
Introduction to Geometry
Introduction to Geometry
H.S.M. Coxeter
John Wiley and Sons, Inc. | New York • London • Sydney
ISBN: 978-0000000000
ISBN-10: 0000000000
Updated: 2024-12-19
By the Same Author
PROJECTIVE GEOMETRY
Blaisdell, New York
THE REAL PROJECTIVE PLANE
Cambridge University Press
NON-EUCLIDEAN GEOMETRY
University of Toronto Press
REGULAR POLYTOPES
Methuen, London
H. S. M. COXETER, F.R.S. Professor of Mathematics, University of Toronto
John Wiley & Sons, Inc., New York • London • Sydney
Copyright
All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or by any information storage and retrieval system, without permission in writing from the Copyright Holder.
ENCODED IN THE UNITED STATES OF AMERICA
¶ Dedication
¶ Preface
¶ Plates
-
The group pg, generated by two parallel glide reflections 57
-
The group cm, generated by a reflection and a parallel glide reflection 59
-
A wire model of the regular 120-cell, {5, 3, 3} 404
-
Close-packed circles in the Euclidean plane 406
¶ Epigraph
¶ I
¶ Triangles
In this chapter, we review some of the well-known propositions of elementary geometry, stressing the role of symmetry. We refer to Euclid’s propositions by his own numbers, which have been used throughout the world for more than two thousand years. Since the time of F. Commandino (1509), who translated the works of Archimedes, Apollonius, and Pappus, many other theorems in the same spirit have been discovered. Such results were studied in great detail during the nineteenth century. As the present tendency is to abandon them in favor of other branches of mathematics, we shall be content to mention a few that seem particularly interesting.
¶ Euclid
Euclids work will live long after all the text-books of the present day are superseded and forgotten. It is one of the noblest monuments of antiquity.
Sir Thomas L. Heath (1861)[1]
About 300 b.c., Euclid of Alexandria wrote a treatise in thirteen books called the Elements. Of the author (sometimes regrettably confused with the earlier philosopher, Euclid of Mégara) we know very little. Proclus (410 a.d.) said that he “put together the Elements, collecting many of Eudoxus’s theorems, perfecting many of Theaetetus’s, and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors.” This man lived in the time of the first Ptolemy, [who] once asked him if there was in geometry any shorter way than that of the Elements, and he answered that “there was no royal road to geometry.” Heath quotes a story by Stobaeus, to the effect that someone who had begun to read geometry with Euclid asked him “What shall I get by learning these things?” Euclid called his slave and said “Give him a dime, since he must make gain out of what he learns.”
Of the thirteen books, the first six may be very briefly described as dealing respectively with triangles, rectangles, circles, polygons, proportion, and similarity. The next four, on the theory of numbers, include two notable achievements: IX.2 and X.9, where it is proved that there are infinitely many prime numbers, and that is irrational [Hardy 2, pp. 32. Book XI is an introduction to solid geometry, XII deals with pyramids, cones, and cylinders, and XIII is on the five regular solids.
According to Proclus, Euclid “set before himself, as the end of the whole Elements, the construction of the so-called Platonic figures.” This notion of Euclid’s purpose is supported by the Platonic theory of a mystical correspondence between the four solids
[cf. Coxeter 1, p. 18]. Evidence to the contrary is supplied by the arithmetical books VII-X, which were obviously included for their intrinsic interest rather than for any application to solid geometry.
¶ Primitive Concepts and Axioms
“When I use a word,” Humpty-Dumpty said, “it means just what I choose it to meanneither more nor less.”
Lewis Carroll (1832)
[Dodgson 2, Chap. 6]
In the logical development of any branch of mathematics, each definition of a concept or relation involves other concepts and relations. Therefore the only way to avoid a vicious circle is to allow certain primitive concepts and relations (usually as few as possible) to remain undefined [Synge 1, pp. 32. Similarly, the proof of each proposition uses other propositions, and therefore certain primitive propositions, called postulates or axioms, must remain unproved. Euclid did not specify his primitive concepts and relations, but was content to give definitions in terms of ideas that would be familiar to everybody. His five Postulates are as follows:
¶ 1.21
A straight line may be drawn from any point to any other point.
¶ 1.22
A finite straight line may be extended continuously in a straight line.
¶ 1.23
A circle may be described with any center and any radius.
¶ 1.24
All right angles are equal to one another.
¶ 1.25
If a straight line meets two other straight lines so as to make the two interior angles on one side of it together less than two right angles, the other straight lines, if extended indefinitely, will meet on that side on which the angles are less than two right angles.[2]
It is quite natural that, after a lapse of about 2250 years, some details are now seen to be capable of improvement. (For instance, Euclid I.1 constructs an equilateral triangle by drawing two circles; but how do we know that these two circles will intersect?) The marvel is that so much of Euclid’s work remains perfectly valid. In the modern treatment of his geometry [see, for instance, Coxeter 3, pp. 161, it is usual to recognize the primitive concept point and the two primitive relations of intermediacy (the idea that one point may be between two others) and congruence (the idea that the distance between two points may be equal to the distance between two other points, or that two line segments may have the same length). There are also various versions of the axiom of continuity, one of which says that every convergent sequence of points has a limit.
Euclid’s “principle of superposition, ” used in proving I.4, raises the question whether a figure can be moved without changing its internal structure. This principle is nowadays replaced by a further explicit assumption such as the axiom of “the rigidity of a triangle with a tail” (Figure 1.2a 1.1):
¶ 1.26
If is a triangle with on the side extended, while is analogously related to another triangle , and if , , , , then .
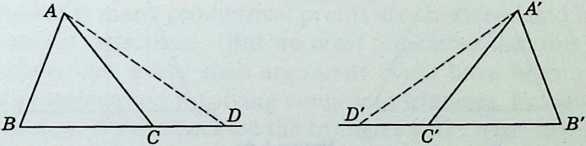 image
image
This axiom can be used to extend the notion of congruence from line segments to more complicated figures such as angles, so that we can say precisely what we mean by the relation
Then we no longer need the questionable principle of superposition in order to prove Euclid I.4:
If two triangles have two sides equal to two sides respectively, and have the angles contained by the equal sides equal, they will also have their third sides equal, and their remaining angles equal respectively; in fact, they will be congruent triangles.
¶ Pons Asinorum
Minos: If is proposed to prove 1.5 by taking up the isosceles Triangle, turning it over, and then laying it down again upon itself.
Euclid: Surely that has too much of the Irish Bull about it, and reminds one a little too vividly of the man who walked down his own throat, to deserve a place in a strictly philosophical treatise?
Minos: I suppose its defenders would say that it is conceived to leave a trace of itself behind, and that the reversed Triangle is laid down upon the trace so left.
C. L. Dodgson (1832)
[Dodgson 3, p. 48]
¶ I.5.
The angles at the base of an isosceles triangle are equal.
The name pons asinorum for this famous theorem probably arose from the bridgelike appearance of Euclid’s figure (with the construction lines required in his rather complicated proof) and from the notion that anyone unable to cross this bridge must be an ass. Fortunately, a far simpler proof was supplied by Pappus of Alexandria about 340a.d. (Figure 1.3a 1.2):

Let be an isosceles triangle with equal to . Let us conceive this triangle as two triangles and argue in this way. Since , the two sides , are equal to the two sides , . Also the angle is equal to the angle , for it is the same. Therefore all the corresponding parts (of the triangles , ) are equal. In particular,
The pedagogical difficulty of comparing the isosceles triangle ABC with itself is sometimes avoided by joining the apex to , the midpoint of the base . The median may be regarded as a mirror reflecting into . Accordingly, we say that an isosceles triangle is symmetrical by reflection, or that it has bilateral symmetry. (Of course, the idealized mirror used in geometry has no thickness and is silvered on both sides, so that it not only reflects into but also reflects into .)
Any figure, however irregular its shape may be, yields a symmetrical figure when we place it next to a mirror and waive the distinction between object and image. Such bilateral symmetry is characteristic of the external shape of most animals.
Given any point on either side of a geometrical mirror, we can construct its reflected image by drawing the perpendicular from to the mirror and extending this perpendicular line to an equal distance on the other side, so that the mirror perpendicularly bisects the line segment . Working in the plane (Figure 1.3b 1.3) with a line for mirror, we draw two circles with centers and radii . The two points of intersection of these circles are and its image .
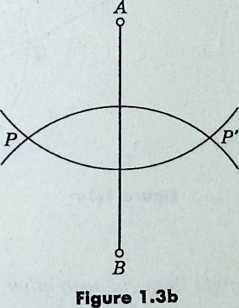
We shall find that many geometrical proofs are shortened and made more vivid by the use of reflections. But we must remember that this procedure is merely a short cut: every such argument could have been avoided by means of a circumlocution involving congruent triangles. For instance, the above construction is valid because the triangles ABP, are congruent.
Pons asinorum has many useful consequences, such as the following five:
¶ III.3.
If a diameter of a circle bisects a chord which does not pass through the center, it is perpendicular to it; or, if perpendicular to it, it bisects it.
¶ III.20.
In a circle the angle at the center is double the angle at the circumference, when the rays forming the angles meet the circumference in the same two points.
¶ III.21.
In a circle, a chord subtends equal angles at any two points on the same one of the two arcs determined by the chord (e.g., in Figure 1.3c, ).
¶ III.22.
The opposite angles of any quadrangle inscribed in a circle are together equal to two right angles.
¶ III.32.
If a chord of a circle be drawn from the point of contact of a tangent, the angle made by the chord with the tangent is equal to the angle subtended by the chord at a point on that part of the circumference which lies on the far side of the chord (e.g., in Figure 1.3c, ).
We shall also have occasion to use two familiar theorems on similar triangles:
¶ VI.2.
If a straight line be drawn parallel to one side of a triangle, it will cut the other sides proportionately; and, if two sides of the triangle be cut proportionately, the line joining the points of section will be parallel to the remaining side.
¶ VI.4.
If corresponding angles of two triangles are equal, then corresponding sides are proportional.
Combining this last result with III.21 and 32, we deduce two significant properties of secants of a circle (Figure 1.3c 1.4):
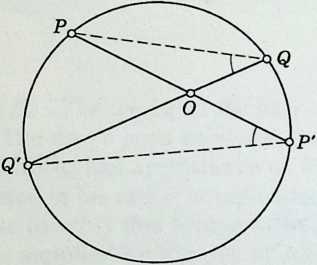
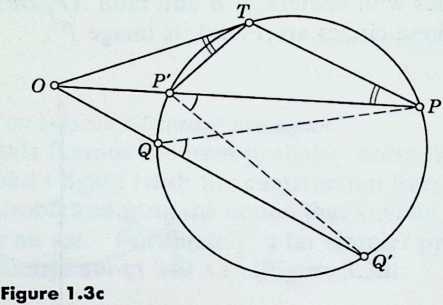
¶ III.35
If in a circle two straight lines cut each other, the rectangle contained by the segments of the one is equal to the rectangle contained by the segments of the other (i.e., .)
¶ III.6
If from a point outside a circle a secant and a tangent be drawn, the rectangle contained by the whole secant and the part outside the circle will be equal to the square on the tangent (i.e., .)
Book VI also contains an important property of area:
¶ VI.19.
Similar triangles are to one another in the squared ratio of their corresponding sides (i.e., if and are similar triangles, their areas are in the ratio .)
This result yields the following easy proof for the theorem of Pythagoras [see Heath 1, p. 353; 2, p. 270]:
¶ I.47.
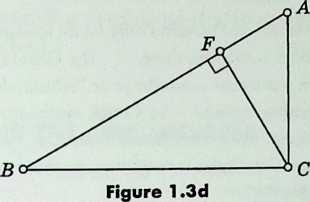
In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the two catheti.
In the triangle , right-angled at , draw perpendicular to the hypotenuse , as in Figure 1.3d1.5. Then we have three similar right-angled triangles , with hypotenuses . By VI.19, the areas satisfy
Evidently, . Therefore .
¶ Exercises
-
Using rectangular Cartesian coordinates, show that the reflection in the reverses the sign of . What happens when we reflect in the line ?
-
Deduce I.47 from III.36 (applied to the circle with center and radius )
-
Inside a square , take a point so that is an isosceles triangle with angles at and . What kind of triangle is ? (Hint: Inside the triangle , take a point so that is congruent to ).
-
Prove the Erdös-Mordell theorem: If is any point inside a triangle and are the feet of the perpendiculars from upon the respective sides , then
Hint:[3] Let and be the feet of the perpendiculars from and upon . Define analogous points and and and on the other sides. Using the similarity of the triangles and , express in terms of , , and . After substituting such expressions into
OA + OB + OC \geq OA(P_{1}P + PP_{2})/RQ + OB(Q_{1}Q + QQ_{2})/ PR + OC(R_{1}R + RR_{2})/QP_{3}$$ collect the terms involving $OP, OQ, OR$, respectively. -
In the notation of Ex. 4,
(A. Oppenheim, American Mathematical Monthly, 68 (1961), p. 230. See also L. J. Mordell, Mathematical Gazette, 46 (1962), pp. 213.)
¶ The Medians and the Centroid
Oriental mathematics may be an interesting curiosity, but Greek mathematics is the real thing. …The Greeks, as Littlewood said to me once, are not clever schoolboys or “Scholarship candidates,” but “Fellows of another college.” So Greek mathematics is “permanent,” more permanent even than Greek literature. Archimedes will be remembered when Aeschylus is forgotten, because languages die and mathematical ideas do not.
G. H. Hardy (1877) [Hardy 2, p. 21]
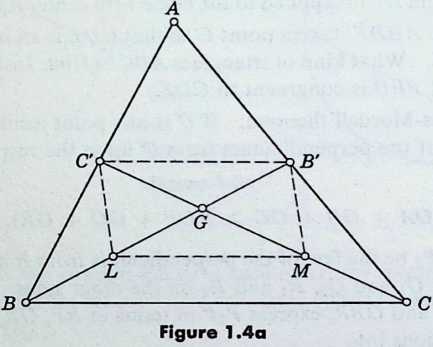
The line joining a vertex of a triangle to the midpoint of the opposite side is called a median.
Let two of the three medians, say and , meet in (Figure 1.4a 1.6). Let and be the midpoints of and . By Euclid VI.2 and 4 (which were quoted on page 8), both and are parallel to and half as long. Therefore is a parallelogram. Since the diagonals of a parallelogram bisect each other, we have
Thus the two medians trisect each other at . In other words, this point , which could have been defined as a point of trisection of one median, is also a point of trisection of another, and similarly of the third. We have thus proved [by the method of Court 1, p. 58] the following theorem:
¶ 1.41
The three medians of any triangle all pass through one point.
This common point of the three medians is called the centroid of the triangle. Archimedes (c. 287 B.C.) obtained it as the center of gravity of a triangular plate of uniform density.
¶ Exercises
-
Any triangle having two equal medians is isosceles.[4]
-
The sum of the medians of a triangle lies between and , where is the sum of the sides. [Court 1, pp. 60.]
¶ The Incircle and the Circumcircle
Alone at nights,
I read my Bible more and Euclid less.
Robert Buchanan (1841)
(An Old Dominie’s Story)
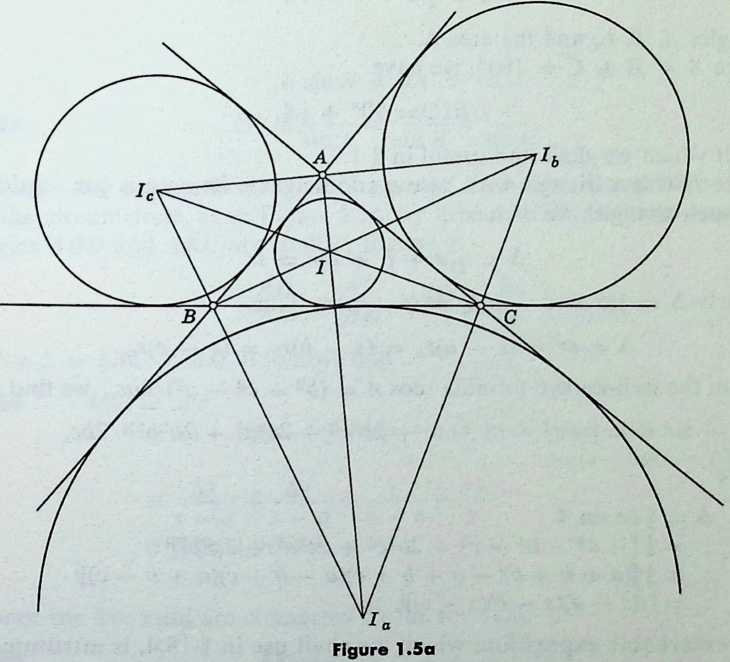
Euclid III.3 tells us that a circle is symmetrical by reflection in any diameter (whereas an ellipse is merely symmetrical about two special diameters: the major and minor axes). It follows that the angle between two intersecting tangents is bisected by the diameter through their common point.
By considering the loci of points equidistant from pairs of sides of a triangle , we see that the internal and external bisectors of the three angles of the triangle meet by threes in four points , as in Figure 1.5a 1.7. These points are the centers of the four circles that can be drawn to touch the three lines . One of them, the incenter , being inside the triangle, is the center of the inscribed circle or incircle (Euclid IV.4). The other three are the excenters : the centers of the three escribed circles or excircles [Court 2, pp. 72. The radii of the incircle and excircles are the inradius and the exradii .
In describing a triangle , it is customary to call the sides
the semiperimeter
the angles , and the area .
Since , we have
¶ 1.51
Similarly $$\Delta = \frac{1}{2}(b + c + - a)r_{a}= (s - a)r_{a}$$ Thus
¶ 1.52
From the well-known formula $$\cos A= \frac{(b^{2}+ c^{2}- a^{2})}{2bc},$$ we find also $$\sin A=\frac{{[}-a^{4}- b^{4}- c^{4}+ 2b{2}c+ 2c{2}a+ 2a{2}b^{\frac{1}{2}}}{2bc},$$
whence
¶ 1.53
This remarkable expression, which we shall use in §18.4, is attributed to Heron of Alexandria (about 60 a.d.), but it was really discovered by Archimedes. (See B. L. van der Waerden,Science Awakening, Oxford University Press, New York, 1961, pp. 228, 277.)
Another consequence of the symmetry of a circle is that the perpendicular bisectors of the three sides of a triangle all pass through the circumcenter , which is the center of the circumscribed circle or circumcircle (Euclid IV.5). This is the only circle that can be drawn through the three vertices . Its radius is called the circumradius of the triangle. Since the “angle at the center,” (Figure 1.5b 1.8), is double the angle , the congruent right-angled triangles , each have an angle at , whence
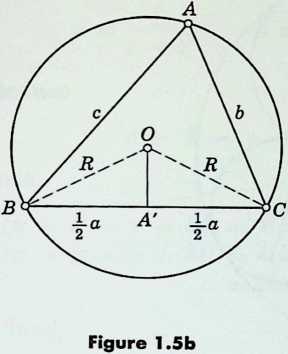
¶ 1.54
2R = \frac{a}{\sin A}= \frac{b}{\sin B}= \frac{c}
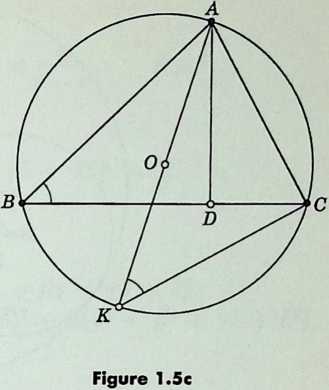
Draw perpendicular to , and let be the diameter through of the circumcircle, as in Figure 1.5c 1.9. By Euclid III.21, the right-angled triangles and are similar; therefore
Since $$\Delta = \frac{1}{2}BC \times AD$$, it follows that
¶ 1.55
[Court 1, p. 73].
The lengths , which appear in 1.52 as well as in Heron’s formula for , are easily recognized as the radii of three mutually tangent circles with centers . Frederick Soddy (1877, who is famous for his pioneering work on isotopes and for his original approach to economics) initiated a fascinating discussion of the two circles that can be drawn to touch all these three, as in Figure 1.5d 1.10, namely a small circle surrounded by the three, and a large one which usually encloses the three (though it fails to do so if the triangle is “very obtuse”). Let these two circles have centers and radii , so that
Also let denote the angles at in the three triangles . Applying to these triangles the familiar formulas
for the angle of any triangle , we obtain
Then we can replace by any three angles whose sum is , such as . Thus
whence
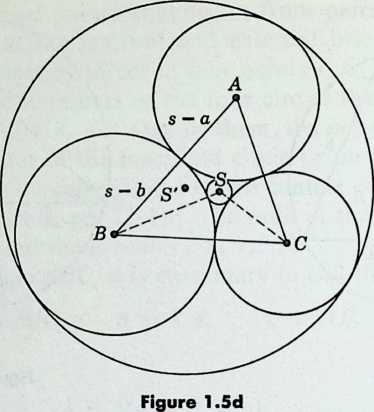
Dividing by and using the abbreviations
we deduce
whence
The upper sign yields the larger bend, that is, the smaller circle. Thus the radii are[5]
¶ 1.58
and $$\sigma^{\prime}= \left[ \alpha + \beta + \gamma - 2 \left( \beta \gamma + \gamma \alpha + \alpha \beta \right){\frac{1}{2}}\right]$$
This last expression is usually negative, indicating a “concave bend”: the circle with center encloses the circles with centers .
Writing for , we find $$\sigma = \Delta / { \frac{\Delta}{s-a}+ \frac{\Delta}{s-b}+ \frac{\Delta}{s-c}+ 2{[}s(s-a +s -b +s-c){]}^{\frac{1}{2}}}$$
¶ 1.59
Similarly, .
¶ Exercises
-
Find the locus of the image of a fixed point by reflection in a variable line through another fixed point .
-
For the general triangle , establish the identities
-
The lengths of the tangents from the vertex to the incircle and to the three excircles are respectively $$s -a, s, s-c, s-b.$$
-
Any triangle having two equal internal angle bisectors (each measured from a vertex to the opposite side) is isosceles. (Hint: If the angles and are not equal, one must be less, say . Then, if the equal angle bisectors are and , there is a point on such that , and a point on such that . Compare the angles at and in the congruent triangles and .)
-
The circumcenter of an obtuse-angled triangle lies outside the triangle.
-
Where is the circumcenter of a right-angled triangle?
-
Let be three points on the respective sides of a triangle ABC. The perpendiculars to the sides at these points are concurrent if and only if $$AW^{2}+ BU^{2}+ CV^{2}= WB^{2}+ UC^{2}+ VA^{2}.$$
-
Given a triangle , for what value of is there a point whose distances from are equal to ? (J.A.H. Hunter.)
-
In Figure 1.54, what happens to if
Sketch the case in which , , so that and .
-
A triangle is right-angled if and only if .
-
Given a point on the circumcircle of a triangle, the feet of the perpendiculars from to the three sides all lie on a straight line. (This line is commonly called the Simson line of with respect to the triangle, although it was first mentioned by W. Wallace, thirty years after Simson’s death [Johnson 1, p. 138].)
-
Given a triangle and a point in its plane (but not on a side nor on the circumcircle), let be the derived triangle formed by the feet of the perpendiculars from to the sides . Let be derived analogously from (using the same ), from . Then is directly similar to . [Casey 1, p. 253.] (Hint: .) This result has been extended by A. Oppenheim from the third derived triangle of a triangle to the th derived -gon of an -gon.
¶ The Euler Line and the Orthocenter
Although the Greeks worked fruitfully, not only in geometry but also in the most varied fields of mathematics, nevertheless we today have gone beyond them everywhere and certainly also in geometry.
F. Klein (1849)
[Klein 2, p. 189]
From now on, we shall have various occasions to mention the name of L. Euler (1707), a Swiss who spent most of his life in Russia, making important contributions to all branches of mathematics. Some of his simplest discoveries are of such a nature that one can well imagine the ghost of Euclid saying, “Why on earth didn’t I think of that?”
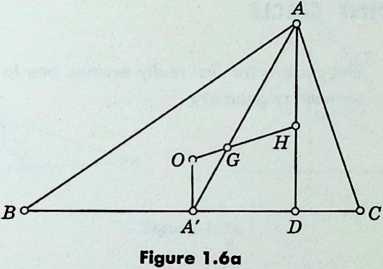
If the circumcenter and centroid of a triangle coincide, each median is perpendicular to the side that it bisects, and the triangle is “isosceles three ways,” that is, equilateral. Hence, if a triangle is not equilateral, its circumcenter and centroid lie on a unique line . On this so-called Euler line, consider a point such that , that is, (Figure 1.6a 1.11). Since also , the latter half of Euclid VI.2 tells us that is parallel to , which is the perpendicular bisector of . Thus is perpendicular to . Similarly is perpendicular to , and to .
The line through a vertex perpendicular to the opposite side is called an altitude. The above remarks [cf. Court 2, p. 101] show that
The three altitudes of any triangle all pass through one point on the Euler line.
This common point of the three altitudes is called the orthocenter of the triangle.
¶ Exercises
-
Through each vertex of a given triangle draw a line parallel to the opposite side. The perpendicular bisectors of the sides of the triangle so formed suggest an alternative proof that the three altitudes of are concurrent. [Gauss 1, vol. 4, p. 396.]
-
The orthocenter of an obtuse-angled triangle lies outside the triangle.
-
Where is the orthocenter of a right-angled triangle?
-
Any triangle having two equal altitudes is isosceles.
-
Construct an isosceles triangle (with base BC), given the median and the altitude . (Hint: The centroid is two-thirds of the way from to .) (H. Freudenthal.)
-
The altitude of any triangle is of length $$2R \sin B \sin C$$.
-
Find the perpendicular distance from the centroid to the side .
-
If the Euler line passes through a vertex, the triangle is either right-angled or isosceles (or both).
-
If the Euler line is parallel to the side , the angles and satisfy $$\tan B \tan C = 3$$.
¶ The Nine-point Circle
This circle is the first really exciting one to appear in any course on elementary geometry.
Daniel Pedoe (1910)
[Pedoe 1, p. 1 ]
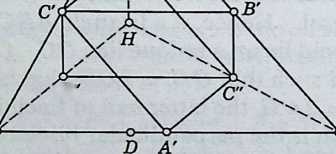
The feet of the altitudes (that is, three points like in Figure 1.6a 1.11) form the orthic triangle (or “pedal triangle”) of . The circumcircle of the orthic triangle is called the nine-point circle (or “Feuerbach circle”) of the original triangle, because it contains not only the feet of the three altitudes but also six other significant points. In fact,
¶ 1.71
The midpoints of the three sides, the midpoints of the lines joining the orthocenter to the three vertices, and the feet of the three altitudes, all lie on a circle.
Proof [Coxeter 2, 9.29]. Let be the midpoints of , and let be the feet of the altitudes, as in Figure 1.7a 1.12. By Euclid VI.2 and 4 again, both and are parallel to while both and are parallel to . Since is perpendicular to , it follows that is a rectangle. Similarly is a rectangle. Hence are three diameters of a circle. Since these diameters subtend right angles at , respectively, the same circle passes through these points too.
If four points in a plane are joined in pairs by six distinct lines, they are called the vertices of a complete quadrangle, and the lines are its six sides. Two sides are said to be opposite if they have no common vertex. Any point of intersection of two opposite sides is called a diagonal point. There may be as many as three such points (see Figure 1.7b 1.13).
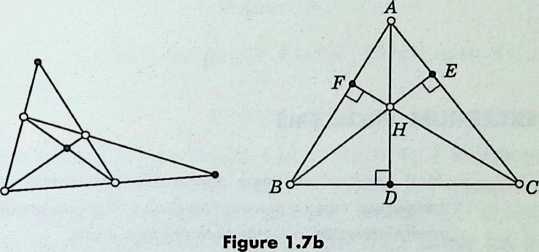
If a triangle is not right-angled, its vertices and orthocenter form a special kind of quadrangle whose opposite sides are perpendicular. In this terminology, the concurrence of the three altitudes can be expressed as follows:
¶ 1.72
If two pairs of opposite sides of a complete quadrangle are pairs of perpendicular lines, the remaining sides are likewise perpendicular.
Such a quadrangle is called an orthocentric quadrangle. Its six sides
which is a path from to , usually a broken fine with angles at and . Such a path from to is minimal when it is straight, as in Figure 1.8a.
Hence, among all inscribed triangles with a given vertex on , the one with smallest perimeter occurs when and lie on the straight line . In this way we obtain a definite triangle for each choice of on BC. The problem will be solved when we have chosen so as to minimize , which is equal to the perimeter.
Since and are images of by reflection in and , they are congruent and
Thus is an isosceles triangle whose angle at is independent of the choice of . The base is minimal when the equal sides are minimal, that is, when is minimal. In other words, is the shortest distance from the given point to the given line . Since the hypotenuse of a right-angled triangle is longer than either cathetus, the desired location of is such that is perpendicular to . Thus is the altitude from . This choice of yields a unique triangle whose perimeter is smaller than that of any other inscribed triangle. Since we could equally well have begun with or instead of , we see that and are the altitudes from and . Hence The triangle of minimal perimeter inscribed in an acute-angled triangle is the orthic triangle of .
The same method can be used to prove the analogous result for spherical triangles[Steiner 2, p. 45, No. 7].
The other problem, proposed by Pierre Fermat (1601), likewise seeks to minimize the sum of three distances. The solution given here is due to J. E. Hofmann.[6]
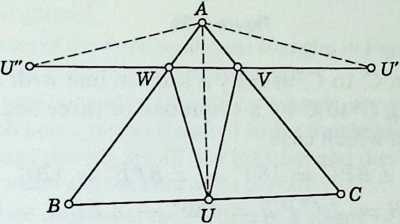
FERMAT’S PROBLEM. In a given acute-angled triangle ABC, locate a point whose distances from have the smallest possible sum.
Consider first an arbitrary point inside the triangle. Join it to and rotate the inner triangle through about to obtain , so that and are equilateral triangles, as in Figure 1.8b. Then $$AP + BP + CP = C\prime P^{\prime}+ P\prime P + PC,$$
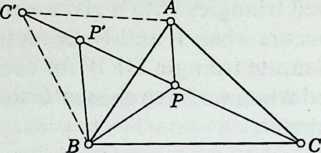
which is a path from to , usually a broken line with angles at and . Such a path (joining C’ to C by a sequence of three segments) is minimal when it is straight, in which case $$\angle BPC = 180^{\circ}- \angle BPP\prime= 120^{\circ}$$ and .
Thus the desired point , for which is minimal, is the point from which each of the sides subtends an angle of . This “Fermat point” is most simply constructed as the second intersection of the line and the circle (that is, the circumcircle of the equilateral triangle ).
It has been pointed out [for example by Pedoe 1, pp. 11 that the triangle need not be assumed to be acute-angled. The above solution is valid whenever there is no angle greater than .
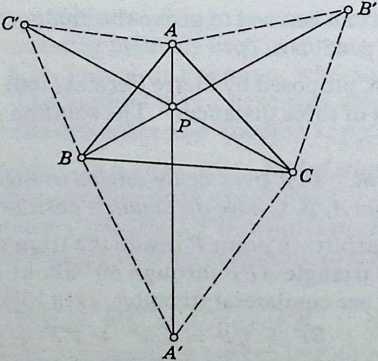
Instead of the equilateral triangle on , we could just as well have drawn an equilateral triangle on , or on , as in Figure 1.8c. Thus the three lines all pass through the Fermat point , and any two of them provide an alternative construction for it. Moreover, the line segments are all equal to . Hence
If equilateral triangles are drawn outwards on the sides of any triangle , the line segments are equal, concurrent, and inclined at to one another.
¶ Exercises
-
In Figure 1.8a, and make equal angles with . Deduce that the orthocenter of any triangle is the incenter of its orthic triangle. (In other words, if is a triangular billiard table, a ball at , hit in the direction , will go round the triangle indefinitely, that is, until it is stopped by friction.)
-
How does Fagnano’s problem collapse when we try to apply it to a triangle in which the angle is obtuse?
-
The circumcircles of the three equilateral triangles in Figure 1.8c all pass through , and their centers form a fourth equilateral triangle.[7]
-
Three holes, at the vertices of an arbitrary triangle, are drilled through the top of a table. Through each hole a thread is passed with a weight hanging from it below the table. Above, the three threads are all tied together and then released. If the three weights are all equal, where will the knot come to rest?
-
Four villages are situated at the vertices of a square of side one mile. The inhabitants wish to connect the villages with a system of roads, but they have only enough material to make miles of road. How do they proceed? [Courant and Robbins 1, p. 392.]
-
Solve Fermat’s problem for a triangle with A \textgreater{}120^{\circ}, and for a convex quadrangle .
-
If two points , inside a triangle , are so situated that , , then .
-
If four squares are placed externally (or internally) on the four sides of any parallelogram, their centers are the vertices of another square. [Yaglom 1, pp. 96.]
-
Let be the centers of squares placed externally on the sides of a triangle .Then the segment is congruent and perpendicular to (also to and to ).(W. A. J. Luxemburg.)
-
Let be the centers of squares placed externally on the sides of any simple quadrangle (or “quadrilateral”) . Then the segment (joining the centers of two “opposite” squares) is congruent and perpendicular to . [Forder 2, p. 40.]
¶ Morley’s Theorem
Many of the proofs in mathematics are very long and intricate. Others, though not long, are very ingeniously constructed.
E. C. Titchmarsh (1899)
[Titchmarsh 1, p. 23]
One of the most surprising theorems in elementary geometry was discovered about 1899 by F. Morley (whose son Christopher wrote novels such as Thunder on the Left.) He mentioned it to his friends, who spread it over the world in the form of mathematical gossip. At last, after ten years, a trigonometrical proof by M. Satyanarayana and an elementary proof by M. T. Naraniengar were published.[8]
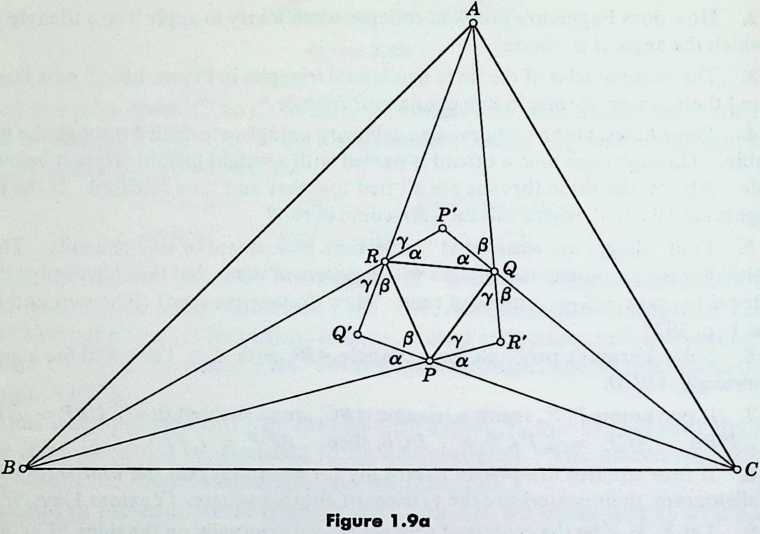
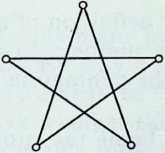
MORLEYS THEOREM. The three points of intersection of the adjacent trisectors of the angles of any triangle form an equilateral triangle.
In other words, any triangle yields an equilateral triangle if the angles are trisected by and and and , as in Figure 1.9a. (Much trouble is experienced if we try a direct approach, but the difficulties disappear if we work backwards, beginning with an equilateral triangle and building up a general triangle which is afterwards identified with the given triangle .)
On the respective sides of a given equilateral triangle , erect isosceles triangles whose base angles satisfy the equation and inequalities
Extend the sides of the isosceles triangles below their bases until they meet again in points . Since , we can immediately infer the measurement of some other angles, as marked in Figure 1.9a. For instance, the triangle must have an angle at its vertex , since its angles at and are and .
Referring to 1.51, we see that one way to characterize the incenter of a triangle is to describe it as lying on the bisector of the angle at such a distance that
Applying this principle to the point in the triangle , we observe that the line (which is a median of both the equilateral triangle and the isosceles triangle ) bisects the angle at . Also the half angle at , and
Hence is the incenter of the triangle. Likewise is the incenter of , and of. Therefore all the three small angles at are equal; likewise at and at . In other words, the angles of the triangle are trisected.
The three small angles at are each similarly atand C. Thus
By choosing these values for the base angles of our isosceles triangles, we can ensure that the above procedure yields a triangle that is similar to any given triangle.
This completes the proof.
¶ Exercises
-
The three lines (Figure 1.9a) are concurrent. In other words, the trisectors of meet again to form another triangle which is perspective with the equilateral triangle . (In general is not equilateral.)
-
What values of will make the triangle (i) equilateral, (ii) right-angled isosceles? Sketch the figure in each case.
-
Let and (on and ) be the images of by reflection in and . Then the four points are evenly spaced along a circle through . In the special case when the triangle is equilateral, these four points occur among the vertices of a regular enneagon (9-gon) in which is the vertex opposite to the side
¶ Regular Polygons
We begin this chapter by discussing (without proofs) the possibility of constructing certain regular polygons with the instruments allowed by Euclid. We then consider all these polygons, regardless of the question of constructibility, from the standpoint of symmetry. Finally, we extend the concept of a regular polygon so as to include star polygons.
¶ Cyclotomy
One, two! One, two! And through and through The vorpal blade went snicker-snack!
Lewis Carroll
[Dodgson 2, Chap. 1 ]
Euclid’s postulates imply a restriction on the instruments that he allowed for making constructions, namely the restriction to ruler (or straightedge) and compasses. He constructed an equilateral triangle (I.1), a square (IV.6), a regular pentagon (IV.11), a regular hexagon (IV.15), and a regular 15-gon (IV. 16). The number of sides may be doubled again and again by repeated angle bisections. It is natural to ask which other regular polygons can be constructed with Euclid’s instruments. This question was completely answered by Gauss (1777–1855) at the age of nineteen [see Smith 2, pp. 301–302]. Gauss found that a regular -gon, say {}, can be so constructed if and only if the odd prime factors of are distinct “Fermat primes” $$F_{k}= 2^{2k}+ 1.$$
The only known primes of this kind are $$F_{0}= 2^{1}+ 1 = 3, F_{1}= 2^{2}+ 1 = 5, F_{2}= 2^{4}+ 1 = 17, F_{3}= 2^{8}+ 1 = 257, F_{4}= 2^{16}+ 1 = 65537.$$
Since 7 is not a Fermat prime, Euclid’s instruments will not suffice for the construction of a regular heptagon {7}. Since the factors of 9 are not distinct, the same is true for a regular enneagon {9}.
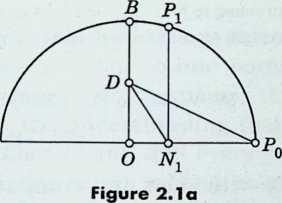
To inscribe a regular pentagon in a given circle, simpler constructions than Euclid’s were given by Ptolemy and Richmond.[9] The former has been repeated in many textbooks. The latter is as follows (Figure 2.1a 2.1).
To inscribe a regular pentagon in a circle with center : draw the radius perpendicular to ; join to , the midpoint of ; bisect the angle to obtain on ; and draw perpendicular to to obtain on the circle. Then is a side of the desired pentagon.
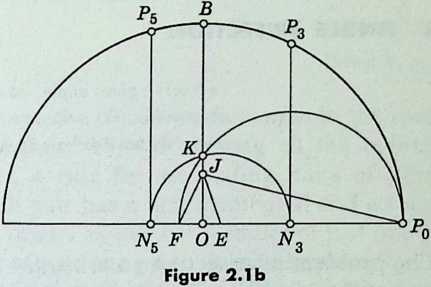
Richmond also gave a simple construction for the {17} (Figure 2.1b 2.2). Join to , one quarter of the way from to . On the diameter through take , so that is one quarter of and is 45°. Let the circle on as diameter cut in , and let the circle with center and radius cut in (between and ) and . Draw perpendiculars to at these two points, to cut the original circle in and . Then the arc (and likewise ) is of the circumference. (The proof involves repeated application of the principle that the roots of the equation are and .)
Richelot and Schwendenwein constructed the regular 257-gon about 1898. J. Hermes spent ten years on the regular 65537-gon and deposited the manuscript in a large box in the University of Göttingen, where it may still be found.
The next number of the form is . Fermat incorrectly assumed it to be prime. G. T. Bennett gave the following neat proof[10] that it is composite [Hardy and Wright 1, p. 14]: the number
must He on the circle with center and radius , and on the circle with center and radius . Since is not on , these circles do not touch each other but intersect in two points, one of which is . Hence is either itself or the image of by reflection in .
¶ Symmetry
Tyger! Tyger! burning bright
In the forests of the night,
What immortal hand or eye
Dare frame thy fearful symmetry?William Blake (1757–1827)
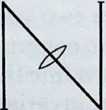
When we say that a figure is “symmetrical” we mean that we can apply certain isometries, called symmetry operations, which leave the whole figure unchanged while permuting its parts. For example, the capital letters E and A (Figure 2.4a) have bilateral symmetry, the mirror being horizontal for the former, vertical for the latter. The letter N (Figure 2.46) is symmetrical by a half-turn, or rotation through 180° (or “reflection in a point,” or “central inversion”), which may be regarded as the result of reflecting horizontally and then vertically, or vice versa. The swastika (Figure 2.4c) is symmetrical by rotation through any number of right angles.

In counting the symmetry operations of a figure, it is usual to include the identity; any figure has this trivial symmetry. Thus the swastika admits four distinct symmetry operations: rotations through right angles. The last is the identity. The first and third are inverses of each other, since their product is the identity.
This use of the word “product” suggests an algebraic symbolism in which the transformations are denoted by capital letters while 1 denotes the identity. (Instead of 1, some authors write E.) Thus if is the counterclockwise quarter-turn, the four symmetry operations of the swastika are
Since the smallest power of that is equal to the identity is the fourth power, we say that is of period 4. Similarly , being a half-turn, is of period 2 [see Coxeter 1, p. 39]. The only transformation of period 1 is the identity. A translation is aperiodic (that is, it has no period), but it is conveniently said to be of infinite period.
Some figures admit both reflections and rotations as symmetry operations. The letter H (Figure 2.4c?) has a horizontal mirror (like E) and a vertical mirror (like A), as well as a center of rotational symmetry (like N) where the two mirrors intersect. Thus it has four symmetry operations: the identity 1, the horizontal reflection , the vertical reflection , and the half-turn .
¶ EXERCISES
-
Every isometry of period 2 is either a reflection or a half-turn [Bachmann 1, pp. 2–3],
-
Express (a) a half-turn, (b) a quarter-turn, as transformations of (i) Cartesian coordinates, (ii) polar coordinates. (Take the origin to be the center of rotation.)
¶ Groups
Symmetry, as wide or as narrow as you may define its meaning, is one idea by which man through the ages has tried to comprehend and create order, beauty, and perfection.
Hermann Weyl [1, p. 5]
A set of transformations [Birkhoff and MacLane 1, pp. 119–122] is said to form a group if it contains the inverse of each and the product of any two (including the product of one with itself or with its inverse). The number of distinct transformations is called the order of the group. (This may be either finite or infinite.) Clearly the symmetry operations of any figure form a group. This is called the symmetry group of the figure. In the extreme case when the figure is completely irregular (like the numeral 6) its symmetry group is of order one, consisting of the identity alone.
The symmetry group of the letter E or A (Figure 2.4a) is the so-called dihedral group of order 2, generated by a single reflection and denoted by . (The name is easily remembered, as the Greek origin of the word “dihedral” is almost equivalent to the Latin origin of “bilateral.”) The symmetry group of the letter N (Figure 2.4b) is likewise of order 2, but in this case the generator is a half-turn and we speak of the cyclic group, . The two groups and are abstractly identical or isomorphic; they are different geometrical representations of the single abstract group of order 2, defined by the relation
¶ 2.51
or [Coxeter and Moser 1, p. 1].
The symmetry group of the swastika is , the cyclic group of order 4, generated by the quarter-turn S and abstractly defined by the relation . That of the letter H (Figure 2.4d) is , the dihedral group of order 4, generated by the two reflections and abstractly defined by the relations
¶ 2.52
Although and both have order 4, they are not isomorphic: they have a different structure, different “multiplication tables.” To see this, it suffices to observe that contains two operations of period 4, whereas all the operations in (except the identity) are of period 2: the generators obviously, and their product also, since
This last remark illustrates what we mean by saying that 2.52 is an abstract definition for , namely that every true relation concerning the generators , is an algebraic consequence of these simple relations. An alternative abstract definition for the same group is
¶ 2.53
from which we can easily deduce .
The general cyclic group , of order , has the abstract definition
¶ 2.54
Its single generator , of period , is conveniently represented by a rotation through . Then is a rotation through times this angle, and the operations in are given by the values of from 1 to , or from 0 to . In particular, occurs in nature as the symmetry group of the periwinkle flower.
¶ EXERCISE
Express a rotation through angle a about the origin as a transformation of (i) polar coordinates, (ii) Cartesian coordinates. If is the equation for a curve in polar coordinates, what is the equation for the transformed curve?
¶ The Product Of Two Reflections
Thou in thy lake dost see
Thyself.J.M. Legare (1823–1859)
(To a Lily)
In any group of transformations, the associative law $$(RS)T = R(ST)$$ is automatically satisfied, but the commutative law $$RS = SR$$
does not necessarily hold, and care must be taken in inverting a product, for example, $$(RS)^{-1}= S{-1}R,$$
not . (This becomes clear when we think of and as the operations of putting on our socks and shoes, respectively.)
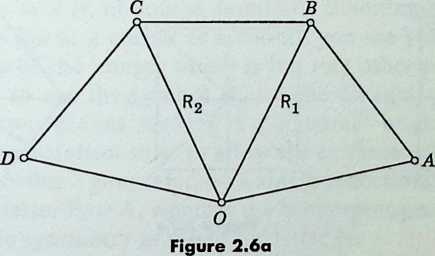
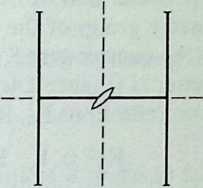
The product of reflections in two intersecting fines (or planes) is a rotation through twice the angle between them. In fact, if are evenly spaced on a circle with center , let and be the reflections in and (Figure 2.6a). Then reflects the triangle into , which is reflected by to ; thus is the rotation through or , which is twice . Since a rotation is completely determined by its center and its angle, is equal to the product of reflections in any two lines through making the same angle as and . (The reflections in and are actually and whose product is .) In particular, the half-turn about is the product of reflections in any two perpendicular lines through .
Since is a counterclockwise rotation, is the corresponding clockwise rotation; in fact, $$R_{2}R_{1}= R_{2}{-1}R_{1}= (R_{1}R_{2})^{-1}.$$ This is the same as if the two mirrors are at right angles, i n which case is a half-turn and .
¶ EXERCISES
-
The product of quarter-turns (in the same sense) about and is the half-turn about the center of a square having for a side.
-
Let and be squares on the sides and of a triangle . If and remain fixed while varies freely, passes through a fixed point.
¶ The Kaleidoscope
is a special case of the general dihedral group , which is , for$n
2$, the symmetry group of the regular -gon, {}. (See Figure 2.7a for the cases .) This is evidently a group of order , consisting of rotations (through the effectively distinct multiples of ) and reflections. When is odd, each of the mirrors joins a vertex to the midpoint of the opposite side; when is even, mirrors join pairs of opposite vertices and bisect pairs of opposite sides[see Birkhoff and MacLane 1, pp. 117–118, 135].
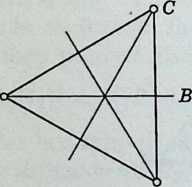
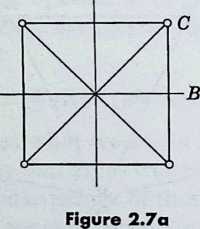
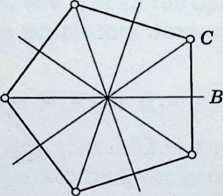
The rotations are just the operations of the cyclic group .Thus the operations of include all the operations of :in technical language, is a subgroup of . The rotation through , which generates the subgroup, may be described as the product of reflections in two adjacent mirrors (such as and in Figure 2.7a) which are inclined at .
Let denote the reflections in their natural order of arrangement. Then , being the product of reflections in two mirrors inclined at times 180°/m, is a rotation through times : $$R_{1}R_{k+1}= S^{k}.$$
Thus , and the reflections may be expressed as
In other words, is generated by and S. By substituting for S, we see that the same group is equally well generated by and , which satisfy the relations
¶ 2.71
(The first two relations come from 2.51 and the third from 2.54.) These relations can be shown to suffice for an abstract definition[see Coxeter and Moser 1, pp. 6, 36].
A practical way to make a model of is to join two ordinary mirrors by a hinge and stand them on the lines of Figure 2.7a so that they are inclined at . Any object placed between the mirrors yields visible images (including the object itself). If the object is your right hand, of the images will look like a left hand, illustrating the principle that, since a reflection reverses sense, the product of any even number of reflections preserves sense, and the product of any odd number of reflections reverses sense.
The first published account of this instrument seems to have been by Athanasius Kircher in 1646. The name kaleidoscope (from /caAos, beautiful; etS o s, a form; and *aKOTreiv,to see) was coined by Sir David Brewster, who wrote a treatise on its theory and history. He complained[Brewster 1, p.*147] that Kircher allowed the angle between the two mirrors to be any submultipl e of 360° instead of restricting it to submultiples of 180°.
The case when is , of course, familiar. Standing between two perpendicular mirrors (as at a corner of a room), you see your image in each and also the image of the image, which is the way other people see you.
Having decided to use the symbol for the dihedral group generated by reflections in two planes making a “dihedral ” angle of , we naturally stretch the notation so as to allow the extreme val ue . Thus is the group of order 2 generated by a single reflection, that is, the symmetry group of the letter E or A, whereas the isomorphic group , generated by a half-turn, is the symmetry group of the letter N.
According to Weyl[1, pp. 66,99], it was Leonardo da Vinci who discovered that the only finite groups of isometries in the plane are
His interest in them was from the standpoint of architectural plans. Of course, the prevalent groups in architecture have always been and . But the pyramids of Egypt exhibit the group , and Leonardo’s suggestion has been followed to some extent in modem times: the Pentagon Building in Washington has the symmetry group ,and the Bahai Temple near Chicago has. In nature, many flowers have dihedral symmetry groups such as .The symmetry group of a snowflake is usually but occasionally only .[Kepler 1, pp. 259–280.]
If you cut an apple the way most people cut an orange, the core is seen to have the symmetry group . Extending the five-pointed star by straight cuts in each ha lf, you divide the whole apple into ten pieces from each of which the core can be removed in the form of two thin flakes.
¶ EXERCISES
-
Describe the symmetry groups of (a) a scalene triangle, (b) an isosceles triangle, (c) a parabola, (d) a parallelogram, (e) a rhombus, (f) a rectangle, (g) an ellipse.
-
Use inverses and the associative law to prove algebraically the “cancellation rule” which says that the relation $$RT = ST$$ implies R = S.
-
Show how the usual defining relations for , namely 2.71 with , may be deduced by algebraic manipulation from the simpler relations $$R1^{2}= 1, R_{1}R_{2}R1 = R2R_{1}R_{2}$$
-
The cyclic group is a subgroup of if and only if the number m is a divisor of . In particular, if is prime, the only subgroups of are itself and .
¶ Star Polygons
Instead of deriving the dihedral group from the regular polygon {}, we could have derived the polygon from the group: the vertices of the polygon are just the images of a point (the of Figure 2.7a) on one of the two mirrors of the kaleidoscope. In fact, there is no need to use the whole group : its subgroup will suffice. The vertex of the polygon can be derived from the initial vertex by a rotation through times .
More generally, rotations about a fixed point through angles transform any point (distinct from ) into other points on the circle with center and radius . In general, these points become increasingly dense on the circle; but if the angle is commensurable with a right angle, only a finite number of them will be distinct. In particular, if , where is a positive integer greater than 2, then there will be points whose successive joins
are the sides of an ordinary regular n-gon.
Let us now extend this notion by allowing to be any rational number greater than 2, say the fraction (where and are coprime). Accordingly, we define a (generalized) regular polygon {}, where . Its vertices are derived from by repeated rotations through ,and its sides (enclosing the center times) are
Since a ray coming out from the center without passing through a vertex will cross of the sides, th is denominator is called the density of the polygon [Coxeter 1, pp. 93–94]. When , so that , we have the ordinary regular -gon, {}. When , the sides cross one another, but the crossing points are not counted as vertices. Since may be any positive integer relatively prime to and less than , there is a regular polygon {} for each rational number . In fact, it is occasionally desirable to include also the digon, although its two sides coincide.
When , we have the pentagon {5} of density 1 and the pentagram{} of density 2, which was used as a special symbol by the Babylonians and by the Py thagoreans. Similarly, the octagram{} and the decagram have density 3, while the dodecagram{} has density 5 (Fi gure 2.8a). These particular polygons have names as well as symbols because they occur as faces of interesting polyhedra and tessellations.[11]

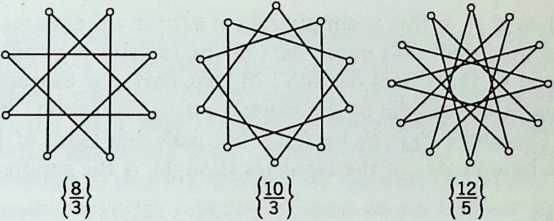
Polygons for whichare known as starpolygons. They are frequently used in decoration. The earliest mathematical discussion of them was by Thomas Bradwardine (1290–1349), who became archbishop of Canterbury for the last month of his life. They were also studied by the great German scientist Kepler (1571–1630)[ see Coxeter **1,**p. 114]. It was the Swiss mathematician L. Schlafli (1814–1895) who first used a numerical symbol such as {}. This notation is justified by the occurrence of formulas that hold for {} equally well whether be an integer or a fraction. For instance, any side of {} forms with the center an isosceles triangle (Figure 2.86) who se angle at is . (As we are introducing trigonometrical ideas, it is natural to use radian measure and write instead of 360°.) The base of this isosceles triangle, being a side of the polygon, is conveniently denoted by . The other sides of the triangle are equal to the circumradius of the polygon. The altitude or median from is the in radius of the polygon. Hence
¶ 2.81
If , the area of the polygon is naturally defined to be the sum of t he areas of theisosc eles triangles, namely
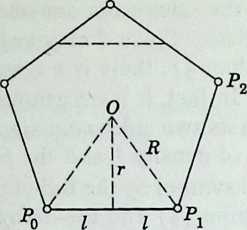
 Figure 2.8b
Figure 2.8b
¶ 2.82
When *d =*1, this is simply ; in other cases our definition of area has the effect that every part of the interior is counted a number of times equal to the “local density” of that part; for example, the pentagonal region in the middle of the pentagram {} is counted twice.
The angle between two adjacent sides of {} , being the sum of the base angles of the isosceles triangle, is the supplement of , namely
¶ 2.83
The line segment joining the midpoints of two adjacent sides is called the vertex figure of {n}. Its length i s clearly
¶ 2.84
[Coxeter 1, pp. 16, 94],
¶ EXERCISES
-
If the sides of a polygon inscribed in a circle are all equal, the polygon is regular.
-
If a polygon inscribed in a circle has an odd number of vertices, and all its angles are equal, the polygon is regular. (Marcel Riesz.)
-
Find the angles of the polygons $${5}, {\frac{5}{2}}, {9}, {\frac{9}{2}}, {\frac{9}{4}}.$$
-
Find the radii and vertex figures of the polygons $${8}, {\frac{8}{3}}, {12},{\frac{12}{3}}$$
-
Give polar coordinates for the th vertex of a polygon {} of circumradius 1 with its center at the pole, taking to be
-
Can a square cake be cut into nine slices so that everyone gets the same amount of cake and the same amount of icing?
¶ Isometry in the Euclidean Plane
Having made some use of reflections, rotations, and translations, we naturally ask why a rotation or a translation can be achieved as a continuous displacement (or “motion”) while a reflection cannot. It is also reasonable to ask whether there is any other kind of isometry that resembles a reflection in this respect. After answering these questions in terms of “sense,” we shall use the information to prove a remarkable theorem (§3.6) and to describe the seven possible ways to repeat a pattern on an endless strip (§3.7).
¶ Direct and Opposite Isometries
“Take care of the sense, and the sounds will take care of themselves.”
Lewis Carroll
[Dodgson **1,**Chap. 9]
By several applications of Axiom 1.26, it can be proved that any point P in the plane of two congruent triangles determines a corresponding point such that . Likewise, another point yields , and . Hence
¶ 3.11
Any two congruent triangles are related by a unique isometry.
In § 1.3, we saw that Pappus’s proof of Pons asinorum involved the comparison of two coincident triangles . We see intuitively that this is a distinction of sense: if one is counter-clockwise the other is clockwise. It is a “topological” property of the Euclidean plane that this distinction can be extended from coincident triangles to distinct triangles: any two “directed” triangles, and , either agree or disagree in sense. (For a deeper investigation of this intuitive idea, see Veblen and Young [2, pp. 61 or Denk and Hofmann [1, p. 56].)
If and are congruent, the isometry that relates them is said to be direct or opposite according as it preserves or reverses sense, that is, according as and agree or disagree. It is easily seen that this property of the isometry is independent of the chosen triangle ABC: if the same isometry relates to , where agrees with , then also agrees with . Clearly, direct and opposite isometries combine like positive and negative numbers (e.g., the product of two opposite isometries is direct). Since a reflection is opposite, a rotation (which is the product of two reflections) is direct. In particular, the identity is direct. Some authors call direct and opposite isometries “displacements and reversals” or “proper and improper congruences.”
Theorem 2.31 can be extended as follows:
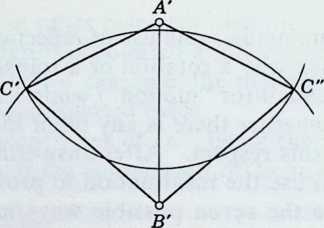
Figure 3.1a
- Two given congruent line segments (or point pairs) AB, AB are related by just two isometries: one direct and one opposite.
To prove this, take any point outside the line , and construct C so that the triangle ABC is congruent to ABC. The two possible positions of (marked C, C" in Figure 3. la) provide the two isometries. Since either can be derived from the other by reflecting in AB, one of the isometries is direct and the other opposite.
For a complete discussion we need the following theorem [Bachmann 1, P-3]:
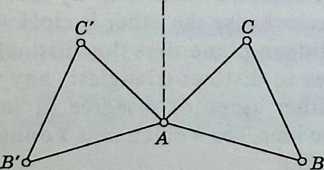
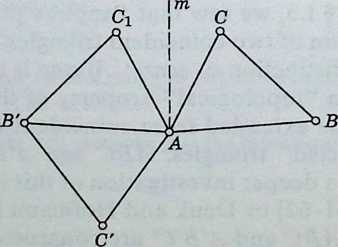
Figure 3.1b
- Every isometry of the plane is the product of at most three reflections. If there is an invariant point, “three” can be replaced by “two.”
We prove this in four stages, using 3.11. Trivially, if the triangles ABC, ABC coincide, the isometry is the identity (which is the product of a reflection with itself). If coincides with A, and with B, while and C are distinct, the triangles are related by the reflection in . The case when only coincides with A can be reduced to one of the previous cases by reflecting in m, the perpendicular bisector of BB (see Figure 3.16). Finally, the general case can be reduced to one of the first three cases by reflecting in the perpendicular bisector of AA [Coxeter 1, p. 35].
Since a reflection reverses sense, an isometry is direct or opposite according as it is the product of an even or odd number of reflections.
Since the identity is the product of two reflections (namely of any reflection with itself), we may say simply that any isometry is the product of two or three reflections, according as it is direct or opposite. In particular,
- Any isometry with an invariant point is a rotation or a reflection according as it is direct or opposite.
¶ Exercises
-
Name two direct isometries.
-
Name one opposite isometry. Is there any other kind?
-
If and A’B’ are related by a rotation, how can the center of rotation be constructed? {Hint: The perpendicular bisectors of AA’ and are not necessarily distinct.)
-
The product of reflections in three lines through a point is the reflection in another line through the same point [Bachmann 1, p. 5].
¶ TRANSLATION
Enoch walked with God; and he was not, for God took him.
Genesis V, 24
The particular isometries so far considered, namely reflections (which are opposite) and rotations (which are direct), have each at least one invariant point. A familiar isometry that leaves no point invariant is a translation [Bachmann 1, p. 7], which may be described as the product of half-turns about two distinct points O, O (Figure 3.2a). The first half-turn transforms an arbitrary point into , and the second transforms this into Pf with the final result that P is parallel to OOand twice as long. Thus the length and direction of are constant: independent of the position of . Since a translation is completely determined by its length and direction, the product of half-turns about and O is the same as the product of half-turns about Q and Q, provided QQ is equal and parallel to OO’. (This means that OOQQ is a parallelogram, possibly collapsing to form four collinear points, as in Figure 3.2a.) Thus, for a given translation, the center of one of the two half-turns may be arbitrarily assigned.
- The product of two translations is a translation.
For, we may arrange the centers so that the first translation is the product of half-turns about Oi and O2, while the second is the product of half-turns about and . When they are combined, the two half-turns about O2 cancel, and we are left with the product of half-turns about (9i and .
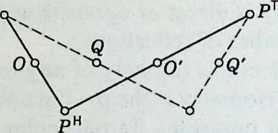
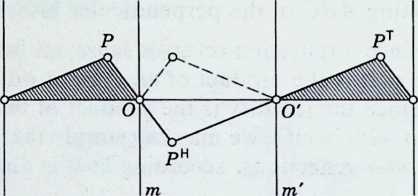
Figure 3.2a Figure 3.2b
Similarly, if m and m (Figure 3.26) are the lines through and O perpendicular to OO, the half-turns about and O are the products of reflections in m and OO, OO and m. When they are combined, the two reflections in OO cancel, and we are left with the product of reflections in m and m. Hence
- The product of reflections in two parallel mirrors is a translation through twice the distance between the mirrors.
If a translation T takes to and Q to Qf, the segment is equal and parallel to ; therefore is a parallelogram. Similarly, if another translation U takes to Q, it also takes to ; therefore $$TU = UT.$$
(In detail, if Q is , Qf is . But U takes to P™. Therefore and coincide, for all positions of P.) In other words,
- Translations are commutative.
The product of a half-turn H and a translation T is another half-turn; for we can express the translation as the product of two half-turns, one of which is H, say T = HH, and then we have
- The product of a half-turn and a translation is a half-turn.
¶ Exercises
-
If T is the product of half-turns about and O, what is the product of half-turns about O and 07
-
When a translation is expressed as the product of two reflections, to what extent can one of the two mirrors be arbitrarily assigned?
-
What is the product of rotations through opposite angles (a and a) about two distinct points?
-
The product of reflections in three parallel lines is the reflection in another line belonging to the same pencil of parallels.
-
Every product of three half-turns is a half-turn [Bachmann 1, p. 7],
-
If , , are half-turns, .
-
Express the translation through distance a along the x-axis as a transformation of Cartesian coordinates. If/(x, y) = 0 is the equation for a curve, what is the equation for the transformed curve? Consider, for instance, the circle .
- GLIDE REFLECTION
We are now familiar with three kinds of isometry: reflection, rotation, and translation. We have not yet considered the product of the reflections in the sides of a triangle. We shall find that this is a glide reflection: the product of the reflection in a fine a and a translation along the same line. Clearly, a glide reflection is determined by its axis a and the extent of the component translation. Since a reflection is opposite whereas a translation is direct, their product is opposite. Thus a glide reflection is an opposite isometry having no invariant point [Coxeter 1, p. 36],
If a glide reflection G transforms an arbitrary point into (Figure 3.3a), and are equidistant from the axis a on opposite sides. Hence
 The midpoint of the line segment lies on the axis for all positions of P.
The midpoint of the line segment lies on the axis for all positions of P.
Figure 3.3a
Figure 3.3b
Let Ri and T denote the component reflection and translation. They evidently commute, so that
We have seen (Figure 3.26) that the translation T may be expressed as the product of two half-turns or of two parallel reflections. Identifying the line a in Figure 3.3a with the line OO in Figure 3.3d, let R, Rdenote the reflections in m, m. Then the product of the two half-turns
is
and the glide reflection is
Thus a glide reflection may be expressed as the product of three reflections (two perpendicular to the third), or of a half-turn and a reflection, or of a reflection and a half-turn. Conversely, the product of any half-turn and any reflection (or vice versa) is a glide reflection, provided the center of the half-turn does not lie on the mirror. [Bachmann 1, p. 6.]
We saw in 3.13 that any direct isometry in the plane is the product of two reflections, that is, a translation or a rotation according as the two mirrors are parallel or intersecting; also that any opposite isometry with an invariant point is a reflection. To complete the catalog of isometries, the only remaining possibility is an opposite isometry with no invariant point. If such an isometry S transforms an arbitrary point into consider the half-turn H that interchanges these two points. The product HS, being an opposite isometry which leaves the point A invariant, can only be a reflection R. Hence the given opposite isometry is the glide reflection
S = H-iR = HR:
Every opposite isometry with no invariant point is a glide reflection.
In other words,
3.31 Every product of three reflections is either a single reflection or a glide reflection.
In particular, the product RT of any reflection and any translation is a glide reflection, degenerating to a pure reflection when the mirror for R is perpendicular to the direction of the translation T (in which case the reflections R and RT may be used as the two parallel reflections whose product is T). But since a given glide reflection G has a definite axis (the locus of midpoints of segments ), its decomposition into a reflection and a translation along the mirror is unique (unlike its decomposition into a reflection and a half-turn, where we may either take the mirror to be any line perpendicular to the axis or equivalently take the center of the half-turn to be any point on the axis).
¶ Exercises
- If is the midpoint of A C, what kinds of isometry will transform
(i) into CB, (ii) into BC?
-
Every direct isometry is the product of two reflections. Every opposite isometry is the product of a reflection and a half-turn.
-
Describe the product of the reflection in OO and the half-turn about .
-
Describe the product of two glide reflections whose axes are perpendicular.
-
Every product of three glide reflections is a glide reflection.
-
The product of three reflections is a reflection if and only if the three mirrors are either concurrent or parallel.
-
If , R3 are three reflections, is a translation [Rademacher and Toeplitz 1, p. 29].
-
Describe the transformation
(x,y) >(x + a,y).
Justify the statement that this transforms the curvef(x,y) = 0 into f(x a,y) = 0.
- REFLECTIONS AND HALF-TURNS
Thomsen* has developed a very beautiful theory in which geometrical properties of points and lines (understood to be all distinct) are expressed as relations among the corresponding half-turns and reflections . The reader can soon convince himself that the following pairs of statements are logically equivalent:
<—> m and mi are perpendicular.
lies on m.
RiR_{2}R^{3}= R^{3}R_{2}R^{X}\textless---\textgreater{}mi,m^{2}, m^
are either concurrent or parallel.
is the midpoint of Oi\textless9^{2}.
HiH = HH^
HiR = RH^
m is the perpendicular bisector of .
¶ EXERCISE
Interpret the relations (a) .
- SUMMARY OF RESULTS ON ISOMETRIES
And thick and fast they came at last. And more, and more, and more.
Lewis Carroll
[Dodgson 2, Chap. 4]
Some readers may have become confused with the abundance of technical terms, many of which are familiar words to which unusually precise meanings have been attached. Accordingly, let us repeat some of the definitions, stressing both their analogies and their differences.
* G. Thomsen, The treatment of elementary geometry by a group-calculus, Mathematical Gazette, 17 (1933), p. 232. Bachmann [1 ] devotes a whole book to the development of this idea.
In all the contexts that concern us here, a transformation is a one-to-one correspondence of the whole plane (or space) with itself. An isometry is a special kind of transformation, namely, the kind that preserves length. A symmetry operation belongs to a given figure rather than to the whole plane: it is an isometry that transforms the figure into itself.
In the plane, a direct (sense-preserving) isometry, being the product of two reflections, is a rotation or a translation according as it does or does not have an invariant point, that is, according as the two mirrors are intersecting or parallel. In the latter case the length of the translation is twice the distance between the mirrors; in the former, the angle of the rotation is twice the angle between the mirrors. In particular, the product of reflections in two perpendicular mirrors is a half-turn, that is, a rotation through two right angles. Moreover, the product of two half-turns is a translation.
An opposite (sense-reversing) isometry, being the product of three reflections, is, in general, a glide reflection-, the product of a reflection and a translation. In the special case when the translation is the identity (i.e., a translation through zero distance), the glide reflection reduces to a single reflection, which has a whole line of invariant points, namely, all the points on the mirror.
To sum up:
3.51 Any direct isometry is either a translation or a rotation. Any opposite isometry is either a reflection or a glide reflection.
¶ Exercises
-
If S is an opposite isometry, is a translation.
-
If Ri, , R3 are three reflections, is a translation along the first mirror. (Hint: Since and are glide reflections, their squares are commutative, by 3.23; thus
that is, Ri and are commutative [cf. Bachmann 1, p. 13].)
- HJELMSLEV’S THEOREM
…a very high degree of unexpectedness, combined with inevitability and economy.
G. H. Hardy [2, p. 53]
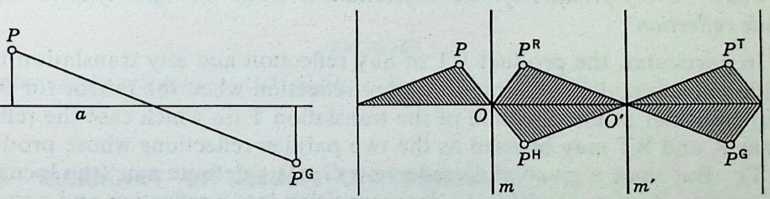
We saw, in 3.12, that two congruent line segments AB, AB, are related by just two isometries: one direct and one opposite. Both isometries have the same effect on every point collinear with and B, that is, every point on the infinite straight line (for instance, the midpoint of is transformed into the midpoint of AB). The opposite isometry is a reflection or glide reflection whose mirror or axis contains all the midpoints of segments joining pairs of corresponding points. If two of these midpoints coincide, the
direct isometry is a half-turn, and they all coincide [Coxeter 3, p. 267]. Hence
HJELMSLEVS THEOREM. When all the points P on one line are related by an isometry to all the points P on another, the midpoints of the segments PP are distinct and collinear or else they all coincide.
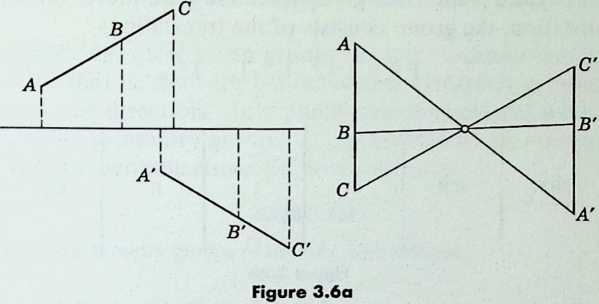
In particular, if A, B, C are on one line and A, B, C on another, with
3.61 AB = AB, BC = BC (Figure 3.6a), then the midpoints of AA, BB, CC are either collinear or coincident (J. T. Hjelmslev, 1873).
- PATTERNS ON A STRIP
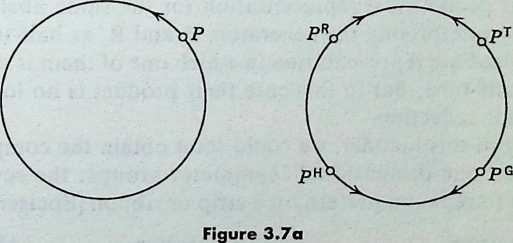
Any kind of isometry may be used to relate two equal circles. For instance, the point on the first circle of Figure 3.7a is transformed into on the second circle by a translation, into by a reflection, into by a half-turn, and into by a glide reflection. (Arrows have been inserted to indicate what happens to the positive sense of rotation round the first circle.) These four isometries have one important property in common: they leave invariant (as a whole) one infinite straight line, namely, the line joining the centers of the two circles. (In the fourth case this is the only invariant line.)
We have seen (Figure 3.26) that the product of reflections in two parallel mirrors m, m is a translation. This may be regarded as the limiting case of a rotation whose center is very far away; for the two parallel mirrors are the limiting case of two mirrors intersecting at a very small angle. Accordingly, the infinite group generated by a single translation is denoted by , and the infinite group generated by two parallel reflections is denoted by . Abstractly, is the “free group with one generator.” If T is the generating translation, the group consists of the translations
m m
Figure 3.7b
Similarly, , generated by the reflections in parallel mirrors m, m (Figure 3.76), consists of the reflections and translations
[Coxeter 1, p. 76]; its abstract definition is simply
This group can be observed when we sit in a barber’s chair between two parallel mirrors (cf. the New Yorker, Feb. 23, 1957, p. 39, where somehow the reflection RRRRR yields a demon).
A different geometrical representation for the same abstract group is obtained by interpreting the generators R and Ras half-turns. There is also an intermediate representation in which one of them is a reflection and the other a half-turn; but in this case their product is no longer a translation but a glide reflection.
Continuing in this manner, we could soon obtain the complete list of the seven infinite “one-dimensional” symmetry groups: the seven essentially distinct ways to repeat a pattern on a strip or ribbon [Speiser 1, pp. 81:
| Typical pattern |
|
Abstract Group |
| (i)…L L L L… | translation | |
| (ii)… L T L r… | glide reflection | r -oo |
| (iii)…V V V V… | reflections | |
| (iv)…N N N N… | half-turns | |
| (v)…V A V A… | reflection and 1 half-turn |
> |
| (vi).. .D D D D… | translation and 1 reflection |
cx x Dr |
| (vii).. .H H H H… | reflections | D X Dr |
In (iii), the two mirrors are both vertical, one in the middle of a V, reflecting it into itself, while the other reflects this V into one of its neighbors; thus one half of the V, placed between the two mirrors, yields the whole pattern. In (vi) and (vii) there is a horizontal mirror, and the symbols in the last column indicate “direct products” [Coxeter 1, p. 42]. For all these groups, except (i) and (ii), there is some freedom in choosing the generators; for example, in (iii) or (iv) one of the two generators could be replaced by a translation.
Strictly speaking, these seven groups are not “1-dimensional” but “Ildimensional;” that is, they are 2-dimensional symmetry groups involving translation in one direction. In a purely one-dimensional world there are only two infinite symmetry groups: , generated by one translation, and , generated by two reflections (in point mirrors).
¶ Exercises
- Identify the symmetry groups of the following patterns:
…b b b b…,
…b p b p…,
…b d b d…,
…b q b q…,
…bdpqbdpq….
- Which are the symmetry groups of (a) a cycloid, (b) a sine curve?
¶ Index
¶ Source Scans
¶ eBook Formats
Heath 1, p. vi. (Such references are collected at the end of the book, pp. 415.) ↩︎
In Chapter 15 we shall see how far we can go without using this unpleasantly complicated Fifth Postulate. ↩︎
Leon Bankoff, American Mathematical Monthly, 65 (1958), p. 521. For other proofs see G. R. Veldkamp and H. Brabant, Nieuw Tijdschrift voor Wiskunde, 45 (1958), pp. 193; 46 (1959), p. 87. ↩︎
It is to be understood that any exercise appearing in the form of a theorem is intended to be proved. It saves space to omit the words “Prove that” or “Show that.” ↩︎
Steiner [1, pp. 60, 524]. See also Hobson [1, p. 216, Ex. 29] and J. Satterly, Mathematics Teacher, 53 (1960), pp. 90. ↩︎
Elementare Losung einer Minimumsaufgabe , Zeitschrift fUr mathematischen und naturwissenschaftlichen Unterricht, 60 (1929), pp. 22. ↩︎
Court [1, pp. 105. See also 1938, p. 293 (footnote, where this theorem is attributed to Napoleon); and Forder [2, p. 40] for some interesting generalizations. ↩︎
Mathematical Questions and their Solutions from the Educational Times (New Series), 15 (1909), pp. 23,47. See also C. H. Chepmell and R. F. Davis, Mathematical Gazette, 11 (1923), pp. 85; F. Morley, American Journal of Mathematics, 51 (1929), pp. 465, H. D. Grossman, American Mathematical Monthly, 50 (1943), p. 552, and L. Bankoff, Mathematics Magazine, 35 (1962), pp. 223. The treatment given here is due to Raoul Bricard, Nouvelles Annates de Mathmatiques (5), 1 (1922), pp. 254. A similar proof was devised independently by Bottema [1, p. 34]. ↩︎
H. W. chmond, Quarterly Journal of Mathematics, 26 (1893), pp. 296–297; see also H. E. Dudeney, Amusements in Mathematics (London 1917), p. 38. ↩︎
Rediscovered by P. Kanagasabapathy, Mathematical Gazette, 42 (1958), p. 310. ↩︎
H. S. M. Coxeter , M. S. Longuet-Higgins, and J. C. P. Miller, Uniform polyhedra, Philosophical Transactions of the Royal Society, A, 246 (1954), pp. 401–450. ↩︎