Beyond the Cube
Beyond the Cube
The Architecture of Space Frames and Polyhedra
Editor: Jean-François Gabriel
Wiley
ISBN: 978-0471122616
ISBN-10: 0471122610
Updated: 2024-12-17
Copyright
All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or by any information storage and retrieval system, without permission in writing from the Copyright Holder.
ENCODED IN THE UNITED STATES OF AMERICA
Beyond the Cube
Beyond the Cube
The Architecture of
Space Frames and Polyhedra
J. Francois Gabriel
Editor
John Wiley & Sons, Inc.
NEW YORK / CHICHESTER / WEINHEIM / BRISBANE / SINGAPORE / TORONTO
This text is printed on acid-free paper.
Copyright© 1997 by John Wiley & Sons, Inc.
All rights reserved. Published simultaneously in Canada.
Reproduction or translation of any part of this work beyond that permitted by Section 107 or 108 of the 1976 United States Copyright Act without the permission of the copyright owner is unlawful. Requests for permission or further information should be addressed to the Permissions Department, John Wiley & Sons, Inc., 605 Third Avenue, New York, NY 10158.
This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold with the understanding that the publisher is not engaged in rendering legal, accounting, or other professional services. If legal advice or other expert assistance is required, the services of a competent professional person should be sought.
Library of Congress Cataloging-in-Publication Data
Beyond the cube : the architecture of space frames and polyhedra / J. Francois Gabriel, editor.
p. cm.
Includes index.
ISBN 0 (cloth : acid-free paper)
1. Space (Architecture) 2. Space frame structures. I. Gabriel, J. Francois, 1930-.
NA2765.B45 1997 97
721 .042dc21
Printed in the United States of America
Contents
J. Francois Gabriel, Syracuse University
- Polyhedra, from Pythagoras to
Alexander Graham Bell 1
Jos Tomlow, Hochschule Zittau/Gorlitz, Germany
- Polyhedrality in the Architecture
Rollie Ristine
Irene E. Ayad
Arthur L. Loeb, Harvard University
- Philip Johnson’s Crystal Cathedral and the
Rhetoric of Its Free-Form Polyhedral Structure 161
Lawrence Davis, Syracuse University
Matthys Levy
- Double Curvature Space Frames Supported
on Four Points: Design and Construction of the International Plaza of Portopia’81 211
Masao Saitoh, Nihon University
Arthur L. Loeb, Harvard University
Pieter Huybers, Delft University of Technology
Rene Motro, Universite de Montpellier
- The Structural Morphology of
Ture Wester, Royal Danish Academy of Fine Arts
- Computer-Aided Processing of
Hoshyar Nooshin, with P. L. Disney and O. C. Champion, University of Surrey
Ariel Hanaor, National Building Research Institute, Israel
- Visual Morphology of Space Labyrinths:
A Source for Architecture and Design 409
Haresh Lalvani, Pratt Institute
- Quasicrystal Architecture:
The Space of Experience 427
Tony Robbin
- Are Space Frames Habitable? 439
J. Francois Gabriel, Syracuse University
¶ Preface
J. Frangois Gabriel
Henry Ford reputedly said that customers could have his automobiles in any color, as long as that color was black. A parallel can be drawn with the shape of our rooms, which could come in any shape but are essentially cubic. Very few rooms are perfect cubes, it is true; most are in the shape of flattened or elongated cubes, but the majority of our buildings are conceived as an assemblage of cubic forms, and that is what they look Eke: piles of shoe boxes.
We use the cube as if it were the only acceptable model for our living spaces and, in doing so, we ignore countless other forms that might lead to more efficient, more beautiful, more economical, and certainly less worn-out environments. Why do we do it? Mr. Ford told us we must drive his black cars, but who told us that we must dwell in square or rectangular spaces, bound by four vertical walls intersecting at right angles?
Would all the painters in the world agree to throw out all their colors and limit their palette to one color only? Would all the writers agree to limit their language to words of three syllables? Would all the composers…? Of course they would not. Yet, like it or not, most of us end up living in cubes, or nearcubes. This book makes a case for a family of shapes that often make more sense than the cube: polyhedra. Indeed, the cube itself is a polyhedron, and many of the forms used or described in this book have a direct, if not always obvious, relationship with the cube. My intention is to show, with the help of contributions from structural engineers, architects, historians, and others whose expertise spans several fields, that polyhedra provide all the elements for a formal language of extraordinary versatility that can satisfy the essential demands of buildings: solidity, beauty, and convenience.
Briefly, this book is organized as follows: We begin, logically enough, with a look at the past. The first chapter contains a historical survey of polyhedra. Then we discuss the attitudes of three great designers of the 20th century toward polyhedral forms. Chapters 5 to 7 look at a more recent past and show how space frames, formed by aggregates of polyhedra, shaped three important buildings, each using a space frame in an original way. In the next five chapters, we focus on the theoretical aspects of polyhedra, their formal bonds with the cube, the kinship that exists between one polyhedron and another, their symbolic meaning, their proportional relationships, their specific structure, and their representation. The subject of the three following chapters is the future: tensegrity, space labyrinths, and quasicrystals, all of which are in their experimental stage, but already suggesting architectural possibilities that may materialize soon.
The most important criterion of architecture is not about looks, but about the quality of the spaces within. An architecture of space frames and polyhedra will be viable if the spaces formed by it are at least as good (as convenient, as beautiful, etc.) as those found within conventional, cubic frameworks. This critical question is discussed in the last chapter of the book.
This is not the definitive book on architecture beyond the cube. Nor can it be, for the field of space frames and polyhedra is continually changing and expanding, enriched by the discovery of new configurations, new design methods, and new applications. However, a genuine effort is made to present a broad, accessible, and faithful picture of the state of the art.
Very few polyhedra are found in the natural world. Most of them are a creation of the mind. With experience in architecture and the history of structural design, Jos Tomlow looks in Chapter 1 at the discovery, the perception, and the use of polyhedra, from Pythagoras to Alexander Graham Bell. With few exceptions, polyhedra were not seen as structural or architectural objects. It is only in this century, and particularly in the last 50 years, that the connection was fully made. Interestingly enough, the representation of polyhedra emerges as one of the most intriguing aspects of their history. Everybody seriously involved with polyhedra knows the challenge of making their forms comprehensible to the onlooker, or even to oneself. The cube is the easiest polyhedron to draw, and I suspect this to be one of the explanations for its extravagant popularity. Of course, the price we pay for using it indiscriminately is a greatly impoverished spatial experience for all of us.
How did some of the most inventive minds of the first half of this century approach problems of structure and architectural modeling? Bruce Goff’s work is characterized by fantasy and ingenuity and he came close to a literal geometry, for he sometimes merged polyhedra and architecture into a single entity. He did not use simple geometric solids in isolation, which is easy to do but which might not be of great significance. He chose to shelter varied architectural functions in regular patterns of polyhedra, or infinite structures, as they are called. He gave polyhedral shapes to his rooms, and he also used the same polyhedra to create different room shapes in the same building, thus proving that it could be done without monotony. He also proved something else. Rollie Ristine, a student of Bruce Goff, shows in Chapter 2 that his teacher was not a geometer, and it is doubtful that he even knew by their names the polyhedra he used in his designs. However, he thought as an architect when giving order to space, and he came intuitively to geometry, showing that geometry is as good a way to organize space as any other. One might even wonder if there is any better way.
With Louis Kahn, in Chapter 3, we come to one of the most widely acclaimed architects of the postwar era. Unlike F. L. Wright, Le Corbusier, or Mies van der Rohe, Kahn had a formal architectural education and earned an architectural degree. The school he attended was traditional, even classical, since at the time architectural education in the United States was completely dominated by the Beaux-Arts system. Far from rebelling against his training, Kahn assimilated the fundamentals of classical architecture and reasserted its principles in his mature work. Simple geometric forms such as the square, the circle, and the equilateral triangle, bilateral symmetry, and clarity, which are typical of classical designs, are among the constants of Kahn’s work. The memorable impression made by his buildings is a direct outcome of classical principles. Geometry infuses Kahn’s designs, and it is no wonder that, under the influence of his collaborator Anne Griswold Tyng, he should have become interested in space frames. The building that first brought him to the attention of the architectural profession at large is the Yale University Art Gallery, where the floor structure is a space frame. The fascinating design for an office structure using a mega-space frame, although not built, gave him the aura of a prophet and made him famous worldwide. Irene Ayad shows how Kahn’s involvement with polyhedra fits in his architectural development.
Kahn, who was also a painter, was intensely visual. Buckminster Fuller, on the other hand, told me in the last year of his fife that he did not care how things looked. He seemed to think that, when things are done right, they end up looking right, for our aesthetic judgments are based on previous experience. Fuller’s geodesic domes, some very large and some rather small, are often as beautiful as pure polyhedra can be. And so is the space frame, which Fuller called the octettruss, and for which we owe him so much. However, those who believe that originality and personal expression are the first goals of architecture do not think much of structuralism. Fuller was neither an architect nor an engineer. He was essentially self-educated, and he has been variously called by others a poet, a philosopher, an inventor, an environmentalist, a scientist, an engineer, a maverick, a crackpot and, by himself, a comprehensivist. In 1952 he did receive an Award of Merit from the New York Chapter of the American Institute of Architects, and in 1960 the Gold Medal of the Philadelphia Chapter of the American Institute of Architects. It is fitting that Arthur Loeb, a maverick himself, should share with us personal recollections of a fruitful collaboration in Chapter 4, Buckminster Fuller and the Relevant Pattern.
Philip Johnson’s approach to design is radically different. Best described as a complex, sectioned, prismatic form, his Crystal Cathedral is a dramatic piece of abstract sculpture. It demonstrates in a masterful way that, far from hindering freedom of expression, space frames can lend themselves to the implementation of any building shape. It is not for ideological reasons that a space frame was selected by the architect, it is because nothing else could do the job, as Mr. Johnson explained to me in January of 1993. Familiar to millions of television worshippers who have seen it on Sunday mornings for 16 consecutive years, the building remains, on many levels, one of the most paradoxical of the second half of the century. In Chapter 5, Lawrence Davis gives us a fascinating account of these paradoxes.
The Javits Convention and Exhibition Center, by Pei, Cobb, and Freed, provides a neat contrast to the Crystal Cathedral. Other than its enormous size, the most impressive feature of the Javits Center is its designers’ sensitive recognition and acceptance of the geometry of a space frame. By geometry, I mean the shape of the “building blocks” and the pattern they form: octahedra juxtaposed to tetrahedra. As Matthys Levy, the engineer in charge of the project, shows us in Chapter 6, this pattern controls and, to a certain extent, determines the shape of the building. One admires, in particular, how smoothly space frames are made to “turn the corners” as well as the expressive effect obtained at the main entrance of this civic palace. Nothing extraneous was added to the space frame, and nothing was subtracted from it. Levy’s no-frills writing style seems perfectly suited to the restraint of the design.
Because of its location and because of its function, a certain austerity is expected in the facade of a building like the Javits Center. What was called for in the theme building of the exhibition “Portopia ‘81’’ in Kobe, Japan, to celebrate the completion of a large artificial island, is very different. The open and cheerful structure is achieved solely with space frames. The airy elegance of this building, all curves and smiles, makes its loss to demolition regrettable. Conceived to resist the effects of typhoons and seismic forces, it would have been interesting to see how it would have fared in the powerful 1995 earthquake. The chapter, entitled Double Curvature Space Frames, is written by the engineer in charge, the talented Masao Saitoh.
It cannot be said too often that a cubic frame with hinged joints is unstable, and that it requires some doctoring to be made indeformable. One treatment consists of adding one member to each square face, placed along one of its diagonals. If the shape one wishes to achieve is a cube, the presence of diagonal members on its faces changes nothing of the interior volume or its bounding surfaces. Because a tetrahedron can be the figure formed by the diagonals alone, it would have been more direct to ignore the cubic frame and adopt a tetrahedral frame to begin with. In other words, a cubic volume fits in a tetrahedral frame as well as it fits in a cube. This little bit of irreverent magic introduces Arthur Loeb’s chapter, Deconstruction of the Cube, where the coupling of tetrahedron to cube is shown to beget many other polyhedra. Names like Stella octangula and rhombic dodecahedron may sound a bit complicated, but they are descriptive and, once you know them, you find that they refer to interesting and friendly personalities. And know them one must if one is considering an expansion of design sources beyond the cube.
As indicated by the title of his chapter, The Polyhedral World, Pieter Huybers reaches away from the cube and sets out to understand the geometric laws that govern these shapes. This understanding is necessary if we are to adapt polyhedra to our architectural and structural needs. Archimedean solids, prisms and antiprisms, domes, and folded-plate structures are included along with space frames in the discussion, which contains a minimum of mathematics.
With Rene Motro in Chapter 10, we look for meaning in space frames and polyhedra. For as long as they have been known, polyhedra have aroused the interest of brilliant minds who, from Plato to Buckminster Fuller, have tried to understand the world as a synergy. The five “perfect” polyhedra are often referred to as Platonic solids, not because Plato discovered them but because each one symbolized one of the five elements in Pythagoras’s cosmology, in which he, Plato, was deeply interested. Thus the cube stands for the earth, whereas the octahedron stands for the air. However, symbolic meaning can be found in everything, and symbolism is not a science. According to Motro, however, one rule applies, and it stipulates that a symbol cannot be defined without suffering mutilation, distortion, or total elimination. As for proportion, it can be more than an attempt to please the eye. Proportion is related to symbolism when it is understood as an expression of divine harmony, that is, perfection. In reading Motro’s chapter, we will see that he is an engineer whose thinking is as clear as it is rigorous.
We return to earth, so to speak, with Ture Wester’s chapter, The Structural Morphology of Basic Polyhedra. Wester is also a structural engineer, and an imaginative one at that. He does not confine his thinking to post-and-beam structures stabilized by triangulation or other means. This would not do with polyhedra, the structural problems of which have little in common with those of their brother the cube. Three of the five regular polyhedra make perfect rigid lattices. They are the tetrahedron, the octahedron, and the icosahedron, which all have triangular faces. Three make perfect plate structures, and they are the cube, the dodecahedron and, again, the tetrahedron. These three have three-branched vertices. This observation forms the basis of Wester’s elegant general theory, structural duality, which leads to the formulation of simple rules for analyzing the rigidity of any arbitrary polyhedra, simple design methods for geometrically complicated but highly efficient plate structures, and other interesting possibilities. Some structures of the natural world are included in his demonstration.
Hoshyar Nooshin has developed a mathematical tool called forniex algebra for the processing of all kinds of configurations. The advent of the computer made the structural analysis of space frames easier and faster. In so doing it became the indirect cause of the profiferation of space frames from the 1950s on. CAD now plays an increasingly useful role in visualization and formal transformations, which are routine in all architectural and structural design, and are even more critical with noncubic forms, where the use of the traditional T-square may be too slow or considered old-fashioned. Nooshin’s chapter, written in collaboration with P. L. Disney and O. C. Champion, lays down the foundations of a comprehensive approach for computer-aided processing of polyhedral configurations.
Chapters 13 to 15 open new horizons for polyhedra in three directions. Tensegrity, a term coined by Buckminster Fuller, represents structures with discontinued compression. All structures include parts that are under compression. In tensegrity structures, these elements are not in direct contact with one another: They are held together by intermediate cables. Tensegrity structures are a marvel to behold. Ariel Hanaor, in Chapter 13, suggests that practical applications may be found in combining tensegrity with deployable, or retractable structures, which are brought on the site in bundles and erected rapidly with a variety of mechanical devices.
Space labyrinths are structures made of a continuous surface dividing space into two parts, one being the inside and the other one being the outside. In some cases, inside and outside are interchangeable and some labyrinths can be constructed with one single module. Space labyrinths are open-ended, meaning that they could theoretically go on forever. One can see from this rough description how space labyrinths could revolutionize our concept of architectural space. Haresh Lalvani conceived his chapter as a pictorial essay that could be part of a visual encyclopedia of form and structure. Higherdimensional diagrams show space labyrinths, some already known, others presented here for the first time, grouped in families. Included are hyperbolic and nonperiodic, that is, quasicrystalline, space labyrinths.
Tony Robbin defines quasicrystals as three-dimensional manifestations of higher-dimensional cubes. Essentially, quasicrystals are assemblies of two different polyhedra with similar topological properties, both derived from the cube, capable of clustering in compact arrangements and capable of forming nonrepeating patterns. This means that the pattern may duplicate itself, but not necessarily at predictable intervals. In his realizations, Robbin aims at making works of art, but he is aware of the structural and architectural capabilities of quasicrystals, which might be realized at full scale in the years ahead.
I have been interested for many years in the shape of spaces generated by space frames. I am even more interested in the architectural spaces that can be found within space frames. What are they like? How can they be connected with one another? How can they be accessed? To what use do they lend themselves? How do they compare with square rooms? How can they be built? Some of my investigations are reviewed in the last chapter of the book. The conclusive ones are given names, such as hexmods and star bea?ns. More are in progress, and many more remain to be discovered. I think we are in the prehistoric phases of discovery in an immense and promising field, which we have only begun to probe.
In general, there is a regrettable shortage of actual polyhedral buildings. This is difficult to understand for those of us who, having explored and experimented for years with these forms, marvel at their inexhaustible richness and have a vision of the poetry that emanates from some of them. This book presents a small but significant portion of the work done around the world by a number of architects, engineers, and others. Some speculate, and others build. Some do both. All our efforts are experiments, and many are successful enough to sustain our enthusiasm. Space frames and polyhedra will change our ways of building. Eventually, they will bring about a gentle revolution in the way we design architecture. I hope readers find pleasure in this book, as the material presented here should stimulate their imagination and encourage them to satisfy their curiosity.
Acknowledgments
The origin of this book can be traced to my teens, when a Monsieur Prevot taught me descriptive geometry for three years with wonderful toughness. He instilled in me a lasting desire to better understand complex relationships between form and space. On this foundation, the training I received at the Ecole des Beaux-Arts developed in me a great respect for the pure, basic, and beautiful forms on which classical architecture is based.
I owe my first insights into space structures to Robert Le Ricolais and Stephane Du Chateau, who both advised me on my thesis. Others who kindly encouraged my independent pursuits are Felix Candela, Keith Critchlow, Buckminster Fuller, Gulzar Haider, Zygmunt S. Makowski, Stefan Medwad- owski, Max Mengeringhausen, Peter Jon Pearce, Duncan R. Stuart, Moshe Safdie, and Yona Friedman.
The students I was privileged to teach, many of them American, played a large part in my continued interest. Their curiosity about spatial relationships, their desire to explore new forms, to understand structural action, and to integrate architecture and structure helped me learn more. John Ray Hoke, Jr., now a Fellow of the American Institute of Architects, was one of these students, and he convinced me to prepare this book.
I am particularly grateful to the fourteen contributors who put aside their own important activities to contribute their talent and their expertise to make this book a remarkable compendium, bringing together aspects of many fields bearing upon architecture: aesthetics, social history, structural engineering, and other fields that do not accept well-defined boundaries. Several contributors also advised me on important matters related to the book.
I am also grateful to the following, who generously gave of their time and wisdom to read and comment on the contents: Edward J. Applewhite, writer, Washington, D.C.; Professor Thomas F. Banchoff, Mathematics Department, Brown University; Dr. John Chilton, Department of Architecture and Planning, University of Nottingham; Dr. H. Martyn Cundy, Kendal, Cumbria, U.K.; Larry Wayne Grantham, architect, Foley, Alabama; Professor Yasuhiko Hangai, Institute of Industrial Science, University of Tokyo; Datuk Lim Chong Keat, Emmanuel College, University of Cambridge; Matthys Levy, Weidlinger Associates, Inc., Consulting Engineers, New York; Dr. Rowland J. Mainstone, D. Eng., Hon. R.I.B.A.; Dr. Robert C. Meurant, Institute of Traditional Studies, Auckland; Professeur Rene Motro, Laboratoire de Mecanique et Genie Civil, Universite Montpellier II; Professor John O’Brien, School of Architecture, University of Tennessee, Knoxville; Peter Jon Pearce, Pearce Research and Design, Studio City, California; Professor Theoman Pekdz, Department of Civil Engineering, Cornell University; Professor Luis Sanchez-Cuenca, Departament d’Arquitectura i Enginyeria de la Construccio, Universitat de Girona; Professor Franz Schulze, Department of Art, Lake Forest College; Professor Ronald Shaeffer, School of Architecture, Florida A & M University; Dr. Charles H. Thornton, Thornton-Tomasetti Engineers, New York; Dr. Anne Griswold Tyng, F.A.I.A.; Professor Patricia Waddy, President of the Society of Architectural Historians; and Bruno Zevi, Director of Architettura.
A number of people helped in several ways. Bruce Abbey, Dean of the School of Architecture at Syracuse University, was instrumental in obtaining for me the leave of absence needed to complete the project. Dr. Gershon Vin-cow, Vice-Chancellor for Academic Affairs, approved the leave. Dr. Ben Ware, Vice-President for Research and Graduate Affairs, believed in the value of my work. Amanda L. Miller, the editor at John Wiley and Sons, Inc., with her assistants Mary Masi and MaryAlice Yates, gave, in addition to technical guidance, the support of her never-flagging enthusiasm for the book project during the entire process. P.G. Wodehouse helped me keep things in perspective.
This book is dedicated to Laura A. Martin, my wife.
Beyond the Cube
¶ Polyhedra, from Pythagoras to Alexander Graham Bell
Jos Tomlow
¶ INTRODUCTION
Writing about the history of polyhedra up to the year 1900 means either lining up repetitive quotations from some 400 editions of Euclid’s Elements or which the author prefersmaking a voyage of exploration through historic objects and images of polyhedral shapes and considering the specialists involved. Indeed, the very materialization of polyhedral form as a two-dimensional image or a three-dimensional object turns out to be one of the keys to the significance of polyhedra in history.
¶ NATURAL CRYSTALS
The history of mathematics did not start with Pythagoras, who built upon the theoretical and practical knowledge of geometry that the Egyptians and the
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
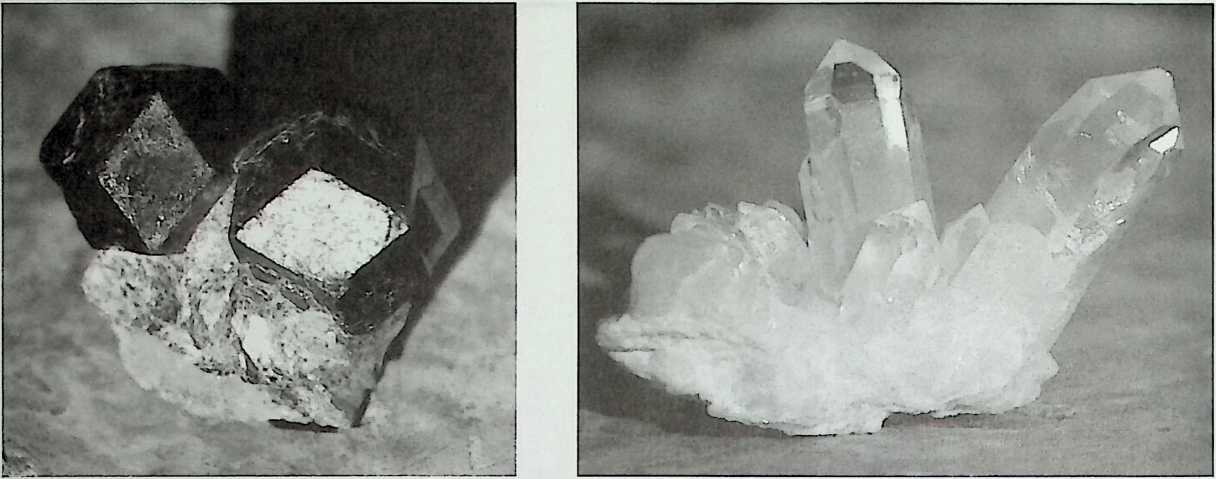Figure 1.2 Quartz, rock crystal, with prismatic shape and pyramidal ends. (Source: Private collection. Photo: Jos Tomlow, Stuttgart.)
Figure 1.1 Natural crystals (Almadin) with the shape of a rhombic dodecahedron. (Source: Private collection. Photo: Jos Tomlow, Stuttgart.)
Mesopotamians had acquired. Even older are Chinese achievements in mathematics. If one wants to reconstruct the earliest human understanding of polyhedral phenomena, one has to think rather of natural polyhedra that occur in certain crystals. So, for a start, we may consider these naturally occurring manifestations that could have urged people to look further. Certain natural crystals show semi-regular or regular polyhedral forms like the rhombic dodecahedron, the tetrahedron, and even the cube.1 The transparent quartz crystal shows a polygonal prism with a pyramidal top. This may have led people to ponder on the geometric properties until someone may have conceived that six square planes fit together in a logical way into a cube.
¶ THE EARLIEST POLYHEDRAL OBJECTS
The next step is the man-made polyhedral object. One such ancient object is the East African foot ring, whose polyhedral ends may be even older in origin than the semi-regular polyhedral pyramids of Egypt or related forms in Mesopotamia. The material is hammered and welded silver. Women wore such lightweight rings loosely around the ankle. The open ring is hollow with two knob-like endings, shaped like cubes with snubbed vertices. This shape, called a cuboctahedron, is a semi-regular polyhedron with six squares and eight triangles. The craftsman took care to smooth some edges of the polyhedra in order to avoid hurting the foot, whereas all other surfaces are adorned with cut lines or stars. Typical °f this kind of jewelry worn by Berber women is its cultural origin and age are difficult to trace.2
Proof that the combination of an open ring with a cuboctahedron is truly
Figure 1.3 Old East African silver foot ring with ends shaped like a semi-regular polyhedron (cuboctahedron). (Source: Private collection. Photo: Gabriela Heim, Stuttgart.)
old can be found in the so-called polyhedral earrings and basket earrings produced in early medieval Europe. One pair of earrings, now in the German-isches Nationalmuseum Niirnberg, was probably found in a grave in Romagna, Italy. The material is silver wire with a tiny solid silver polyhedral knob attached to it.3 Another type of earring, an example of which is in the Landesmuseum in Stuttgart, was found near Basel in an Alamannic woman’s grave (end fifth century). One end of the so-called basket earring, made of either gold or silver, has an open cuboctahedron or similar form, in which a precious stone (e.g., garnet) is held. Although later on these polyhedral forms were copied by regional artists, their origin is thought to be Mediterranean, imported by trade or war.4
¶ THE ANCIENT GREEKS ON POLYGONS
In my hypothetical chronology, the ancient science of polygons and polyhedra began only after craftsmen had made simple polyhedral objects like the early cuboctahedra mentioned previously.
Pythagoras (ca. 570 B.C.) is attributed with developing a basic geometric theorem, the graphic demonstration of the algebraic formula a2 + b2 = c2. The square and the right-angle triangle play a major role in his proof.5To underline the importance of his work, we may recall here the story of how Pythagoras sacrificed a hundred fat oxen to the gods in gratitude for his having discovered the 90° angle.8
In Euclid’s Elements we find a discussion of the Pythagorean theorem. An illustration survived, dating from a time when European prints did not yet exist and can be found in an Arabic transcription of Nasr ad-Din at-Tusi (who died in 1247). If we consider the quality of the drawing, we see some interesting, progressive features: Letters permit cross reference to the text and the figure is drawn in red, whereas the lettering uses dark ink. Negative features also exist: The drawing is roughly executed with some lines shown double; the squares do not show true right angles; and the illustration is awkwardly squeezed between the accompanying text. The non-right angles are especially puzzling, as they concern the very essence of the geometric construction described. One may think that the illustration has no meaning on its own and can only be understood in relation to the mathematics in the text. We may call this a diagrammatic use of the drawn image.9
Figure 1.4 The five “Platonic” regular polyhedra and their symbolism together with concave or stellated polyhedraas depicted by Johannes Kepler in Harmonices Mundi (1619). (Source: J. Kepler, Die Weltharmonik, R. Oldenbourgh Verlag, Munich, 1990.)
¶ THE ANCIENT GREEKS ON POLYHEDRA
The Greeks started to theorize about the relationship between polygons and polyhedra and, in this way, entered into a hermetic realm of knowledge. The observation that only five regular and convex polyhedra can exist and the notion that these bodies were a symbol for all and everything were formulated as a doctrine by Timaeus of Lokri: Fire is represented by the tetrahedron, air by octahedra, water by icosahedra, earth by cubes and, since a fifth arrangement is possible, God has zised the dodecahedron to serve as a contozir of the zmiversecited from Timaeus by Plato (427/347 B.C.).5
Euclid (ca. 323 B.C.) described the basic geometric principles of these five polyhedra in his Elements.10,11 As we shall see, it was a long time before the visual image of polyhedra matched the mathematical rigor of Euclid. It is only from the 18th century onward that book illustrations can be regardedmore or lessas geometrically correct projections.10,12
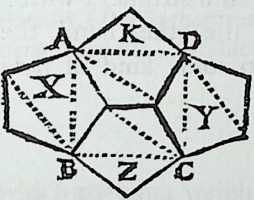
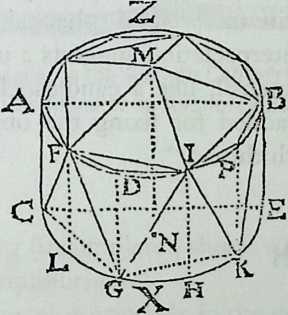
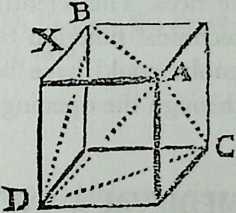
Figure 1.5 Polyhedra illustrations, showing poor standard of representation in 18th-century mathematical handbooks. (Source: B. Lamy, Les Elemens de Geometrie ou de la Mesure de Ietendue; qui comprennent les elemens dEuclide;…, Paris, 1731.)
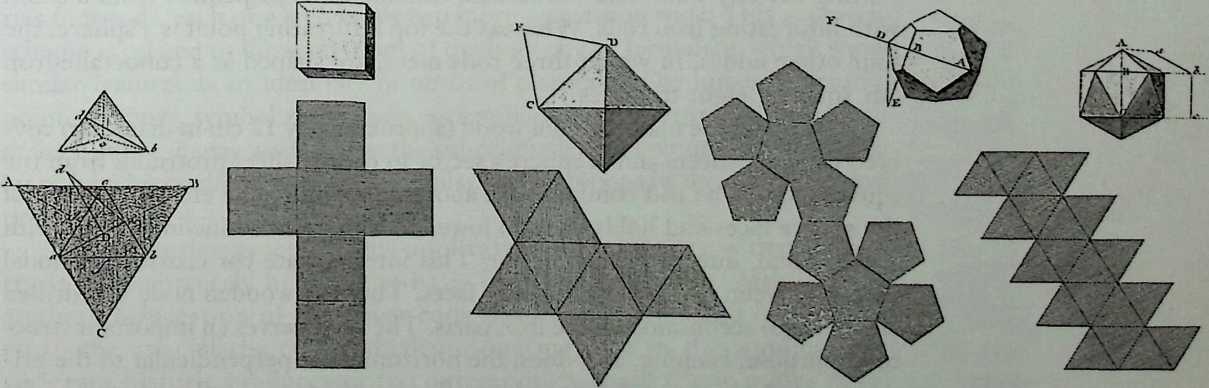
Figure 1.6 Polyhedra illustrations in a leading architectural handbook of the early 19th century. (Source: J. Rondelet, Traite theorique etpratique de Iartde batir, Paris, 1812.)
Furthermore, note that it is in 320 A.D. that Pappus published the 13 semi-regular polyhedra described by the great physicist Archimedes (ca. 287 B.C.).6-7
¶ ANCIENT POLYHEDRAL MODELS
Let us return to the interesting question of polyhedra as three-dimensional objects. Referring to their autonomous beauty, Plato himself speaks in Phile-bos of the making of such objects “with a plane iron” and with the help of “guideline and triangle.”13
In a recent contribution Malkevitch states that polyhedral objects were being made in late Roman times. He mentions icosahedra of steatite and faience with Greek letters incised on their faces.
Quite significant is a bronze dodecahedron found in Carmarthen, Wales (Society of Antiquaries of London). It is a hollow dodecahedron with 12 circular openings in the faces. The circular openings are of six different sizes and paired together on opposite faces. Solid spherical knobs are added on the 20 vertices. The scientific interpretation suggests a use as an instrument with a technical function or a utensil, like a candlestick. On the other hand, the knobs could have been added for fixing the object to some land of pole through the openings with thread.14
¶ MEDIEVAL APPROACH
Mature ingenuity is shown in the semi-regular polyhedra in the Barbarossa Chandelier in the Aachen Cathedral (ca. 1270). The Barbarossa Chandelier is one of the few remaining of this type in Germany, others being in Hildesheim and Gross-Comburg. These chandeliers symbolize the city of Jerusalem. Individual miniature towers are attached on a metal ring representing the city wall. The Barbarossa Chandelier is suspended from a chain with bifurcating iron rods. Whereas the top bifurcating point is a sphere, the four other nodes, in which three rods meet, are shaped as a cuboctahedron (six squares, eight triangles).
The nodes are made of solid wood (approximately 12 cm in diameter) covered by silver sheets and a sphere’s sector in copper sheet protrudes from the square faces. The rod coming from above enters the node element in one of the square faces and holds the two lower rods in a shared inclined plane with a horizontal, intermediate iron bar. This intermediate bar crosses the nodal object between two opposite square faces. Thus the wooden node was drilled crosswise to accommodate the iron parts. The node serves an important structural purpose, keeping, as it does, the horizontal bar perpendicular to the primary rod. As both secondary rods are fixed to the horizontal part with eyelet hinges, the structural solution for the chandelier and the even heavier chain,
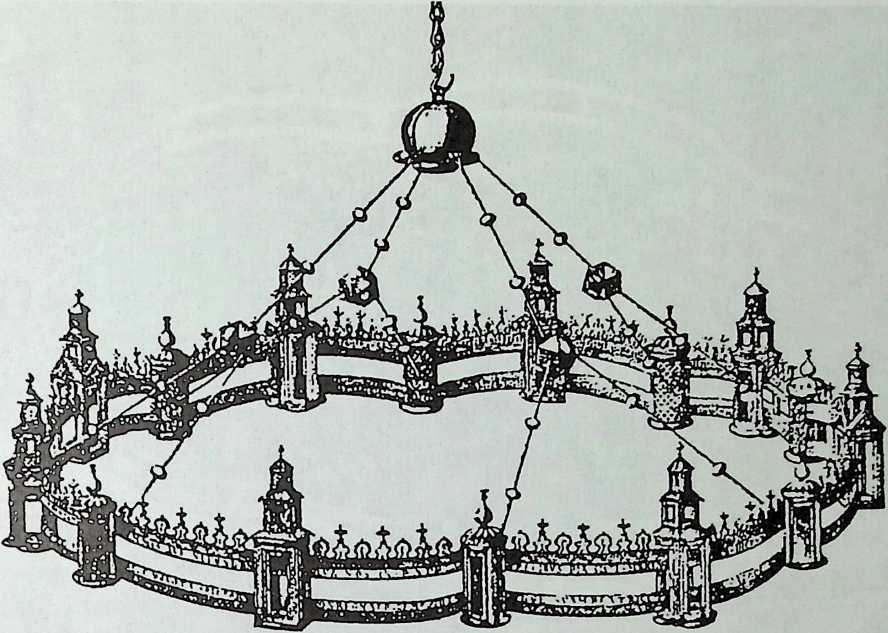
Figure 1.7 The Barbarossa Chandelier in the Aachen Cathedral (1170). (Source: Die Kunst-denkmaler dec Stadt Aachen, I. Das Munster zu Aachen, Dusseldorf, 1916.)
which together weigh 640 kg (incomplete), shows a maximum degree of freedom within a symmetrical equilibrium.15
Polygonal geometry is a major principle in the design, not only as applied to the node element but also in relation to the whole chandelier and even its position in the centralized space of the Aachen Cathedral, called the Octagon. The chandelier’s ring is divided into eight segments and carries eight three-story towers, alternating with smaller towers. Forty-eight lamps are regularly spaced around the wall. The bifurcation occurs in two stages: The chain carries four rods, each of which holds two more suspension rods. This geometric scheme is related to the symbolism of the holy city of Jerusalem, which shows similar features as an ideal city in terms of planning. The upper bifurcation point, a sphere, symbolizes the sun, as can be seen from texts on these chandeliers, and one may assume that the other smaller spheres and the semi-regular polyhedra could be interpreted as planets and moons in their ordered position in space.15,16
The inventive aspect of this application of polyhedra is that geometry is used correctly here as the basis for a spatial design. Although the angle of bifurcation of the lower rods was a free choice and is not related to the axes of the cuboctahedron, one may see in this application a very rare historic predecessor to contemporary space frame nodes developed from polyhedra.
Figure 1.8 The structural parts of the Barbarossa Chandelier in the Aachen Cathedral (1170). (Source: Aachener Dom, Domkapitel. Photo: Herta Lepie, Aachen.)
Figure 1.9 Semiregular shaped knot (snub cube) of the suspension of the Barbarossa Chandelier in the Aachen Cathedral (1170). (Source: Aachener Dom, Domkapitel. Photo: Herta Lepie, Aachen.)
¶ CONTRIBUTIONS FROM THE ARABIC WORLD
Other medieval examples of polyhedral objects are rare and there seems to have been little theoretical development during this period. This may be because Greek mathematical sources were only fragmentarily known in Europe and there was only limited communication with the Arabic world and its fruitful scientific use of Greek sources.9,17
Although Arabic knowledge of polygons and their use in design, for instance, in tile mosaics, was brilliant and common, no evidence could be obtained that the Arabs took the logical next step to polyhedra-based applications in three-dimensional space. However, Critchlow refers to Arabic cosmological speculationssimilar to Kepler’sbased on ancient polyhedra symbolism.18
Of decisive importance for the understanding of three-dimensional space will be the understanding of the way in which the eye receives a certain image. On the basis of Euclid’s book on optics, Arabic authors such as al-Kindi (who died in 873) and Abu Ali al-Hasan (965), known as Alhazen, contributed to the scientific understanding of basic notions like the cone of vision, the working of the pupil of the eye as a lens, and the necessity of light for visibility of any object. These Arabic books were translated for use and interpretation throughout Europe. Subsequently, Arabic knowledge on optics added to the understanding of the physical part of perspective projection in Italy, outside the tradition of its authors. Richter defends the hypothesis that a model by Alhazen showing the working of the eye was based on the torus shape consisting of polygons, which will be discussed in more detail in the following section.”
¶ PAOLO UCCELLO (ca. 1397) AND THE “MAZZOCCHIO”
As Gothic gave way to the Renaissance, a Florentine painter named Uccello became interested in the main problem of early Renaissance painting: perspective. Vasari describes Uccello as an artist who should have given less time to geometry and more to painting.19 Uccello’s fascination with perspective and geometry led him to concentrate on details. Overall, his paintings show a complex composition with several different perspective vanishing points.20
Drawings from his hand show objects, often of circular shape, reduced to quasi-polyhedral forms. His favorite is the torus shape, not as a pure abstract form but depicted in some paintings as the cylindrical hat worn by the men of his time, the so-called “mazzocchio.” Preparatory drawings of such faceted rings measure up to 20 cm and are extremely precise perspec-tival projections in ink. The rings, sometimes enriched by pyramidal forms, are divided into 16 or 32 sectors and each ring’s cross section consists of a regular hexagon or octagon. Because all points of the ring are shown in most of these drawings, the ring appears transparent, much like today’s CAD line
Figure 1.10 Perspective ink drawing of a faceted ring, seen from below, attributed to Paolo Uccello (1397). (Source: F. Borsi and S. Borsi, Paolo Uccello, Florenz zwischen Gotik und Renaissance, Belser Verlag, Stuttgart, Zurich, 1993.)
drawings. The reason for the consistent use of this drawing method may be to show up any mistake in the perspective projection of the ring through a disturbance in the continuity of the lines. Afterwards these drawings could be copied with all hidden lines eliminated. The drawings are in one-point perspective and they have an axis of symmetry common to two of the sector borders. In his painting Bernardino della Ciardi Pushed out of His Saddle (part 2 of The Battle of Sail Romano), four men with such hats are depicted from various points of view. In order to emphasize the geometric structure, the hats’ facets are colored like chessboards.20
Figure 1.11 Drawing of a 72-faceted irregular polyhedron with pyramid points attributed to Paolo Uccello (ca. 1440). (Source: F. Borsi and S. Borsi, Paolo Uccello, Florenzzwischen Gotik und Renaissance, Belser Verlag, Stuttgart, Zurich, 1993.)
The epitome of these studies is a drawing of a vase with 32 sectors and some 64 nodal points in its section. Another very interesting drawingsimilar to some of the other drawings not positively identified as Uccello’s but executed according to his drawing methodis a “sphere with diamond pyramids.”13,20,21 The sphere turns out to be a 72-faceted irregular polyhedron. Another depiction of a polyhedrona stellated dodecahedron surrounded by a polyhedral ring is attributed to Uccello. It is a colorful floor mosaic in the basilica of San Marco in Venice dating from 1429.22
¶ PDERO DELLA FRANCESCA (ca. 1420) AND HIS PERSPECTIVE LESSONS
Unlike Uccellowho often placed the boldly drawn volumes of his figures in dark and somewhat ill-defined settings in his paintingsPiero della Francesca, one of the major Renaissance painters, achieved an impression of perfect harmony by using lighter colors and placing his figures in clearly defined architectural settings masterfully rendered in central perspective.23
In his old age when almost blind, he produced a work on perspective De Prospectiva Pingendi, dictating the text to a pupil, who also executed the drawings. Being a major source of publications by Albrecht Durer and Luca Pacioli and of La Pratica della Perspettiva (1569) by Daniele Barbaro, this work was highly influential. It was through it and the others that many artists and architects learned about perspective and geometry.13,24
Piero della Francesca’s didactic approach is characterized by great care in the choice, composition, and manner of execution of the illustrations. In the Codex Palatin manuscript, in order to make the procedures as clear as possible, the construction fines are drawn in red and the finished perspectives of the objects in black. The geometric construction of the mazzocchio torus form (here called “torculo”) is explained as well as that of a polyhedral cupola similar to Uccello’s 72-faceted polyhedron. However, the text is very dry and tedious, consisting of page-long listings of the points to be connected as the construction proceeds.25
¶ LUCA PACIOLI (ca. 1445) AND THE MODEL APPROACH
The theology professor Luca Pacioli from Borgo San Sepolcro (hence who was also known as Fra Luca di Borgo) was involved in a research project for the Duke of Urbino, Guido Ubaldo, and Bishop Valletari, seeking to define correctly the mathematical shapes of polyhedra, which were thought to have high symbolic significance. His scientific publications included the first Italian translation of Euclid’s Elements.13,24
A new departure in the search for representation is the devising of different kinds of models of polyhedra. Pacioli’s method of working essentially develops new forms by truncation (cuboctahedron) or addition (stellated poly-hedra). His presentation of results is unique for his time. One can distinguish no fewer than four levels of presentation in his book De Divina Proportione (1497), which was highly influenced by Piero della Francesca. First, there is the text, a mixture of dry descriptions of mathematical relationships and witty accounts of architectural praxis. In this text a treatise on the golden section is followed by a discussion of polyhedra and their variants. Second, the text contains figures, which are simple line drawings of the schematic Euclidean type, without proper perspective or perpendicular projection when they show three-dimensional forms. Third, there are correct perspective drawings of the more complex stellated polyhedra, drawn on Pacioli’s request by Leonardo da Vinci, one of his many artist friends.21 These drawings were based on the fourth level of Pacioli’s presentation, the three-dimensional models of polyhedra. Even a fifth level of presentation is allowed for by leaving ample white space around the printed parts on the pages, to enable the reader to add his or her own sketches or notes.8
In his book Pacioli refers to the usefulness of perspective drawings and he especially recommends that the reader should visit the models in a sort of exhibition room or laboratory.
He describes the modelswhich were lattice structuresas being suspended and in his perspective drawings Leonardo took care to show how they were suspended with thin threads. The fact that the models were suspended may have practical reasons. As we know from experience, lattice models are rather vulnerable to deformation. By suspending them, one ensures that only their own weight is loading the structure. Even when somebody touches one, it will simply swing until balance is recovered again.
Other information provided by Pacioli in Chapter LXX of De Divina Pro-portione is that the Latin names of the polyhedra were written on paper labels attached to the suspension threads of the models with two pegs (of amber, which is extremely fight). He humbly excuses himself for the poor material he had to use for his models, owing to a lack of funds, and he remarks that the noble theme of polyhedra deserves to be proclaimed in precious metals decorated with precious stones.8
The monk Pacioli’s interest in polyhedra is further documented in a double portrait painting by Jacopo de’ Barbari (1495), showing him with a young nobleman in the role of a pupil.13,24,26 A solid wooden dodecahedron is shown on a desk with other objects relevant to geometry and drawing. Of particular interest is the model of a semi-regular polyhedrona rhombicuboctahedron, as Kepler named this shape, made of 18 squares and 8 triangles. This polyhedron of glass polygons, probably blown in one piece, is half filled with water. A thread crossing the glass bowl in its center is fixed to its bottom and suspends it in an unstable equilibrium from the ceiling. It should be remarked, however, that, in an otherwise perfect painting, the polyhedron shape is flawed with a small perspective mistake: The water level is not parallel with the top and bottom triangles.
This water-filled glass polyhedron can be interpreted as a measuring device, making use of physical laws. Because the suspension is vertical and the water level horizontal, any horizontal section of the polyhedron can be generated by varying the amount of water and the result can be compared with drawings. This polyhedron and its geometric constructionwithout referring to the model is explained in De Divina Proportione, Chapter LIU. Another example of Pacioli’s concern for the physical aspects of his models is that he mentions the possibility of enlarging the form by adding triangular or square pyramids, leading to stellated shapes that will always stand on the tops of three pyramids “as one can verify by observation on the materialized shape.”
The 72-faceted polyhedral sphere, already mentioned in the discussion of Uccello’s work, is presented in Chapter LIV Pacioli points out that domes like that of the Pantheon in Rome with its faceted coffers may be regarded as being derived from a similar geometric approach.
Pacioli’s aim in his concise presentation of stereometry was to advocate the training of good craftsmen and he indicates this by warning anecdotes. In Chapter LVII he recounts that he, together with a painter, once convinced a client to build a pillar capital in a polyhedral form for its aesthetic impact. The master builderthinking it would be an easy jobfollowed the proposal, but in twenty days of work many marble blocks were spoiled and compensation had to be paid. This awkward situation was only resolved when Pacioli offered to teach the workers about polyhedra. A modest type of polyhedra-based decoration by Pacioli is diamond-faceted masonry, probably developed from a dodecahedron.24
In a rather mean waytypical of the feeling of superiority of the academic toward the common workerPacioli proposes in Chapter LVH to expose the ignorance of stonemasons by asking them to make a regular shaped block with 12 regular polygons, but using no pentagons.
In Chapter XVIII of his book De Architectlira (1509), Pacioli again encourages architects to build pillar bases and capitals according to polyhedral forms. He mentions Roman literary references to the famous sculptor Phidias from Cercio, who executed a part of a work in icosahedron shape (the symbol of water). This icosahedron attracted the speculative attention of philosophers, more than any other part of his outstanding work.8
Yet only few architects of his time followed Pacioli’s optimistic vision of polyhedra. Vasari reports about Michelangelo (1475) that he “had the goldsmith Piloto make a ball of seventy-two facets” as a decorative finial for the cupola of San Lorenzo.19 An illustration of the ball consisting of irregular triangle planes is shown in Mainstone’s book.27
¶ LEONARDO DAVINCI (1452) AND THE LATTICE STRUCTURE
Leonardo da Vinci’s illustrations for Pacioli’s De Divina Proportione were probably the first to show polyhedra as lattice structures.21,28 Drawing the edges of a polyhedron with more than one line allows the artist to show which edges are in front and which are behind, which is a great help in visualizing structures in space.
Leonardo’s skill as a draftsman shines especially in his drawings of machines and complex building designs and there is clearly a connection between his illustrations for Pacioli of latticed polyhedra and his linear stereometric images of architectural structures.29 Compare his drawings from the Codex Atlanticus: f. 190 r-a, f.3 v-b, and £.335 v-e.
¶ ALBRECHT DURER (1471) AND THE CLEARING OF POLYHEDRAL IMAGES
Diirer’s interest in polyhedra is well known from his copperplate engraving Melancholia of 1514. In Melancholia an angel contemplates an oversized truncated stone block in a puzzling setting referring to building praxis, eternal time, and religion.
Being influenced by humanist philosophy and Renaissance universalism, Diirer was fond of any geometric problem relating to art. Around 1506 he visited Italy for the second time and he himself tells of a master in Bologna who taught him the “secret perspective.” This master is thought to have belonged to the circle around Pacioli. In Venice Diirer bought a Latin copy of Euclid’s Elements in order to understand the theoretical background of his newly acquired knowledge.13,24,\ 30,31
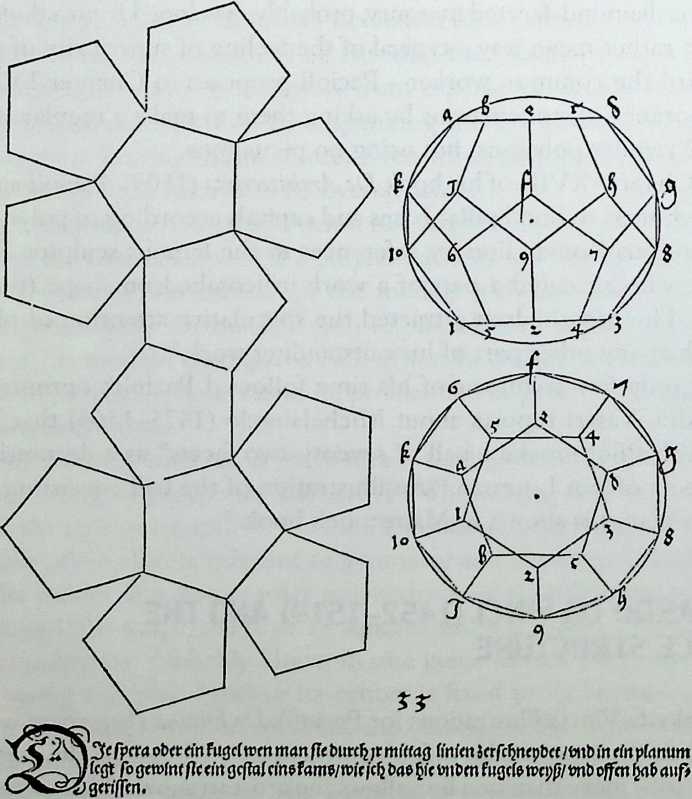
Figure 1.12 Albrecht Diirer: projective image of a dodecahedron and a cutout plan for a paper model, as depicted in Underweysung der Messung (1525), fourth book, Fig. 33. (Source: A. Diirer, Unterweisung der Messung, Verlag Dr. Alfons Uhl, Nordlingen,1983.)
In the fourth book of his Underweysung derMessung (1525), polyhedra are illustrated in a new way. Here, Durer, probably the most able woodblock cutter of all time, developed a layout of beautifully worked out lettering with ample space for the illustrations. As in other figures, polyhedra are shown by line drawing of plan and section, representing the body, as it were, transparent. Letters facilitate the understanding of the drawings. Other figures show chains of polygon plans, which can be cut out to make paper models.32
Diirer’s clear-looking images of polyhedra nevertheless often contain mistakes, showing that he was not quite aware of the mathematical rigor of geometry. For example, he draws the circumscribing circle of the polyhedral body as if the two-dimensional projection in plan or section would touch it in all its vertices. Being an artist teacher, his major aim may have been to give a clear, methodical description rather than to show exact geometry. Similar criticism may be made of his description of the conical section, the ellipse, to which he gives the name “eyerlini” (egg line) because of the asymmetrical result in his drawn construction. Later Kepler will point out that Diirer’s “egg line” should be interpreted as a bisymmetrical form when speaking about the ellipse.24,\ 33,\ 34
Figure 1.13 Nicolas
Neufchatel: Portrait of the Calligrapher and Mathematician Johann I Neudorfer and His Son (1561), both studying a lattice model of a dodecahedron. (Source: German-isches Nationalmuseum, Niirnberg.)
Yet Durer’s method of drawing polyhedra and conical sections was far more accurate than the illustrations in early manuscripts or editions of Euclid’s Elements, which often seem to be mere diagrammatic adjuncts to the mathematical text.
¶ JOHANN NEUDORFER (1497) AND THE DDDACTBC MODEL
The founder of German calligraphy and a teacher of calligraphy as well as calculation was Johann Neudorfer (1497) from Nurnberg. He executed the text for Durer’s print series Apostles. A painting (Germanisches Nationalmuseum Nurnberg) by Nicolas Neufchatel (1561) shows Neudorfer as a mathematician, measuring with compasses a dodecahedral lattice model of approximately 20 cm diameter, while Neudorfer’s son writes down the results. A cube model is seen hanging on the wall.
The dodecahedron in the painting shows a profile in L-shape for the bars?1 This may, on the one hand, save some weight in comparison with a simple trapezoidal profile. On the other hand, it makes it easier to close the faces with pentagon-shaped boards for demonstration purposes.
¶ WENZEL JAMNITZER (ca. 1508) AND RENAISSANCE AESTHETICS
Durer’s hometown of Nurnberg offered the best quality in book production and art printing. Nobody was more fond of generating new polyhedral configurations than Wenzel Jamnitzer, a gold-and silversmith and instrument maker, who was also from Nurnberg.
His perfectly produced book Perspectiva Corporum Regularium (1557) shows a large quantity of variations, generated from the five regular polyhedra. Beautifully adorned images of the Platonic symbols (fire, air, water, earth, universe) with short texts introduce four pages with six polyhedral variants for each polyhedron. Each of them is represented inside a hollow half-sphere.13 The second part of the book shows polyhedral “fantasies” in architectonic arrangements: for example, a monumental grave, diamond-like faceted cones, and a latticed dodecahedron on a richly worked base.
In Jamnitzer we recognize an artist with a systematic approach to geometry but ignorant of scientific language. Jost Amman, a copperplate engraver, executed Jamnitzer’s designs with precision.35 Jamnitzer’s method of inventing and drawing complex polyhedra is known, although he did not describe it himself. Using simplified models of polyhedra, he drew a correct image based on the empirical perspective method described by Diirer. On the basis of these drawings, he could generate variations by connecting different nodes or surfaces.
Portraits show Jamnitzer as an elderly looking, rather heavyset man with
Figure 1.14 Wentzel Jamnitzer: allegory on “Water,” Plato s symbol of the icosahedron, from his Perspective Corporum Regularium (1568). (Source: Germanisches Nationalmuseum, Niirnberg.)
Figure 1.15 Wentzel Jamnitzer: dodecahedron variants (1568). (Source: Germanisches Nationalmuseum, Niirn-berg.)
Figure 1.16 Jost Amman: engraving print of Wentzel Jamnitzer working on his installation to analyze perspective (ca. 1568). (Source: Germanisches Nationalmuseum, Niirn-berg.)
a long beard. It is amazing that a person with such a physiognomy could like some brilliant pianists with short thick fingersproduce the most delicate work of such natural beauty. Of his silverwork it was said that he could make trees with miniature leaves that were of such fine workmanship that they would move when one blew on them.
Jamnitzer’s instruments were also inventive and precise. The portrait by Jost Amman in a copperplate print (ca. 1568) shows Jamnitzer with his perspective apparatus. From a given viewpointthe top of a pole on the righta thread is stretched to the object to be drawn and is held by a vertical stick with a foot plate on the other side. The thread is kept under tension by a free-hanging weight inside the pole. (Another possible interpretation is that the weight hangs in front of the pole but is not shown in the print.) A second vertical stick, with a small console that can move vertically, is attached on a rail. The console’s end, fixed by a vertical stick and horizontal rail, gives the coordinates of one of the points on the projection surface of the drawing. By changing the direction of the thread toward other marked points of the object, all necessary points of the drawing can be determined and measured. A special aid was a plate with the drawing pinned on it, which is fixed with a horizontal hinge parallel to the rail on the table. If one turns the drawing into a vertical position, the console could make a small hole to mark the corresponding point on the paper. To permit turning the paper vertically, the thread and its lower fixture would have to be turned away temporarily.36
The polyhedral construction in the niche shows a model that Jamnitzer might have used to draw his polyhedra variants. The model, of rather modest appearance, is of some mathematical interest as showing the cube in three different positions of balancestable on a face and unstable on an edge and a vertex.
As an instrument maker, Jamnitzer would have been accustomed to improving an existing apparatus and his perspective instrument should be regarded as a product of his cooperation with other perspective researchers in the Niimberg circle, such as Hans Lencker, Lorenz Stoer, and Hans Hayden. This development of perspective instruments was known and illustrated by Paulus Pfinzing in Ein schoner kurtzer Extract der Geometric und Perspectiva (1598, privately printed with handdrawings) and later published with woodcut illustrations as Optica (1616).13,36
Both the goldsmith Jamnitzer with his work in gold and silver and the engraver Jost Amman were famous artists who worked for the imperial family. One wonders why such an odd book project on abstract polyhedral shapes was established. The engravings by Jost Amman mostly depict historic events and people against a background of architecture or landscape with decorative embellishments.
Apart from the preparatory drawings for the book illustrations, Jamnitzer’s remaining working drawings only once (in the Berlin Sketchbook, page 21) show a sketchy representation of some polyhedra.36 The isolated position of his polyhedra studies in relation to his usual themes leads one to interpret Jamnitzer’s purpose as the creation of a training method for drawing three-
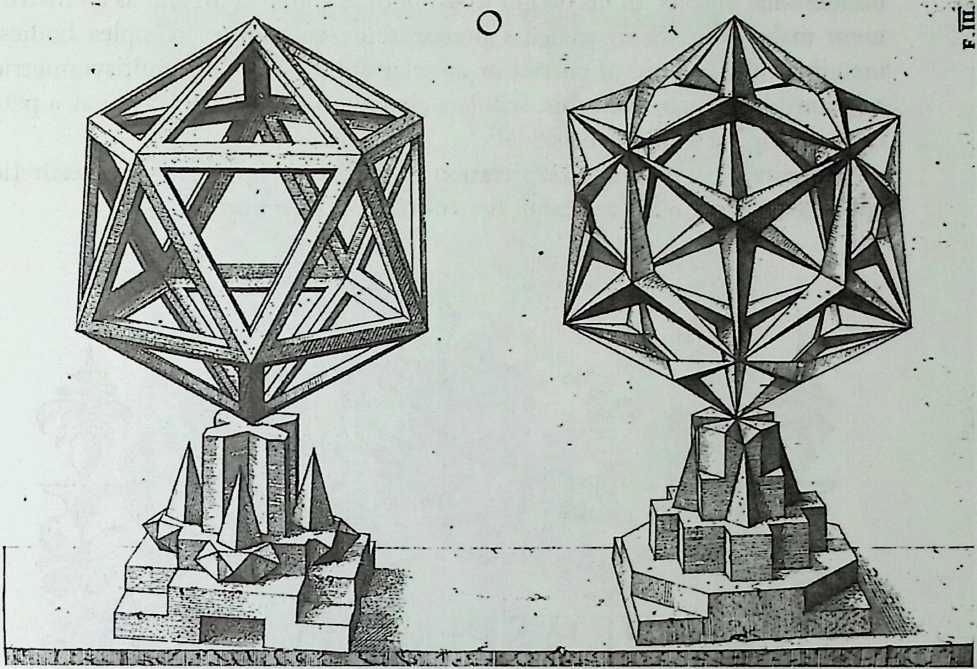
Figure 1.17 Wentzel Jamnitzer: polyhedral fantasy (1568). (Source: Germanisches Nationalmuseum, Niirnberg.)
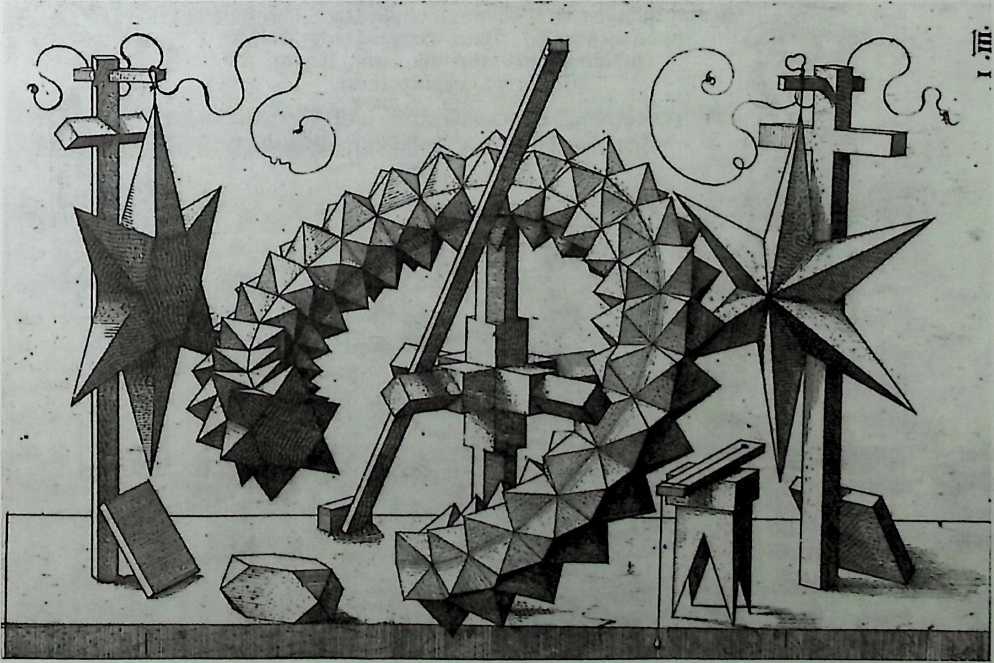
Figure 1.18 Wentzel Jamnitzer: monumental grave as a polyhedral fantasy (1568). (Source: Germanisches Nationalmuseum, Niirnberg.)
dimensional objects. In his design work, both as a goldsmith and as an instrument maker, Jamnitzer needed a precise representation of complex bodies, including any volume of curved or angular appearance and multisymmetric relationships. Apart from this, scholars characterized the book type as a pattern catalog for use by artists.13,37,38
Jamnitzer’s symbolic interpretation is the best example of the aesthetic approach to polyhedra typical of the 16th and 17th centuries.
&efc$2te&en/ mitepempclnavffnct fcnban
tag gegeben tvirb/ei n newer befonber turner/ bodj gcrecfjter onnb
feln leicfcter weg/roie allerlep bing/ea ffren (£oxpoxa/©ebe ro/ober
wa$ mdglidj juerbemfenvnbingrunbju(egeni(i/venucftober
enuerruef t/ferner in bit Pcrfpcetpf gebxacfjt werben mag/ on eini«
ge sergeblice linie/rip vff puneten/xcbergleicften weg biffitio noefc
nit betant gewcfen/ ©urefj fianfen_£encferQ3urger
ju$?iirmberg/allenfieb(jabern guter tflnflen
Ju e(nen vnb ge fallen publieirt.
Figure 1.19 Hans Lencker: front page of his Perspec-tiva (1621), depicting technical applications of polyhedral forms like sundial, balance, wheel axis, and chain. (Source: Germanisches Nationalmuseum, Niirnberg.)
WWW \\\\
[Srwj]
PERSPECTIVA
ttK5m.2ey.C50ay.freibeit/ auff feebsfar.
©ebxutft ju Shlrmberg/ burdj Sictricfe ©crlafc.
M. D. LXXI.
Figure 1.20 Lorenz Stoer: polyhedral fantasy from his Geometria et Perspectiva (1567).
(Source: Germanisches Nationalmuseum, Nurnberg.)
¶ JOHANNES KEPLER (1571) AND POLYHEDRAL NOMENCLATURE VERSUS COSMOLOGY
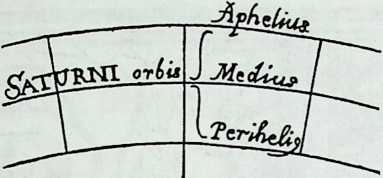
One of the sadder chapters in the history of science is the retrograde emphasis on polyhedra in Kepler’s cosmology. As a physicist of Newtonian stature, he made a major contribution to astronomy by showing that the orbits of the planets were ellipses having the sun as one focus. However, his pursuit of the idea that the distances of the planets from the sun were proportionate to the dimensions of the five regular polyhedra nested inside one another was, in retrospect at least, a stultifying mistake. Even when empirical observations did not seem to fit this idea, he defended it with great logical ingenuity, seeing no inconsistency between doing this and indulging in furious polemics against those astrologists who saw metaphysical meaning in certain number combinations.39
However, as a positive result of his otherwise fruitless battle, Kepler contributed to the best known astronomical tabellarium of the day, that of Tycho Brahe (1546), and in his book Hormonices Mundi (1619) he discussed new concave polyhedral solutions and developed a systematic Latin nomenclature, which is still in use today.39
BUS
Figure 1.21 Johannes Kepler: representation in Harmonices Mundi (1619) of Keplers speculative theory that the planets have the same distances as regular polyhedra, which fit exactly to each other. (Source: J. Kepler, Die Weltharmonik, R. Oldenbourgh Verlag, Munich, 1990.)
LORENZ ZICK (1594) AND POLYHEDRAL SCULPTURE AND TOYS
In the early 17th century, the mathematical story of polyhedra and the precise depiction of their shapes reached maturity. Craftsmen (fine wood turners), silversmiths, and ivory workers found an interest in the possibilities they offered. The increasing complexity of geometry in Renaissance and early baroque art and a general fascination with machinery contributed to this interest.4244 In some European courts turning craft had become part of the modern teaching
system and some noblemenlike August of Saxony (reign 1553) were taught in the preparation of ivory objects on turning machines.
In Historische Nachricht von den Niirnbergischen Mathematicis und Kiinstlem (1730), Doppelmayr published some sculptures by Lorenz Zick. The central part of one sculpture is a body with some concentric parts inside, which can all turn separately. Twelve circular openings are regularly located on the sphere’s surface. Hence one could describe this form as dodecahedral. Doppelmayr refers to the making “of all kind of polygonal bodies, which are much alike the dodecahedron and which have inside them 8, 10, 12, 16 identical bodies…and which later often were copied.”45
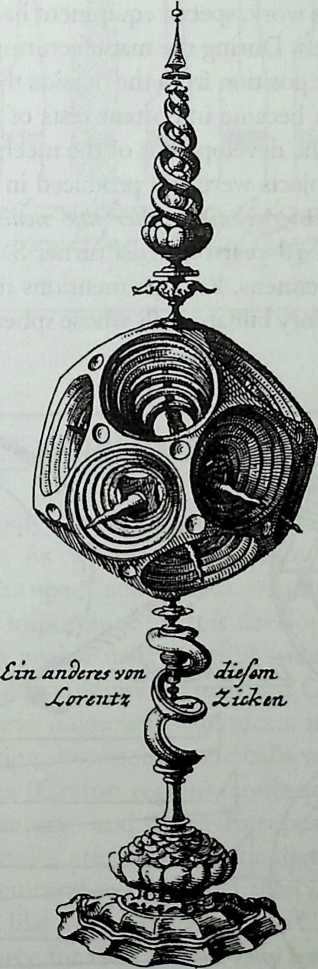
Figure 1.22 Lorenz Zick (1594): dodecahedron-based concentric ivory showpiece with stellated nucleus as published by J. G. Doppelmayr, Historische Nachricht von den Niirnbergischen Mathematicis und Kiinstlern,… , Niirnberg, 1730, Tab. 5 (Source: Wurttem-bergische Landesbibliothek, Stuttgart. Photo: Joachim Siener.)
In spite of Doppelmayr’s statement, which suggests that these polyhedral ivories were invented in Niirnberg, such ivory polyhedra were already being made in Dresden around 1581 by the court turner Georg Wecker, who came from Munich. Other important artists were Giovanni Ambrogio Maggiore from Milan and Egidius Lobenigk, probably from Cologne. Beautiful specimens were produced in Dresden until 1620, many of which were recently restored and can be seen in the famous Grime Gewolbe museum in Dresden. A certain contribution to the unique quality of the Dresden samples may be attributed to Niirnberg artists such as Christof Koller, who was charged in 1559 with the installation of the first turning workshop in the Dresden court, and Hans Lencker, who from 1576 onward gave lessons in perspective related to the problem of turning ivory.44
To complete such fine work, special equipment had to be developed, including spherical curved chisels. During the manufacturing process, the spheres had to be fixed in a concentric position from the outside through the openings. Such applications of polyhedra became important tests of mastery in fine carpentry and thus contributed to the development of the mechanics of precision.43
Similar polyhedral objects were still produced in the 20th century and the book Drechslerkunst Meistertechniken alter zmd neuer Zeit by Hugo Knoppe (1929) is dedicated to the 70-year-old artist turner Saueracker from Niirnberg, who made many fine specimens. Knoppe mentions that the polyhedral objects were derived from used ivory billiard balls whose spherical shape was damaged.43
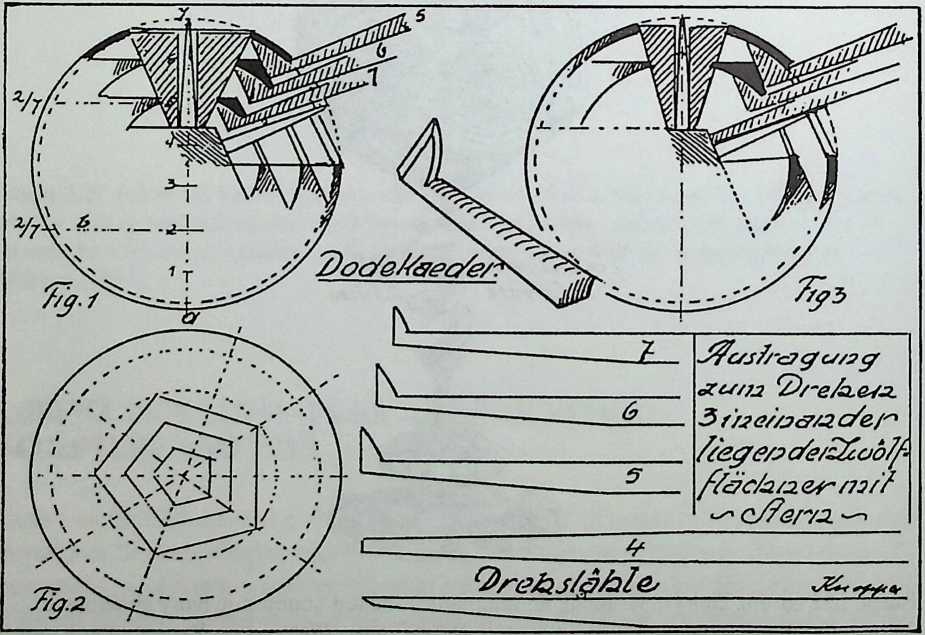
Figure 1.23 Hugo Knoppe: working drawing and special chisel equipment for concentric dodecahedra (1926). (Source: H. Knoppe, Meistertechniken derDrechslerkunst,\er\ag Th. Schafer, Hannover, 1986.)
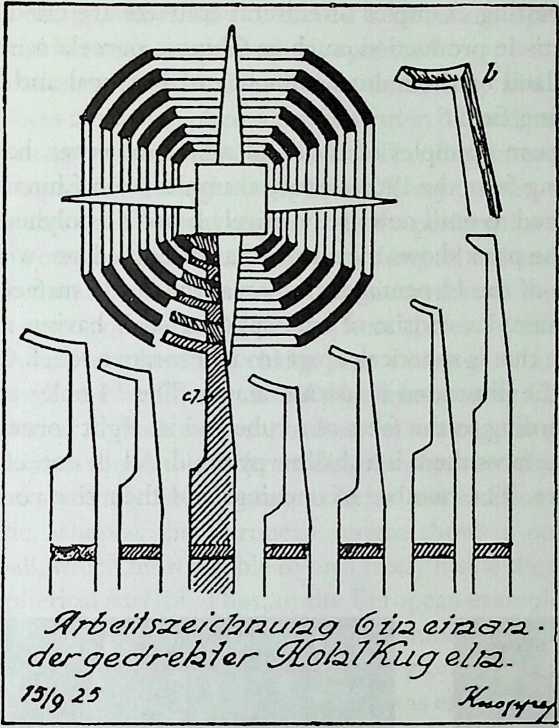Figure 1.24 Hugo Knoppe: working drawing and special chisel equipment for concentric spheres, similar to the Chinese examples (1926). (Source: H. Knoppe, Meistertechniken der Drechslerkunst, Verlag Th. Schafer, Hannover, 1986.)
¶ THE CHINESE “DEVIL’S WORK BALLS”
The ivory “devil’s work ball,” as the Chinese call it, is the most famous of all polyhedra-based objects. As we have seen, knowledge of polyhedra was acquired only slowly in Europe. Euclid’s Elements and the development of perspective were of decisive importance for this development. However, in nonEuropean cultures with a proper mathematical sciencefor instance, among the Arabs, the Mayas, and in cultures of India and Chinaperspective analysis of comparable rigor was unknown. Therefore, it seems important to ask how the tradition of carving these concentric balls was established in China.
In the south of China (Canton region), concentric ivory balls have been carved since the 14th century and direct European influence is unlikely.46 First, no European examples are known from that age, and, second, there seems to have been little cultural contact other than indirect trade at that time, apart from rare examples like Marco Polo’s visit to China in the late 13th century. The most likely source for the Chinese may have been their own earlier handicraft techniques for the carving and turning of precious stone (jade), wood, and ivory. Ivory has been carved since very early times, as it is a very fine-structured material and yet soft enough to be carved.
Another hypothesis is that the influence of China on the European examples resulted from colonial trade. Some literature suggests such influence and interesting examples of cultural contacts are cited after 1500 for comparable artistic production, such as Chinese porcelain imitated in Portugal and Holland or the mutual influence of Portugal and West Africa in the ivory-carving field.47
The European examples of Zick and others, however, have some major features differing from the 19th-century examples from China. The European examples referred to until now are positively based on polyhedra. The exterior surface of the parts shows the shape of a dodecahedron, with a hole in the middle of each of the 12 pentagons, whereas the inside surface is spherical.
Chinese examples consist of true spheres, each having an exterior and interior surface that is spherical, apart from decorative relief. Often they have 14 holes, like the illustrated modern example. The 14 holes are conceptually organized according to the faces of a cube and its eight corners, and on each of the cube’s six faces there is a shallow pyramid. All 14 corner points touch a common sphere. The number of openings and their size correspond to the
Figure 1.26 Ivory “devils work ball” with all holes in common axes (Hong Kong, contemporary). (Source: Institut fur leichte Flachentragwerke (IL), Stuttgart University. Photo: Gabriela Heim, Stuttgart.) specially shaped chisels, which have to carve a large enough spherical sector to loosen all material between two concentric spheres.43
Figure 1.25 Sphere-in-a-sphere object with eight independent turning concentric partsa “devils work ball,” as the Chinese call itmade out of one piece of ivory. The holes are divided like the 14 vertices of a semi-regular polyhedron (Hong Kong, contemporary). (Source: Institutfur leichte Flachentragwerke (IL), Stuttgart University. Photo: Gabriela Heim, Stuttgart.)
Some speculation on the function of such objects may also be appropriate. They are showpieces in the first place: a demonstration of handicraft virtuosity.42,46 However, one can also regard them as puzzles. Tiny fingers or thin sticks may turn the spheres separately through the openings. Every puzzle or play has a purpose, and in this case the first goal may be to find a position for all spheres with one opening on a common axis. One can reach this goal rather easily. The final goal would be to turn all spheres into such a position that all their openings are organized in the same position as the outer sphere’s holes. In this way the initial impression of a massive sphere will change into an image of a ball that seems transparent through its core. In the case of the contemporary Chinese example, the final goal is rather difficult to reach, because its semi-regular geometric organization with 14 holes shows two different distances between the holes.
The Chinese system is finer because interior and exterior surfaces are all really concentric, whereas the European system shows a polyhedral outer form for each ball, which must be able to turn freely inside the next larger ball with an inner spherical surface. Thus, in the European example, some material waste cannot be avoided. Consequently, the number of parts that can turn around differs: Modern examples of the Canton region reach up to 45 spheres. A sphere that consisted of 25 concentric pieces was exhibited at the Panama-Pacific World’s Fair in 1919.48
On the other hand, some European examples are spherical like the Chinese balls and we can find no topological differences between these and the Chinese specimens.43
¶ BROOK TAYLOR (1685) ON PERSPECTIVE PROJECTION OF POLYHEDRA
One of the few English contributors to the development of perspective geometry is Brook Taylor, a Cambridge Doctor of Law, who was also interested in polyhedra.
His Linear Perspective (1715) and Nero Principles of Linear Perspective (1719) take a more abstract approach than most books, which derive an object image by parallel projection from plan and front view. Taylor’s approach integrates images as perspective projections on a plane.49
In these rather short books Taylor prefers to take polyhedra as his examples for demonstrating perspective projection, probably because the distorted plans of a point-symmetrical polyhedron can be understood more easily than similar plans derived from a nonsymmmetrical object, such as an architrave piece resting in an inclined position on a stone block.
Although his geometrical work is considered difficult and his method painstaking, Taylor became quite famous. An illustration of polyhedra in an architectural setting in Thomas Malton’s A Compleat Treatise on Perspective (1779) reminds us of Taylor’s interest.49
¶ MAX BRUCKNER (1860) AND HIS PAPER MODEL COLLECTION
In the preface of his book Vielecke und VielflacheTheorie und Geschichte (1900), Max Bruckner explains that the interest of mathematicians in poly-hedra was diminishing because many known problems were solved by then, although a compendium such as his, bringing together a historic survey and an encyclopedic classification of polyhedral examples, still seemed worthwhile to him.5,14
A very interesting parallel to Pacioli is Bruckner’s care for visual presentation. By means of many conventional drawings and photographs of 146 paper models, which were made by Bruckner over the course of many years, a clear overview of the possible range of polyhedral forms is presented. The reader is kindly invited to study the actual models at Bruckner’s work place.5
¶ ALEXANDER GRAHAM BELL (1847) AND INVENTIVE USE OF TETRAHEDRA
Better known as the inventor of the telephone, Alexander Graham Bell was creative in quite a universal sense. An active participant in the expanding industry of the late 19th century, he had an unrestricted vision of the commercial potential of technical improvements of the production process. He apparently did not aim at solving some specific problem but followed the reverse procedure: He looked at a technical or mathematical principle and sought a useful application for it. The accretion of such simple elements as latticed tetrahedra led him to invent a major structural system: the space frame.
Around 1900 he applied this system to enormous kites: compositions of tetrahedra of approximately 20 cm on the side. The frames were partly covered with fabric. By means of his tests he articulated many properties of tetrahedral form, not only in structural, but also in technical terms.50
He recognized that the latticed tetrahedron, by virtue of its triangles, is stiff against deformation. Actually, it requires the minimal number of bars needed to generate a rigid frame. Because of this the structure’s weight is optimal, resulting in a lightness that is decisive for any flying object. Part of Bell’s research into kites is that their form should be variable in order to reach optimal flying behavior empirically. For this reason he prefabricated the basic elements. Like cubes, tetrahedra can be added in a closed packing, but Bell also understood the possibility of minimizing structural weight through the omission of tetrahedra at the center of the structure.
Building on the experience gained with his tetrahedral kites, Bell found other uses for space frames, including a complete architectural structure built in Canada in 1907: a watch tower 28 m high with a weight of only 5 tons. The edge length of the modular elements is approximately 160 cm. They were prefabricated as complete tetrahedral elements (six rods and four nodes) and were transported and stored on site as a compact pile of 10 elements. For this pur-
Figure 1.27 Paper models of polyhedra variants by Max Bruckner (1900). (Source: M. Bruckner, Vielecke und VielflacheTheorie und Geschichte, Leipzig, 1900.)
pose details had to be such that two or three nodes met in one point. Presumably, this problem was geometrically solved by reserving modular zones in the node area and specifying the exact node form for each position in the system. Even the conventional stairway was integrated into the tetrahedral logic by shaping it as a triangular prismatic frame in one of the legs.50
The tower was erected in only 10 days by unskilled laborers. In order to manage it with the least effort, two tower legs and the platform were assembled on the ground, using the third legby assembling it in sectionsas a jack for the whole structure. Dining the building process, in which the legs owing to their almost horizontal starting positionbehaved as beams, Bell installed an additional triangular frame as a prop in the middle of the tetrahedral configuration.
For static purposes the three continuous border rods of each tower leg were thicker than the normal rods.50 It is notable that, at the point where the legs met on the hexagonal platform, Bell used rods of normal section in the borders, surely because he expected weaker forces in the compact platform frame than in the three inclined legs. Thus a remarkably transparent tower was obtained.
¶ CONCLUSIONS
Polyhedraspatial bodies of perfect geometric shapehave fascinated human beings throughout history. Although their major laws were already recognized by the ancient Greeks, further progress turned out to be extremely difficult and only the best mathematicians, geometers, and artist-craftsmen preferably in collaborationachieved substantial advances in knowledge.
A typical phenomenon of polyhedra research became the “mixed visualization” of scientific results, combining the text with diagrams, drawings, and even models. Durer offered cutout plans for paper models, and Pacioli, Jam-nitzer, and Bruckner relied on spatial models as empiric proof and control of drawn speculations.
Research into polyhedra has also been historically interpreted as a dangerous field of study. Its hermetic nature expressed, for instance, by the multitude of symmetry axes in each regular polyhedron or the finite number of
Figure 1.28 Polyhedral chandelier piece, ground from a glass sphere (Belgium, 19th century). (Source: Institut fur leichte Flachentragwerke (IL), Stuttgart University. Photo: Gabriela Heim, Stuttgart.)
only five regular polyhedra, made the field a source of metaphysical speculation. In Jamnitzer, the artist, we find a positive result of this kind of metaphysics, rendered harmless through joyful humor and presented with considerable artistry. In Kepler’s fate we find a sadder outcome.
However, in most cases, history demonstrates the creative potential of consistent polyhedra research. A special result is their role in the development of turning wood and ivory. The mathematical understanding of “infinity” had its counterpart in the manufacturing of infinitely precise or infinitely small objects. Ivory sphere-in-the-sphere objects were made in both Chinese and European cultures. The beauty of thesevoid of any substantial usefulness made them an ideal subject for testing precision in handicraft.
Leonardo da Vinci invented lattice structures based on polyhedral forms. Their brief history ends around 1900 with the tetrahedron-based space frame of Alexander Graham Bell, which shows a concise understanding and an original use of polyhedra. Bell’s approach may be seen as the legacy of all those persons who, in the past, have been drawn affectionately toward polyhedra.
¶ METHODOLOGY
A remark on the methodology and the specific goal of this chapter may be appropriate. In February 1993, J. Francois Gabriel wrote to the Stuttgart Institut fiir leichte Flachentragwerke (IL), asking if somebody could work on the history of the science of polyhedra and their applications in architecture. The author accepted such a vast undertaking, encouraged by his experience with similar studies on the history of geometry (ruled surface structures by Suchov, Gaudf, and Candela and late-Gothic vault geometry). A basic research approach was discussed and it was agreed that the study would focus on the time before 1900, as there is little scientific research and documentation available from this time period. In order to find connections between the use of polyhedra in science and architecture, the author was forced to construct a hypothetical historic path, as only in a few cases are polyhedra instantly recognizable in old architecture. The main stress was given to the technical aspects of the visualization of polyhedra and of the making of polyhedral models, often related to the arts. Because of this technical viewpoint, however, decorative aspects from the international art-nouveau style (Berlage and Gaudi) were not relevant, as was the case with Haeckel’s interpretation of biological specimens (radiolaria) as polyhedral shapes.51
My research methodology had to focus on isolated historic examples that favored by luckcould be traced during continuous investigations in museums or literature. Thus the result is quite fragmentary. In some cases, like the early use of the cuboctahedron shape or the Chinese concentric ivories, the craftsmen may not even have known they were working with a polyhedron. To the author these examples still seem valuable because a polyhedron is not only qualified as some geometric shape or material object, as such, but also by the structure of its axes with its specific technical implications.
Because of this research approach, giving priority to the visual aspects of the polyhedron, the science of polyhedral geometry was not dealt with systematically. Although the author tried to establish a chronology of mathematical inventions, this goal could only be reached very superficially.
The illustrations were chosen with care but they serve different goals. Some were chosen because they show a plentitude of beauty and can be regarded as symbols of the equal emphasis on art and science. Others illustrate complex geometrical relationships, necessary because they are still ill documented. Finally, some illustrations are informative about the cultural setting of an artist or architect. The first results of my studies on polyhedra history were presented at the seminar Application of Structural Morphology to Architecture in Stuttgart.52
¶ ACKNOWLEDGMENTS
Many people were helpful in finding polyhedral examples and the material gathered substantially exceeds that presented here. I want to thank all the people and institutions that provided information, especially the editor Jean-Frangois Gabriel, who took the initiative for this historical survey. Next to him my referees Rowland J. Mainstone and Pieter Huybers took greatest care in strengthening the meaning and beauty of this chapter on such a demanding subject matter, for which I am grateful. Furthermore, I would like to thank Rainer Graefe, Jurgen Hennicke, Frieder Klenk, Werner Muller, Martin Trautz, and Ture Wester for supplying valuable information.
The city of Niirnbergwhich historically has played a prominent role in polyhedral research and related artopened its archives; special thanks goes to Dr. Slenczka, the library director, and Dr. Locher, the painting gallery director of the Germanisches Nationalmuseum. Similarly important was a visit to the Griine Gewdlbe museum of the Staatliche Kunstsammlungen, Dresden, where Christine Wendt kindly showed me recent restoration work by the Erbach ivory museum. Other material was found in the Landesmuse-um Baden-Wurttemberg and the Wurttembergische Landesbibliothek, both in Stuttgart. Much literature was checked in the library of the mathematical faculty (Air. Denninger) of Stuttgart University. Thanks also goes to Dr. Lepie, the director of the department of goldsmith art (Aachen Cathedral), who provided detailed information about her forthcoming restoration of the Barbarossa Chandelier in Aachen.
I would like to thank the following collaborators who were instrumental during the preparatory studies at the Institut fur leichte Flachentragwerke of Stuttgart University, which is directed by Prof. Werner Sobek: Elisabeth Trautz-Fiilop (archives), Gabriela Heim (photographs and reproduction), and Brigitte Trappe. The original English manuscript text was edited by Frieda Piersma-Spanjersberg.
¶ NOTES
-
J. M. Montesinos, Classical Tessellations and Three Manifolds, Heidelberg, 1987.
-
A. Fischer, Afrika im Schmuck, Cologne, 1991.
-
W. Menghin, Gotische und langobardische Funde aus Italien, Germanisches Nationalmuseum, Niirnberg, 1993.
-
R. Christlein, Die Alamannen: Archdologie eines lebendigen Volkes, Aalen, Stuttgart, 1991.
-
M. Bruckner, Vielecke und VielflacheTheorie und Geschichte, Leipzig, 1900.
-
D. J. Struik, Geschiedenis van de iviskunde, Amsterdam, 1980.
-
H. Gericke, Mathematik in antike und OrientMathematik im Abendland, Wiesbaden, 1993.
-
Fra L. Pacioli, Divina Proportione, Die Lehre vom Goldenen Schmitt, nach der venezianischen Ausgabe vomjahre 1509, C. Winterberg, ed., Vienna, 1889.
-
A. Sabra, “The Exact Sciences,” in The Genius of Arab CivilizationSource of Renaissance, Oxford, 1978.
-
B. Lamy, Les Elemens de Geometric ou de la Mesure de Petendtie; qui comprennent les elemens dEuclide;…, Paris, 1731.
-
M. Folkerts, E. Knobloch, and K. Reich, Mass, Zahl, und Gewicht, Mathematik als Schlussel zu Weltuerstandnis und Weltbeherrschung, Herzog August Bibliothek, Wolfenbiittel, 1989.
-
J. Rondelet, Traite theorique etpratique de Part de batir, Paris, 1812.
-
F. Richter, Die Asthetik geometrischer Kiirper in der Renaissance, Stuttgart, 1995.
-
J. Malkevitch, “Milestones in the History of Polyhedra,” in Shaping SpaceA Polyhedral Approach, M. Senechai and G. Fleck, eds., Boston, Basel, 1988, pp. 80.
-
H. Lepie, “Radleuchter mit 16 Tiirmen im Karlsdom,” in Kirch enzeitung fur das Bistum Aachen, Jan. 1992, pp. 24.
-
Die Kunstdenkmaler der Stadt Aachen, I. Das Munster zu Aachen, Dusseldorf, 1916, pp.138.
-
S. Hunke, Allahs Sonne uber dem Abendland: unser arabisches Erbe, Stuttgart, 1960.
-
K. Critchlow, Islamic Patterns, an Analytical and Cosmological Approach, London, 1976.
-
B. Burroughs, ed., Vasaris Lives of the Artists, New York, 1946.
-
F. Borsi and S. Borsi, Paolo Uccello, Florenz zwischen Gotik und Renaissance, Belser Verlag, Stuttgart, Zurich, 1993.
-
K. H. Veltman, Studies on Leonardo da Vinci, I, Linear Perspective and the Visual Dimensions of Science and Art, Munich, 1986.
-
J. Bohm and E. Quaisser, Schonheit und Harmonie geometrischer Former, Berlin, 1991.
-
A. Angelini, Piero della Francesca, Florence, 1985.
-
L. Olschki, Geschichte der neusprachlichen Literatur, ersterBand, Heidelberg, 1918.
-
Petrus Pictor Burgensis, De prospectiva pingendi, [Ozz the Perspective of Painting by Piero della Francesca from the codex of the royal library in Parma, translated into German by C. Winterberg], Strasbourg, 1899.
-
H. A. Millon, in The Renaissance from Brunelleschi to Michelangelo The Representation of Architecture, V Magnago Lampugnani, ed., Milan, 1994.
-
R. Mainstone, Develop?nents in Structural Form, Cambridge, MA, 1975.
-
M. Cianchi, Die Maschinen Leonardo da Vincis, Florence, 1984.
-
C. Pedretti, Leonardo Architect, London, 1986.
-
Albrecht Dilrer 1471, Germanisches Nationalmuseum, Niirnberg, Munich, 1971.
-
Albrecht Dilrer aux Pays-Bas, son voyage (1520), son influence, Palais des Beaux-Arts, Brussels, 1977.
-
A. Diirer, Unterweisung der Messung, Niirnberg, 1525; Verlag Dr. Alfonse Uhl, Nordlingen, 1983.
-
P. Jesberg, Vom Bauen zivischen Gesetz and Freiheit, Braunschweig, Wiesbaden,
1987.
-
J. Sellenriek, Zirkel und Lineal, Munich, 1987.
-
W. Jamnitzer, Perspectiva corporum regularium, A. Flocon (Preface), Niirnberg, 1568, Madrid, 1993.
-
P. May, “Die Kunstfertigkeit der Perspektive zu Niirnberg,” in Wenzel Jamnitzer und die Niirnberger Goldschmiedekunst 1500, Germanisches Nationalmuseum, Niirnberg, 1985, pp. 161.
-
W. Miiller, Kunstwerk, Kunstgeschichte und Computer, Munich, 1987.
-
O. PatzeXt,Faszination des Scheins, 500Jahre Geschichte der Perspektive, Berlin, 1991.
-
J. Kepler, Die Weltharmonik, translated into German and introduced by M. Caspar, Munich, 1990.
-
D. J. Struick, ed., The Principal Works of Simon Stevin, Volume II, Mathematics, Amsterdam, 1958.
-
P. Huybers, “De geometric van uniforme polyeders,” Technische Hogeschool Delft, Stevin Rapport 10, March 1976.
-
E. v. Phillippovich, Elfenbein, Munich, 1982.
-
H. Knoppe, Meistertechniken de?’ Drechslerkunst, Original title: DrechslerkunstMeistertechniken alter iind netier Zeit, Leipzig, 1926, Hannover, 1986.
-
WiedergeroonnenElfenbein Kunststucke aus Dresden Eine Sammlung des Griinen Gewdlbes, Deutsches Elfenbein Museum, Erbach, 1995.
-
J. G. Doppelmayr, Historische Nachricht von den Niiiiibergischen Mathe?naticis und Kunstlern,…, Niirnberg, 1730.
-
L. A. de Boger and H. Batterson-Boger, The Dictiona?y of Antiques and the Decorative Aits, New York, 1967.
-
E. Bassani and W. B. Fagg, Africa and the Renaissance Ait in Ivory, New York,
1988.
-
Schiitze Chinas aus Museen der DDR, Roemer-und Pelizaeus-Museum, Hildesheim, 1990.
-
K. Andersen, Brook Taylors Work on Linear Perspective, New York, 1992.
-
K. Wachsmann, Wendepunkt im Bauen, Wiesbaden, 1959.
-
K. Bach a.o., “Radiolarien,” Mitteilungen des Institut filr leichte Fliichentragwerke, Vol. 33, Stuttgart, 1990.
-
J. Tomlow, “A Bouquet of PolyhedraSome Remarks on the Image and Significance of Polyhedra in History,” in: Proceedings 2. Int. Seminar: Application of Structural Morphology to Architecture, Stuttgart, October 8/9, 1994.
Polyhedrality in the Architecture
of Brace Goff
Rollie Ristine
¶ INTRODUCTION
Bruce Goff (190A-1982),1 architect, painter, educator, and composer,2 created in over six decades of architectural practice, primarily in the Midwest, an impressive array of buildings and designs exhibiting an extraordinary profusion of geometric formspolyhedral, spherical, cylindrical, conical, toroidal, helicoidal.3 Much of his work also contains less easily defined configurations.4 This chapter examines only that family of forms in Goff’s work directly related to polyhedra.
We will first define polyhedra and discuss their geometric and nongeometric attributes, including historical, psychological, and symbolic aspects. We will speculate on why Goff used polyhedra in his work and mention some of his architectural influences. Comments are included from Herb Greene on 20th-century thinking about geometry as related to Goff’s use of geometry. We will touch on formalism and the difficulties of description of polyhedra. A taxonomic framework is proposed involving four stages of polyhedrality in Goff’s work. Finally, salient polyhedral aspects of selected buildings are illustrated and discussed with observations from several who have lived in or worked on those buildings.
Definition of Polyhedra
A polyhedron is a solid bounded by plane faces. A “regular” polyhedron is arranged according to a system of symmetries. The boxlike spaces comprising the bulk of the world’s architecture, from tract house to international style office building, are a special class of polyhedrarectangular parallelepipeds, or rectangular prisms; that is, spaces bounded by pairs of parallel rectangles at right angles to one another. They occur in Goff’s work as well, but are mentioned in this chapter mainly as a takeoff point.
Regular Polyhedra
Regular polyhedra include the five well-known Platonic solidsthe cube, tetrahedron, octahedron, icosahedron, and dodecahedronwith their simple, powerful, and all-encompassing symmetries, and the thirteen less familiar Archimedean solids, that is, truncated versions of the Platonics, and others such as the cuboctahedron and icosidodecahedron.5 Geodesic domes are an outgrowth of these family members.
Further Classes of Polyhedra
Other branches of the polyhedra family include extrusions (prisms), pyramids, dipyramids, truncations (e.g., a frustum, or pyramid with its top cut off), skewed and elongated volumes, and so on. Still other variations are evident in specialized fields such as crystallography, which identifies by shape, among many other factors, the several thousand of earth’s naturally occurring minerals, for example, quartz and feldspar.6 “The mineral world expresses pure volumetric geometry with the greatest clarity, but it is important to remember that these solids do not exist in nature. In their perfect form they exist only on a metaphysical plane, as pure, creative ideation, and can be represented, for the mind to grasp, only through geometry.”7 Pure, complete, and intact polyhedra belong, in various conceptual garb, to the world of mathematics. Geometric space, a rigorously well defined set of symbols and abstractions, is different from architectural space, which is not usually so well defined or so abstractand yet the two are intimately related.
Why Polyhedra?
Being an architect and not a geometer, why did Goff employ polyhedrasince a major portion of his oeuvre might be called “beyond the polyhedron”? Probably the most compelling reason, in terms of childhood development, is that “Goff’s father was a jeweler and gave the boy crystals to play with. Pyrites, crystalline rocks, and semi-precious stones are to be found all over the American southwest.”8
Mental Tools
There may be a universal appeal in polyhedra that Goff felt in common with many other architects. The abstractions, definitions, and symbols of the world of solid geometry are among the essential mental tools required for the invention, discovery, and modeling of space in the real world. One of the major means of delimiting and enclosing space and creating volumes is by the use of planes (another is through the use of curved surfaces). Polyhedra provide a rich source for the interrelation of planes and Goff has drawn on that stock. As Goff said, “Some people open doors and others walk through them.”
Imperfect Polyhedra
In architecture, spaces are enclosed or defined by fragments, repetitions, distortions, proliferations, and other variations of geometric solids (like the polyhedra examined in this chapter) realized in “concrete” form. Just as in biological forms “…the geometry” says mathematician H.S.M. Coxeter, “… developed to perfection by our soap-films in the twinkling of an eye, is only roughly developed in an organic structure, even one so delicate as elderpith; the conditions are no longer simple, for friction, viscosity and solidification have vastly complicated the case.”9 In every example of Goffs architecture, where simple, pure, idealized geometric form is involvedthere are functional, spatial, and circulational, that is to say, organic, elements that modify, develop, anchor, and objectify that ideal. In spite of his respect for Wright’s “organicity,” Goff suggested taking the “nature of materials” with a grain of salt. Rigorous intellectual and philosophical purity in architectural realization can be self-defeating. Architectural solutions require unparallel (epiped?) coordination of large arrays and tangled hierarchies of conditions, levels, elements, and evaluations so it is not surprising that one does not often find complete and pure expression of Platonic and Archimedean polyhedra in architecture.
Historical Position of Polyhedra
A brief glance at architectural history will find Goff, along with a number of other 19th-and 20th-century architects, for example, Antonio Gaudi, R. Buckminster Fuller, and Frank Lloyd Wright, to mention just several, creating at the growing tip of an evolution of ever more complex spatial “conceptioning” (to use a Fullerism).
Architecture as metaphor could probably be applied as far back as the big bang, but we will not go quite that far. Animal architecture is free, curved, rough, organic10 examples of more or less perfectly straight lines and flat planes are rare as, say, a spider hanging from a strand of its own silk in a still cave or the planes in a honeycomb. Straight line and plane are more apt to be approximated in natural inorganic formsthe surface of a pool of perfectly still water, a fine icicle, a patch of glare ice, but especially in minerals, for example, an iron pyrite cube.
Geometry is a human endeavor that brings the straight line and plane to building, whence in architecture the rectangular parallelepiped rears its ubiquitous head the cube, the box. To protect the box, the traditional pitched roof appears enclosing a triangular prism of space.11 The tent appears as a variation of pyramid, frustum, prism, or cone. An early basic geometric solid was the Egyptian pyramida mass, not spatial. The pyramid’s developmental precursor was the frustum, or mastaba. Both are polyhedra in the general sense, but they are not regular polyhedra. Nonpolyhedral forms were exemplified in structures from the domes (hemispheres) of the igloo to Greco-Roman stonework, in the cones of the Plains Indians’ tepees, variations on intersections of half-cylinders in vaulting throughout the ages, full cylinders in masonry towers, warped surfaces and solids generated by rotation about axes in African paraboloids, the Islamic dome on top of a cube, and so on.12
Goff’s Work in the Context of the history of Architectural Geometry
Goff’s architectural forms take their place in the historical evolution of an ever more subtle, complex, and sophisticated knowledge and use of geometry. This is not to say that architectural work in the past did not have its mind-boggling intricacies, for example, Gothic masonry, Japanese joinery, Islamic ornament13 as well as the subtleties of proportional systems such as the ancient Greek orders.
I mention architectural influences on Goff in spite of Ben Allan Park’s daunting challenge: “It is useless to consider Goff’s influences. He has a much wider appreciation of the work of his contemporaries than might be supposed.”14
Claude Bragdon’s early-20th-century books on the generation of geometric forms were well known to Goff. When Projective Ornament by Bragdon was published in 1915, Goff would have been 13 years old when Bragdon’s The Frozen Fountain was published in 1924.
Furness, the Vienna Secessionists, Finsterlin, Mendelsohn, and other late-19th-and early-20th-century spatial innovators and geometers were among Goff’s interests and exemplified the subject matter of his modern architectural history courses, which he taught at the University of Oklahoma.
Goff was not only a dedicated “student” of Wright’s work (although never an apprentice) but also a friend. Other influences, to mention just a few, were Sullivan, art nouveau, Islamic, Balinese, Japanesein short, the expanse of world architecture.
In Goff’s own words:
I prefer Paestum to the Parthenon …it’s more vigorous. I admire almost all Hindu temples …Madras …Fatehpur-Sikri…the Japanese works, of course …the Ise Shrines. I love the detachment of the Katsura Palace, the Imperial Coronation Hall in Kyoto and the palaces there …the Golden Pagoda. In China, the Temple of Heaven in Peking …the whole Peking complex. …I have so many favorites…the Gothic at Cologne and Rheims. I like Scandinavian wood architecture …pre-Columbian …the Monadnock building and others in Chicago …Sullivan’s banks. I admire lots of buildings that are not supposed to be architecture: the hut houses of Samoa, African huts. …Wright, the Heber master …and the greatest of them all, Gaudf. A completely dedicated man.15
Goff’s complex use of geometry with its triangulated precursors to geodesics, its paraboloidal reinterpretations of organic lines of structure and growth predates but is unsurpassed in inspiration by 20th-century developments.
To try to show how specific Goffian forms were derived from such historical osmosis is perhaps part of the “uselessness” that Park is implying. Goff’s output should be regarded as an original and consistent unity, informed by and part of global architecturein spite of the apparent differences between his varied projects. Here we are spotlighting only that fraction of Goff’s output that utilized a spectrum of polyhedral prototypes.
GeometryTheoretical Versus Applied
The practical application of geometric forms in architecture may lag considerably behind the development of new mathematical concepts, but architectural composition has its own distinct systems of organizationalbeit often related to spatial configurations: from circulation networks, functional hierarchies, environmental interfaces, and microclimate control to configurations affected by the strength of materials, safety, security, and ease of use.
Practical Necessity of a Conceptual Framework
In order to build, such function complexes must be integrated into spatial configurations. This is where the intimate working sense of sohd geometric forms comes into play as the conceptual grid for the organizational/functional entities. Years of experience permit a designer to coordinate, to marry the substance, skeleton, and skin with appropriate forms through novelty and inspirationto create.
Crystallization of an Idea
From these systems of architectural organization several functional vectors might provide the germ of an idea, which would act as a catalyst to produce a polyhedral concept, just aswhen in a chemical bathat a certain temperature and pressure an initial prod produces a rapidly spreading crystallization, unique for those specific conditions.
Goff and Computers?
Goff’s polyhedral designs, accomplished just before the advent of computers, would have been facilitated and perhaps made more complex had he used computers. The “human biocomputer”16 was already therethe brain; however, we will speculate that Goff would have used the computer to further the unity of the arts with architecture. A computer could be used, for example, to replicate metaphorically the shapes derived from Trois Morceaux en Forme de Poirethe music of the “spheres” as embodied in a pear by Erik Satie (another Goff favorite), who was in turn alluding to painting. We are reminded of Philip Johnson’s designing by carving up a pear, the resultant shapes of which were to have been digitized in Frank Gehry’s (French developed) Catia computer program for a joint venture.17
Computer usage, logic, and mathematics have much in common with music. Goff had a wide-ranging interest in music, especially that of the 20th century. One of his favorites was Claude Debussy whose L’Apres Midi dhm Faun was illustrated by Goff in a painting for Joe Price’s Studio. (The painting is reproduced in Architectural Design Profiles 16.) Goff felt a strong kinship between music and architecture and invited his students to regular listening sessions from his extensive record collection. To teach design, Goff used musical principles such as theme, variation, development, rhythm, and counterpoint, specifying their direct analogs to visual and spatial elements in architecture.
In any case, students and designers who utilize the computer today will be better situated to assimilate, certainly to manipulate, complex polyhedral and other geometries. Among the problems that might be expected in using polyhedral forms, for which computers will prove useful, are: conceiving, visualizing, grouping, drawing orthographically and in perspective, linear and volumetric measuring, dealing with nonparallel planes, marking, and aligning. In construction the computer facilitates stereolithographylayout, fitting, joining, and cutting. Walking tours through computer-animation perspectives are becoming more accessible.18 However, as the electronically aided visual representation of more and more complex forms becomes easierso their verbal description becomes more difficult but perhaps more importantessential to the linkage of the visual/emotional world with the moral/historical perspective.
Herb Greene on 20th-Century Thinking About Geometry and Goff’s Use of Geometry
Berkeley architect, painter, author, educator, and Goff student Herb Greene, discusses the mystique of geometry in architectural thinking among the European rationalists early in this century contrasted with the position that geometry occupied in Goff’s work:
In the Nineteen Twenties when the functional, mechanical and technological revolution in architecture was replacing historical eclecticism, the rationalists began to use geometry with conscious intent to create architectural forms denoting function, machine technology and an image cleansed of historical associations. The geometry selected by the rationalists, however, drew heavily on a narrow range of Euclidean forms. The rationalists unconsciously inherited the classical belief that value can reside in explicit forms. The faith expressed by le Corbusier in the flat plane, cube and cylinder characterized much of the spirit of the times. The Euclidean forms were conceived as embodying ultimate simplifications of nature. Exceptions and overlaps were sometimes to be found in the works of the leading rationalists, but the rectangular flat plane tended to become a symbol eliciting a response to function, technology and a feeling for contemporary dynamics. The point is that architects, then as now, tend to regard historical forms, cubes for instance, as possessing in themselves the subjective values that only mankind can project into forms. That familiar forms in the environment are of vital importance to human psychological experience is not questioned; what is questioned is the belief that certain forms, such as Euclidean forms, possess immutable value and are to be imposed on the architectural design situation. Mies van der Rohe was probably the apotheosis of the modem acceptance of this belief.
Bruce Goff has been cautious of using geometry, or any other “tool” of architecture, to express a predetermined type of perfection to be applied wholesale to a variety of architectural programs. Architecture, rather than assuming a geometry sanctified by familiarity and unconscious psychological associations, should evolve its geometry by responding more intimately to conditions in the immediate design situation. For Goff, the final design form must show evidence of being derived from a multifarious world. There are the particular conditions of the site, climate and context, the life experiences of the client or user, the building program, the limitations of materials and construction techniques, and there are the notions of order and art influenced by the life experiences of the architect. Goff does not pay lip service to these ideas. It is his belief that a wholehearted attention to these factors is required, and that it can only produce a unique solution to every design situation. He maintains that the architect is both obligated and free to use whatever form that is suggested by a determinedly open-minded examination of the problem….
…the variety of new geometric forms appearing in the architecture of recent years should be mentioned. The best of these have been derived from structural and technological sources: shells, space frames, air forms and others. Goff, in addition to using structural determinants, has, since the early forties, been deriving his unique shapes from cultural, social, esthetic, perceptual and psychological determinants. There is a difference in intention as well as in results.19
Preconscious Meaning in Polyhedra?
To overlay Greene’s “structural…perceptual and psychological determinants” with a reconsideration of formal determinants, we ask whether the nodes of precision in three-dimensional geometry and the symmetry in regular polyhedra resonate in our mind with some as yet undiscovered inherent preconscious intensity? Is there a structure within our inherited neural network that corresponds to such three-dimensional geometries? Perhaps something of this ilk will be discovered among the multidimensional “point sets” that comprise the brain’s universe of synapses.
Psychological Effects and Symbolic Aspects of Polyhedra
According to the philosopher Suzanne K. Langer, “Symbolic expression is something miles removed from provident planning or good arrangement. It does not suggest things to do, but embodies the feeling, the rhythm, the passion or sobriety, frivolity or fear with which any things at all are done. That is the image of life which is created in buildings; it is the visible semblance of an ‘ethnic domain,’ the symbol of humanity to be found in the strength and interplay of forms.”20 The affective properties of polyhedra impart a palpable spatial feeling. This is due both to their multiple three-dimensional symmetries and to their contrast to conventional “extruded” architectural space, to which most of us have been acclimated. Goff pointed out that the acute angle, for example, could represent anger, whereas the obtuse angle has a more relaxed feeling and the circle is more intuitive. As visual symbols polyhedra grab and hold attention. Polyhedra are jointed, three-dimensional, straight-line abstractions of the structure of tree branchesthe limbs within which the capabilities of human hand and eye coordination evolved and are thus inextricably attuned. They convey a feeling of strength, and, indeed, the triangulated geometry of many polyhedra gives them an inherent structural rigidity. They convey a presencea sculptural sense of unified containment beyond the overly familiar square and rectangular world of grids. Because of this they must be handled carefully and with knowledge and discipline. The Goff work discussed in this chapter provides examples of such use.
Monumentality as an Effect of Polyhedral Usage
Monumentality is another ancient phenomenon on the border between illusion and symbolism. Detailing, massing, scale, and texture can be made to work together to create a larger-than-life entity. Polyhedral usage appears to contribute to this effect in Goff’s structures. The term “monumental” is related to the word mountain. There is something symbolic of the mountain in the angular and crystalline forms of polyhedra.
Golden Mean Ratio
The golden mean ratio, occurring so frequently in nature, is inherent in certain Platonic polyhedra. Le Corbusier, for example, found the ratio and its extension into the Fibonacci series so vital that he wrote two volumes on the subject.21 As far as I know, however, Goff did not exploit this mathematical phenomenon in his designs and the topic will not be pursued here. De Long and others have discussed Goff’s use of magic square proportional systems and the like.
Parallelepiped Architectural Spaces
The ubiquity of parallelepiped architectural spaces in Western culture makes them invisible, transparentone is almost oblivious to such spaces. Mies van der Rohe’s “Less Is More” with its rectangular box embodiment would seem to arise from a hostage-like or perhaps, Machiavellian, acquiescence to this convention; however, atop our 21st-century perch we may lose sight of the excesses of cluttered Victoriana from which these minimalist Miesian urges arose. Goff’s approach to spatial experience, on the other hand, is emotional and it is expressed in other words, brought to one’s attention; meant to be seen, felt, delighted in; made available to the senses. Does this arise out of necessity from the lonely midwestern plainsan emotional crescendo, up from pragmatic subsistence in contrast to the anhedonic, rationalist cubic formulaa decrescendo from Victoriana. Though affective and emotional, we experience a powerful intellect at work in Goff’s architecturealways striving for an exuberant expression of space.
Opposition to “Formalism”
Marcel Proust’s character, M. De Norpois, complains, “All those Chinese puzzles of form, all these deliquescent mandarin subtleties seem to me to be quite futile.” However, to reject the significance of form, its study, and its conscious application (e.g., formalism?) is to ignore one of the primary elements of the creative process in architecture (or any other art)the conceptual spatial matrix.
Acquaintance with Polyhedra
Practical gain aside, world expositions and the increasing use of space structures are familiarizing many with the rudiments of polyhedra in architecture; still, few are practiced in the verbal and visual languages of form necessary for the description of such spaces.
Description Difficult
Goffs geometric ingenuity makes description difficult. According to former Goff assistant, Larry Wayne Grantham, Goff said, “There are two reasons for an element of architectural designthe reason one gave the client and the real reason.” Still, becoming aware of the language of solid geometry and knowing that some of these forms yield to description and analysis might give some legitimacy to Goffs work for those who are not practiced in the perception of architecture, or for those seeking “rationale.” If one already appreciates his work, another layer of meaning might be added. Grantham says further, “In my experience with Mr. Goff, when he was from 72 to 76 years of age, I have no recollections of his describing his work using technical descriptions of the forms…. I will concede, though, that Goff knew his work would be analyzed thoroughly. I do not understand that some individuals need such descriptions. The danger, as I believe Goff would have commented, is that people might use such analysis as a means to create formulas for copying. Goff often spoke of things growing from the problems to be solved outward to define the space. Such forms are always unique to each design opportunity.”
Describing Complex Forms
Descriptive attempts, however, indicate why visual means are preferable to verbal. With twinnings, abuttings, intersections, interpenetrations, truncations, and so on, the formal descriptions of polyhedra in architecture tend to be overwhelmed by the complexity of spacesthe nomenclature can quickly become unwieldy or superfluous. Goff’s architecture, however, seems to teach itself, nonverbally. The rewards are raised consciousnessgreater satisfaction in architectural usein the appreciation of the play of light and shadow, in an awareness of space. Goff had confidence in the inevitable power and rightness of his work.
Four Stages of Polyhedrality
Goff’s use of polyhedra can be conveniently, if somewhat arbitrarily, placed in four stages from less to more polyhedrality, as follows: (1) virtual polyhedra, (2) nonregular polyhedra, (3) single-cell regular polyhedra, and (4) multicell regular polyhedra.22
These “stages” are not intended to carry an implicit value judgment of the worth or beauty of such forms, for example, that a close-packing arrangement of Stage 4 is somehow better than, say, a simple horizontally extruded prismatic space. Each should be considered according to its purposes and situation.
Stage 1: Virtual Polyhedra
(Pseudopolyhedra would be too negative a term.) This category sees surface effects “striving” toward polyhedra and depth, but stymied by limits of economics or function. It includes diagonal motifs, beveling, truncation, champfers, ornament, and related nonrectilinear elements occurring within the confines of rectangular boxes. Two-dimensional iterations (i.e., repetitions, rhythms) would be included. Triangular patterns are also used frequently.
Some Goff designs have an illusory qualitywhat might be called “virtuality” (a concept taken to its extreme today by the spread of computer virtual reality) the semblance of the third dimension upon a two-dimensional surface. If it were not economically feasible to develop a full polyhedral theme for a client, Goff might provide, because his thinking was spatial, a more limited, two-dimensional representation of polyhedraor, more generally, of “depth cues”23 through the manipulation of ornament, fenestration or, say, the beveling or inclining of surfaces such as railings, walls, soffits, mullions, or struts. An impression of depth is thus enhanced in forms and surfaces where it might not otherwise be economically obtainable. There is a hint of art deco here with its geometric surface pattern orientation; however, this stage is more concerned with allusions to depth. The effect is apparent in many Goff designs, for example, the Page Warehouse, Tulsa, Oklahoma, 1927, and the Floral Hills Memorials, Project, 1959. Still, the love of rhythm and pattern for its own sake is obvious in Goff’s work.
“Virtuality” is also evident in Frank Lloyd Wright’s use of ornament, especially his leaded glasswith its overlappings, repetitions, and angles often giving a strong sense of a third dimension not unlike the effect of an isometric drawing. The illusion is made more complex when looking, through such a depth pattern, at the three-dimensional world outside the window.
Among examples illustrating this stage are the Hyde and Snyder Houses and the Floral Hills Mortuary complex. In the Blackwell Building, Project, Dallas, Texas, 1961, two three-story-high 45° triangles side to side at a prominent corner act together to imply a tetrahedron.
Stage 2: Nonregular Polyhedra
(Proto-polyhedrality; proto-Platonic, or proto-Archimedean geometry) This category includes nonvertical extrusions, vertical extrusions of nonrectilinear shapes, polygonal prisms, pyramids, and various sloping surfaces. Extrusion of triangular forms is prevalent.
Limitations of Extrusion. Goff discussed with his students the tired limitations of creating space via vertical (gravity generated) extrusion from the floor plan. This concept is expressed in Goff’s work through (1) extrusions along axes other than vertical (e.g., prisms) and (2) nonextruded spaces such as pyramids and frusta.
Prisms. Prisms are a recurring theme in Goff’s work, prisms, that is, with nonrectilinear basesextrusionsbut often nonvertical extrusionsvery likely terminated by other than simple planes, but if planar, usually at angles other than perpendicular to the direction of extrusion, for example, the horizontal prisms of the Price Studio 2.
Prisms as Proto-Polyhedra. To give a polyhedral “boost” to a form, that is, to enhance its three-dimensional character, one could apply similar operations to different dimensional axesthat is, to front and side elevations as well as plan. An extrusion could be terminated (the ends closed) with a shape similar to its base or cross section. Take a rhombic prism, for example. Rather than trimming or closing the ends with flat planes, those ends might be shaped by dihedral angles, acute or obtuse, creating concavities or convexities or virtual tetrahedra. In the Snyder House, Project, Dewey, Oklahoma, 1958 (Figure 2.1), V-shaped terminations at the ends of the very prominent “bay windows” are virtual tetrahedra, defined by two pairs of opposite edges (Figure 2.2). Variations on this idea appear frequently in Goff’s work.
Examples of Stage 2 are the Nicol, Bass, and Gutman Houses and the Price Studio (as built).
Stage 3: Single-Cell Regular Polyhedra
(Or single-volume polyhedral space) This stage is made up of Platonic and Archimedean solids and their duals and facially subdivided variations (geodesic domes) in single units or separated multiple groupings in which the single polyhedra are still obvious units. This stage might occur in the building as a wholethe Crystal Chapel is a prime exampleor in regions or details of a building, for example, the Rudd House projects. Another characteristic might be “soft packing” or “unpacking” (as opposed to “close packing and hard packing”). This is simply the repetition of polyhedra without abutting; see the Rudd House discussion.
Geodesic domes fall into Stage 3. Buckminster Fuller (discussed in Chapter 4) lectured at the University of Oklahoma once or twice when Goff held the architecture department chair in the late 1940s and early 1950s.24 Although Goff’s polyhedra were usually subordinated to a personal architectural gestalt, curiously enough, in the several of Goff’s designs involving patented geodesics the domes’ triangulated configurations remained dominant and essentially unaltered, for example, the Fitzgerald Realty Office Building, Project, Tyler, Texas, 1965; the Le Boeuf House, Project, La Grange, Texas, 1967; and the Harry Goff House, Project, Tulsa, Oklahoma, 1962. Each used, according to De Long, “…a patented wood version of a geodesic structure …developed by the Pease Company and manufactured by Geodesic Domes Inc., Davidson, Miss. Two diameters were offered: 26 feet and 39 feet. In 1960 these cost $1,300 and $2,600 respectively.”25 These domes were, polyhedrally speaking, based on the triacontahedron.
Stage 4: Multicell Regular Polyhedra
(Cell iteration) Stage 4 comprises clusters of Platonic and Archimedean solids or their duals in space-filling, perhaps close-packing arrangements the polyhedra abutting, side to side, front to back, and/or up and down regularly or irregularly. Among the prominent actors seen on Stage 4 are structural space lattices (three-dimensional matrices that owe their inherent
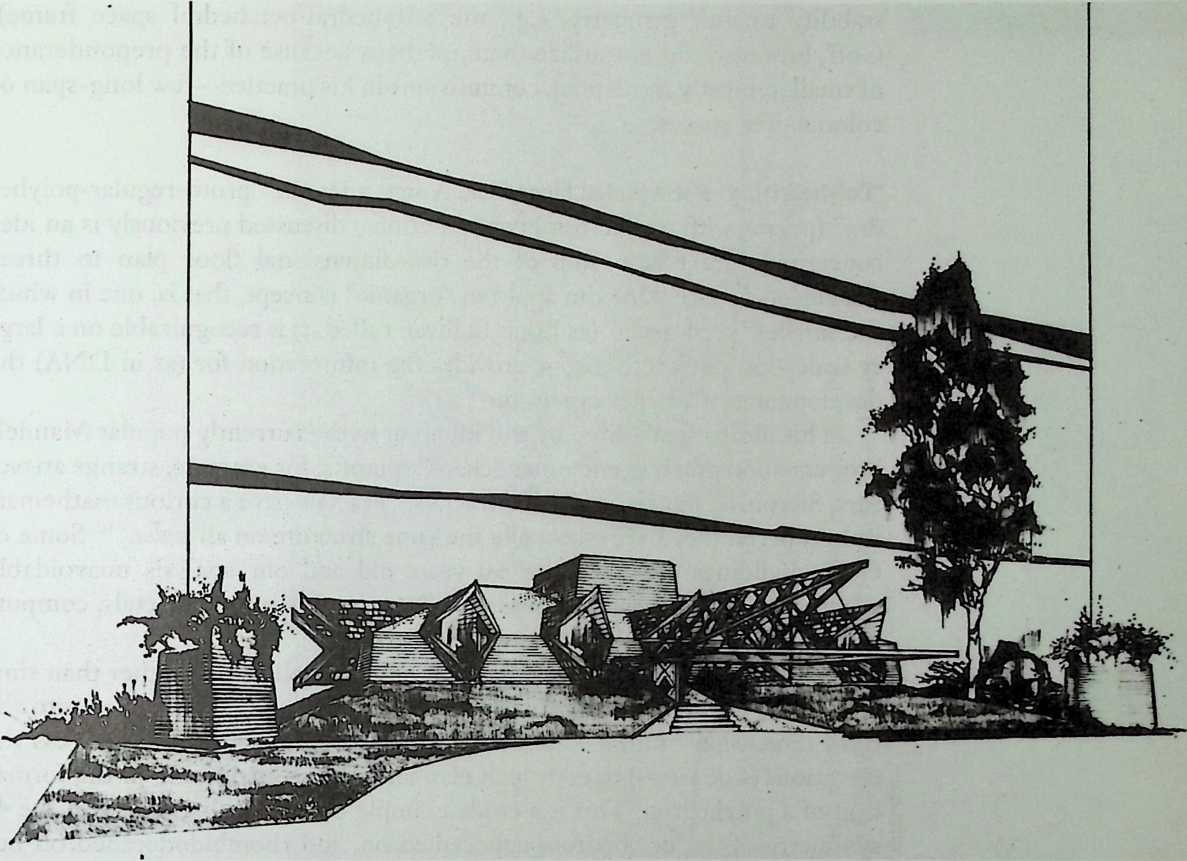
Figure 2.1 Russell B. Snyder House, Project, El Dorado, Kansas, 1958. Rendered perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
Figure 2.2 Snyder House. Virtual tetrahedron.
stability to unit geometry, e.g., the tetrahedral/octahedral space frame). Goff, however, did not utilize them, perhaps because of the preponderance of smaller, mostly residential, commissions in his practicefew long-span or column-free spaces.
“Polyhedrizing” a Tessellated Floor Plan. A step after the “proto-regular-polyhe-dra” (prisms with certain basal configurations) discussed previously is an idea concerning the relationship of the two-dimensional floor plan to three-dimensional space. One can apply an “organic” concept, that is, one in which the smaller “seed-germ” (as Louis Sullivan called it) is recognizable on a larger scaleor, put another way, provides the information for (as in DNA) the development of a larger organism.
This idea is symbolized by and inherent in the currently popular Mandelbrot equation graphics and other “chaos” spinoffs, for example, strange attractors, Sierpinski figures, and other fractals. “Fractals have a curious mathematical property: they have essentially the same structure on all scales.”16 Some of Goff’s buildings are now over 50 years old and our analysis unavoidably attempts to superimpose various latter-day concepts such as fractals, computer graphics, deconstruction, and postmodernism.
A floor plan composed of polygonal units (tessellations), rather than simply serving as the base for a vertically extruded space, could be taken into the third dimensioninto a volumeby using a similar polygon to express the elevations (side views) of each such plan unit, thus contributing to the formation of a polyhedron. This is a crude example that works literally with the 4-symmetry of the octahedron, cuboctahedron, and rhombidodecahedron but would not be sufficient for development of the 5-symmetry icosahedron and dodecahedron. In this way a tessellated plan could serve as the base for a Stage 4 space-filhng polyhedral matrix of which the Wilson and Pollack/Warriner Houses are examples.27
Table 2.1 fists stages and polyhedral configurations for representative buildings and projects.
This list is by no means exhaustive. Most of these works are described and illustrated by De Long.
Summary of Stages of Polyhedrality
Stage 1. Surface application of triangulation. Boxes striving to go beyond. Stage 2. Vertical extrusions or pyramids from polygons other than square. Nonvertical extrusions of triangular and other polygons. Composites from pyramids.
Stage 3. Archimedean/Platonic polyhedral single-cell space or overall massing. Same, but in smaller detail regions, not overall.
Stage 4. Cell iteration, close-packing, “far packing” (e.g., the Rudd House, discussed later). Same, but in smaller detail regions. Vertical packing.
2 Interior of balcony, looking east (Photo: J. Francois Gabriel. Reproduced with permission.)
3 Exterior framed by eucalyptus trees. (Photo: J. Francois Gabriel. Reproduced with permission.)
4 Exterior of northeast entry ventilation louvres and large pulpit doors in closed position. (Photo: J. Frangois Gabriel. Reproduced with permission.)
5 Detail of space truss. (Photo: J. Francois Gabriel. Reproduced with permission.)
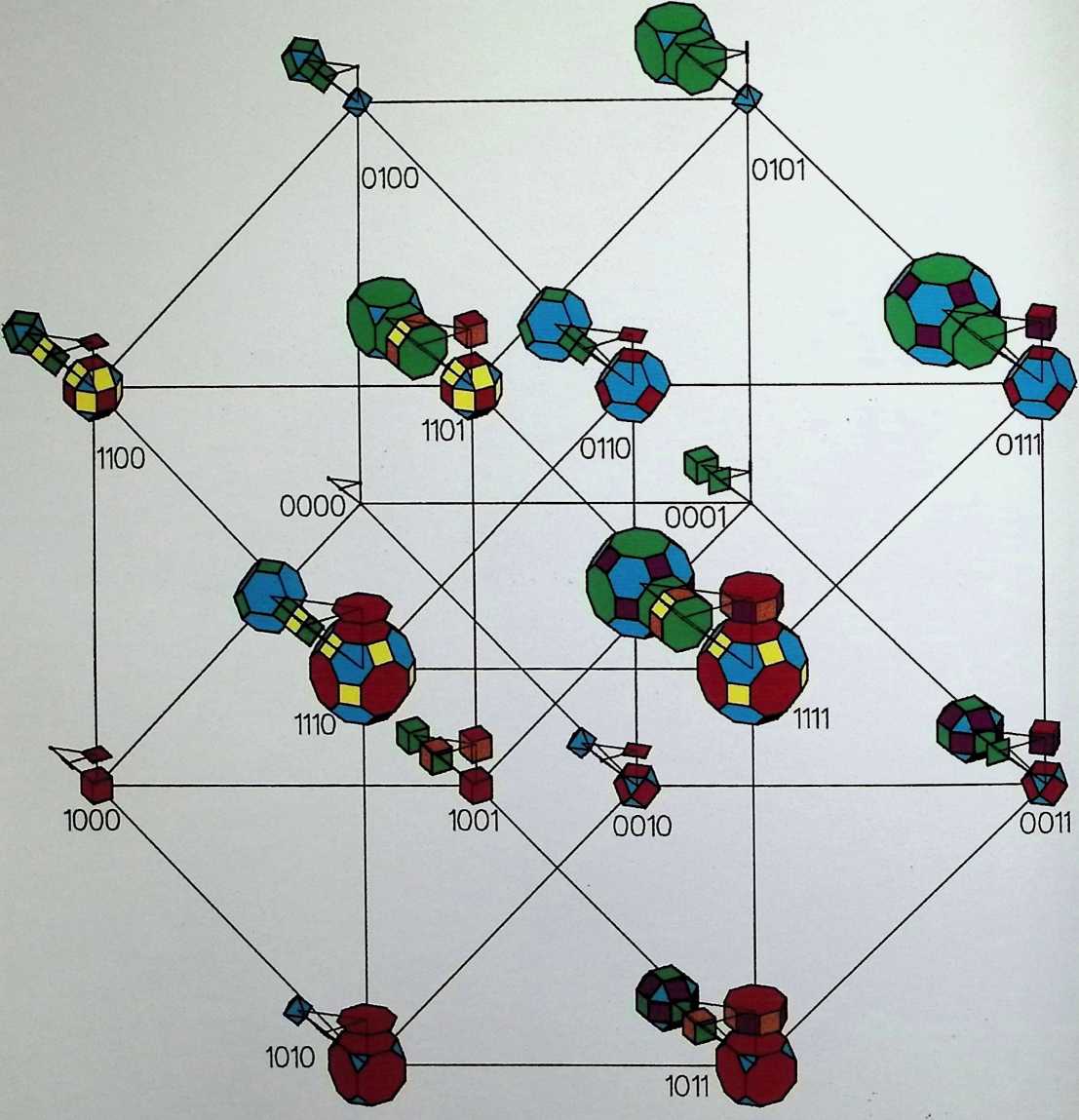
6 Four cells of the 16 structures of the family (434) obtained by locating a vertex at every available position within the fundamental region (shown in exploded view). The structures are arranged on the vertices of a four-dimensional cube and indexed accordingly.
7 Portions of 16 periodic spacefilling structures corresponding to Color Art 6.
8 Cells of 16 structures of family (434) obtained by removing red and green faces from the structures of Color Art 6.
-
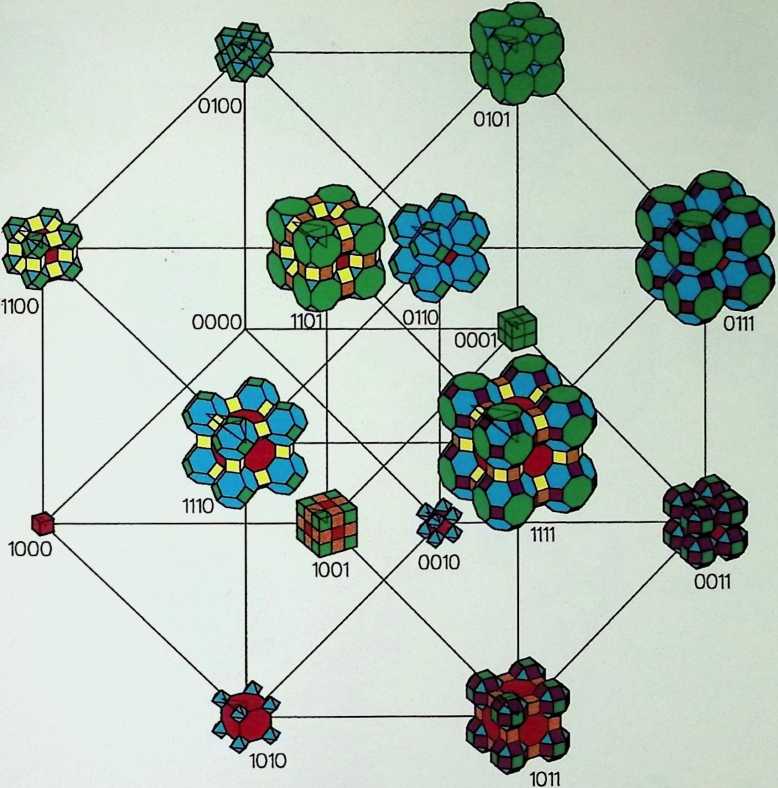
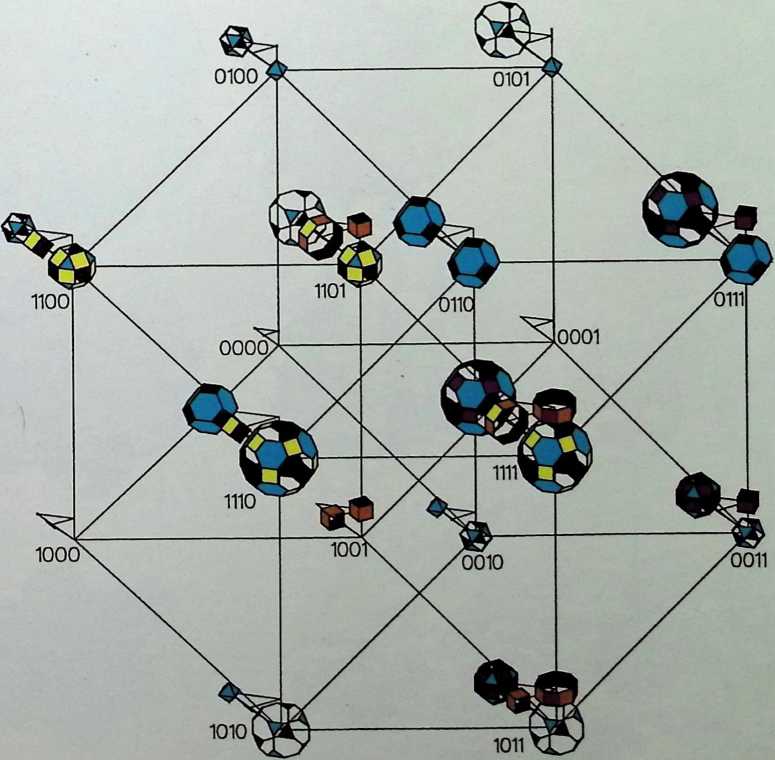
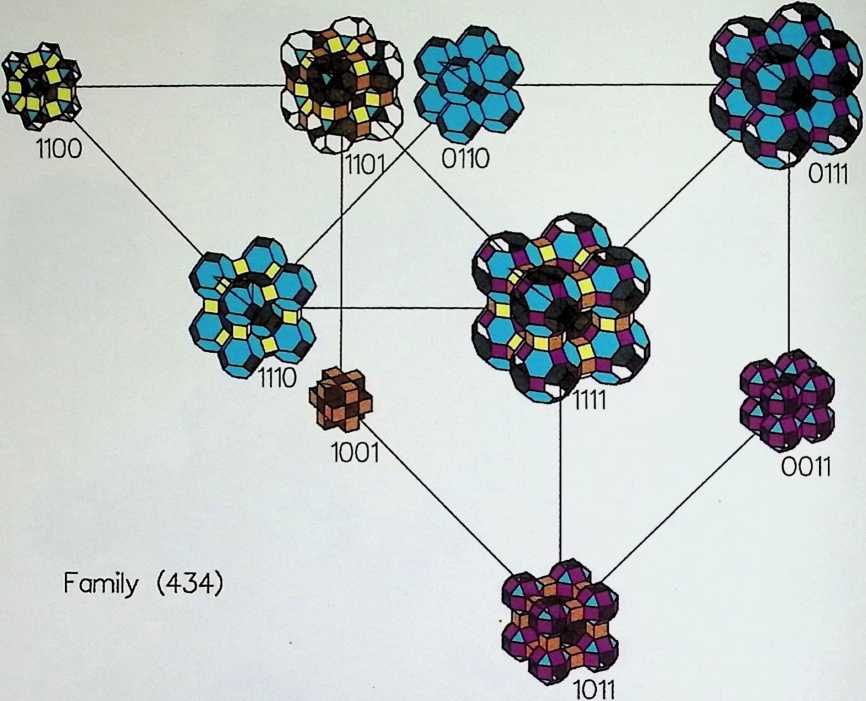
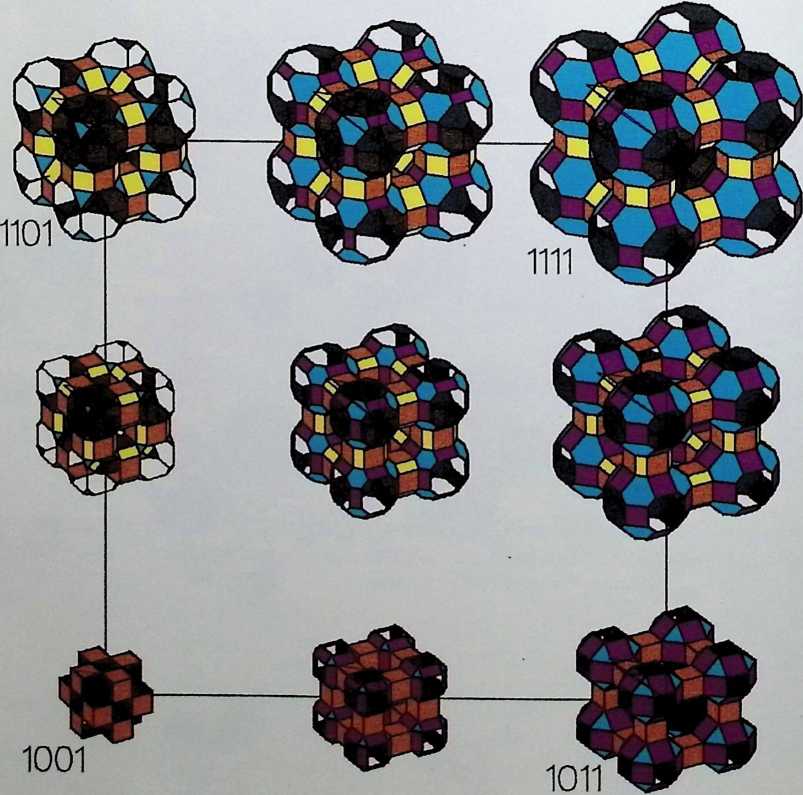
Portions of nine labyrinths of family (434) having red and green faces removed, corresponding to part of Color Art 8.
-
A two-dimensional lattice of continuous transformations between four different labyrinths of family (434) shown in Color Art 9.
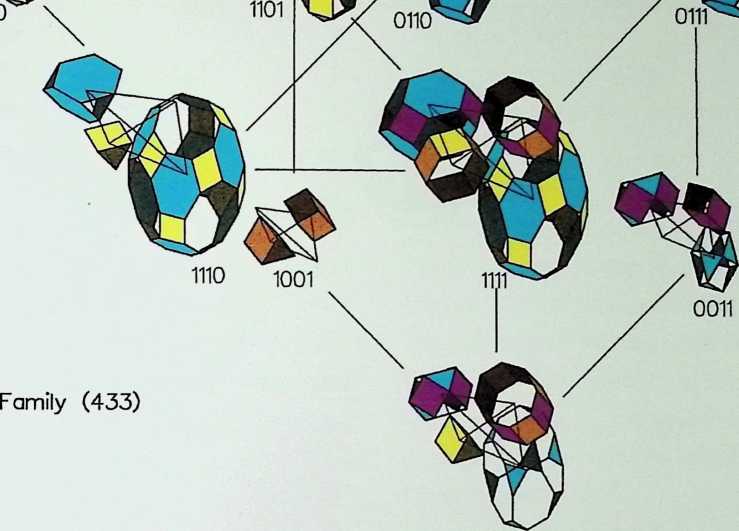
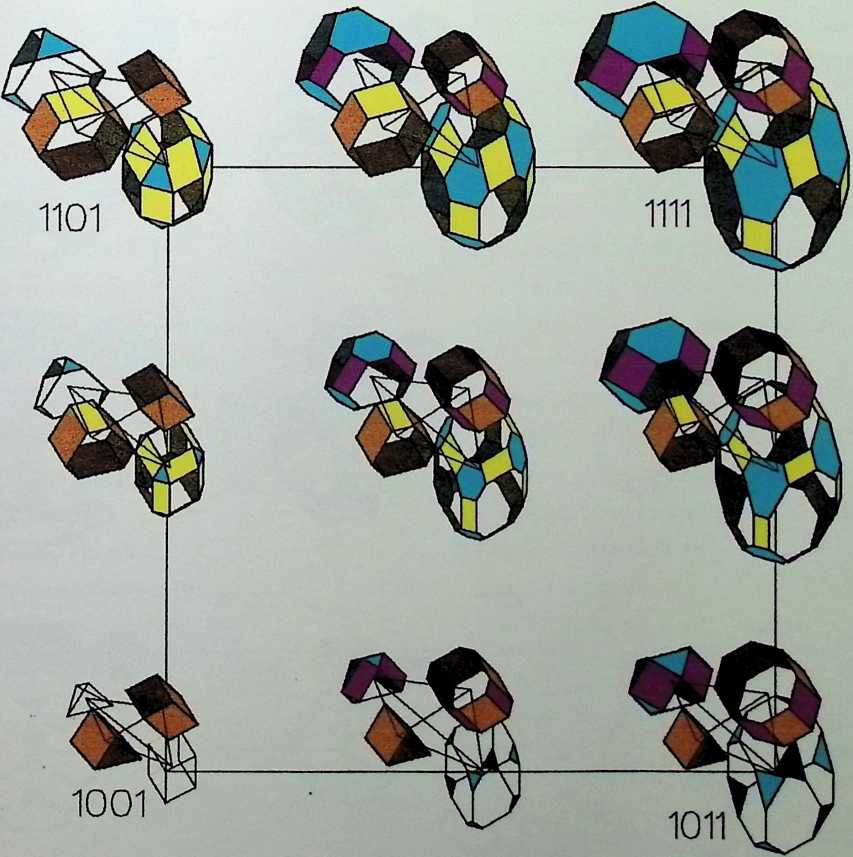
1011
-
Cells of nine labyrinths of family (433) having red and green faces removed (shown in exploded view).
-
Atwo-dimensional lattice of continuous transformations between four different labyrinths of family (433) shown in Color Art 11.
13 Cells of nine labyrinths of family (533) having red and green faces removed (shown in exploded view).
1011
14 A two-dimensional lattice of continuous transformations between four different labyrinths of family (533) shown in Color Art 13.
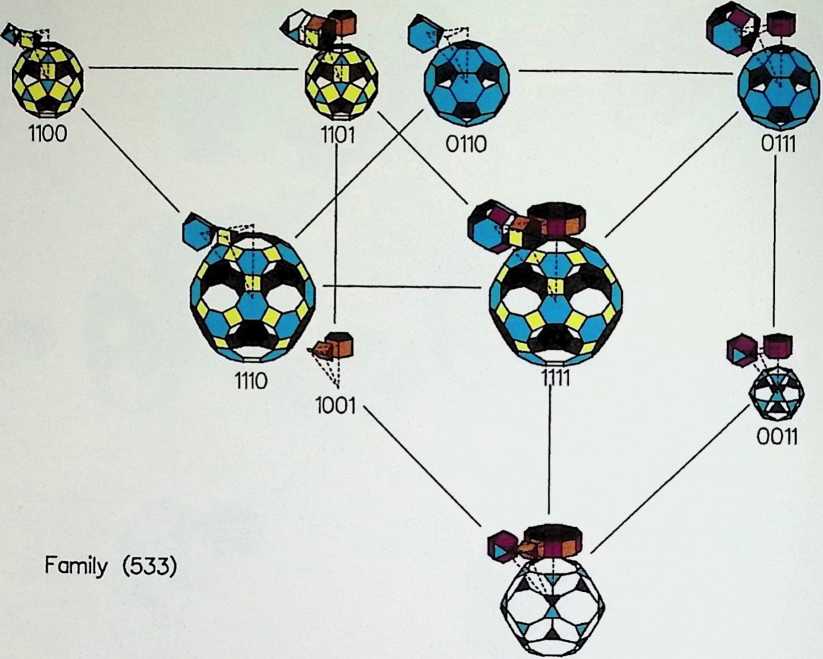
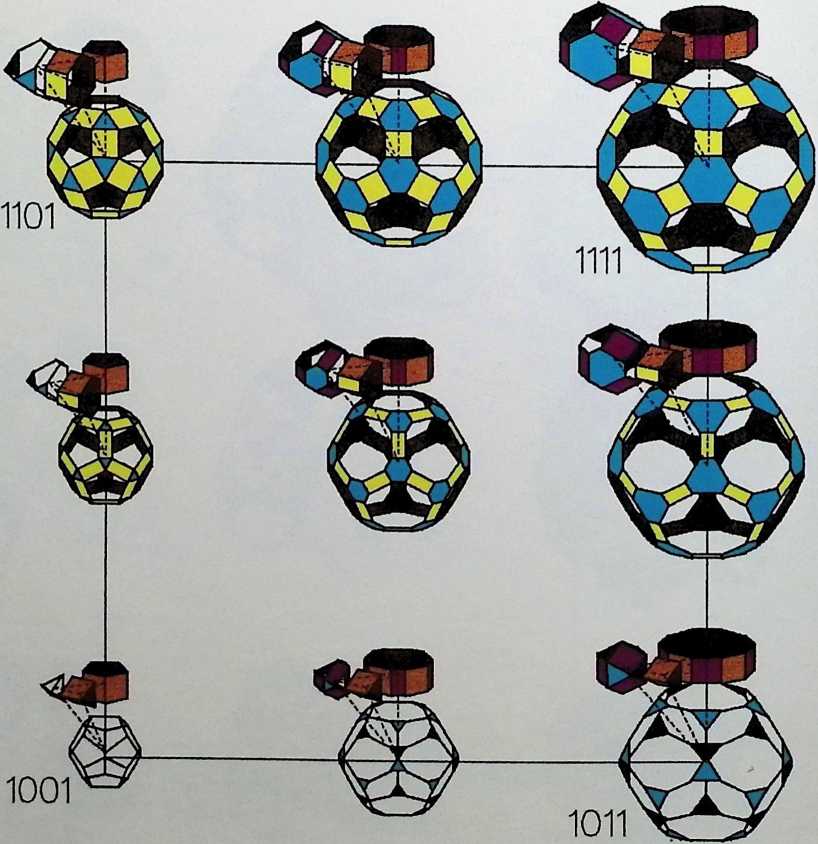
Summary of Stages of Polyhedrality □ 49
TABLE 2.1 Polyhedrality in Goffs Work
| Building | Stage | Polyhedra |
| Hyde/Lane House | Champfers, bevels | |
| Floral Hills Complex | Virtual dual transformations | |
| Ledbetter Cottage | Virtual pyramid of tension rods intersecting a square prism | |
| Blackwell Building | Virtual tetrahedron | |
| Searing House | ,2 | Hexagonal prism |
| Briar Cottage A | ,2 | Truncated triangular prism |
| Black Bear Motor Lodge | ,2 | Triangular prism, tetrahedron, stellated tetrahedron |
| Phi Beta Delta Fraternity House | ,2 | Trapezoidal prism, virtual tetrahedron |
| Pi Lambda Phi Fraternity House | ,2 | Triangular prism, half-cuboctahedron |
| Phi Sigma Epsilon Fraternity House | ,2 | Triangularly arrayed rectangular parallelepipeds |
| Snyder House | ,3 | Virtual tetrahedra, window bays |
| Unseth House 1, Project | ,4 | (Quasi) tetrahedra/octahedra space frame |
| Unseth House 2 | Triangular prism | |
| Nicol House | Octagonal prisms and pyramid | |
| Bartman “Triaero” Cottage | Hexagonal diprism enclosed by a truncated octahedron | |
| McCullough House | Dodecagonal prism | |
| Hopewell Baptist Church | Multisloped dodecagonal pyramid | |
| Bass House | Partially stellated dodecahedra (or intersecting pentagramal pyramids) | |
| Gutman House | Truncated triangular dipyramid | |
| Miller House (porch) | ,3 | (Undefinedfacets somewhat like a cut gem) |
| Freeman House (porch) | ,3 | Pyramid and inverted frustum |
| Price Studio 1 | Interpenetrating square and rhombic difrusta | |
| Price Studio 2 | Horizontally extruded trapezoidal prisms | |
| Jones House | Interpenetrating octagonal prisms and pyramids | |
| Crystal Chapel, Norman | Quasistellated rhombic hexahedron, elongated tetrahedra | |
| Crystal Chapel, Artesia | Intersecting or multislope pyramids | |
| Gerald, Boeuf, and H. Goff Houses | Geodesic domes of triacontahedron base | |
| MacBryde House | Flattened cuboctahedron or elongated tetrahedron | |
| Adams House | Triangular diprism or “octahedroid” | |
| Rudd House | Truncated icosahedra, truncated tetrahedra | |
| Wilson House | Rhombic cuboctahedra | |
| Pollock/Warriner House | Rhombic dodecahedra | |
| First National Bank | ,2,4 | Octagonal pyramid, horizontal prism |
Limitations of the Four Stages
The four suggested “stages” are rough-cut categories that overlap and intertwine even though one or the other stage may predominate. Unlike the biologist’s taxonomy, they do not indicate a chronological progression or evolution. I am not attempting a rigorous comparative anatomy but rather taking snapshots of different areas of unique designs. Nor are they categories that Goff claimed, taught, or even mentioned. He did, however, discuss the concept of “variation” in the sense of theme and variations as in musical compositionemphasizing the possibilities of a gradation or range of possibilities for any given design principle. For example, the effects of light involve transparency, translucency, and opacity; the relationship of a building to its site could be blending or contrasting or a mix.
SELECTED GOFF WORKS
The following are more detailed descriptions of salient polyhedral aspects of selected Goff buildings:
The Lawrence Hyde/Scott Lane Mouse, Kansas City,
Missouri, 1965
The Hyde/Lane House (Figure 2.3) is an example of Stage 1in which diagonal details modify and overcome primarily rectilinear volumes. The plan of the Hyde House consists of rectangular rooms that have been extruded vertically within a Greek cross perimeter, but with many 45° and other angled details striving toward the polyhedral. Such angled details consist of comer fenestration, storage, garage placement, beam terminals, end-wall terminals, door, window, and railing design, a cathedral ceiling over the living room, roof facia, and an apron at the bottom of the exterior siding. These disparate elements are focused and epitomized in a central, open, fireplace, with pyra-
Figure2.3 Lawrence Hyde/Scott Lane House, Kansas City, Missouri, 1965. Rendered perspective.
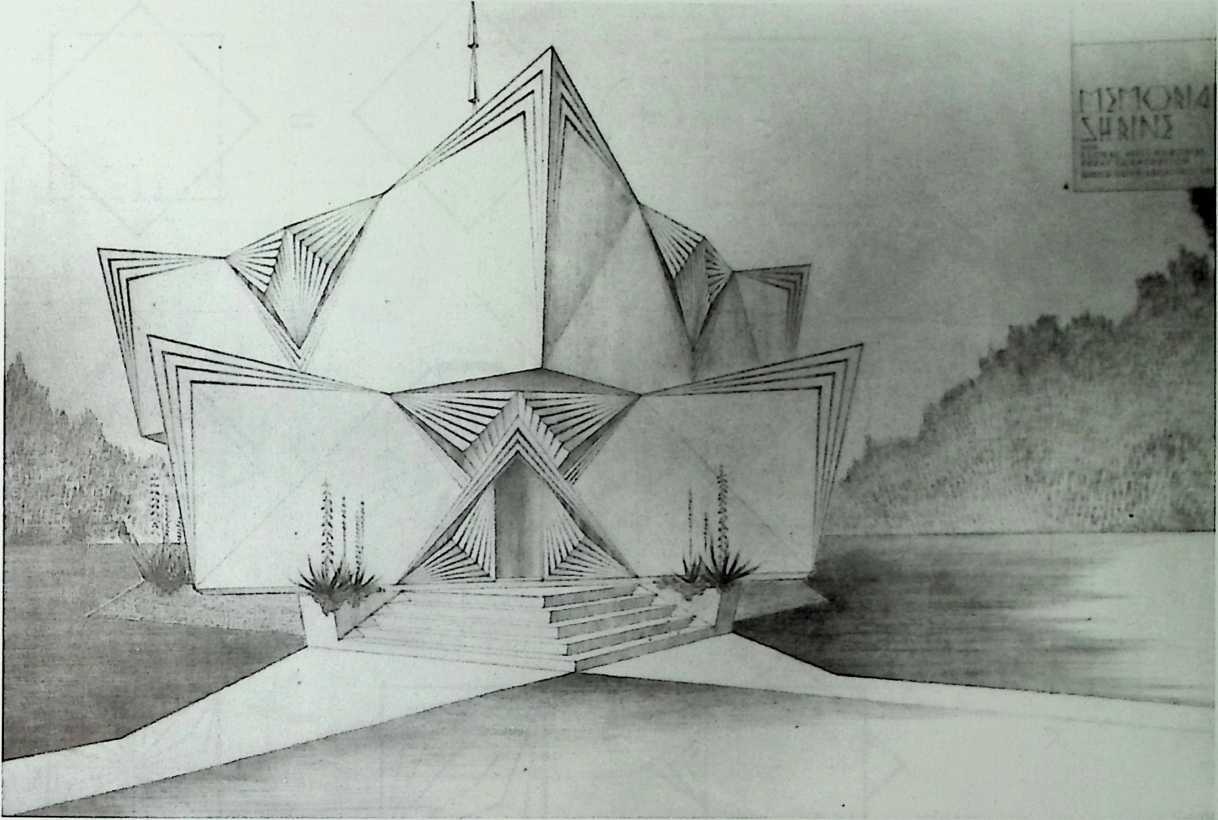
Figure 2.4 Floral Hills Temple of Rest, Project, Las Vegas, Nevada, 1960. Perspective rendering. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
midal hood and large triangular mirror backdropapproximating a virtual octahedron. De Long discusses the “earth, air, fire and water” symbolism in this convergence.28
The Floral Hills Temple of Rest, Project, Las Vegas, Nevada, 1960
This mortuary complex is another example of Stage 1 (Figure 2.4). Goff had taken the square and “made it his own,” as he might have said. Variations on the theme of one square overlapping another at 45° resulted in octagonal motifs varied by bends, folds, uplifts, thicknesses, contrasts, diagonal placement, and the like. Comers were stretched into tetrahedra and emphasized by bracketing lines at intervals of several degrees either more or less than 90° (Figure 2.5).
Mr. and Mrs. James Nicol House, Kansas City, Missouri, 1965
The Nicol House, as built (Figure 2.6), is the third and simplest of three designs.29 The first two schemes involved curvilinear forms cylinders, cones,
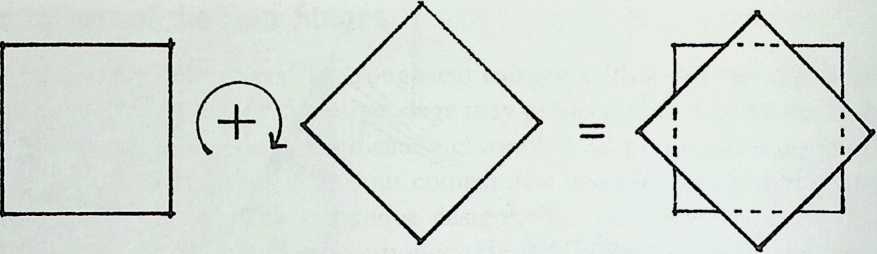
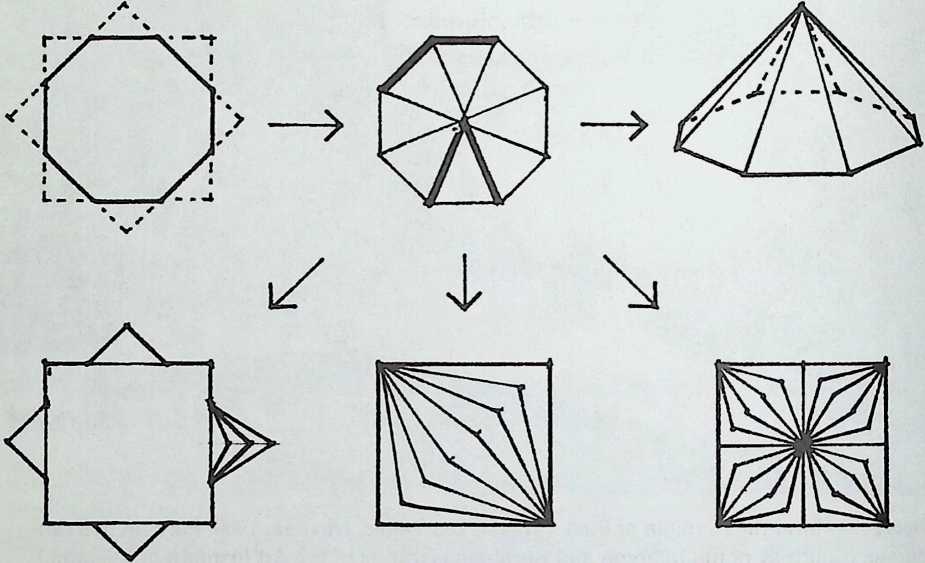
Figure 2.5 The Floral Hills Temple of Rest. Variations on the theme of one square overlapping another at 45°.
beehive-like forms, warped planes, a helix, and so forth, probably beyond budget constraints.
The third and finally built design for the Nicol House is a prototypical step “beyond the cube,” relying on vertical extrusion from forms other than the square and rectangle (Stage 2), principally variations on the octagon.
Plan Octagons
The floor plan’s most obvious pattern is based on an outer ring of eight octagons, each about 12 feet wide, with sides of approximately 5 feet, linked (or separated) by eight squares of the same edge length. Each of these outer octagons is thus centered on one of the eight vertices of a larger imaginary octagon (Fig. 2.1a). This outer ring of eight encircles four interior octagons, which in turn surround a fifth, central, focal octagon “conversation pit” (Figure 2.1b). These comprise the largest expression, although almost completely intangible, of a square-octagonal tessellation, creating the somewhat cruciform central living area or atrium (Fig. 2.1c). Other
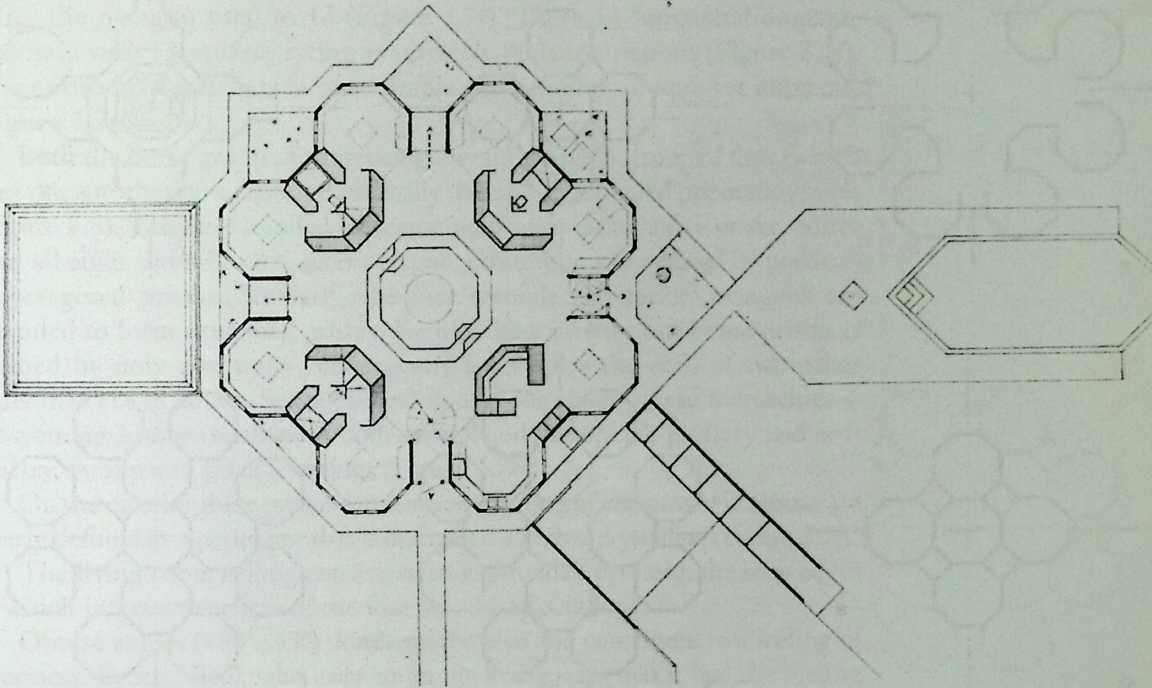
Figure 2.6 Mr. and Mrs. James Nicol House, Kansas City, Missouri, 1965. (a) Plan; (b) exterior photo. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
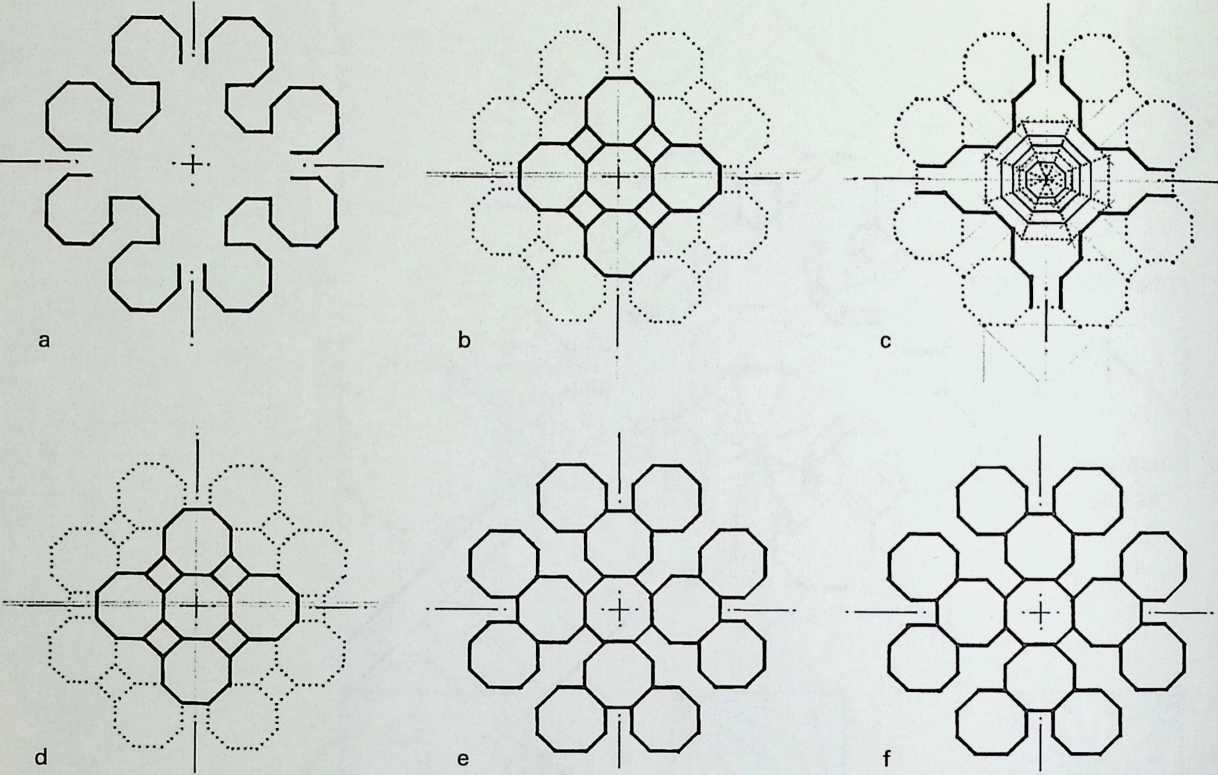
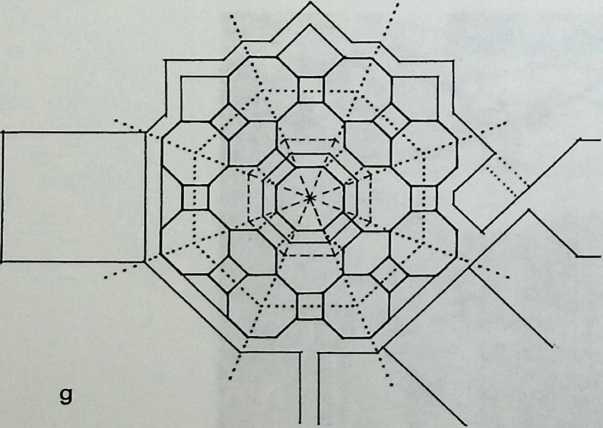
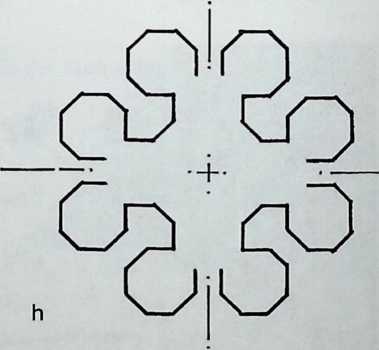
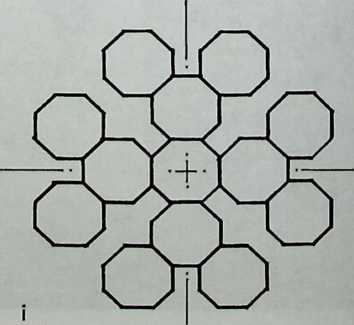
Figure2.7 Nicol House. Octagons: *(a)*ring of octagons; central square/octagon tessellation; (c) central living commons; (d) Examples of other square/octagon tessellation regions; (e) all 13 octagonal units; (f) all 12 square service/circulation units; (g)the complete grid; (h) a mandala of primary and secondary spaces; (i) perimeter, both floral-like and crystalline. clusters of two and three octagons occur as fragments of a square-octagonal tessellation (Figure 2.7d). The outer ring of 8 plus the atrium ring of 5 bring the octagon total to 13 (Figure 2.7e). These 13 functional domains alternate with 12 squares acting as service/circulation regions (Figure 2.7/). The entire grid system is at once simple and complex, unique yet universal (Figure 2.7g).
Both the outer group of eight octagons and the inner group of four (which abut one another) are extruded vertically to imply eight-sided prismatic spaces (Figure 2.8). They are impliedbecause walls occur at only five or six, rather than all eight, sides of each outer octagon, creating spaces defined by portions of octagonal prisms. Similarly, the four secondary (interior) octagons are extruded to form octagonal prisms. Each of these interior octagonal prisms is defined by only two walls on opposite sidesplus the ends of two other walls that act as edges. Space “flows” in and out among these hierarchiesblossoming in a mandala with both central and peripheral, primary and secondary, family and private settings (Figure 2.7Zz).
On the exterior these prisms formed from the ring of eight outer octagons are clearly defined in a perimeter that is both floral-like and crystalline (Figure 2.1 i).
The living room ceiling consists of an eight-sided pyramid, the base edges of which intersect vertices of the four secondary octagons.
Obtuse angles (180°±45°) dominate the plan and contribute to a feeling of openness. Bruce Nicol, who grew up in the house, says that it had the feeling of “space without walls.”
Windows on the four exterior walls of each octagonal prism, and in two cases on interior walls, consist of inverted 45° isosceles triangles. Their downward pointing 45° angle is the same as the angle subtended by the side of an
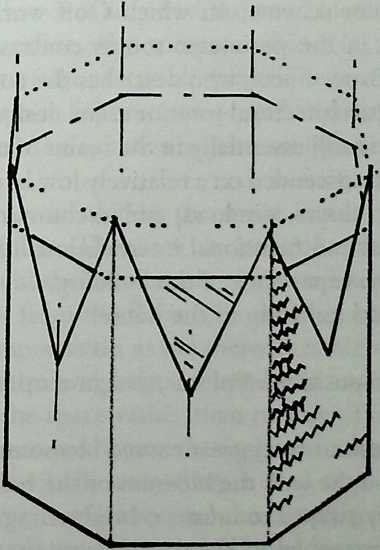
Figure 2.8 Nicol House. Octagons extruded into octagonal prism units.
octagon. Why the triangular windows? The use of conventional rectangular double-hung or casement windows would have ignored the octagonal schemata, squelched the visual dynamics, and destroyed the unity (Figure 2.8). Between each pair of triangular windows is a triangular region consisting of two walls meeting in a dihedral angle. This fold is both more and less than a “corner” because it is at a 135° angle and is emphasized by being at the central spine, or altitude, of a triangular motif. The ceiling and floor lines of these prismatic rooms participate in this angular dance.
The plurality of rhythmically spaced downward-pointing triangular windows complements the unity of the upward-pointing, octagonal-pyramid, central roof (and its similar pyramidal skylight). The herringbone shingle pattern is a textural reflection of this theme.
According to David De Long:
…The recessed, octagonal shaped area at the center focused upon an elaborate construction of Goff’s design: a wire sculpture linking the skylight above with a circular pool below. Again Goff had created a central feature in which a pool and skylight were linked, here enhanced by the addition of a third elementfireand by the subtle motion and sound of the water as it moved down the wires, reinforcing unities. Its dramatic amplification of changing light added to its focal strength, transforming the room into an almost ceremonial space as strongly evocative of family position as any Roman domus. And like the atrium of a Roman house, or any number of similarly traditional models, the space was not conceived as a container of conventional furniture, but rather as a place of grander assembly, with more intimate, less formal areas provided elsewhere.30
In the original color scheme, on which Goff worked closely with Airs. Nicol, electric colors in the perimeter rooms contrasted strongly with the green central carpet. Bruce Nicol, who describes the colors as “very ‘60s,’’ has become a specialist in architectural interior color design.
The Nicol House is still essentially in the realm of the (vertical) extrusion, although ingeniously transcended on a relatively low budget. Variations on the octagonal theme affect doors, windows, tables, counters, and cabinets. However, their subtle visual and functional interrelations can only be understood and deeply felt through experience of the building.
Kathy Nicol reflects on living in the house:
…is a home a composition of pieces, design motifs, or a whole…
“O chestnut tree, great rooted blossomer, Are you the leaf, the blossom or the bole? O body swayed to music, o brightening glance, How can we know the dancer from the dance?”
W.B. Yeats, “Among Schoolchildren”
It is a question which needs to be raised about many of Goff’s constructions but few traditional buildings.
…invariably one of us would drag (Goff) off to see something in the house; the way in which a moon door framed a red bud limb or the reflection from the lily pool on a bedroom ceiling. BG always was pleased that someone had noticed and always claimed credit for having anticipated just such a phenomenon…BG stayed in the house for a month in 1969 when the entire family went away. It was the first, and I think only time he ever lived in one of his designs. He was singularly uncommunicative about the experience except to say that it was interesting…
The building itself inculcates a sense of possibility. It is not set squarely on the lot with a front door facing the street. Each room is visually open to nature on all sides and above. One need not look out a window or up through the skylight to know what the weather is. These serve more as frames than windows or skylights. The view from no two windows is the same. There is a sense of integration with the outside. The house changes dramatically during the day and during the year. In the winter when snow covers the skylights there is a sense of enclosurenot the sense of being protected from the elements but being enclosed by them. Snow never looks as soft and comforting on the ground as it does when one sees it from below on a skylight with the reflected light of a fireplace. In spring, the many trees which surround the house change from day to day. As they begin to blossom and then leaf, one is aware of the gradual change. Branches are close to windows and skylights so once again there is no need to look “out” a window; the “out” is brought into close proximity to the “in” and becomes a part of the interior decoration. The relationship is not only visual…one knows when the first rain falls and the sound of leaves falling and the wind blowing them about on the roof makes one realize why someone living in a cube might crave a recording of a waterfall or birds chirping. The two large moon doors also contribute to the noise factor; openone hears not only birds, but squirrels, frogs and even the splashes as bats swoop at the pools drinking and eating bugs.
The sense when inhabiting the space is not of forms connected to other forms but of flow. There are no dead ends in the building…. Those corners which would shelter a corner chair are lined with built-in shelving at about three feet from the floor. The shelving keeps one back about 18 inches but more importantly, as the shelves are highly wood grained, a soft color, about fingertip level from a relaxed arm and continuousthe sense is to move about the space rather than to stop. The more prevalent cornerare they convex and concave? is that which protrudes. These move the eye and even the body away from a dead end. They force movement along the line of one surface around the comer to the next which invariably leads into the central living area. The beds are on platforms which are continuous. If one sits in the living room and looks into the bedroom the color and texture continues from where one is sitting over the top of the conversation pit, across the floor and up the bed platform. There is flow rather than stasis. (…occasionally first time visitors say they get turned around in the house. I don’t understand but know that this would never happen in a cube.)
BG used Pella doors throughout the house so even the actual shapes seem to change with the closing and opening of these temporary divisions. The structure of the doors is a simplified microcosm of the building. The rolling feel of the shape and the sense of expansion or enclosing.
My parents have done no redecoration or modifications to the house, other than maintenance and removing my brother’s suspended bed, since the house was built. This is pretty weird when one considers that the house is almost thirty years old. However, the impetus to change and redecorate is subverted by the structure itself. The interplay with nature provides constant seasonal change. Additionally, as spaces are not confining but rather interrelated, visually expandable areas, one’s perception of the structure changes.
Having spent much of my formative years in the house, I must heartily agree with Winston Churchill’s belief: “We make our buildings then our buildings make us.”
…The shingles on our house are grey stain and the interior carpet is green bordering on chartreuse. The “wire” fountain was long ago replaced by BG with a string and mirror sculpture. The lily pool is a square while the swimming pool is the elongated hexagon which is the shape of the shingles. Tvo tables are circular while two low tables are the negative space of the moon doors where the glass was inserted. These were impromptu designs which Goff devised when he saw the quality of the grain in the Japanese Ash which is used throughout the house. He felt the wood too beautiful not to use. This inspired the salvaging of most of the negative spaces…These forms and anti-forms provide a pleasant repetition and visual reversal throughout the house. …Both staircases are standard metal spiral staircases. The treads of these have been wrapped in carpeting but would more closely approach a triangular shape than an octagon. The stools which Goff designed are metal reinforcing bars with balls on one end and circular cushions on the other the configuration repeats the crossed reinforcing bar design above each large skylight, over the chimneys and those on either post of the front gate.
Goff trimmed many areas with square mirrors in various sizes and textures. In the central skylight area there are downward pointing pyramids of these in the spaces where shingles come together. Along the front of the carport there are little rows of these mirrors set on edge. Although Goff used the octagon as a unifying shape, it does not in practice feel dominant. The drawer pulls are triangles and many cabinets and shelves are rectangles, cubes, or triangles. The doors have compressed squares and pyramids as metal trim. In living in the house and viewing the interior one is impressed by the interplay of many geometric forms rather than the dominance of one. The polyhedrality is to my mind far more complex than the repetition of octagons.
As to the personal side of living in an unusual structure, it has been a fascinating experience. It is hard for me to pull apart the influences and dissect what comes from being reared by people who hired BG, spending great quantities of time with him over a four or five year period when I was especially open to new ideas, and the influence of growing up in one of his creations. I always enjoyed living in the house growing up and often rated people by their reaction to it. I have been living here again recently and have a more developed respect for the design elements and the functionality. I am however still surprised by the fact that Kansas City or maybe the world in general has not yet caught up with Goff. It still rather startles me when people comment on the house. I have been dealing with realtors and potential buyers in the past few months and am flabbergasted that many people believe it demands some strength of character to not five in a box. When we first moved into the house I was about 14 and thought it very cool and wanted all my friends to comment. Gradually however, I began to feel that those who felt compelled to comment on the house were simply displaying a very narrow mind-set. Time has moderated my stance somewhat. It was a fabulous house for teenagers in the sixties; a great place for slumber parties; a great place to awaken one to the value of environment and the importance of living with beauty and many other very valuable lessons. . . .
P.S. I just finished this after nightfall and forgot to include how the house is never really dark. There is always some moonlight or even reflected city lights it’s never like a windowless apartment bathroom. …Also during full moons when the moon is over my bedroom skylight I understand “lunacy.”31
William H. Bass House, Project, Tulsa, Oklahoma, 1956
Before discussing polyhedra in the Bass House (Figure 2.9), we will let others summarize its formal and functional aspects:
According to Architectural Design:
The car port is screened from the road by a low wall of translucent glass along two sides of a lily pool. A covered walk leads through the car port across the forecourt of white raked sand, with reflecting pools, to the main entrance at the right. Tall louvered aluminium “light trees” illuminate this area at night. The entrance door is of pale green marble, as are all closet walls and sliding doors for same. From the entrance hall we may go into the kitchen, at the left, or into the “powder room,” coat closets and stairs up to the balcony. Sliding translucent glass doors in gunmetal frames open into the marble-floored recreation room with fountain. This space opens out on to the screened porch and sliding translucent glass walls open to the carpeted parents’ living-room and the daughter’s living-room.
Figure 2.9 William H. Bass House, Project, Tulsa, Oklahoma, 1956. (a) Plan; (b) rendered aerial perspective; (c) roof plan. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
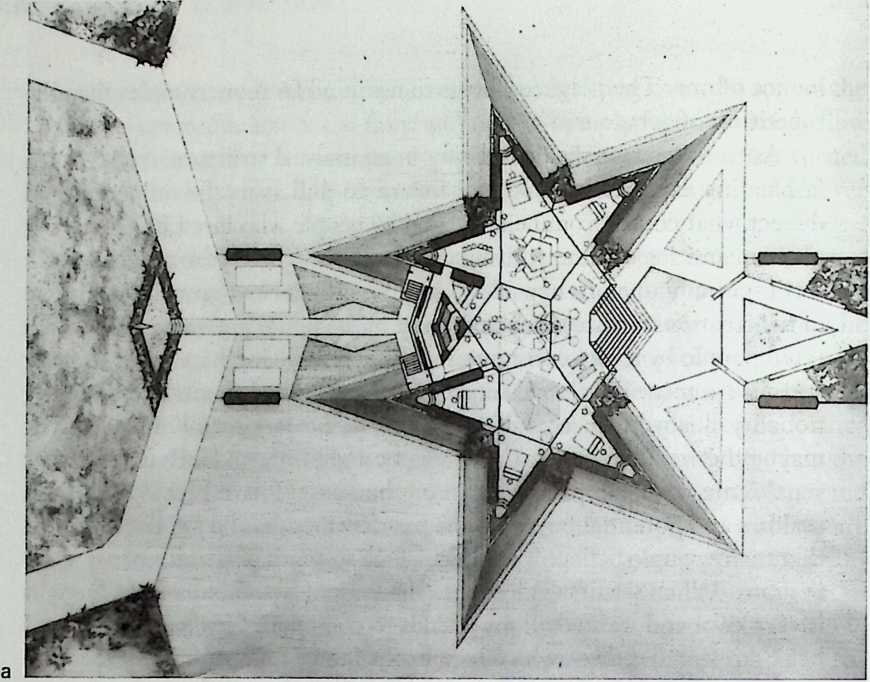
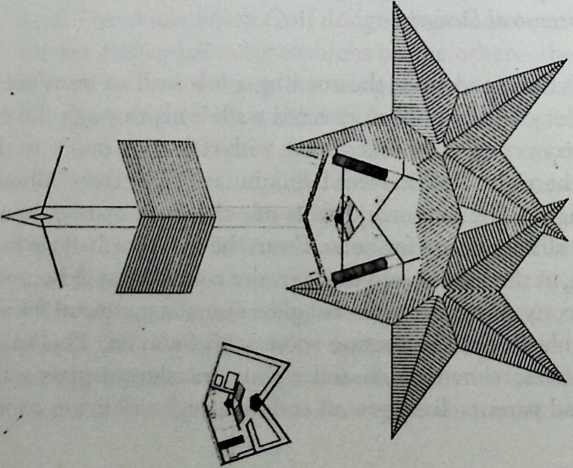
Bedrooms open off these living rooms, each with marble closet walls, dressing areas and baths. The dining-room opens off the parents’ livingroom and has direct service from the kitchen. A service entrance opens into this space, with servants’ stairs leading down to their rooms in the semibasement. A swimming pool adjoins the porch and dressing rooms and showers are connected by a wisteria-covered arbor.
The entire house is built on a star-shaped grass-covered berm, with gravel strip surrounding it for drainage. Sim bathing areas flank the swimming pool. The roof is of Stran-steel construction, covered inside with metal lath, sprayed with white acoustic-insulating asbestos …all furniture, including dinnerware, glasses, etc., will be designed by the architect. All baths are sunken marble-lined pools screened with translucent glass with planting beyond….32
And De Long:
…the Bass house projectresembles the Price Studio in appearance but is composed differently, for it extends the theme of the McCullough project…with modular shapes overlapped to form systematic variations of interior space. The repeating unit, however, is itself more complex: a five-pointed star. Four are overlapped to order both interior and related exterior spaces, and within the house a regular pattern of hierarchies results, with shared, private, and service areas given specific spatial character. These are programatically identical to the McCullough Scheme, and reinforce Goff’s tendency to express a Ghent’s desire for privacy through clearly defined geometries. Again he had produced a geometric metaphor for interlocking family structure [my emphasisRR], one that stood in marked contrast to the more conventionally open and unstructured designs of the time, almost as if compensating for that which he had rarely experienced but perhaps sought to honor. Typical of Goff’s approach is his three-dimensional realization of the modular unit, here achieved by angled planes that reinforce the star image…. The house was to have been constructed of steel joists, with an exterior cladding of pale blue anodized aluminum. Inside, pale green marble was to be used for floor and wall surfaces and, in sheets suspended from wheeled ceiling tracks, as movable partitions. Goff explained that while the clients approved the design, they were discouraged from building by the strong protests of the neighboring residents.33
The floor plan of the Bass project was based on three abutting pentagons suggesting dodecahedral development; however, the scheme developed instead toward a stellated pentagon (pentagram, or five-pointed star, two-dimensionally speaking). Two nonadjacent pentagon sides were extended until they intersected, creating an isosceles triangle, the base of which was the included side of the pentagon. In plan, the pentagon modules were each stellated on fewer than all five of their sides, resulting in partial pentagrams (Fig-
Figure 2.10 Bass House. Pentagon modules “stellated” into pentagrams.
ure 2.10). The plan is based on a stellated pentagonal grida small region of a quasicrystalline grid.
A startling expression of the pentagonal geometry was the double-star roof. Two intersecting pentagrams covered three pentagonal cores, their ridges bisecting the 36° pointed ends of the stars in a natural outgrowth of the plan. The roofs stars interpenetrated like mirror-image, twinned crystals. The owner was a two-star admiral! (Goff himself was in the Navy during World War II)not the first Goff literal translation of a client attribute into a specific formnote Goff’s entry in the Cowboy Hall of Fame competition for Oklahoma City, 1956, in which the buildings were shaped like horseshoes!
Interiors consisted of free-flowing regions defined by pentagramal pyramid ceilings whose bases were low triangular walls resting on perimeter facias or light troughs, the soffits of which became the ceilings of the star arms. The pentagons were further defined by screens, glass, storage walls, seating areas, and so on at key vertices. As in the Nicol House, major spaces were virtual prisms generated by plan elements capped by corresponding pyramids, with subsidiary outcroppings around their edges.
The roof over a typical star arm had conventional two-slope pitch; however, the following handling of surface planes contributed to the polyhedral character (Figures 2.11 and 2.12):
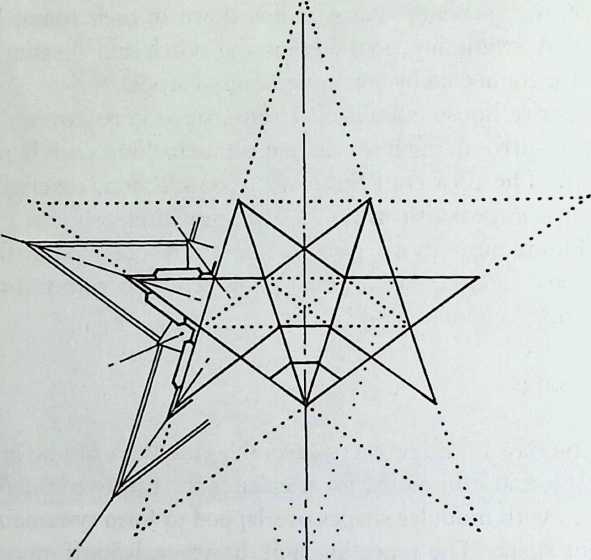
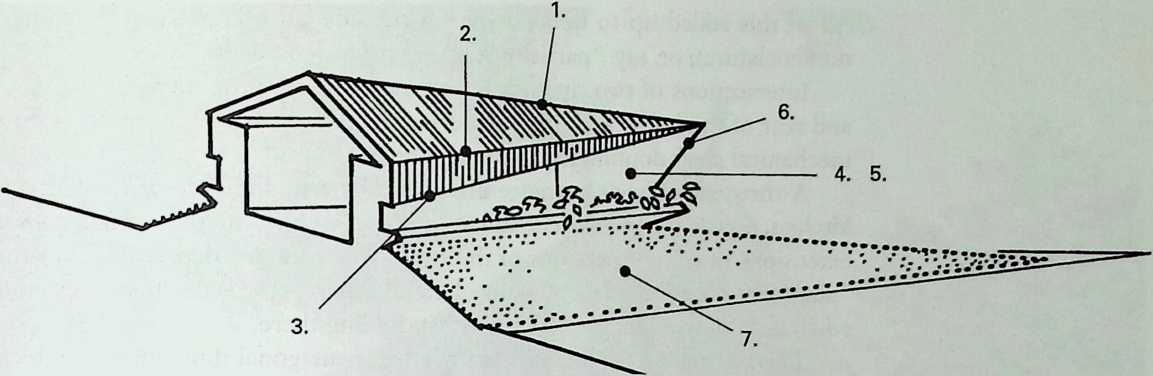
Figure 2.11 Bass House. Polyhedral star arm.
-
The ridge sloped upward from the outer tips of the star arms as the roof widened.
-
The roof consisted of four planes with three foldsthe eave folds are horizontal.
-
The lower roof surfaces wrapped down vertically onto the walls, in effect becoming siding, their bottom edges sloped downward from the end points, circumventing the conventional wall/roof dichotomy. The roof predominated and walls became secondary. Examples of other Goff designs that employ this device are the Rudd icosahedral bedrooms, the Price Studio, and the Crystal Chapel.
-
Glazing the ends of the star arms removed the vertical wall planes and let the roof polyhedra dominate.
-
These glass walls tilted out at the topcreating a pentagonal cross section.
-
The apparent slope of the glass was doubled where the two sloping glass planes abut at the pointed ends of the star arms.
-
Landscape berming repeats the dihedral, pointed roof pattern, emphasizing the pentagram fingers. Angular planters articulate vertices where the star arms meet.
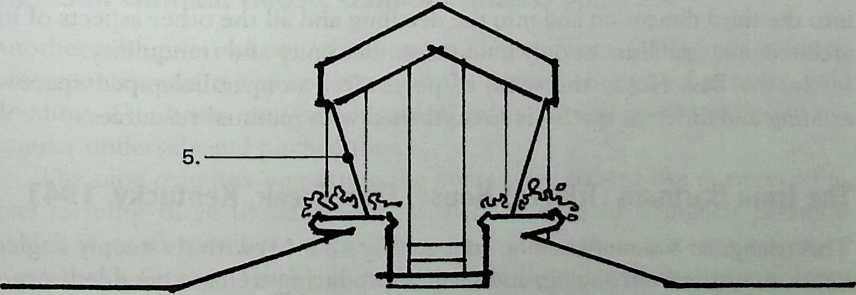
Figure 2.12 Bass House. Section through star arm.
All of this added up to quin-or pentapyramids (an extension of di-pyramid nomenclature); or, say, “partially-stellated-proto-icosahedra.”
Intersections of two tip ends of the star arms are prominent in the front and rear of the housethe front intersection being articulated further into a mechanical shaft doubling as entrance totem.
A three-story front entrance area contains a multiplicity of functions kitchen, powder room, closets, and utility rooms. Covering these elements are extensions of central portions of the roofin a complex departure from the “purity” of the twinned pentagrams. Lateral halves of the star arms are extended straight beyond the ridge, rather than folding there.
The star theme proliferates in skylights, pentagonal diprism glass tables, stools and chairs, exterior planting, walkways, and sunken seating areas.
John Sergeant observes:
On a larger scale, the same problem [i.e., an “erosion” of the centralized geometry for an “act of entering” which is “somewhat mean”] is exhibited in the Bass project…. A two-star admiral merits a grand plan with family pentangles; but ultimately there is the same clash between entrance and kitchen, which duel for the same geometric slot. The brilliantly developed geometrical hierarchy suffers from one of its points being a dining room while the others are bedrooms.
It has been argued that this very abstract, “frozen” geometry is unworkable; it has been called “heraldic.” De Long, however, feels that it represents only an extreme development, and draws attention to the geometry as pattern. He suggests that the complication and ambiguity of architectural experience which result from such plans parallel the aims of Sufi architecture, where complex overlapping pattern was used to sustain contemplation. This may be so, but Goff’s handling of symmetry must also be set in Western culture.54
As this design is unbuilt, no one can vouch for the static-ness versus the fluidity of the interior space from direct experience. However, based on built designs with similarly strong generating patterns, for example, the Pollock/Warriner, Wilson, Nicol, and Price residences, the strength of the geometry and the rigor and variety with which the Bass pentagonal theme is carried into the third dimension and into the detailing and all the other aspects of its architecture, establish not only uniqueness, but unity and tranquillity.
In the Bass House the sense of polyhedral, nonparallelepiped spaceexciting and different spaceis strengthened with minimal resources.
The Irma Bartman (Triaero) House, Fern Creek, Kentucky, 1941
This triangular summer vacation cottage (Figure 2.13) with its steeply angled struts, dramatic overhanging, and shadow-producing trellises heralded several features that were later to appear in the Bass design: glass end walls, inclined wall storage units, and wraparound, ribbed siding. Together these elements
Figure 2.13 Irma Bartman House (Triaero), Fern Creek, Kentucky, 1941.
dramatized the acutely angled corners of the plan, producing a feeling of more than just a prismatic, vertically extruded volume, in short, creating the emotional dynamics resulting from the use of polyhedra. The storage areas and glass end walls are a sort of hexagonal diprism, capped and enclosed by a triangular roof and stanchions that form a truncated octahedron.
The Emil Gutman House, Gulfport, Mississippi, 1958
Another triangular scheme, the Gutman House (Figure 2.14), built in hurricane country, was raised one story off the ground on pipe columns to avoid flooding. The house was “wind-proofed” by its “airfoil” profile of sloped triangular underside and pitched roof.
The pipe columns supporting the house were arrayed like outspread fingers forming three tetrahedra-like clusters or inverted triangular pyramids (which were to have been enclosed in the first design, as were the towers of New York’s George Washington Bridge). In three tetrahedral pipe column clusters, a single one-inch-diameter steel rod tension member tied down the cantilevered floor trusses. Professor Robert Faust, of Auburn University, who
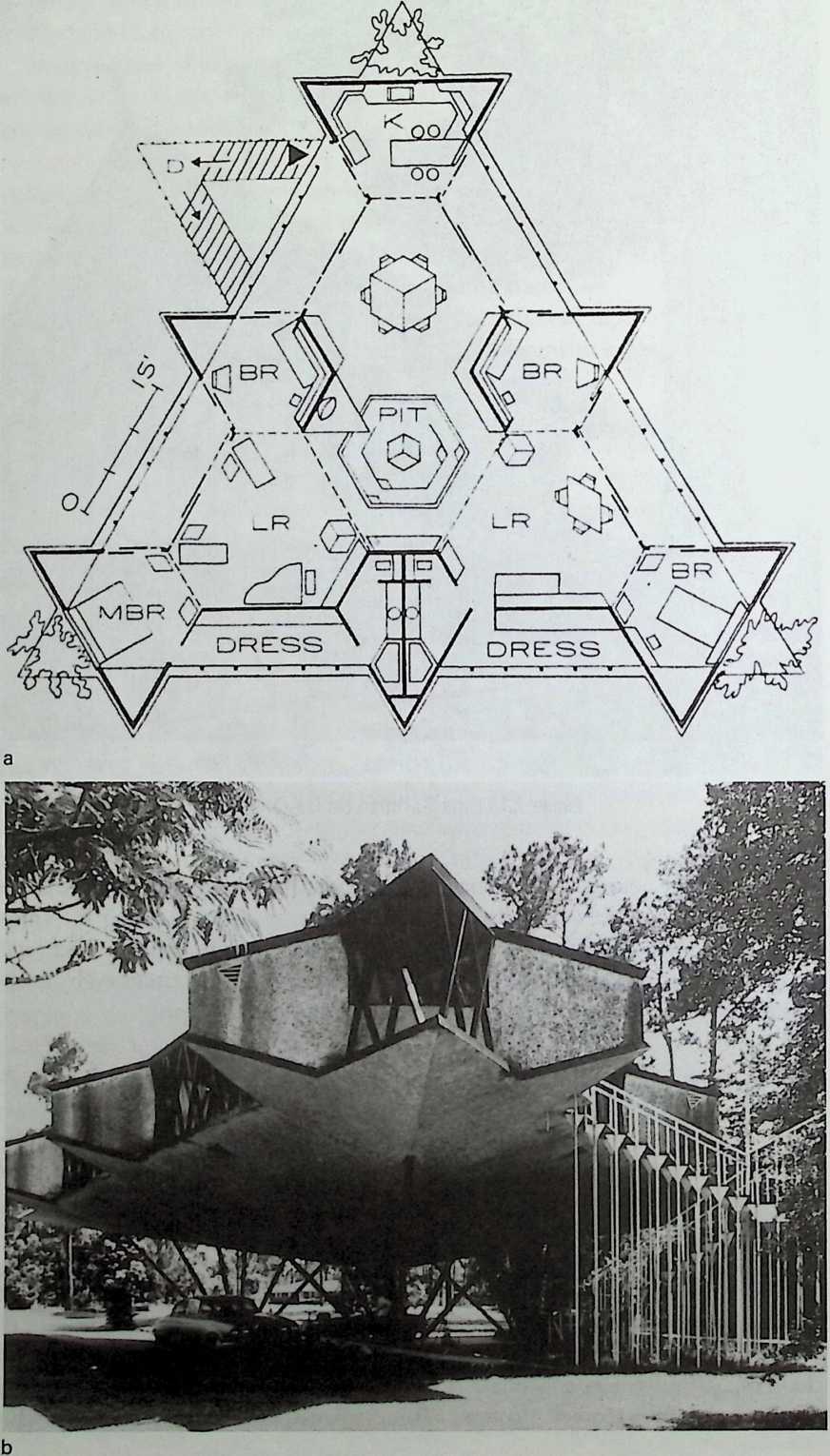
Figure 2.14 Emil Gutman House, Gulfport, Mississippi, 1958. faPlan; (b) exterior photo. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
organized and supervised the construction was worried about those rods if anything happened to one of them (e.g., a fire), presumably down would come the house. There was a fire, but it affected other parts of the house.
Faust said construction work on the house, which went smoothly, caused a great deal of excitement. Passers-by (many of whom were from the local Pensacola area) thought it was a bridge under construction, among other things.
The geometry of the scheme as a whole is based on a triangular grid hierarchy with a unit triangle of 7 feet on a side (Figure 2.15a). The structural supporting legs conform to this geometrythree inverted pyramids forming a tetrahedral/octahedral space-frame-like unit (Figure 2.15#). The interior spaces were generated by vertically extruding into prismatic volumes a plan tiling of triangles with one, two, or three comers truncated, creating both truncated rhombi and hexagons with unequal sides arranged within a larger overall triangle. The resultant plan is essentially a tessellation of equal-and unequal-sided hexagons with sides defined by partitions of varying degrees of
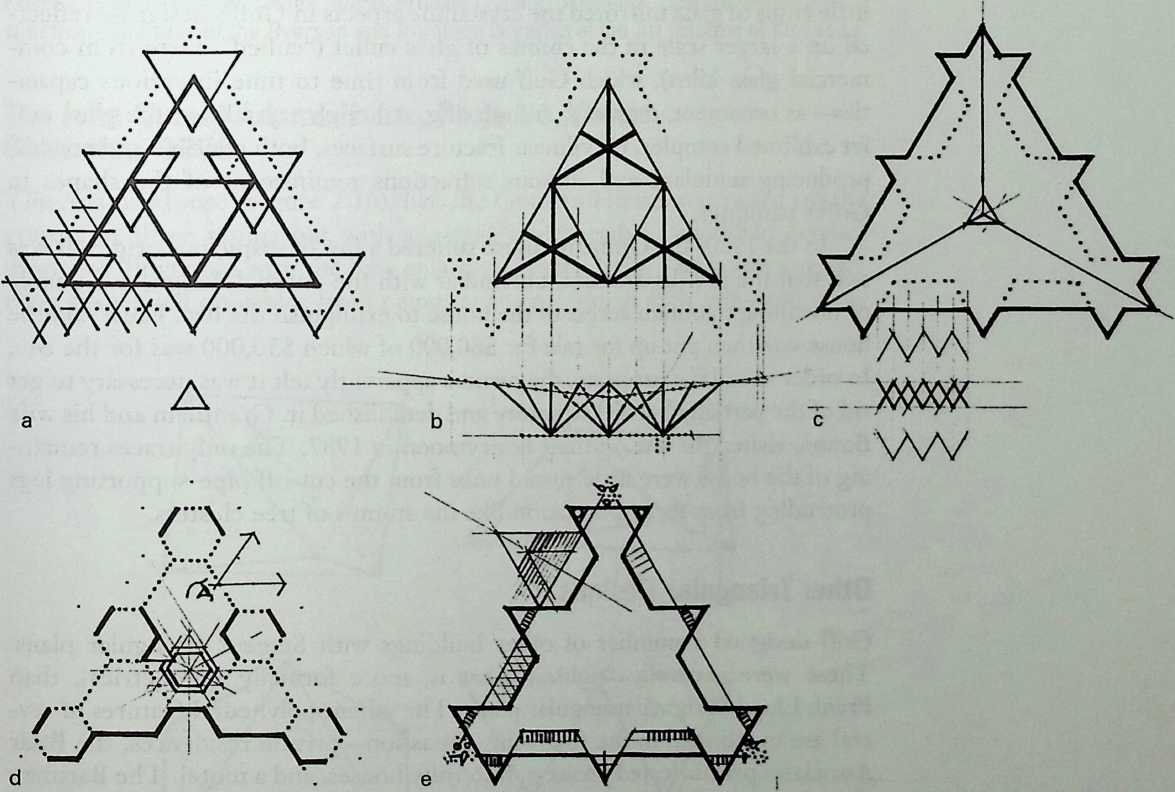
Figure 2.15 Gutman House, fa) Geometry, triangular grid hierarchy; (b) structure, inverted pyramids of supporting legs form a tetrahedral/octahedral space frame (with elevation). (c) roof plan, pyramid, soffit under similar (with elevation of diagonal structure), (d) open interior spaces hexagonal tessellation, partition transparency and views, (e) peripheral service elementsclosets, planting, porches, utilities.
transparency and movability, for example, drywalls, sliding glass doors, fixed glass, and folding wood doors as room dividers and closet doors (Figure 2.15d). In plan, again the polygon variations differentiated private, family, utility, and server spaces. In the Gutman House, however, most of the service elements closets, planting areas, porches, utilities, stairsare on the periphery (Figure 2.15e). The regularity, truncation, and size gradation of opposing triangular modules is clear in the Gutman House. Alternate triangular prisms are expressed on the exterior corners and midsides of the larger triangle. All are sandwiched between shallow triangular dipyramids (hence “airfoil”). In other words, the roof (Figure 2.15c) is a shallow pyramid capped by a single-module tetrahedral skylight; the underside or soffit is a similar, but inverted, pyramid, the bottom of which accommodates a sunken seating area, the floor framing and mechanical equipment while portions of the upper pyramid are recessed to reveal sloped ceilings.
Faust said one thing that did not work as well as Goff expected for the Gutman House was the use of little chips of broken plate glass added to the stucco and to the driveway to make them sparkle. Albeit unsuccessful, these little chips of glass mirrored the crystalline aspects in Goff’s designsreflected on a larger scale in the chunks of glass cullet (“culled” waste from commercial glass kilns), which Goff used from time to time in various capacitiesas ornament, masonry, and glazing. Athough crystalline, the glass cullet exhibited complex, curvilinear fracture surfaces, both concave and convex, producing undulant and sinuous refractions reminiscent of the shapes in Goff’s paintings.
In the 1980s the Gutman House suffered a fire of suspicious origin. It was said that the fire department, unfamiliar with the unusual design, was unable or unwilling to obtain access to the house to extinguish the fire. Faust said the house was then put up for sale for $80,000 of which $50,000 was for the site. In order to sell the property, the owners apparently felt it was necessary to get rid of the partially burned structure and demolished it. Grantham and his wife Bonnie visited the site on their honeymoon in 1987. The only traces remaining of the house were little rusted nubs from the cut-off pipe-supporting legs protruding from their foundation like the stumps of tree clusters.
Other Triangular Designs
Goff designed a number of other buildings with Stage 2 triangular plans. These were generally “tighter,” that is, more formally symmetrical, than Frank Lloyd Wright’s triangular plans. The salient polyhedral features of several are mentioned in the following discussionprivate residences, the Briar Associates prefabricated projects, fraternity houses, and a motel. The Bartman (Triaero) House was discussed previously in conjunction with the Bass House. The Price Studio designs and the Crystal Chapel are covered further on. The Searing House was noted in passing. Each provides a unique example of a variation on the triangular themebut they are by no means all simply prismatic spaces extruded vertically from triangular plans.35
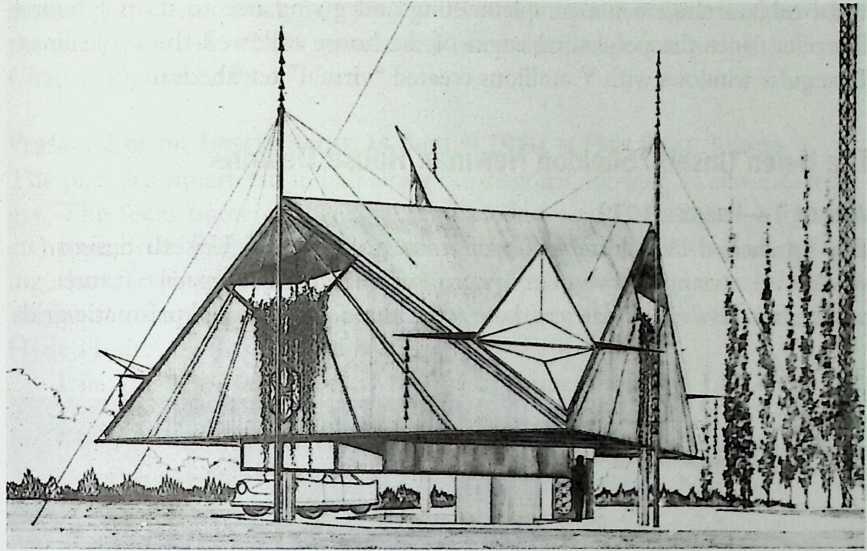
Figure 2.16 John Quincy Adams House, Project 1, Vinita, Oklahoma, 1958. Rendered perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
The John Quincy Adams House, Project 1, Vinita,
Oklahoma, 1958
The Adams House (Figure 2.16), like the Gutman House, was raised off the ground at three points but with a garage underneatha modified octahedron or dipyramid with the base enlarged (Figure 2.17). The house was partially suspended on cables from pylons at the centers of each sidethe pyra-
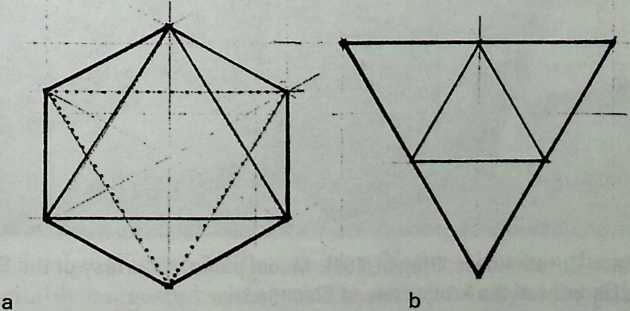
Figure2.17 Adams House.
(a) Octahedron, two views; f/V Adams House, side view and plan.
midal cable arrangements complementing and giving rise to its polyhedral character, since the polyhedral edges of the house followed the cable lines. Triangular windows with Y mullions created “virtual” tetrahedra.
The Helen Unseth/Sheldon Newman House Designs
Version 1Project, 1939
The tetrahedral-like clusters of roof trusses of the first Unseth design (an equilateral triangle in plan) were not rigorous space frame or tetrahedral-octahedral matrices, but rather, three-dimensional prismatic grids
Figure 2.18 Helen Unseth House, Project, 1939. Model photo. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
resulting from interlocking two-dimensional trussesan early suggestion of the Sierpinski arrowhead mentioned below in connection with the Crystal Chapel (Figure 2.18).
Version 2 of the Unseth House, as Built in 1940, in Park Ridge, Illinois
The plan is a square cut in half along the diagonal, forming an isosceles triangle. The focal point of this small and modest-seeming house is a dynamic composition of fireplace opening, sunken hearth, flue, windows, and skylight, together carrying into the third dimension the diagonally cut-square theme. A similar functional/polyhedral cluster surrounding a fireplace was seen in the Hyde House, discussed previously.
Triangular windows are covered with shutters that are “die cut,” as it were, from the continuous diagonally lapped board siding. When opened, a shutter, together with its window opening, create a virtual tetrahedron. A similar polyhedron is implied in a corner of the bathroom by two back-to-back triangular windows.
The present owner of the house, Sheldon Newman, feels that the house is a bit small for his present needsbut that the character of the house more than compensates. Mr. Newman said he felt that to know a Goff house one should know about the client, because Goff carefully tailored his designs to their needs. From neighbors he found out that Ms. Unseth was an artist and horticulture lover who had planted most of the sitenow fully mature over half a century later. From the interiors the windows bear a striking relationship to the trees and bushes outsidethe 45° angled sloping sills provide surprisingly harmonious frames for the spreading crowns of the yard foliage. (The same is true of the Nicol House windows.) A tiny triangular window at the floor level may have provided a view of a favorite plant outside.
Briar Associates Projects, Bartlesville, Oklahoma,
1963 and 1964
Goff again used triangular and hexagonal prisms (vertically extruded Stage 2) in the several designs for the Briar Associates prefabricated structures. House A was based on the hexagon whereas House B and Cabin A were based more on truncated triangular prisms. Cabin A, with its clearly expressed riveted metal shell, was supported and raised above grade, like the Gutman House, on three steel finger-like “quadripod” arraysinverted pyramids. Triangular windows at the corner truncations of Cabin A (similar to those of the Nicol House) were shaded by the sharply pointed cantilevered prows of the roof, which extended the equilateral triangle of the plan out to its vertices.
Black Bear Motor Lodge, Project, Jackson Hole, Wyoming, 1961
The tepee-like tetrahedral “dormer” windows that enliven the roofs of the Black Bear Lodge (Figure 2.19) connote a Native American themea theme that is inevitably suggested whenever a conical (or many-sided polygon-based
Figure 2.19 Black Bear Motor Lodge, Project, Jackson Hole, Wyoming, 1961. Rendered perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
pyramid) form is used, as in Goff’s Crested Butte Lodge and a number of other projects. The Black Bear motel rooms are grouped into three rectangular blocks, which in turn are arranged as a triangle. Within this triangle are three dining, communal, and service tetrahedral spacesall one story above grade. This frees up the ground level for parking, circulation, landscaping, and a swimming pool at the center, which is open above. Tapered skylights cap the ridges of the tetrahedral roof of each major space and, together with a similar tapered spire from the peak, create a four-pronged (tetrapodal), stellated-like crown (Figure 2.20) three of which dominate the motel silhouette. Zigzag masonry walls enclose the whole and frame sharply pointed balsam fir and spruce trees, which echo the rooftop spiresall set against and perhaps inspired by the jagged mountainous backdrop.
Figure 2.20 Black Bear Motor Lodge. Tetrapodal crown/skylight.
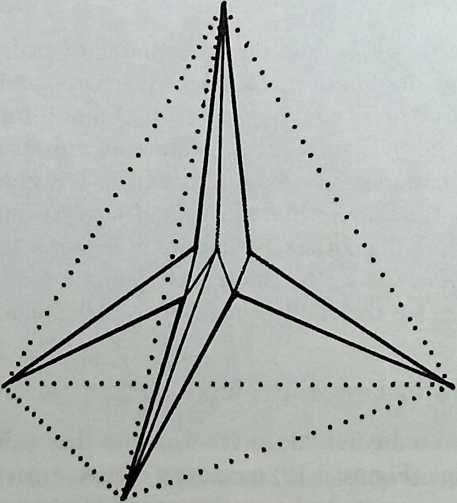
Figure 2.21 Phi Sigma Epsilon Fraternity House, Project, Talequah, Oklahoma, 1962. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
Phi Sigma Epsilon Fraternity House, Project, Talequah, Oklahoma, 1962
A series of “A-frame” structural members created a triangular prism upon the sloping wall/roofs of which nestled rows of complementary triangular prism “dormer” windows (Figure 2.21). A similar volume, but a negative variation on the prism, provided an inviting and protective entrance. Related clusters of rooms occur in the fraternity houses and the motels as they are both multiunit residences.
W.R. MacBryde House, Project, Kansas City, Kansas, 1959
The MacBryde House (Figure 2.22), like the Gutman and Adams houses, is raised one story with the garage remaining at grade. Diagonal corner porches are joined visually by railing walls with sloping tops that create an illusion of the entire house resting on a flattened half-cuboctahedral base. Like the Gutman House, interior volumes are expressed on the exterior as triangular prisms with sloping bases, penetrating the partial cubocatahedron that defines the perimeter. As in the Pollock/Warriner House, here the structural framing runs at a 45°angle to the overall massing of the house.
Figure 2.22 MacBryde House, Project, Kansas City, Kansas, 1959. (a) Birds-eye perspective; fworms-eye perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
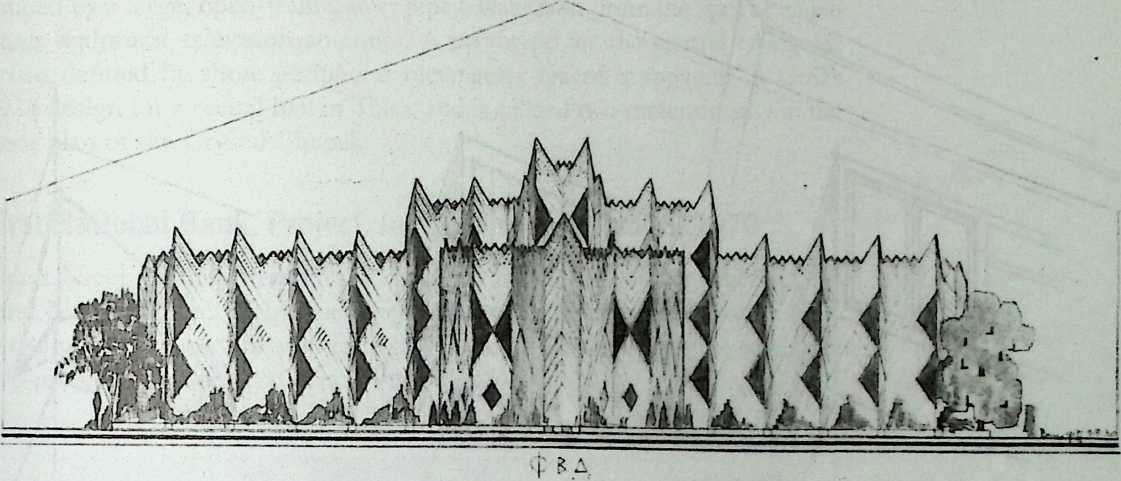
Figure 2.23 Phi Beta Delta Fraternity House, Project, Norman, Oklahoma, 1930. Rendered elevation. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
Phi Beta Delta Fraternity House, Project, Norman,
Oklahoma, 1930
The Phi Beta Delta Fraternity House (Figure 2.23) was an elaborate Stage 1 project, basically a T-shaped plan, with its member cells cantedproducing a “sawtooth” plan, which gave each room a corner window, expressed the multiplicity of rooms, and created a dynamic, spatial exterior. Goff had designed a high school in 1930 along similar, serrated lines. The corridor between two banks of rooms, as a result of this canting, contained wedge-shaped volumes, which would have invited “schmoozing.” A typical cell comer window consisted of back-to-back triangles again, the virtual tetrahedron (Figure 2.24). These “tet” volumes dominated the exterior of the building and the balance of the exterior wall surfaces were diagonally and triangularly patterned and scaled so as to unify them into an abstract composition (what today we might lazily call art deco), emphasizing the vertical stacking of rooms and downplaying the horizontal. Frank Lloyd Wright used the wraparound window early on (e.g., the Henderson House, 1901), as did Le Corbusier (e.g., the Amedee Ozenfant Studio, 1922).
Pi Lambda Phi Fraternity House, Norman, Oklahoma, 1955
As in the Black Bear Lodge, the mostly rectangular spaces in the Pi Lambda Phi Fraternity Housea dining room, private rooms, and offices were contained in three longer rectangles, which in turn defined the edges of a large, two-story, interior triangular commons (Figure 2.25). At the three comers where these rectangles met, the resulting triangular entrance and related spaces were extruded vertically into prisms. A very flattened half-cuboctahe-
Figure 2.24 Phi Beta Delta Fraternity House. Corner windows compared: (a) Frank Lloyd Wrights Henderson House, 1901; (b) Le Corbusiers Ozenfant Studio; (c) Goffs Phi Beta Delta Fraternity House, virtual tetrahedron.
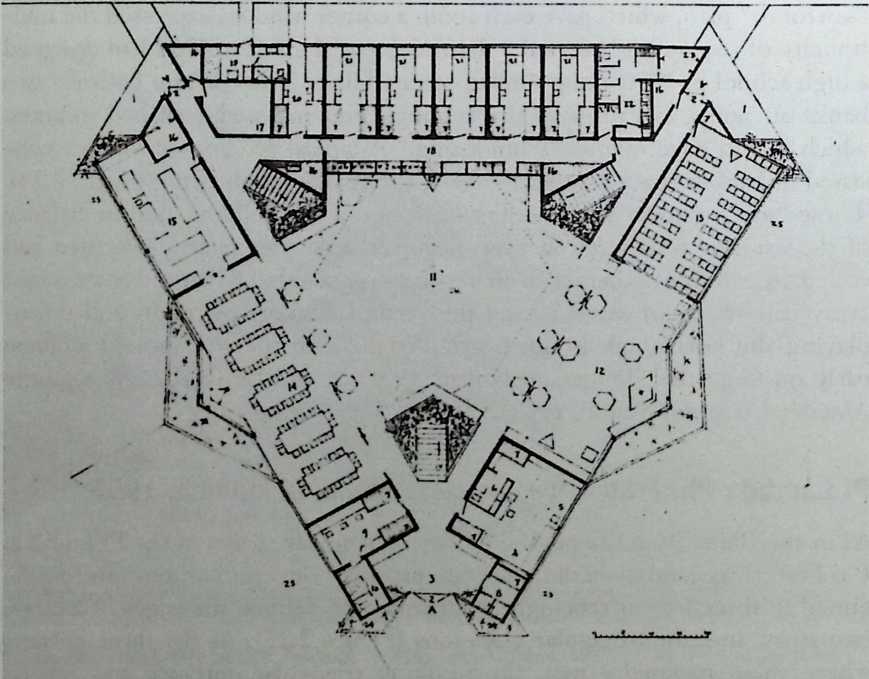
Figure 2.25 Pi Lambda Phi Fraternity House, Norman, Oklahoma, 1955. Plans. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
dron roof with triangular clearstory windows covered the communal area, topped by a large, open-frame, steel pipe tetrahedron, from the apex of which hung sculptural television antennas. A prototype for the central triangular prism defined by three peripheral rectangular spaces is apparent in Goff’s 1924 design for a recital hall in Tulsa, and is echoed two-dimensionally in the floor plan of the Crystal Chapel.
First NatioiniaD Bank, Project, Independence, Missouri, 1970
James Nicol (of the Nicol House discussed previously) was an officer of the First National Bank of Independence (Figure 2.26) and was instrumental in getting Goff the commission for a new building for the bankthe second of two projects (the first had been a remodel).
Figure 2.26 First National Bank, Independence, Missouri, 1970. Rendered perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
The core of the bank was a load-bearing structural steel frame enclosing stairs, elevators, and utilities. The structural members of the core were exposed at the top of the building and cutaway into a crown that formed half of a virtual cuboctahedron. From this core were cantilevered floors of graduated lengthsone could argue that this might lend variety to rental potentialcreating the most striking polyhedral element of the buildinga tower mass as a square rotated 45° to stand on its corner. The visual device of increase in width toward the top was used occasionally by Wright, for example, the Rogers Lacey Hotel project in Dallas, 1946,56 and, of course, the Guggenheim Museum in New York. Goff’s design, however, increases in width much more rapidly from the base upward to its midpoint and then decreases equally. A square with this orientation seems less a squaremore a quadrangular polygon its corners predominant. The edges we are used to in conventional architectural boxes are either parallel to the ground or vertical, the comers scarcely noticed. This portion is Stage 2a horizontally extruded, nonrectilinearly oriented, rectangular parallelepiped.
Adding to the dramatic mass of the square on its corner was a robust, deeply patterned Cor-ten steel curtain wall. Although he obtained commissions for a variety of high-rise buildings, Goff never had occasion to use modular polyhedral units in vertical close packingonly a suggestion appeared in the First National Bank curtain wall. Was the honeycomb-like cladding intended to allude to the beehive of the office environment?
This polyhedral curtain wall was based on a familiar tessellation of octagons and smaller squares with the same edge length as the octagons, turned 45° in sync with the office tower massing. This grid appears in the plans of the Jones, Wilson, Pollock/Warriner, and Nicol houses discussed in this chapter and in the Innis House, Project, Coronado, California, 1943, among others. The octagons of the First National project acted as the bases of shallow (having a short altitude relative to the width) but visually powerful pyramidsthe octagons were largeequal to the story height. The intermediate squares and their vertically pivoting window sashes when opened 90° formed virtual octahedra (Figure 2.27).
The purpose of this pyramidal dimpling was the same as that of the pressed metal patterns employed frequently for cladding of commercial buildings from the 1950s onward, such as the aluminum curtain wall of the 666 Building in New York to stiffen a thin metal sheet and simultaneously provide some tex-ture/omament. Goff’s wall had a real depth but, at the same time, imparted an even greater illusion of depth through its pyramid symbolism.
Fitting the multipyramidal integument to the sloping ends of the 45° office block was accomplished by a slide transformation in which the pyramids were cut so that five segments stayed in place and three slid inward to the next story (Figure 2.28). “Slide” surfaces resulted in an accordion pleat, strongly defining the sloping end walls. This curtain wall is a proto-Stage 4 polyhedral tessellation.
Cor-ten steel was the rage for a while in the 1950s and 1960sit was a preoxidized (rusted) steel alloy that would presumably oxidize only up to a
Figure 2.27 First National Bank, Independence, Missouri. Virtual octahedron window.
Figure 2.28 First National
Bank. “Slide” surfaces result in accordion pleat.
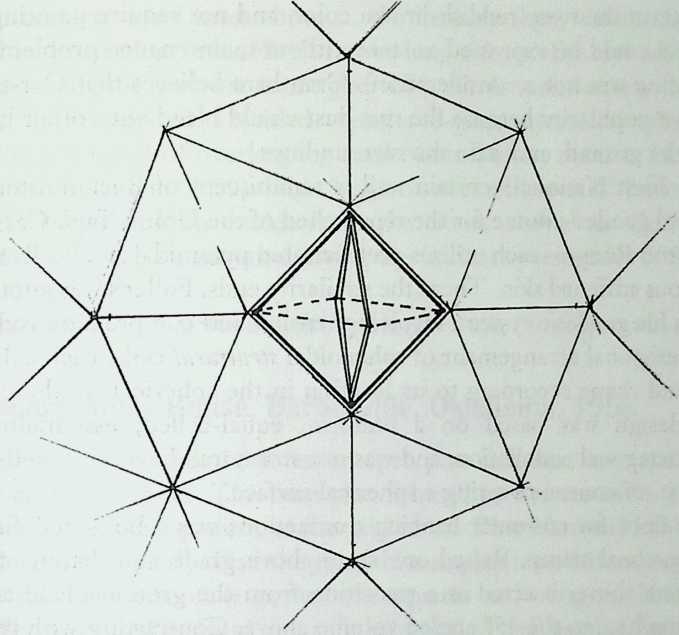
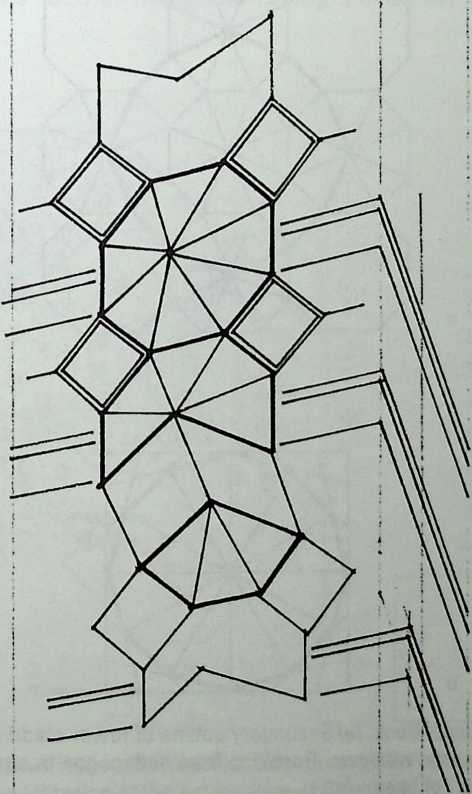
point, retain die rusty reddish-brown color, and not require painting. Structural steel could be expressed as steel without maintenance problems (where fireproofing was not a consideration). Grantham believes that Cor-ten eventually lost popularity because the rust dust would bleed onto other buildings, drip to the ground, and stain the surroundings.
The First National’s curtain wall is reminiscent of Buckminster Fuller’s 1958 steel geodesic dome for the repair shed of the Union Tank Car Company in Baton Rouge each utilizes prefabricated pyramidal steel cells to form a continuous stiffened skin. There the similarity ends. Fuller’s was another variation on his geodesic system, involving tension and compression rods as part of the hexagonal arrangement of sphenoidal structural cells, each cell varying in size and shape according to its location in the spherical geodesic pattern. Goff’s design was based on a uniform, equal-celled, essentially planar, square-octagonal tessellation, and was not structural, beyond its self-bracing, nor was it, of course, covering a spherical surface.
The floor for customer banking transactions was a boxredefined with Goff’s personal stamp. Raised one story above grade and distinct from the office zone above, it acted as a transition from the ground plane and as an underlying base to the 45° angled volume above. Contrasting with the opaci -
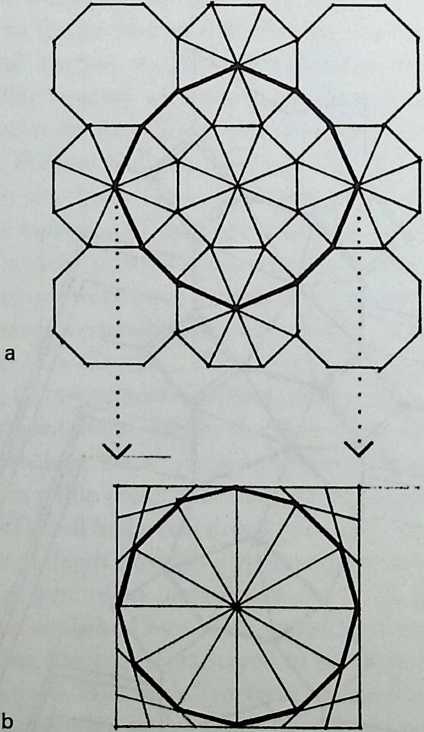
Figure 2.29 First National Bank, (a) Secondary outline of tower cladding is reflected in (b) banking floor rondelle windows. Transition from dodecagon to square frame is done with “curve stitching” of beams.
ty of the textured steel mass above it, the banking floor was transparent enclosed by giant glass “rondelles” on one long side, on the end walls, in the ceiling as skylights, and set in the floor as well. A variation on the tower cladding, it comprised 12-sided, tempered-glass pyramids whose base perimeters consisted of overlapping steel beam frames, another example of curve stitching (Figure 2.29). This “cage of steel and crystal” hovered over the plaza, suspended on cables from the floors above. As Goff said to Grantham (who spent a month drawing the intricate perspective), “Same old unusual stuff.”
When First National was bought by a larger bank, the project was dropped.
The Howard Jooues House, Bartlesville, Oklahoma, 1958
The Jones House (Figure 2.30) has an open plan that does not readily admit to polyhedral discoveries. The floor plan is based on squares and octagons in tessellationthe same pattern as the grid of the First National Bank curtain wall discussed previously. Had the Jones House plan tessellation been carried into the third dimension (e.g., had the squares and octagons been orthographically projected in front and side elevation as well as plan) to create an aggregation of polyhedral cells, it might look something like the schematic representation of a sodalite crystal.”
Major functions such as living and dining inhabit the various octagons,
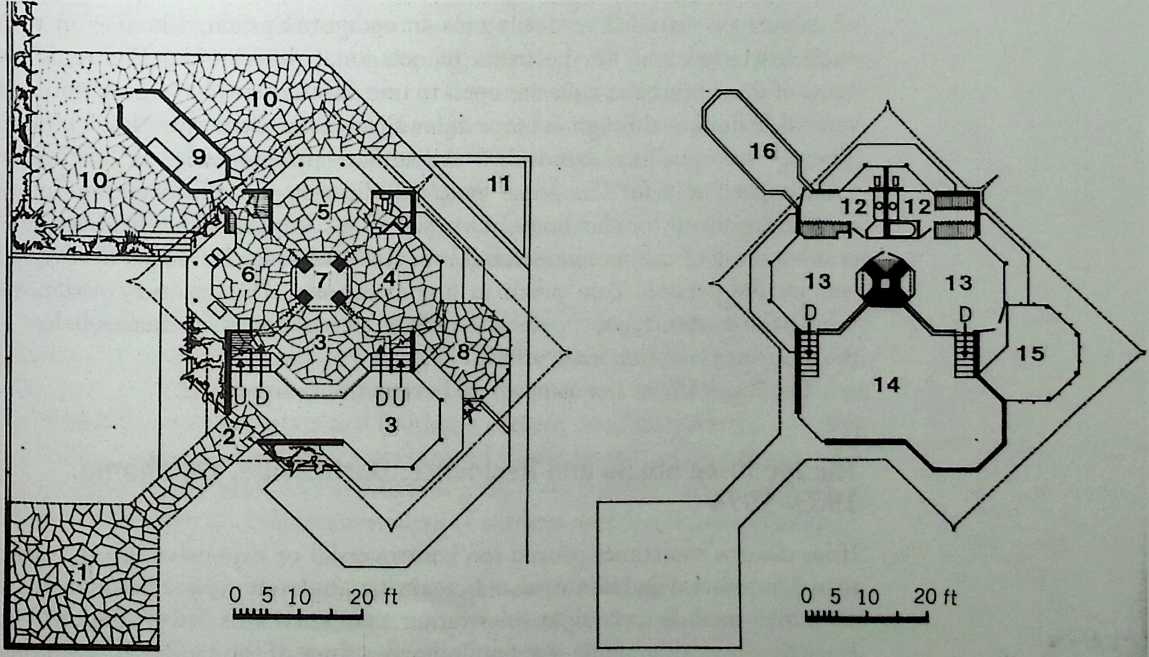
Figure 2.30 Howard Jones House, Bartlesville, Oklahoma, 1958. Plans. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
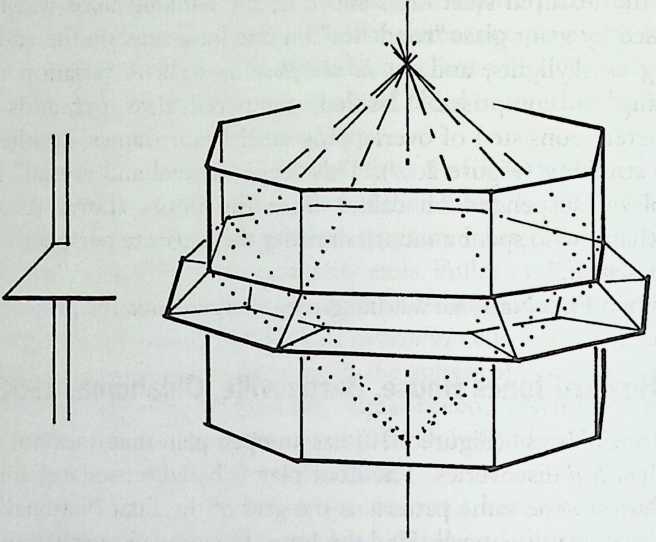
Figure 2.31 Howard Jones House. Octagonal prism penetrated by octagonal dipyramidsschematic view and section.
which He at different levels, whereas the square elements comprise circulation and service modulesstairs, fireplace, and so on. A basic unit of space consists of an octagon extruded vertically into an octagonal prism, which is in turn encircled by portions of the frusta of octagonal dipyramids (Figure 2.31). Most of these prismatic units are open to one another and have only minimal vertical definition through exterior sidewallsfewer than the Nicol House. The frusta girdling bands of triangular prismsact as showcase window/shelf units for Airs. Jones’ pottery collectionan important architectural determinant for this house. One senses a complex and spacious openness a sense of the monumental. Three 1892 Oak Park houses by Wright contain the pyramid cum prism in a conventional 19th-century juxtapositionwith steep octagonal pyramid roofs on octagonal prism spaces belowthe Thomas Gale, Emmond, and R.P. Parker Houses.
The Jones House Hes somewhere between Stages 1 and 2.
The Joe Price Studio and Residence, Bartlesville, Oklahoma, 1953
If his designs sometimes proved too controversial or expensive, Goff, rather than compromise and dilute, would create a completely new scheme, using a simplified module or straight lines rather than curves or fewer angles. The Price Studio is an examplestepping down a rung of the ladder to a simpler polyhedral stagefrom Stage 3 to Stage 2.
Morphologically, the Price Studio designs were (in brief): Scheme 1lin-
ear clusters of rhombic frusta along the x, y, and z axes. This scheme was rejected for reasons discussed later. Scheme 2a was a “pinwheel” theme with vertical walls and a pitched roof. Scheme 2b had a similar plan but with sloping walls, creating less conventionally prismatic spaces. This scheme was built in 1956 and will be referred to in the following discussion simply as Scheme 2. It received two additionsa gallery and a meditation room.
Scheme 1
Scheme 1 (Figure 2.32), unbuilt, consisted of variations on rhombic frusta arranged in additive series or stacks along the x, y, and z axes. The approximately 90° opposition of each axis to the other two created a three-pronged reference armature in space, strongly expressive of three-dimensionality. The application of this spatial toolindividually articulated x, y, and z axiality (Figure 2.3 3zz)occurs not only in the multiplanar work of Frank Lloyd Wright (e.g., the Robie House) but also in that of Le Corbusier and Mies van der Rohe (the Barcelona Pavilion is an easily read example). In the Price Studio 1 nonrectilinear volumes, that is, frusta and prisms, rather than planes or boxes, are oriented along the x,y, and z axes (Figure 2.3 3£). The slight inclination of these axes to one another parallels a common property of crystals.
XAxis. The thematic unit volume of the Price Studio 1 was the rhombic frustum (Figure 2.34zz), extending horizontally and approximately perpendicular to the slope of the hillside site (Figure 2.34#). The cushioned, carpeted lower inclined surfaces of these frusta were seating/lounge surfaces.
Variations on this theme aboundlarge and small, frustum, pyramid, and prism, vertical, horizontal, and sloping, abutting and branching, and so on. The main studio space was a linear series consisting of two frusta of rhombic pyramids of different “altitudes” (I emphasize “altitude” because in this case it is horizontal, whereas we usually think of the altitude of a pyramid as being vertical) with their truncation faces abutting, plus two rhombic pyramids, in a generally ABB\AX relationship, with pyramid and frustum bases back to back (Figure 2.3*5a)*or two pyramids interpenetrating vertex to vertex with a rhombic pyramid terminating each end.
At each end of the x-axis array, dormers frusta sprouted like crystal growths or plant buds, a literal expression of organic architecturepart window, part skylight (inspired by the unfolding spout of a milk carton?) glazed by boring holes in the glass and bolting it direcdy onto the gasketed opening.
Side planes of the B frusta overlapped to shield and define bands of skylights, fighting fixtures, and ventilation grillesat the same time emphasizing the frustum edge and the separateness of surfaces and downplaying solidity.
Y Axis. Penetrating the x’-axis volumes at not quite a right angle in plan (in keeping with the rhombic theme, i.e., angles other than right angles) was a prism extruded parallel to the slope of the hill. The hill slope appears to have been a major determinant of the rhombic themethe hill’s angle of repose projected onto each of the x, y, and z dimensionsschematically, if
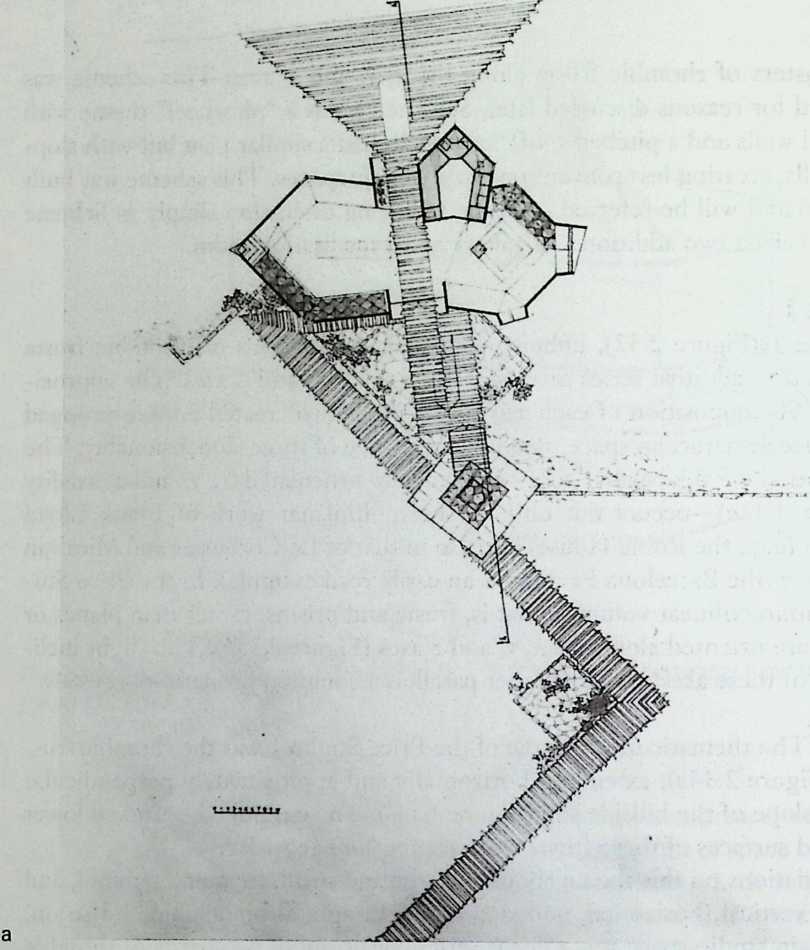
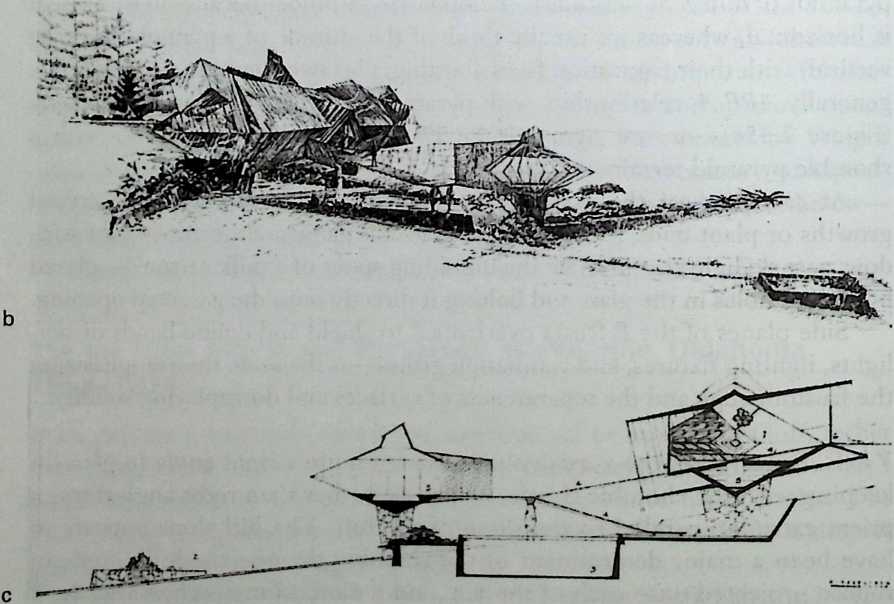
Figure 2.32 Joe Price Studio and Residence, Project (Scheme 1), Bartlesville, Oklahoma, 1953. (a) Rendered plan; (b) rendered exterior perspective; (c) section. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
Figure 2.33 Joe Price Studio, Scheme 1 (project), (a) Generalized x, y, and z axiality; (b)x, y, and zaxiality in the Price Studio.
Figure 2.34 Price Studio, Scheme 1. (a) Rhombic frusta; (b) hillside slope as generator of the angles of the rhombus.
not strictly. The base of this inclined prism was a square tilted at 45°. (The First National Bank was a variation on this theme.) A wood ramp within served as circulationcarport, entrance, and bridge. The prism acted as tunnel and watercourse for a stream passing through the house, terminating in a waterfall on the downhill side. In addition to square and triangular elements, the pentagon (if somewhat modified) can also be found in the Price Studio 1.
ZAxis. Several variations on the prism array were related to the (vertical) z axis. One was an outdoor lounge or screened porch (Figure 2.35Z>). This was an ABBiAi stack on a vertical axis, the bottom A acting as a stone base holding up the central BBi porcha dipyramid. A horizontal deck was placed within the canted sides of the inverted pyramid. It was topped by another A1 frustum
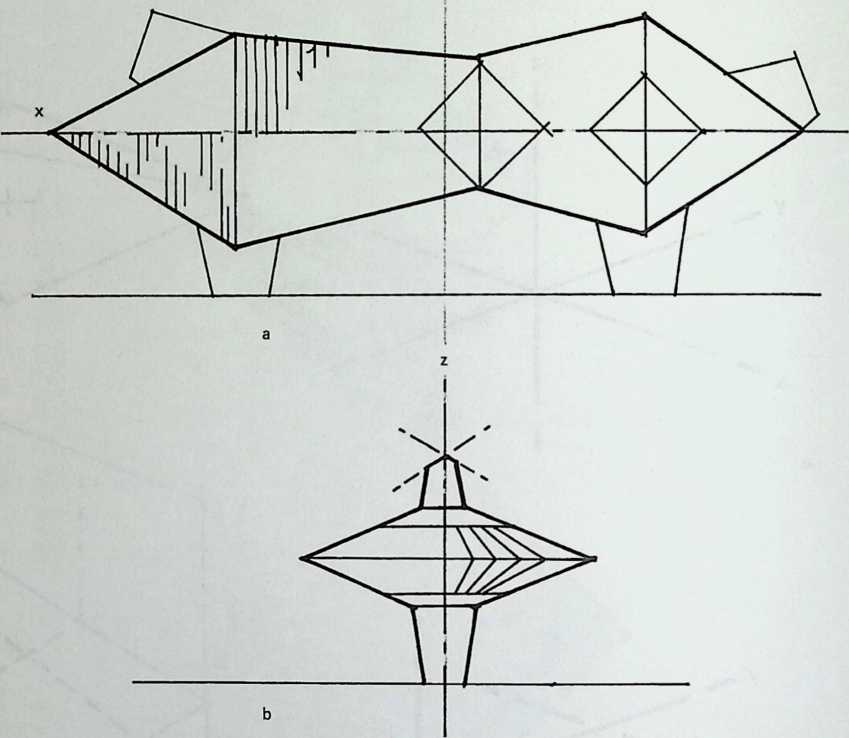
Figure 2.35 Price Studio, Scheme 1. (a) Main living area with horizontal ABBA arrangement of units; (b) screened porch, with a vertical variation of the ABBA sequence.
lighting fixture. The z-axis array consisted of, in other words, back-to-back bent pyramids. Another variation on the z-axis grouping was a kitchen/bath-room/darkroom service module near the entrance.
The rhombic polyhedra of Scheme 1 hint at the illusory effect of that well-known psychology experiment in which an object at the end of an experimental room with diminishing dimensions seems larger than normal because of the unexpected distortion in perspective. In other words, a frustum might exaggerate its own perspective, a property we will encounter again in the Crystal Chapel.
Early in the 1920s Goff heeded Wright’s admonition to his followers not to copy his forms but rather to find their own way. Goff was motivated to steer clear apparent in his propensity to create crystalline forms as spaces that could be occupied. According to Larry Grantham, who feels that Goff’s work can be interpreted as “building-as-ornament,” such spaces came about as the logical development of two-dimensional ornament being made three-dimensional. Goff contrasted this concept of “building-as-ornament” (a concept that he explored in his “273” design lab at the University of Oklahoma) with that of applied local ornament. In teaching, Goff characteristically neither advocated nor rejected these ideas, but simply put them forward as possibilities of which to be aware.
The Price Studio was sited directly across a shallow valley facing the Harold Price House designed by Frank Lloyd Wright. Wright reacted negatively to the design for the first Price Studio. After seeing the plans, Wright wrote a scathing letter to Goff in December of 1954, calling the design a “travesty,” an “elaborate and expensive fiasco,” and a “manifest aberration” that “violated the concordant repose.”38 (Similar barbs had been thrown at Wright’s work from time to time, e.g., against the Guggenheim Museum!) According to Grantham, Goff “altered his course forever after Wright pulled in the reins.” Scheme 1 was abandoned.
Scheme 2
Scheme 2 (Figure 2.36), built in 1956 (three years before Wright’s death), has a cross section similar to Taliesin West’s sloping rectanglewhich carries into three dimensions the nonrectilinear angles of the plan. To this angle of cross section, Goff compounded another angular motifthe diagonal orientation (approximately 20°-70°) of the gold anodized aluminum roofing/siding. The effect is both dynamic and illusionary, approaching a helix (Figure 2.37). (Nor is, incidentally, the 45°-90° grid of Wright’s Taliesin West plan repeated in its elevation/section it is approximately 15°recalling the slope of the background Paradise Valley mountains.)
Figure 2.36 Joe Price Studio and Residence (Scheme 2), Addition, Bartlesville, Oklahoma, 1956. (a) Loft; (b) photo of tile bathroom with pool above. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
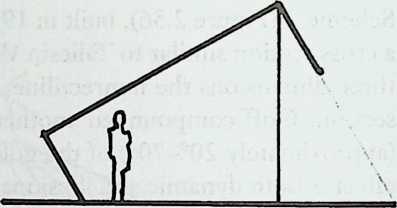
Figure 2.37 Price Studio, Scheme 2 (built). Schematic roof plan, elevation, and section.
The Price Studio is the most opulently appointed of Goff’s residences with its deep pile carpets, its famous goose-feathered ceiling, and its built-in Goff designed murals, sculpture, and stained glass; however, in terms of spatial concept, other designs were more daring, for example, the studio’s first scheme, the Bavinger House, the Dewlin Aparture project, and the first Garvey House design (the latter three are curvilinear).
Still, the Price Studio, as built with its additions, is a symphony of Stage 2 triangular and hexagonal prisms and dipyramids, of truncations, elongations, shifting axes, twinning, bi-and triaxial and rotational (pinwheel) symmetries of plan and roof structure (Figure 2.38), finials, stretching, bending, rhythms, branching, ornamentation, and texture.
For example, an aquarium at the center of the Japanese Painting Gallery (the first addition to the studioa hexagonal prism motif) consists of an inverted hexagonal pyramid, the faces of which are subdivided into shallow triangular (triakis) stellations (or pyramids). The water reflects and refracts, multiplying the edges, vertices, and planes, adding to the pool’s crystalline, polyhedral quality, giving it the feeling of a large cut diamond.39 A similarly framed skyfight was designed for the roof directly above.
A meditation room (the second addition to the studio), described by some as “kaleidoscopic,” reprises the rhombic frustum theme of Scheme 1, like Petroushka’s ghost. Its roof is a rhombus folded into an elongated tetrahedron (in crystallographic terms a tetragonal bisphenoid) and truncated at the ends to produce smaller, similar virtual tetrahedra (Figure 2.39). The windows of Scheme 2 are another variation of the folded rhombus/virtual tetrahedron.
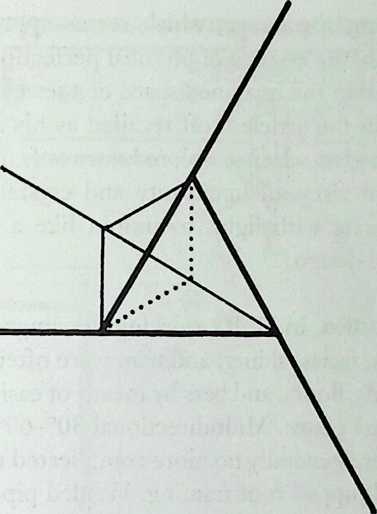
Figure 2.38 Price Studio, Scheme 2. Schematic “pinwheel” roof framing and pyramidal skylight over living room.
De Long discusses further symbolic and metaphoric aspects of the crystalline nature of Goff’s design:
Images of crystals …permeate his work, from such large-scale expressions as the Crystal Chapel…to such small-scale applications as the windows of the Snyder project…. In no example does such imagery seem more clearly intended than in the Price studio, beginning with the unbuilt project of 1953, where shapes shown in the exterior perspective closely resemble a quartz crystal Goff had in his collection…. In the built design of 1956 the crystalline forms of the aluminum-clad structure, reinforced by the prismatical details of the windows, sustain the image…. The studio appears to emerge from foundations of coal and encrusted glass as if it were a crystal in formation, recalling Expressionist postulations regarding the transformation of coal into precious gems, a form symbolic of the highest ideals. Manipulations of glass, mirrors, and coal within the Price
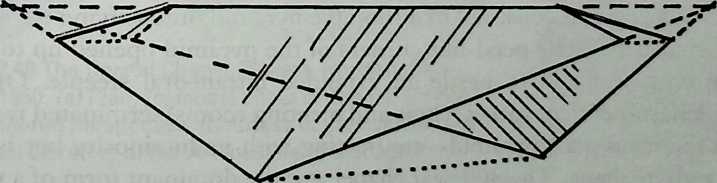
Figure 2.39 Price Studio, Scheme 2, second addition. Schematic roof configurationvirtual truncated tetragonal bisphenoids.
studio augment the image, which seems appropriately symbolic, for it would embody the essence of physical perfection and provide for an ideal retreat set within the imagined space of a jewel itself. This seems close to a statement in the article Goff recalled as his introduction to such concepts: “Thick glass, clear or colored, for roofs or walls or floors, opens up unconjectured vistas of luminosity and crystalline splendour, causing a house to vibrate with light, to unfold like a jewel of many forces, of dynamics and design.”40
A Note on Construction. In Goff’s working drawings 30°-60° elements such as window mullions, facias, siding, and trim were often anchored to 90° components such as studs, floors, and bars by means of easily shaped transition pieces such as bent metal plates. Multidirectional 30°-60° cuts and fillets in woodwork for walls were generally no more complicated than those encountered in, say, conventional hipped roof framing. Welded pipes and rods were easier to bend and join in a nonrectilinear way. Beveling was accomplished as it is in ordinary construction. In short, the construction process was not inherently differentthere were just more non-90° angles. Scheme 2 was based on a triangular grid (as were, incidentally, many Wright houses).
Joe Price said, “I didn’t want to go out and build an angular house.” That had been Goff’s way of fulfilling his client’s needs. “One result of living in it is that I knew it. When you have glass cullet in the wall you’re conscious of it and you never go up against itif it’s in your mind. Oh, I’ve had a couple of guests who were drunk and got some scrapesnothing serious. But nobody soberbecause you’re always conscious of it.” The Prices have since moved west and now five in a house designed by another former Goff assistant, architect Bart Prince. Price quips, “There isn’t an angle in it. We knew we could run into it head on and not get a bruise!”
The the former Price residence was tragically destroyed by fire in December 1996 (arson is suspected).
The Crystal Chapel, Project, Norman, Oklahoma, 1950
The Crystal Chapel project (Figure 2.40), developed for a University of Oklahoma site in 1950, was to have been, as its name implies, a chapel that was literally and figuratively quite crystallinea jewel-like pyramid, faceted with roseate glass (hailproofimportant for Oklahoma!) mounted on a 3O°-6O° angled stainless-steel grid structuredouble glazed and translucently insulated. Each glazing unit consisted of a rhombic pyramid, intensifying the organic “self-similarity.” The petal-like corners of the pyramid opened up to act as inviting entrances and to nestle an extended tetrahedral steeple. Opaque, tetrahedral, subservient spaces (choir and meeting rooms) terminated two corners of the main glass pyramidcontrasting with its luminosity but harmonizing with its shape. The 300-seat chapel was the dominant form of a pair of buildings. The other contained a multiuse student religious center with classrooms, meeting rooms, and ancillary spaces, within a rectangular plan. Its
Figure 2.40 The Crystal Chapel, Project, Norman, Oklahoma, 1950. (a) Plan; (b) model photo of chapel; (c) interior rendered perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
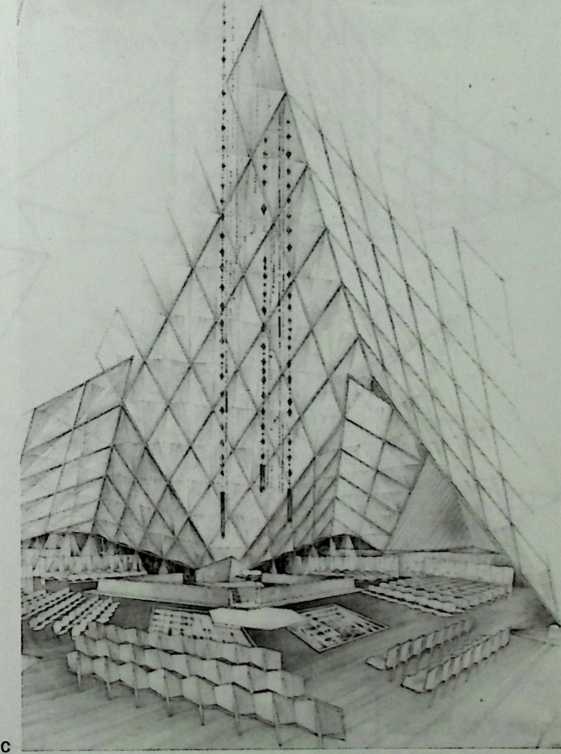
sloping side walls of rhombic glass were held in a grid similar to the chapel’s a tessellation with roots in Goff’s 1922 hypothetical study for a cathedral.41 A variation of the chapel’s elongated tetrahedral steeple marked its entrance.42
The Crystal Chapel nearly realized the self-fulfilling prophecy of Goff’s youthful dream “to design a diamond palace for a maharaja.” Recall that Goff’s father had been a jeweler.43
The polyhedral basis for the pyramidal form of the Crystal Chapel can be interpreted in several waysowing to the fact that certain regular polyhedra are interrelated. The interrelationships include component counts, axial orientation, face configuration, distribution of vertices, dihedral angles, face angles, and dual transformations. In biology the phenomenon of similar forms arising from different functions is called “convergence” (although here we are just concerned with geometry).
The following are several interpretations of the chapel’s geometry:
A Developed (Opened and Laid out Flat) Cuboctahedron
Schematically, the Y-shaped plan of the chapel was a central triangle bounded by three square arms, or wingsor four faces of a developed cuboctahedron (Figure 2.41).
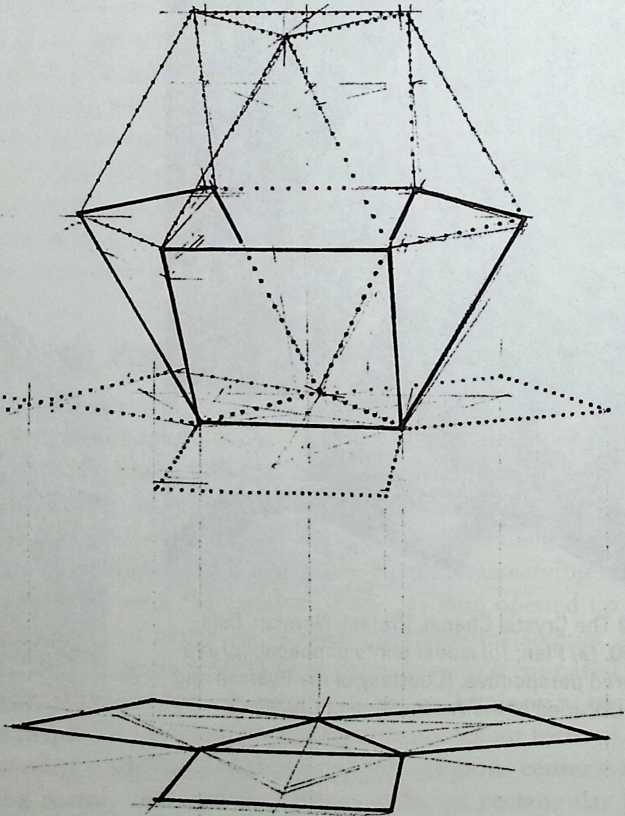
Figure 2.41 Crystal Chapel. Schematic plan elements of the chapel folded into a portion of a cuboctahedron.
A Tetrahedron
The third dimension in the chapel’s development was derived not from the cuboctahedron but rather from the central plan triangleand from the tetrahedron (triangular pyramid). The triangular comers at the base of the tetra faces were folded outward like tent flapsthree pairs in all, not unlike the wide starched wings of the coronet of the Sisters of Charity or Japanese origami birds (Figure 2.42).
Effects of the “Tent Flaps.” On so opening, the bottom edges of the flaps were no longer hugging the ground, a problem similar to that encountered in relating geodesic domes and other polyhedral volumes to the ground plane encountered in the Pollock/Warriner, Wilson, and Rudd Houses. Transition from the sloping bottom of the wall to the horizontal ground plane was accommodated by a series of graduated pink granite supporting piers, each of
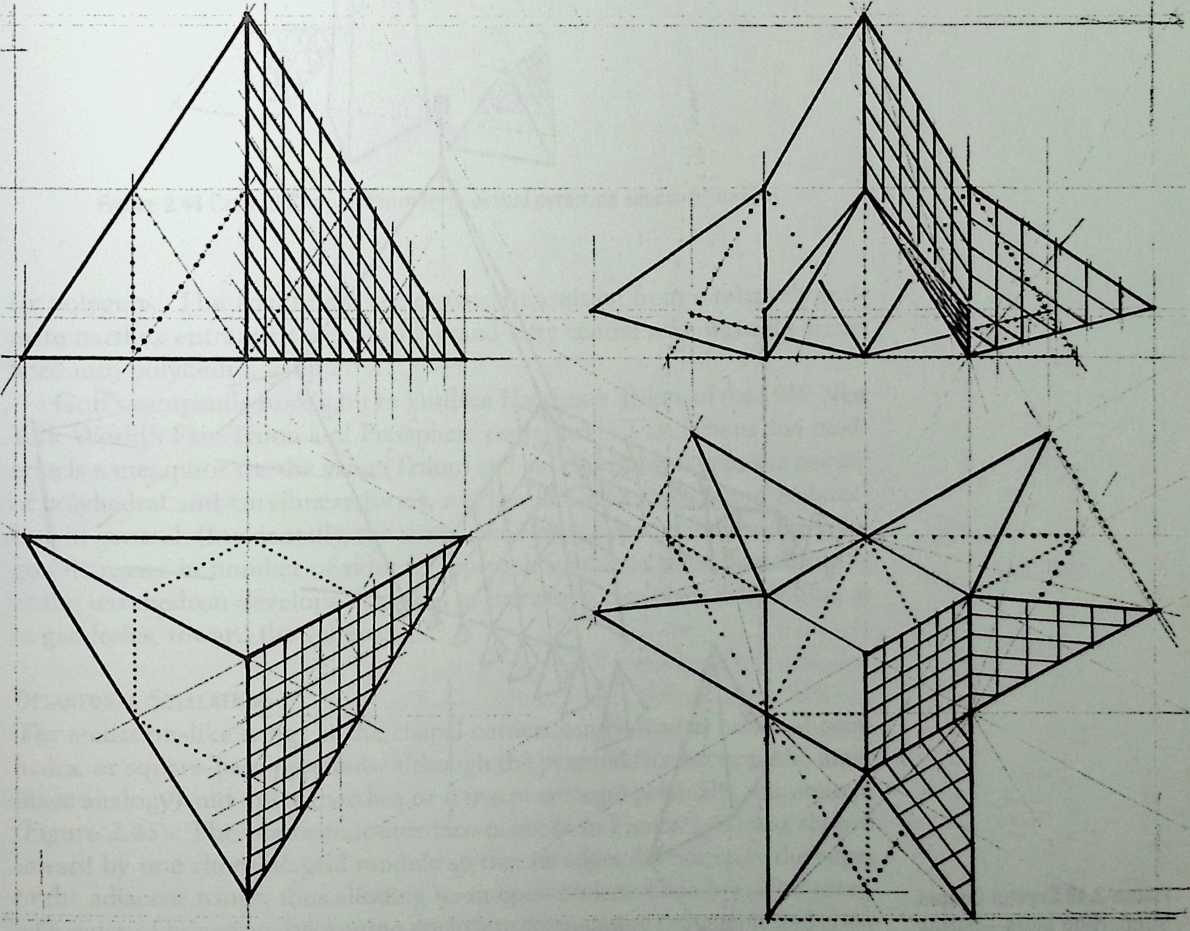
Figure 2.42 Crystal Chapel. Origami-like folding of a tetrahedron. Coronet.
which was an equilateral triangle in elevation and a rhombus in plan a rhombic pyramidor half of an oblate octahedron (Figure 2.43). These shrinking triangles acted as cross sections of attenuated, virtual, horizontal pyramidsmatching in scale and flanking, but at right angles to, the main steeple (Figure 2.44). Their repetition suggested procession and their receding size would have created the perspective illusion of a longer passage and diminishing scale as one approached the central major space of the chapel, making the latter seem more monumental. Nave bays and other elevation features (balconies? planters?) in Goff’s hypothetical study for a cathedral in 1922 foreshadow the gradation of dimension and the repetition of the isosceles triangle.44 This “forced” perspective recalls Bernini’s shrinking Scala Regia (or expanding, depending on which way one is headed). The enabling “depth cue”45 is the “slope,” that is, a gradual change in size of a series of similar objects, or the angular relationship of lines in a triangular motif. Two adjacent legs of a triangle have a more pronounced convergence toward their common vertex than do, say, two adjacent sides of a square or of other regu-
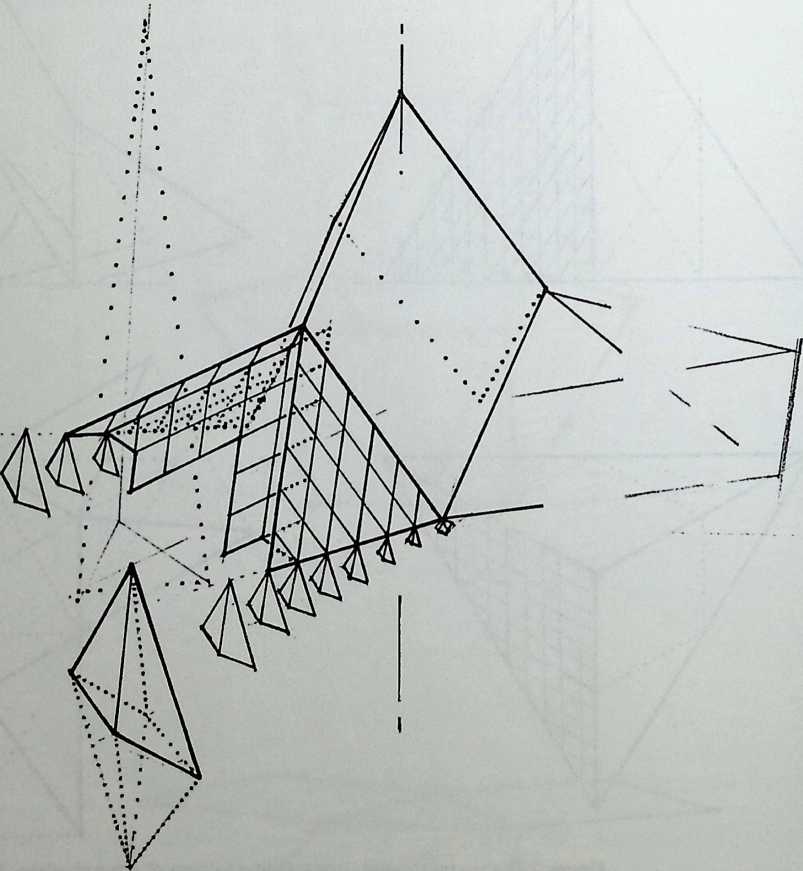
Figure 2.43 Crystal Chapel. Supporting piershalves of an oblate octahedron.
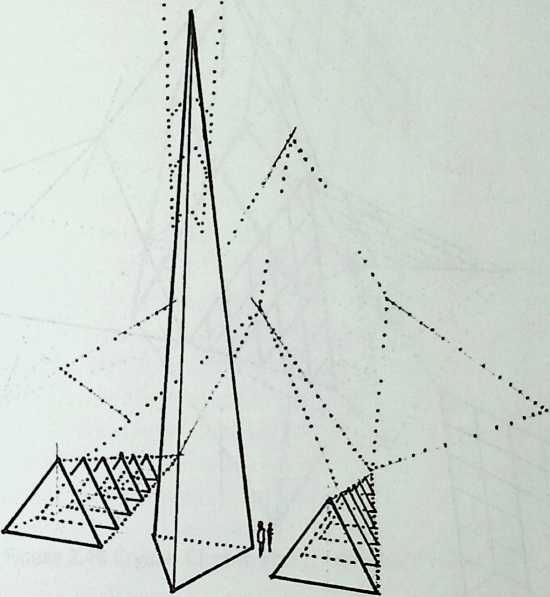
Figure 2.44 Crystal Chapel. Piers form virtual pyramids similar to steeple.
lar polygons. The traditional ecclesiastical transition from a relatively intimate narthex entrance space into a grand lofty central nave was thus translated into polyhedral geometry.
Goff’s campanile nods a bit to Wallace Harrison’s Trilon, of the 1939 New York World’s Fair Trilon and Perisphere centerpiece. That famous duo mod-erne is a metaphor for the yang (Trilon) and yin (Perisphere) opposite pairing of polyhedral and curvilinear forms, not just in Goff’s work, but in architecture in general. (Incidentally, the twain could meet hypothetically as the polygon increases in number of sides to approach a circle or three-dimensionally as the tetrahedron develops by stages of increasing face plane subdivision, as in geodesics, toward the sphere.)
Octahedral Stellation
The stellation-like wings at the chapel comers can be read as halves of octa-hedra, or square-base pyramids, although the pyramid face between the inner (nave analogy) and outer (narthex or transept analogy) polyhedra was omitted (Figure 2.45). The opposite, outer face plane (a in Figure 2.45) was slipped inward by one rhombic grid module so that its edges did not meet the edges of the adjacent wings, thus alluding to an open projected window. This created a sense of hovering, beckoning enclosure surrounding the steeple and choir and gave the glass a sense of folded, enveloping surfaceof weightlessness.
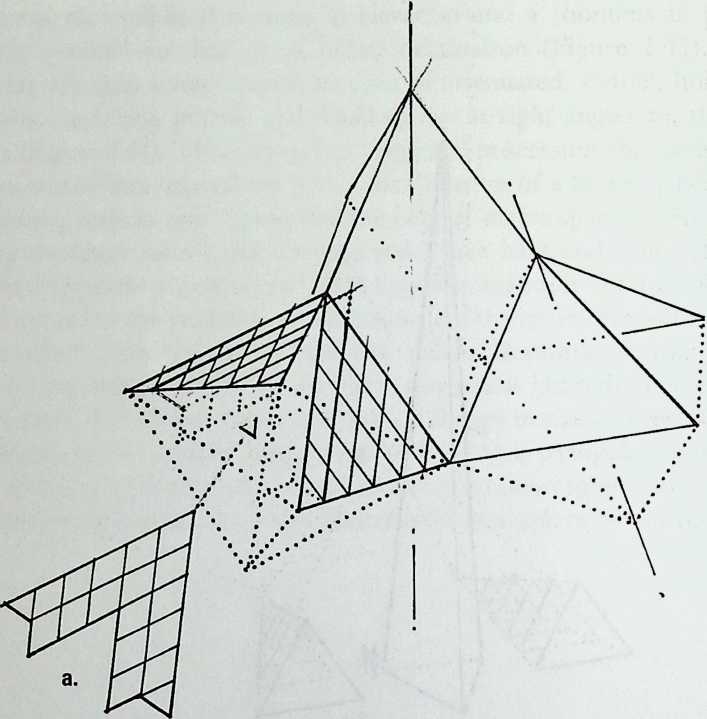
Figure 2.45 Crystal Chapel. Octahedral “stellation.” Face plane “slippage.”
The feeling of solidity and mass that is imparted by closed, opaque faces with abutting, congruent edges was thus substantially decreased. A similar overlapping and offsetting of planes occurred in the Price Studio 1.
Rhombic Hexahedron
These comer “flaps” surround, isolate, and emphasize three major central 60°-120° rhombi of the chapel roof, defining half of a rhombic hexahedron (Figure 2.46). A rhombic hexahedron (or oblate rhombohedron) is like a cube (hex = six, i.e., six faces) that has been distended by pulling two diagonally opposite comers so that the cube’s faces become diamonds (rhombi). In the PoUock/Warriner House we encounter one-half of a related polyhedronthe rhombic dodecahedron (12 faces). The half, rather than the whole, in each case is due to the truncating intersection of a polyhedron with the ground plane.
In the Crystal Chapel did the conception of the tetrahedron come first, origamicized, as it were, with its flapsan example of a modified Platonic solid projected orthographically onto the ground plane, or was it one of the other polyhedra mentioned previously? Or does it matter? Because in the finished design square, triangle, hexagon, rhombus, tetrahedron, octahedron, rhombic hexahedron,and so on are orchestrated into a complex composition of variations.
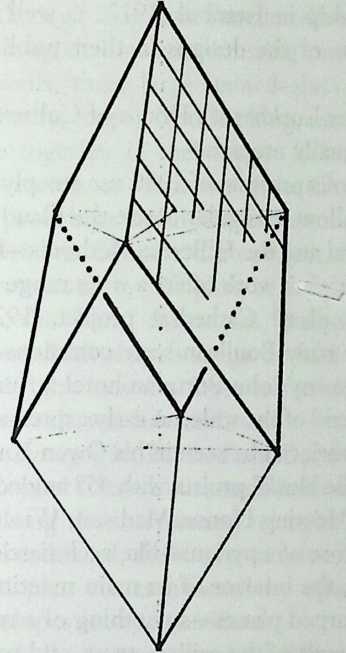
Figure 2.46 Crystal Chapel. Haifa rhombic hexahedron.
The Crystal Chapel: A Historical Perspective
The Crystal Chapel’s position in modern architectural history is a fascinating adjunct to its geometry. It is linked by evolution and influence from the early 19th century through the present. It is a mid-2 Oth-century focal point for noteworthy unified major spaces enclosed by metal and glass. Suffice it to mention here a few precedents and antecedentsdesigns involving transparent or translucent pyramidal forms with more or less triangulated or rhombi-cally faceted surfaces. These related buildings anchor the Crystal Chapel in time like prongs securing a jewel in a settingupholding Goff’s design as an important statement of spatial unity, impact, and grandeur. As composer James Heath put it in the title of a composition dedicated to fellow musician John Burkes Gillespie, “Without You, No Me.”
By the mid-19th century, metal-and-glass construction had come into its own heralded by the budding greenhouses or “palm furnaces” erected in Europe, and later long-span structures such as train shedsclimaxing in the mammoth 1,851-foot-long prefabricated Crystal Palace Exhibition Hall in London, 1851, designed and built by Sir Joseph Paxton. Perhaps Goff, who taught the history of 19th-and 20th-century architecture, intended the Crystal Chapel as a centenary homage to Paxton’s structure.
A throng of experiments arose in the early 20th centuryBruno and Max Taut’s expressionist Glass Pavilion for the Cologne Exhibition of 1914 (actually a pointed dome, rather than a pyramid) and their competition entry for
a House of Friendship in Istanbul, 1917, as well as the various crystalline mountain-like forms of the designs in their publication, “Alpine Architecture,” 1919.46
Wassili and Hans Luckhardt’s House of Culture and other projects (circa 1919) were equally utopian.47
Two Goff religious projects of 1930 use steeply pointed triangular motifs interacting with shallow triangular bases: the Gaudf-influenced Hypothetical Study for a Cathedral and the Hillcrest Methodist-Episcopal Church, Tulsa.48
Frank Lloyd Wright’s work offers a wide range of crystalline examples:
His Steel (and glass) Cathedral project, 1926, with its staggeringly immense atrium a truly Boullean scale commensurate with Wright’s talent and visionpredates any John Portman hotel atrium.
At the opposite end of the scale, an early expression of the pyramidal idea in Wright’s domestic work can be seen in his Owen Young House, Chandler, Arizona, 1927 a “textile block” project with 45° angled fenestration and massing.
The Unitarian Meeting House, Madison, Wisconsin, 1947, with its magnificent prow is more of a pyramid-like ecclesiastical extension of a Usonian house. Surprisingly, the interior of its main meeting area is ceilinged not by pyramidal but by warped planessomething of a rarity in Wright’s work in this case a natural result of the ceiling, truss, and roof configurations.
Wright’s Trinity Chapel project, 1958, designed some 10 years later for the same site as Goff’s Crystal Chapel on the University of Oklahoma campus, was also unbuilt (Figure 2.47). Wright’s design (the barest hint of a precursor to a Sierpinski arrowhead49) appears to be a variation on Goff’s Crystal Chapel. Although not so much a “crystalline” building, it is still a variation on pyramidal formswith a gradual transition from the completely flat and horizon-
Figure 2.47 Trinity Chapel project by Frank Lloyd Wright. Transition from horizontal to vertical.
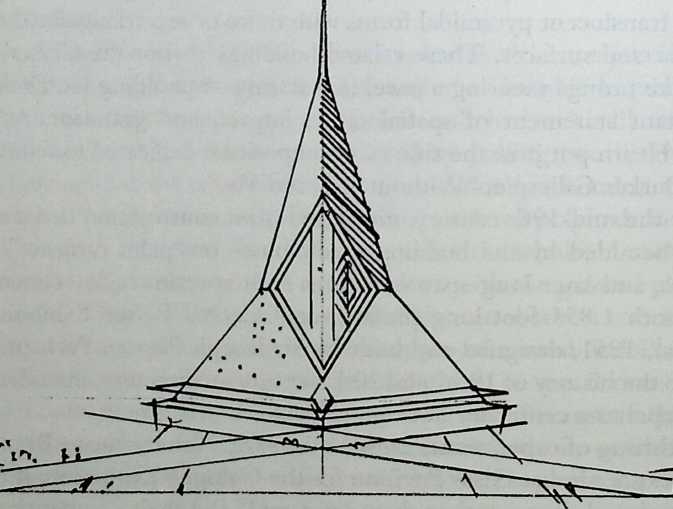
tai ground plane upward through four basic functional/massing elements to a vertical spire at the peak: long shallow criss-crossing ramps, a trio of opaque buttress-like tetrahedral walls, three large stained-glass rhomboid windows nestled among these tetrahedra, topped by three long, narrow, folded, leaf-like roof forms,50 which come together in their upper halves to terminate in a tapered spire. There are even echoes of the top of the Chrysler Building here! The roofs are V-textured, probably standing-lock-seam metal and reminiscent of the roofs of Wright’s Nekoma Country Club project.
Thus Goff’s chapel is echoed by Wright’s in at least four themes: the rhombus, the tetrahedron, the “bent” theme (i.e., graduated slopes), and the triangular symmetry of plan. Both chapels assign distinct materials for different functions; however, Wright uses the more traditional architectural elements of individuated base, wall, window, and roof.
Wright’s Beth Sholom Synagogue, Elkins Park, Pennsylvania, 1953, bears comparison to the Crystal Chapel. Although its two intertwining tripod structural frames (symbolizing the intersecting triangles of a Star of David) hark back to Wright’s steel cathedral, the roof is translucent and three comers of its modified hexagonal plan are terminated by opaque tetrahedral-like masses, and the changing slopes are again evident.
The Wayfarer’s Chapel, Portuguese Bend, California, 1946, by Frank’s son, Lloyd Wright, is not pyramidal (although it is dramatically sited, like a Greek temple, on a hillside overlooking the Pacific Ocean), but it is more or less rhombically faceted and wholly transparent.
Skidmore, Owings, and Merrill’s U.S. Air Force Academy Chapel, 1957, is neither transparent nor pyramidal, but its rhombically faceted (“folded-plate”) structure, rectangular plan, and serrated roofline recall the classroom wing of Goff’s Crystal Chapel complex.
The Religious Center, Project, Artesia College, New Mexico, 1976, by Goff, once again in an academic setting and also called “Crystal Chapel,” is a series of multisloped or “bent” pyramids with extensive transparencya variation on his chapel in Norman, with “intensified angularity, less symmetrical massing of the pyramidal shapes, and less regular glazing,” according to De Long.
The Artesia chapel was a transparent pyramid. Its decreasing mullion spacing and the resultant wedge shapes of the glazing acted together to create gradients depth cueswhich increased the apparent slopes and heights (Figure 2.48). Transverse mullions spiraled gradually upward. Motion was symbolizedappropriately ascendant. Dynamism, however, was only implied here, in contrast to the literal kineticism of Goff’s Rudd House (discussed later), which had movable walls. Of course, large moving sections of buildings, such as entire roofs (covering stadiums) or rooms, are not uncommon, as in some works by, to name a few, Calatrava, Lautner, and Site.
The Artesia multisloped pyramids had a family resemblance to the frustum clusters of the first Price Studio projectnotably the latter’s freestanding screened pavilionas well as Goff’s Ski Lodge, Crested Butte, Montana, 1965 (Figure 2.49), based on a 16-sided pyramid (with this many sides it is
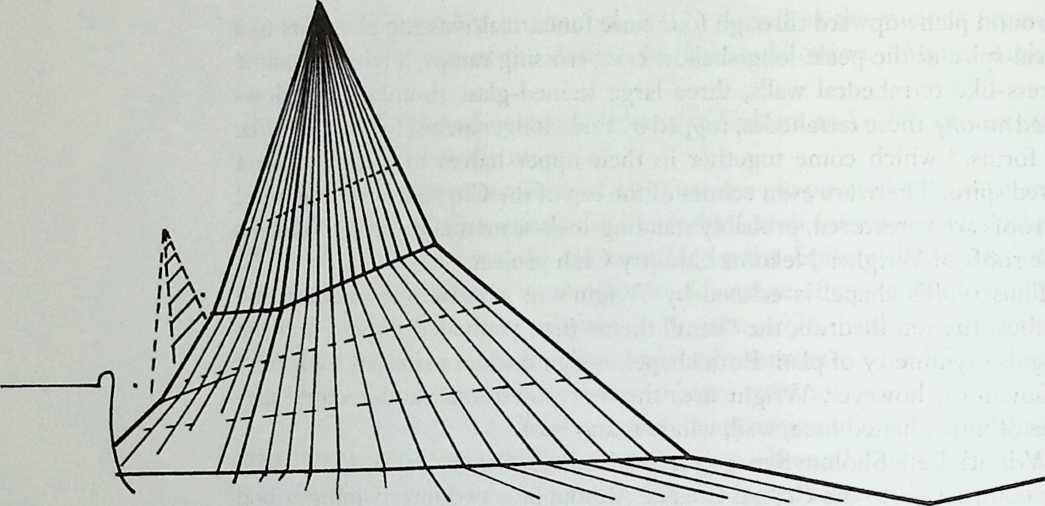
Figure 2.48 Artesia Religious Center. Multisloped pyramids.
Figure 2.49 Ski Lodge, Crested Butte, Montana, 1965. Photo. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
approaching a cone) and Goff’s Hopewell Baptist Church, Edmund, Oklahoma, 1948 (Figure 2.50).
Philip Johnson’s Crystal Cathedral, 1980, Garden Grove, California (see Chapter 5), with its massive space truss walls and roofs, does not appear to be directly influenced by the Crystal Chapel, other than in its “crystallinity” and in the fact that Johnson was aware of Goff’s design.
Similar to Johnson’s Crystal Cathedral in its use of an all-encompassing space frame with pyramidally faceted glazing is the BioSphere 2 designed by architect Phil Hawes, both Wright apprentice and Goff student. BioSphere 2 utilizes a commercially available space truss throughout, enclosing just about everythingbiological habitats, offices, and mechanical equipmentas Goff enclosed both of his major plan functionsthe Crystal Chapel and its multipurpose wing with the same rhombic envelope. (An example of an architectural precursor of an all-encompassing envelope is Paxton’s prefabricated glass.) In the BioSphere 2 in the late 20th century, the transparent structure has come full circle from the mid-19th centuryback to its use as a “palm furnace.”
R. Buckminster Fuller and Shoji Sadao’s Tetrahedron City project at Yomiuriland, near Tokyo, 1970, was a megadream proposed perhaps more for the sake of publicizing prototypical possibilities than for its communal perfection. The glass-clad spherical space frame of Fuller’s U.S. Pavilion at Montreal’s Expo ‘67 could be considered a “perisphere” to the Pyramid City “trilon.” Although Fuller’s continuous presence hovers patently over all “three-dimensionally triangulated” structures of whatever-hedra, it does not,
Figure 2.50 Hopewell Baptist Church, Edmund, Oklahoma, 1948. Rendered perspective. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
in my opinion, establish hegemony over the Crystal Chapel.
LM. Pei’s pyramidal addition to the Louvre, an ultimate in mansard roofs (as Egyptian pyramid follows mastaba), and its smaller companion octahedra, are glazed with rhombisimilar to the Crystal Chapel. His Rock-and-Roll Hall of Fame, Cleveland, 1995, contains much larger but less elegant pyramidal elements Miesian interpretations of the pyramid.
The black pyramid of the 2,500-room Luxor Las Vegas Hotelwith its layer of rooms hugging the exterior walls and appropriately straddling the River Styxis a gaudy geometrical Goliath that runs rampant over history in yet a further display of the American (or perhaps just human) love of the buck and yet another lurch in the mindless romantic exploitation of the pyramidal past.
Several other recent entries in the pyramid sweepstakes are Moshe Safdie’s 1988 Canadian National Gallery in Ottawa and “Pyramid City” for 100,000 byTRY2004.51
The Jones Memorial Chapel as finally built at the University of Oklahoma, over protests from many prominent architects praising Goff’s project, is timid, conformist, and prosaically neo-Georgian. Philip Johnson was, incidentally, among those who protested.52
Vernon E. Rudd House, Projects, San Mateo, California, 1959
In the three unbuilt designs for the Rudd House, the prominent polyhedral features are the bedrooms, individually attached “like melons on a vine,” as Goff put it, to an S-curve of corridor and common living areas (Figures 2.51 to 2.53 show Schemes 1 to 3, respectively). Their heritage includes Wright’s Usonian house concept with its linear arrangement of bedrooms on a long corridor; however, in the Rudd House the individual chambers are completely separated surrounded by their own open spacelike pavilions or cabins.53 If “polyhedral privacy pods” (my terminology) is too hard to take, I would suggest “truncated tetrahedral sequestration receptacles” or “individuated icosa-hedral enclaves.” The possibilities have yet to be exploredpolyhedoir? poly-hedranctum? icosahedriculum? tetratorium? Goff did not shrink from exploratory terminologyhe called his house for the Dewlins (a design that, incidentally, did not include polyhedra) an “aparture.”
In the first version of the Rudd House, truncated tetrahedra (Figure 2.51 a-c) were used as bedrooms hung from cable and mast to keep them clear of the rough, wooded site. Scheme 2 kept the truncated tetrahedra but mounted each of them on six short legs (Figure 2.52). Contrast this Scheme 1 polyhedrathe geometry of the truncated tetrahedron54with the (slightly modified) icosahedronone of the five Platonic solids, used for the same purpose in Scheme 3 (Figure 2.53zz-e).
The “icosa-pods” of Scheme 3 rested on and were lifted above the irregular grade on short trunks (Figure 2.53ZJ. These raised units are a modest reminder of the late California architect John Lautner’s spectacular 1960 Malin House (“Chemosphere”) an entire house, not just a room, octago-
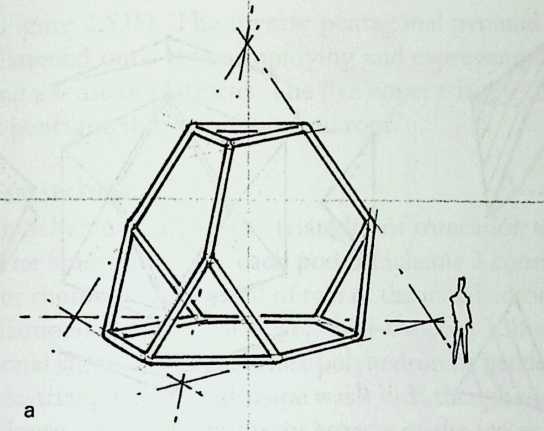
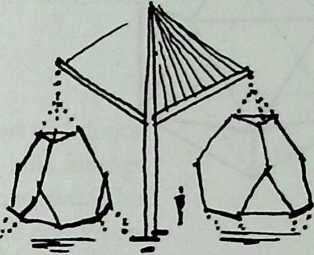
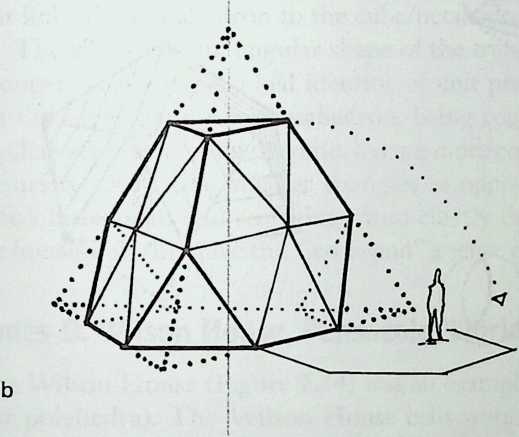
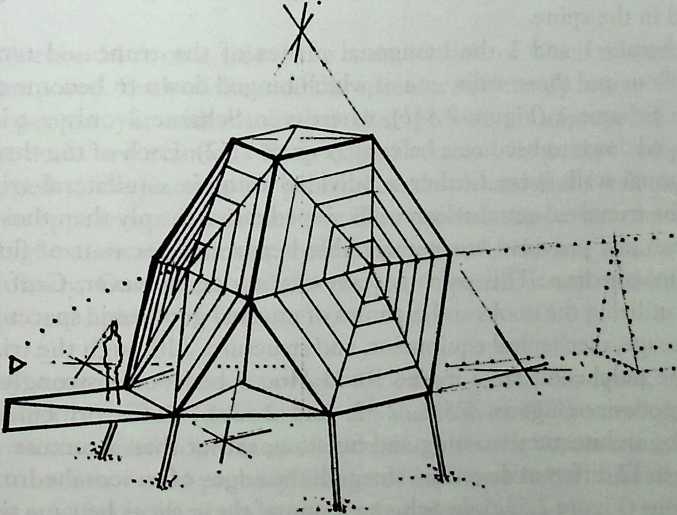
Figure 2.51 Rudd House, Scheme 1. Truncated tetrahedron units. Theoretical Vierendeel structural frame, similartothatof the Wilson House unit; *(b)*triangulated panels of the hexagonal faces, one of which hinged down to create an open porch.
Figure 2.52 Rudd House. Scheme 2. Truncated tetrahedron with six legs and triangular hinged-down porch.
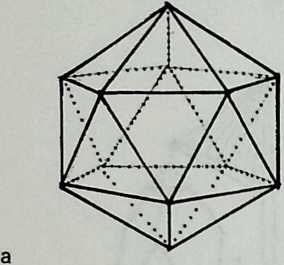
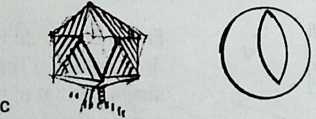
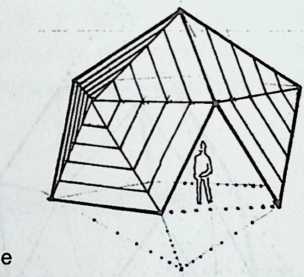
Figure 2.53 Rudd House. Scheme 3. Icosahedron units: (a} Icosahedron; (b) exploded view; (c) “cats-eye” window; M4-symmetry aspects of the icosahedron; pentagons emphasized by paneling pattern.
nal in plan, perched on a very tall concrete stem to accommodate a steep slope in the Hollywood hills. Each o£ the Rudd pods was connected to the house corridor with a short prismatic passage. Bathrooms and storage were contained in the spine.
In Schemes 1 and 2 the hexagonal planes of the truncated tetrahedra served as floor and three walls, one of which hinged down to become an open terrace in Scheme 1 (Figure 2.51£), whereas in Scheme 2 only a triangular panel hinged down to become a balcony (Figure 2.52). Each of the three sloping hexagonal walls were further subdivided into six equilateral triangular panels. The truncated-tetrahedron walls sloped more steeply than those of the icosahedron and provided less comfortable headroom per unit of floor area than the icosahedron. This point is somewhat moot, however, Goff being a master at utilizing the nooks and crannies of unusual geometric spaces for furniture, storage, mechanical equipment, and structure. Although the triangulation of the polyhedral faces in the Rudd House bedrooms strongly recalls Fuller’s geodesics (Figures 2.5lb, 2.52, and 2.53*?), Goff’s principal thrust seems to be architectural massing and function, rather than structure.
Slices in 12 different directions through the edges of an icosahedron result in pentagons (Figure 2*.53a).* In Scheme 3 one of these slices became the floor
(Figure 2.53). The inverse pentagonal pyramid under this slice of floor was flattened outthus simplifying and expressing the floor structure and creating a sense of platform. The five upper triangles of the icosahedron comprised a pentagonal pyramid pitched roof.
Fenestration
In Schemes 1 and 2 the triangles of truncation served as windows and doors. The fenestration for each pod of Scheme 3 consisted of a single bold lozenge (or rhombus, composed of two of the icosahedron’s equilateral triangles). This diamond-shaped “cat’s-eye,” half-window, half-skylight, gave the pod a personal signature beyond just polyhedron or geodesic (Figure 2.53c). This double-triangle diamond shape was a link, though not further utilized in the Rudd House, to the 4-symmetry aspects of the icosahedron, that is, the symmetry that links the icosahedron to the cube/octahedron family (Figure 2.53c).
The slightly more angular shape of the truncated tetrahedron imparted a stronger sense of individual identity, of unit presence, than the icosahedron. On the other hand, the icosahedron, being roundish, being perhaps a more familiar geometric solid to some, having more equitably distributed and smaller surface facets (the smaller triangles as opposed to the truncated tetrahedron’s hexagons), and so fitting more closely the curved circulation areas of the houseall this gave the “icosa-pod” a sense of repose and appropriateness.
James D. WSHsomi Mouse, Pensacola, Florida, 1950
The Wilson House (Figure 2.54) was an example of Stage 4 (multicelled regular polyhedra). The Wilson House cells were cubelike and, in fact, conveniently called cubes: “A cube module of 14 ft. was used, so that the space in each unit is intimate and is easily expandable. This was the first use of a three dimensional module in this way.”55
As stated in Progressive Architecture:
A cube 14 ft on a side is the space module of which this entire house is composed. Each of the modular spaces is sufficiendy intimate for one or two people, yet added together they provide an appropriate space for large-scale entertaining. Each cube is framed in welded boiler tubing. Clipped to the framing are prefabricated redwood-faced wall panels, similar in appearance inside and out. The beveled corners have been filled in with glass jalousie units to provide cross ventilation and a sense of spatial continuity. Corrugated translucent plastic panels at the roof-line provide additional light.56
They were nevertheless “beyond the cube”truncated cubes, to put it in the simplest of terms. However, to see the Wilson House modules only as cubes with truncated edges (and corners; if not for the comer truncations, the edge truncations would produce elongated hexagons rather than rectanglessee Figure 2.55a) is to miss a number of subtleties.
Figure 2.54 James D. Wilson House, Pensacola, Florida, 1950. fajSection; exterior photo; (c) plan. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
c
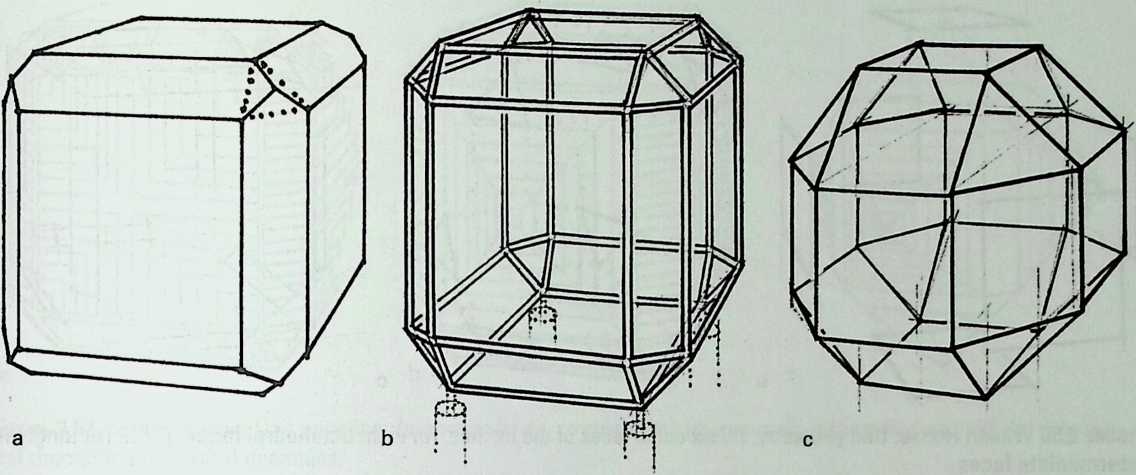
Figure 2.55 Wilson House, (a) Edge-truncated cube; (b) pipe frame module; (c) Rhombicuboctahedron.
The modular floor plan of the Wilson house, entrance, and carport consisted of a dozen abutting truncated squares. In plan, the modules defined the various functions, for example, living, dining, sleeping, and carport, whereas four truncated corners together provided servicesfenestration, column locations, a fireplace, sliding doors, and circulation. The plan units were translated into three-dimensional modules (“close packed”somewhat like a tray of muffins), which define and enclose the space within the house. L. Lines refers to closely packed polyhedra as “parallelohedra…. Congruent polyhedra that can be stacked together so as to fill space completely….”57 This definition applied only very loosely to the Wilson and Pollock/Warriner housesin the Wilson modules there were gaps left between, and in the PoHock/Warriner the modules overlap.
The Wilson module exemplified the creative possibilities of prefabricated production for architecturean idea that reappears occasionally and seems to go nowherefor example, during World War H and later with Operation Breakthrough in the 1960s. Prefabrication of the Wilson modules was more in the symbolic sense, as there was considerable on-site fabrication.
The generation of the Wilson module can be described in several ways as:
-
Truncation. An edge-and corner-truncated cube (Figure 2.55).
-
Dual transformation. Dual transformation of either a cube, an octahedron, or a rhombicuboctahedron (Figure 2.55c).58 The face planes enclosing the Wilson module consist of:
6 square cubic faces (Figure 2.56a)
8 triangular octahedral faces (Figure 2.56b)
12 rectangular intermediate faces (Figure 2.56c)
If the design is seen as an RCO transformation, the octahedral edges and faces become reduced, and the intermediate faces, which would
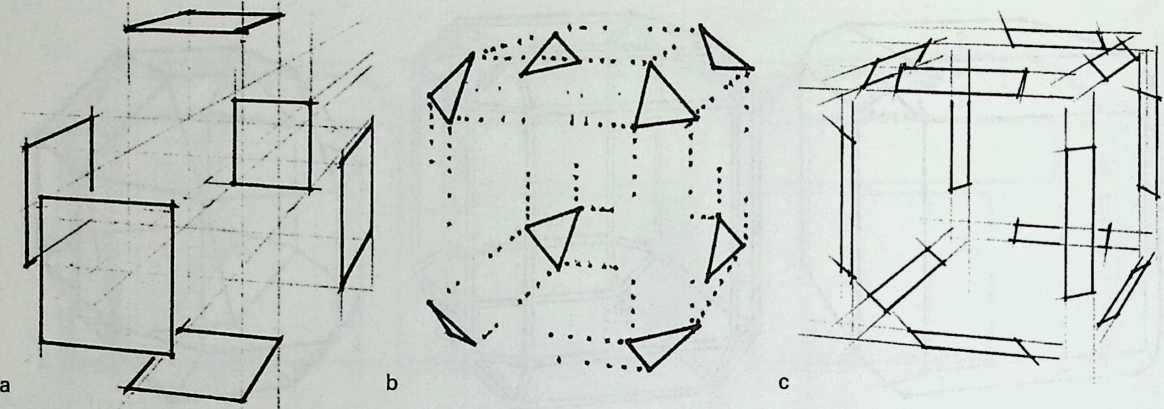
Figure 2.56 Wilson House. Unit geometry: (a)s\ x cubic faces of the module; (b) eight octahedral faces; (c) 12 rectangular intermediate faces.
have been square in the initial RCO, become rectangles. Dihedral angles remain the same. Other ramifications of such a transformation can be seen in the Wilson module.
3. Tesseract. The double-edged effect of the Wilson module resembles one of the possible three-dimensional projections of a tesseractthat curious four-dimensional relative of the cube, which is illustrated and discussed at some length by Bragdon.59
Each geometric component of the Wilson module was assigned a specific architectural function, as follows:
Edges. The edges of the RCO module were structural, consisting of 4-inch-diameter boiler pipe (Figure 2.55£). The joints (vertices) were welded, creating a kind of three-dimensional Vierendeel truss. The geometry necessitated welding because RCO geometry does not have the inherent stability of triangulation (even though the corners are triangles).
One of the RCO modules was left unclad and open, with the pipes describing the edges of its volume. This particular unit performed a multitude of tasks: It illustrated the module’s abstract geometry, contrasted with the enclosed bulk of the rest of the house, supported the carport roof, and served as an entrance totem.
Cubic Faces. On the exterior, the cubic faces dominated the transformed RCO module in size, pattern, and texture (Figure 2.56a and 2.57). Prefabricated wood siding “membranes” were intended originally for both walls and roofs, with the boards lapped in a series of nested squaresboth inside and outrecalling the Wright trademark and its Chinese, Japanese, and Native American precedents. If, instead, the siding had been applied at 90° to the pipe frames, forming a cross pattern, it would not have emphasized the square face
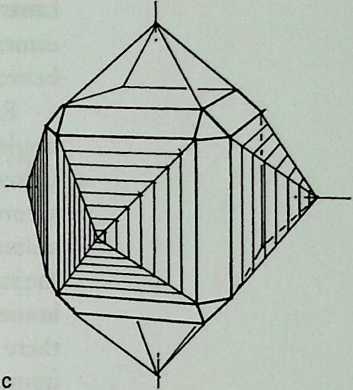
Figure 2.57 Wilson House. Unit paneling: (a) perpendicularto pipe frame (theoretical); (b) paneling as built; theoretical rhombidodecahedral dynamics.
and would have fought with the corner jalousie window lines (Figure 2.57 a). Nor would the overlap of the boards have fit properly against the pipe frames. On the interior of the house, the nested squares regulated the dimensions of doors and other openings.
Having been designed originally for a California hillside site with an approach from above, with an identical pattern on the roofs of the modules as well as their sides, the house would have read clearly as a cluster of three-dimensional units. The units would become “supercubes,” as it were, in spite of their RCO characteristics, that is, each of the geometric elements of the cubecorner, edge, and face (i.e., point, line, and planewhich Goff emphasized in first-year design courses) being articulated and emphasized in its own right.60
Redwood siding was to have been used in California. When the Wilsons retired instead to Florida, Goff changed the design to cypressbut none was available so he stayed with the redwood; however, on the flat Florida site because the roof surface was not visible a conventional built-up tar-and-grav-el roof was used. As built, the interior of the module had equivalent side and ceiling surfaceson the exterior, only equivalent sides.
Another interpretation of the pattern of nested squares of wood siding is that they symbolize the stages of transformation through which a rhombicuboctahedron might pass on its way to becoming a rhombidodecahedron, thus energizing and reinforcing polyhedral spatial presence and implying movement and change (Figure 2.57c).
Upper Sloping Planes and Triangles. The long, narrow upper sloping intermediate planes of the RCO and the upper comer, triangular, octahedral faces held fixed translucent glass fiber clearstorys (Figures 2.56c and 2.57 b).
Vertical Rectangles. These rectangles contained glass jalousie windows, which were sandblasted for privacy in two bathrooms (Figures 2.56c and 2.57b).
Lower Sloping Planes and Triangular Faces. These components were opaque cement asbestos board, comprising an apron that concealed the crawl space between the floor deck and grade (Figures 2.56b and c and 2.57ti).
Rex Slack, another Goff student, did additional drawings on the site as needed and supervised the construction along with fellow student Ray Cobb. Unseen in the completed house and, in fact, not on the working drawings, according to Slack, were short, stub pipe columns on which the larger RCO units rested (Figure 2.55Z>), necessary for anchoring to footings and leveling the stub pipes being concealed by the gentle slope of the gravel grade near the house. Some of the upper pipes were slotted to serve as gutters. Slack said that there had been some condensation on the interior faces of some of the pipe frames but he knew of no roof leaks. Larry Grantham visited the site in 1982 and observed that “pipes were rusted through at the horizontal roof areas. Roof leaks were subject to continual maintenance. There could have been many years without problems, though. One of the typical problems, needless to say, with these perfect geometric concepts is that such planes create difficult to impossible places to fabricate without leaking problems. Something to be considered by students….”
The occurrence of the plane of the floor inside rather than on the surface of the RCO module characterizes a common concern in adapting pure geometric solids such as polyhedra and geodesics to architecture, that is, the need for flat circulation areas accompanied by human-scaled headroom. The plane of the floor intersected the Wilson modules at the bottom edge of the large square wall membranes, permitting significantly more usable floor space (by getting the canted triangular corner pieces and their connecting frame members out from under foot) than had the floor level been at the lowest square face (Figure 2.58). This created a crawl space, which contained floor bracing plus the usual mechanical and electrical necessities. It caused the exterior and interior expressions of the RCO to differ somewhat. Whereas the exterior read clearly as a set of modules, the interior, although still retaining the modules, appeared as a grove of abstract tree trunks and branches.
Other elements of the house interacted with the RCO module as inter- penetrations (e.g., a pool and a four-way fireplace) and as variations (light fixtures, folding doors, and shed roof). The fireplace chimney was capped by an ornamental octahedral sculptureto symbolize a free passageway for smoke?
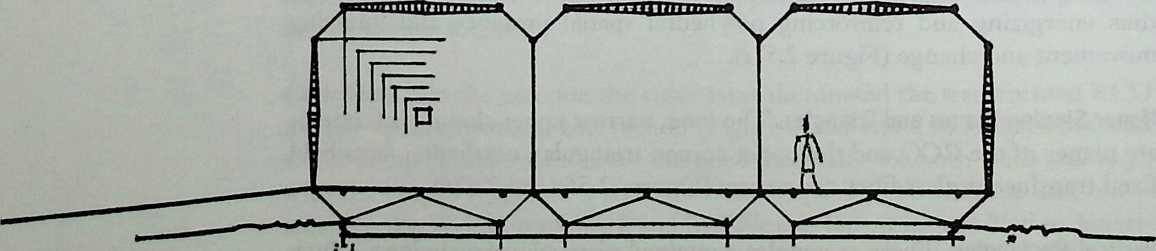
Figure 2.58 Wilson House. Schematic section.
The Wilson House was destroyed by fire in the 1980s. The present owner, an architect, cut up and reassembled the frames, using the original floor structurebut it is entirely different now, according to Grantham.
The Donald Pollock [House, Oklahoma City, 1957, Remodeled by Goff for John and Laura Warriner, 1977
The Pollock/Warriner House (Figure 2.59), like the Wilson House, is based on adjacent, repeated polyhedra derived from a floor plan consisting of abutting truncated squares; however, the joining of the Pollock/Warriner
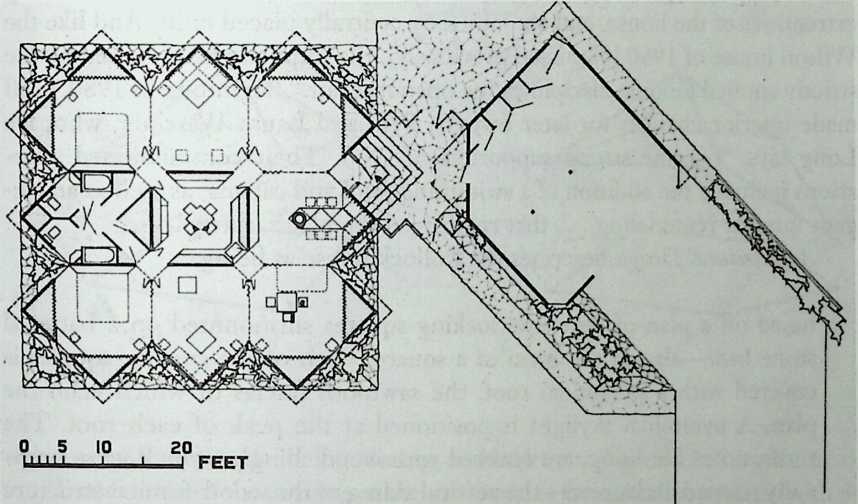
a
Figure 2.59 Pollock/Warriner House, Oklahoma City, Oklahoma, 1957. (a) Plan; (b) photo.
modules is more complicated. Like the Wilson module, the Pollock/Warriner module can be depicted as having been generated in several ways. Of these, incidentally, the most likely involves a design process that probably did not start with the polyhedra that we see in the completed house.
To give an overview of the Pollock/Warriner House, we turn to others:
De Long writes, “In plan, nine interlocking squares are arranged symmetrically upon a large square plinth. Nine pyramidally shaped roofs, each with an individual skylight at the peak, give volumetric expression to the module. In this realized design, shingles laid along angled lines further emphasize a crystalline quality, as do the faceted panels of translucent plastic over a porch joining house and garage. As with the McCullough and Bass projects [discussed previously], the parents’ and children’s areas are clearly defined along extremities of the house, and are joined by centrally placed units. And like the Wilson house of 1950 [discussed previously], the implied grid imposed by the strictly applied module disciplines the open interior.” Beginning in 1980, Goff made interior changes for later owners, Paul and Laura Warriner, who, De Long says, “became strong supporters of Goff. Their commissioned alterations included the addition of a swimming pool and cabana, as well as an elegant interior remodeling…that reinforced the plan’s clarity.”61
Architectural Design describes the Pollock house as being
based on a plan of nine interlocking squares surmounted on a battered stone basealso in the form of a square. Each of the smaller squares is covered with a pyramidal roof, the sawtooth fascias of which echo the plan. A pyramidal skylight is positioned at the peak of each roof. The roofs, notes De Long, are covered with wood shingles which were originally painted dark green the vertical siding of the wood-framed structure is painted fight green. At each interlocking corner of the squares are narrow full-height windows overlooking triangular planters formed between the sawtooth plan of the walls and the stone base. Between the garage and the house, and spanning the entrance, is a large screened enclosure which follows the geometry of the rest of the house, but on a slightly reduced scale, and slightly taller. This structure is wholly glazed and finished with pyramidal formed, translucent, green plastic roof panels. The structure of this outdoor living area encompasses part of the garage roof which is used as a sun-deck. Inside, the house is organized around a central kitchen (at Mrs. Pollock’s request) and divided into various spatial configurations by accordion doors. Against Goff’s advice the Pollocks commissioned landscape architects who repeated the 45° geometry of the plan in a hard-edged pattern of planting areas.”62
The polyhedral module of the Pollock/Warriner House is the rhombidodec- ahedron (occasionally referred to below as “RD”), which has 12 rhombic faces (Figure 2.60zz). It is, incidentally, the dual of the cuboctahedronan Archimedean solid.
The plan schemata starts with nine 13-foot truncated squares arranged in a three-module-by-three-module grid, each square anchoring a major func-
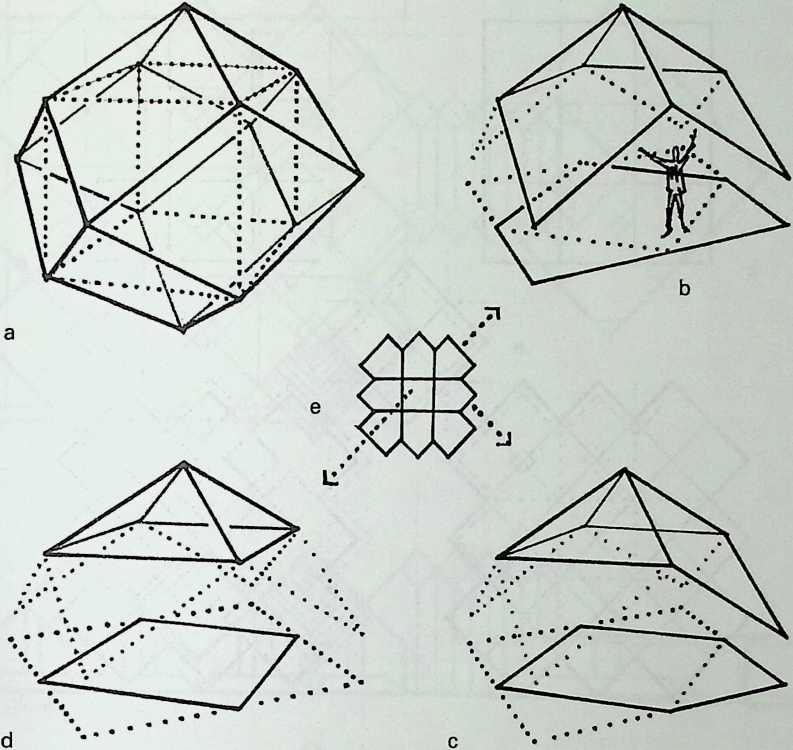
Figure 2.60 Pollock/Warriner House. Rhombidodecahedral unit geometry:
-
rhombidodecahedron relative to inscribed cube;
-
typical corner unit and plantrace; fc/typical edge unit and plan; (d) interior unit and plan; (e) schematic roof plan key.
tional area, for example, living, dining, and bedroom (Figures 2.59a and 2.61a).
Truncations of the comers of the grid squares form smaller squares (with 4-foot diagonals) at 45° to the original larger squares (Figure 2.61b). These areas, again as in the Wilson House, serve as circulation nodes, column locations, and window and door frames. Other elements in the house occur in harmony with the scale of these truncations, for example, skylights (one at the peak of each pyramid, recapitulating in miniature the RD shape of the roof below), distance of floor level to low point of roof, and screened porch mullions.
The truncations are extended at the exterior walls until they meet, forming the edges of yet another group of squares (about 16 feet) at 45° to the original group of squares and overlapping one another (Figure 2.61c). These new 45° “outcroppings” expand the original squares to provide storage, seating, dining, and bathroom space around the perimeter of the house. This group (discounting the roof overhangs) comprises plan sections of partial rhombidodecahedra.
The Pollock/Warriner module is related through transformation to the tetrakis hexahedron (Figure 2.62a) and the triakis octahedron (Figure 2.62b) stellation-like derivatives of the cube and octahedron, respectively. They would not have played a part in the generation of the design, although the “stellation” aspect of the “outcroppings” mentioned in the preceding paragraph invites comparison.
The cluster of pitched-roof rhombi are the primary expression of these
Figure 2.61 Pollock/War-riner House. Development of plan grid: (a) square grid; (b) corner truncations; (c) truncations extended to form another grid at 45°; (d)roof plan; (e) rhombidodecahedral roof plan unit.
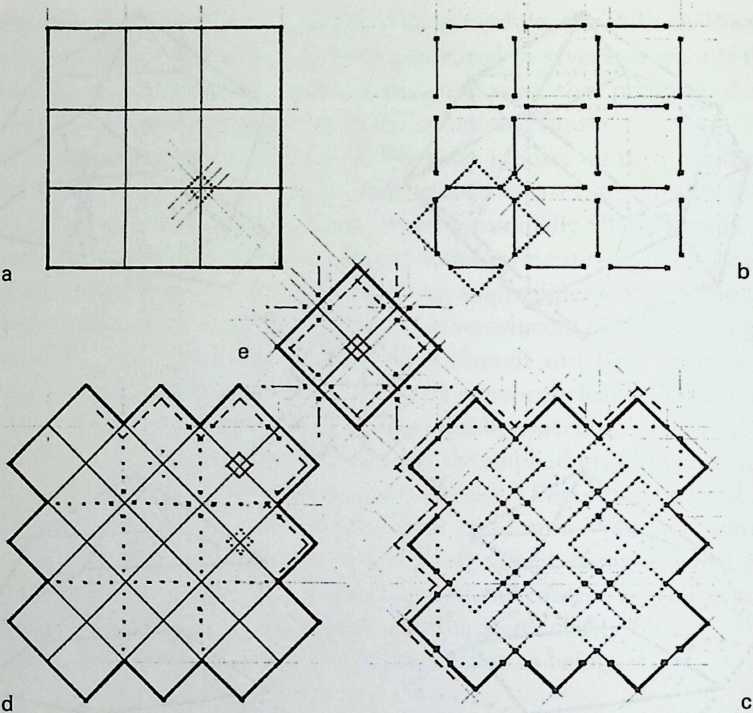
RDs, with half-and quarter-rhombi comprising exterior walls (Figures 2.61c and d and 2.63). However, nowhere is an entire 12-faced rhombidodecahe-dron completed. If it were, the obvious problem of how to provide a flat floor would occur. As to the roofs, the working drawings referred to them simply as hipped roofs, and so they are. They are similar to the “helm” roofs of Romanesque bell towers (e.g., Limburgh, Cologne, and Speyer Cathedrals), though the rhombi of these roofs are much more elongated than the Pol-lock/Warriner module (Figure 2.64). The central portion of the Crystal Chapel is a triangular version of the helm roof (Figure 2.46).
b
Figure 2.62 Pollock/War-riner House. Related geometry: (a)tetrakis hexahedron; (b) triakis octahedron.
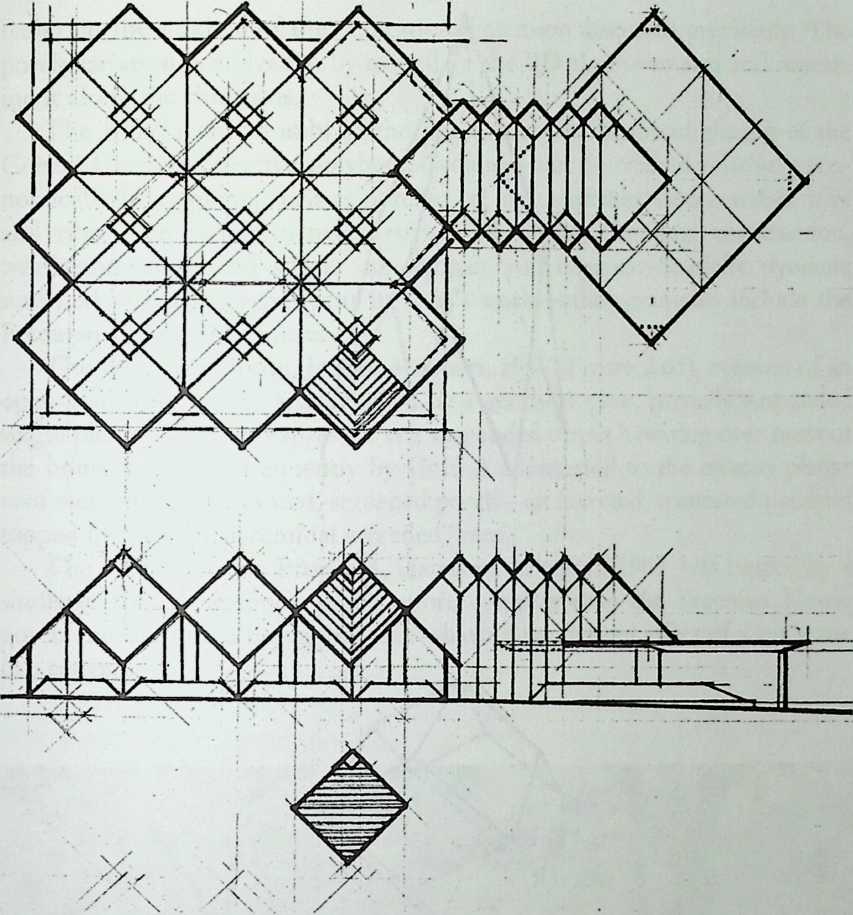
Figure 2.63 Pollock/Warriner House. Roof plan and elevation.
The ceilings under these hipped roofs rise to 15 feet at the top of the skylights and to just under 3 feet at their low points. The lower areas are consigned to the backs of closets and alcove-like portions of seating areas, with the underside of the main 4x10 beams at a height to accommodate a conventional 6-foot, 8-inch wood folding door.
The axial, or orthographic, projections of an RD are square grids (Figures 2.6\ d and e and 2.63). A “4-axis” is that projection onto a plane that is perpendicular to an axis through opposite vertices at which four edges meet. The actual face angles, however, are 70° 32 and 109° 28 hence the ‘rhombi’ in rhombidodecahedron.63
This square projection appears in both plan and elevation of the polyhedra and in the design and working drawings of the houseand the actual roof slopes are 45°. Looking at the drawings, an unsuspecting builder might not be aware of the rhombus nature of the roof segments until construction was underway. An untoward effect would be the fact that plywood sheathing would not fit as neatly on the rhombi as onto 90° rectangular shapes. The original
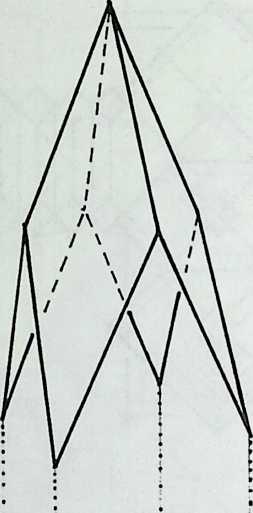
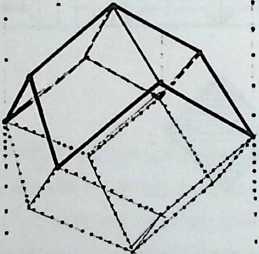
Figure 2.64 Pollock/Warriner House. Unit roof compared to medieval “helm” roof.
shingle pattern of nested V’s, which followed and emphasized the rhombi’s lower edges (a counterpart to the nested squares of the Wilson House redwood siding) was long ago replaced with conventional horizontal rows of shingles, eliminating one of the strong echoes of the RD profile (Figure 2.63).
A rhythm is created by the Pollock/Warriner House modules by three identical geometric shapes. Similar triplets occur in other Goff works, for example, the square faces of the Wilson House and the dodecagons of the First National Bank, among many others. The repetition of the regular faces of polyhedra or other structures symbolizes rationalitybut in Goff’s work it also creates “music” rhythm.
The simplicity of the flat-roofed, corner-truncated, square-on-a-45°-angle garage contrasts strongly with the sculpted cluster of rhombi of the main house and is derived from the plan module formed by the roof ridges (Figure 2.63). The two are joined by a translucent green corrugated glass-fiber-roofed, screened porch that is a transparent, crystalline variation of the RD based on the module of the truncation dimension discussed previously. The porch variation is arrived at by extending the RD along two axes and repeating it along the third axis.
The translucent rhombi of the porch echo the diamond glazing of the Crystal Chapel. Effective polyhedral volumes can be created relatively economically in elements such as porches by means of inexpensive screen wire and ribs. The requirements of structural design, detailing, construction, weatherproofing, and so on are simpler and cheaper. Spatially dynamic screened porches are frequent in Goff’s work other examples include the Freeman and Miller Houses.
The Freeman House, Joplin, Missouri, 1958 (Figure 2.65), consists of an open-plan, rectangular space roofed by a gently sloping, partially suspended single plane. The roof expressed as a suspended carpet hovering over most of the house was used frequently by Goff. A counterfoil to the opaque planar roof element is an elevated, screened porchan inverted, truncated pyramid topped by another pyramidal screened “roof.”
The Miller House, Project 3, Harrison, Arkansas, 1963, was topped by a similarly spatial screened porch, more complex than the Freeman House porch and built on a hexagonal planhaving the faceted effect of a cut stone in a setting.
Figure 2.65 Freeman House, Joplin, Missouri, 1958. Photo of screened porch. (Courtesy of the Ryerson and Burnham Libraries of the Art Institute of Chicago.)
Frank Lloyd Wright frequently increased the sense of space and size in his designs with the comparatively economical use of porches and carports, which extended axes and elongated ground-hugging planes and masses.
The composition of the Pollock/Warriner House involved three major elements: (1) the cluster of roof polyhedra of the main house, (2) the flat-top garage, and (3) the polyhedral variations of the screened porch. The interaction of these three components, along with their exterior/interior spatial complexities and the attention to color, material, and detail, results in a grandeur, an atmosphere beyond the modest size, material, and construction methods of the dwelling.
Dr. and Airs. Warriner were asked to describe how it felt to live in this house with emphasis on the polyhedral aspects. Laura Warriner, a painter, said:
I could never live in an “ordinary” house. The forms of light and shadow in this house are an education. It feels like living in a giant palace. It amazes people when I tell them it’s only 1,500 square feet. It was confusing when I first moved inmaze-like. …It’s amusing to see peoples’ reactions to the house when they first come in.
The light changes during the day because each room has its own skylight. Thunderstorms the house puts you in tune to naturedie outside comes in (visually, that is)you can see completely through the house. It’s like living outsidethe sense of shelter. If it’s snowing it’s like snowing on you. It’s like being inside a cut diamondthe faceted light.
I felt that [polished stone] surfaces would magnify the effect. The house is angular but it does not seem to have harsh or sharp angles. There are no problems with headroom or bumping into things.
Repairs and maintenance are no more difficult than for any house.
It is not hard to furnish. When Bruce redesigned the house for us he said every other house of mine has a pit in it, let’s put a pit in this one. Most houses have too much furniture. This one doesn’t need much but I still have too much. But mostly it has art…
I’m sorry that everybody in the whole world can’t live in a Bruce Goff house!64
¶ GOFF’S LEGACY
Goff left a rich body of work both with and without polyhedrality. Some of these have been lovingly and carefully tended and preserved. Others have suffered neglect, emasculating alterations, fires, and demolition, and need public attention and nurturing. The Gutman and Wilson Houses and the Phi Lambda Fraternity House were demolished after damaging fires. Other Goff houses are gonethe Glen Harder House near Mountain Lake, Minnesota, was completely destroyed by fire recently. In December 1996, Goff’s masterpiece, Shin’enkan, the former Oklahoma residence of Joe and Etsuko Price, burned to the ground. Arson is suspected. The Frank Cole House in Park Ridge, Illinois, an example of Stage 1 polyhedrality, was demolished several years ago. A number of structures have undergone radical alterations, for example, the 1967 Mercedes-Benz Building in Atlanta.
“…The process of designating as landmarks many of his best designs has just begun, and will continue as the structures pass the 50-year mark required for official recognition. It is our hope that the remaining body of Goff’s extant designs will be recognized and preserved as a testament to one of America’s great architectural minds.”65
Goff’s contribution to the use of polyhedra in architecture did not originate in a spirit of rigorous polyhedral form making. Rather, it translates the concepts of Bragdon, Wright, et al., by creating new transcendental environments, incorporating polyhedra in their place among the universe of architectural form/structure/space possibilities.
¶ ACKNOWLEDGMENTS
I would like to thank the following for their assistance: Robert Bowlby, Nelson Brackin, Susan Bresler, Ernest Burden, David De Long, Jean Eckenfels, Robert Faust, Jack Golden and the Friends of Kebyar, Larry Wayne Grantham, Herb Greene, Grant Gustafson, Randolph Helming, David Milstead, Mrs. James Nicol, Kathy Nicol, Bruce Nicol, Joe Price, Rex Slack, Laura Warriner, and Mary Woolever and the Art Institute of Chicago.
¶ NOTES
-
For a comprehensive, “rich and definitive account of the life and work of the brilliant maverick from the western plains,” according to Helen Searing (whose 1996 Goff-designed house in Kansas City, Kansas, includes variations on extruded truncated hexagonal prisms), refer to David G. De Long, Bruce Goff. Toward Absolute Architecture, MIT Press, Cambridge, MA 1988.
-
Refer to Sidney K. Robinson, “Bruce Goff and Music,” in The Architecture of Bruce Goff, 1904, Art Institute of Chicago/Prestel, 1995.
-
Examples of Goff’s buildings utilizing forms other than polyhedra include: the Ford/Robinson House, Aurora, Illinois, 1948 (torus, cone); the Bavinger House, 1950 (helix, cylinder); the Garvey House 1 project, 1952 (sphere, torus, helix); Sid Lodge, Crested Butte, Montana, 1965 (16-sided, polygonal pyramid approaching cone); and the Struckus House, Woodland Hills, California, 1983 (cylinder). In 1978 the Bavinger House was recognized with a “Twenty-Five Year Award” from the American Institute of Architects as an “extraordinary work of imagination …a vivid expression of American values.”
-
For example, the undulating and ragged “free forms” of the Don Leidig House project, 1946, and the Ledbetter House, Norman, Oklahoma, 1947. Tension structures also occur in Goff’s output, e.g., the aforementioned Bavinger and Lei-dig Houses, the Plunkett Guest House project, the Shin’enKan Museum in Los Angeles, etc. Tension structures employ cables deployed in straight-line configurations. Both two-and three-dimensional arrays of cables occur in Goff’s work, in the latter case resulting in subtle geometric volumescylindrical, conical, pyramidal, etc. Tension arrays were often used ornamentally by Goff, frequently as “curve stitching,” i.e., the overlapping of a group of straight lines such that their intersections result in polygonal or curved shapes.
-
Many books illustrate and analyze these figures, e.g., Anthony Pugh, Polyhedra, A Visual Approach, University of California Press, 1976; Magnus J. Wenninger, Polyhedron Models, Cambridge University Press, 1971. The latter covers both regular and semi-regular polyhedra, or more generally, the 75 “uniform” polyhedra, including stellations.
-
Crystallographers study centers, planes, and axes of symmetry and the relative orientation of x, y, and z axes in minerals, using terminology such as “monoclinic,” “brachypinacoid,” and “orthorhombic.” A recent concern of crystallographers is the hypercrystal, which is an irregularly organized, quasiperiodic structure. See Chapter 15 for a discussion of quasicrystals.
-
Robert Lawlor, Sacred Geometry, Philosophy and Practice, Crossroad Publishing, New York, 1982, p. 104. Here is another source on polyhedra, “gnomonic expansion,” the spiral, the golden section, metaphor, and universal order, etc., with many good illustrations and diagrams.
-
John Sergeant, Architectural Design Profiles 16, p. 55.
-
D’Arcy Thompson, On Growth and Form, John Tyler Bonner, ed., Cambridge University Press, abridged Ed., 1966, p. 122. Bonner, a biomorphologist, is the author of Morphogenesis, An Essay on Development, Atheneum, 1963, which discusses three basic determinants of form in the biological world: growth, differentiation, and morphogenetic movement. As architectural metaphors, growth is cell (module) iteration or duplication; differentiation represents the functional variations of spaces such as living room, dining room, entry, and storage; and morphogenetic movement represents uniform characteristics carried throughout different parts of the same building, e.g., structural members, mechanical lines, and materials assemblies.
-
The startling architecture of the zoological world is revealed in Karl von Frisch, Animal Architecture, Harcourt Brace Jovanovich, 1974. This book covers habitations and devices actually built by animals, not the anatomy of the animals themselves.
-
A steel frame sculpture objectifies this abstraction in Venturi and Rauch’s Franklin Court, Philadelphia, 1972. It is illustrated in Charles Jencks, The Language of Post-Modern Architecture, Rizzoli, 1984, p. 89.
-
For a capsule visual history of architectural form covering 111 “styles,” including a profusion of recent entries, in 25 pages, see Chap. 1 of Ernest Burden, Elements of Architectural Design, A Visual Resource, Van Nostrand Reinhold, 1995. For a capsule history of Goff’s work, see the graphic, multipage pull-out sectionpp. 7in I’Architecture d’Aujourd Hui, No. 227, June 1983.
-
Islamic ornamental patterns are illustrated and analyzed in Syed Jan Abas and Amer Shaker Salman, Symmetries of Islamic Geometrical Patterns, World Science, River Edge, NJ, 1995. The 17 unique symmetry groups are used as a basis for this study. Another source of clear graphic analysis of intertwining Islamic tessellation (not only in architecture, but in planning, poetry, and music!) is Issam E. Said and Ayse Parman, Geometric Concepts in Islamic Art, World of Islam Festival Publishing Co., London, 1976.
Grids related to the Islamic can be found in Kaiyama Kyusaburo, The Book of Japanese DesignBansho Shin Hinagata, Bijutsu Oyo, Crown, New York, 1969. Two-dimensional patterns attempt to rise off the paper into the third dimensionsome quite similar to Goff designs in the Price Studio. The three-dimensional metal curtain walls of Goff’s First National Bank are related to these patterns.
-
“The Architecture of Bruce Goff,” Architectural Design, May 1957, p. 151. Author and historian Park was the University of Oklahoma architectural school librarian during Goff’s chairmanship. Goff, incidentally, explaining the bland conformity throughout the profession, said, “We all read the same magazines.”
-
Francine du Plessix and Cleve Gray, “Bruce Goff, Visionary Architect,” Art in America, Winter 1965.
-
See John C. Lilly, Programming and Metaprogramming in the Human Bio-Computer, Julian Press, 1972.
-
Mentioned in an interview with Johnson in Vanity Fair, June 1993, p. 157.
-
An increasing number of three-dimensional graphics programs are available for computers, e.g., Truespace. One can start with a polygon, drag (extrude) it to make a prism, shrink one end, see it in three dimensions, and rotate it here is an embryo polyhedral unit of the Price Studio. Or one could call up a preformed “organic,” i.e., a single geometric volume and transform it by pulling it through a “deformation lattice” or “energy field.” Then one can apply a surface texture, shades, and shadows, etc. Artifice contains a “solid modeling program” in which a three-dimensional background “space” appears with the cursor attached to a “wireframe,” e.g., lines representing the x, y, and z axes, in perspective. Typical commands are “linear duplicate,” “wallify” and the like. Not to mention the ubiquitous Autocad and animation programs such as Lightwave and Video Toaster. Information can be obtained from Computer Chronicles Newsletter, 1. See Chapter 12 for a discussion of computers and polyhedra.
-
Introduction to A Portfolio of the Work of Bruce Goff, designed and compiled by William Murphy and Louis Muller, Architectural League of New York and American Federation of Arts, 1970. For an elaboration of these ideas, see Herb Greene, Mind and Image, Ait Essay on Art and Architecture, University Press of Kentucky, 1976, and Building to Last, Architecture as Ongoing Art, with Nanine Hillard Greene, Architectural Book Publishing Co., 1981. The Greenes go on to say (in the latter, p. 77), “Nature seems patient of as many systems of geometries as we can discover. At this time who can say which warrants the highest metaphysical status.”
-
Suzanne K. Langer, Feeling and Form, A Theory of Art Developed from Philosophy in a New Key, Scribner’s, New York, 1953, p. 99.
-
Le Corbusier’s treatises: Modulorl irll, Harvard University Press, 1980. For a discussion of the golden mean or golden section, the ratio 4>> i-e., 1:1.618…as inherent in certain polyhedra, e.g., the icosahedron and dodecahedron, see H. E. Hunt-ley, The Divine Proportion, A Study in Mathematical Beauty, Dover, 1970.
-
This taxonomic series could be continued with a similar grouping for curvilinear formsfirst, extrusions of two-dimensional curves, then curves beyond the flat plane, i.e., spheres, etc., singly and in clusters continuing further with combinations of spherical surfaces and polyhedral forms and finally “free forms” and beyond. A transition from the polyhedral to the curvilinear can be seen in polygons with increasing numbers of edges but this is for another study. A number of Goff designs were curvilinear in the first go round and later revised to polygonal to fit the budget. Scaling down occurs with the Price Studio designs, but away from complex polyhedra rather than away from the curvilinear.
In his article “Bruce Goff, The Strict Geometrist,” in Architectural Design Profiles 16 (a special issue on Goff), John Sergeant divides Goff’s work into crystalline (with three categoriesrectangular, diagonal, and triangular) and curvilinear (four categoriescircular, radial, spiral, and processional).
-
For a discussion of depth cues, see James J. Gibson, Perception of the Visual World, Riverside Press, Cambridge, 1950.
-
As a student of Goff in the early 1950s, I felt that Goff was neither particularly interested in nor impressed by Fuller’s ideas, unlike a few of his students, myself included. Goff was, rather, politely respectful and appreciative of Fuller’s work, as he was with that of technologists such as Ibrroja, Candela, Nervi, and Maillart, to name a few.
The Louis Kahn/Ann lyng high-rise space frame office tower, part of Kahn’s Plan for Central Philadelphia, was well publicized at this time (mid-1950s). As a classroom assignment this writer attempted to design a “High-Rise Monastery for Downtown Houston,” incorporating living, circulation, and service spaces within a story-high tet-oct grid (i.e., a space frame whose structural members were composed of a “close packing” of alternating tetrahedra and octahedra).
We also designed a Chinese restaurant using the Fuller/Kenneth Snelson concept of discontinuous compression in the form of a sphere, or, more accurately, a tensegrity-modulated icosidodecahedron, as a structural/envelope matrix. In both cases almost the entire time allotted for the projects was taken up just trying to figure out the projective geometrical drawing of these forms, which today would be a snap on the computer. A pentagonal prism core/mast of concrete containing vertical circulation, kitchens, mechanical equipment, etc., served and supported the tensegrity bubble, which enveloped and supported the dining platforms. Goff grasped the nature of the beast and was most helpful in overcoming problems for the utilization of these forms in an architectural setting.
Just as a reminder of the typically strong effect Buckminster Fuller had on students across the country during the 1950sanother Goff student, New York architect Robert Tieger, says, “Fuller gave a talk at the O.U. Student Union. He talked on and on. The janitor wanted to turn the lights out at 10pm but Fuller went on ‘til about 12. It was the greatest thing I’d ever listened to.’’
-
De Long, Bruce Goff.
-
Michael Field and Martin Golubitsky, Symmetry in Chaos, A Search for Pattern in Mathematics, Art and Nature, Oxford University Press, 1992, p. 160.
-
The variety of space-filling polyhedral units and their manipulation via twisting, tipping, and other metamorphoses are explored in Donald G. Wood, “Space Enclosure Systems, The Variables of Packing Cell Design,” Bulletin 205, Engineering Experimental Station, Ohio State University, 1968.
-
De Long, Bruce Goff, p. 304.
-
Ibid.
-
Ibid., pp. 232.
-
Kathy Nicol, letter to author, August 25, 1995.
-
Architectural Design, May 1957, p. 173.
-
De Long, Bruce Goff, pp. 152.
-
John Sergeant, “Bruce Goff, The Strict Geometrist,” Architectural Design Profiles 16, Vol. 48, No. 10, 1978, p. 58.
-
Ibid. This article provides thumbnail illustrations of some two dozen floor plans on a single page (!) for comparison. Sergeant’s “crystalline” categorization of Goff’s work is mentioned elsewhere in this chapter.
-
The Lacey Hotel was, incidentally, a forerunner of a rhombic grid of glass claddingrecalled by Goff’s Crystal Chapelalthough Wright’s diamonds were arranged in an overlapping shingle-like pattern, whereas Goffs were set flush within a supporting grid.
-
As illustrated in George T. Kerr, “Synthetic Zeolites,” Scientific American, July 1989. Zeolites are minerals composed of silicon or aluminum and oxygen molecules, which form truncated octahedra. A cross section through the center of a truncated octahedron is an octagon. This may provide a clue to the subtle yet complex sense of space imparted in the Jones House that complex, repeating, spatial symmetries can be suggested by a few pieces of the grid.
-
For the full text of the letter, see De Long, Bruce Goff, p. 126.
-
This preceded by some years a scene from the sci-fi film Zardoz, in which Sean Connery is trapped within a magic gemstone. Note Mrs. Warriner’s crystalline comment near the end of this chapter.
-
De Long, Bruce Goff, p. 305. The quote within is from Herman George Schef-fauer, “Dynamic Architecture,” Dial, Vol. 70, March 1921, pp. 323.
-
Ibid., p.13.
-
For further descriptions of functions, see De Long, ibid., and Jeffrey Cook, The Architecture of Bruce Goff, Harper and Row, 1978, pp. 41.
-
Sergeant, “Bruce Goff.”
-
De Long, Bruce Goff, p. 13.
-
James J. Gibson, Perception of the Visual World, Riverside Press, Cambridge, 1950.
-
See Dennis Sharp, Modern Architecture and Expressionism, Braziller, New York, 1966. An untoward side effect of some of these projects is the chilling recall of the Nietszchean mountain-climbing mystique in German films of the 1920s such as The Blue Light by Leni Riefenstahl, who later became a propagandist for Hitler.
-
Ibid.
-
Both illustrated in De Long, Bruce Goff.
-
The Sierpinski arrowhead, a sponge-like tetrahedral fractal, will probably be used sooner or later as a basis for high-rise office or apartment buildings, if it hasn’t already. The figure is illustrated in John Briggs, Fractals, The Patterns of Chaos, Discovering a New Aesthetic of Art, Science and Nature, Simon and Schuster, 1992, p. 68.
-
Reminiscent of the roof trusses of Goffs very low budget Hopewell Baptist Church, Edmund, Oklahoma, 1949. In this dodecagonal pyramid the subtlety of the basic “tepee” is increased by using over a dozen variations of the angle of the sloping roofin walls, bell armature, truss chords, etc.
-
Safdie, “Pyramid City,” p. 90; Christian W. Thomsen, Visionary Architecture, From Babylon to Virtual Reality, Prestel Verlag, Munich, New York, 1994, p. 164. Several others in this bookBruno Taut’s 1918 “The Crystal Mountain,” p. 81, and Wassili Luckhardt’s 1919 “Project for a Sacred Building” in concrete and colored glass, p. 85.
-
For Johnson’s comment about Goff’s Crystal Chapel, as well as high praise from other architects in support of the Crystal Chapel over a traditional period piece, see De Long, Bruce Goff, p. 104.
-
This has a spherical/helical counterpart in Goff’s first Garvey House.
-
At Expo ’67 in Montreal, multistoried truncated tetrahedra were constructed from space trusses for (appropriately) the Space Frame Exhibition Hall by architects Affleck, Desbarats, Dimikopolous, Lebensold, and Sise; structural engineers de Stein and Associates, Eskenazi, and Barass.
-
Architectural Design, Vol. 28, May 1957, p. 163. More on the Wilson House can be found in Sergeant, “Bruce Goff,” p. 22.
-
Progressive Architecture, Dec. 1962.
-
L. Lines, Solid Geometry, Dover, 1965. Lines illustrates close packing in polyhe-dra such as hexagonal prisms, “rhomboidal dodecahedra,” “rhombo-hexagonal dodecahedra,” and truncated octahedrain order to prove properties relating to vertices, centers, etc.
-
See Haresh Lalvani, Transpolyhedra, Dual Transformations by Explosion Implosion, Lalvani, New York, 1977. See also Chapter 14.
-
Claude Bragdon, Projective Ornament, Dover, New York, 1992, p. 28.
-
“Supercube” was a term used by Lester Walker, New York architect, teacher, and author, for a cubic device, totally different from the Wilson module, which he designed, patented, and built in the 1960sa prefabricated, unfolding, expanding, “exploding” multipurpose studio furnishing module with a miscellany of built-in functions such as bed, desk, storage, and fighting.
-
De Long, Bruce Goff, pp. 154, 325
-
Architectural Design Profiles 16, p. 27.
-
Anthony Pugh, Polyhedra, A Visual Approach, University of California Press, 1976, p.43.
-
Laura Warriner, telephone conversation with author, 1994.
-
Annemarie van Roessel, “Bruce Goff’s Built Works,” in The Architecture of Bruce Goff, 1904, Design for the Continuous Present, Pauline Saliga, Mary Wbolever, and Sidney K. Robinson, eds., Art Institute of Chicago and Prestel Verlag, 1995the catalog issued in conjunction with the 1995 exhibition of Goff’s architecture and paintings at the Chicago Art Institute. The Institute holds Goff’s archives.
¶ BIBLIOGRAPHY
Abas, S. J., and Salman, A. S.: Symmetries of Islamic Geometrical Patterns, World Science, River Edge, NJ, 1995.
Baukunst und Werkform, No. 7, Frankfurt, 1953.
Bonner, J. T: Morphogenesis, An Essay on Development, Atheneum, 1963.
Bragdon, C.: Projective Ornament, Dover, New York, 1992.
Briggs, J.: Fractals, The Patterns of Chaos, Discovering a New Aesthetic of Art, Science and Nature, Simon and Schuster, New York, 1992.
Burden, E.: Elements of Architectural Design, A Visual Resource, Van Nostrand Reinhold, 1995.
Cook, J.: The Architecture of Bruce Goff, Harper and Row, New York, 1978.
Coxeter, H. S. M.: Introduction to Geometry, Wiley, New York, 1961.
De Long, D. G.: Bruce Goff, Toward an Absolute Architecture, MIT Press, Cambridge, MA, 1988.
Field, M., and Golubitsky, M.: Symmetry in Chaos, A Search for Pattern in Mathematics, Art and Nature, Oxford University Press, 1992.
Frisch, K. v.: Animal Architecture, Harcourt Brace Jovanovich, 1974.
Fuller, R. B.: Ideas and Integrities, A Spontaneous Autobiographical Disclosure, Robert W. Marks, ed., Collier Books, Macmillan, 1963.
Ghyka, M.: Geometrical Composition and Design, Alec Tiranti, London, 1952.
Gibson, J. J.: Perception of the Visual World, Riverside Press, Cambridge, 1950.
Goff, Bruce, Architect (boxed folio), distributed by Prairie School Press, Chicago, 1978.
Gray, C., and du Plessix, E: “Bruce Goff, Visionary Architect,” in Art in America, Winter 1965.
Greene, H.: Mind and Image, An Essay on Art and Architecture, University Press of Kentucky, 1976.
Greene, H.: Introduction to A Portfolio of the Work of Bruce Goff, designed and compiled by Louis Muller and William Murphy, Architectural League of New York and American Federation of Arts, 1970.
Greene, H., with Greene, N. H.: Building to Last, Architecture as Ongoing Art, Architectural Book Publishing Co., 1981.
Hambidge, J.: The Elements of Dynamic Symmetry, Yale University Press, 1919, reprinted 1948.
Holden, A.: Shapes, Space and Symmetry, Columbia University Press, 1971.
Huntley, H. E.: The Divine Proportion, A Study in Mathematical Beauty, Dover, 1970.
Jencks, C.: The Language of Post-Modern Architecture, Rizzoli, 1984.
Johnson, P.: Vanity Fair, June 1993.
Kerr, G.T.: “Synthetic Zeolites,” Scientific American, July 1989.
Kyusaburo, K.: The Book of Japanese DesignBansho Shin Hinagata, Bijutsu Oyo, Crown, New York, 1969.
Lalvani, H.: Transpolyhedra, Dual Transformations by Explosion-Implosion, Lalvani, New York, 1977.
Langer, S. K.: Feeling and Form, A Theory of Art Developedfrom Philosophy in a New Key, Scribner’s, New York, 1953.
Lawlor, R.: Sacred Geometry, Philosophy and Practice, Crossroad Publishing, New York, 1982.
Le Corbusier: Modtilor I ir II, Harvard University Press, 1980.
Lilly, J. C.: Programming and Metaprogramming in the Human Bio-Computer, Julian Press, 1972.
Lines, L.: Solid Geometry, Dover, 1965.
Mohri, T.: Bruce Goff in Architecture, Kenchiku Planning Center Co., Tokyo, 1970.
Park, B. A.: “The Architecture of Bruce Goff,” in Architectural Design, Vol. 28, May 1957.
Parman, A., and Said, I. E.: Geometric Coticepts in Islamic Art, World of Islam Festival Publishing Co., London, 1976.
Progressive Architecture, Dec. 1962.
Pugh, A.: Polyhedra, A Visual Approach, University of California Press, 1976.
Robinson, S. K.: “Bruce Goff and Music,” in The Architecture of Bruce Goff, 1904, Art Institute of Chicago/Prestel, 1995, catalog to the exhibition.
Scheffauer, H. G.: “Dynamic Architecture,” *Dial,*Vol. 70, March 1921.
Sergeant, J.: “Bruce Goff, The Strict Geometrist,” in Architectural Design Profiles 16, Vol. 48, No. 10, 1978.
Sharp, D.: Modem Architecture and Expressionism, Braziller, New York, 1966.
Thompson, D’A. W.: On Growth and Form, Abridged ed., John Tyler Bonner, ed., Cambridge University Press, 1966.
Thomsen, C.W.: Visionary Architecture, From Babylon to Virtual Reality, Prestel Verlag, Munich, New York, 1994.
van Roessel, A.: “Bruce Goff’s Built Works,” in The Architecture of Bruce Goff, 1904, Design for the Continuous Present, Pauline Saliga, Mary Woolever, and Sidney K. Robinson, eds., Art Institute of Chicago and Prestel Verlag, 1995.
Wenninger, M. J.: Polyhedron Models, Cambridge University Press, 1971.
Wood, D. G.: “Space Enclosure Systems, The Variables of Packing Cell Design,” Bulletin 205, Engineering Experimental Station, Ohio State University, 1968.
¶ Louis Kahn and Space Frames
Irene E. Ayad
¶ INTRODUCTION
During the 1950s, Louis I. Kahn (1901) inspired by his contemporariesBuckminster Fuller, Anne Griswold Tyng, and Robert Le Rico-lais briefly experimented with space frames. The Beaux-Arts-educated Kahn, however, was less interested in the technological and economic advantages of three-dimensional construction than in its spatial, structural, and formal potentials.
Kahn was particularly interested in the hollow spaces embedded within the frame, which he first discovered while designing the celebrated tetrahedral ceiling for the Yale University Art Gallery (1951) and subsequently used to harbor the gallery’s mechanical ducts and conduits.
Stimulated by the Yale project, Kahn joined forces with Tyng and examined in earnest the language of space frame architecture, an endeavor that culminated in the City Tower project, a municipal high-rise complex conceived within the context of Philadelphia’s redevelopment efforts. The final version (1956), an immense self-bracing concrete helix, was a total triangulated habitable space frame in which primary and secondary spaces were hierarchically integrated. The building offered a visionary alternative to the layered space frame trusses and to the modern braced post-and-beam structures. Except for
□ 127
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
the Yale University Art Gallery, none of the other largely visionary schemes were ever built.
BEGINNINGS: THE YALE UNIVERSITY ART GALLERY (1951)
In 1951, while a visiting critic at the Yale School of Architecture, Louis Kahn was commissioned to design the addition to the Yale University Art Gallery.1 The Yale project was to kindle his brief but decisive involvement with space frames. At the time of the commission, Kahn was a well-respected architect and design critic. Like many of his contemporaries, he had abandoned his Beaux-Arts roots and embraced the tenets of modern architecture, including its concerns with social housing, urban and community development, and technological issues. Most of his housing and community schemes were small scale in nature and located in the vicinity of Philadelphia, his hometown.
The Yale Art Gallery was Kahn’s first truly prestigious assignment. The building was to be a modern loft structure with extremely flexible spaces that could be subdivided at will to accommodate a host of functions.2 Kahn first considered a conventional post-and-beam structure with widely spaced concrete columns and concrete floor slabs.3 Suspended acoustical plaster vaults were to span the preconceived rectangular spaces from east to west. The spaces above the vaults were to accommodate the building’s mechanical systems. Because the vaults determined the position of the room dividers, Kahn eventually rejected the proposal.4 Keen to find a more compelling and innovative solution, he developed a rather ingenious multiplanar truss system that was to unite floor and ceiling.5 In this the horizontal planes consisted of equilateral, hollow, and open-base concrete tetrahedra. Adjacent tetrahedrons were joined at the vertices so that the reinforcing rods located at the base of each triangle could run in three directions without interference. The rods were to absorb the tensile stresses in the lower horizontal plane constituting the ceiling. A continuous concrete slab, connecting the apices, provided the floor’s base.
To satisfy the New Haven building codes, which required a beam system, and to eliminate shear where the tetrahedrons joined, Kahn and Henry A. Phisterer, the consulting engineer, modified the proposal while trying to preserve its original formal and spatial qualities. The modified scheme called for inclined concrete beams braced by V-shaped elements covered by a thick top slab spanning 40 feet.6 Though no longer a true space frame, the ceiling maintained its tetrahedral character (Figure 3.1).7
In the hollow channels running between beams, Kahn threaded the ducts for the electrical and ventilating systems. The mechanical equipmentwhich he considered the bane of modern architectthus became an integral part of the structure’s hollow fabric.8 Kahn’s desire to integrate the mechanical with the structural system was a pioneering idea, and one that modern architecture had largely ignored.9
Figure 3.1 Yale University Art Gallery (1951) interiorview showing ceiling and column. (Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Commission.)
The beginning of the 1950s witnessed a renewed interest in three-dimensional construction.10 This change from “plane” to “space” construction resonated in the work of Buckminster Fuller and Anne Tyng, who were both associated with Kahn. Indeed, each claimed some responsibility for inspiring the Yale ceiling.11 Fuller’s association with Kahn began during the 1930s in Philadelphia and was renewed in 1951 when he was a visiting critic at Yale.12 Fuller believed that his “exhaustive” descriptions of the theoretical premise underlying his geodesic structures had led to the development of the “octettruss in the Yale Art Department.”13 These marathon lectures supposedly took place on their joint railroad trips to New Haven. Kahn first admitted but later denied that Fuller’s work had any bearing on his scheme, noting that it was “structurally more advanced” and not applicable to a “flat ceiling.”14
The link between Fuller and Kahn was established by Tyng, who had joined Kahn’s office in 1945 and later worked with him on the gallery.15 Fascinated by Fuller’s ideas,16 she had experimented with his octet truss in a proposal for an elementary school project (1949) using a multilayered truss system.17 The school consisted of individual buildings, housing three classrooms. Each classroom was contained within its own frame which grew from a single triangular unit into wider layers eventually branching horizontally to cover the classroom space. Here vertical and horizontal elements formed an organic unit. Tyng’s work demonstrated that Fuller’s single-layered octet truss could be adapted to both a multilayered truss system and to a conventional building type with its traditional emphasis on facade, orientation, and division of spaces. In the Walworth Tyng house (1951) located on Maryland’s eastern shore, she extended the triangulated frame to embrace the entire building: roof, wall, sunshades, dormers, entrance, and balcony. Applying the octet geometry to a rectangular house with a pitched roof demanded that she turn the “geometry so that the squares in the octahedrons were in the horizontal plane.”18 The Walworth Tyng house was probably the first habitable space framea concept that was to intrigue Kahn.19
Although Fuller and Tyng were the catalysts, the Yale ceiling lacked the structural sophistication of Fuller’s work and the organic growth concept Tyng had pursued in her projects. A lattice support, for example, would have been a more efficient system for a noncontinuous space slab, providing a structural and visual continuity between the gallery’s vertical and horizontal members. Nevertheless, the ceiling slab was the art gallery’s most prominent and discussed feature.20 Its bold geometric concrete forms not only transcended the gossamer and lightweight quality that characterized the work of his peers, but also signaled a new monumentality in Kahn’s work.
The development of the slab had stimulated Kahn’s interest in three-dimensional construction. He was particularly fascinated by its hidden spatial potential, which he examined more closely in a project that became known as City Tower.21
THE SPACE FRAME AND ITS ARCHITECTURAL IMPLICATIONS
City Tower (1952)
The City Tower was a proposal for a triangulated frame that Kahn and Tyng designed during their spare hours. The scheme was based on Kahn’s 1952 Civic Center proposal for Philadelphia, which included a tall prism-shaped triangular building. After the city planning commission had rejected the project on the grounds that it was too abstract, Kahn and Tyng developed the prism-shaped structure into a space frame later known as City Tower.22
The tower was designed in several stages. The first version, whose biological emphasis suggests the hand of Tyng, was conceived as a total triangu
lated cantilevered structure with open and trussed spaces that could be further subdivided into smaller levels.23 Whereas the open spaces were to accommodate the building’s honorific areas, the trussed spaces were set aside for municipal offices and workshops.
In this early scheme, the tetrahedral floors were stacked above each other and connected to the angled frames (Figure 3.2). The actual form was inspired by an illustration of a diatom (Figure 3.3), a type of algae depicted in D’Arcy Wentworth Thomson’s On Groivth and Form.™ The book was held in high esteem by progressive architects. Kahn probably leafed through its pages studying the images, which revealed that in nature geometry and structure were organically related.25 The undulating floors are an iconic interpretation of the diatom whose form was derived from a skewing pattern of hexagonal cells. Later Kahn was to credit Tyng for recognizing “the aesthetic implications of the geometry inherent in biological structures bringing us in touch with the edge between the measurable and the unmeasurable.”26
To free the center from internal supports, the angled frames were placed at the periphery and the vertical circulation shafts for elevators and stairwells were incorporated within its hollow fabric, creating a clear distinction between what Kahn would soon call “served” and “servant” spaces. The
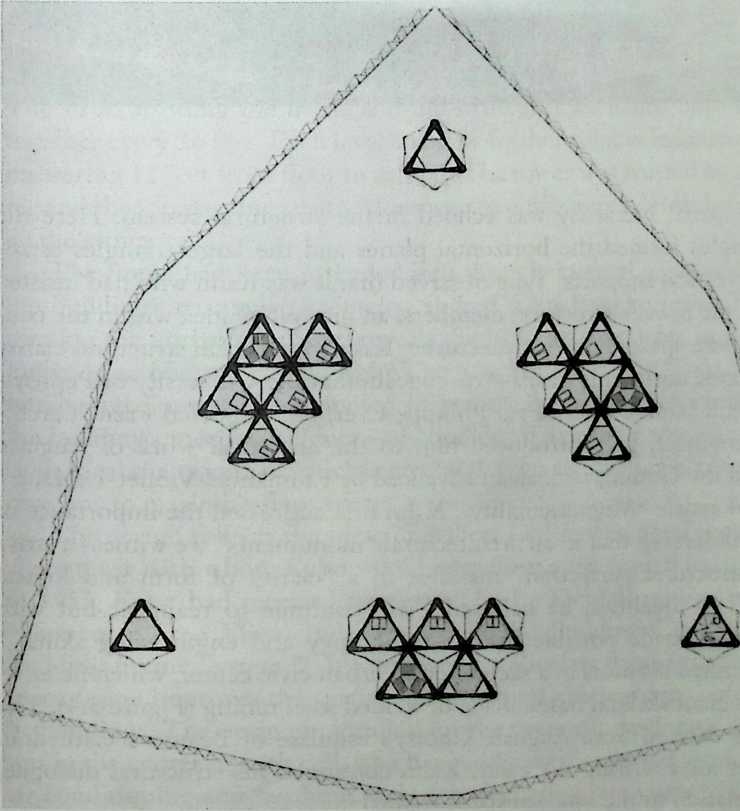
Figure 3.2 City Tower, Philadelphia, Pa., structural floor plan, first version (1952/53). (Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Commission.)
Figure 3.3 A diatom showing skewing pattern of hexagonal cells. (From D Arcy Wentworth Thomson, On Growth and Form, Cambridge University Press, 1948.)
building’s spatial hierarchy was echoed in the structural system. Here the small triangles formed the horizontal planes and the large triangles established the vertical supports, Tyng observed that it was Kahn who had insisted on seating the tower’s structural members, an innovative idea within the context of modern space frame architecture.27 Kahn’s interest in structural clarity was developed during his Beaux-Arts education at the University of Pennsylvania in Philadelphia where Paul Philippe Cret, the respected French architect and engineer, had introduced him to the analytical work of Auguste Choisy and the Gothic rationalism advanced by Emmanuel Viollet-Le-Duc.28 In his 1944 article “Monumental!ty,” Kahn first addressed the importance of structure, observing that in all architectural “monuments” we witness a striving for “structural perfection” manifest in a “clarity of form and logical scale.”29 These qualities, he believed, “will continue to reappear but with added powers made possible by our technology and engineering skills.”30 Kahn illustrated his ideas in a sketch for an urban civic center, which he envisioned as a giant skeletal frame made of welded steel tubing (Figure 3.4). The design was derived from Auguste Choisy’s esquisse of Beauvais Cathedral. Eight years after writing the essay, Kahn continued his structural dialogue, albeit in relation to the modem space frame.
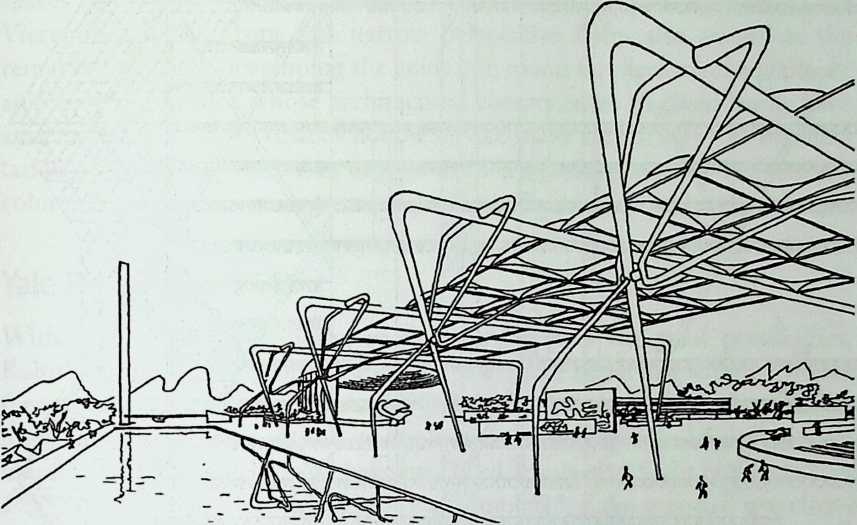
Figure 3.4 Civic Center, perspective view, 1944, illustrating monumentality. (From Paul Zucker, ed„ New Architecture and City Planning, New York Philosophical Library, 1944.)
In the summer of 1953, the City Tower was published in Perspecta, the Yale University architectural journal.31 By then the scheme had evolved into a 216-foot concrete frame covered with an angled faceted exterior (Figure 3.5).32 The struts forming the frame and the structure’s six major floor levels came together every 36 feet. Each level could be further subdivided into three floors measuring 12 feet from floor to ceiling. The tower was trussed by cross-framing and the intersecting struts. Moreover, two mezzanine levels helped to stiffen the structure.
The floors had been extended into three hexagonal areas and, following the building’s triangular geometry, shifted from level to level. The idea of rotating the horizontal planes reveals the hand of Tyng who, as Buckminster Fuller later observed, “was Kahn’s geometrical strategist.”33 As at Yale, the tetrahedral floor slabs, composed of precast lightweight concrete, harbored the building’s mechanical duct and conduits. The center was occupied by six cylindrical shafts, one of which accommodated a stairwell. This central service core was to maximize floor spaces.
The design reflects the ideas of Robert Le Ricolais, the French structural engineer with whom Kahn would later form a life-long friendship.34 Early in 1953, Kahn had received two essays by Le Ricolais respectively entitled “Hexacore ‘Free Flow’ Industrial & Public Buildings” and “ ‘Multicore’ Building Frame System.”35 In summary, Le Ricolais argued that a hexagonal space frame improves the spatial and structural efficiency in multistory public buildings. The optimum location for the supporting columns, he believed, was in the center of each cell, which could be used in part as service shafts for air conditioning and “as drain pipes for evacuating rain water.”36 After seeing
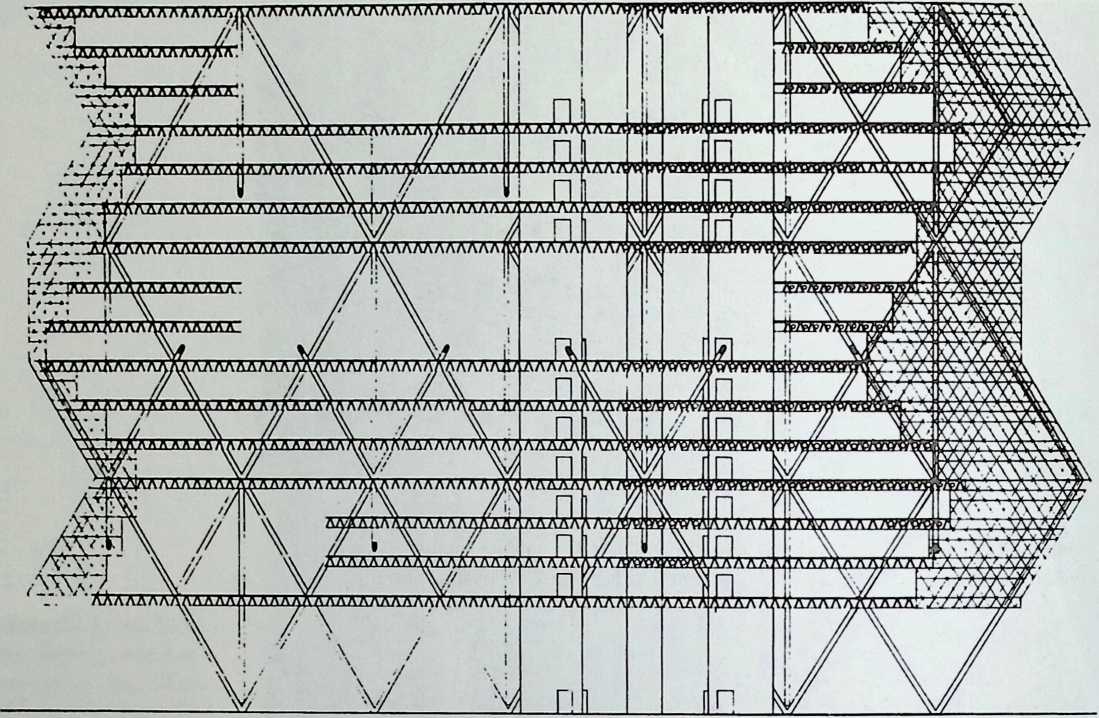
Figure 3.5 City Tower, Philadelphia, Pa., section, later version (1953), illustrating shifting horizontal planes. (Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Commission.)
the Perspecta publication, Le Ricolais sent a letter to Kahn congratulating him on the project.37
In tandem with Perspecta, Kahn offered his first and only extended discussion on space frame architecture:
In Gothic times, architects built in solid stones. Now we can build with hollow stones. The spaces defined by the members of a structure are as important as the members. These spaces range in scale from the voids of an insulation panel, voids for air, lighting and heat to circulate, to spaces big enough to walk through and live in.38
Immediately following these observations Kahn proclaimed:
The desire to express voids positively in the design of structure is evidenced by the growing interest and work in the development of space frames.39
Reflecting the growing emphasis Kahn placed on integrating the mechanical with the structural system, Kahn is primarily interested in the interstitial
spaces that he would later examine in other structural systems including the Vierendeel truss. From this narrow perspective Kahn also arrived at the remarkable idea of developing the voids into rooms for mechanical equipment and services, an idea whose architectural consequences he could hardly have anticipated. The City Tower’s hollow service shafts are the very first manifestation of Kahn’s suggestion to express voids in a positive manner. The “hollow column” would soon emerge in his work as a distinct architectural feature.
Yale Revisited (1954)
With a better understanding of the space frame’s structural possibilities, Kahn’s thoughts invariably returned to Yale. As he noted in a letter to Walter Gropius: “My work on the Yale Art Gallery has led me to think about three-dimensional construction and its implications architecturally. I failed to command the forces which could have produced a truly significant building.”40 In 1954, about a year after the gallery was completed, Kahn prepared two closely related sketches depicting the building as a cantilevered structure with enormous tetrahedral columns connected to a tetrahedral floor slab (Figure 3.6). In this conjectural scheme, the vertical supports are in structural sympathy with the geometry of the spanning members. After reviewing the scheme, Kahn observed: “A tetrahedral floor asks for a column of the same structure.”41 Kahn had considered both a rectilinear and a hexagonal plan. The latter, of course, would have been a logical continuation of the building’s triangulated geometry. In subsequent publication of the scheme, however, Kahn favored the rectilinear plan, an obvious concession to the existing site conditions.
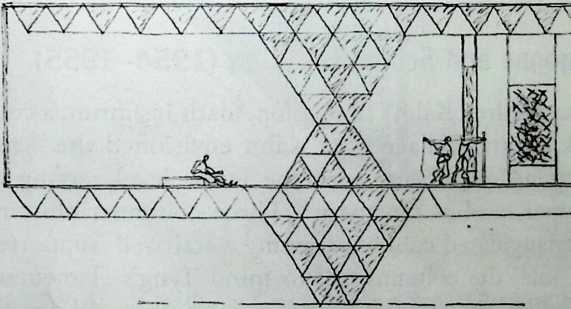
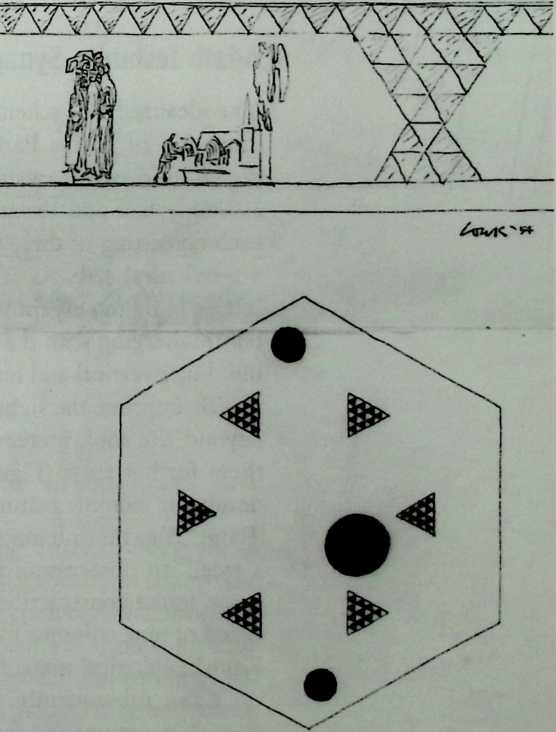
Figure 3.6 Yale University Art Gallery, section and plans showing reevaluation of structural system (1954). (Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Commission.)
The dwarfed figures and artifacts occupying the gallery spaces illustrate that Kahn envisioned a building of truly impressive scale. Indeed, if we take the figure holding a tape as a module measuring about 5 feet 7 inches (the height of an average person) and multiply this number by the triangles constituting the height of the columns, we find that the ceiling height comes close to 30 feet the actual height is approximately 10 feet. In the second sketch, the columns are placed closer together, yet the lofty feeling of the gallery spaces is maintained. These sketches illustrate that Kahn was more interested in creating impressive monumental spaces than addressing mere utilitarian concerns, a quality he greatly admired in Imperial Roman architecture.42 The Baths of Caracalla was his favorite building: “Here was the will to build a vaulted structure 100 feet high in which men could bathe. Eight feet would have sufficed.”43
Adath Jeshurun Synagogue and School Building (1954)
The idealized Yale scheme inspired Kahn’s design for Adath Jeshurun, a congregation in Elkins Park, North Philadelphia. Kahn envisioned the synagogue as a two-story tetrahedral scheme with the lower level serving as assembly hall and the upper level as sanctuary.44 Three columnar clusters, each consisting of three triangulated columns framing a stairwell, supported a tetrahedral slab. As at Yale, the columns call to mind Tyng’s elementary school building, except that here the triangulated layers contract and expand before merging with the ceiling, thus making a clear distinction between the building’s vertical and horizontal members.
To improve the fight within the stairwells, Kahn extended the columns beyond the roof, increased the number of columns per cluster, and pulled them further apart (Figure 3.7). The column was not only emerging as the dominant tectonic feature in Kahn’s work, but as he explained in a letter to Tyng: “Now the column must be hollow like the stem of a leaf or the trunk of a tree,” an observation that, for sure, owed much to his involvement with space frame construction.45 In this final scheme, each columnar cluster consisted of nine columns forming a 26-foot triangle.46 Its “hollow trunk,” to use Kahn’s biological metaphor, housed the triangulated staircase.
Kahn subsequently prepared this color sketch to emphasize the synagogue’s structural and formal characteristics (see Color Art 1). Reflecting his desire to make a clear “distinction between things,”47 the yellow and teal effectively show the difference between the scaled geometry of the structural members and the building’s horizontal and vertical elements. The color
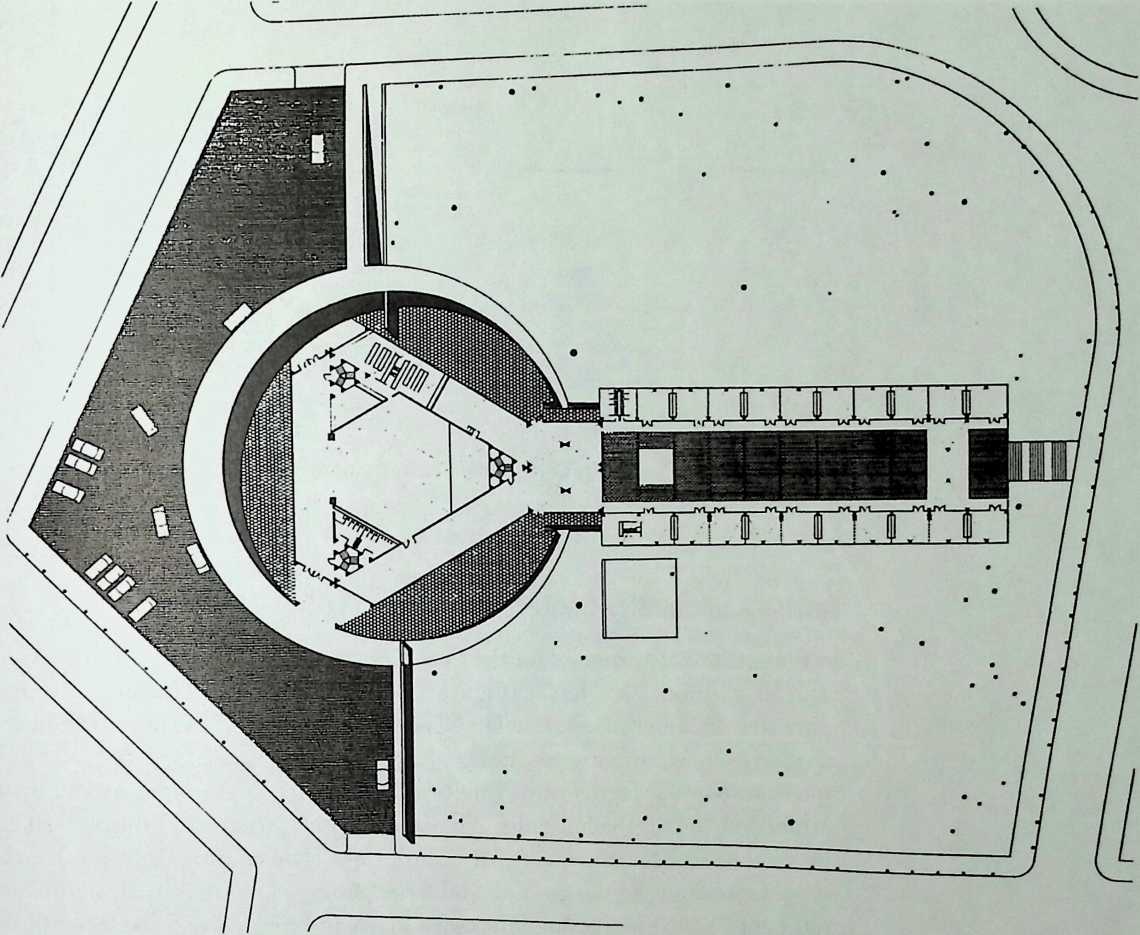
Figure 3.7 Adath Jeshurun Synagogue and School Building, Elkins Park, North Philadelphia, Pa., plan (1954). (Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Commission.)
sketch, more than the plan, demonstrates that the servant spaces have emerged as the building’s salient feature.
A review of the synagogue reveals Kahn’s growing desire to integrate all parts of the building by using a consistent geometric vocabulary to resolve the conflict witnessed at Yale where he had used different compositional models.48 In the Yale Art Gallery, the preconceived rectilinear plan was at odds with the triangulated geometry of the ceiling.49 For the synagogue, Kahn had originally considered a hexagonal plan before settling on the triangular arrangement. But even then, he failed to achieve an organic unity between structure and space, an objective he had mastered in his trabeated projects. With Adath Jeshurun, which was never built,50 Kahn’s interest in three-dimensional construction was beginning to wane.
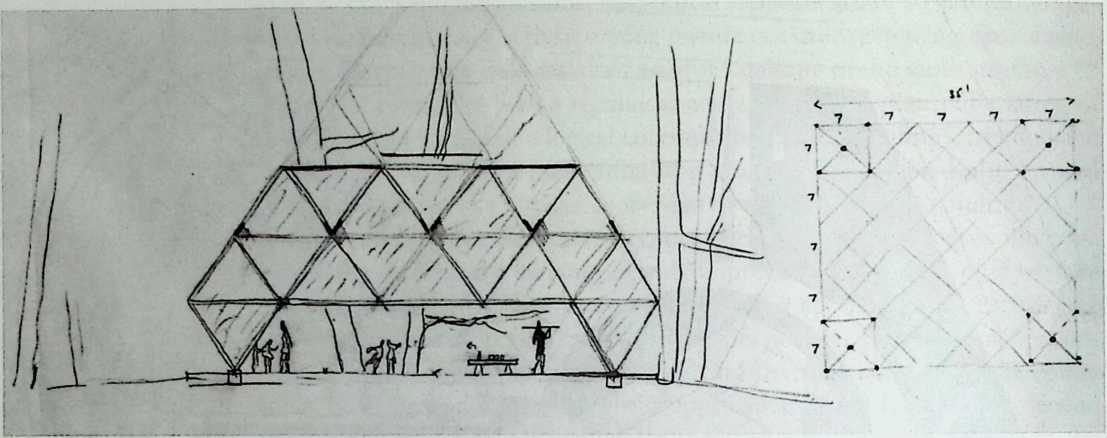
Figure 3.8 Jewish Community Center-Day Camp, Trenton, N.J., section and plan, preliminary proposal (ca. 1955).
Jewish Community Center/Day Camp (1955)
In the preliminary proposal for the Day Camp of the Jewish Community Center near Trenton, New Jersey (Figure 3.8), Kahn continued his quest to integrate structure and space. The Day Camp was conceived as three tetrahedral pavilions set within an open field.51 Each building was based on a 35-foot square whose four comer posts supported a truncated pyramidal frame of half tetrahedral and octahedral units. The steel tubular structure, however, lacked the sinuous and graceful quality of Kahn’s 1944 civic center. With its truncated roof, proximity to the ground, and large geometric units, the design brings to the fore Kahn’s increasing interest in mass, and his desire to wed the building with the ground.
Indeed, the Day Camp was modeled after Kahn’s Trenton Bath House (1955) comprising four square pavilions grouped around a central atrium. The comers of each square were occupied by a small cubicle whose concrete block walls supported the building’s truncated pyramidal roof. The cubicles could be used for a myriad of services. The building marked a watershed in Kahn’s career: not only were structure and space unified by one compositional model, the square, but the hollow column had evolved into a separate servant room. In the Trenton Bath House Kahn first fully realized his “served” and “servant” space concept, the generative force for all his subsequent work.52
City Tower (1956)
In 1956 Kahn returned to the City Tower and, in collaboration with Tyng, developed the project into an imposing 616-foot-tall skyscraper (Figure 3.9). This final version was prepared for the Universal Atlas Cement Company’s advertising campaign to promote and show the versatility of concrete.55 The model was to be published in both the Architectural Record and
Architectural Fomm. Kahn and Tyng elaborated on the project’s urban significance, its “servant spaces,” and the structural shortcomings of the earlier project.
The building was to rest on a 700-foot square platform comprising three levels: a parking and service floor below grade, a shopping concourse at street level, and a pedestrian plaza above ground. Cylinders placed at the periphery acted as fight and air wells for the lower levels, which could be reached by ramps, escalators, or staircases. The substructure served as a transitional element between the surrounding streets and the tower whose triangular geometry was anticipated in the plaza’s pavement. Here two intersecting triangular systems, one facing north to south, the other east to west, were superimposed on an orthogonal grid. The tower was a totally triangulated precast and prestressed concrete frame whose awesome physicality bore little resemblance to the earlier scheme. Whereas the building’s monumental scale showed little regard for the surrounding urban domain, its basic structural unit was an 11-foot tetrahedron, the height of an average ceiling.55 In this final version, the shifting planes were fully coordinated with the threefold column clusters.56 The concrete struts forming the frame intersected with the nine structural levels at 66-foot intervals. Kahn and Tyng prepared a host of sketches to identify the natural growth of the triangular geometry that gave the tower its distinct bodily configuration: a helix bracing itself diagonally against the wind. From this moment, Tyng observed, “Kahn was able to see the tower as a form which grew itself.”57
The column clusters were crowned by “hollow capitals” measuring 11 feet, a variation on the hollow-column theme. The bell-shaped capitals harbored ancillary spaces for toilets, mechanical services, and storage. In the section drawing of the capitals, Kahn included a standing figure to illustrate his earlier claim that voids should be large enough for people to walk through and live in. In the absence of any decorative details, the servant spaces assumed an ornamental quality. Like the earlier scheme, the hollow spaces within the tetrahedral floor slabs carried the air-conditioning ducts, electrical wiring, and plumbing. The center was occupied by shafts for pipes, which in turn were surrounded by three stairwells. The vertical circulation shafts, however, were independent of the structural system.
With its natural growth form, the tower was conceived as an alternative to the modern post-and-beam slab diagonally braced for wind loads.58 In contrast to Mies van der Rohe’s Seagram Building, for example, in which the diagonal bracing is hidden to preserve the structure’s pristine rectilinear frameKahn once called the building “a beautiful bronze lady in hidden corsets”59the tower expressed the very idea of wind bracing.60 However, as Robert Venturi noted, it did so at the expense of public spaces and elevators.61 In addition to its spatial shortcomings, the building would have been expensive and difficult to build.62
Concern for natural elements gave rise to what Kahn called a higher order of construction. To shade the tower from sun and wind, and to regulate its temperature, the entire structure was covered by glass panels held in place with permanent sun louvers made of aluminum strips resembling filigree. The panels, like the planes, shifted from level to level, creating a texture of light and shade. As Kahn explained: “I didn’t want to graft on a wind idea but to find an order which takes care of the wind.”63 Kahn later compared the tower to a fairy tale, an affirmation that the geometric language, transcending any aesthetic and functional concerns, had determined what the building “wanted to be.”64
Civic Center-Foram (1957)
In 1957 Kahn included the final version of the City Tower in his Civic Center-Forum project, one of his ongoing redevelopment proposals for Philadelphia (Figure 3.1O).65 Like its Roman predecessors, the forum was to be the city’s new civic center, housing all of its public institutionscivic, academic, social, and commercial. The triangulated tower was the crowning element. Within this setting, its visionary vocabulary assumed symbolic overtones, heralding the renewal of the city and its institutions, which Kahn had come to regard with increasing reverence. With the City Tower, later shown at the Museum of Modern Art’s exhibition Visionary Architecture, Kahn’s involvement with three-dimensional construction had come to a close.66
Figure 3.10 Market Street East Studies, Philadelphia, Pa., Civic Center Forum, perspective view (1957). (Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Commission.)
¶ CONCLUSION
Kahn’s experiments with space frames, which owed much to the collaborative effort of Tyng, produced several memorable and rather visionary projects, as did his writings on three-dimensional construction, leaving us with the indelible image of the “hollow stone” and, by extension, the “hollow column.” Yet the largely experimental nature of his work, his brief and limited engagement with the structural system paralleled by his growing interest in orthogonal planning and mass, all suggest that Kahn never truly felt comfortable with the triangulated vocabulary of this structural system. Kahn was at heart a master builder and, like Frank Lloyd Wright, Le Corbusier, and Mies van der Rohe before him,67 did not belong to the age of space frame architecture.
Nevertheless, Kahn’s foray into three-dimensional construction played a crucial role in the development of his work. It was here that he discovered that voids could be extended into servant spaces and that structure and form were explicitly related; and here he also reexamined the structural ideals of his Beaux-Arts roots, dormant during his encounter with modern architecture. These themes were to inform his mature work,68 which established Kahn as a leading voice among 20th-century architects.
¶ ACKNOWLEDGMENTS
I am grateful to Anne Tyng for the information and material she offered in preparation for this paper and to Professor John O’Brien, at the University of Tennessee-Knoxville, for his thoughtful review of this manuscript. I also would like to thank Professor Elefterios Pavlides, at Roger Williams University, for his interest in the project and Julia Moore Converse, director of the Architectural Archives at the University of Pennsylvania, for her unfailing support to obtain the photographic images.
¶ NOTES
-
The definitive monograph on Kahn is David B. Brownlee and David De Long, Louis I. Kahn: In the Realm of Architecture, Rizzoli, New York, 1991.
-
For a history of the Yale Art Gallery, see Patricia Cummings Loud, The Art Museums of Louis I. Kahn, Duke University Press in association with the Duke University Museum of Art, 1989, pp. 55.
-
Heinz Ronner and Sharad Jhaveri, Louis I. Kahn: Complete Work 1935, 2nd ed. Birkhauser, Boston, 1987, p. 67.
-
Kahn, interview with John W. Cook and Heinrich Klotz, From Conversation with Architects, reprinted in Richard Saul Wurman, ed., What Will Be Has Always Been: The Words of Louis I. Kahn, Access Press and Rizzoli International, New York, 1986, p. 206.
-
“Tetrahedral Floor System: Yale’s New Design Laboratory Conceals Lighting and Ductwork Within a 31” Deep Floor Structure,” ArchitecturalForum, Vol. 97, Nov. 1952, pp. 148.
-
George A. Sanderson, “Extension: University Art Gallery and Design Center,” Progressive Architecture, Vol. 35, May-Aug. 1954, pp. 88. Boris Pushkarev, “Yale University Art Gallery and Design Center,” Perspecta, No. 3, 1955, pp. 46.
-
Vincent Scully Jr., Louis I. Kahn, Braziller, New York, 1962, p. 21.
-
In reference to the Yale Art Gallery Kahn noted: “The builders of the past had it much easier than those of the present in one important respect: they did not have to worry about pipes, ducts, conduits, and innumerable mechanical intestines.” Kahn, quoted in Ronner and Jhaveri, Louis I. Kahn: Complete Work, p. 68.
-
Kenneth Frampton, Modern Architecture, Oxford University Press, New York, 1980, p. 244.
-
For example, in December 1951 the Architectural Forum was planning to hold a symposium on “Space Frames and Stressed Skin Construction.” Kahn was invited to participate in the discussion. Telegram, Vernon Read (associate editor, Architectural Forum) to Kahn, December 9, 1951. Louis I. Kahn (Personal) 1953, Box LEK 60, Louis I. Kahn Collection, University of Pennsylvania and Pennsylvania Historical and Museum Collection, Philadelphia (hereafter cited as Kahn Collection).
-
Letter, Fuller to John D. Entenza (director, Graham Foundation), April 5, 1965. Fuller, R. Buckminster, correspondence 1965, Box LEK 55, Kahn Collection. In conversation with Patricia Cummings Loud, lyng asserted that she helped Kahn with developing “the concept,” but the design was his. Cummings Loud, The Art Museums of Louis I. Kahn, p. 94 note 6.
-
Scully, Louis I. Kahn, p. 15. Letter, Fuller to Entenza.
-
Fuller, Ibid.
-
Scully, Louis I. Kahn, p. 21. Kahn, quoted in From Conversation with Architects, in Wurman, p. 206.
-
lyng joined Kahn’s office in 1945, a year after receiving her graduate degree from the School of Design, Harvard University. Kahn was then associated with Oscar Stonorov. After their separation in 1947, lyng stayed with Kahn. Until 1959, she collaborated with him on numerous projects. Later she was less frequently in Kahn’s office. Anne Griswold lyng, interview with Alessandra Latour (May 2, 1982) in Louis I. Kahn: Vuomo il maestro, Latour, ed. Edizioni Kappa, Rome, 1986, p. 55.
-
In 1949 lyng attended Fuller’s lectures at the University of Pennsylvania, Philadelphia, which introduced her to his theories and work. Anne Griswold lyng, “Louis I. Kahn’s ‘Order’ in the Creative Process,” in Latour, p. 285. Anne Griswold lyng, “Inner Vision Toward Architecture of Organic Humanism,” to be published in International Journal of Space Structures, (Special Issue on Morphology and Architecture), Vol. 6, No. 1/2.1 am grateful to Anne lyng for furnishing me with a draft of her article.
-
Anne Griswold lyng, “Synthesis of a Traditional House with a Space Frame,” International Journal of Space Structures, (Special Issue on the Architecture of Space Frames), Vol. 6, No. 4, 1991, pp. 267 am grateful to Francois Gabriel for providing me with a copy of this issue.
-
lyng, “Synthesis of a Traditional House,” p. 269.
-
Handwritten draft, Kahn, n.d. In the draft Kahn refers to a house in which “The same geometry follows thru [sic] consistently forming the roof walls sunshades dormers and entrance balcony. This is the only house built with the concept of the space frame in which you live.” In the margin Kahn noted “concept.” Louis 1. Kahn 1955, Box LIK 65, Kahn Collection.
-
The project was praised but also criticized for being about “60% heavier than equivalent 40 spans in ordinary beam and joist construction.” In part this was justified to satisfy local fireproofing regulations. “Tetrahedral Floor System,” Architectural Fonini, p. 114.
-
“The concept of hollowing out random spaces in the totally consistent order of the tetrahedron-octahedron geometry intrigued Kahn, and made it possible for me to persuade him to collaborate with me on the tower based on the same geometry.” Tyng, “Louis I. Kahns ‘Order’ in the Creative Process,” p. 287.
-
Peter S. Reed, “Philadelphia Urban Design,” in Brownlee and De Long, Louis I. Kahn, pp. 306.
-
Louis I. Kahn, “Plan for Midtown Philadelphia,” Perspecta, No. 2, Aug. 1953, p. 27.
-
D’Arcy Wentworth Thomson, On Growth and Form, Cambridge University Press, 1942, 1948, pp. 510 description of Figure 3.3.
-
Kahn recommended the book to his nephew “to help him explain architecture.” Years later he admitted that he had never read it. Alan Kahn, “Conversation about Lou Kahn,” Los Angeles, California, June 20, 1981, in Latour, p. 65.
-
Letter, Kahn to John D. Entenza (director, Graham Foundation), March 2, 1965. “Letters of Recommendation, 1964,” Box LIK 55, Kahn Collection.
-
“[Kahn] incorporated the notion of the Yale Art Gallery ceiling as the ceilings for the tower. The ceilings would be a smaller scale geometry for the total space frame so that he developed the first expression for the hierarchy of the geometry.” Tyng, interview with Latour, p. 51.
-
Kenneth Frampton, “Louis I. Kahn and the French Connection,” Opposition, No. 22,1980, reprinted in Latour, p. 225. Brownlee and De Long, Louis I. Kahn, p. 43.
-
Louis I. Kahn, “Monumentality,” in New Architecture and City Planning, Paul Zucker, ed., Philosophical Library, New York, 1944, pp. 577.
-
Ibid, p. 579.
-
Louis I. Kahn, “Toward a Plan for Midtown Philadelphia,” pp. 23.
-
Ibid.
-
Letter, Fuller to Entenza.
-
Brownlee and De Long, Louis 1. Kahn: In the Realm of Architecture, p. 56. Kahn and Le Ricolais would later teach jointly the Master Class at the University of Pennsylvania. G. Holmes Perkins, “Louis Kahn: Teacher,” in Latour, pp. 367.
-
Kahn received the first Le Ricolais paper, entitled “Hexacore ‘Free Flow’ Industrial & Public Buildings,” from James Fitzgibbons, South Carolina University, March 1953. Letter, Kahn to James Fitzgibbons, May 7, 1953. North Carolina State College, Box LIK 56, Kahn Collection. Kahn acknowledged the material saying that it was “highly appreciated.” In April 1953, Le Ricolais sent Kahn his paper “ ‘Multicore’ Building System.” Letter, Le Ricolais to Kahn, April 3, 1953. “Louis I. Kahn” (Personal) 1953, Box LIK 60, Kahn Collection. The Le Ricolais papers are filed in Le Ricolais, Box LIK 56, Kahn Collection.
-
Le Ricolais, “Hexacore ‘Free Flow’ Industrial & Public Buildings,” n.p.
Tyng, in conversation with the author Nov. 21, 1995, rejected the idea that Le Ricolais’s work had any bearing on the project.
-
Tyng, interview with Latour, p. 51.
-
Kahn, “Toward a Plan for Midtown Philadelphia,” p. 23.
-
Ibid.
-
Handwritten draft, Kahn to Walter Gropius, n.d. “Louis I. Kahn (Personal) 1953,” Box LIK 66, Kahn Collection.
-
Kahn, quoted in Ronner and Jhaveri, Louis I. Kahn: Complete Work, p. 76.
-
Between Dec. 1950 and Feb. 1951, Kahn was a resident architect at the American Academy in Rome, Italy. In a letter to his office colleagues in Philadelphia he wrote: “I firmly realize that the architecture of Italy will remain as the inspirational source of the work of the future….What is necessary is the interpretation of the architecture of Italy as it relates to our knowledge of building and needs.” Letter, Kahn to Dave [Wisdom], Anne [Tyng] as well as others, Dec. 6, 1950. “Rome 1951,” Box LIK 61, Kahn Collection.
-
Kahn, quoted in Ada Louise Huxtable, “What Is Your Favorite Building,” New York Times Magazine, May 21, 1961. A copy of the article is filed in “Misc.,” Box LIK 53, Kahn Collection.
-
Ronner and Jhaveri, Louis I. Kahn: Complete Work, pp. 74.
-
Letter, Kahn to Tyng, April 5, 1954, reprinted in Alexandra Tyng, Beginnings: Louis I. Kahns Philosophy of Architecture (Wiley, New York, 1984), pp. 65.
-
Louis I. Kahn, “A Synagogue,” Perspecta, No. 3, 1955, pp. 62.
-
Tyng, in conversation with the author, Nov. 21, 1995.
-
Enzo Frateili, “Louis Kahn,” Zodiac, No. 8, 1968, p. 16.
-
Alexandra Tyng observed that Kahn believed the plan of the Yale Art Gallery should have been “triangular rather than rectangular.” Tyng, Beginnings, p. 35. Scully, Louis I. Kahn, p. 22.
-
Kahn’s design was rejected for being “out of spirit with the type of building wanted by the Board.” Letter, Weiss to Kahn, April 29, 1955. “LIK Miscellaneous 1954,” Box LIK 65, Kahn Collection.
-
Ronner and Jhaveri, Louis I. Kahn: Complete Work, p. 84.
-
“The hollow columns which I invented for it [the Trenton Bath House], which were containers, became the servant areas and all other spaces became open, served by these hollow columns. From this came a generative force which is recognizable in every building which I’ve done since.” Kahn, in conversation with Peter Blake, July 20, 1971, reprinted in Wurman, p. 130. Walter McQuade, “Architect Louis Kahn and His Strong-Boned Structures,” Architectural Forum, Vol. 107, July-Dec. 1957, p. 140.
-
Tyng, in conversation with the author, Nov. 21, 1995. Tyng, interview with Latour, p. 51.
-
Louis I. Kahn and Anne Griswold Tyng, “A City Tower: A concept of natural growth,” Universal Atlas Cement Company United States Steel Corporation Pubfication No. ADUC-707 (5-BM-WP), 1957.
-
Kahn, quoted in From Conversation with Architects, in Wurman, p. 184.
-
“In our earlier schemes this shift in plan was not fully coordinated with the completion of the three-fold column clusters sloping in three directions. By shifting the centers of the column clusters in plan, I was able to eliminate edge conditions where only one or two out of the three columns were contained by the volume of the tower.” Tyng, in conversation with Latour, p. 51.
-
Ibid.
-
Kahn and Tyng, “A City Tower.”
-
Scully, Louis I. Kahn, p. 27.
-
Walter McQuade, “Wind Bracing Comes out of Behind the Curtain,” Fortune, Vol. 7, May 1965, p. 145.
-
Robert Venturi, Complexity and Contradiction in Architecture, Harry N. Abrams, New York, 1966, p. 50. Venturi worked in Kahn’s office and helped with drafting the sketches for the model. See Invoice, Atlas Cement-City Hall Model, March 25, 1957. Universal Atlas Cement Co., Box LIK 80, Kahn Collection. Kahn seemed sensitive to the criticism that the building had no elevators. In conversation with Cook and Klotz, he observed that, “The vertical spaces needed for elevators were inherent in the course of the spiraling of the structure upward.” Kahn, quoted in From Conversation with Architects, in Wurman, p. 185.
-
August E. Komendant, 18 Years with Architect Louis I. Kahn, Aloray Publishers, Englewood, NJ, 1975, Chap. 10.
-
“I knew that one had to take care of the wind when a skyscraper is built, but I didn’t know anything about the formulas for wind. I didn’t want to graft on a wind idea but to find an order which takes care of the wind. I knew the triangle was nonde-formable, and I trusted that this would do it.” Kahn, quoted in From Conversation with Architects, in Wurman, p. 193.
-
“You might say that the tetrahedral skyscraper was something which had truly to do with the fairy tale: You wanted a skyscraper to come about and not have to learn anything about skyscrapers. Just wave your wand and have it. It is the employment of freeing nature, the way nature makes things with a very inaccessible answer to what dictates its making. Its dictates are tremendously irrefutable. It’s very far away from history.” Ibid.
-
Reed, “Philadelphia Urban Design,” pp. 10. Ronner and Jhaveri, Louis I. Kahn: Complete Work, pp. 34.
-
‘Visionary Architecture,’’ Industrial Design, Vol. 7, Nov. 1960, p. 18. “The Dream Builders, Time, Oct. 17, 1960, p. 86. In “The Dream Builders,” the critic compared the tower to a “tottering, concrete Erector set.”
-
The reference to Wright, Le Corbusier, and Mies was by J. Francois Gabriel in “Space Frame: An Alternative to the Architectural Cube,” Intel-national Journal of Space Structures, (Special Issue on the Architecture of Space Frames), Vol. 6, No. 4, 1991, p. 293.
-
Frampton, Modem Architecture, p. 244.
¶ Buckminster Fuller and the Relevant Pattern
Arthur L. Loeb
¶ INTRODUCTION
In the early sixies R. Buckminister Fuller and I discovered that we were using the same coordinate system, based on tetrahedral-octahedral space filling, the former for the design of architectural trusses, the latter in order to understand why minerals have the structure they do. We both rejected the cube, Fuller because of its instability, myself because it concealed the natural design of crystals, rather than rendering it obvious.
This chapter explains this coordinate system, explores Fuller’s discomfort with irrational numbers and continuous structure, and relates my role in the writing of Synergetics. The five-fold way of dome structures and its influence on recent molecular physics and on the metallurgy of alloys is stressed.
¶ THE RELEVANT PATTERN
Spinel is a mineral and semiprecious stone. Its chemical formula is MNX, where M and N represent small, positively charged metal ions and X stands for large, negatively charged ions such as oxide or sulfide. The chemical formula indicates that there are one M ion and two N ions for each pair of X ions. Over 35 years ago, it was my task1 to investigate the mechanism by which information in the form of a magnetic flux could be held in materials having a spinel-like configuration of oxide and magnetic metal ions.2 The magnetic flux results from the interactions between the various types of ions in the spinel, and especially from their spatial interrelations.
The configuration of the ions in spinel is apparently complex; a ball-and-rod model of the “cubic unit cell” was forbidding and did not reveal any mechanism explaining why nature would have chosen to arrange these ions in such a perversely complicated manner. This configuration was revealed experimentally by means of X-ray analysis; X-ray crystallographers traditionally index the locations of ions in a solid like spinel relative to a cube, creating the so-called unit cell.
I decided that the first step in developing an understanding of the interactions of the ions in spinel was to see what sort of structure each of the metal ions would separately form in conjunction with the oxide ions, in other words, what the structures of the individual oxides would be. In spinel, the oxide ions occupy the vertices and the centers of a cubic unit cell, as shown in Figure 4.1. However, a slight but useful change in perspective results if we abandon the traditional unit cell, remembering that the crystal is made up of stacked unit cells. If, instead of slicing out the cube of Figure 4.1, we move over half a cube edge length, we can slice out a different cube, as shown in Figure 4.2: Now
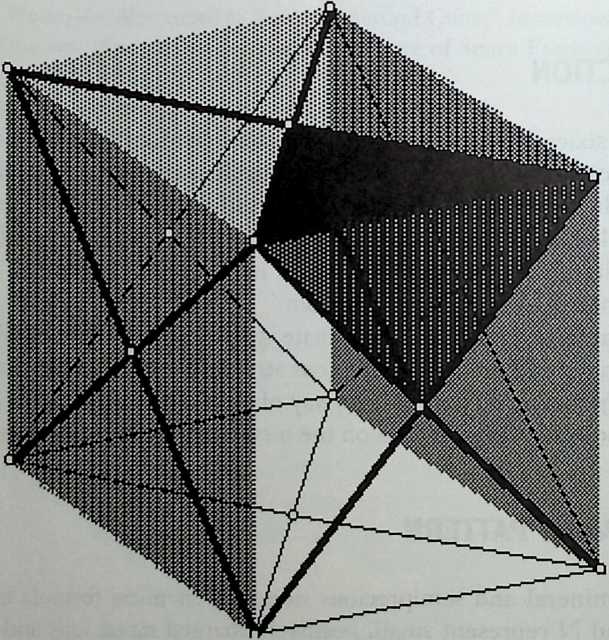
Figure 4.1 Face-centered cubic unit cell.
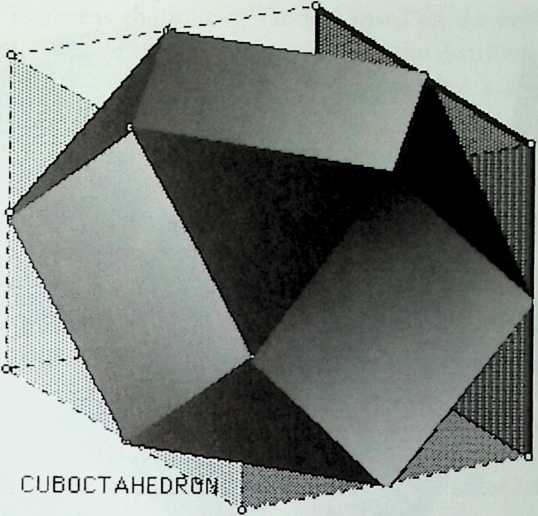
Figure 4.2 Cuboctahedron in a cubic cell.
the oxide ions occupy the centers of the new cubes as well as the centers of each of its 12 edges. The oxide ions are now seen to occupy the vertices of a polyhedron known as the cuboctahedron, called by R. Buckminster Fuller the “vector equilibrium.”
The cuboctahedron has six square and eight triangular faces. It can be constituted of eight regular tetrahedra and six square pyramids, each of which is half of a regular octahedron (cf. Figure 4.3). Accordingly, the large oxide ions, located at the center and the vertices of the cuboctahedron, have octahedral and tetrahedral interstices in between, which may be occupied by the smaller metal ions. Once one knows whether these metal ions occupy tetrahedral or octahedral ions in their simple oxide crystals, one has a clue as to where these ions would go in composite oxides containing several different kinds of metal ions.
In Figure 4.4 four different hexagonal cross sections through a cuboctahedron are shown. The center of the cuboctahedron is surrounded by six vertices in each of four regular hexagonal cross sections; that is to say, of the twelve vertices of the cuboctahedron, six form a regular hexagon around the center, three He on one side, and the remaining three He on the opposite side of that hexagon. In the crystal each oxide on a vertex of the cuboctahedron is in turn the center of a cuboctahedron, the original center being one of twelve vertices of this new cuboctahedron. Thus we have come by a series of steps from a unit-cell model to one of stacked, closely packed layers of oxide ions having tetrahedral and octahedral interstices in which smaller metal ions may be accommodated. It then turned out that the most symmetrical distribution of the various types of metal ions over these interstices consistent with their chemical composition produces not only the spinel structure but also the structures of many other minerals and man-made materials
Figure 4.3 Cuboctahedron made up of regular tetra- hedra and half-octahedron.
Figure 4.4 Four hexagonal cross sections through a cuboctahedron.
CUBOCTAHEDRON WITH
CONSTITUENT TETRAHEDRA
AND OCTAHEDRA
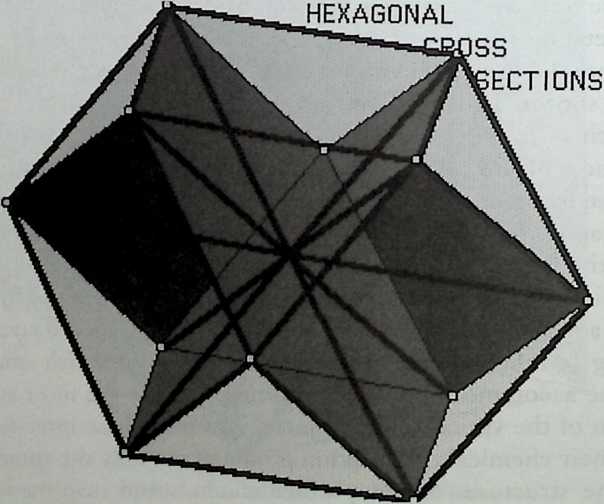
(Figure 4.5). Whereas the unit-cell model based on the cubic unit cell was obscure and did not offer any explanation for the distribution of ions in a crystal, the octahedron/tetrahedron model provided a simple geometric insight into crystal structures.
In 1960 the International Congress of Crystallography took place in Cambridge, UK. I felt like a real iconoclast in presenting an alternative to the cubic unit cell so sacred to the crystallographer. When I had finished my presentation, I saw Elizabeth Wood, head of the U.S. delegation, charging toward me. Somewhat apprehensive, I was surprised to hear her say: “All my life I have wanted to say ‘TO HELL WITH THE UNIT CELL!’, and now you have done it.”
To implement my systematic ordering of crystal structures, I designed four types of modules,3 two tetrahedral and two octahedral (Figure 4.6), which, in various combinations and permutations, could represent a multitude of crystal structures (Moduledra). Two of these polyhedra contained a colored sphere in the center, representing a metal ion; the other two were empty.
| octahedra: | tetrahedra: | ||
|
All | None | Niccolite BX |
|
1/2 | None |
|
| 2/3 | None | Corundum B2X3 |
|
Spinel AB2X4 |
/2 | /8 | |
|
None | 1/4 | |
|
None | /2 | Wurtzite AX |
Antifluorite A2X |
None | All |
|
Carborundum AX |
None | 1/2 |
|
Figure 4.5 Systematic overview of common crystal structures.
Figure 4.6 Moduledra™ crystal building blocks.
Because regular tetrahedra and octahedra together can fill all of space in a ratio of two tetrahedra per octahedron, it was possible to arrange these modules without fasteners. The vertices of the modules represent the centers of the large ions, whereas the spheres in the centers of the modules represent metal ions. The empty modules represent unoccupied interstices; if for no other reason, these modules were unique in that there was an explicit representation of an empty space. I had designed these modules to be attractive and pleasant to handle, with the result that they were exhibited here and there.
In 1962 the Educational Network was making a television series on Richard Buckminster Fuller. William Wainwright, an associate of Fuller’s, had seen my Moduledra on exhibit and suggested that these should be included in the films. Accordingly, the authors of the films interviewed me and invited me to meet Fuller. At lunch Fuller told me that he had hoped to find in nature, and specifically in crystals, building blocks like tetrahedra, octahedra, cuboctahedra, and others, but not cubes, which are inherently unstable. All the crystallographers whom he had met, however, referred to the cube as the basic building block, the unit cell that was encountered previously. Fuller felt encouraged to learn from my work that a model based on tetrahedra and octahedra gave a clearer understanding of crystal structure than one based on the unit cell.
Since that first meeting, I have always been impressed with Fuller’s genius in recognizing the relevant pattern and rejecting the trivial one. Although known primarily for his lightweight structures capable of spanning large areas with a minimum of matter, he had also studied the very opposite, namely, the densest packing of spheres.4 The cuboctahedron and its deconstruction into eight tetrahedra and six half-octahedra were basic to his understanding of sphere packings.5 The fact that the distance between adjacent vertices of the cuboctahedron equals that of each vertex to the center of that polyhedron caused him to call the cuboctahedron vector equilibrium: If there is an optimal distance between the centers of two interacting objects, then the cuboctahedron is an optimal configuration of such objects, conserving an optimal number of such optimal distances.
Fuller kept wrapping layers of spheres around the 12 constituting the vertices of the inner cuboctahedron and counted the number of spheres in each successive layer. He noted that these numbers, successively 12, 42, 92, 162…, could be written as the squares of successive integers followed by the digit 2. I am told that the renowned geometer H.S.M. Coxeter first greeted this observation with disbelief, but by that time I had already written a proof for Synergetics.6 Fuller’s preoccupation with numbers found an outlet in Chapter 1200 of Synergetics, called Numerology. In all this work Fuller plays with numbers, delighting in the patterns that turn up. When, in the preface to Synergetics, I wrote: “… Fuller…discerns patterns and accepts their significance on faith. His is not the burden of proof: the pattern is assumed significant unless proven otherwise.” Fuller expressed surprise, because he thought that he had provided a proof.
Some of my students similarly feel that a demonstration is actually a proof; when mathematics is transformed into an experimental science, proofs become inductive rather than deductive. A proof then consists of a generalization encompassing as many diverse phenomena as possible. Very few physics theorems have withstood the test of time: Even Newton’s laws of motion eventually were found to be approximations valid only at sufficiently large scales. The proof of a theorem will, however, offer an insight into the constraints within which the theorem is valid. I offer two instances in design science as an illustration:
William Varney was working at Fuller and Sadao’s architectural office in Cambridge while finishing the requirements for his bachelor’s degree at Harvard through a tutorial on design science with me. I had shown him that a necessary, but not sufficient condition for the stability of polyhedra is that
(4.1)
3I/-F<6
where V equals the number of vertices and E the number of edges of the polyhedron.7 For tensegrity structures, if C is the number of compression members and T the number of tension members8:
£= 7+ C
T=4C
V=2C
Hence
(4.2)
C<6 Varney had noted that tensegrities having more than six compression members, although holding together on a small model scale, tended, when constructed on a large scale, to sag more than the classical six-strut tensegrity, and was delighted to see that a mathematical analysis actually proved the fundamental stability of the six-strut tensegrity.
Some years later, Varney was teaching the design science seminar-workshop with me. We were examining the rhombic triacontahedron, a structure related to domes, having 30 rhombic faces.9 He related to me that Shoji Sadao, Buckminster Fuller’s partner, was using arctan 2 as a convenient approximation for the surface angle of the triacontahedron. Because the ratio of the lengths of the diagonals of each of the faces of this polyhedron exactly equals the golden fraction 4>, defined by the equation
<) = 1/(1 + <b) (4.3)
it seemed unreasonable that the surface angle of the triacontahedron should be independent of the golden fraction. Wasma’a Chorbachi,10 moreover, had discovered medieval Islamic design manuals giving rules of thumb for geometrical constructions, which work well on a moderate scale, but which we could prove to be approximations. Accordingly, I decided to calculate the tangent of the surface angle of the triacontahedron, which is also the angle between the diagonals of a golden rectangle. It turned out that the sine of that angle equals 2cf>/(2-d>), the cosine of <J>/(2-<h). Their ratio, the tangent of the surface angle of the triacontahedron, accordingly equals exactly 2, and Sadao’s “approximation” was, in point of fact, no approximation at all, but rigorously correct, and thus valid at any scale! It was not until May of 1995 that I was able to give Sadao this proof of the exactness of his “approximation,” which still surprised him.
Fuller was uncomfortable with irrational numbers11 and would have been delighted with the elimination of the irrational golden fraction from the expression for the surface angle of the triacontahedron. This discomfort relates to his discrete rather than a continuous view of matter: a circle is not the locus of all points equidistant from a given point, but rather a polygon with a great many, but a finite number, of sides, and the number it should therefore be rational.
Following our first meeting, Fuller sent me two books about his work. Although I had myself written two books by then, I did not think that their subject matter, the electric double layer around spherical lyophobic colloid particles and wave mechanics, would hold the slightest interest for Fuller. Therefore, I decided to send him a book on the Dutch graphic artist M.C. Escher instead. At the same international congress in Cambridge, where I had presented my Moduledra crystal building modules, Escher had been invited to deliver an address, and our meeting there turned into a lasting friendship. Fuller was so impressed with Escher’s art that I decided to organize a symposium to introduce these two pivotal figures in design science to each other.
In the fall of 1964, a small number of scholars gathered at the Ledgemont Laboratory of the Kennecott Copper Corporation in Lexington, Massachusetts, for a symposium on structure systematics. Both Fuller and Escher were scheduled to be among the speakers, but at the last moment Escher became ill in Canada, so that I had to read his paper. When Fuller began his own contribution, he characteristically squirmed, complained about the heat, and removed his jacket for the first five minutes, then launched into a brilliant survey of design science and fascinated, charmed, and entertained his sophisticated audience for hours.
My young colleague Eric Haughton, a psychology graduate student of behaviorist Fred Skinner, delivered a paper on his work with programmed instruction. Instantly, some of the scholars turned into parents, interrupting the speaker with their concerns. Suddenly, Fuller said: “I am amazed. I thought this was an audience of scientists, yet you keep a scholar from presenting you his quantitative data.” The parents sobered up, and Haughton continued without further interruption.
Fuller had been with us for the entire week but had to leave early Friday afternoon to get a flight at Logan Airport. The next Monday my phone rang. It was Buckminster Fuller. “Where are you?” I asked. “At Logan Airport” was the answer. “Did you spend the whole weekend there?” was my reaction. No, it turned out that he had gone home to California over the weekend and happened to be passing through Logan again on his way elsewhere. He graciously thanked me for including him in the symposium and invited me to collaborate with him on the forthcoming synergetics book.
Eleven more years were to pass before the actual publication of Synergetics. Fuller invited Escher to contribute some illustrations to his volume, which the artist agreed to do. Unfortunately, completion of Synergetics was delayed until well after Escher’s passing, so nothing came of that collaboration. It was interesting to compare the working methods of these two geniuses. Interestingly, Fuller, the architect and inventor, appears to have been the more intuitive (Fuller even named one of his boats as well as one of his books Intuition), whereas Escher, the artist, was very precise and analytical. Both became icons of the 1960s counterculture, yet each was very traditional in demeanor and dress.
In 1972 Buckminster Fuller invited us to his island off Camden, Maine. As I had just joined the Department of Visual and Environmental Studies at Harvard, which was having a faculty meeting the day following our visit to Bear Island, I decided, knowing Fuller’s propensity for long conversations, that it would be the better part of valor to spend the night on the mainland so that we could get an early start the next morning. On the appointed day a boat was to meet us at the dock in Camden. I wondered how we would recognize the boat, or be recognized, but I need not have worried, for Fuller was navigating the Intuition himself. When we first met, Fuller quickly noted that I had done a lot of sailing in my day. Indeed, growing up in Amsterdam, I had been a Sea Scout; accordingly, Fuller entrusted the rudder to me.
As we neared a cruising windjammer, Fuller instructed me to pull up beside her because there was a person aboard with whom he desired to speak. The passengers looked rather anxious, apparently fearing piracy, but the party was found quickly and invited to Bear Island with a promise that he would be restored to his cruise in due time. The surprised man took a few minutes to collect his wife and some baggage and then joined us on the Intuition. Fuller told me that he had a group of students working on a dome on Little Bear Island who were anxious to talk with me, so after lunch we adjourned there, painted the floor of the new dome being built so that it could survive the next winter before being completed, and then returned to Bear Island itself for dinner and one of Fuller’s famous roundtable discussions about the state of the whole earth. Fuller showed me the various islands in the distance where his relatives and friends from Milton, Massachusetts, had summer houses; clearly, this world citizen still felt that his real home was right there. His grasp of the relevant pattern clearly harks back to his roots in New England transcendentalism, notably to his great aunt Margaret Fuller. Late at night Fuller himself was kind enough to take us back to Camden.
Peter Pearce was to be the editor of Synergetics, and we met several times during the next few years. Fuller’s original intention had been to have my contributions interspaced in a different typeface as running comments between his text. This did not appear practical, however, and so I wrote a preface and a number of chapters. I recall a gathering at our house on a very wintry day, including Fuller, Pearce, and a number of associates. We had had snow and frost, then a sudden thaw accompanied by a torrential rain. Suddenly, one of our guests felt wet, and we discovered water leaking through the living room ceiling. The bathroom upstairs was flooded with backup from the gutters, and soon the whole house was leaking like a sieve. There was nothing to do but to place whatever buckets we had in crucial locations and to continue with whatever we had been doing, which was madrigal singing in the music room, an investigation of Fuller’s A-and B-modules in the living room, and the refilling of the buffet in the kitchen.
Fuller suggested installing electric wires on the roof to melt the snow when it started to accumulate on the roof. We thought that this Yankee architect would be the best expert we could hope for, but after the installation, the first snow, upon being melted, slid down the roof, taking the wires with it. Fuller had not realized that we still had a slate roof, which was too slippery to hold on to the wires!
After Peter Pearce had spent two years on Synergetics, subsidized by a grant, Fuller did not feel the volume was ready for publication, and the project lapsed. Some time in the early 1970s, I received a call from EJ. Applewhite, who introduced himself as the editor of Buckminster Fuller’s next book. Applewhite requested from me a reprint of my article in the Journal of Solid State Chemistry11 of which I had sent Buckminster Fuller a copy because it dealt extensively with the vector equilibrium. I gathered during our conversation that Applewhite had a background in security, for he asked me a great deal of questions but was reluctant to reveal any information about the book. I found out, however, that indeed the new book was Synergetics, and Ed Applewhite told me later that he realized then that the few bits and pieces from my contributions that he had come across were but the tip of an iceberg. Fuller had apparently rather indiscriminately distributed my contributions, but I, being apprehensive about having unpublished results so generally accessible, had bundled them into a copyrighted technical report, which I could then send to Applewhite.
In the mid-1970s I was working on my Space Structures." Concerned about the fate of my contributions to Synergetics, I wrote Fuller that regretfully I would need to withdraw these contributions and instead include them in my own forthcoming book if Synergetics were not published by 1975. Ed Applewhite told me that the letter built a fire under Fuller, with the result that Synergetics did appear with my contributions in 1975, followed by my Space Structures in 1976.
One of the first, and probably one of the few, people to read Synergetics from cover to cover was Amy Edmondson, who did so as an undergraduate student at Harvard-Radcliffe during a junior tutorial under my direction. Fuller would often state that a bicycle wheel is actually a tensegrity structure, a statement that Amy checked out as her senior thesis. I proposed that she construct a bicycle wheel in which the spokes were strings instead of metal bars and test out its strength. Although it is sometimes believed that the spokes in a bicycle wheel are compression members, they are actually tension members, with the hub suspended from the rim by the spokes. She actually built a tensegrity cart supported by a set of tensegrity wheels, positioned her brother in the cart, and then proceeded to cut the spokes one by one, until the inevitable catastrophe occurred. Interestingly, none of the remaining string spokes snapped, but the rim eventually collapsed; the function of the spokes is indeed to distribute the load over the rim. In that sense the wheel is a tensegrity structure.
Upon graduation, Amy Edmondson went to work with Buckminster Fuller in his Philadelphia office. Just before Harvard Commencement 1983, she called me to say that Fuller had decided to attend and asked whether we could have dinner with him the night before. We had a delightful evening, joined by Gyorgy and Juliette Kepes and my father, who had come over from his home in the Netherlands to celebrate his 90th birthday with us. Fuller, Amy, my wife, and I made a date to meet in Maine for a working session, but that dinner turned out to be the last time we met, for early in July we learned of the passing of both Buckminster and Anne Hewlett Fuller. After the interment in the Fuller family lot, near great aunt Margaret, in Mount Auburn Cemetery, Amy and I decided that the best tribute to Fuller would be a book explaining his ideas in more traditional language than Fuller’s own, which I proposed to Birkhauser for the Design Science Collection. The result was Amy’s A Fuller Explanation.
Already before Buckminster Fuller’s death, materials scientists began to recognize the importance of fivefold rotational symmetry.14 The geometer H.S.M. Coxeter lectured at Harvard on a range of virus structures having fivefold rotational symmetry; I wrote Fuller afterwards that Coxeter had declared that the viruses most resembling miniature Fuller domes were also the most deadly. Characteristically, Fuller replied that he was not surprised, because those would be the most stable and hence the most virulent viruses. Because fivefold rotational symmetry15 is incompatible with translational symmetry, crystals, which do necessarily have translational symmetry, cannot also be fivefold symmetrical.
Fivefold rotational symmetry occurs frequently in organic structures (plants, flowers, shells, viruses), which have a single symmetry axis, but not in crystals. Crystallographers were therefore surprised to find alloys whose X-ray diffraction patterns were fivefold symmetrical. After a characteristic period of denial, they had to abandon the superstition that fivefold symmetry in the X-ray pattern implies fivefold symmetry in the crystal. When the ions in a crystal diffract X-rays to generate the pattern from which crystallographers deduce the location of these ions in the crystal, they do so through the interaction between close neighbors in the crystal. If the immediate vicinity of each ion appears to be fivefold symmetrical, then, regardless of the fact that the entire crystal lacks fivefold rotational symmetry, the diffraction pattern will have fivefold rotational symmetry. Materials having this special structure are called quasicrystals.
With his dome structures, Buckminster Fuller introduced fivefold rotational symmetry into our visual culture. The U.S. Pavilion at Expo ‘67 in Montreal was a Fuller dome; altogether, the exposition was rich in untraditional polyhedral forms. The three-dimensional theme icon was a truncated regular tetrahedron, and Moshe Safdi’s Habitat abounds in space-filling poly-hedra. When Smalley and Kroto identified a molecule consisting of 60 carbon atoms, (C60), one of them used the dome kit he had bought for his young son to construct a possible model for this new structure.
Much successful science is a matter of pattern recognition, and one cannot recognize that with which one is not already familiar. Buckminster Fuller familiarized us with many unconventional structures, among them the truncated icosahedron, already familiar as the soccer ball but less so as the Fuller dome. That Fuller selected the relevant structure on the basis of its stability is borne out by his reaction to the Coxeter lecture. When C60 was named Buckminsterfullerene, popularly known as Buckyball, the attribution was a proper one because Fuller knew that the structure is stable and because his dome kit provided the means of constructing a stable structure having 60 mutually equivalent atoms.
¶ NOTES
-
A. L. Loeb, “The Architecture of Crystals, or Simplicity in Design,” in Vision and Value: Module, Proportion, Symmetry, Rhythm, Gyorgy Kepes, ed., Braziller, New York, 1966.
-
J. B. Goodenough and A. L. Loeb, “A Theory of Ionic Ordering, Tetragonal Phase Formation, Magnetic Exchange and Lamellar Precipitation due to Covalent Forces in Spinels,” Physical Review, Vol. 98, 1955, pp. 391. A. L. Loeb,
“A Systematic Survey of Cubic Crystal Structures,” Journal of Solid State Chemistry, Vol. 1, 1970, pp. 237. A. L. Loeb, “Hierarchical Structure and Pattern Recognition in Minerals and Alloys,” Per., Mineralogia, Vol. 59, 1990, pp. 197.
-
A. L. Loeb and G. W. Pearsall, “Moduledra Crystal Models,” American Journal of Physics, Vol. 31, 1963, pp. 190.
-
R. Buckminster Fuller, Synergetics, Macmillan, New York, 1975, pp. 33.
-
Ibid., Fig. 222.30.
-
Ibid., p. 857.
-
A. L. Loeb, “Vector Equilibrium Synergy,” International Journal of Space Structures, Vol. 1, 1985, pp. 99. A. L. Loeb and W. Varney, “AStabilized Cuboctahedron Frame,” International Journal of Space Structures, Vol. 7, 1992, pp. 83.
-
Fuller, Synergetics, Chap. 700.00.
-
A. L. Loeb, J. C. Gray, and P. R. Mallinson, “On the Icosahedron, the Pentagonal Dodecahedron and the Rhombic Triacontahedron,” Symmetry, Vol. 1, 1989, pp. 29. A. L. Loeb and W. Varney, “Does the Golden Spiral Exist, and if Not, Where Is Its Center?” in Spiral Symmetry, Istvan Hargittai, ed., World Scientific, Singapore, 1992, pp. 238.
-
W. K. Chorbachi and A. L. Loeb, “A Pentagonal Seal (from Scientific Manuscripts of the Geometry of Design), in Fivefold Symmetry, Istvan Hargittai, ed., World Scientific, Singapore, 1992, pp. 283.
-
A. L. Loeb, “R. Buckminster Fuller Versus the Irrational, a Double Entendre,” International Journal of Space Structures, to appear.
-
Loeb, “A Systematic Survey of Cubic Crystal Structures.”
-
A. L. Loeb, Space Structures, Their Harmony and Counterpoint, Addison-Wesley, Reading, MA, 1976, Birkhauser, Basel/Boston/Berlin, 1991.
-
N. G. de Bruijn, “Algebraic Theory of Penrose’s Non-periodic Tilings of the Plane,” Kon. Nederl. Akad. Wetensch., Proc. Ser. A, Vol. 88,1981, pp. 38. A. Katz, and M. Duneau, “Quasiperiodic Crystals and Icosahedral Symmetry,” Journal de Physique, Vol. 47, 1981, pp. 181. A. Mackay, “Crystallography and the Penrose Pattern,” Physica A, Vol. 114, 1982, pp. 609.
-
An object has ra-fold rotational symmetry if it appears unchanged when turned 360/tz degrees. It has translational symmetry if it appears unchanged when moved a given distance parallel to itself, maintaining its orientation but not its position. Translational symmetry characterizes patterns infinite in extent. Because crystals contain so many millions of ions, they are essentially infinite in extent.
Philip Johnson’s
Crystal Cathedral
and the Rhetoric of
II
Its Free-Form
¶ Polyhedral Structure
Lawrence Davis
¶ INTRODUCTION
Philip Johnson and John Burgee’s Garden Grove Community Chapel is one of the more enigmatic buildings of its time. Better known as the “Crystal Cathedral” and constructed between 1978 and 1980, its curious nature has not only to do with its purpose, form, and treatment but includes the often puzzling intent and ultimate behavior of its polyhedron structure. The distorted geometry of the building causes a transformation of the tectonic system referred to ubiquitously as a “space frame.” Because there is little consensus regarding a precise definition for the term, many structural specialists often prefer the term “space truss.” Most architects and engineers use “space frame”
Figure 5.1 Exterior: carillon and small chapel in base completed in 1990. (Photo: Richard Payne, F.A.I.A. Reproduced with permission.)
as a catch-all to describe a multi-directional structural system made up of linear elements that are exclusively in compression or tension. Nearly all descriptions of the system type make no explicit reference to it in relation to a Platonic and rigorous geometry. Yet it is intriguing that widely held perception suggests that “space frames” ally themselves and represent a rigorous geometric and mathematical logic and arrangement.
It is precisely the departure from such expectation that allows the structure of the Crystal Cathedral to materialize physically Philip Johnson’s expressive vision for the building. The “free form” of the building suggests that the rhetoric of the system’s surface and the volume it creates are more compelling than the internal control of a geometric order. (See Color Art 2.) The building delineates a paradox common to many contemporary buildings and reflects a number of society’s present architectural expectations. In late-20th-century America, the meaning of geometry as a metaphysic and organic order influencing the composition of building components and programmed space
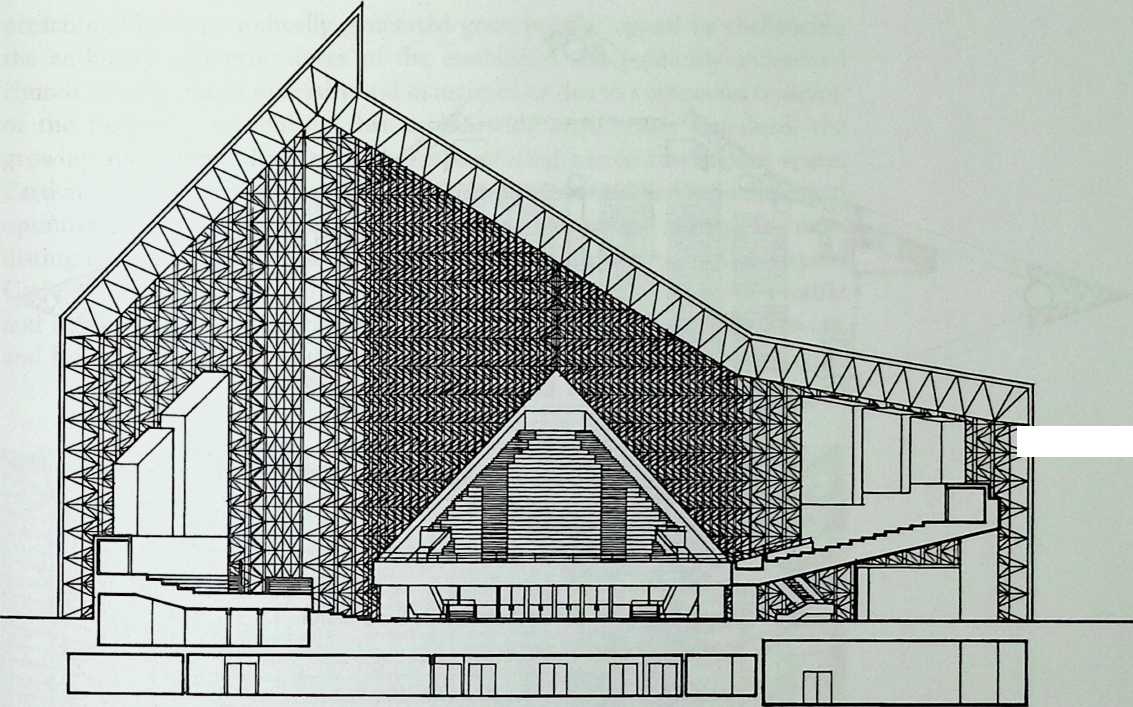
Figure 5.2 Section toward east. (Illustration: Kristin Simonson.)
is, if not decreased, at least transformed in value. In many instances strict Euclidean geometry is replaced by an architecture of easily recognizable and “consumable” emblematic shapes and objects. The Crystal Cathedral is embedded in a common negotiation in the built environment between a representation of rigorous geometry and expressive form. This dialogue demands an acceptance of the often mercurial readings that come from such work. Indistinct and frustrating indicators seem characteristic of much of postwar building. At the same time the potential richness of such inconsistent interpretations suggests a device through which to observe an era of considerable social conversion. In addition to an architectural description of the Crystal Cathedral and its structure, a comparison of the elements to historic influence and evolving societal circumstance can position the building within a set of intrinsic contemporary myths and values that sustain them.
¶ AMERICAN EVANGELISM: IMPROVISED RITUAL AND SPACE
The Crystal Cathedral is not only the product of a mix of common contemporary social conditions, the visions of the architect and client, but a little documented history of the evangelistic built environment in the United States. Exported from Puritan Britain, the informality and inventiveness of “gospel
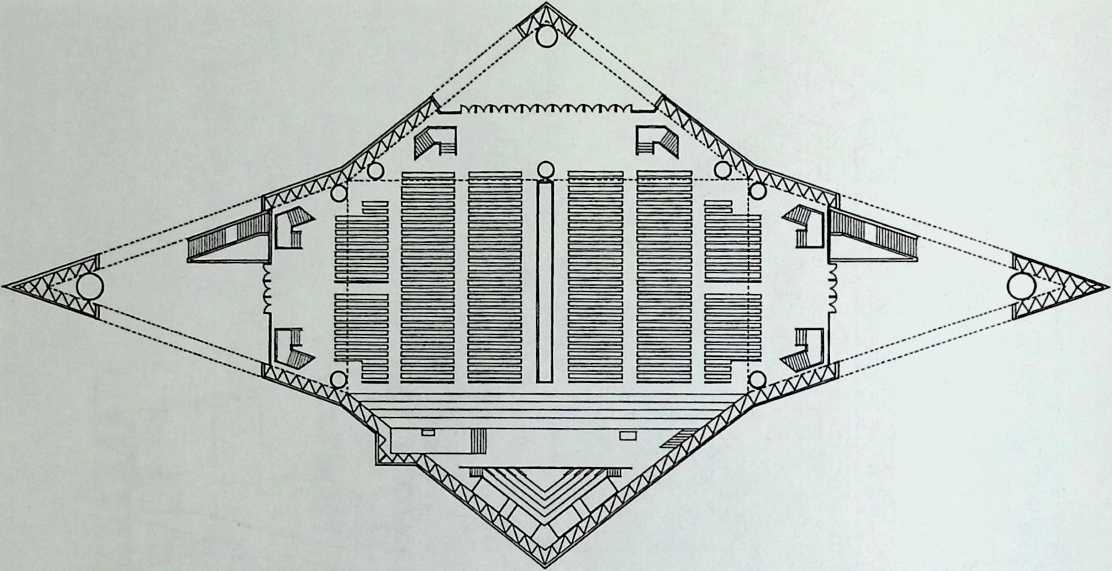
Figure 5.3 Ground floor plan. (Illustration: Kristin Simonson.)
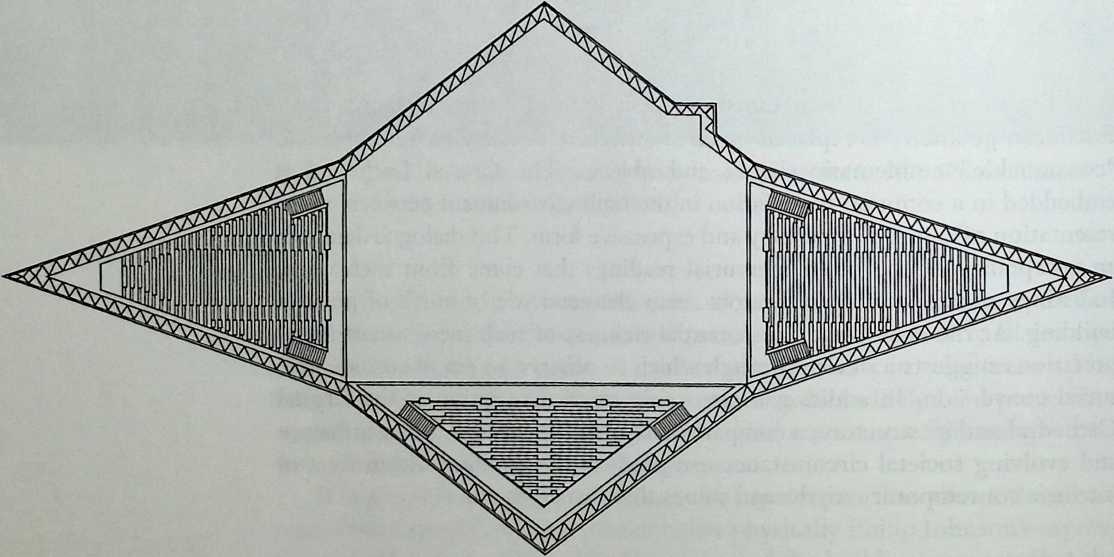
Figure 5.4 Balcony floor plan. (Illustration: Kristin Simonson.)
preaching” have periodically generated great popular appeal by challenging the authority and procedures of the established and politically authorized church.1 Partly out of necessity and in many cases due to a conscious rejection of the instituted symbolism that ecclesiastical architecture contained, the growing movement threatened the preconceived notion of religious space. Particularly in the rural South and West, the emotional and antiintellectual optimism of evangelical revivalism has evolved into what is perhaps the most distinguishing quality of America’s common spiritual heritage. The Crystal Cathedral, and its principal client, Dr. Robert Schuller, are a part of a fertile and resourceful revivalist tradition that includes D.L. Moody, Billy Sunday, and Billy Graham and stretches back to what many religious historians agree
Figure 5.5 Interior of pulpit and organ, looking north. (Photo: Richard Payne, F.A.I.A. Reproduced with permission.)
was the seminal Cane Ridge, Maryland, “Camp Meeting” organized by Barton Warren Stone in 1801.
Revivalism in the United States has always benefited from at least the appearance of spontaneity. In most cases the representation of informality is highly planned. This dexterous character allows revivalism to transform as society changes. Examples of this include the early circuit ministries of the Methodists who were able to follow the frontier, D.L. Moody’s use of big business money and methods to preach “old time religion” in large 19th-century cities, the vaudevillian and ethically questionable tactics of Billy Sunday in the early 20th-century circuit, and, after World War II, Billy Graham’s highly organized manipulation of all forms of media within a given city during his crusades.2 Like Graham, Schuller’s evangelical message gives a charismatic voice to conservative Protestants frustrated with the increasingly progressive social agenda followed by mainline Protestant churches. Although their followings are often characterized as “nondenominational,” they do not embrace the ecumenical movement, which is supported by established churches and is seen to broaden the civil rights movement to include religious plurality.
Because of its often consciously peripheral political position, revivalism has historically been transient, moving from place to place. The camp meetings of the young nation were often in rural and socially developing locations. The newness of the tents, like the land itself, became a symbol of rebirth and salvation. As society industrialized, revivals moved to the larger cities. D.L. Moody and Billy Sunday both conducted successful urban crusades, filling to capacity large auditoriums and exhibition halls. In the late 20th century, revivalism has continued the temporal theme by using the ephemeral “space” of broadcast media versus the established power of a particular location. Recalling the traveling revivals of frontier and rural America, but using the media’s expanding influence, Billy Graham established a national reputation with his enormously successful 1949 “tent meeting” in Los Angeles, California? Originally using the Hollywood Bowl, Graham would frequently utilize the large spaces of stadiums and auditoriums.
From the start of his ministry, Dr. Schuller has been part of the non traditional spirit of the American evangelical tradition. Unlike his counterparts, he seldom, if ever, embarks on physically mobile campaigns. Delivered from a single location, Schuller’s ministry nevertheless relies on the itinerant character of revivalism. As with physically mobile campaigns, Schuller uses television to diffuse questions about the relevance of physical and established ritual that plagues traditional religion. Schuller is among those who understood the gaining influence of broadcast media in the daily lives of common Americans. Aware of its effect on social and intellectual change, he takes advantage of television as an efficient means for capturing the public’s attention.
In 1970 Dr. Schuller began to televise his weekly service, “The Hour of Power.” Through television he offered a populist spiritualism for what Peter Rowe, author of Making a Middle Landscape, paraphrasing Robert Wood, describes as, “ . . the hardworking corporate yeoman, who while materially
consumptive wants both economic security without risking personal ambition.”4 One might speculate that this “inner-directed man” from the “19th century” might be seeking spiritual security as well. The often corporate style of Schuller’s message differentiates his sermons from those of other evangelists. He often laces his message with a marriage of “self-help” psychology and the terminology of a motivational retreat for middle-and high-level managers. It is often argued that what John Pastier described in a 1979 article as Schuller’s “I’m O.K., You’re O.K.” approach is a means for caressing further financial support from his strong associations with big business.5
¶ THE REPRESENTAT8ON OF MORALITY: THE CATHEDRAL AND THE HISTORICAL AVANT-GARDE
The Crystal Cathedral, like other recent evangelical structures, is a large arena-like auditorium. In addition, the scale, technical spirit, and function of this relatively new building type are oddly reminiscent of the self-promoting qualities of Tatlin’s 1919 Monument to the Third International. Both are used for administration and for the dissemination of information through a broadcast theater. In expression, construction, and purpose, the Crystal Cathedral is part of a new breed of large-scale churches that in themselves become enormous metaphors bepraising a new evangelical social order. As with the difference in Schuller’s corporate preaching style, the uniform character of the polyhedron structure distinguishes the Crystal Cathedral from other structures in this emerging class of church architecture. The cathedral’s space truss is indicative of the industrial power and prestige of American corporate culture. Its homogeneous texture and transparency are similar to much of the architecture of postwar big business: a language codified best in the later work of Mies van der Rohe, simultaneously referring to the diaphanous and optimistic compositions of the suprematists as well as to the stable heritage and order of Roman classicism.6
The surface and space of the cathedral connect it to a mythic and transitory religious building tradition associated with evangelism. The white translucent scrim of the entire space truss system recalls the light and space of revivalist tents. The naturally fit tentfike space suggests a connection to Le Corbusier and Pierre Jeanneret’s Pavilion de Temps Nouveaux in the Paris World Exposition of 1937: a pavilion advocating the ethicacy of the industrialized aesthetic. More to the point, in Towards a New Architecture, Le Corbusier identifies the tent as an essential temple paradigm. Although he is using the example primarily to discuss the virtues of geometric regulation, Le Corbusier discusses the instinctive and sophisticated act of inhabiting a location, regardless of the modesty of the means for doing so.7 The use of structure as the prime generator of architectonic form connects Le Corbusier’s example with a Franco-structuralist tradition that includes Viollet le Due and originates in Gothic architecture. There is no evidence that Johnson intended the Crystal Cathedral to recall this specific legacy. What is more certain is that the simple nature of the building’s tentlike interior suggests a compelling reference to the informal structures of American evangelism. The structure’s ephemeral symbolism can be read to intentionally challenge established theological authority often enclosed in the heavy, dark, and “enduring” buildings. The transparent polyhedron structure of the Crystal Cathedral continues to express the improvisational and resistive nature of evangelical spirituality. As in the revivals of early America, which offered an exhilarating social and spiritual occasion to break from the lonely and monotonous life of the frontier, Schuller’s intention seems to create a crystalline “tent” as an analogous inspiring experience for the deserted souls of the grueling uniform world of postmodern America.
As well as connecting it to the history of evangelical space, the white color of the cathedral’s interior structure bespeaks of an ethicacy found in much of the modern movement. This is particularly true of the cubistic architecture of Le Corbusier. In The Decorative Arts of Today, written to protest the 1925 Decorative Arts Exposition in Paris, Le Corbusier discusses “The Law of Ripolin: A Coat of White Wash.” Finding beauty in the functional and rational forms of the Machine Age, Le Corbusier wrote that every citizen should be required to paint everything on the interior of their homes with a coat of white ripolin. This “moral act” would establish a sense of “inner cleanliness” that would “improve conditions.”8 Le Corbusier seems to feel that the decorative nature of most interior spaces was overly sentimental and undermined its rational beauty as a functional object. He also considered the prevalent use of “white wash” in the built environments of the less industrialized cultures to be an agent that bound all segments of the society. He describes the socially objective spirit of white wash in a metaphor: “bread, milk and water are the wealth of slave and king.”9
Although Johnson’s selection of white for the color of the structure is useful in reflecting natural light, it also refers to an idealized and moral side of early modem architecture with which the architect is well acquainted. The connection between the salvation found in the machine and that of “The Word of God” becomes an association that reconciles the conservative politics of Schuller’s congregation with a common technical and corporate representation found in today’s society. As with Le Corbusier’s recommendation of the use of “white wash” in preindustrial society, the vast white field of structure in the Crystal Cathedral unifies an electronically connected multitude of individuals, frequently of different economic and social backgrounds. This consensus by structure strengthens the universal intentions of the nondenomina- tional organization of Schuller’s ministry.
Philip Johnson has stated that the nave on the short axis of the deformed star shape of the plan is inspired by Bernini’s San’ Andrea al Quirinale in Rome. This exposes a difference in background and intention with regard to the essential geometry of the building. Whereas Johnson, albeit randomly, appropriates from the history of European architecture, he seems less impressed with this pedigree and sees a plan that falls clearly within the evangelical spatial tradition that brings the congregation closer to the speaker. Whereas older, more liturgical faiths emphasize the mystery of ritual associated with the Eucharist performed from the altar, the evangelical Protestant tradition emphasizes the spectacle of the sermon about the “Gospel” performed from the pulpit. This influences the nature of the service and very often the shape of the space in which it is performed. In many cases American Protestant sanctuaries have shorter, less hierarchical naves, frequendy containing a semicircular arrangement of pews facing a central pulpit. Along with the pulpit, the altar and choir become part of a tabernacle-like stage that faces, and is surrounded by, the audience. This more intimate relationship allows the sermon and service to be easily experienced by the congregation and represents a God that is accessible to the common man.
Perhaps because of the tradition of a less formal relationship between minister and audience, many evangelical ministers found radio and television uncompromising to the sacred nature of the “Gospel.” The very definition of evangelical ministry implies an emphasis on the importance of preaching, as contrasted to ritual. Whereas rejection of established ceremony was a means for challenging the authority of mainstream churches, the evangelical movement would create its own unofficial power base through the media. Many found the emerging broadcast media the most efficient means for projecting their message and influencing as many as possible.
Dr. Robert Schuller was among those who had been willing to innovate in his ministry and to pioneer new techniques for relating to and enlarging his congregation. Because a traditional, or even enclosed, structure was unattainable at the time, he began preaching to people on Sunday mornings in 1955 from the roof of the concession stand of an Orange County drive-in theater.10 What he discovered was an untapped audience in need of spiritual inspiration who felt more at home in their automobiles than in a conventional church setting. When, in the late 1950s, Schuller commissioned Richard Neutra to design his first chapel in Garden Grove, California, the sanctuary was arranged to house both a congregation within the building and an audience seated in an adjacent “amphitheater of cars.” Presumably because of his experience with his “drive-in” ministry and the pioneering ministry of such leaders as Billy Graham, Schuller recognized and embraced the power of television, too. Like the car, it presented a comfortable and familiar setting to experience the service. The eventual broadcast of the service allowed him to reach an increasingly larger audience. Today the services are televised to an estimated audience of two million viewers each week across North America and Australia.11 The success of the televised ministry meant that Schuller could not only spread his message to more people but appeal to a much larger audience for the funding of his growing organization and its projects. Additionally, television allowed the Crystal Cathedral to become an important focal point in Orange County. Schuller’s cathedral is an additional stop on the constellation of Southern California tourist destinations as well as a contemporary pilgrimage church attracting religious travelers from across the United States, Canada, and Australia.
Different from the evangelical movements of the 19th and early 20th centuries, many of which were located in destitute urban areas and had strong social service components to their missions, Schuller’s broadcast ministry is based in the relatively affluent suburb of Garden Grove. Many criticized Dr. Schuller’s organization for channeling the bulk of its fund raising toward ever more extravagant and expensive broadcasts. The flexibility and openness of the structure and volume support transforming spectacles that match the circus-like “theater of action” proposed in Walter Gropius’s unrealized Total Theater project of 1927.12 Although arguably these productions create a new consciousness in the congregation, critics of Schuller contend that the economic energies of the organization might focus more on the disadvantaged. The theatrical broadcast format has the net effect of cultivating a rather passive congregation, one that is not physically active in the day-to-day pursuits of the church. Questions arise regarding the intentions of the message, means, and mission of the cathedral. The facile manipulation of perceived purpose is arguably a distinctive trait of the evangelical movement in particular and postmodern society in general.
The appeal of experiencing what had traditionally been a physically public event, namely, the church service, from, at first, one’s automobile and later from one’s television transforms the idea of “space” through which “public” dialogue is maintained. The allure of this spatial type represents a perceived anxiety toward an increasingly uncontrollable and misunderstood public realm. Schuller seems to understand that the automobile and television are tools that allow people to experience culture without having to contend with many of the daily problems of society. The car and the television have become controllable capsules from which to observe the volatile production of culture and a selective portrait of society.
One suspects that Schuller also recognizes that the television and automobile are artifacts that are part of what David Harvey has identified as basic changes in contemporary human psychology, emerging in large part from the volatility and ephemeral nature of culture and contributing to the swift change of values and a breakdown of consensus.13 Schuller might propose a contrary argument: that television and the auto instead of eroding society actually assist in coping with disorienting contemporary conditions. Both “spaces” allow people to be selective about what they experience and at what distance they choose to experience it. Because of their limitations, the automobile and, in particular, television contribute to culture’s oversimplification. As suggested previously, Schuller and the Crystal Cathedral take advantage of this. On the other hand, many think, as David Harvey, that the television and the auto appear to reinforce a sense of denial of problems that exist outside one’s immediate experience. This significantly contributes to a general blase attitude in society at large.14
Schuller, at least intuitively, understands both the negative and the positive effects of the television and car. Regarding the design of the Crystal Cathedral, he knows how they influence the character of contemporary built environments. As with the television and car, a sense of security, contentment, and choice is the principal goal of most contemporary common commercial
spaces. Schuller has claimed that the Crystal Cathedral is a “22 acre shopping center for Jesus Christ.” Shopping malls and privately owned urban atria are prosaic spatial paradigms that block out uncontrollable stimuli, simplify the meaning of the message in order to appeal to a larger audience, and often restrict access to marginalized segments of the population. This last quality, in particular, contributes to what Harvey has described as a “collective sense of denial” toward the unpleasant aspects of society. The refusal to respond to the full range of circumstances, including those that are lamentable, changes the nature of public space.15
¶ THE GLASS CHAIN BORN AGAIN
Schuller’s attempt to connect with the common built environment may begin to explain why he rejected the first scheme proposed by Philip Johnson. Dr. Schuller felt the initial proposal was too dark and introverted. The second scheme was inspired, according to Johnson’s own account, by the early expressionist work of Bruno Taut and the glass office tower projects of the early 1920s proposed by Mies van der Rohe.16 In particular, Johnson was intrigued by the free form plan of the Friedrichstrasse, Berlin Project of 1921 and the instinctive and emotional character of Taut’s “Stadtkrone,” or City Crown.17 Taut’s crystalline universal paradigm for religious buildings simultaneously connected the building to the tradition of cathedral making as an urban and cultural centerpiece (see Color Art 3). Taut’s commitment to a new architecture of glass allowed the tectonic vision to respond to and exaggerate the potential of contemporary transparent construction materials. For Taut this position is epitomized by his 1914 Werkbund Exhibition Pavilion. Has articulation of the idea additionally influenced a broader audience of emerging designers who were beginning to experiment with transparent construction of skin and frame, among them Mies van der Rohe.
In a recent interview Johnson claims that he has always been an “expressionist” and not a “structuralist” architect.18 It is not clear if this assertion is made retroactively. It does seem to connect this particular work with the instinctive factions of the earfy-20th-century avant-garde. It can also be argued that such an expressive streak is consistent with some of Johnson’s earlier work and explains Kenneth Frampton’s observation that his work is many times “determined to obscure structure through surface manipulation.”1’ There was, in fact, an additional motivation for referring to Taut’s Stadtkrone. The promotion by Taut and “The Glass Chain” of an architecture of individually asserted and expressive “will to form,” or “Kunstwollen,” offers a further ideological justification for Johnson’s historically conscious architecture. The terse and optimistic text Glasarchitektiir of 1914 by Paul Scheerbart, a member of Taut’s expressionist group “The Glass Chain,” advocates a new crystalline architecture that has the potential of “restructuring society.”20 It is unknown whether Johnson referred to Scheerbart’s position when presenting the second scheme to his client. However, one can imagine that the connec-
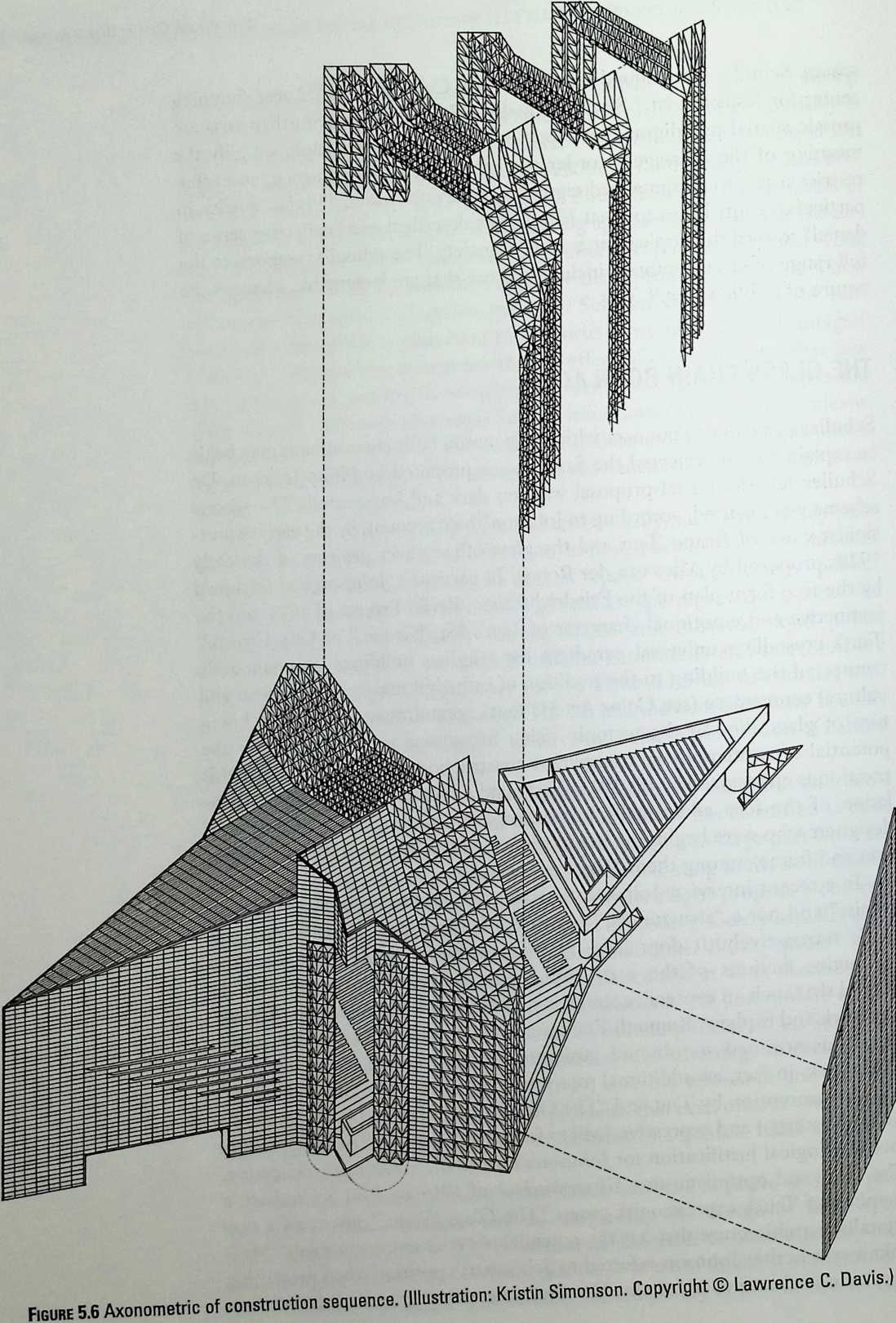
tion between the inspirational qualities of “The Glass Chain” and Schuller’s ministry is more than coincidental. It is also intriguing to note that the Stadtkrone character appears to have migrated into the design of a number of glass office towers that were erected around the time of the Crystal Cathedral, placing the church in a larger body of corporate work executed by Johnson and Burgee in the 1970s and 1980s: among them the PPG Headquarters in Pittsburgh and the Transco Tower in Oak Park near Houston.
More to the point of this chapter, understandingjohnson’s position is critical in evaluating the architect’s means for realizing the Crystal Cathedral’s idea. The free-form interpretation of the polyhedral structure of the building allows the architect to disregard the collective expectation of the normative and Euclidean configuration of the “space frame.” Johnson’s expressionist position no longer obliges him to represent the scientifically and mathematically driven spatial agenda begun in the Enlightenment. The architect is able to engage in a new and dexterous organization of form and meaning that not only recalls the beginnings of the modern movement but, because of its varied and simultaneous readings, positions the building as representative of the postmodern condition. The intuitive crystalline form permits the work to become both historically grounded and, at the same time, a volatile and ephemeral piece of “fashion en masse” that scholars such as David Harvey and Jean-Frangois Lyotard describe as essential to the palette of characteristics ascribed to postmodernism.
It was Johnson’s initial intention to use a space frame to accommodate the crystalline form without “posts or beams.”21 The scenographic program is enclosed in a vast interior landscape that includes a large tabernacle stage with space for the altar, pulpit, choir, and organ. These iconographic elements are set against the suburban Southern California landscape viewed through the lattice of the polyhedron structure and the transparent skin that clads it. Because of the distorted geometry of the building volume, Johnson was forced to abandon the use of a common multidirectional polyhedral system.22 The varying spans caused by the shape of the building in plan and section demanded that increasingly greater depths be generated toward the center of the building’s longer dimension.23 Johnson and his structural engineer, John Muller of SeverudPerrone-Szegezdy-Strum, designed a system of parallel “space trusses.” These were intended to be a series of parallel and coincident one-way structural systems.24 Because of the structure’s height and relative thickness, stiffness is achieved through a diaphragm action created by the parallel trusses acting together as a shear wall. This wall of combined space trusses, when tied to the independent balcony structures at the lateral comers, creates a stiff homogeneous “beam-like” unit.25 Each 5-foot-wide space truss was assembled off site, driven on flatbed trucks, and erected in prefabricated segments of two and three space trusses each. Two rows of shoring were used to stabilize the structure during construction.26
The compositional emphasis on the vertical dimension of the interior suggests a similar emphasis found in Gothic interiors. The outside surface of the assembled structure comprises horizontal and vertical members. The inside
Figure 5.7 Detail of space truss. (Photo: J. Frangois Gabriel. Reproduced with permission.)
surface has no primary horizontal or diagonal members.27 Like the Gothic interior, the vertical members express structure as a series of one-way systems. The compositional difference between the inside and the outside also separates the building’s structure from a common plate-like structural system, typically a means for transmitting loads on both interior and exterior surfaces. It is a fortuitous irony that the combination of many one-way space trusses in the Crystal Cathedral results in what structural engineers often refer to as “space effect”: The shedding of the loads laterally creates a two-way behavior that shares the essential characteristics of a normal “space frame.”28
Ideally, to have each element and node support the loads equally, a space frame should be a flat plate of a geometrically pure shape and have supports on all sides at each node.29 When support conditions are not consistent, as is usually the case, all loads on all members are different. Support conditions are more important than the overall shape of the surface or volume when sizing individual elements and designing connections. In most cases the rhetoric of a continuous and uniform system requires that the system’s members be sized to carry the largest load. This means that many of the members are often oversized and redundant. In some cases, in order to achieve an apparently uniform diameter of all members, their actual wall thickness is varied to address different loading conditions. In extreme cases members are solid where loads are highest. This technique is relatively expensive because of the retooling required to create the different casts for the various wall thicknesses necessary to maintain consistent diameters.
More than most polyhedral structures, the unusual shape of the Crystal Cathedral generates a number of different loading conditions. This problem is addressed by varying the depth of the space trusses to accommodate the various moments created by the increasingly larger spans toward the center of the plan. This solution produces a large number of diameter types for the individual pipe sections. This also demands a complex and idiosyncratic set of joints.30 This strategy is opposite to the techniques that manipulate the wall thickness of members to retain uniform diameters. The diameters of the members of the Crystal Cathedral vary from 2 to 5 inches to accommodate inconsistent loading conditions throughout the structural network.31 One suspects the relatively modest project cost, $10 million, required that the space truss system comprise a modified “off the shelf’ system, in this case, tubular sections from preexisting stock. This frugal strategy eliminates the option of varied tube wall thickness as a technique for accommodating dissimilar loads. The irregularity of the member sizes and the complex geometry produced a widely varied set of joint conditions. Johnson and Muller’s solution contrasts greatly with the typical space frame, which attempts to minimize the number of joint conditions as a method for achieving a consistent or uniform surface treatment. The architect and engineer devised an arrangement of connections that call for the pipe members to be welded at their slotted ends onto gusset plates.32 Owing to the distorted geometry, these are often complicated because as many as 11 members come into one joint. Where the roof meets the wall, castings are added to the gusset plates.33 The castings themselves were so complex that George Kent, a steel detailer and consultant to the structural engineer, had to model them with rubber balls and cardboard tubes in order to understand their configuration.34
Although somewhat compromised with regard to a typical space frame, there is an effort by the architect to minimize the heavy visual impact of gusset plates, service ladders, catwalks, and fighting fixtures by burying them deep within the truss system.35 In addition, ventilation is achieved through natural means. The glass itself is tinted to allow only 8 percent of the daylight and heat into the interior. A series of glass panels on the exterior skin are mechanically operable and comfortably modify air movement and the interior temperature.36 By using the depth of the space truss as a service zone, Johnson produces a discrete version of Kahn’s “served and servant” space idea. The structure becomes a tectonic and rhetorical object containing mechanical and electrical systems whose regularized surface dominates the character of the interior. Simultaneously, the frame supports a singular exterior glass wall whose smooth, reflective, and atectonic surface comes from a world of contemporary industrial production and the glossy veneers of many modern consumer goods.37 The atectonic exterior recalls the nearby Los Angeles Pacific Design Center built in 1971 by Cesar Pelli. The dialectic between the glazed exterior and the skeletal interior is part of a rhetorically industrialized tradition that includes buildings such as John Paxton’s Crystal Pavilion of 1851 and Norman Foster’s Sainsbury Centre of 1978.
Each of these examples is informed by industrial lofts. Kenneth Frampton has labeled such restatement of the uninterrupted volume typology as “productivism.” Specifically, the term is used to describe a class of innovative commercial and office structures built since the mid-1960s. It is closely allied to the original modernist idea of the building as “an elegant act of engineering.”38 The Crystal Cathedral is representative of the American branch of productivism that demonstrates little concern for the elegantly detailed and revealing tectonic language of its British counterpart, led by such figures as Sir Norman Foster and Sir Richard Rodgers.39 Because of its reductive form and deemphasized detail, Johnson’s cathedral can also be placed at the end of a line of postwar American minimalists who include Eero Saarinen, Kevin Roche, Gunnar Birkerts, and Cesar Pelli. Often monumental in scale and institutional or corporate in purpose, the work of this group frequently places an emphasis on the making of a refined abstract shape: The taut quality of the building’s language makes it difficult to manipulate in a manner that signifies such familiar architectural moments as building entry and individual window.
The transparent skin as well as its romantic framing of the sky and landscape connect the Crystal Cathedral to a second species of modernism specific to Southern California. Predominantly domestic in function and thus vastly smaller in scale than the cathedral, work by Richard Neutra and Charles and Ray Eames and the buildings of the Case Study House Movement share some tectonic characteristics and existential themes. The lightweight cladding and steel frame construction of this group derive inherent tectonic qualities from a concern for an improved programmatic and spatial relationship with natural elements. The California architects felt that the building should take advantage of the psychological and physiological benefits of the mild arid climate of the region.40 In particular, Frampton has characterized the works of Eames and the Case Study Movement as possessing a concern for standardization and mass production. This suggests a connection with the work of the later, albeit more heroic, productivist agenda. Using a more lyrical and personal formal vocabulary, the work of the Los Angeles architect Rudolf Schindler offers a vocabulary more intuitive and far less committed to standardization than other California modernists of the era. Johnson has never claimed to be influenced by Schindler’s work in the design of the Crystal Cathedral. In fact, Johnson has been accused of being indifferent to Schindler, a criticism that has its roots in the California architect’s absence from the 1932 Museum of Modem Art’s exhibition on the International style. What is striking is that many of the California projects by Schindler and the Crystal Cathe-
dral share an instinctive character that modifies normally standardized systems of construction to create expressive form.
The Crystal Cathedral corresponds to a set of larger attitudes that reveal values and conditions peculiar to postindustrial America: one of a technological monument emblematic of a productivist postwar economy and another of a building that engages in the changing American mythology of nature. In addition, the Crystal Cathedral can be connected with the previously described American tradition of temporary and makeshift environments in which religious revivals were staged.
¶ FROM BOULLEE TO OLDENBURG: THE STRUCTURE IN A POSTMODERN CONTEXT
Philip Johnson claims that the enormous geometric volume of the cathedral alludes to an expressionist utopia. Others have found the Crystal Cathedral to be similar to the architecture of the Enlightenment and more recently much of pop art. The building’s boldness and heroic scale recalls the projects by Boullee and Ledoux. This courageous yet eccentric architecture from the Enlightenment, among other things, spoke in confident terms of the power of reason and a comprehension of natural laws of the universe. American society has been a principal descendant of this legacy because of (1) the society’s commitment to capitalistic production, (2) its historically strong individual work ethic, and (3) its view that the natural environment is a resource meant to be transformed through the laws of nature for the good of society. In particular, the Anglo-American Enlightenment was the parent of a number of evangelical and reform movements. These two sets of offspring have often radically alternated between being mutually supportive of or distincdy at odds with each other. Albeit for vastly different reasons, they both currendy participate in a broader contemporary critique of America’s philosophical commitment to science and technology.
A departure from the “reasoned” spirit of the Enlightenment appears to contradict a primary reading of Johnson’s polyhedral structure: a group of evangelical Christians being housed in a system that symbolizes a secular heritage. This apparent discrepancy makes sense when one considers that Dr. Schuller’s ministry is unique in that it is not part of the “creationist” branch of the modern evangelical movement. The rhetoric of technology is compatible with Schuller’s rejection of the common evangelical belief of “original sin.” Schuller contends that “sin” is the primary source of “guilt,” a principal inhibitor of human potential. For Schuller, technology becomes a symbol of the material, psychological, and spiritual maximization of human nature. This positions him on the edge of more familiar reactionary strains of evangelism, placing him closer to moderate contemporary American belief.
In addition to its compatibility with a secular society, the building is also part of a 19th-and 20th-century tradition that embraces the revelatory nature of technology. This mystic optimism is epitomized in the exhibition structures
Figure 5.8 Interior toward east across nave. (Photo: Gordon H. Schenck, Jr. Reproduced with permission.)
of the 19th century, the reconsideration of architectural language of the 20th century, and the built artifacts of the space program of the 1960s and 1970s. Ironically, it is the social upheaval of this last period that most recendy called into question the credence of this shared faith in science.
The overt representation of technology in the Crystal Cathedral can be interpreted as nostalgia for America’s historic leadership and prestige in the first two-thirds of the century in science, technology, economics, and politics. Many have interpreted the structure’s white tubular members and the intricate shadows they produce as connoting the assembly building and launch towers of Cape Canaveral. According to the architect, the cathedral’s large 70-foot-high doors, which, when open, connect the pulpit to the audience in their cars in the parking lot, were inspired by the poetics of the structures at NASA’s Florida rocket-launching facility.41 The large doors require a motor the size of that needed to operate a washing machine to open; ironic because their motion alludes to the incomprehensible nature of a powerful cybernetic apparatus (Color Art 4).
On first inspection, the inspirational reading of the structure and doors seems consistent with what Manfredo Tafuri describes as the “mystic transparency” pursued by the “Glasarchitektur” of the early modem movement in Germany.42 Conversely, Tafuri has also suggested that the building’s lack of technical development, manifest in the crudeness of its detail, keeps it from truly achieving its revelational potential. The large scale and the undiscriminating character of the structural connections deny a specific identity that reduces both the interior and the exterior surface to an indifferent quotation free from a profound reading of the relationship between material, craftsmanship, and gravity. The lack of differentiating inflection of the building’s structure to its external context, which includes Richard Neutra’s most recognized works, or the internal context of specific programmatic or technical requirements implies that the building is emblematic of the passive, casual, and overly inclusive nature of the contemporary built environment: a set of qualities shared with much of current culture and the media in particular.
It is tempting to read Johnson’s design as an intentional and subtle critique of common life, a highly considered piece of “culture en masse,” that is, at the same time, as Schuller claims, a “22 acre shopping Center for Jesus Christ” to be inhabited by the common man. Its bluntly assembled off-the-shelf building system has the ability to be a powerful icon of contemporary times. The generic nature of the structure recalls the mechanical and serial form making of pop art (Color Art 5). As with pop art, the nondiscriminating nature of Johnson’s work, particularly the Crystal Cathedral, has attracted both a critical and a popular following. The boldness of the imagery and candor of the overall statement can be considered more consequential than a classically inspired elaboration of a glass-and-steel construction. It is often argued that such technical bluntness distinguishes American art and architecture from that of Europe.43 This rejection of the seriousness of “high culture” and its art has been described as characteristically “American” as well.44 These contentions become difficult to defend when one considers that the “anti-art” segments of dadaism began in Europe. On the other hand, its descendant, American pop art, simultaneously embraces and critiques the popular culture of postwar America as well as both historical and contemporary avant-garde. For the inhabitant and viewer the Crystal Cathedral, like much of pop art, can be impersonal, monotonous, banal, lonely, disturbing, and oddly at the same time, glorifying.
Ultimately, comparing the Crystal Cathedral to pop art becomes problematic. Missing from the Garden Grove Chapel is the intentional wit or derision of Warhol, Lichtenstein, Oldenburg, and others of the movement. One senses that Johnson is not consciously iconoclastic in the design of the church. In fact, Johnson’s stated reference to the architecture of expressionism and the optimistic reading of technology suggest that the building is very traditional in that it is conspicuously heroic. It is precisely the underarticulated character of the building systems that undermines this reading, reinforcing instead the mechanical and potentially “senseless” ritual of viewing a televised service.
¶ THE STRUCTURE AND AMERICAN MYTHOLOGIES OF NATURE
The nation’s transforming relationship to nature and spirituality is arguably of greater metaphysical significance to American society and culture, and the Crystal Cathedral in particular, than the pragmatics of pop. The American connection to nature and God gives the building its serious dimension. Understanding changes in the American mythology of nature is useful in comprehending the relationship of the cathedral to the contemporary natural environment.
Leo Marx’s paradigm and the title of his influential text published in 1964, The Machine in the Garden, describes a set of important models for grasping the historic relationships of American society and the landscape. Initially, the New World was understood by Europeans through a set of conflicting views of the vast unsettled continent: one as a terribly untamed and savage realm; the other a pure unspoiled opportunity to recast and reform European civilization. This perception would significantly change with the rise of industrialism. In no small part due to the 19th-century romantic movement in Britain, the philosophical debate about nature in America centered around a pair of attitudes that saw the natural environment, on the one hand, as an endless resource in service to the accumulation of commercial wealth and, on the other, as a finite and diminishing realm, aiding individual initiative and prosperity.
In his book The Machine in the Garden, Leo Marx describes this conflicting set of 19th-century views about the utility of nature as “pastoralism.” In Making a Middle Landscape, Peter Rowe contends that, “Pastoralism,” as defined by Marx, is “a cornerstone of American intellectual and artistic experience….”4S In the 19th century the politics and culture of the pastoral ideal evolved to serve simultaneously the symbolic interests of the individual and the collective interests of industry. Small property owners and big
business both saw the natural environment as an energetic and inspiring mythology coming from wilderness and a means to exchange and generate wealth. The 19th-century landscape painter Thomas Cole, in particular, depicts the unique relationship Americans have with nature.4* His work often juxtaposes cultivated landscapes with wild landscapes. Cole’s somewhat didactic paintings frequently imply a Biblical narrative that propounds the transformation of a raw and sublime wilderness to a productive garden because of the persistent and virtuous progress of civilization. These portrayals place American nature myths with the future, or at least the here and now. This is in contrast to the conventional European mythology about nature, which often cultivates cultural relationships with the past.47 It is interesting to compare Cole’s work with the views of nature portrayed by European, and classically romantic, painters such as William Turner. Turner’s atmospheric work depicts a less optimistic image, indicating that nature and culture are both cast as a sublime, terrifying, and ultimately incompatible dichotomy. This melancholic view is often described as being nostalgic toward a perceived “semiprimitive” time before industrialization. Selected works of George Inness represent an important shift in the 19th-century American pastoral metaphor. His painting The Lackawanna Valley creates an idyllic pastoral setting but moderates the scene by introducing the dialectical promise of technology: a railway locomotive pulling a train of freight cars in the middle ground. In contrast to the dominant British view of technology, later placed in architectural terms by John Ruskin, William Morris, and others, that enslaves the individual, Inness portrays the machine as something that can free the individual and tap into a new constructive potential for the benefit of society. This is consistent with the American proclivity to place industry in a visionary light. Peter Rowe describes this as an accommodation in American pastoralism that allows the coexistence of nature and technology.48 This historically has allowed society the material advantages of industry and the moral benefits of honest social values associated with a Virgilian rural existence.49 Over the course of the nation’s life, this contention becomes an important element of the complex imprecise environment of the American suburb, a cultural and social condition critical to understanding the character of the Crystal Cathedral.
¶ THE CONTEMPORARY PASTURE: A CATHEDRAL IN A PARK
In coming to terms with the contemporary state of pastoralism in the city and suburb, Peter Rowe describes a fundamental difference between the pastoral ideal and society’s technical alignment: the former prescribing a state of being and the latter, a means for doing things. He submits that contemporary society awkwardly attempts to quantify the pastoral condition. This occurs in such practices as describing the qualitative social benefits of open space and parks in empirical terminology.50 Rowe suspects that the tendency to measure conventionally qualitative criteria has to do primarily with the modem and universal means of production, the technocratic method of managing things, and the scientific manner of interpreting the world. He also describes how a technocratic orientation has the unfortunate characteristic of bypassing the “symbolic realm of human experience,” favoring instead limited but empirical modes of measurement.51
In the postindustrial context, although transformed, the pastoral ideal still has much to do with explaining the character of the suburb, particularly in the domestic setting. Rowe describes the current state of the natural myth as becoming a nostalgic presentation of a bucolic landscape framing “kitsch” period-style structures. The image of moral superiority of the 19th-century pastoral ideal over the tainted traditions of European society is transferred to the 20th-century American suburb. The lower-density parldike setting of suburbia represents the perception of a more virtuous environment compared to the decay of the inner city.52 Corporate and commercial suburban environments are often just as committed to a dialogue with nature. These nonresi-dential types usually have an architectonic vocabulary and site strategy that are less nostalgic toward historic styles and are often more overtly expressively “rational” and “functional” in nature.55
More than most buildings that are open to a large segment of the public, the Crystal Cathedral engages in the two themes of modern pastoralism. First, its sheer transparency, informed by the expressive architectural language of the early-20th-century avant-garde, connects the interior with the suburban landscape, one that, through decentralization, portrays a socially natural and ideal terrain. Recalling the work of Thomas Cole, the view of the contemporary pastoral setting suggests a Biblical reference to the “Garden of Eden” and American mythology, which romanticizes the cultivation of the frightening wilderness. In the case of Orange County, California, a prototypical suburban version of a “New Jerusalem,” one suspects that the definition of “wilderness” includes not only the historic vision of undeveloped land but, more importantly, the chaotic and threatening nature of “Babylon” in the form of America’s contemporary urban and threatening inner-city “wilderness.”54
Second, the use and reading of nature and the garden as a recreational diversion is now significantly different from what it was in the 19th century. Today, nature and God are seen to be therapeutic resources. In an age of overstimulation and a proliferation of morally undifferentiated choice, the white structure and transparent skin of the cathedral open to the sky and to an idealized landscape suggest a soothing, if not semiconscious, state separate from the profane nature of the everyday environment. The diversion of idyllic nature becomes a remedy for dealing with the estrangement caused by the fragmentation of daily rituals, necessary where international and regional affiliations have become more important than local relationships. As the traditional separation between city and country becomes blurred, nature becomes a more exceptional experience. Green space becomes a distinct realm, readily available to be manipulated by those who control their environments.
In the Crystal Cathedral nature is highly controlled and is used to represent the rehabilitative effects of Christian spiritual salvation. In addition to the panorama of suburban Garden Grove, the resplendent interior houses a row of gentle fountains lined in a pool that is on axis with the altar, itself overgrown with tropical ferns and flowers. Between services, a bath of religious Muzak further acoustically tranquilizes the interior. As well as recalling the integrated environment of a shopping mall, these attributes further strengthen the perception of the cathedral as a suburban “Garden of Eden.” The Crystal Cathedral becomes a condensed and collective version of the ideal Southern California backyard comprised of house, pool, and lawn. David Hockney portrays this emblematic personal space in his 1967 painting?! Lawn Being Sprinkled. Peter Rowe describes the work as representing a paradigmatic space of the postmodern condition, a realm supporting the “blank good life…loaded with intriguing cliches that are simultaneously surreal, energetic, alienating and filled with a deep sense of ennui.” ” The contemporary view of nature is distinct from the traditional separate character of city, suburb, and countryside of the past. It is now part of the synchronic ubiquitous matrix of the urban/suburban metropolis.
The coincident usage of the contemporary city structure suggests an alternate reading of the Crystal Cathedral’s polyhedral structure. The articulated and non-rectangular frames refer to the uniform texture of the endless metropolitan environment. Like Jennifer Bartlett’s famed Rhapsody, which uses the grid as a symbol and means for creating semiautonomous image fragments from a larger image, Johnson’s white lattice structure creates a pictorial quilt of the exterior landscape’s segregated and diverse functions stitched together by a relentless system of high-speed roadways. Unlike in the 19th century, nature is no longer a civilized and separate pastoral ground. Today, nature is a set of figures woven into an uneven context with an indistinct purpose. At the scale of an individual plot, nature’s figural function takes the shape of the autonomous suburban backyard. At the scale of the metropolis, nature is formed in city, regional, or national parks; the latter being a paraurban destination intended psychologically and physiologically to separate people from their customary environment, thereby refreshing the mind from its fatigued condition. It is easy to contend that nature’s commodified and isolated image is itself compromised and itself “un-natural.” At its best nature is rewoven into the placeless space of the metropolitan terrain. At its worst it becomes a nebulous decoration used as a green skirt for industry, recreational facilities, residential districts, and commercial zones.
In addition to engaging with a transformed pastoral ideal found in the contemporary decentralized city, the Crystal Cathedral is participating in a traditional, though no less converted, relationship between technology and a natural context. To many architects and urban designers, most suburban residential architecture presents a discrepancy between its practical purposes, which are often arranged in a highly functional manner by accommodating the most sophisticated consumer technology, and its use of decorative styles, which are firmly entrenched in the often quasihistoric or pseudorustic pretensions of the architecture that society desires. Along with a body of his smaller-scale work in the 1950s and 1960s, Johnson’s Crystal Cathedral through its transparent glazing and its polyhedral shape begins to imply a 20th-century pastoralism for contemporary suburban culture. Particularly given the historicist nature of the work he and John Burgee designed and built shortly after the Garden Grove Chapel, it would be inaccurate to portray Johnson as a utopian committed to reshaping the nature of the American pastoral tradition. Although smaller and more private in function, the Glass House in New Canaan, the Roofless Church in New Harmony, and the Underground House in suburban Cincinnati offer a body of conceptually imaginative work in parklike settings. More than most works of this century, these are very close to Leo Marx’s “machine in the garden” paradigm. In all three buildings and the cathedral, the visual and often spatial movement between a modem building and the landscape is uninterrupted, highly contemplative, and ultimately intensely poetic.
What separates the Crystal Cathedral from Johnson’s earlier body of work is its somewhat more frightening and indifferent relationship to the landscape. Whereas its transparency connects the inside with the outside world, its large scale, reflective treatment, and prismatic form seem to render a sense of imposition and disengagement with the scale of its surroundings. This may have much to do with the fact that Reverend Robert Schuller did not retain Johnson and Burgee to plan or coordinate the landscape immediately surrounding the building. It may also have to do with an intention, or at the very least a reading, that links the building to the pandemonium of signs and visual stimuli of the local suburban environment.
The directness of the building creates an ironic contrast to the bucolic character of its suburban setting. The chapel’s graphic vitality recalls a suburban “Babylon,” a “city of vice” found in the “architecture of the strip” that Robert Venturi and Denise Scott Brown describe in their studies of highway iconography. In the case of the Crystal Cathedral, the form and treatment together recall the figurative, though no less symbolic, quality of the surrounding suburban office parks and the mysterious tinted glass of limousines slipping by on the nearby Santa Ana and Garden Grove highways. Like other buildings in the suburban realm, the client priorities often reduce the design of such landscape elements as parking lots to their most basic level to keep the cost of the entire project down. This places most of the emphasis on the more efficient symbolic reading of the building’s form and materiality. Such subtraction denies the possibility of developing an architecture that is sensitive to many scales. By spatially modulating the building’s surroundings, a more concentric and intimate set of scales could have been introduced. By not adequately dealing with the leftover spaces, namely, the parking lots, the Crystal Cathedral contributes to the unfortunate perception that most modem architecture is indifferent to the scale of human occupation and that the rhetoric of the frame and massing dominates the conceptualization of the project, precluding any attempt to foster an intimate relationship between humans and architecture.
SOME
¶ CONCLUSION
S
The paradoxical structure and space of the Crystal Cathedral represent the religious organization that uses the building and are emblematic of many rich inconsistencies found in American society. Through monumental form and mannered geometry, the expressive and unorthodox character of Johnson’s design addresses not only a desire for informality but the need for validation of a historically controversial and spiritually conservative segment of the nation’s population. The cathedral’s glass skin and structure both frame the idealized suburban Southern California context: a part of the United States that, more than most, romanticizes the benefits of civil fiberties and unlimited choice. The building’s overt embrace of the television and the automobile, two of the most important postwar technological influences of contemporary culture, adds ammunition to the project’s ability to accommodate an additional and, one suspects, an increasingly authentic set of myths. Its transparency and polyhedron construction connect the Crystal Cathedral to the familiar atria of malls and shopping centers to reinforce: (1) the reading of the American terrain as a cultivated palimpsest of public and private gardens dedicated increasingly to diversionary activities; and (2) the nation’s historic and characteristic attachment to standardized technology, which appears to encourage corporate capitalism as long as it serves the concept of unlimited consumer choice.
The geometric distortion of Philip Johnson’s polyhedron structure is both intriguing and banal because it is the result of, and at the same time exemplifies, contemporary circumstances. Johnson and Burgee’s structure was never intended to position itself in the long line of geometrically precise structuralist designs that historically and intellectually owe much of their existence to the philosophical traditions of Europe. It is easy to contend that, although Johnson has been strongly influenced by European architecture, his appropriations have favored an, at times, random and expressionist set of architectural projects and movements. If there is a consistency in Johnson’s work it is that Euclidean geometric order, particularly with regard to structure, is of little metaphorical concern. This indifference toward intellectual precision and cosmologic arrangement, while troubling to many of the profession’s theoreticians, is of no small importance because it seems that the American public does not often care either. What this chapter attempts to suggest is that such apathy to external order is part of the American cultural and social legacy and goes a long way to explain the dearth of representational geometric space in the Crystal Cathedral, Johnson’s work, and in the current built environment.
¶ NOTES
-
Sydney F. Ahlstrom, A Religious History of the American People, Yale University Press, 1972, p. 263.
-
Ibid., general references, pp. 743.
-
Ibid., p. 957.
-
Peter Rowe, Making a Middle Landscape, MIT Press, Cambridge, MA, 1991, p. 36.
-
John Pastier, “An Evangelist of Unusual Architectural Aspirations,” American Institute of Architects Journal, May 1979, p. 52.
-
Kenneth Frampton, Modern Architecture: A Critical History, Thames and Hudson, New York, 1980, p. 232.
-
Le Corbusier, Towards a New Architecture, Dover, New York, 1986, pp. 69.
-
Le Corbusier, The Decorative Arts of Today, MIT Press, Cambridge, MA, 1987, p. 188.
-
Ibid.
-
Pastier, “An Evangelist of Unusual Architectural Aspirations,” p. 49.
-
Doctor Robert Schuller, “The Hour of Power,” Television Broadcast, Dec. 2, 1995.
-
Frampton, Modem Architecture, p. 139.
-
David Harvey, The Condition of Postmodemity, Basil Blackwell, Cambridge, MA, 1989, p. 286.
-
Ibid.
-
Pastier, “An Evangelist of Unusual Architectural Aspirations,” p. 52.
-
Philip Johnson, Author’s interview, New York, Nov. 13, 1995.
-
Ibid.
-
Ibid.
-
Frampton, Modem Architecture, p. 240.
-
Ibid., p. 116.
-
Johnson interview.
-
Johnson interview.
-
Ibid.
-
Robert E. Fisher, “The Crystal Cathedral: Embodiment of Light and Nature,” Architectural Record, Nov. 1980, p. 82.
-
John Muller, Author’s telephone interview, Syracuse, NY, Nov. 21, 1995.
-
Fisher, “The Crystal Cathedral,” p. 82.
-
Ibid.
-
Muller interview.
-
Fisher, “The Crystal Cathedral,” p. 82.
-
Ibid., p. 83.
-
Ibid.
-
Ibid.
-
Ibid., p. 82.
-
Ibid.
-
Ibid.
-
Ibid.
-
Frampton, Modem Architecture, pp. 302.
-
Ibid., p. 304.
-
Ibid., p. 303.
-
Ibid., p. 249.
-
Fisher, “The Crystal Cathedral,” p. 82.
-
Manfredo Tafuri, “Subaqueous Cathedral,” Domus, No. 608, 1980, p. 12.
-
Barbara Rose, American Painting: The Twentieth Century, Rizzoli, New York, 1969, p. 89.
-
Ibid.
-
Rowe, Making a Middle Landscape, p. 226.
-
Ibid., p. 222.
-
Ibid.
-
Ibid., p. 225.
-
Ibid., pp. 225.
-
Ibid., p. 232.
-
Ibid., p. 233.
52.Ibid.
53.Ibid.
-
Ibid., p. 245.
-
Ibid., p. 54.
¶ BIBLIOGRAPHY
Ahlstrom, S. E.: A Religious History of the American People, Yale University Press, 1972.
Engh, M. E., SJ.: Frontier Faiths: Church Temple and Synagogue in Los Angeles, 1846, University of New Mexico Press, 1992.
Fisher, R. E.: “The Crystal Cathedral: Embodiment of Light and Nature,” Architectural Record, Nov. 1980, pp. 77.
Frampton, K.: Modern Architecture: A Critical History, Thames and Hudson, New York, 1980.
“Garden Grove Community Church, Garden Grove, California,” Global Architecture Document, No. 3, A.D.A. Edita, Tokyo, 1981, pp. 22.
Gaustad, E. S.: A Religious History of America, Harper and Row, New York, 1966.
Goldstein, B.: “New Crystal Palace: Crystal Cathedral, Garden Grove California,” Progressive Architecture, December 1980, pp. 76.
Habermas, J.: “ModernityAn Incomplete Project,” The Anti-Aesthetic: Essays on Postmodern Culture, H. Foster, ed., Bay Press, Port Townsend, WA, 1983.
Harvey, D.: The Condition of Postmodernity, Basil Blackwell, Cambridge, MA, 1989.
Huyssen, A.: After the Great Divide: Modernism, Mass Culture, Postmodernism, Indiana University Press, 1986.
Jacobs, J. M.: Philip Johnson, Braziller, New York, 1962.
Johnson, P.: Johnson/John Burgee: Architecture, Random House, New York, 1979.
Johnson, P.: Johnson/John Burgee Architecture 1979, Rizzoli, New York, 1985.
Johnson, P.: Philip Johnson: In His Own Words, Rizzoli International, New York, 1994.
Le Corbusier: The Decorative Arts of Today, MIT Press, Cambridge, MA, 1987.
Le Corbusier: Towards a New Architecture, Dover, New York, 1986.
Lyotard, J. E: The Postmodern Condition: A Report on Knowledge, University of Minnesota Press, 1979.
Marx, L.: The Machine in the Garden: Technology and the Pastoral in America, Oxford University Press, 1964.
Miyakawa, T. S.: Protestants and Pioneers: Individualism and Conformity on the American Frontier, University of Chicago Press, 1964.
Pastier, J.: “An Evangelist of Unusual Architectural Aspirations,” American Institute of Architects Journal, May 1979, pp. 48.
Perez-Gomez, A.: Architecture and the Crisis of Modem Science, MIT Press, Cambridge, MA, 1983.
Rose, B.: American Painting: The Twentieth Century, Rizzoli, New York, 1969.
Rowe, P.: Making a Middle Landscape, MIT Press, Cambridge, MA, 1991.
Schulze, E: Philip Johnson: Life and Work, Knopf, New York, 1994.
Tafuri, M.: “Subaqueous Cathedral,” Domas, No. 608, 1980, pp. 8.
¶ Tetrahedral Purity: The Javits Center
Matthys Levy
¶ INTRODUCTION
New York’s Javits Center, one of the world’s largest exhibition spaces contained in a single building, sits on Manhattan’s waterfront on a 9-hectare site. Its distinctive architectural profile is identified by a unique space frame that both encloses and defines interior spaces. Because the center is a major public facility, the building’s architect, James Ingo Freed of Pei Cobb Freed, sought to create a design that welcomes the public while creating a dynamic interplay between the purely commercial and the public uses of the project. To achieve this result, Freed took advantage of the special features of the site: the views toward the river, the changes in ground elevation over the site, and the difference in relative importance of the surrounding streets.
¶ ARCHITECTURE AND POLITICS
The building is oriented along 11th Avenue, which slopes down from the southern to the northern end of the site, permitting the development of a two-level entry system. A ceremonial entrance at the highest point leads directly to a great entrance hall on the level of the upper exhibit hall. A roadway entered from the northern end provides access to a 300-m-long bus and taxi dropoff that is directly outside the concourse, which is at midheight between the two exhibit floors. The lower exhibit floor, with a 6-m ceiling height, contains about 60,000 m2 of space, including restaurants, meeting rooms, and a specialevents hall. The upper exhibit hall, with a ceiling height of 10 m and an area of 50,000 m2, is over 300 m long. A galleria floats above this hall in an east-west direction, providing access from the entrance hall to a future restaurant and bar overlooking the Hudson River. At the back of the exhibit halls, along 12 th Avenue, truck bays are provided on both levels with direct access to each exhibit floor.
The exhibit hall, the galleria, the concourse, and the entrance hall are all covered with a continuous space structure with a plan area of over 53,000 m2 supported on a grid of columns spaced 27 m on center. This roof structure climbs in giant steps from the general roof line over the exhibit hall to a point 47 m above the entrance hall. The multilevel cubes give the appearance of a crystalline structure reminiscent of the 1851 Crystal Palace.
New York had long sought to build a new convention center to meet the ever-growing demand of the public and trade show sectors that were inadequately served by the small (30,000 m2) coliseum. After a failed attempt in 1972, the needed legislation for a new center was passed in the spring of 1979 and married the state’s Urban Development Corporation, which had construction and planning expertise, to the Triborough Bridge and Tunnel Authority to provide the necessary financing. To further complicate matters, separate development and operating corporations were established to build and manage the new facility. This proved to be an awkward arrangement that was finally changed, centralizing all responsibility in one agency, but only after the building was completed.
GEOMETRY AND STRUCTURAL FORM
The two most challenging problems in the overall design were first to devise a structural system to unite the building’s diverse functions in a coherent pattern of visual and spatial rhythm, and, second, to articulate this structure in a way that visually reduced the scale of so large a building. The center’s form represents a synthesis between these related objectives (Figure 6.1).
Derived from the 27-m spans used within the exhibition halls, the basic structural unit of the exhibition center is a 27-m bay covered with a space frame roof supported at each 8.725-m-high column at four comers of an inverted pyramidal column capital on 400-mm-diameter circular base plates 3 m apart. At each of these points, the space frame is either fixed, free, or permitted to slide in either the N-S or E-W directions, depending on the location of expansion joints in the roof and the requirement for restraint to support lateral loads. Below the inverted pyramidal top are four 400-mm shafts centered on the four comers of a 1.5-m square that are welded to a base plate bolted to the concrete floor of the upper exhibition level. The sculptured
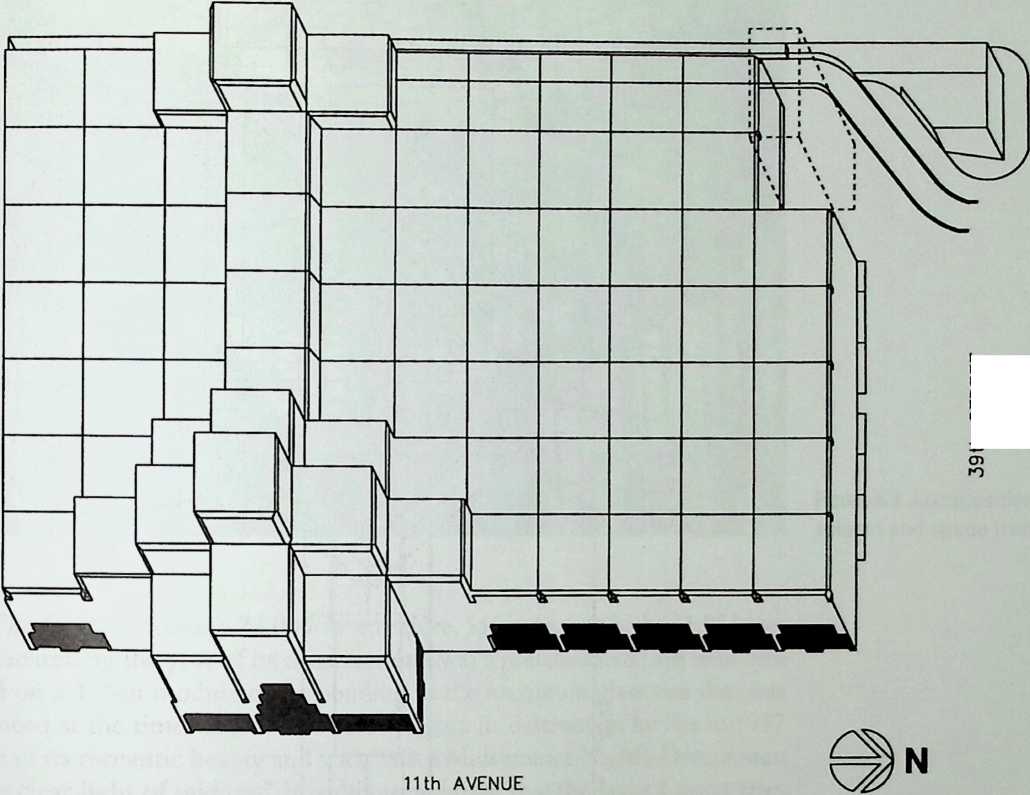
38th STREET
Figure 6.1 Axonometric view of the Javits Center.
th STREET
shape of these columns somewhat resembles delicate, multistemmed champagne glasses rather than gross single-legged piers (Figure 6.2).
The 27-m repetitive bays, visible throughout the building, unify the structural rhythm of the entire exhibition center: The concourse and galleria are the width of one bay, whereas the exhibition halls are formed by the repetition of many such bays. Through the variety of heights defined by the space frames and the sculptural quality of the frames themselves, the design achieves a reduction of scale in the formation of the building itself.
Along the building’s exterior, the form of the space frames and columns is mirrored in the building’s facade. The skin of the building is modulated by the metal of the frames and a range of reflective glasses. Transparent glass forms the lower facade of the entrance hall and the concourse, as well as that of the galleria and restaurants; the remaining facades are translucent or opaque glass. The skin articulates the functions of the building and expresses the form of the structural unit. The result is a single, unified rhythm, integral to the structure, patterned to reduce scale (Figure 6.3).
The interior illumination of the building differs significantly from most
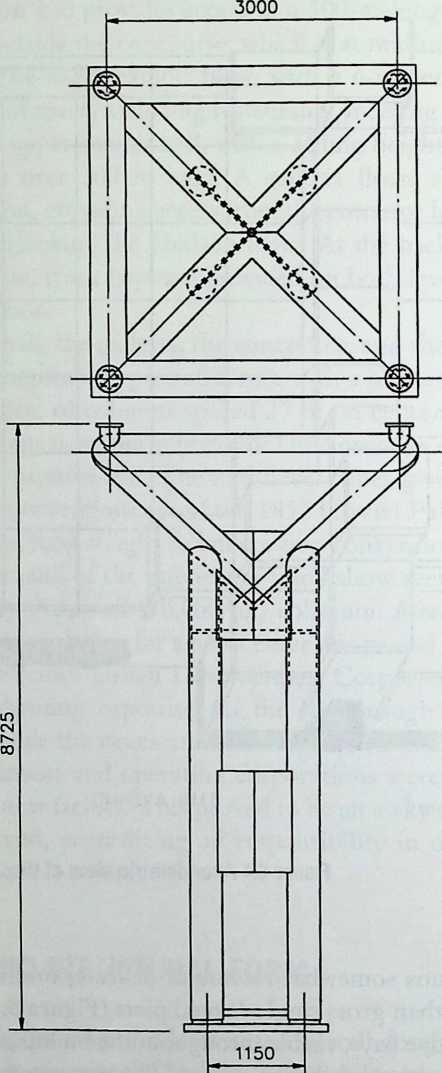
Figure 6.2 Column elevation.
glass architecture in realizing the possibility of using natural light as a means of visually defining interior spaces. The public spaces are articulated, not by walls, but by a soft, evanescent fight filtering in from outside the building through the tinted glass that reduces the light entering the building and permits views outside the building.
The center’s design presents a rare opportunity, in the tradition of the great exposition palaces of the 19th century, to demonstrate the innovative use of modem technology. It is perhaps closest in concept to the Crystal Palace built for the 1851 London Exhibition, although images are also present of the Galerie des Machines built for the 1889 Paris Exhibition.
Figure 6.3 Juxtaposition of column and space frame.
The Crystal Palace, a 72,000-m2 structure, 555 m long (which is 1,851 feet long, matching the year of its construction), was a prefabricated iron structure based on a 1.2-m module corresponding to the maximum glass size that was produced at the time. Those who saw it before its destruction by fire in 1937 spoke of its romantic beauty and said, “it is a Midsummer Night’s Dream seen in the clear light of midday.” It is this same image that the Javits Center tries to evoke. Clearly, it is the structure of the building, more than any other element, that contributes to the crystalline quality of the design.
What is interesting is the process leading to the solution. From the beginning, an organic approach was sought that would tie together the various forms. The space frame, which covers the horizontal planes, turns comers, climbs in steps to the top of the great hall, and descends to the ground, does so without violating the “pure tetrahedral geometry” of its smallest unit. Specified as an assembly of steel pipes and spherical steel nodes, the space frame geometry is the master to which the designer is the servant. The deft and elegant maimer in which the elements are handled demonstrates how imaginatively prefabricated elements can be handled by a competent designer.
Based on a 3 X3-m horizontal module, 1.5 m deep, the space frame is stiffened along the column lines by diamond trusses formed by a second layer of the standard tetrahedral geometry. The whole assembly behaves much like a flat plate with reinforced column strips. At the columns, a third layer of space frame creates a drop panel completing the analogy. The column itself contains the capital, an inverted pyramid, sitting on four stiffened shafts of steel-clad reinforced concrete (for fireproofing) (Figure 6.2). The column capital member sizes use 400-mm tubes, 40 mm thick for diagonals and 13 mm thick for horizontals. Material for these tubes is ASTM A618 Gr 2 (F7 = 345 MPa). The crossed base of the inverted pyramid consists of butt-welded 38-mm-thick gusset plates of ASTM A3 6 steel (F? = 248 MPa). These are, in turn, welded to bearing plates at the top of the four vertical 400-mm-diameter concrete-filled steel shafts.
¶
JOINTING
Because of its size, it was necessary to divide the roof area into eight units, each of which would respond independently to movements and deformation resulting from temperature variations (Figure 6.4). Two conditions were considered:
-
Maximum temperature variations during construction: 3 5 °C with large permissible deformations and stresses.
-
Maximum ambient temperature variation during operation, after the building is closed in: 15°C with small deformations and stresses.
Figure 6.4 Layout of roof regions.
PLAN
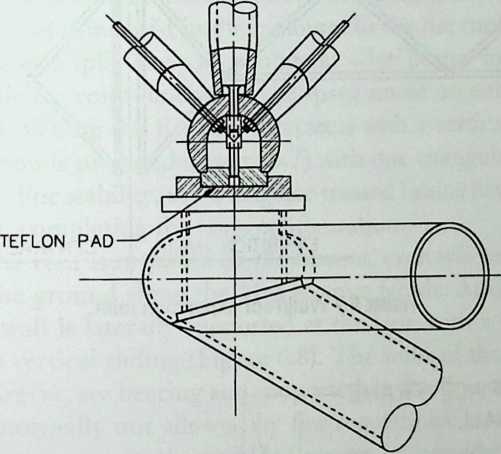
Figure 6.5 Unidirectional sliding bearing.
Figure 6.6 Expansion joint
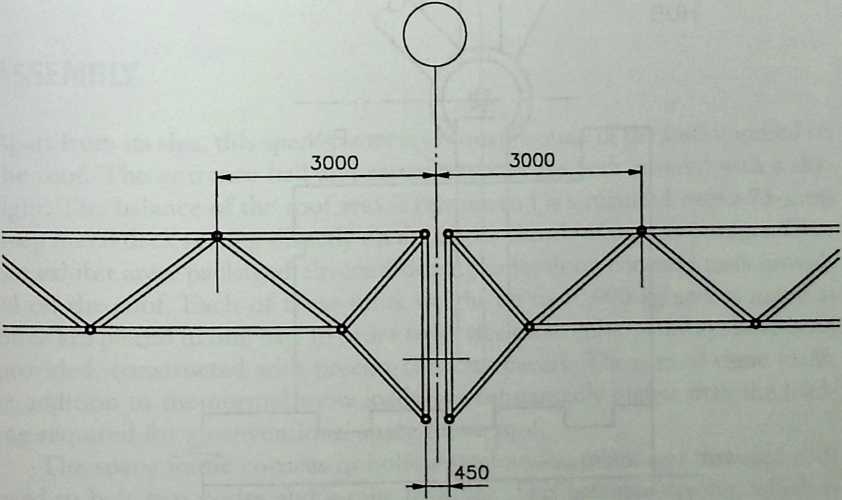
EXHIBITION HALL
CENTRAL HALL
Figure 6.7 Wall/roof expansion joint.
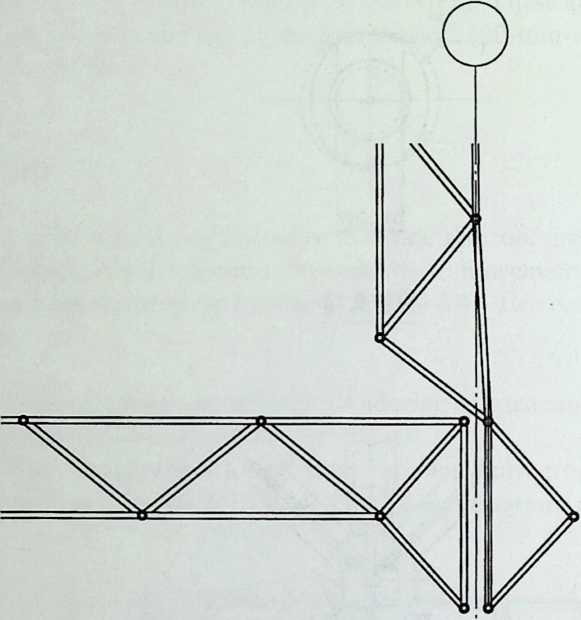
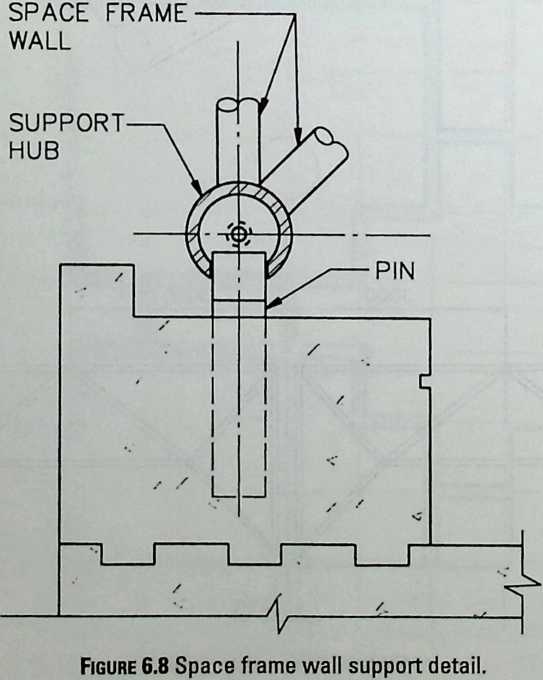
Consistent with these principles, three types of supports were designed for the space frame at the top of the columns: fixed, free, and one-way sliding (in one of the two orthogonal directions). In general, the center of a unit between expansion joints was fixed and the unit was permitted to expand outward from this center. As a result, no more than two bays, or 54 m, of the continuous space frame is fixed against expansion and the resulting bar forces are no more than 10 percent of the total design forces.
Most of the roof units are required to resist lateral wind forces, because they are either continuous with exterior walls or support mullions from entrances or curtain walls. These wind forces are resisted at fixed supports as well as sliding supports that are perpendicular to the wind direction (Figure 6.5).
In plan, the repetitive grid of column locations is carried out without regard to the location of expansion joints. As a result, the pure geometry of the space frame is distorted at these locations to accommodate the expansion joints. Two such conditions exist in the building. In the flat roof area, the diamond-shaped beam is split into two triangular edge beams spaced 450 mm apart, each of which is continuous with the space frame on either side of the joint (Figure 6.6). Where the flat roof intersects with a vertical wall, a more complicated division is provided (Figure 6.7) with one triangular beam hanging from the wall. For stability, the triangular trussed beams have diagonals in the vertical plane, completing the truss configuration.
In general, the roof is supported on the columns, even where the wall continues down to the ground along the 11th Avenue facade. At these locations, the space frame wall is laterally supported at the base with a detail connection that permits vertical sliding (Figure 6.8). The walls of the three bays on 12 th Avenue, however, are bearing and supported on the floor slab. This condition, which is normally not allowed by fire regulations, was permitted on the condition that an automatic sprinkler system be provided covering the full area of the walls.
ASSEMBLY
Apart from its size, this space frame is unusual because of the loads imposed on the roof. The entrance hall and restaurant area are both covered with a skylight. The balance of the roof area is opaque and is structured with a 75-mm-deep metal deck resting directly on the upper chords of the space frame. Over the exhibit area, packaged air-conditioning units sit on concrete pads provided on the roof. Each of these units weighs up to 10,000 kg and as many as three are placed in one bay. In order to service these units, pathways have been provided, constructed with precast-concrete pavers. The sum of these loads, in addition to the normal snow loads, are substantially higher than the loading required for a conventional space frame roof.
The space frame consists of hollow steel nodes, tubes, and threaded rods used to bolt two nodes and a tube together. This patented system, which is known as the PG System, operates as follows: The tubes carry all compressive
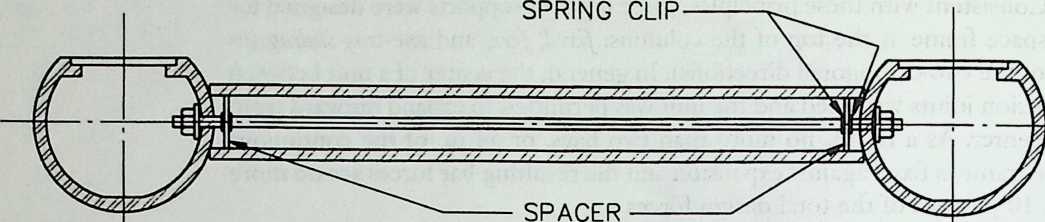
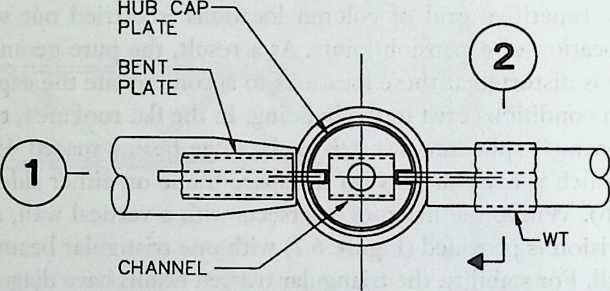
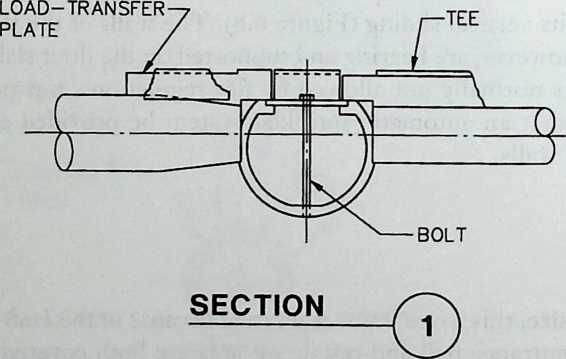
WASHER
Figure 6.9 Typical member-hub connection detail.
PLAN
SECTION
Figure 6.10 Top chord roof deck support.
forces, and rods, all tensile forces. The rods, which run from node to node, provide a level of prestress to the system, which varies depending on the rod size (Figure 6.9). The diameter of the rods varies from 13 to 83 mm and they are made of high-strength steel with an ultimate strength of 1,035 MPa and a yield strength of 863 MPa. A total of 75,000 rods are used in the project.
Tubes, which vary in diameter from 75 to 215 mm, are 365-MPa-yield- strength material. The actual tube strength varies by ± 13 percent, depending on the tube diameter. Larger tubes are swaged (tapered down at the ends) to avoid interference with adjacent tubes at nodes. Where tubes are required to support transverse loads, such as at the top chord of the roof, they are reinforced with a tee or channel. This reinforcing extends onto the node to provide a positive load transfer device (Figure 6.10). For light lateral loads, a bearing washer between the tube and the rod placed within 20 mm of the end of the tube provides the load transfer mechanism. Tubes are cut square at the ends and therefore bear on the spherical node along a line. Local yielding is assumed to take place along this line bearing due to the Hertz contact pressure.
Hollow nodes used on this project have an outside diameter of 215 and 240 mm and vary in thickness from 19 to 38 mm. These nodes, with a strength of 863 MP a/1,03 5 MPa (yield/ultimate), were originally conceived as cast steel. In order to provide the required 19,000 nodes in time, it was necessary to seek more than one supplier. A Japanese manufacturer (who eventually supplied one-third of the total required) was found who was able to forge the nodes rather than casting them.
ANALYSIS
The analysis of the structure was performed using the NASTRAN program, modeling the space frame as a truss system. Each region defined by expansion joints or free edges was analyzed separately.
The largest region, with over 20,000 bars and 5,100 nodes, is the central hall area. It is also the most complex with both vertical and horizontal surfaces as well as columns made up of space frame elements. The second-largest region, a portion of the exhibit hall roof, has almost 15,000 bars, and the smallest region is a single bay with 1,500 bars (on average, there are four bars per node). Each region was analyzed for five loads, dead loads, wind and temperature effects as well as snow loads in a checkerboard pattern. Various combinations of these loads were considered and the most critical combination was determined for each member in the roof. An iterative approach was used to size members with corrections introduced in each subsequent run. A maximum of three iterations was used to produce a final list of members.
In addition to the design analysis, a progressive collapse analysis was performed to determine the sensitivity of the structure to local failure. As a starting point for this analysis, it was assumed that a critical member failed for whatever reason. For this purpose a critical member was defined as the bottom chord of the diamond beam at the center of the span, or a diagonal just above the support column. Nonlinear member properties were defined for the bars: Tension bars were modeled as elastoplastic members; compression bars were modeled as nonlinear elastic bars approximating the buckling behavior obtained from actual tests of a range of tube diameters (Figure 6.11). An additional criterion was imposed stating that if a node became unstable due to failure of all but two bars connected to the node, the load applied at that point was removed. From a physical viewpoint, this implies that the load falls to the ground if the node fails. A stepwise solution of the problem using the MARC program was performed with four load increments. In order to obtain preliminary indications of the extent of a potential collapse, static runs were performed with critical bars removed at various locations. The inherent strength of the continuous indeterminate space frame is apparent from these preliminary analyses. Removing members anywhere within the fabric of the structure was shown to be not critical and redistribution of forces easily accommodated the loss of the member. Only on the perimeter bays was any significant collapse shown to occur due to removal of a critical member. Even here, the extent of the potential collapse was shown to be limited to the affected bay.
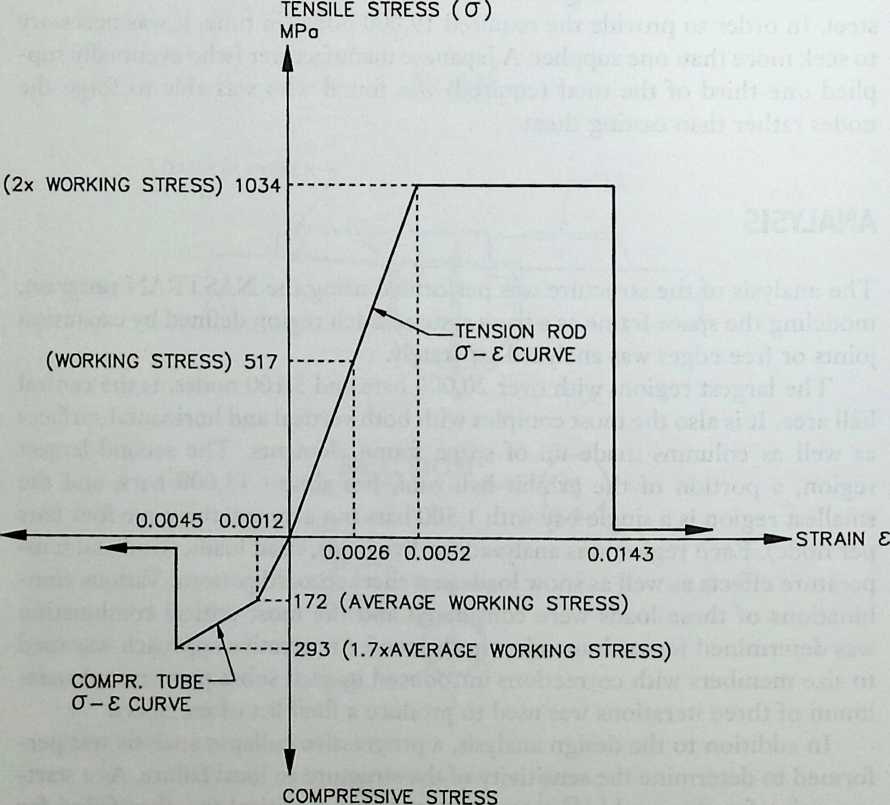
MPa
Figure 6.11 Stress-strain diagram for tension rod and compression tube.
FABRICATION AND CONSTRUCTION
For ease of fabrication, the roof was assumed to be built without any camber. As a result, the natural deflection of the roof under load results in a low point at the center of a bay. For redundancy against possible ponding, two drains were provided in the vicinity of this point. In addition, a minimum deflection was specified to assume adequate slope for drainage of the roof. The bays covered by skylights, on the other hand, drain to channels that were incorporated into the skylight construction along a square 3 m from the edge of the roof. In this case, the skylight channel is posted up from the space frame and sloped to these drains. This imposed a stiffness requirement on the space frame as maximum deflections were specified.
On the facade and at entrances, the design of the space frame is controlled by stiffness rather than strength requirements. The limitation on the deformation of glass panels and entrance doors, both of which are attached to the space frame, limits the permissible deflection of the space frame. This requirement resulted in oversizing members and, in the case of the concourse facade, in adding a stiffened edge to the space frame wall. Two criteria were the determinants for this condition: First, the racking of a 3-m square facade panel is limited to 6 mm and, second, the out-of-plane twist is limited to 6 mm.
The sculptural columns supporting the space frame were required to conform to a building code ordinance that the columns be fireproofed to a point 7.5 m above the floor. This requirement was met by filling the four steel shafts with reinforced concrete. Under symmetrical loads, the pyramidal capital acts essentially like a truss with tension in the horizontal tie members and compression in the diagonals. Under nonsymmetrical loads, significant bending is introduced in the diagonals, which tend to act as cantilevered branches from the vertical trunk of the column. The details at the four comers of the capital were developed without external gussets to provide an elegant solution. The 400-mm-diameter space frame base plate is supported by a 250-mm vertical pipe, which is, in turn, welded to an inclined 38-mm-thick plate welded to the diagonal arms of the capital. The horizontal tubes are then welded to each other and the 250-mm vertical pipe at the mitered comer. After welding, a reinforced epoxy filler was used at the mitered comer to form a clean curved fine after welding, a solution that proved to be more economical than filling with weld metal and grinding (Figure 6.3). The comers themselves were originally conceived as three-dimensional cast-steel elements, but because the same visual and structural result could be obtained by a weldment at substantially lower cost, the welded solution described here was chosen.
The four 400-mm-diameter columns below the capital are filled with 40- MPa concrete as are the midlength cross braces. This concrete was pumped in from the bottom prior to the attachment of the capital. At the base of the columns, both the shell and the reinforcing bars are welded to the base plate, achieving the required tensile resistance against overturning moments.
Stringent vertical and horizontal tolerances had to be maintained in the assembly and fabrication of the capital. The four bearing points have a center-to-center tolerance of 2 mm in 3 m and were required to be in plane within 3 mm. In order to meet these tolerances, a sequence of welding and assembly was developed to minimize thermal distortion due to welding and a jig was used for both the subassemblies and the final assembly. Welding procedures required both preheat for all heavy plates and tubes and the use of E70XX electrodes. In the final assembly, a boxed cover enclosed the crossed plates below the capital to match the dimensions of the cross-stiffeners of the vertical shafts of the column. Apart from this concession to visual architectural requirements, the structure of the column assembly is totally exposed, protected by a thin film of epoxy paint.
CONSTRUCTION
Stringent tolerances were maintained throughout the fabrication and erection of this structure. These tolerances started with the column location, which was controlled to within 8 mm in the two orthogonal directions. For the space frame itself, individual tubes are within 1 mm of specified length and the overall assembly is within 8 mm per 27-m bay. These strict tolerances were required to ensure proper fit of the elements without forcing and inducing built-in stresses into the assembly. In order to obtain these tolerances, extraordinary controls were established for the fabrication and assembly process. Jigs were used to check each tube length and subassemblies were prepared in highly accurate frames.
The erection process was devised taking into account the required final tolerances. The flat roof of the exhibit hall was divided into subassemblies, each of which was transportable. A typical bay consisted of four beam elements, two of which sat on the columns, and a central 18-m square divided into three 6X18-m strips. These three strips were joined together by stitching on the ground prior to lifting (Figure 6.12).
Erection started with the four beam elements. When these were stitched together to form a ring, the center section was lifted in one piece and temporarily suspended from four corners at an elevation slightly below that of the adjacent beams while the stitching process took place. Stitching members were first loosely installed. Torquing of nuts at the end of the rods pulled the central section into alignment with the previously placed beams.
Erection of the cubes over the central hall presented a further complication. Each cube, except the one at the center, is supported by four walls, one of which belongs to the cube at the next-higher level. This required a sequence whereby the supporting walls had to be erected first before placing the central sections, which, in turn, entailed temporary cable bracing particularly for the four space frame columns in the central hall.
The schedule for erection required completion of a minimum of two bays per week. As there are a total of 71 bays, a total erection time of nine months was anticipated and met!
Figure 6.12 Layout of subassembly units.
Stringent controls were established for every step of the fabrication and erection process. The cast-steel nodes were subject to visual, magnetic particle, and radiographic inspection. Flaws in the castings such as cracks or voids, which were not repairable by welding, were cause for rejection. Particular attention was focused around the open mouth of the casting where high stresses were shown to exist by analysis. The high-strength rods with upset rolled threads were inspected for defects. Rolled threads were called for, instead of cut threads, to avoid notch sensitivity. The material for the rods has
a high Charpy notch toughness, which alleviates sensitivity to stress corrosion, a concern for the extended life span of the structure.
COMPONENT TESTS
A series of load tests of the elastic and inelastic behavior of the rods and tubes were conducted to confirm properties used in the space frame analysis. The resulting force-deformation relationships for both rods in tension and tubes in compression (including postbuckling behavior) were used to define the material properties in the progressive collapse analysis described previously. Verification of the design was provided by a full-scale load test of a 14-bay region of the roof. In order to further probe the safety of the structure, the response of the structure to a series of improbable events was explored, culminating in a progressive collapse analysis.
RISK MODELS
Five events that might cause failure of a space frame component were identified:
-
Defective Member: Critical defects in a member are likely to be detected during construction. The probability of failing to detect a defective member should be very low. The probability of a small 13- mm-diameter tension rod having a significant defect is greater than that of a large 83-mm rod, because the smaller tension rods are more susceptible to discontinuities and notches introduced during the manufacturing and fabricating process and possibly because of less stringent inspection during erection. In addition, the majority of the large tension members greater than 36 mm in diameter were proof-tested before installation. The probability of a significant defect in a tube is also low, because compression members are less sensitive to loss of strength due to defects.
-
Abnormal Loading: Loading exceeding the design load is considered abnormal. A 1.9 kN/m2 overload above the design five load over at least one bay, owing to an accumulation of slushy snow, for example, would be a very rare occurrence. Even application of the full design five load of 1.9 kN/m2 , with no overload, over at least one bay would be an uncommon occurrence, happening perhaps only a few times during the lifetime of the roof.
-
Human-Induced Accident: The probability of failure as a result of an event such as a crane hitting a critical member or uncontrolled welding on a sensitive, highly stressed member is very low. Fire was not included in this analysis.
-
Catastrophic Event: Events such as an airplane or a large wind-driven missile crashing into the structure are also extremely rare. Even with the high level of air traffic in the area, the annual probability of such a catastrophic event is on the order of 1 in 1,000,000.
5. Unknown Deterioration: Corrosion inside tubular members, or inside joints, could be missed by normal maintenance procedures. This deterioration is possible, although very unlikely, in an inside environment over a normal service life.
Approximate probability values were assigned to each of the five initiating events for three different types of members (13-mm-diameter tension rods, 76-mm-diameter tubes, and 83-mm-diameter tension rods). These values are summarized in Table 6.1, where
P(A) is the annual probability that an initiating event
will occur;
P(M/A) is the probability of a critical member failing and
becoming unavailable for loading given that the initiating event has occurred; and
P(M)=P(A) X P(M/A) is the overall probability of member failure.
It should be pointed out that the estimates of probabilities in Table 6.1 are subjective; the available data are limited and the probabilities should be considered in terms of their orders of magnitude rather than exact numerical values. Even with these limitations, the analysis shows that the risk of failure is several times greater for the 13-mm-diameter tension rod than for the tube or larger rod. It is recognized that the risk of failure during a catastrophic event is the same for all members. However, the analysis suggests that the probability of failure for all of the other events may be 10 times higher in the small 13-mm tension rods (approximately 2 X 10-6) than in the compression tubes (approximately 2 X 107) or 50 times higher than in the large rods (approximately 10*). More importantly, the analysis also indicates that, in absolute terms, the annual probability of failure is low even for the small rods: on the order of 1 in 500,000.
TABLE 6.1 Annual Probabilities of Critical Members Becoming Unavailable for Loading Given the Occurrence of an Initiating Event and Probabilities of Initiating Events
| P(M/A) | P(A) | m | P(M/A) | P(A) |
|
P(M/A) | P(A) | P(M) | |
| 1. Defective member | * | * | * | * | * | * | * | * | * |
| 2. Abnormal loading | * | 6 | * | ” | * | * | * | * | * |
| 3. Human-induced accident | * | * | 2 | * | * | * | * | * | |
| 4. Catastrophic event | * | * | * | * | * | * | |||
| 5. Unknown deterioration | ” | * | * | ” | * | * | * | * | * |
| Summation YP(M/A) P(A) | = | 3x10* | * | * |
ULTIMATE LOAD CAPACITY
Based on the results of the risk analysis, four cases were explored to determine the ultimate capacity of the roof structure. The region of the roof that was analyzed consisted of the 14 bays on the north end, with a uniform live load of 1.9 kN/m2, in addition to the dead load applied over the entire roof. The corner bay (Figure 6.13) was then loaded until a large number of members had failed as defined by fracture of tension members and postbuckling of compression members. The four cases that were studied and the results are as follows:
Ultimate Load Capacity
as a Multiple of Design
Case Condition Live Load (1.9 kN/m2)
-
Roof as built 3
-
Smallest tension member: 3
13-mm rod removed from
bottom chord of diamond truss
- Small compression member: 3
76-mm tube removed from
bottom chord of diamond truss
- Largest tension member: 0.75
83-mm rod removed from
bottom chord of diamond truss
The analysis on which these results are based considered nonlinear member properties and assumed a 3 percent sliding friction coefficient at the Teflon support bearings. Intermediate cases were also studied with results similar to those shown previously.
COLLAPSE ANALYSIS
A nonlinear model of the structure includes separate force-deformation relationships for tubes and rods. For tubes, the postbuckling behavior is modeled based on earlier tests. For tension rods, yielding and fracture are similarly based on tests with the tensile area at the thread used to define member strength. Because of different steel quality, the ductility of rods below 18 mm in diameter was less than that of large bars (Figures 6.14 to 6.16).
Using a nonlinear version of the SAP IV program run on a CDC 7600 mainframe, loads were applied incrementally to the roof, making multiple runs to obtain convergence of the solution. Initial load increments were large (0.9 kN/m2) and were decreased to 0.2 kN/m2 as the capacity of the structure was approached. Loading was continued until a load level was reached for which no stable solution was achieved. The following table summarizes the results obtained for the five cases studied:
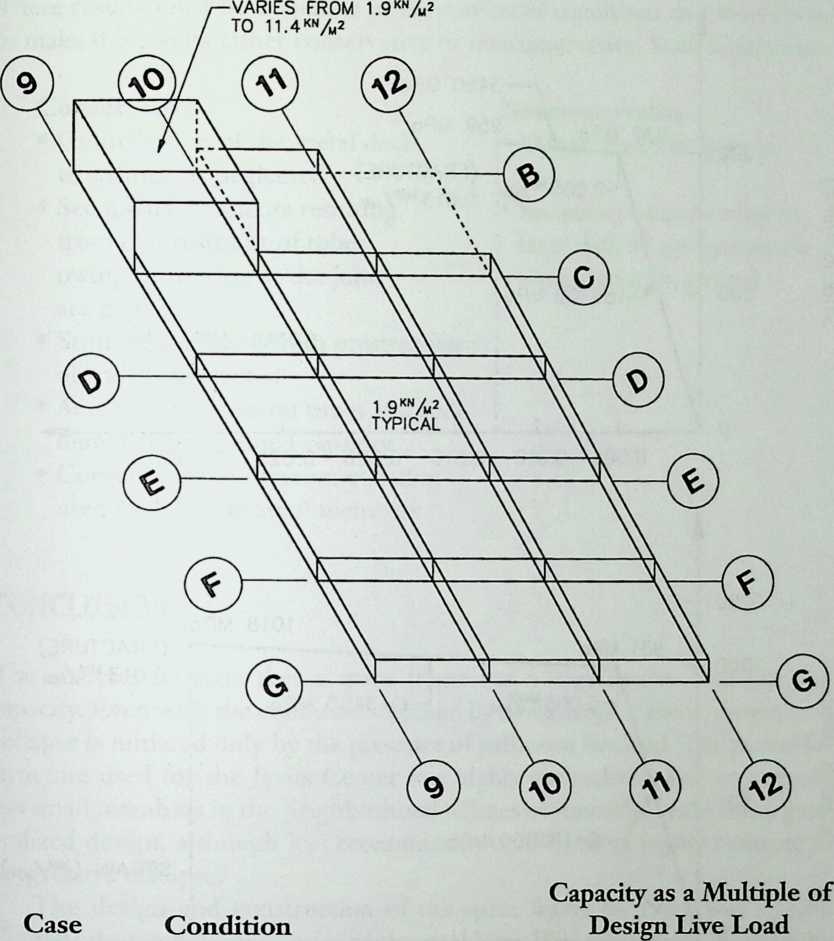
Figure 6.13 Loading condition for ultimate load capacity.
- As builtuniform dead load plus 3+
0.9 kN/m2 over entire roof. Loaded
in the southwest corner incrementally.
- 13-mm tension rod removed from 3+
bottom chord of diamond truss. Same loading as case 1.
- As builtincrementally applied load over 3.5+
entire roof.
- 8 3-mm tension rod removed from 0.25+
bottom chord of diamond truss.
Incrementally applied load over entire roof.
- Catastrophic event: diamond truss and 0.10+ portion of adjacent space frame removed. Incrementally applied load over
remaining roof.
cn tn Ld or
tn
Figure 6.14 Force-deformation relationship for 13-and 16-mm tension rods.
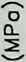
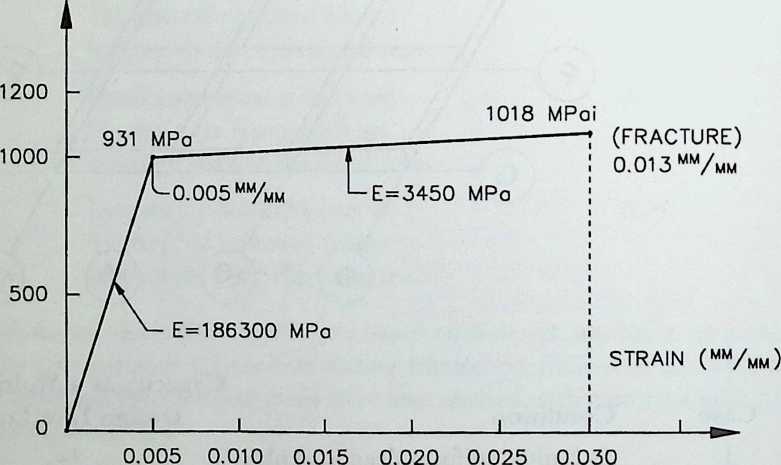
tn tn Ld (Z i
tn
Figure 6.15 Force-deformation relationship for 18-mm and largertension rods.
Figure 6.16 Force-deformation relationship for typical compression tube.
1.0
3.0
8.4
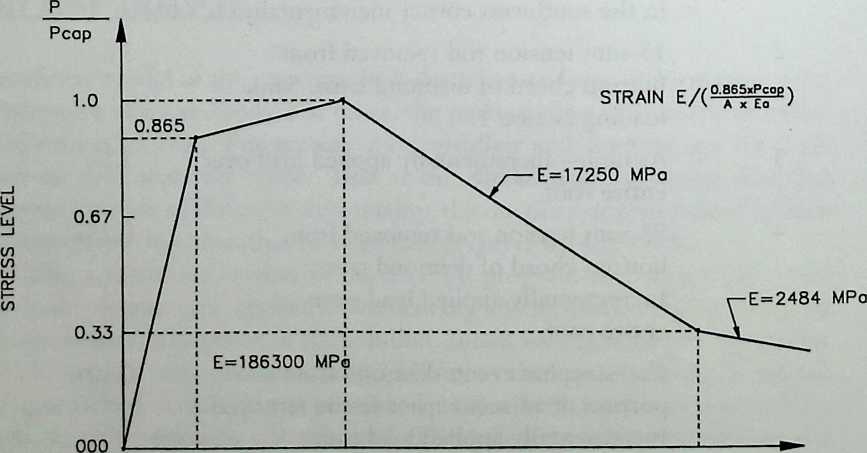
These results must be evaluated in the context of conditions that would tend to make the results either conservative or nonconservative. Such factors are:
Conservative
Nonconservative
-
Dynamic effects ignored
-
Secondary effects owing to large deflections (geometric nonlinearity) neglected
-
Contribution of the metal deck to stiffness is neglected
-
Secondary moments resulting from end restraint of tubes owing to friction at the joint are neglected
-
Stiffness resulting from prestressing of rods is neglected
-
Actual test results on tubes and rods higher than assumed capacity
-
Conservative interaction equation used to define flexural members
¶ CONCLUSION
The analyses indicate that a space frame has a large reserve load-carrying capacity. Even with the condition imposed by a catastrophic event, progressive collapse is initiated only by the presence of sufficient live load. The particular structure used for the Javits Center was highly optimalized, and, as a result, has small members in the neighborhood of lines of contraflexure. A more generalized design, although less economical, would be more highly resistant to progressive collapse.
The design and construction of the space frame for New York’s Javits Center presented unique and complex problems. The solutions to these problems demonstrate the adaptability of the space frame concept to specialized applications. Starting with a defined geometric configuration, modifications to a standard-component prefabricated system are shown to be readily made. The flexibility of the system extends to the originality of the construction solution. Although few structures of such a large scope may be built, lightweight, steel, space frame construction should find application to more modest enclosure problems and should be an integral part of the design repertoire of architects and engineers.
¶ BIBLIOGRAPHY
Levy, M.: “New York Convention Center Space Frame,” IASS Symposium, Dortmund, 1984.
Levy, M., and C. Chow: “Load Test Verification of Space Frame Roof Design, Space Structure,” International Journal of Space Structures, Vol. 3, No. 1, 1988.
Wiss, Janney, and Elstner: “Results of Analysis II for J.K. Javits Convention Center Space Frame.”
¶ Double Curvature Space Frames Supported on Four Points: Design and Construction of the International Plaza of Portopia ‘81
Masao Saitoh
¶ INTRODUCTION
Port Island, which is off the coast of Kobe, is the first large-scale man-made marine city in the world. It has an area of 436 ha in which a hundred baseball stadiums could entirely be laid out. Fifteen years after the reclamation work began, major urban facilities such as hotels, hospitals, residences, and parks, as well as a fully automated mass-transit system, were completed in 1981.
The exhibition, called PORTOPIA’81, to commemorate the completion of Port Island was held during a 180-day period beginning March 20, 1981, in an area of about 65 ha in the south of Port Island (Figures 7.1 and 7.2). The
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
□ 211
Figure 7.1 Aerial view of P0RT0PIA.
main theme of the exhibition was “Creation of a New Marine City of High Culture” with the aim of presenting an ideal future-oriented marine city as well as promoting international friendship and peace. The International Plaza was plarmed as the main facility for the exhibition.
The International Plaza is an open space for events in which an octagonal space shelter covers the spectators’ seats. In this plaza such international events as dances, choral concerts, and dramatic presentations were held every day during the entire period of the exhibition. Sixteen hundred spectators’
Figure 7.2 Aerial view of International Plaza.
Figure 7.3 Interior view of space frame.
seats and a stage with a width of 18 m and a depth of 8 m were installed around an open space with an area of 700 m[1] [2]. The plaza had a seating capacity of 2,600 with the addition of movable seats from the adjacent vacant lot.
The shelter that covered the International Plaza was in the shape of four triangular eaves connected to a central elliptical paraboloid shell, giving the appearance of open flower petals. The plan of the shelter was a square with sides of about 51m and was supported by hinges at the center of each side.
The spectators’ seats and the stage were designed to be enclosed under one roof. At the same time, the external shape was designed so that many people would be interested in entering the plaza. The shape chosen for the International Plaza was arrived at after a survey of shapes having either a static and closed image of an internal space or a dynamic and expansive image of an external atmosphere (see Figure 7.3). Both the shelter and the International Plaza were removed after the end of the exhibition.
OUTLINE OF THE STRUCTURE
In order to realize a column-free large-scale roof with an area of about 2,600 m2, which possesses the shape of such a unique doubly covered surface, a double-layer space truss structure composed of a system truss was employed (Figure 7.4). This structure was chosen for the following four reasons:
-
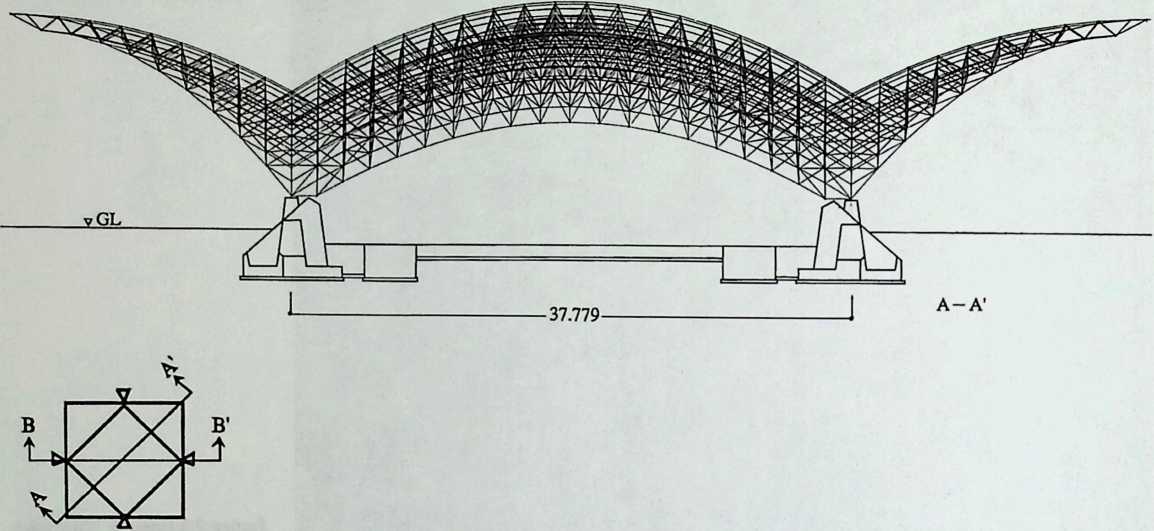
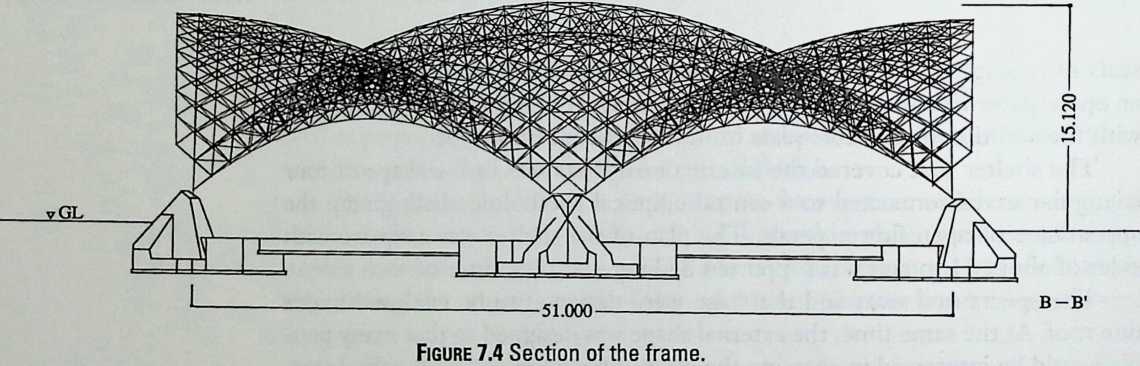
Manufacturing accuracy of members is high owing to the fact that they are made in a factory with a dimensionally controlled production system.
-
A short construction period is possible.
The roof truss consists of upper and lower layers with a two-way square grid of about 2 m and a depth between layers that varies from 1 to 2 m. The TM (Taiyo-Mero) system adopted for this roof has 5,600 steel tubes for the chords and web members and 1,560 steel nodes for its joints. The self-weight of the roof truss is about 85 tons corresponding to 33 kg/m2 and the long-term design load is estimated at 50 kg/m2, including the weight of the roof fabric.
In general, the structural design followed the flow diagram shown in Figure 7.5. It is important to note that there are two phases, a preliminary design to decide the structural system and a final design to examine the structural behavior.
Architectural
Requirement
-
image & function •scale
-
boundary
t
( Structural Form )<■
4
Internal Structure -. system of internal str.
- strength and stiffness
of subassemblies
- arrangement
/ unit, pattern \
\ depth, frequency /
4
( Structural System )
Form Finding
Method
. geometrical
. mathematical
. experimental
-Connection -
-
joint mechanism
-
statical property
-
eccentricity
Analytical Method
-
theoretical
-
numerical
-
experimental
Structural
Analysis ~
-
stress analysis
-
stability analysis
. limit analysis
- dynamic analysis
Additional Load
dead & live
snow wind earthquake temperature erection
support movement
( Structural Behavior )
”
-
internal str.
-
joint str.
-
boundary str.
Design of
Structural Element
Figure 7.5 Structural design flow of space frame.
STRUCTURAL PLANNING
During the design of the space frame, attention was paid to three basic factors:
-
Form
-
Arrangement
-
Connections “Form” is the shape of the overall space frame, “arrangement” in the internal structure means the arrangement of the individual members consisting of several elements, and “connections” refers to the joint system of the space frame. When the support conditions and the perimeter conditions of the space frame are predetermined, its structural properties are determined by the factors mentioned previously. In this chapter we shall discuss form and arrangement.
Finding the Form
Finding the form of the roof surface is the starting point in the preliminary design of a shell structure. It is also the approach used in the design of a space frame and starts with a general forma surface curved in space which is then replaced with a similar structure composed of discrete elements.
Therefore, the technique for the form design of space frames is the same as the technique in the design of shell, tension, or pneumatic structures. Three methods of design can be distinguished: geometrical, mathematical, and experimental.
In this case, from the architectural point of view, the form was desired not only to provide the enclosed space for the audience but also to be attractive as monumental architecture. One can imagine a number of curved surfaces with four supporting points. Here, the author proposed three forms of shells, characterized by the curved edge line as shown in Figure 7.6.
Type A has four wing shells spread from a central dome, type B is obtained by the combination of four hyperbolic paraboloid surfaces, and type C is the continuous surface as a whole having both properties of types A and B. Types A and B are pure geometrical surfaces and type C is a free form that can be determined mathematically or by experimental methods such as by hanging a weighted net.
To compare the structural behavior of the proposed form of types A and B (Figures 7.7 and 7.8), stress and displacement analyses were carried out for the case of self-weight, which is dominant in large-span space frames. Using the finite-element method of numerical analysis, units are replaced with equivalent beam sections. Consequently, the effective stiffness in tension and
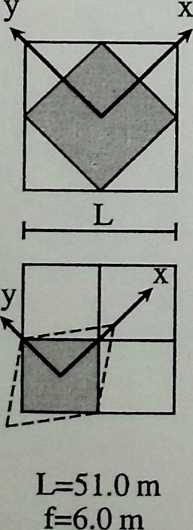
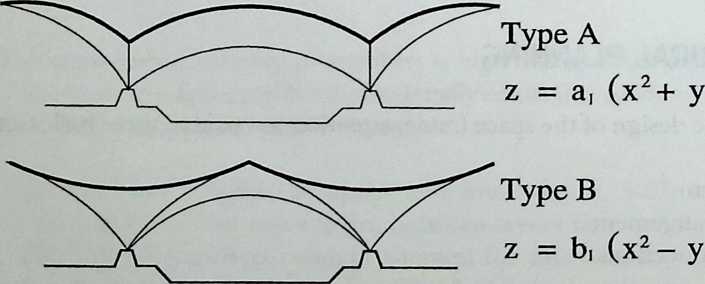
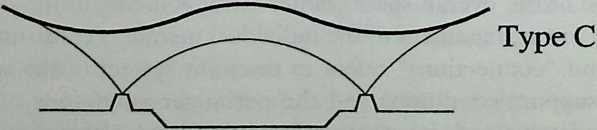
Figure 7.6 Proposed form of the roof.
Figure 7.7 Model of Type A.
bending and shearing of two kinds are measured in the unit and are put into the equivalent beam that makes up the grid surface of the shell roof.
Figure 7.9 shows the results of calculations using the equivalent-grid model. Both the deflection and the bending moments of type B shells are smaller than those of type A. On the other hand, the axial force along OC is larger in type B than in type A. From these results, type B behaves more like a membrane than type A.
After considering the architectural requirements, especially the creation of a theater-like space, type A (composed of transitional surfaces of an elliptical paraboloid) was adopted for the actual shell roof.
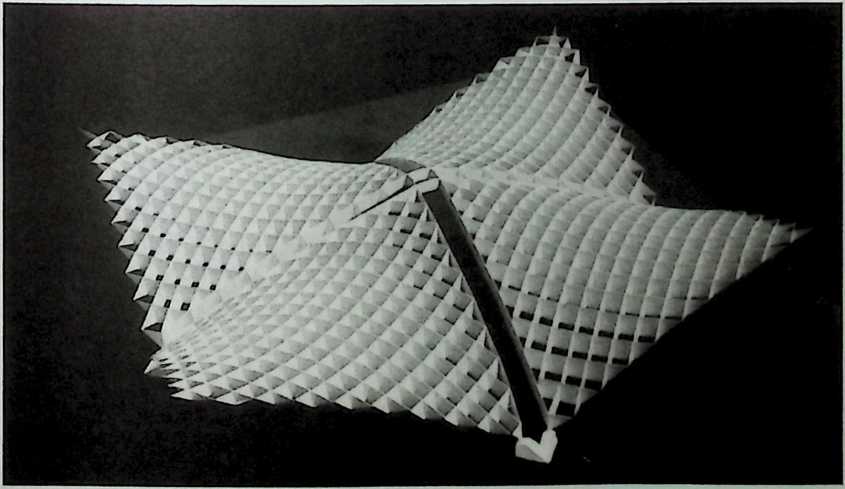
Figure 7.8 Model of Type B.
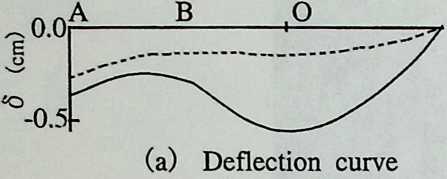
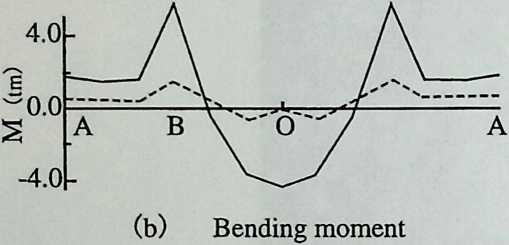
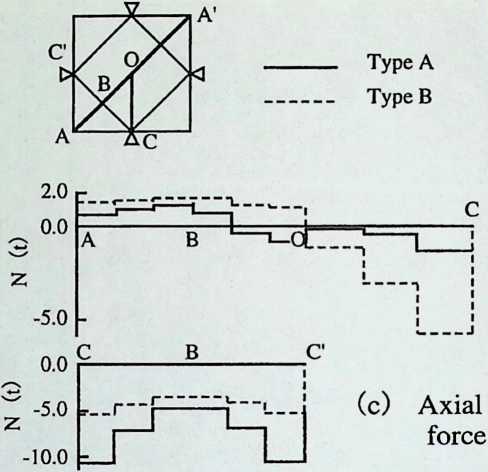Transition to the Curved Surface
Figure 7.9 Comparison of Types A and B.
In order to comprehend the structural effect obtained by the curvature in the type A shell, the models that demonstrate the stages of development, starting with a plate to arriving at a final structure, are presented in Figure 7.10.
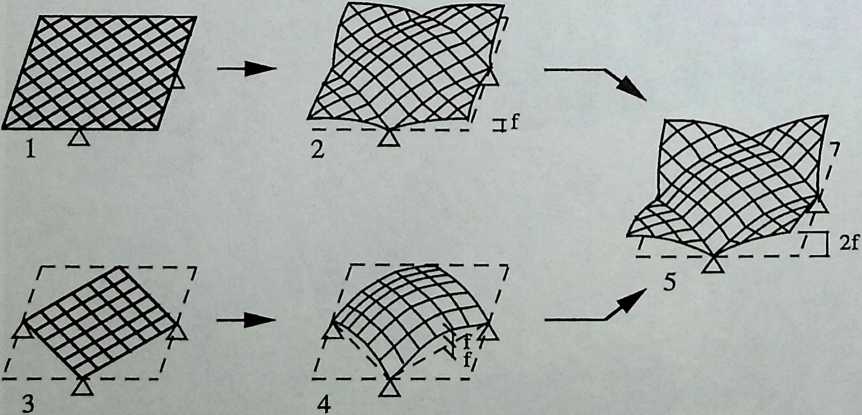Each stage of the models was subject to uniform loads (50 kg/m[3] [4]) and the structural behavior was calculated by the equivalent-grid method. The following
¶ CONCLUSION
s are drawn from the deflection and bending-moment distribution (Figure 7.11):
Figure 7.10 Five stages in the development of the shell.
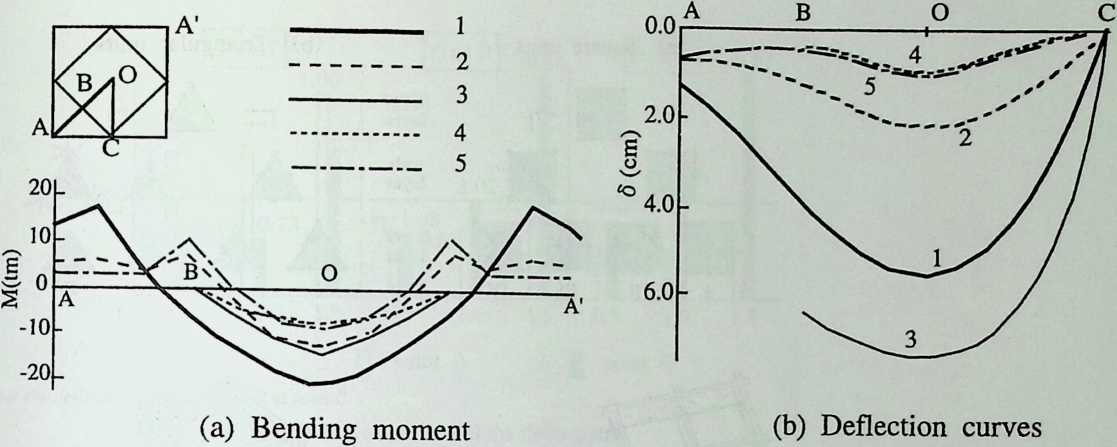
Figure 7.11 Transition of the structural behavior.
-
The apparent effects of the curvature in shell structures can be seen in the deflection of stages 2 and 4.
-
Because the change in deflection is only slighdy different between stages 4 and 5, the structural rationality of stage 5 to cover a larger area is evident.
Member Arrangement
The fundamental patterns of double-layer space frames can be obtained geometrically by various combinations or arrangements of the upper and lower layers and web elements, as shown in Figure 7.12. Unit HI, which is the most popular square unit type, the so-called offset grid, was adopted for this structure.
Because this unit has no twisting rigidity and is not internally stable, sufficient external supports have to be provided to compensate for the lack of internal stability. It should be noted that with internal stability (such as is provided by triangular grids) additional stresses during construction or due to differential settlements may be avoided.
Member arrangement and the constituent frequency (the scale ratio of the element dimension to the overall dimension) determine the stiffness and the load-carrying capacity of a space frame.
For the purpose of studying the influence of depth and frequency on structural behavior, a numerical analysis was carried out for the unit models as shown in Table 7.1. In this table the frequency ratio and the depth ratio for the basic unit used in the realized structure are presented as a (the ratio of unit frequency) and Ji (the ratio of unit depth) respectively. The numbers in parentheses represent the ratio of total volume of truss members used in the whole structure.
The analytical method used was the one mentioned earlier and only the effective rigidities are changed for the beams of the grids of the shell. Figure 7.13 shows the deflection at points A and 0 in nondimensional units with a=y?=1.0.
(a) Square units
(b) Triangular units
upper layer
web layer
lower layer
Unit
Unit n
Figure 7.12 Fundamental pattern of units.
Table 7.1 Analytical Models of Different Units.
| un o | Q V (2.00) |
■(0.85) | w (0.55) | |
o T-< |
T7 y (2.74) | V(1.00) | q p \ (0.60) ¥ |
|
| CQ. | v-~< | V7 V (3.53) |
Sms) | P 1 / \/(0.67) |
b
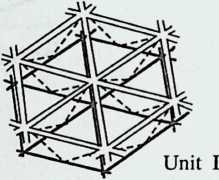
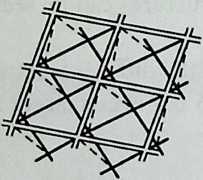
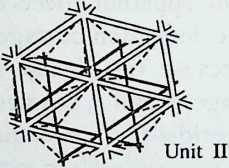
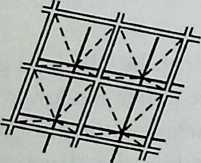
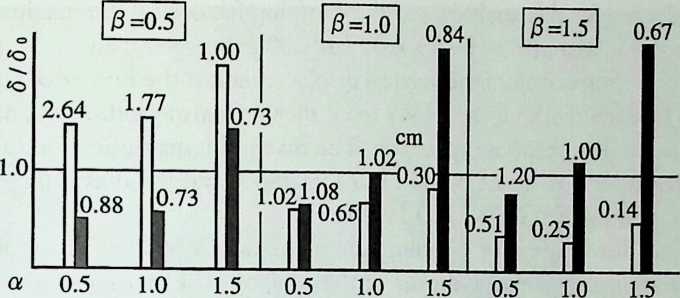
point A point O
So: the deflection of the basic unit at point 0
Figure 7.13 Comparison of the deflection.
In this figure two numbers are shown: the deflections for each case divided by the deflection of the basic unit at point 0 and the actual values of deflection.
As the depth ratio / becomes large, the deflection decreases considerably and the point of maximum deflection moves from point A to 0, corresponding to increasing bending rigidities.
The economical efficiency concerning the depth and frequency is difficult to estimate. Although the deflections have a tendency to decrease as a and Ji increase, care should be taken to ensure that the tolerable force due to buckling decreases simultaneously.
NUMERICAL ANALYSIS OF THE SPACE TRUSS SHELL
Static Analysis
The structure was analyzed as a grid framework in the preliminary design to select the form and member arrangement of the structural system. A final calculation was made using the displacement method, assuming a hinged connection at every intersection of the truss elements. Axial forces on truss members and the deflection of all points were numerically obtained under dead load (50 kg/m2), horizontal earthquake force (seismic coefficient = 0.3) and wind force (v = 35m/sec). Wind tunnel tests were performed on a 1/100 scale model to obtain the design loads.
Because the roof is fight and an open-air type, the wind force has considerable influence on its structural behavior. The maximum tensile axial force of truss members due to wind forces was 4.6 times as large as that due to dead loads.
Furthermore, for the case of temperature forces, the elongation of the tie beam and differential settlement of the supports were examined.
Dynamic Analysis of the Roof
The dynamic analysis for seismic forces was carried out using a model composed of 85 nodal points and 168 equivalent beams. A lumped mass system was adopted for this analysis, and the damping factor and the maximum acceleration were assumed to be h = 0.02 and 200 gal respectively .
For a comparison of the vertical displacement of the influence coefficients given by each method, the RMS (root mean square) method of analysis was used based on a response spectrum. The maximum magnification of acceleration response is 8.43 (EL CENTRO UD 1940) and the maximum deflection is 14.2 mm (MIYAGIOKI UD 1978).
The distribution of bending moments was obtained from the above response displacement by means of the replacement method with equivalent beam. It is important to emphasize that the axial forces in this case are very large. That is, the maximum force of 15.6 ton corresponds to a magnification of 10.9 of the one due to horizontal earthquake forces (seismic coefficient = 0.3) and 0.96 of the one due to wind forces (q= 148 kg/m2; return period = 30 years).
STRUCTURAL DESIGN
The member size of the steel tubes used in the roof are of eight kinds, 114.34> X6.0 to 48.6<J>X3.2, with slenderness ratios of about 50, 80, and 60 for upper chords, lower chords, and diagonal members, respectively. The ball joints used for the intersections have five different diameters ranging from 150c> to 85< j>.
The roof has eight supporting pin joints at the lower chords sitting on the four reinforced concrete supports. To resist the rotation due to the horizontal thrust of wind or earthquake, these supporting columns are fixed to a complex foundation and are also connected to each other by an underground tie beam (Figures 7.14 and 7.15).
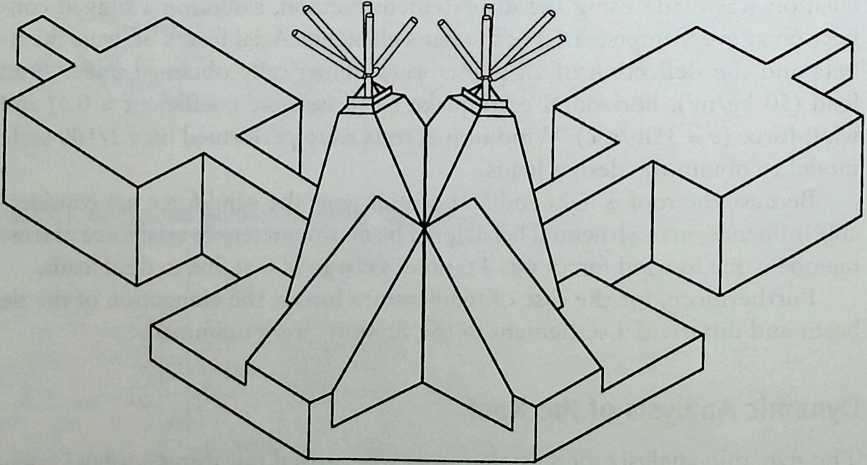
Figure 7.14 Supporting point.
Figure 7.15 View of supporting point.
The catwalks for maintenance were provided in the space frame by utilizing the space within the roof depth. From the viewpoint of statics, the depth of the wing shell changes from 2 to 1 m. Therefore, the upper and lower surfaces of the roof are defined by two kinds of elliptical paraboloid.
The lower surface of the whole roof and the upper surface of the central shell are given by Zo and the upper surface of the wing shell is given by 7,\ as follows:
Zo = -(x2 + y2) + 2f
iy
u f2
Z1=(f1 + f“+h1)--(x2 + y2)-z lyz
A-J lx2ly2
Using the geometrical nature of transitional surfaces, all chords of the lower surface and the upper chords of the central shell have the same length, equally dividing the parabola (Figure 7.16).
CONSTRUCTION
The assemblage and the erection of the roof truss were completed on the ground. After the central shell was set on supporting columns, four wing shells were attached to it one by one (Figures 7.17 and 7.18). It took about 30 days to construct the truss shell, including checking the torque in the joints.
Although the TM (Taiyo-Mero) system, in which a tolerable error in member length is 1 mm, has no error-absorbing capacity, the construction was achieved without scaffolding or adjusting of the support position. The reason
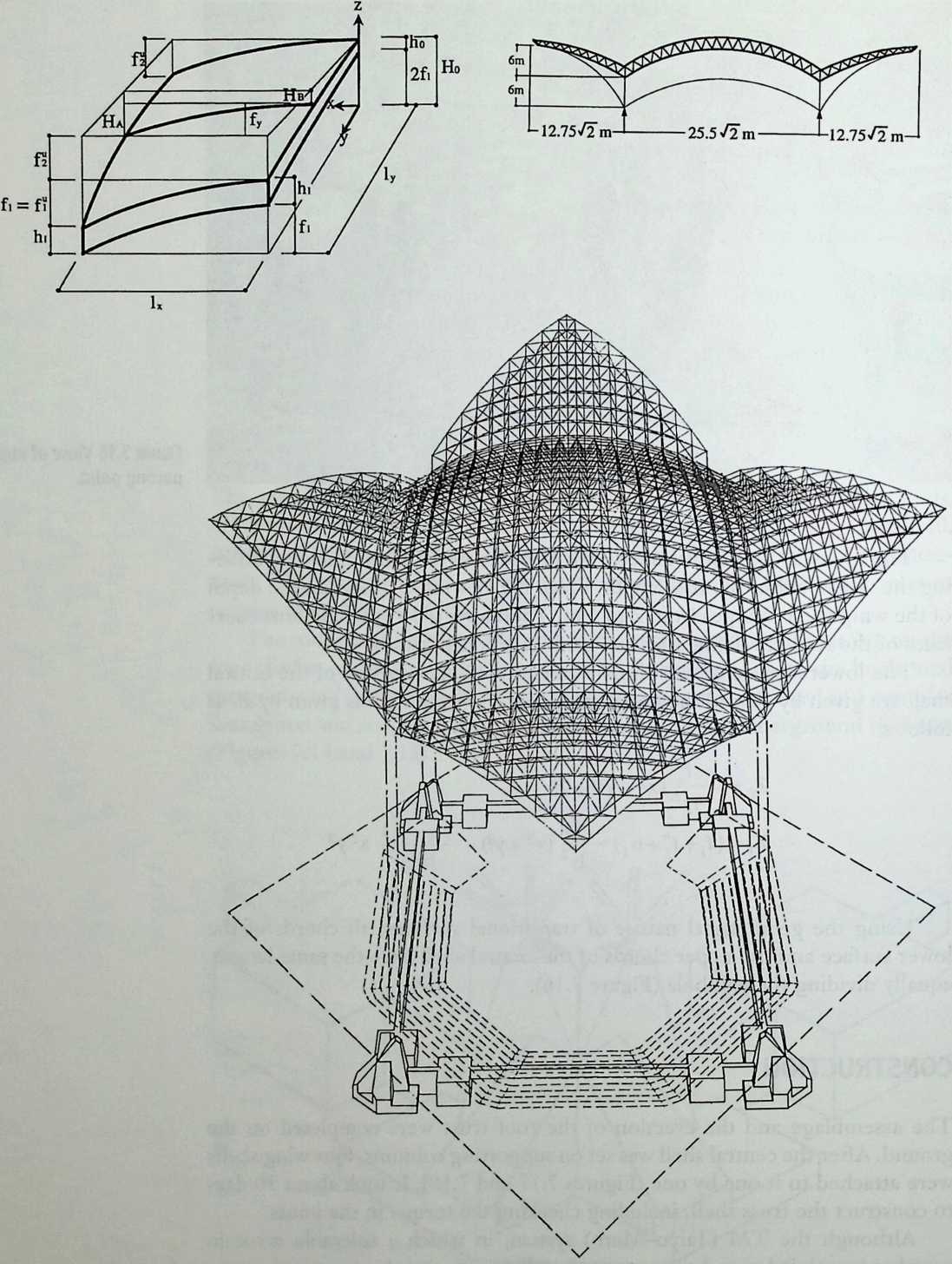
Figure 7.16 Surface of the shell.
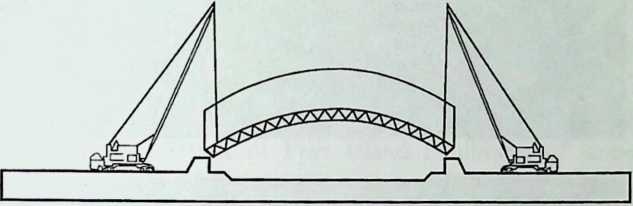
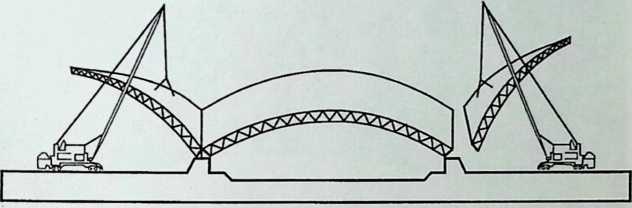
Figure 7.17 Process of the construction.
for adopting this construction method was because this structure is not too large and the unit of space frame used has no twisting rigidity. In the construction of a large-span space frame, particular attention must be paid to member deformation due to temperature change and self-weight.
¶ CONCLUSION
At present, many double-layer space truss structures of the type described in this chapter are being constructed. However, we often forget that this type of structure has low applicability to shapes formed by such permanent finishing materials as glass and membranes, although it can be freely formed as a structure. As for the roof finish, a membrane material was adopted and attached to each upper joint of the space frame. Sometimes the existence of secondary members to support finishing roof material seems to prevent the rationalization of a space frame in which all members are attached with pin joints.
We live in an age when “any kind of shape can be formed” because of the remarkable development in computer and analytical technologies. It is now true that the degree of freedom for conceiving any design and shape seems to have become unlimited.
Figure 7.18 View of space frame during construction.
Consequently, a firm concept concerning the “integration of structure and design” must be established. As this chapter shows, a sound and attractive structure with a double-layer space truss can be developed based on this concept.
ACKNOWLEDGMENTS
The author wishes to express his sincere gratitude to the late Dr. Yoshikatsu Tsuboi and other colleagues who recommended this manuscript to the IASS, and for their fruitful discussions. This paper was completed in collaboration with Mr. Akira Okada, a research assistant at Nihon University. The author also wishes to thank the following organizations for allowing publication of this manuscript: Association of Port Island Exhibition of Kobe; Nikken Sekkei, Ltd., planners, architects, and engineers; Kajima Corporation, general contractor; Taiyo Co., Ltd., space frame contractor; Saitoh Laboratory, Nihon University, and TIS & Partners, engineering consultants; Kawamura Laboratory, Osaka City University, wind tunnel testing; and Tajimi Laboratory, Nihon University, vibration testing.
¶ Deconstruction of the Cube
Arthur L. Loeb
¶ INTRODUCTION
The arbitrary assumption that a cube having unit edge length has unit volume has given the cube an undeserved fundamental significance. This notion is a superstition in the sense that it has been handed down for many generations without ever having been subjected to experimental verification: It is, in point of fact, an assumption that cannot be experimentally proven or disproven. The cube is a space filler but, then, so are other forms such as the rhombic dodecahedron and the truncated cube, each of which is more fundamental to an understanding of crystal structure than is the cube.1 Although it is true that the edges of a cube define a forward-backward/up-down/left-right system of reference in which we move, Rudolf von Laban in his time-motion and dance notation actually preferred the icosahedron to the cube as a frame of reference. Unfortunately, he found that dancers are culturally conditioned to the cube as a reference frame, whereas von Laban’s choreography stressed diagonal motions.2
The cube has six square faces, twelve edges, and eight vertices. It is unstable, that is to say, when eight flexible joints at the vertices of a cube are joined by twelve struts along that cube’s edges, this structure will collapse, because it has six degrees of freedom.3,4 It will be stabilized by joining the vertices by six additional struts. There are many ways of accomplishing such stabilization,
Figure 8.1 Tetrahedron inside a cube.
one being the creation of a tetrahedron inscribed inside the cube in such a manner that the six edges of the tetrahedron constitute the face diagonals of the cube (Figure 8.1). The inscribed tetrahedron occupies exactly one-third of the volume of the cube.5
¶ THE REGULAR TETRAHEDRON AND OCTAHEDRON
A regular tetrahedron may thus be considered as a truncation of the cube: Four comers of the cube are completely removed. These four corners may be juxtaposed to form a square pyramid whose four lateral faces are equilateral triangles (Figure 8.2). This pyramid constitutes one-half of a regular octahedron: Its volume equals exactly two-thirds of that of the original cube. Accordingly, this regular octahedron has a volume exactly four-thirds of that of the cube. We may therefore conclude that the volume of a regular octahedron equals exactly four times that of a regular tetrahedron having the same edge length. The portions truncated from the cube to produce a regular tetrahedron are called octants of an octahedron: Eight of them constitute a regular octahedron. The regular tetrahedron is the polyhedron with the smallest number of vertices and the only one in three-dimensional space in which all vertices are equidistant from each other. It is also the most resistant to compression.
The cube does not occur much in nature,6 nor does the right angle occur in the art and architecture of peoples much in touch with nature. It is, however, a convenient reference solid; as we have just noted, it may be deconstructed into an inscribed tetrahedron and half of a regular octahedon. I shall
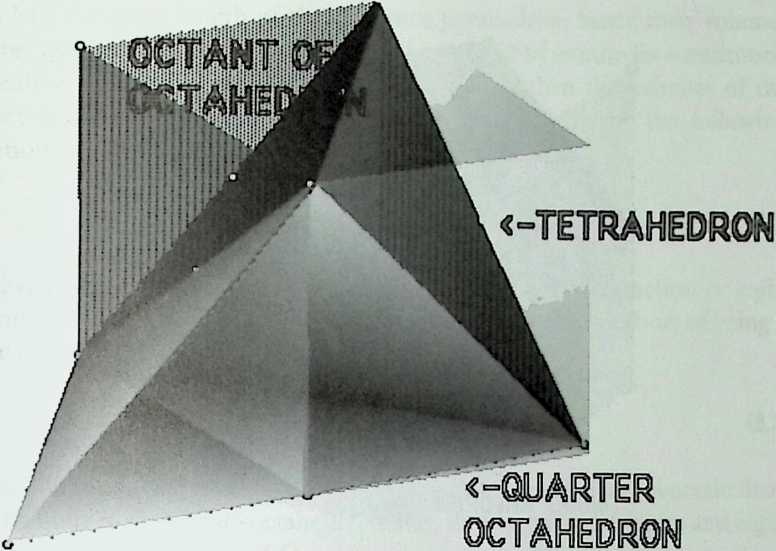
Figure 8.2 Cube deconstructed into a tetrahedron and half an octahedron.
call this tetrahedron the reference tetrahedron and assign it a unit volume; then the cube circumscribed around it (the reference cube} has volume 3, and the octahedron having the same edge length as the tetrahedron (the reference octahedron) has volume 4. (For a discussion of units of volume, see Chapter 4.) The cube is a space filler; that is, it and its clones may fill all of a space without gaps or overlaps. Therefore, its components, the regular tetrahedron and half-octahedron, which individually are not space fillers, may together fill a space in the ratio of one tetrahedron per half-octahedron, which amounts to two tetrahe-dra per octahedron. Structures that have the same symmetry as the cube, and that includes all polyhedra considered here (with the possible exception of the regular tetrahedron whose symmetry is a subsymmetry of the cube), may be built out of octahedra sharing faces with tetrahedra only and of tetrahedra sharing faces with octahedra only.
¶ THE CUBOCTAHEDRON
The cube may also be truncated as far as the midpoints of its edges (Figure 8.3); eight octants of an octahedron are removed, leaving a polyhedron having eight triangular and six square faces, called the cuboctahedron. The octahedron thus removed from the cube has half the edge length of the reference tetrahedron; its volume therefore equals one-eighth the volume 4 of the reference octahedron, that is, 1/2. Because the reference cube has a volume equal to 3, the volume of the cuboctahedron that remains after the truncation equals one-half less, that is, 5/2.
In Figure 8.4 we note that the cuboctahedron has four hexagonal cross
Figure 8.3 Truncation of a cube to form a cuboctahedron.
sections: Each vertex of the cuboctahedron functions as a vertex of two of these regular hexagons. Accordingly, the cuboctahedron has 12 vertices, each at the center of one of the edges of the reference cube. The distance between the center of the cuboctahedron and each of its 12 vertices equals exacdy the edge length of the cuboctahedron, a characteristic that led R. Buckminster Fuller to name the cuboctahedron vector eqtiilibrium.
The cuboctahedron may itself be constructed out of regular octahedra and tetrahedra. As neither of these constituent forms has square faces and the cuboctahedron has six of these, the regular octahedra need to be bisected, so that their equatorial cross sections may supply the square faces for the cuboctahedron. The tetrahedra and octahedra constituting the cuboctahedron all
have half the edge length of the reference tetrahedron; hence their volumes are, respectively, 1/8 and 1/2. If we call the number of tetrahedra constituting the cuboctahedron x and that of the octahedra y, then the volumes of the cuboctahedron and its constituent polyhedra are related by the following equation:
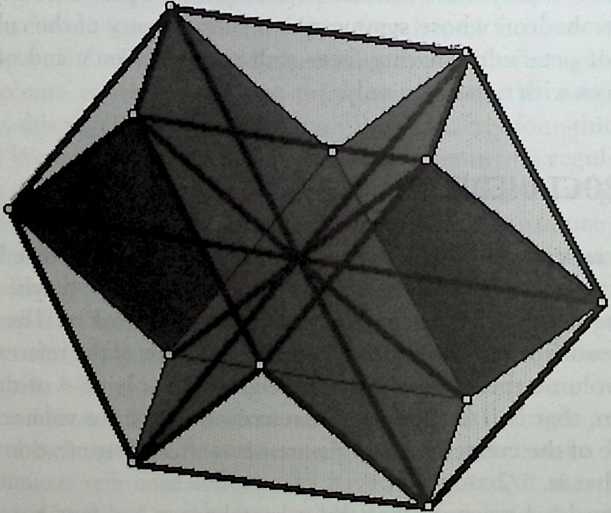
Figure 8.4 Four hexagonal cross sections of a cuboctahedron.
(1/8) x+(1/2) y= 5/2 or x+4/=20 (8.1)
Furthermore, since the cuboctahedron results from the subtraction of eight octants of the octahedron from the cube, it is one octahedron short of being a space filler. Hence
x=2(y+1) (8.2)
From Equations (8.1) and (8.2) it follows thatjy = 3, x = 8: The cuboctahedron may be built from six half-octahedra, that is, three regular octahedra and eight regular tetrahedra (Figure 8.5).
¶ THE STELLA OCTANGULA
A tetrahedron inscribed in a cube shares four of its vertices with the cube. The remaining four cube vertices could be shared by a second tetrahedron (Figure 8.6), whose six edges are each perpendicular to one of the edges of the first tetrahedron. The two tetrahedra overlap: The space shared by them is occupied by a regular octahedron. The space not shared by the two overlapping tetrahedra is constituted of eight tetrahedra having an edge length half that of the reference tetrahedron; their volumes are therefore 1/8 each. The central octahedron has four times that volume, that is, 1/2. Together, this octahedron and its eight satellite tetrahedra form a Stella octangula, or eight-pointed star, having a volume equal to 3/2 (Figure 8.6/z).
Accordingly, the Stella octangula occupies one-half of the cube in which it is inscribed. Nevertheless, it is not a space filler, because it is constituted of one regular octahedron and eight tetrahedra, six tetrahedra in excess of the ones required for space filling. For the purpose of filling space, these six excess tetrahedra would require three additional octahedra; indeed, 12 quarter-octa-hedra at the edges of the cube will exactly fill the space between the inner walls of the cube and the external faces of the Stella octangula.
THE TRUNCATED OCTAHEDRON
A Riddle: Imagine a hollow cube partially filled with water up to a level where the water surface is a regular hexagon. What fraction of the cube volume is filled with water? (Do not turn the page until you have at least considered the question.)
¶ CUBOCTAHEDRON WITH CONSTITUENT TETRAHEDRA AND OCTAHEDRA
Figure 8.5 Exploding cuboctahedron.
Figure 8.6 Two tetrahedra inscribed in a cube.
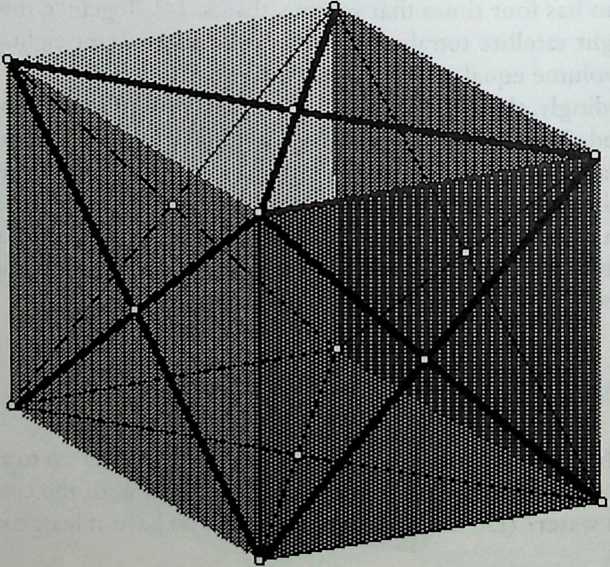
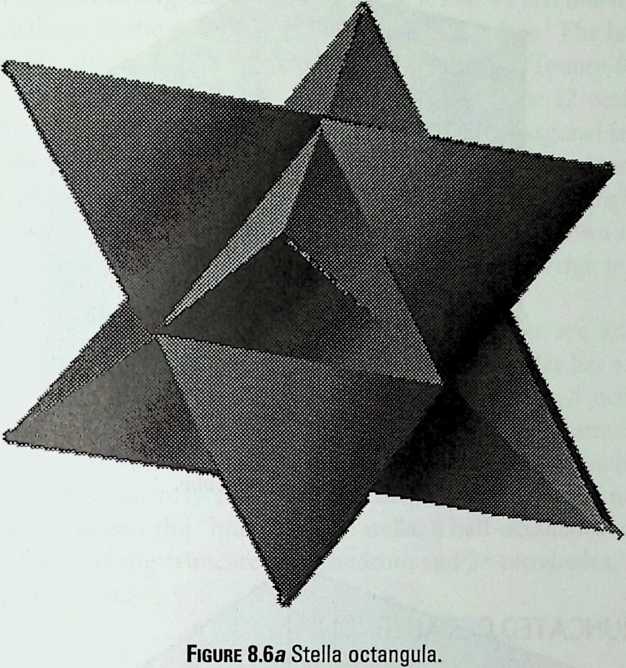
The answer is one-half: The cube was placed with one vertex on a table and its body diagonal vertical, or, as our editor asserts, hanging by a thread attached to one of its vertices. The cube can thus be bisected into two halves (Figure 8.7) having one hexagonal, three triangular, and three irregularly pentagonal faces, which, of course, are space fillers as well. These half-cubes are themselves octants of a truncated octahedron (Figure 8.8), that is, a regular octahedron with its six vertices amputated. If we consider the truncated octahedron inscribed in the reference cube, the volume of the cube will be 3. Hence the volume of the truncated octahedron equals 3/2, exactly the same as that of the Stella octangula inscribed in the cube. The truncated octahedron may itself be constructed out of tetrahedra and (half) octahedra; at least six half-octahedra are needed to provide the six square faces. These octahedra and tetrahedra have an edge length one-quarter that of the reference octahedron and tetrahedron, so that their respective volumes are 1/16 and 1/64. Once again, if x is the number of tetrahedra and y the number of octahedra in the truncated octahedra:
(1/64) x + (1/16) y= 3/2 or x+4/=96 (8.3)
and
x=2y (8.4)
Therefore, x= 32 andy= 16: The truncated octahedron maybe built from 32 tetrahedra and 16 octahedra. Of the latter, three need to be halved. Because
Figure 8.7 Bisection of the cube.
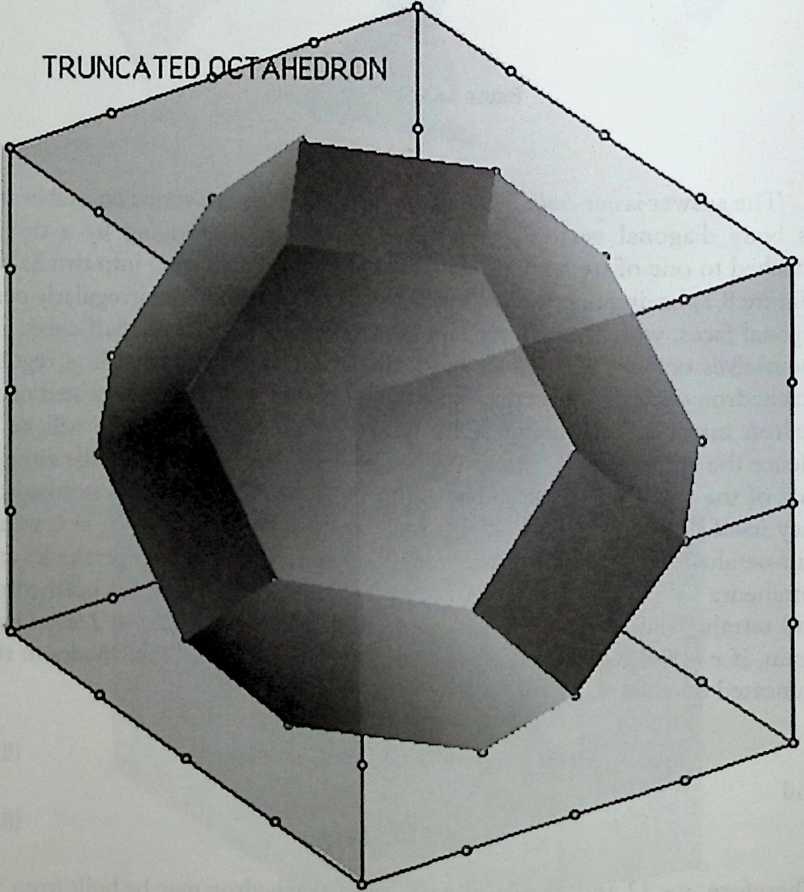
Figure 8.8 Truncated octahedron.
the number of remaining octahedra, 13, is odd, it follows that one of these 13 octahedra will go in the center of the truncated octahedron. The latter polyhedron has 36 edges, of which 24 bound the square faces. Twenty-four tetrahedra are configured adjacent to the six square faces. The 12 octahedra all have the same dihedral angles as the angles between the hexagonal faces of the truncated octahedron, for these hexagons and their adjoining edges are what is left of the faces of the original truncated octahedra. Accordingly, the 12 remaining octahedra will be situated at the intersections between hexagonal faces, of which there are just 12, namely, the edges of the large octahedron from which the truncated octahedron was generated.
This leaves eight tetrahedra unaccounted for. These are attached to the faces of the central octahedron; each of these tetrahedra has a vertex in the middle of one of the hexagonal faces of the truncated octahedron. Together, the central octahedron and the eight tetrahedra attached to it constitute a small Stella octangula inside the truncated octahedron. The truncated octahedron may therefore be constituted of a Stella octangula, 12 octahedra between the “horns” of the Stella, 6 half-octahedra to provide the square faces of the truncated octahedron, and 24 tetrahedra, three for each hexagonal face.
¶ THE RHOMBIC DODECAHEDRON
We shall show now that this form may be considered as a special stellation of either the cube or the regular octahedron. There are [?z(?z-l)]/2 connections between n points. There are, accordingly, 28 connections between the eight vertices of a cube. Of these, 12 are edges of the cube. Another 12 are the diagonals of the six faces of the cube, constituting the edges of the two tetrahedra inscribed in the cube. The remaining four connections pass through the center of the cube; they are the four body diagonals of the cube.
These body diagonals intersect at the center of the cube, at angles arc- cos±(l/3) to each other. The cube may be subdivided into six mutually congruent square pyramids whose lateral edges run along the body diagonals of the cube. Two of these pyramids may be joined along their square faces to form an octahedron; because the triangular faces of the pyramids are not equilateral, this octahedron is not regular. However, because the cube is a space filler, this octahedron will also fill space by itself: Three of such octahedra may be bisected into six square pyramids, which may then be reassembled into a cube and thus fill space.
When the six constituent square pyramids of the cube are each positioned with a square face contiguous with one of the faces of a second cube, the result (Figure 8.9) is a rhombic dodecahedron,7 which, accordingly, may be considered a special stellation of the cube. Of the 12 rhombic faces the 12 short diagonals are the 12 edges of the reference cube from which it was generated. Because the volume of the reference cube is 3 and the dodecahedron was generated from two such cubes, the volume of the rhombic dodecahedron equals
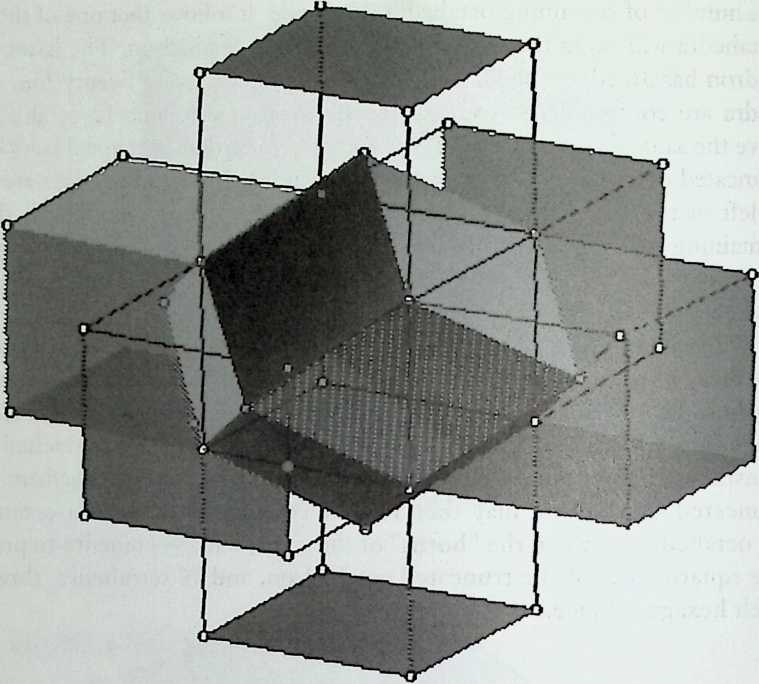
Figure 8.9 Rhombic dodecahedron in an array of cubes.
- The edges of the dodecahedron correspond to the body diagonals of the cube; the surface angles of the rhombic dodecahedron are therefore arc-cos±(l/3).
The 12 long diagonals of the faces of the rhombic dodecahedron constitute the edges of a regular octahedron, which is equal in size to the reference octahedron: Its volume equals 4. The space between this octahedron and the outer shell of the rhombic dodecahedron has a volume equal to 2; this space will just accommodate eight quarter-tetrahedra, of which one is shown in Fig-
Figure 8.10 Quarter-Tetrahedron.
ure 8.10, supplying just the two needed volume units. The rhombic dodecahedron may therefore be considered as well as a regular octahedron stellated by eight quarter-tetrahedra.
DUALS
The valency of a vertex of a polyhedron is defined as the number of edges meeting at that vertex. The valency of a face equals the number of edges around that face. Two polyhedra are each other’s duals if to each face of one there corresponds a vertex of the other, and vice versa. A cube has eight trivalent vertices and six quadrivalent faces, whereas an octahedra has eight trivalent faces and six quadrivalent vertices: Cube and octahedron are a pair of duals. The rhombic dodecahedron has twelve quadrivalent faces and eight trivalent and six quadrivalent vertices. Its dual should have twelve quadrivalent vertices and eight trivalent and six quadrivalent faces: We have seen that this is the cuboctahedron. The tetrahedron has four trivalent faces as well as four trivalent vertices; it is self-dual. Duals always have the same number of edges.
¶ CONCLUSIONS
The term deconstruction, which is being used by historians of art and architecture in a figurative sense, has been applied here in its original literal sense of taking apart. The cube can be deconstructed in many different ways, but stronger, more stable, and more fundamental building blocks to be retrieved from it are the regular tetrahedron and octahedron. These fill space in a ratio of two tetrahedra per octahedron. In turn, the regular tetrahedron and octahedron may be combined in a diversity of ways to construct semi-regular solids: truncated octahedron, cuboctahedron, Stella octangula, rhombic dodecahedron, and others. Conversely, the cube may be constructed out of its component parts; these component solids may be combined in various ways to fill space.
When these various forms are juxtaposed so that their three fourfold axes of rotational symmetry are aligned, their volumes are found to be related by simple rational numbers. Such “nesting” is possible because the numbers of vertices, edges, and faces of these polyhedra are all products of their rotational symmetry values 2, 3, and 4, as shown in Table 8.1.
In Table 8.1 all volumes are normalized with reference to their circumscribed or inscribed cube. When the vertices, edges, or faces are of two different kinds, their numbers are shown as a sum, for instance, the truncated octahedron has 6 square and 8 hexagonal faces, and the Stella octangula has 12 edges corresponding to its internal octahedron and 24 edges corresponding to the 8 corner tetrahedra.
In three-dimensional design it is useful to know how diverse numbers may be represented spatially by means of polyhedra. These numbers are obtained from Table 8.1 and listed in Table 8.2.
TABLE 8.1 Parameters of Diverse Polyhedra Having Cubic Symmetry
| Polyhedron | Number of Number of Number of Vertices Edges Faces Volume |
Cube Tetrahedron Octahedron Truncated Octahedron Cuboctahedron Stella octangula Rhombic dodecahedron |
12 . 6 3 4 6 4 1 6 12 8 4 24 12+24 6+8 3/2 12 24 6+8 5/2 6+8 12+24 24 3/2 6+8 24 12 6 |
Note that for each of these forms Euler’s relation holds: The sum of the number of faces and vertices is two units greater than the number of edges.
In summary, then, in spite of the cube’s use as a space filler and because its faces may be aligned parallel and perpendicular to gravitational forces, the tetrahedron and octahedron and their symmetrical subdivisions are stable and offer an expanded view of the possibilities of three-dimensional forms, their interrelationships and transformations, and their ability to fill space in an attractive diversity of permutations and combinations.
TABLE 8.2 Polyhedral Representation of Numbers
|
Equals the Number Of |
|
Vertices of a tetrahedron Faces of a tetrahedron |
|
|
|
Faces of an octahedron |
|
Vertices of a cuboctahedron Edges of a cube Edges of an octahedron Faces of a rhombic dodecahedron |
|
Vertices of a Stella octangula
Faces of a cuboctahedron |
|
Vertices of a truncated octahedron Edges of a cuboctahedron Edges of a rhombic dodecahedron Faces of a Stella octangula |
|
|
ACKNOWLEDGMENTS
The author gratefully acknowledges the comments and suggestions from Professors Thomas Banchoff and Anne Tyng, which have been incorporated into the final draft of this chapter.
¶ NOTES
-
A. L. Loeb, “A Systematic Survey of Cubic Crystal Structures,” Journal of Solid State Chemistry, Vol. 1, 1970, pp. 237.
-
Juana de Laban, private communication.
-
A. L. Loeb, “Vector Equilibrium Synergy,” InternationalJournal ofSpace Structures, Vol. 1, 1985, pp. 99.
-
A. L. Loeb and W. Varney, “A Stabilized Cuboctahedron Frame,” International Journal of Space Structures, Vol. 7, 1992, pp. 83.
-
A. L. Loeb, “Remarks on Some Elementary Volume Relations Between Familiar Solids,” The Math Teacher, Vol. 58, 1965, pp. 417.
-
A. L. Loeb, “The Architecture of Crystals,” in Vision and Value: Module, Proportion, Symmetry, Rhythtn, Gyorgy Kepes, ed., Braziller, New York, 1966.
-
A. L. Loeb, Space Structures, Their Harmony and Counterpoint, Addison-Wesley Advanced Book Program, Addison-Wesley, Reading, MA, 1976, Birkhauser, Basel/Boston/Berlin, 1991, pp. 147.
¶ The Polyhedral World
Pieter Huybers
¶ INTRODUCTION
It seems that the cube and the prism are at present the most common building shapes. As these two belong to the family of the so-called Platonic and Archimedean polyhedra, or, in other words, that of the regular and the semi-regular solids, this preference means a very limited choice out of a much greater source of available forms. Most of these solids have a form that is so perfect that they exert a great attraction to artists, scientists, and engineers. We find many examples in nature the shape of which is based on one of these forms, like some of the monocellular beings and crystals. However, they are also of great aesthetic as well as of practical importance. When we look more closely at the building structures around us, it appears that the polyhedral solids are actually used as a form-giving principle in building to a much greater extent than we would at first sight realize (Figure 9.1). The tetrahedron and the octahedron, for instance, have often been used in building for the composition of space structures, and the icosahedron usually serves as the starting point for a further subdivision of spherical surfaces. However, there are many more possibilities for the use of the other polyhedra, and of the forms that are derived from them, in building applications. It is therefore necessary to know in what form they occur and what their characteristics are.
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
□ 243
Figure 9.1 Houses in the shape of tilted cubes by Pieter Blom in Rotterdam, the Netherlands.
¶ WHICH POLYHEDRA DO WE KNOW?
Definition of a Polyhedron
First of all we must agree on a workable definition of what we consider in this context to be a polyhedron.1 We assume that:
-
They are covered with a closed pattern of plane, regular polygons. At this point we shall only look at the so-called Platonic solids, which are composed of identical polygons, and at the Archimedean solids, which consist of two or three different polygons. Both groups are named after the ancient scientists to which their discovery is usually ascribed.2,3 The different polygons that occur in these solids have either 3, 4, 5, 6, 8, or 10 edges.
-
All vertices of a polyhedron lie on one circumscribed sphere.
-
All the vertices are identical. This is so because around each vertex of a particular polyhedron the polygons are grouped in the same number, kind, and order of sequence.
-
The polygons meet in pairs at a common edge.
-
The dihedral angle at such an edge is always convex. This means that the dihedral angle between two adjacent polygons is less than 180°, if seen from the interior, or, in other words, the sum of the polygon face angles that meet at a vertex is always smaller than 360° (see Table 9.1).
The Various Kinds of Polyhedra
It is easy to understand that under these conditions the minimum total number of polygons around a vertex is three, the maximum number five, and it is also simple to prove that not more than five totally regular polyhedra can exist (Figure 9.2). These are the regular or Platonic solids and they are each composed of one kind of face. Polyhedra are called semi-regular, or Archimedean, if more than one kind of polygon is used for their construction. According to the first condition of the previous definitionnamely, that the polygon has no more than 3, 4, 5, 6, 8, or 10 edgesa group of 15 principally different semi-regular polyhedra is found (see Figures 9.3 to 9.5).
The polyhedron numbers in Table 9.1 were introduced by the author and they are merely used here and in the following discussion in an “administrative sense.”4 They indicate an order of sequence, based on the numbers of their faces. The Euler formula is applicable, which means that: V -E + F =2.
The names of the semi-regular solids show that they are generally considered to be derived from the regular solids by truncation. If this truncation is done through the vertices, so that the original faces convert to polygons with double the number of sides (i.e., triangle becomes hexagon, square becomes octagon, and pentagon becomes decagon), five new polyhedra are found: the truncated versions of the regular solids (Figure 9.4: Nos. 6, 8, 9, 13, and 14). The original face edges are divided into three parts. The truncation procedure can be carried out a little bit further so that the original edges are exactly
Figure 9.2 Derivation of the five possible Platonic polyhedra, composed of one kind of polygon, with three, four, or five sides.
Figure 9.3 Sketch of the 5 Platonic and the 15 Archimedean polyhedra, including two left-handed versions.
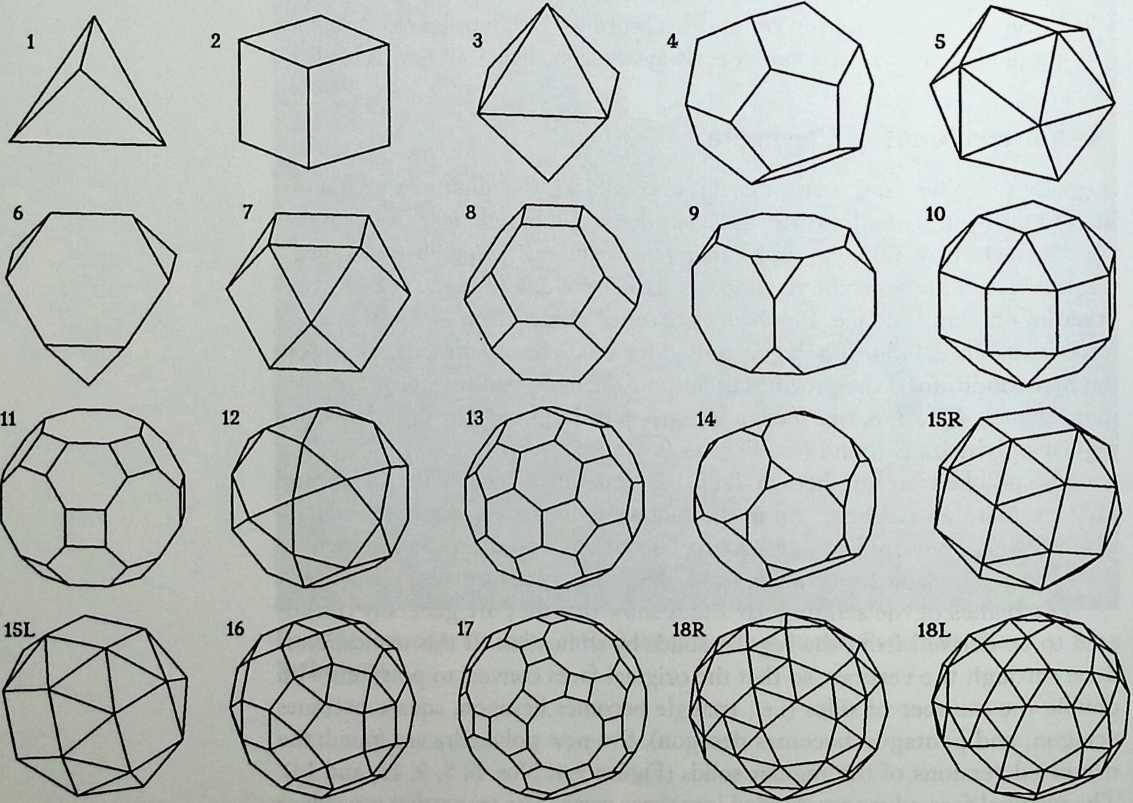
Figure 9.4 Photograph of the Archimedean solids.
b
Figure 9.5 The different polygons in the regular and semi-regular polyhedra.
TABLE 9.1 Some Characteristic Aspects of the Platonic and Archimedean Polyhedra
| p Number | Code | Name | F | E | IT | Total Angle | Deficient Angle | Radius |
| -3 | Tetrahedron | |||||||
| -4 | Cube | |||||||
| -3 | Octahedron | |||||||
| -5 | Dodecahedron | |||||||
| -3-3 | Icosahedron | |||||||
| -6 | Truncated tetrahedron | |||||||
| -3 | Cuboctahedron | |||||||
| -6 | Truncated octahedron | |||||||
| -8 | Truncated cube | |||||||
| -4 | Rhombicuboctahedron | |||||||
| -8 | Truncated cuboctahedron | |||||||
| -3 | Icosidodecahedron | |||||||
| -6 | Truncated icosahedron | |||||||
| Truncated dodecahedron | ||||||||
| -3-4 | Snub cube | |||||||
| -5 | Rhombicosidodecahedron | |||||||
| -10 | Truncated icosidodecahedron | |||||||
| -3-5 | Snub dodecahedron |
P = polyhedron index. Code = side numbers of respective polygons that meet in a vertex. V, E, and F = number of vertices, edges, and faces. Total angle = summation of face angles that meet in a vertex. Deficient angle = 360° (or flat situation) -Total angle. Radius = radius of circumscribed sphere.
bisected. This gives two new solids, the cuboctahedron (No. 7) and the icosi-dodecahedron (No. 12). These two are peculiar ones and they are called quasiregular, because they are, as their names already suggest, compounds of two pairs of regular solids. P7, the cuboctahedron, is composed of six squares (like the cube P2) and eight triangles (like the octahedron P3). Pl2, the icosido-decahedron, is composed of 20 triangles (like the icosahedron P5) and 12 pentagons (like the dodecahedron P4).
Truncation can also take place along the edges. This generally produces square extra faces and it yields four new semi-regular solids (Nos. 10, 11, 16, and 17).
Finally, there are two other solids that are found by truncation of the corners and a double truncation of the edges. There are, in fact, four of them, as they occur in a right-handed as well as in a left-handed (enantiomorphic) version. These are the snub cube (No. 15) and the snub dodecahedron (No. 18). These two are called after their circumscribed figures. The snub cube has six squares, each completely surrounded by triangles, whereas the snub dodecahedron has 12 pentagons in a corresponding location. They have the common characteristic that they all are based on a polygon or p-gon with a variable number/; of edges, and that these p-gons come together in a vertex with four triangles. As this variable p can have any valuewith six as a maximum (one
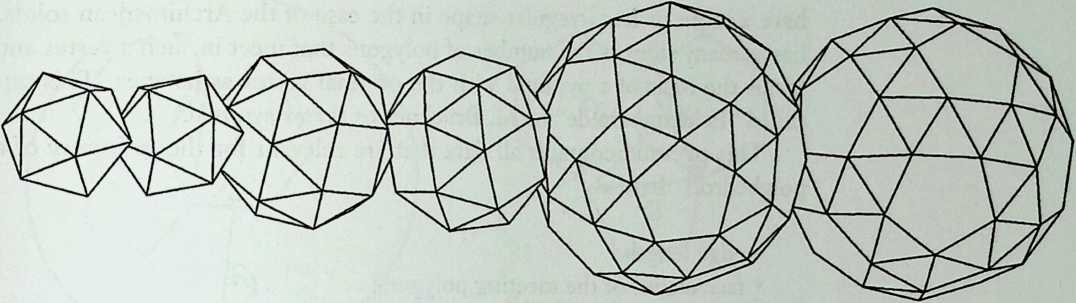
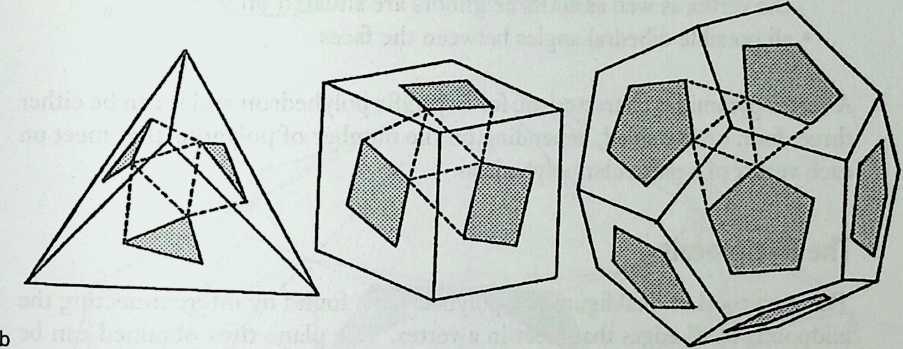
Figure 9.6 (a) The row of hypothetical “snub” solids. (b)The snub solids P18, P15, and P5.
hexagon and four triangles form a plane grid)a row of figures with common characteristics is found havingp-gons with a successively increasing number of sides: six at one end and three at the other end (icosahedron). One can even go further and also take into consideration the combination of a 2-gon, which is, in fact, a line of unit edge length with four triangles. This would produce an octahedron. Thus the complete row of “snub figures” consists of: octahedron, icosahedron, snub cube, snub dodecahedron, plane tessellation of triangles, and hexagon.5 (See Figure 9.6a.)
It is also possible to obtain the snub cube and the snub dodecahedron by truncation from the octahedron and from the icosahedron, respectively. These are two Platonic solids that are composed of triangles only and they differ by the fact that a variable number of triangles meet on each vertex: four in the octahedron and five in the icosahedron. There are indications that the latter derivation from the triangular regular solidsis even more logical than the first. This would mean that the two snubs could as well be called “snub octahedron” and “snub icosahedron.” Correspondingly, the snub tetrahedron is identical to the icosahedron. (See Figure 9.6b.)
Vertex Situations
If one connects the outer ends of the edges that meet in a vertex of any of the convex polyhedra, one obtains asometimes irregular polygon, which is called a vertex figure. This polygon is regular for the Platonic solids, but it can have a more or less irregular shape in the case of the Archimedean solids. It has as many sides as the number of polygons that meet in such a vertex and it forms the basis of a pyramid with the original vertex as its apex. This cap is called “Eckenpyramide” by M. Bruckner or vertex pyramid.6
This pyramid contains all data that are relevant for the geometry of the polyhedron, that is:
-
edge length
-
face angles of the meeting polygons
-
curvature of the circumscribed sphere, which is defined by the fact that the vertex as well as all its neighbors are situated on it
-
all possible dihedral angles between the faces
A vertex pyramid is characteristic for a specific polyhedron and it can be either three, four, or five sided, depending on the number of polygons that meet on each vertex of a particular polyhedron.
The Reciprocals
The reciprocal or dual figure of a polyhedron is found by interconnecting the midpoints of all edges that meet in a vertex. The plane thus obtained can be expanded until it meets similar adjacent planes. The section lines between these planes bisect the original edges of the polyhedron perpendicularly and are also perpendicular to the line that connects the midedge with the center of the polyhedron.7,8 (See Figures 9.7 and 9.8.)
The reciprocals of the semi-regular or Archimedean solids have the following characteristics (see also Table 9.2):
-
All faces are identical and have as many edges as the number of the polygons, meeting on the vertices of the original polyhedron.
-
The number of faces is equal to the original number of vertices.
-
The number of vertices is equal to the original number of faces.
-
The number of edges remains the same.
-
The edges bisect the original edges perpendicularly and tangent to the midsphere (Figure 9.10).
-
All dihedral angles in a reciprocal solid are equal and specific for each of them.
The Reciprocal Faces
The face of a reciprocal figure can have either three, four, or five edges, depending on the number of w-gons in the original solid that occur on each vertex (Figure 9.9).
The five regular polyhedra appear to be self-reciprocal, for example, tetrahedron-tetrahedron, octahedron-cube, and dodecahedron-icosahedron (Figure
deficient angle
Figure 9.7 faThe vertex pyramid of a polyhedron (in this case P13). 6W The Dorman-Luke construction method of the reciprocal solids.
Figure 9.8 The Dorman-Luke construction demonstrated on the polyhedron P7.
9.10). The reciprocals have in this case regular polygon faces. The reciprocal faces of the semi-regular polyhedra, however, are more or less scalene. They can be constructed by drawing tangent lines around the circle through the midpoints of the edges (Figure 9.11). This construction is known as the Dorman-Luke construction (see Figure 9.7).9 Two famous representatives of this group are the rhombic dodecahedron (honeycomb cell) and the triacontahe-dron (Nos. 7 and 12) (Figure 9.12zz and V).
TABLE 9.2. Names and Numerical Data of the Reciprocal Figures
| R Number | Name | V | E | F | Dihedral Angles |
| Tetrahedron (edge = 1) | ° 31” | ||||
| Octahedron (edge = /T) | ° 28 16.39” | ||||
| Cube (edge = 1/2 /T) | ° 00 00.00” | ||||
| Icosahedron (edge = t) | ° 11” | ||||
| Dodecahedron (edge = 1/t) | ° 33 54.18” | ||||
| Triakis tetrahedron | ° 31 16.31” | ||||
| Rhombic dodecahedron | ° 00 00.00” | ||||
| Tetrakis hexahedron | ° 07 48.37” | ||||
| Triakis octahedron | ° 21” | ||||
| Trapezoidal icositetrahedron | ° 07 04.65” | ||||
| Hexakis octahedron | ° 04 55.85” | ||||
| Rhombic triacontahedron | ° 00 00.00” | ||||
| Pentakis dodecahedron | ° 43 06.79” | ||||
| Triakis icosahedron | ° 36 45.19” | ||||
| Pentagonal icositetrahedron | ° 18 33.24” | ||||
| Trapezoidal hexecontahedron | ° 07 16.9” | ||||
| Hexakis icosahedron | ° 53 16.41” | ||||
| Pentagonal hexecontahedron | ° 10” |
Thenames in this table give an indication of the number of faces. The suffix “-kis” means: number of subdivision. Furthermore, r = 11 + J 5 ):2 or the golden section. The numbers in the first column of this table refer directly to that of their related polyhedra in Table 9.1.
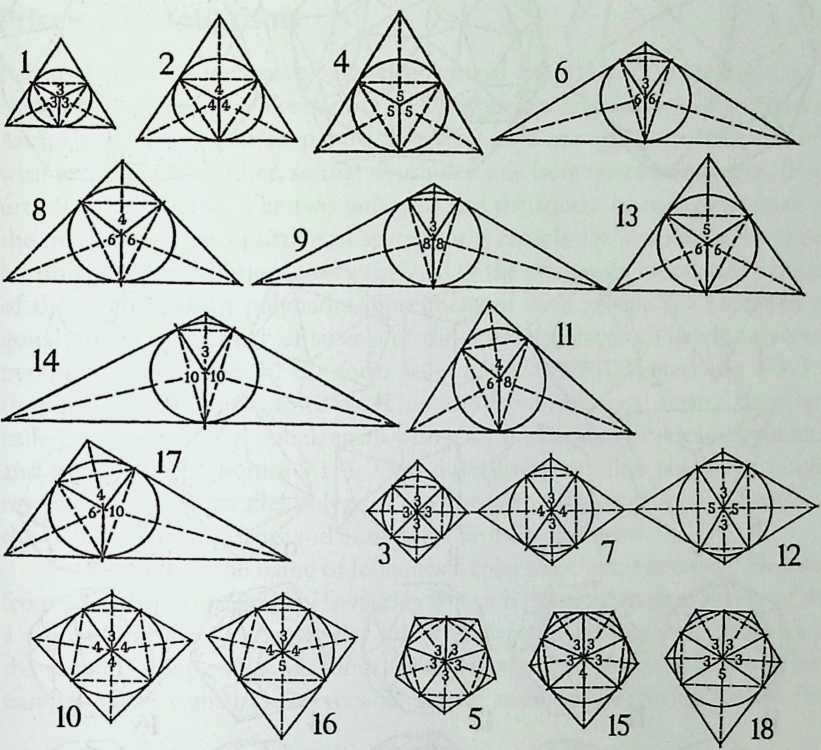
Figure 9.9 Sketch of the reciprocal faces.
Figure 9.10 The mutual reciprocity of the regular polyhedra.
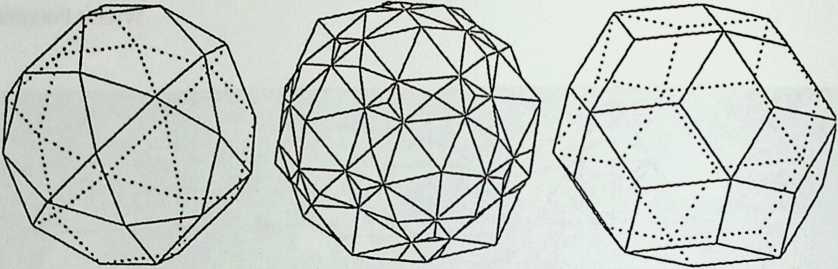
Figure 9.11 The derivation of the rhombic triaconta- hedron (P12).
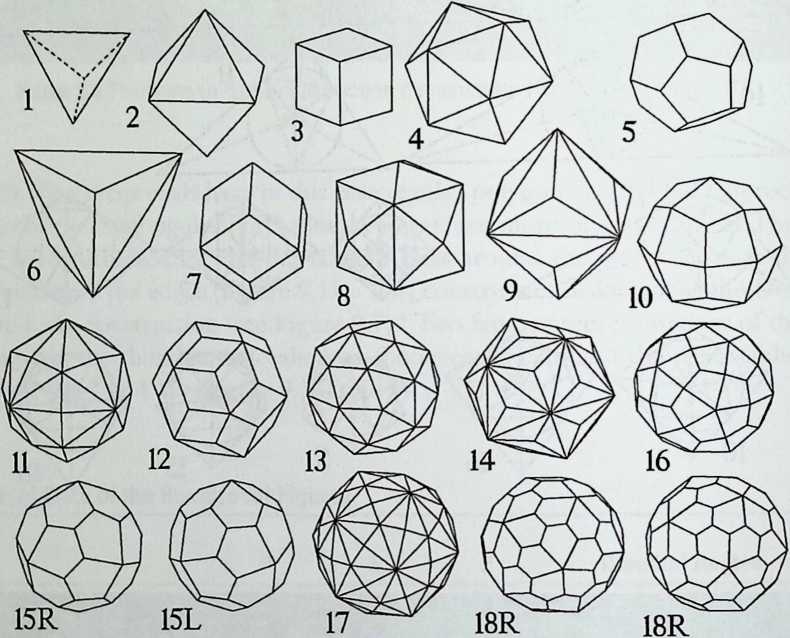
Figure 9.12 (a) Sketch of the reciprocal figures. The numbers refer to those of the solids from which they are derived (see also Figure 9.3). (6/The reciprocal figures of the semi-regular solids.
b
Prisms and Antiprisms
Prisms have two identical, parallel polygonal faces that are kept apart by a closed ring of squares, like the top and bottom of a box with square side faces. Antiprisms are similar to prisms, but they have one polygonal face rotated with respect to the other, so that the square side faces turn into triangles (Figures 9.13 and 9.14). The two polygons and the square or triangular faces of the mantle enclose a portion of space that is completely surrounded by regular polygons. In addition, they satisfy all of the previously mentioned criteria of the Archimedean polyhedra. Specimens of both groups can be called p- gonal after the number of sides p of the parallel polygons.They have vertex pyramids with a basis of the form 4-x for prisms (triangular) and 3-3-x (trapezoidal) for the antiprisms. They too have reciprocal forms; these are called polygonal (or /i-gonal, again with p for the number of sides) dipyramids and trapezohedra (Figure 9.15). They differ from the other polyhedra in one respect: The two parallel polygons can have any number of sides. Therefore, the two groups of prisms and antiprisms form endless rows.
In this context the name of Johannes Kepler must be mentioned.10 He lived from 1571 and in his Harmonices Mundi he gave a complete survey of the 5 regular and the 13 semi-regular solids. As explained before, two members of the second group, the snub solids (Nos. 15 and 18 in Figure 9.3) have a lefthanded and a right-handed version. Kepler mentioned explicidy for the first
Figure 9.14 Regular antiprisms.
time in history the prisms and antiprisms and showed them in sketch form. He introduced the principle of duality and he gave all these figures the Latin names by which they are still known. There are a few overlaps with the other solids: The square prism is identical to the cube and the triangular antiprism is identical to the octahedron. It is sometimes interesting to include also the 2-gonal antiprism, as it is identical to the tetrahedron (Figures 9.14 and 9.18&).
The Stellated or Kepler-Poinsot Polyhedra
Kepler also mentioned two stellated figures, the small and the great stellated dodecahedra (Figure 9.16). The small stellated dodecahedron (No. 3) can be constructed by placing on the faces of a dodecahedron pentagonal pyramids of such a height that they are in extension with some of the adjacent faces of the basic polyhedron. The result is that they have the appearance of 12 interpenetrating, pentagonal star polygrams, or pentagrams (Figure 9.17). The great stellated dodecahedron (No. 4) is derived similarly by the placement of triangular pyramids on an icosahedron. This also results in a compound of 12 pentagrams. Poinsot in 1809 discovered two more stellated regular polyhedra: the great dodecahedron (No. 2) and the great icosahedron (No. 1), which, respectively, can be considered as an intersection of 12 pentagons or of 20 triangles.11 The star polyhedra, in fact, do not satisfy the fifth condition of the definition that was given for polyhedra, as they are not convex at all places.
Figure 9.15 (a) A number of compounds of polyhedra and their reciprocal figures. 6W Antiprisms and their reciprocals.
Figure 9.16 The four regular star polyhedra.
Both prisms and antiprisms also have star-shaped versions (Figure 9.18). The two parallel polygonal faces can be replaced by regular stars or polygrams. This produces two new families: star prisms and star antiprisms. In the first group a mutual distance, equal to the unit edge length, can be chosen, as in the normal prism. The resulting figure has a mantle, consisting of rectangles. The star antiprisms have a somewhat unexpected appearance. On closer examination the forms with even numbers of sides seem to be composed of two antiprisms with half the number of faces, but with a greater edge length. Among these the square version is a peculiar one. The four-sided polygram, or tetragram, is identical to a set of crossing lines and it therefore leads to a figure, which can be considered as a pair of intersecting tetrahedra. This figure was also discovered by Kepler and he called it the Stella octangula (No. FS-4 in Figure 9.18).
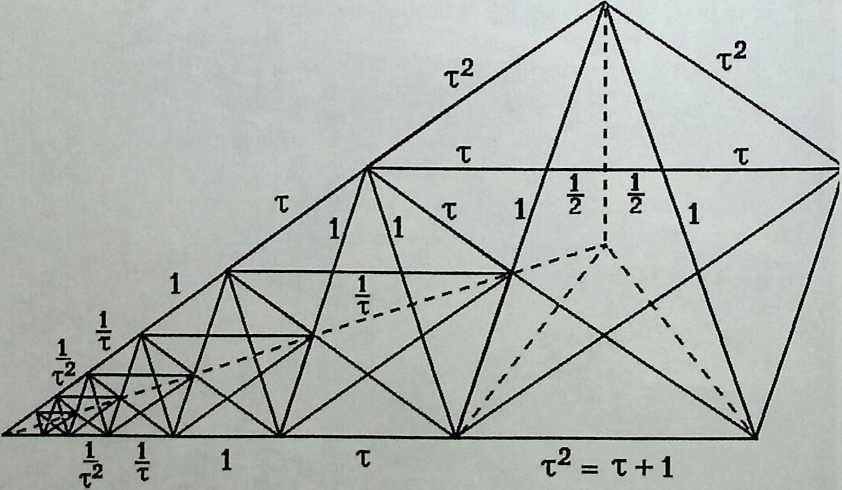
Figure 9.17 A row of successive pentagrams, with t = (1 + /5~):2.
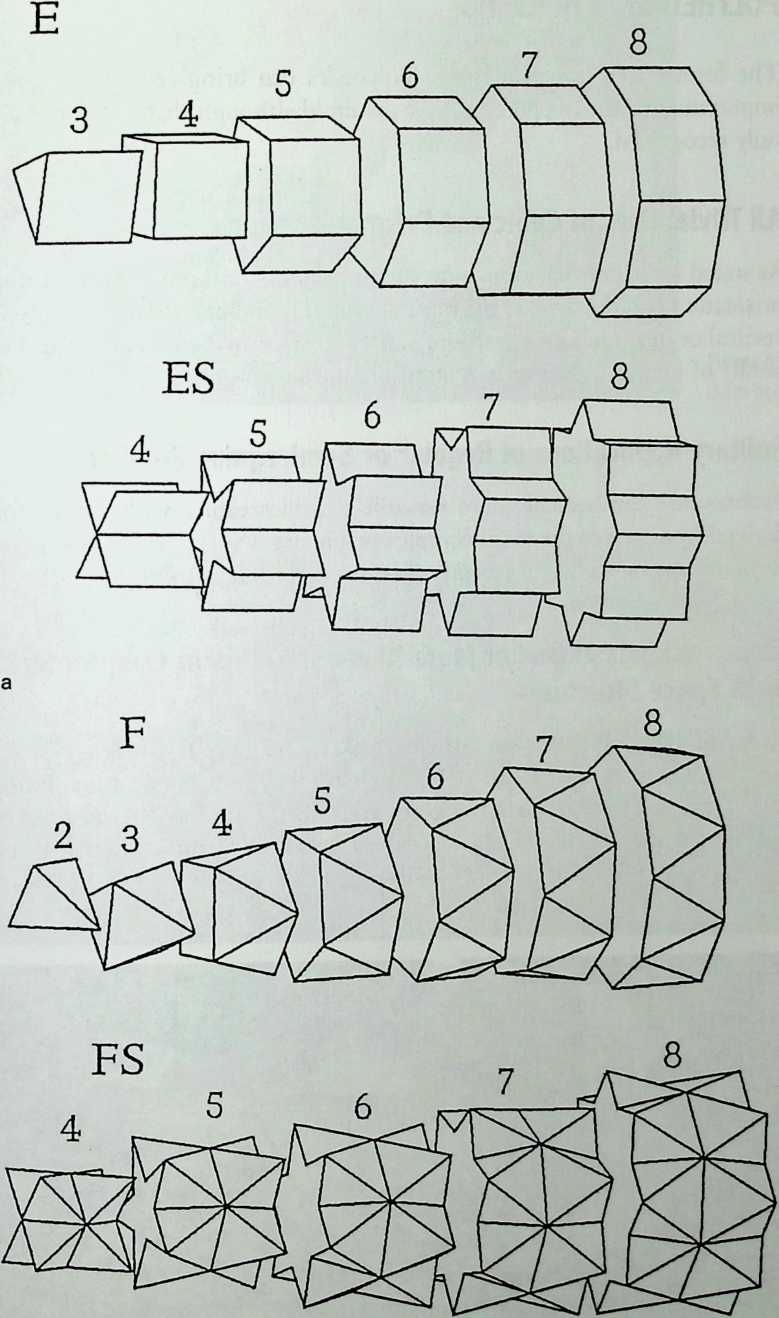
b
Figure 9.18 Star prisms and antiprisms.
POLYHEDRA IN BUILDING
The form-giving possibilities that polyhedra can bring to buildings is very important, and their applications are manifold although this fact is not always fully recognized.
All Trivial Uses of Cubic and Prismatic Shapes
As stated in the introduction, most of our present-day architectural forms are prismatic (with the cube as the most common member). Prisms are used in a vertical or in a horizontal position, in pure form or in distorted versions. This family of figures is therefore of utmost importance for building.
Solitary Applications of Regular or Semiregulair Polyhedra
Architecture can become more versatile and interesting with macro forms, derived from one of the more complex polyhedra or of their reciprocal (dual) forms. Unfortunately, this has not often been done (Figures 9.19 to 9.22).
Close Packings of One or More Kinds of Solids in Conglomerates or in Space Structures
Some of the polyhedra lend themselves to being put together in tight packing formations (Figure 9.23). In this way quite complex building forms can be realized. Such packings are also suitable as the basic configuration for space frames, because of their great uniformity: identical mem-
Figure 9.19 Full-scale cardboard house based on P8.
Figure 9.20 Scale model of a polyhedron house.
Figure 9.21 Office building in Bamako, Mali, based on P10.
Figure 9.22 P16 model, made of GRP sandwich panels.
Figure 9.23 Packing of polyhedra (P11).
bers meeting at specific angles. These members usually meet at joints having a polyhedral form. The rhombianboctahedron (PIO) is well known in this respect, as it is the node of the famous MERO system. The struts meet the joint on the square faces. The joint has 18 such faces that have mutual positions and angles allowing the formation of various frame shapes (Figures 9.24 to 9.27).
Prismatic and Antiprismatic Forms
The simplest structural forms are the prismatic shapes. They usually fit well together and they allow the formation of many variations of close packings. Figure 9.28 shows examples of such applications: Matrices can be formed with regular or deformed prisms, parts can be linked up in rows to make cylinders, or elongated prisms can serve as the struts of space frames. If a number of antiprisms is put together according to their polygonal faces, a geometry is
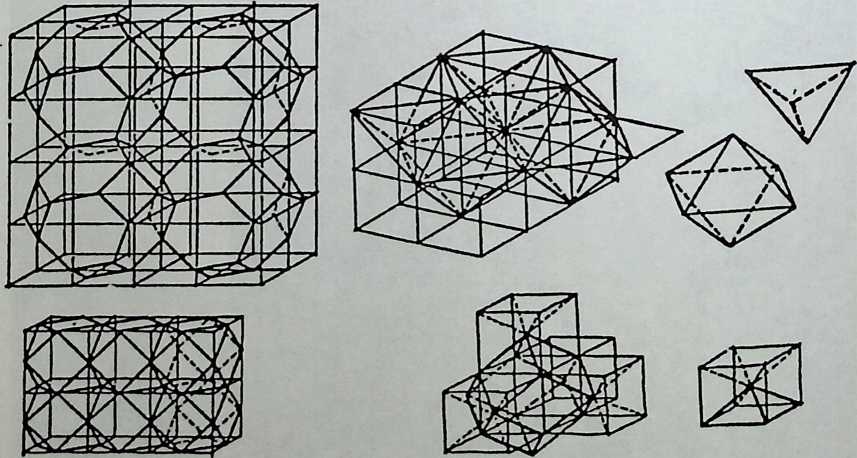
Figure 9.24 Possible space frame configurations.
Figure 9.27 Triple-layer space grids, based on P7.
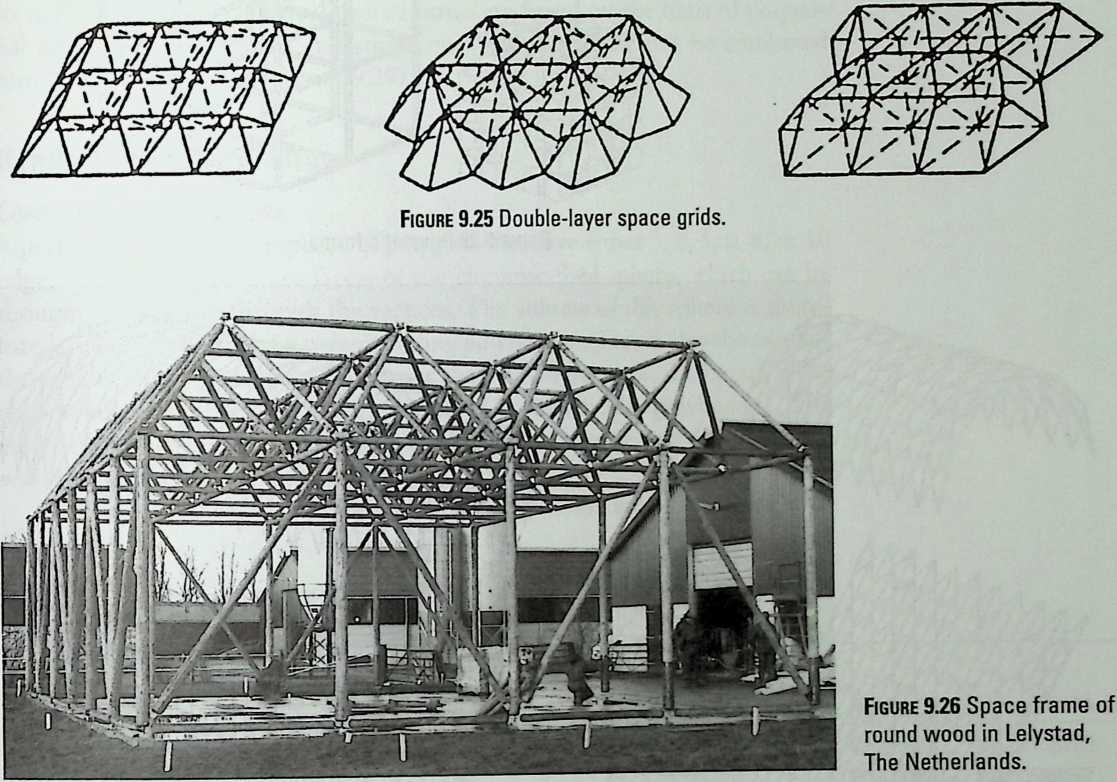
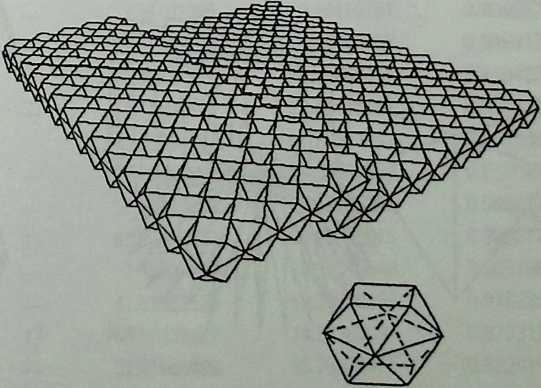
Figure 9.28 Prismatic forms.
obtained that is often used as the basis for structural applications. The outer mantle has the appearance of a cylindrical, concertina-like folded plane. These forms can be described with the help of only a few parameters. Tonon mentions methods that modify the general shape of antiprismatically folded planes.12 This has been worked out by the author for circular transformations, so that toroidal and spherical overall forms are found on the basis of polygonal or star-formed prisms and antiprisms.13 Parts of these can be combined into larger compounds (Figure 9.29).
Hemispherical Structures
Compactness of Polyhedra
A polyhedron can be composed of polygons that have either 3,4, 5, 6, 8, or 10 edges. These polygons are facets of the circumscribed sphere, which can be thought of as going through the vertices. The volume of this sphere is therefore larger than that of the corresponding polyhedron. This is also the case for the area of their envelopes. The closer these two values are, the better is the approximation of the sphere that is reached by a particular polyhedron. The closeness of this approximation can be expressed in a value called the compactness of a polyhedron (Table 9.3).
The compactness Cp is equal to the quotient of the area of a sphere with
TABLE 9.3 Compactness of Polyhedra
| 3 | 4 | 5 | 6 | 10 | |||||
The values of Volume, Area, and Compactness are expressed in unit edge length.
the same volume as the polyhedron with index p, divided by the surface area of this polyhedron. This value is given by the following equation:
Vse-ir* Volume,2
Cp =
Area,
Pyramided or Polar Versions of Solids
Pyramidization or “sphere point raising” is a technique whereby the center of a polygonal face of a polyhedron is raised until it lies on the circumscribed sphere. If these new polar points are connected to the polygon corners with inclined lines, a further subdivision is obtained that has a better approximation to the sphere. The technique is often applied in order to reduce the size of larger polygons. It can therefore be considered as the first grade of subdivision of the circumscribed sphere, which can be done with any of the known poly- hedra. It is clear that the 8-and 10-gon are not very useful in this respect, as we would get long inclined edges and narrow triangular faces. We know, however, of a number of applications where polyhedra consisting of polygons with smaller numbers of edges have been used. Many radomes have been built of hexagonal and pentagonal pyramids, usually made of GRP (glass-fiber-rein-forced polyester) (Figures 9.30, 9.31, and 9.43).14
Polyhedral Sphere Subdivisions
Triangular Subdivision Methods. For the further subdivision of spherical surfaces in most cases the icosahedron is used as a starting point, because it consists of
Figure 9.30 Scale model of pyramidized P8 compound.
Figure 9.31 Octagon House by K. Critchlow, based on a compound of truncated and pyramidized reciprocal solid R7. (Source: R. Sheppard et al., Paper Houses, Survival Scrapbook 4, Unicorn Bookshop, Caerffydin, USA, 1974.)
20 equilateral triangles that can be easily covered with a suitable pattern that is subsequently projected upon a sphere. This leads to economical kinds of subdivisions up to high frequencies and with relatively small numbers of different member lengths. There are two other triangular regular solids that can be used similarly: the tetrahedron and the octahedron.15"20
The original polyhedron triangle has to be subdivided up to a suitable frequency, so that elements are produced of the required maximum or minimum length. This can be done using several methods, each of which has its own advantages.
Generally, two main methods are considered:
-
Subdivision of the polyhedron edge in equal parts and successive interconnection of corresponding points on opposite edges of the triangular face, so that a pattern of regular small triangles is found. This pattern is then projected from the center onto the surface of the sphere.
-
Subdivision of the polyhedron edge in equal parts of the spherical angle under which this edge is seen from the center, so that, in the case of the sphere, equal chords are found. The parts into which the edge is subdivided are no longer equal and, if opposite points are interconnected, the connection lines therefore do not intersect in points but form small triangular “windows,” as Clinton calls them.21 The centers of these windows are successively projected onto the envelope.
Polygonal Subdivisions. Similar kinds of subdivisions can be made on any of the other regular and semi-regular solids. Even their reciprocals as well as regular prisms and antiprisms can be used this way, as long as they are properly subdivided.19,22,23 Subdivision patterns are written on the faces of these figures and the coordinates of the intersection points can be converted from Cartesian into polar coordinates. If all distances are then taken equal to the radius of the circumscribed circle, the originally polyhedric form is turned into a sphere. The spherical coordinates can also be written in a general form, so that the shape of the sphere can be modified.
It was previously mentioned that the polyhedra considered here are composed of polygons with 3, 4, 5, 6, 8, or 10 sides. In the literature one discerns mainly three so-called classes of subdivision of the triangular faces; see, for example, Ki trick.18 Class I is the basic subdivision type for triangles and is generally used in combination with icosahedra (only rarely with octahedra); Class II is, in fact, reciprocal (the rhombic triacontahedron); and Class III is the snub dodecahedron type (P18 in Figure 9.3).
The subdivision of the polygons can be worked out more or less analogously to the general concept used by Kitrick et al. (Figures 9.32 to 9.36).
Class I: Radial Type. The triangle is taken as the starting point. This can be subdivided into smaller triangles. Two basically different methods are in use: edge based and arch based. The polygon is first subdivided into its own plane and each intersection is projected radially onto the sphere (Figure 9.37). In the next part, byway of example, triangular patterns with frequencies of 3 or 6 are used and also a particular hexagonal pattern. This equilateral triangle can be
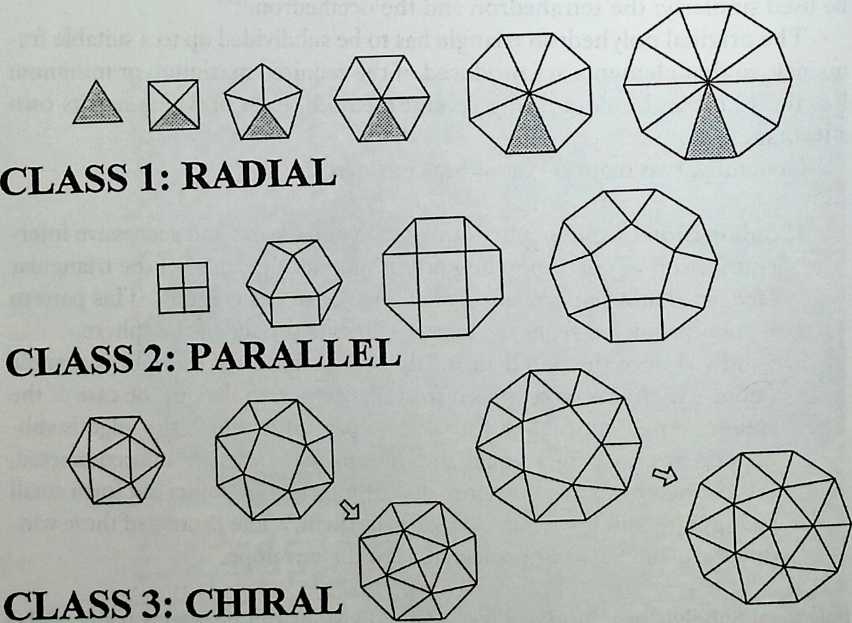
Figure 9.32 Three kinds of subdivision of polygons.
Figure 9.33 Further breakdown of the polygons.
Figure 9.34 P7 with hexagonal pattern, pumped up to spherical form.
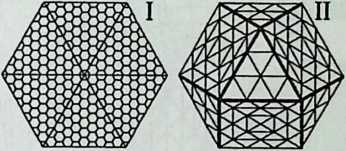
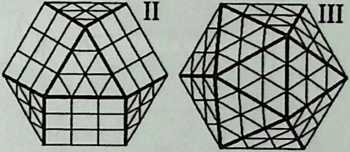
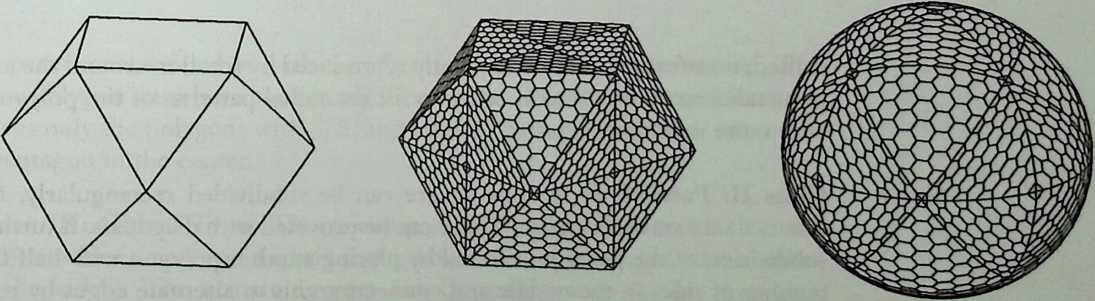
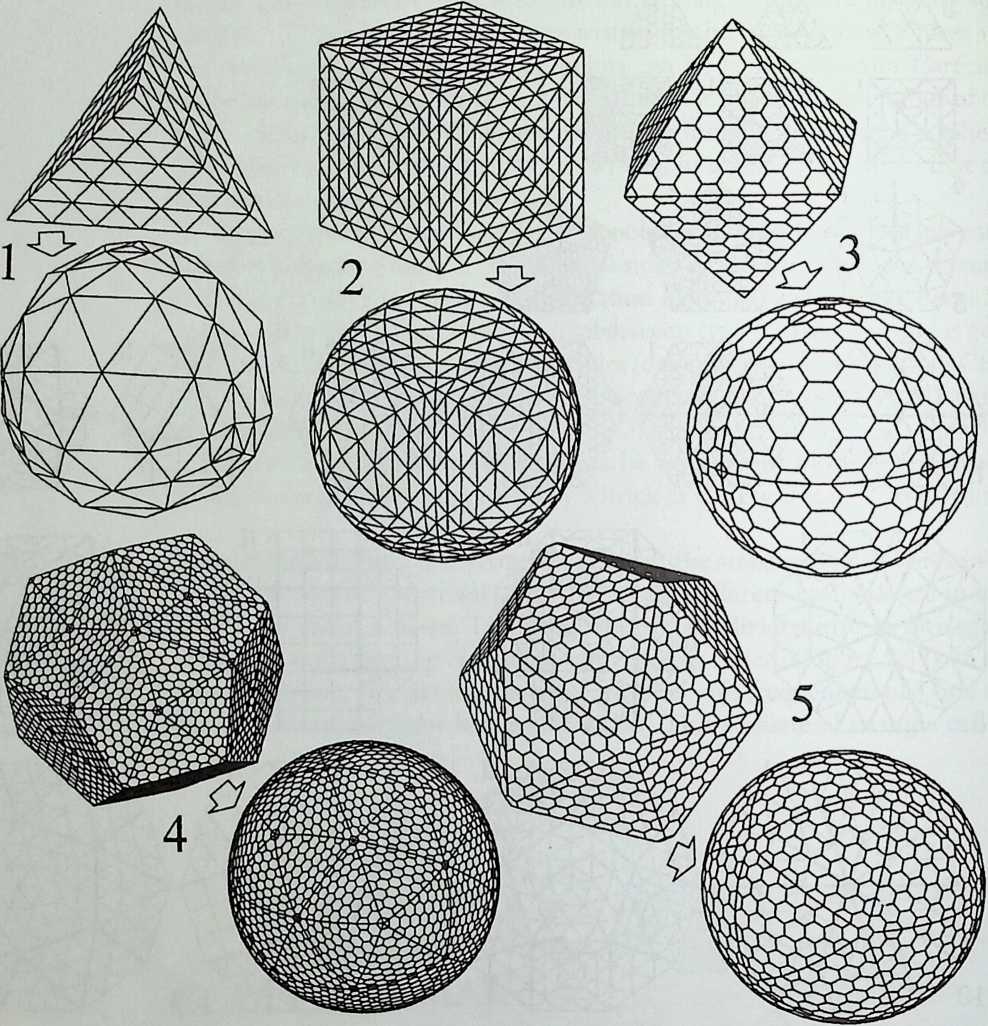
Figure 9.35 Examples of polyhedral breakdowns of spherical surfaces, based on the Platonic solids.
shifted, transformed, and subsequently reproduced by rotation around the axis perpendicular to its plane in order to fill the radial patterns of the polygons with more than three sides.
Class II: Parallel Type. The square can be subdivided rectangularly, for instance into smaller squares. These can be provided with diagonals. A further subdivision of the polygon is found by placing another polygon with half the number of sides in the middle and connecting this to alternate edges by rectangles. The remaining parts are triangular. The triangular and the rectangu-
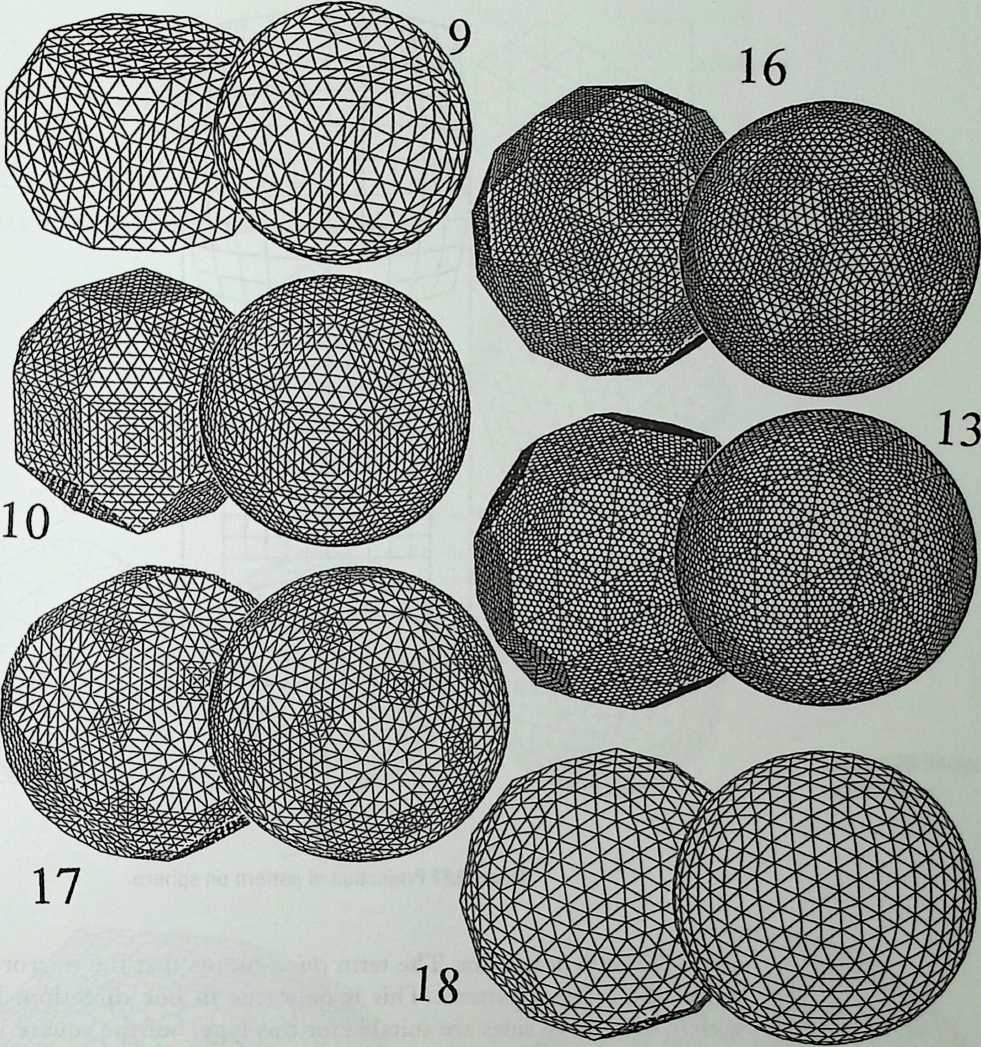
Figure 9.36 Further examples of breakdowns, based on some of the Archimedean solids.
lar parts can be filled in with transformations of the regular versions. The basic polygon must have an even number of sides. The square is trivial and this leaves only the polygons with 6, 8, and 10 sides having a triangle, a square, or a pentagon in the center.
Class III: Chiral Type. This is comparable to Class II but with the central smallerpolygon slightly rotated over the angle ir/n (n is the number of the sides). The remaining part can be made up of smaller triangles, which can again be subdivided. If seen from above, this type recalls very
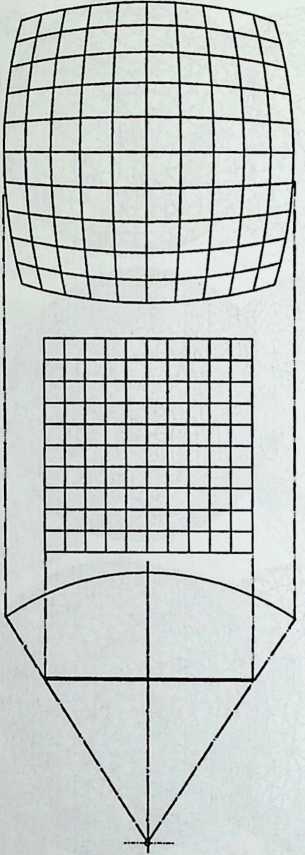
Figure 9.37 Projection of pattern on sphere.
much the snub polyhedra. The term chiral means that the mirror image is unlike the original pattern. This is only true in one direction. Polygons with 4, 6, 8, or 10 sides are suitable for this type, but the square leads to a somewhat trivial solution.
Reciprocal Sphere Subdivisions
The dual or reciprocal versions of the polyhedra can also be further subdivided (Figures 9.38 and 9.39). This is easily understandable for those that have a triangular composition, such as those with the numbers Rl, 2, 4, 6, 8, 9, 11, 13,14, and 17. These do not particularly throw a new light on the subject, but there are two others that are much more interesting in this respect: R7 and R12, or the rhombic dodecahedron and triacontahedron. R3 (cube), which can be considered as the dual of the octahedron, also belongs to the category of rhombic polyhedra by analogy. So there are three reciprocals that act as the counterparts of the three triangular regular polyhedra. The subdivision of the spherical surface is accomplished in this group in a way similar to the Class H triangle.
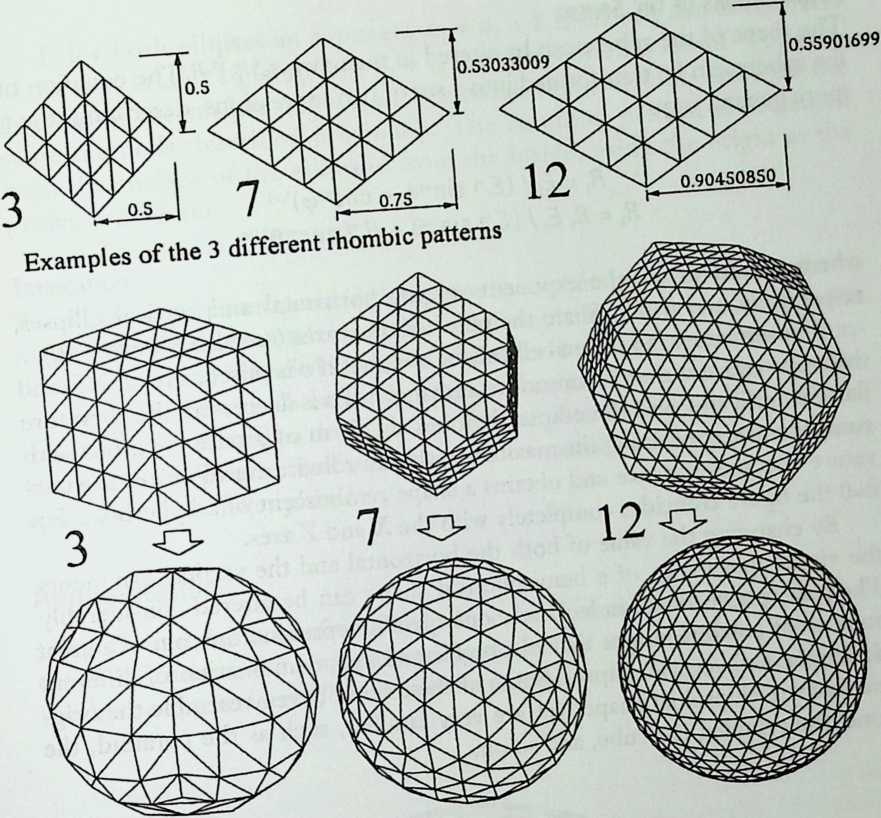
Figure 9.38 Reciprocal subdivisions.
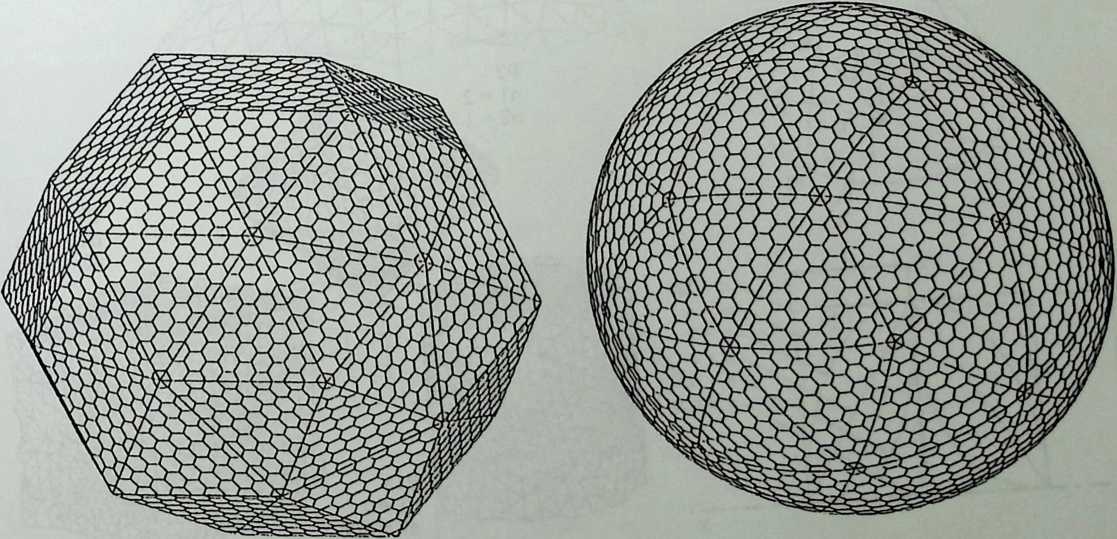
Figure 9.39 Hexagonal geodesic, based on R12.
Modifications of the Sphere
The shape of the sphere can be altered in many ways.4,16,l7,27 The equation of the sphere can be transformed into a set of two expressions, describing it in a more general way:
/?, = EJ sin"> + cos",(p),/n
/?2 = /?,£/ (£?* sinn20 + Rf2 cos"2"2
where nx and n2 are the exponents of the horizontal and vertical ellipses, respectively, and E1 and E2 are the ratios of their axes (see also Figure 9.40).
The curvature is a normal ellipse for m=2, but if n is raised, a form is found that approximates the circumscribed rectangle. If n is decreased, the curvature flattens until 72=1 and the ellipse then has the form of a pure rhombus with straight sides, connecting the maxima on the coordinate axes. For n<\ the curvature becomes concave and obtains a shape reminiscent of a hyperbola. For ?z=0 the figure coincides completely with the X and Y axes.
By changing the value of both the horizontal and the vertical exponents, the visual appearance of a hemispherical shape can be altered considerably. The pure sphere forms, in fact, only one specific representation out of a great number of possible shapes that can be formed by a combination of different horizontal and vertical ellipses. Some of these do not even resemble the original convex ellipsoidal shape, yet are very familiar, such as the pyramid, the cone, the cylinder, the cube, and so on.
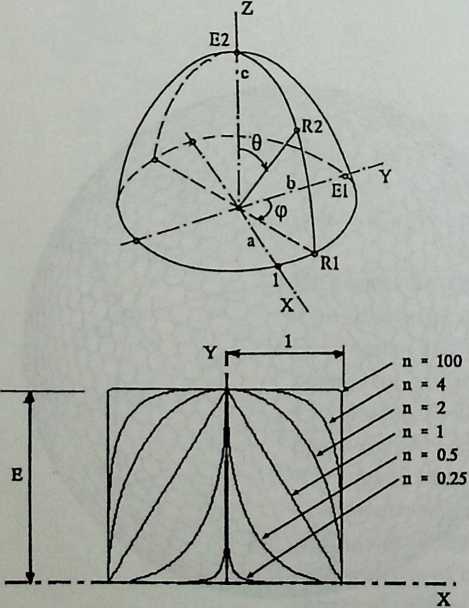
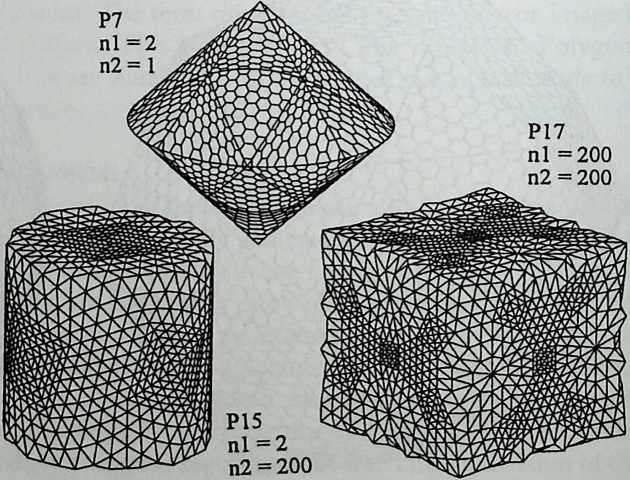
If for both ellipses an exponent nx = n2 = 2 is chosen and if the ratio of the axes is kept equal to = E2 = 1, the pure sphere is found. The subdivision of the surface of such an ellipsoidal shape may be based on the same methods described previously. The resulting pattern is projected onto the surface of the ellipsoid from the inside, using the origin as the projection center.
Truncation
For practical purposes, parts of the sphere have often been cut off in order to make it fit on horizontal or against vertical planes. This can be done as demonstrated in Figure 9.41. A certain value for the angle of the desired truncation plane has to be chosen and an area around it where all occurring nodes have to be transferred to this plane in order to obtain a properly closed lower boundary. The pattern itself can be rotated or translated before the projection upon the sphere takes place.
Augmentation
Upon the regular faces of the polyhedra other figures can be placed that have the same basis as the respective polygon. In this way polyhedra can so to speakbe “pyramidized,” as already mentioned earlier. This means that shal-
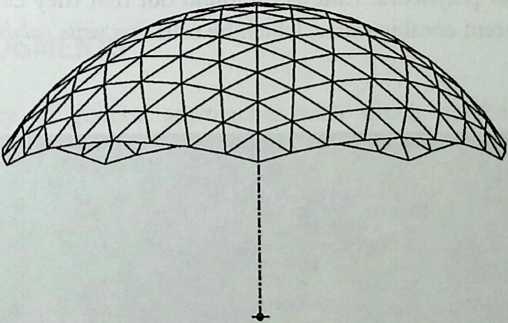
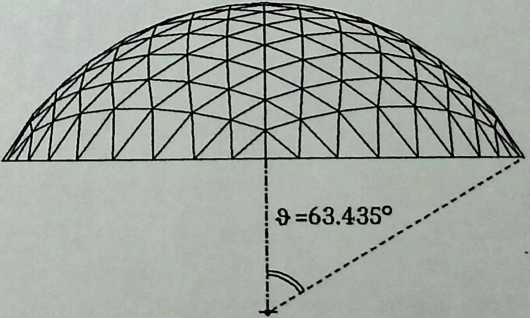
Figure 9.41 Truncation and adaptation to horizontal plane.
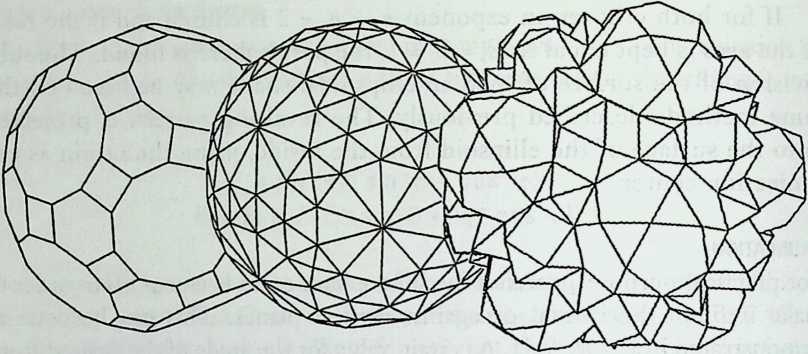
Figure 9.42 Augmented polyhedra.
low pyramids are put on top of the polyhedral faces, having their apices on the circumscribed sphere of the whole figure. This can be considered as the first frequency subdivision of spheres.
In 1582 Simon Stevin introduced the notion of “augmentation” by adding pyramids, consisting of triangles and having a triangle, a square, or a pentagon as a base, to the five regular polyhedra.3 In 1990, the late D.G. Emmerich extended this idea to the semi-regular polyhedra (Figure 9.42). He suggested using pyramids, with 6-, 8-, or 10-sided bases, that are composed of regular polygons. There are seven such pyramids, that are suitable for this purpose and that are, in fact, parts of other polyhedra. Emmerich found out that they can be combined to form 102 different combinations, which he calls composite polyhedral
Figure 9.43 Structure of pyramidized pentagonal and hexagonal GRP panels.
Figure 9.44 Model of augmented P9 and P11.
ACKNOWLEDGMENTS
The availability of general approaches with which polyhedra and related forms can be described so that they become visible and tangible is very important. The computer is a substantial help in reaching this goal. Some of the shapes generated remind one of crystalline elements or aggregates of composite materials. There appears to be great similarity in the way in which structural elements or systems as a whole are described. Both environments can be approached using one comprehensive method only. The application of physical properties to such micro or macro structures opens the way to their interactive design and also to the computer-aided production of the constituent members.
Most of the figures in this chapter have been made with the help of the computer program CORELLI, which is being developed by the author in close cooperation with Gerrit van der Ende.13,22,25
¶ NOTES
-
H. S. M. Coxeter et al., “Uniform Polyhedra,” Philosophical Transactions of the Royal Society of London, Series A, Vol. 246, 1954, pp. 401450.
-
L. A. Lyustemik, Convex Figures and Polyhedra, Dover, New York.
-
D. J. Struik, The Principal Works of Simon Stevin, Vol. 2, Swets en Seitlinger, Amsterdam, 1958.
-
P. Huybers, “De Geometri van Uniforme Polyeders” (The Geometry of Uniform Polyhedra), TUD-Report 10, Delft, 1976.
-
P. Huybers, “The Snub Polyhedra on Closer Examination,” Proceedings of the IASS-CSCE International Congress on Innovative Large Span Structures, Toronto, July 12, 1992, Vol. 2, pp. 2910.
-
M. Bruckner, Vielecke and Vielfliiche, Theorie und Geschichte, Druck und Verlag von B. G. Teubner, Leipzig, 1900.
-
P. Huybers, “The geometry of the Dual Uniform Solids,” First International Seminar on Structural Morphology, Sept. 7, 1992, Vol. 2, pp. 1.
-
T. Roman, Regulate und halb-regulare Polyeder, VEB Deutsche Verlag der Wis-senschaften, Berlin.
-
A. Holden, Shapes, Space and Symmetry, Columbia University Press, 1971.
-
J. Kepler, Harmonices Mundi, Liber II (1571).
-
L. Lines, Solid Geometry, Dover, New York, 1965.
-
O. L. Tonon, “Geometry of the Spatial Folded Forms,” Fourth Conference on Space Structures, Sept. 5, 1993, Guildford, England, pp. 2042.
-
P. Huybers and G. van der Ende, “Prisms and Antiprisms,” Proceedings of the International IASS Conference on Spatial, Lattice and Tension Structures, Atlanta, April 24, 1994, pp. 142.
-
R. Sheppard et al., Paper Houses, Survival Scrapbook 4, Unicorn Bookshop, Caerffyrdin, USA, 1974.
-
Domebook, Pacific Domes, London, 1971.
-
P Huybers, “Super-Elliptic Geometry as a Design Tool for the Optimization of Dome Structures,” in Optimization of Structural Systems and Industrial Applications, S. Hernandez et al., eds., Computational Mechanics Publications and Elsevier, Southampton/London, 1991, pp. 387.
-
P. Huybers, “About the Manipulation of Spheroidal Forms,” Proceedings of the IASS-CSCE International Congress on Innovative Large Span Structures, Toronto, fitly 12, 1992, Vol. 2, pp. 55.
-
C. J. Kitrick, “A Unified Approach to Class I, II & DI Geodesic Domes,” International Journal of Space Structures, Vol. 5, No. 3/4, 1990, pp. 223.
-
H. Lalvani, “Continuous Transformations of Subdivided Periodic Stirfaces,” International Journal of Space Structures, Vol. 5, No. 3/4, 1990, pp. 255.
-
A. Pugh, Polyhedra, a Visual Approach, University of California Press, 1976.
-
J. D. Clinton, “Advanced Structural Geometry Studies,” NASA Contract Report CR.1735.
-
P. Huybers and G. van der Ende, “Polyhedral Sphere Subdivisions,” Proceedings of the IASS Conference on Spatial Structures: Heritage, Present and Future, Milan, fine 5, 1995, pp. 189.
-
H. Nooshin and D. Tzourmakliotou, “An Approach for Generation of Geodesic Forms,” Fourth International Conference on Space Structures, Guildford, Sept. 6, 1993, pp. 1085.
-
D. G. Emmerich, “Composite Polyhedra,” International Journal of Space Structures, Vol. 5, No. 3/4, 1990, pp. 281.
-
P. Huybers, “The Formation of Polyhedra by the Rotation of Polygons,” Fourth
International Conference on Space Structures, Guildford, Sept. 6, 1993, pp. 1097.
-
P. Huybers, “Dome-Type Space Structures of Ellipsoidal Form, International Journal of Space Structures, Vol. 5, No. 3/4, 1990, pp. 297.
-
H. Kenner, Geodesic Math and How to Use It, University of California Press, London, 1976.
10
¶ Proportion and Symbolism in Polyhedra
Rene Motro
¶ INTRODUCTION
The task of understanding the “architecture” of polyhedra can be made easier by the study of proportion and symbolism in polyhedra, which gives access to some fundamental meanings. Since ancient times, polyhedra and their associated symbolism were a matter of thinking and contemplation: Readers can refer to the major works of Plato1 and Fra Luca Pacioli.2 Papers concerning the symbolic approach have been recendy published by Critchlow,3,4 Meu-rant,5 and Lawlor8 among others. Concerning proportion and specifically the golden one, a major contribution was made by Ghyka.9 Coxeter and Hilbert are the authors of comprehensive studies that give the necessary mathematical basis.10,11 As far as the golden proportion is concerned in relation to architecture, Le Corbusier’s work The Modular plays a major role.12 Moreover, Lal-vani paid attention to hyperspaces based on polyhedra.13
In such a context, we only present here the main features of proportion and symbolism in polyhedra, and focus on the five so-called Platonic or regular polyhedra, which can be related to one another in geometric and symbolic terms.
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
□ 281
PROPORTION AND POLYHEDRA
It may be necessary to recall some elementary definitions regarding polyhedra before we proceed. Most of these developments are included in the previously cited references with more details, but they are given in this chapter in order to allow an easier reading for people who are not familiar with this topic.
A polyhedron is a closed surface composed of plane polygons assembled by their edges in such a way that each edge is common to two of them. It is convex if it is entirely positioned on one side of the planes that form the faces. Only the first three regular polygons, the equilateral triangle, the square, and the pentagon, can be assembled to make a regular polyhedron, which is characterized by the fact that all of its faces, edges, and apices are identical. While the geometrical construction of the first two polygons can be achieved simply with a ruler and a compass, knowledge of the golden proportion is necessary for the pentagon. This proportion also plays a major role in the geometrical construction of regular polyhedra and their relative inscription. We introduce it now in relation to the pentagon.
The Golden Proportion and the Pentagon
The Golden Proportion
Mathematically speaking, a proportion is the equality of two ratios and can be understood as a comparison and, furthermore, as an analogy. It is not surprising to learn that Jamblique used the Greek word “avaXoyia” (analogy) for the golden proportion that establishes a specific relation between three numbers or, if extended to a symbolic approach, between three concepts. The value of the ratio in this specific case was called the “golden number” and was designated by the letter 4>; in reference to the architect Phidias who used it in his architectural works.
According to historical evidence, the “golden number” was related to the observations made by the Greek astronomer Meton: Every 19 years, the moon’s cycles were identical at the same dates (related to the motion of the earth around the sun). This discovery allowed for improvement of the calendar. This 19-year period, known as “Meton’s cycle,” was adopted in 453 B.C. and inscribed in golden letters on the columns of Minerva’s temple; the rank of any year of the cycle was its golden number. Later on, a golden number designation was conferred on the whole cycle. The relation between this historical explanation and the mathematical value of the golden number is not obvious. Perhaps it could be found in the proportions of Minerva’s temple.
Only three terms, a, b, and c, are necessary to establish a proportion. One of them, say b, will be considered as the “middle term” (xe8i6Te in Greek) between the two others. In the same way, one idea can relate the two others, allowing a better understanding of their relationship.
From the algebraic point of view, three main kinds of proportions are known. In the case of the arithmetic proportion, the three terms are related by the equality
a-b= b-c
where b is the arithmetic mean between a and c:
a+ c
2
The harmonic proportion is governed by
a-b _a
b-c~ c
A specific case of this proportion occurs when
c= a+ b
which leads to
b=a-/2
The golden proportion is a special case of the geometric proportion characterized by
c_ b
b~ a
or
b = yj a-c
where
c= a + b
If we write
the governing equation becomes
<>2 + 4> -1 = 0
This equation has two roots
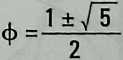
The approximate absolute root values are 1.618 and 0.618 and they are both known as “golden numbers.” Many mathematical developments have been made based on the golden number and specifically in terms of the Fibonacci series. However, if we are interested in the symbolic approach, then it can be noted that, c being the result of the combination of a and b, “b is to c as a is to b.” Establishing in such a way a continuous relationship between the whole and its parts, the division in mean and extreme ratio for a segment is such that the ratio of the smaller segment to the larger is the same as that of the latter to the whole. It is of great importance when c is considered as the “principle,” the “primal unity,” the “one”; and it is interesting to notice, as did Ghyka, that this irrational number can be reached with calculations made only with the number 1. It can be demonstrated that
1
= lim ;
and
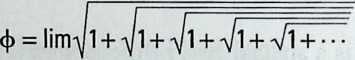
In symbolic studies, the number 1 has a great importance; it is the principle from which all things are derived, and expressions of <±> based on this value attest to its direct filiation with unity, known as the key to harmony in many fields, particularly in architecture.
Besides the algebraic approach, the geometrical approach can also be used and two geometrical constructions are traditionally described. We give these two constructions next.
For a given segment AB (Figure 10.1), the division must be done in such a way that “the smaller part be to the greater what this last one is to the initial segment,” achieving by geometrical means the specific case of geometric proportion.
On the straight line perpendicular to AB at B, we transfer a segment BC =
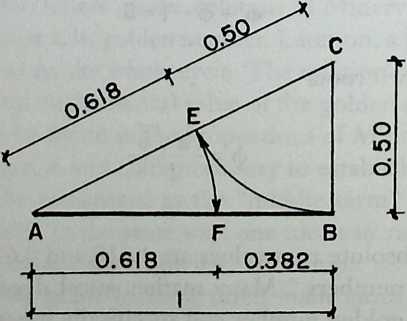
Figure 10.1 First geometrical construction of the golden proportion.
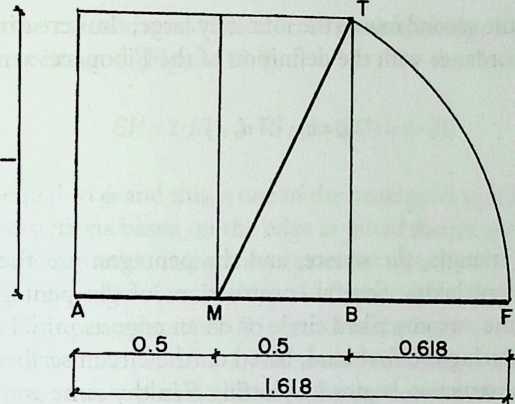
Figure 10.2 Geometrical construction of the golden proportion based on a square.
AB / 2. On CA we plot point E defined by CE = CB and on AB a point F such that AF = AE. This point produces the required division and it can be verified, by calculation of the different lengths, that
1.618
rD
The other geometrical construction commonly used is as follows: A square with unity-length edge AB is first divided into two equal rectangles (Figure 10.2). M being the middle point of AB, pointFis taken on the line AB and its position is defined by MF = MT (MT being the diagonal of either one of the two rectangles).
These two constructions are based on the division of the initial segment AB into two equal parts and the drawing of a square angle, which can be done with a compass. They can be grouped together in a single diagram (Figure 10.3). When it is repeated again and again, the first construction leads to the
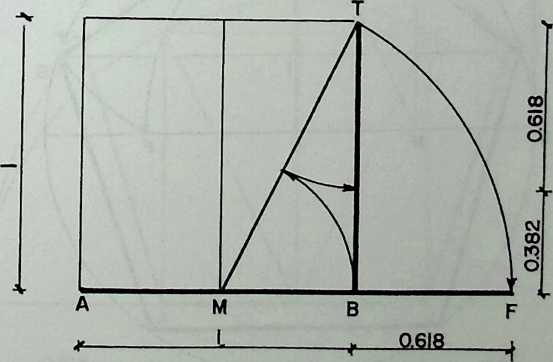
Figure 10.3 Geometrical construction of the golden proportion: synthesis.
infinitely small, the second one to the infinitely large, thus creating a sequence of lengths in accordance with the definition of the Fibonacci series for which
un=un_1+un_2
The Pentagon
The equilateral triangle, the square, and the pentagon are the constitutive faces of regular polyhedra. Several constructions of the pentagon are used, based either on the circumscribed circle or on an edge as initial data.
When considering the first kind, based on the circumscribed circle (Figure 10.4), the construction begins by plotting F in the same way as in Figure 10.3, AB being the circle radius. It can be verified that TF is the required edge of the pentagon. The resulting value is
7F = Vl + 0.6182 =1.176
which is in accordance with the algebraic value calculated with trigonometry, that is,
7F=2-sin (tt/5) = 1.176
It is interesting to notice that the pentagon apex angle is equal to 108°, and that sin (54°) = 0.809 = <j> / 2
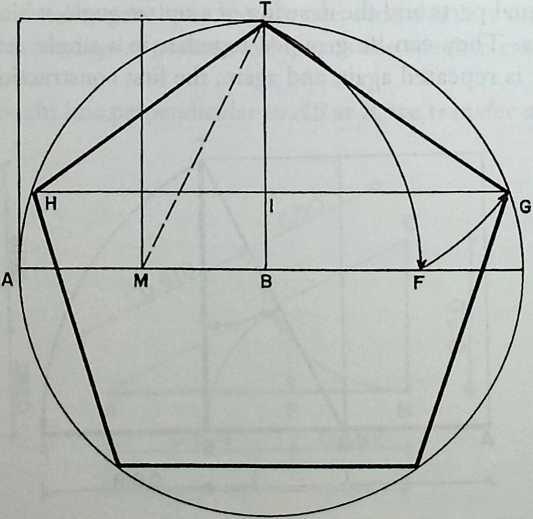
Figure 10.4 Pentagon inscribed in a circle.
which allows the calculation of the ratio between the edge TG and the diagonal GH in the pentagon (Figure 10.4):
GH = 2-IG = 2-TG -sin (54°) = c>-TG
This ratio is equal to <f> and this is one of the pentagon’s significant properties. Two constructions based on the edge as initial datum are described next. The first construction using the edge as basis rests on this property (Figure 10.5). AB is the edge of unit value, and Fis defined as in Figure 10.2. Then AF = <b and a first pentagon apex E is found at the intersection of two circles: one of center A and radius AB = 1, the second of center B and radius BE = c{). Other apices are simply obtained from a similar construction.
A second construction using the edge as basis can also be employed (Figure 10.6). We draw two circles Cl and C2 (centers A and B, radius equal to AB) that intersect at J and J. A third circle (center J, radius equal to AB) intersects Cl and C2, respectively, at points G and H, and straight line at point I. Apex E is given by the intersection between Cl and the line HI. Apex C is given by the intersection between C2 and the line GL The last apex D Res on line JJ’ and on a circle of center f and radius equal to 1. (This last construction is graphically sufficient but resulting apex angles are not strictly equal to 108°.)
Polyhedra
Five Regular Polyhedra
There are five regular polyhedra and only five. For each of them, faces, edges, and apices are identical. The faces are regular polygons characterized by their
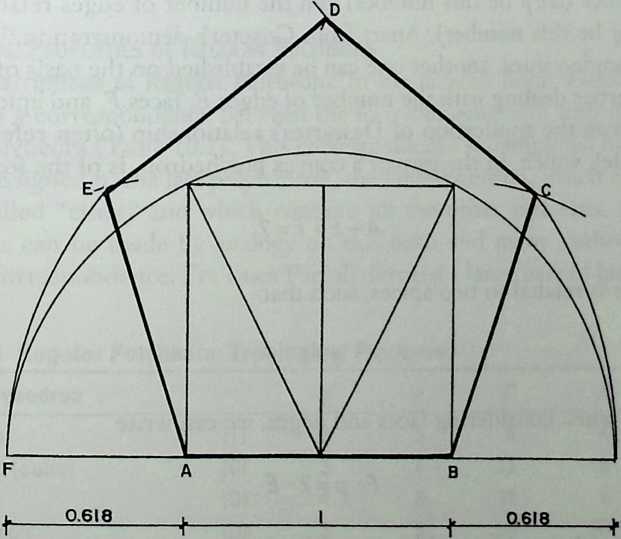
Figure 10.5 Pentagon of a given edge, exact construction.
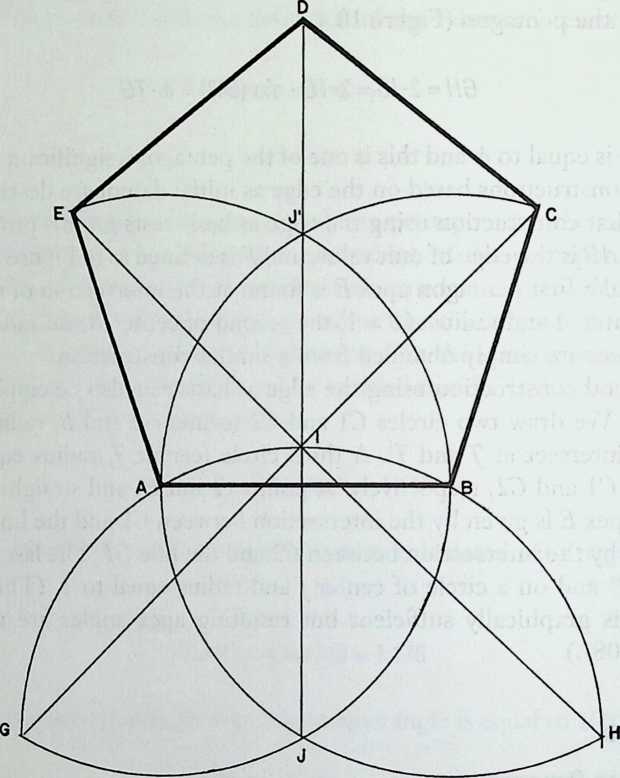
Figure 10.6 Pentagon of a given edge, approximate construction.
edge number (let p be this number) and the number of edges related to one apex (let q be this number). Apart from Coxeter’s demonstration,10 based on the apex angle values, another one can be established on the basis of topological properties dealing with the number of edges E, faces F, and apices A. It is derived from the application of Descartes’s relationship (often referred to as Euler’s rule), which, in the case of a convex polyhedron, is of the form:
A-E+F=2
Each edge is related to two apices, such that
A-q=2-E
Similarly, when considering faces and edges, we can write
F-p = 2-E
Descartes’s relationship can be expressed only in terms of E, p, and q in the following form:
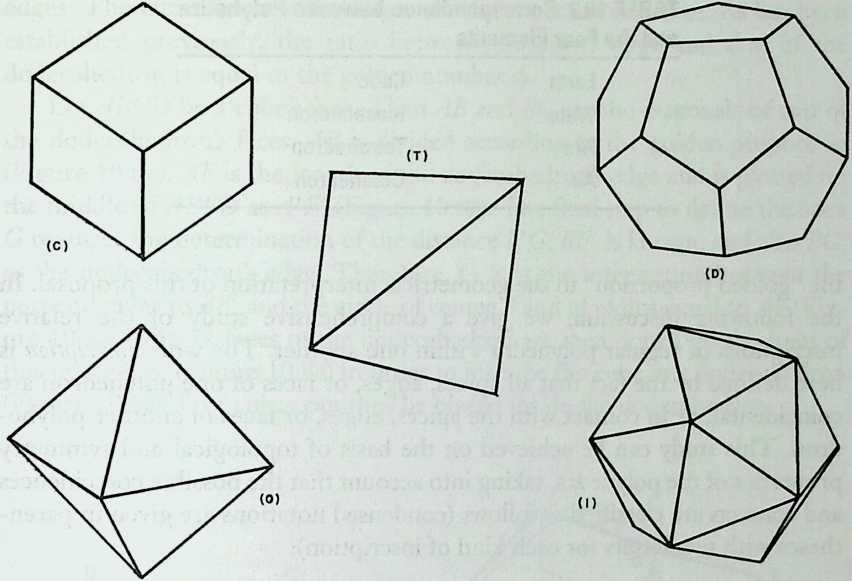
Figure 10.7 The five regular polyhedra: (C) cube, (0) octahedron, (T) tetrahedron, (I) icosahedron, (D) dodecahedron.
Taking into account that p and q, which are integers, must satisfy
p>3, q>3
because faces are at least equilateral triangles, there are only five admissible values for the couple {p, q}. Denomination and topological characteristics of these five regular polyhedra (Figure 10.7) are fisted in Table 10.1.
Geometrical Properties of Regular Polyhedra
Relative Inscriptions of Regular Polyhedra. In his famous book Timaeus, Plato establishes a correspondence between the four elements with four of the five regular polyhedra (Table 10.2). This correspondence is completed by the specific role assigned to the last polyhedron, the dodecahedron, which represents what is called “ether” and which contains all the other elements. Symbolic derivations can be made by analogy on this basis and many authors agreed with this correspondence. Fra Luca Pacioli devoted a large part of his book on
TABLE 10.1 Regular Polyhedra: Topological Properties
| Regular Polyhedron | P | E | A | F | ||
| Tetrahedron | (T) | |||||
| Hexahedron (cube) | (C) | |||||
| Octahedron | (0) | |||||
| Dodecahedron | (D) | |||||
| Icosahedron | (1) |
TABLE 10.2 Correspondence between Polyhedra
| Earth | Cube |
| Water | Icosahedron |
| Fire | Tetrahedron |
| Air | Octahedron |
the “golden proportion” to the geometrical interpretation of this proposal. In the following discussion, we give a comprehensive study of the relative inscriptions of regular polyhedra within one another. The word inscription is here defined by the fact that all apices, edges, or faces of one polyhedron are coincidental, or in contact with the apices, edges, or faces of another polyhedron. This study can be achieved on the basis of topological and symmetry properties of the polyhedra, taking into account that the possible coincidences and contacts are classified as follows (condensed notations are given in parentheses with two letters for each kind of inscription):
-
an apex with an apex (AA)
-
an edge with an apex (EA)
-
a face with either an apex (FA) or an edge (FE)
From the systematic study of mutual correspondence between one polyhedron and the other four, the inscriptions given in Table 10.3 can be estab-fished. Table 10.3 shows that only the dodecahedron can “receive” the other four polyhedra in accordance with the geometrical interpretation given by Plato. Simultaneously, the tetrahedron is inscribable in the other four. These geometrical properties will be subsequently exploited at the symbolic level. The relative inscriptions of the four polyhedra in the dodecahedron will first be described in detail. No calculations are given here in terms of angles and length ratios: They have been carried out on the basis of spherical and Cartesian coordinates in order to obtain the appropriate size required for display.14
Dodecahedron and Cube.The cube’s construction is very well known and is not presented here. Proceeding “Beyond the Cube,” we begin with a description of the drawing procedures for the dodecahedron.
Each of the dodecahedron’s 12 faces is related to corresponding cube’s
TABLE 10.3 Relative inscriptions of regular polyhedra
| Tetrahedron | Cube | Octahedron | Icosahedron | Dodecahedron | |
| Tetrahedron | EA | ||||
| Cube | EA or FE | FE | |||
| Octahedron | EA | EA | |||
| Icosahedron | FA | FA | FA | ||
| Dodecahedron | AA | AA or FE | EA | FE |
edges: The latter become the diagonals of the pentagonal faces. As has been established previously, the ratio between the cube’s edge and that of the dodecahedron is equal to the golden number <£>.
Let ABCD be a cube’s face. Then AB and BC are the diagonals of two of the dodecahedron’s faces. AB is divided according to the golden proportion (Figure 10.8/z). AF is the length of the dodecahedron’s edge and is plotted on the middle of ABCD as AF (Figure 10.Sb). The final step to define the apex G requires the determination of the distance FG; BF is known, and also BG, as the dodecahedron’s edge. Therefore, G is at the intersection between the perpendicular to BF and the circle of center B and of radius equal to AF (Figure 10.8c). The 12 faces of the dodecahedron are then drawn on the basis of this procedure (Figure 10.8d) in order to inscribe the cube in a dodecahedron (Figure 10.8c). Five cubes can thus be placed inside the dodecahedron.
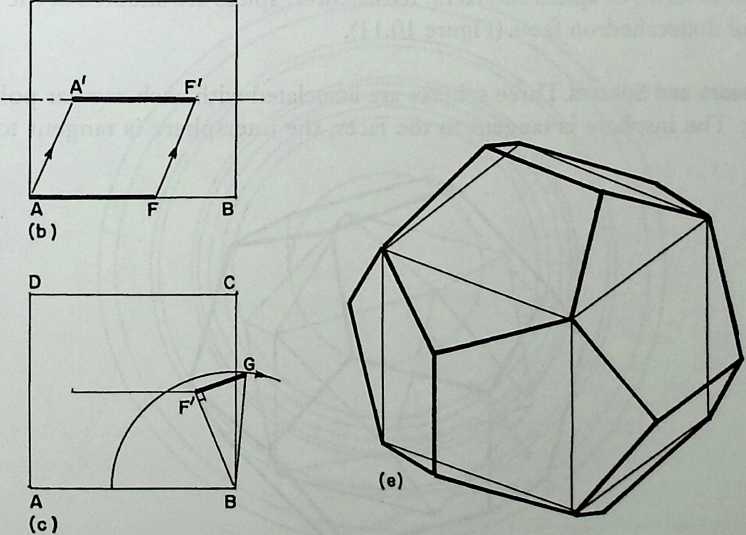
Figure 10.8 Dodecahedron and cube: (a) determination of dodecahedrons edge length; (b) plotting A F, projection of dodecahedrons edge on ABCD; (c) determination of FG; (d) two dodecahedrons faces on the cube; (e) cube inside a dodecahedron.
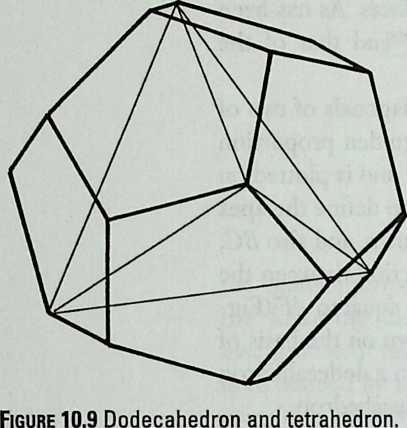
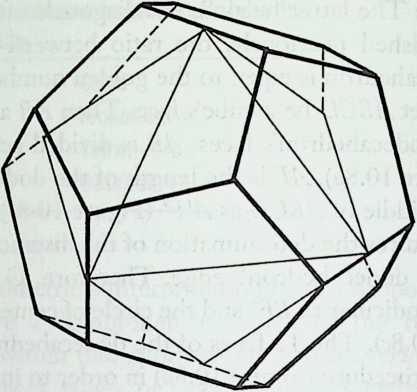
Figure 10.10 Dodecahedron and octahedron.
Dodecahedron and Tetrahedron. As the tetrahedron is inscribed in the cube by coincidence between its four apices with four of those of the cube, one position is immediately determined (five positions can be found according to the relative number of apices between the dodecahedron and the tetrahedron) (Figure 10.9).
Dodecahedron and Octahedron. Identical orthogonal symmetries exist for both of these polyhedra; inscription is obtained from contact between the six apices of the octahedron and six of the thirty edges of the dodecahedron at their middle (Figure 10.10). Five octahedra can be placed inside a dodecahedron.
Dodecahedron and Icosahedron. Correspondence between these two polyhedra is dual in terms of apices and faces: Icosahedron apices are situated at the centers of dodecahedron faces (Figure 10.11).
Polyhedra and Spheres.Three spheres are associated with each regular polyhedron: The insphere is tangent to the faces, the intersphere is tangent to the
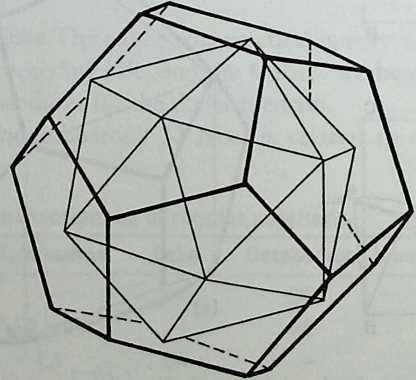
Figure 10.11 Dodecahedron and icosahedron.
TABLE 10.4 Radii of Associated Spheres
| Polyhedron | Circumsphere Radius | Intersphere Radius | Insphere Radius |
| Tetrahedron | |||
| Octahedron | |||
| Cube | |||
| Icosahedron | |||
| Dodecahedron |
edges, and the circumsphere contains all the apices of a regular polyhedron. This a geometrical characteristic of regular polyhedra.
Corresponding radii have been calculated (Table 10.4) for the inscription situation of all polyhedra inside a dodecahedron. As a basis, we chose an edge cube equal to 2. It can be seen that there are 10 distinct spheres because some of them are common to two or three polyhedra (Figure 10.12). Table 10.4 corresponds to the inscription of the four polyhedra in the dodecahedron (Figure 10.13). In symbolic terms, the number 10 is important; it recalls the famous Pythagorean tetraktis and is, of course, closely associated with the number 5 and also the golden number. It can also be related to the 10 sephiroth of the cabala.
¶ CONCLUSION
From the preceding discussion we want to underline, among the important properties that have been described, the inscription of regular polyhedra in
Figure 10.12 Ten spheres.
the fifth one, the dodecahedron (Figure 10.13), and the number of associated spheres.
¶ SYMBOLISM AND POLYHEDRA
Introduction
Because this book is concerned with architecture, in the following discussion we will give some landmarks that relate geometrical properties and symbolic meanings for polyhedra which are inherent in architecture.
The purpose of this section is necessarily humble because of the very subject under discussion: We only hope to indicate a pathway or two for research in the visible and the invisible. The guide to these pathways can be the symbolism of polyhedra, which is as present in polyhedral architecture as it was in Plato’s cosmogony in his Timaeus.
On Symbolism
The symbolic approach is rare enough in these days to justify a few reminders concerning this procedure. The essence of the “symbol” is that it cannot be
Figure 10.13 Inscription of the four elements inside a dodecahedron
defined without being mutilated, limited, deformed, or even eliminated. Indeed, the question is not to define “a” specific symbol but to determine what is found under the heading “symbol.” “The” symbol is a collective singularsimply indicating symbolism that must be investigated from a multiplicity of angles. It is usually accepted that the origin of the word is the Greek symbolon, which was a sign of recognition formed by two halves of a broken object; joining two members of the same brotherhood. The verb symballein also implies the idea of togetherness through the prefix “sym” but includes the idea of throwing or projection. A symbol is an image presenting an analogical representation of its object. It consists of three elements: the outward, that is, the visible, perceptible, concrete, and rational representation, the word; what is represented, that is to say, the invisible, the irrational, the idea represented by the symbol; and, finally, the relation between the outward and the idea. The symbol moves from the visible and rational to the hidden and irrational. The symbol requires both comprehension from analysis of each of its components and intuitive perception. However, although the symbol expresses an ideaor enables it to be expressedit does not provide an explanation because the visual image given by the symbol is only the reflection of what is not known. It awakens, suggests, and provokes.
The symbol underlines the connections between the various parts of the cosmos. It reveals the harmony of the world and the bonds that join what is separated, or that which seems to be separated. It gives homogeneity of meaning to what is represented. It reveals by veiling and achieves while destroying. As a prism between body and spirit, the symbol returns light and image in a different manner depending on the illumination that it is given and depending on the direction from which it is regarded. In this, it is a living, perpetually changing, and moving image, which remains constant in its metaphysical span.
A simple illustration of this is what Vieux15 called “le Pavilion des Can-tonniers” (the roadmenders’ hut), consisting of a cube topped by a squarebased pyramid of four faces with identical slopes (Figure 10.14).14 We are here at the heart of an elementary polyhedral construction. The layout of the four slopes is obtained from a pentagon whose side is equal to that of the square; only four sectors of the pentagon are used. The symbol associated with this form recalls the need to divide the pentagon. This construction, consisting of a cube topped by a pyramid, symbolizes a call for spiritual elevation from the visible world (the cube corresponds to the quaternary of the visible and material, e.g., to Plato’s four elements: earth, air, fire, and water). The notion of ascension is suggested by the slopes of the pyramid, whose summit is the final point. The outline of this pyramid contains the symbolism of the golden number. It requires the construction of a pentagon, which cannot be obtained, as we previously remarked, without tracing with a compass the proportion of the golden number. As such, this structure contains the elements required to awaken consciousness and acts as a catalyst on the imagination. It acts as any symbol in leading from the concrete to the idea.
Elevation
Figure 10.14 Roadmenders hut: geometrical construction.
Plato’s Cosmogony in Timaeus
The Four Elements
The symbolic role of polyhedra reaches its full dimensions in Plato’s cosmogony.1 Plato’s writings are not analyzed hereinterested readers can profitably consult Critchlow’s work.4 In brief, three ideas should be stressed: harmony, duality, and ternary. The first idea is that of harmony in the Greek sense of the term, the idea being that any and all manifestations of the principle must preserve a harmonious relationship between the elements created and must be complete. This idea is discussed in the following quotation:
The Platonic Cosmos, then, in the words of Timaeus, was created by a “maker” who, wishing to make this world most nearly like that intelligent thing which is best and in every way complete, fashioned it as a single visible creature, containing within space itself all living things, whose nature is of the same order space. (Timaeus 30d)
Now that which comes to be must be bodily, and so visible and tangible; and nothing can be visible without fire, or tangible without something solid, and nothing is solid without earth. Hence the god, when he began to put together the body of the universe, set about making it of fire and earth. (Timaeus 31b)
These two elements cannot be satisfactorily united without a third; for there must be some bond between them drawing them together. And of all the bonds the best is that which makes itself and the terms it connects a unity in the fullest sense; and it is of the nature of a continued geometric proportion to effect this most perfectly. (Timaeus 31c)
…The “maker” set water and air between fire and earth, and made them so far as was possible, proportional to one another, so that as fire is to air, so is air to water, and as air is to water, so is water to earth, and thus he bound together the frame of a world visible and tangible. (Timaeus 32b)
The world is then a living being, whole and complete, of complete parts … and he turned its shape round and spherical, equidistant every way from center to extremitya figure the most perfect and uniform of all; for he judged uniformity to be immeasurably better than its opposite. (Timaeus 33b)1
¶ The Constitution of Polyhedra and Their Interrelations
Recall that the regular polyhedra that symbolize the four tangible elements are: the tetrahedron for fire, the octahedron for air, the cube or hexahedron for earth, and the icosahedron for water. A fifth and last regular polyhedron, the dodecahedron, is taken to represent the etherthe quintessence of which the heavenly bodies are made and in which the four other elements are impregnated.
…To the tetrahedron they ascribed the fire, for that it is ascendeth upward according to the figure of the Pyramis. To the ayre, they ascribed the Octohedron for that through the subtle moisture which it hath, it extendeth it selfe every way to the one side, and to the other, accordyng as the figure doth. Unto the water, they assigned the Ikosahedron, for that it is continually flowing and moving, and as it were makyng angles on every side according to that figure. And to earth they attributed a Cube, as to a thing stable, firme and sure as the figure signifieth. Last of all a Dodecahedron, for that it is made of Pentagons, whose angles are more ample and large than the angles of the other bodies, and by that meanes draw more to roundnes, & to the forme and nature of a sphere, they assigned to sphere, namely, to heaven. Who so will read Plato in his Timeaus, shall read of these figures and of their mutual proportion, straunge matters, which here are not to be entreated of, this which is sayd, shall be sufficient for the knowledge of them and for the declaration of their definitions. …16
The geometrical inscriptions of the four elements in the dodecahedron, described in the previous section, are in total agreement with the symbolic approach described by Plato.
We know that there cannot be other polyhedra satisfying the definition of regularity. It is fundamental to note that these five polyhedra, together with the thirteen Archimedean polyhedra and all those subsequently studied by scholars, form part of a continuum, which makes it possible to return to the source by simple geometrical transformations of truncation, duality, similitude, and so forth. Numerous authors have discussed this question using different approaches but displaying a common desire to return to the principle. Noteworthy research includes that of Pacioli,2 with the collaboration of Leonardo da Vinci, and more recently the works of Critchlow,4 Lalvani,13 and Pearce.171 beg to be forgiven for only mentioning a few bibliographical landmarks, knowing that, as with symbols, one idea leads to another.
The symbolism of polyhedra cannot be dissociated from the symbolism of numbers. This relationship is illustrated, for example, by distinguishing three classes among the regular and semi-regular polyhedra. One class consists only of the tetrahedron and the truncated tetrahedron; the second comprises the cube, the octahedron, and their Archimedean derivatives; and the third consists of the icosahedron, the dodecahedron, and their Archimedean derivatives. This classification reveals a symbolic analogy. Through rotational symmetries, the first class can be linked with the number 3; the second with the number 4, the outwardness number, and the third with the number 5, representing the quintessence and the proportion between mean and extreme ratio characterized by the golden number. This series 3, 4, 5 is reminiscent of the Isiac triangle dear to the Egyptians, and at the same time shows which geometrical procedure can be used to move from one of these classes to another. It is known, for example, that obtaining the volumes of the icosahedron class requires the truncation of a polyhedron edge with a ratio of 4>.
¶ CONCLUSION
Many architects design their projects in accordance with the proportions of the human figure, which are close to the golden proportion. Ancient temples were built on the basis of man’s measurements; it was sufficient to use a 13-node rope to trace a double square and the Isiac triangle. Builders knew the golden proportion, which is present in numerous constructions. With his Modular Le Corbusier tried to put together the double square and the golden proportion and generated a human scale of measurements. Symbolism gave meaning to architecture by using suitable proportions, which are inherent in polyhedra. Today, proportion and symbolism in polyhedra are a way, among others, to give sense to architecture “beyond the cube.”
¶ NOTES
-
Platon, Sophiste-Politique-Philebe-Timee-Critias, Gamier Flammarion, Paris, 1969.
-
Fra Luca Pacioli di Borgo san Sepolcro, La Divine Proportion, reprinted by Librairie du Compagnonnage, Paris, 1988.
-
K. Critchlow, “The Platonic Tradition on the Nature of Proportion,” Lindisfarne Letter on Geometry and Architecture, Lindisfarne Association, 1980.
-
K. Critchlow, Order in Space, Thames and Hudson, London, 1971.
-
R. C. Meurant, “A New Order in Space-Platonic and Archimedian Polyhedra and Tilings,” International Journal of Space Structures, Vol. 6, No. 1, 1991.
-
R. C. Meurant, The Aesthetics of the Sacred, a Harmonic Geometry of Consciousness and Philosophy of Sacred Architecture, 3rd ed., Opoutere Press, Boulder and Auckland, 1989.
-
R. C. Meurant, “The Myth of Perfection of the Platonic Solids,” Proceedings of the Conference on Myth Architecture History Writing, University of Auckland, New Zealand, July 1991.
-
R. Lawlor, Sacred GeometryPhilosophy and Practice, Thames and Hudson Art and the Imagination Series, London, 1982.
-
Matila C. Ghyka, Le nombre dlor. Gallimard, 1959.
-
H. S. M. Coxeter, Regular Polytopes, Dover, New York, 1973.
-
D. Hilbert and Vossen S. Cohn, Geometry and the Imagination, Chelsea, New York, 1952.
-
Le Corbusier, Le Modular, Editions de 1’Architecture d’Aujourd’hui, 1965.
-
H. Lalvani, “Non-Periodic Space-Filling with Golden Polyhedra,” First International Conference on Lightweight Structures in Architecture, SLA 86, V. Sedlak, ed., Vol. l,pp. 202.
-
R. Motro, “Etude geometrique et symbolique des polyedres reguliers,” Note de recherche 95, LMGC Universite Montpellier II, July 1995.
-
M. Vieux, Les Secrets des Batissettrs, Collection les Enigmes de 1’Univers, Robert Laffont, ed., Paris, 1975.
-
S. K. Heninger, Touches of Sweet HarmonyPythagorean Cosmology and Renaissance Poetics, The Huntington Library, San Marino, CA, 1974.
-
P. Pearce, Structure in Nature Is a Strategy for Design, MIT Press, Cambridge, MA, 1978.
-
R. Motro, “The Symbolism of Polyhedra in Space Structures,” International Journal of Space Structures, Vol. 6, No. 4, 1991.
¶ The Structural Morphology of Basic Polyhedra
Tore Wester
¶ INTRODUCTION
The fascinating world of polyhedra has a long and diverse history. These archetypical geometrical configurations have influenced numerous aspects of art and science. When introduced in a theme or subject, polyhedra seem to be the carriers of a strange and satisfying basic order to the subject, for example, Plato’s pythagorean cosmology, Kepler’s planet shells, the crystal symmetry groups, and so forth. Different fields, such as crystallography, engineering, mathematics, astronomy, architecture, art, cosmology, astrology, and religious and divine orders, have all been affected by the scientific and philosophical conceptual content of polyhedra.
Polyhedra almost always play a role in architecture as architects think in terms of plane facets such as walls, roofs, ceilings, facades, and so on, combined to form spatial configurations, making up what are basically nothing other than clusters of polyhedra! Unfortunately, the connection with polyhedra is often unperceived and unreflected, and the cube seems to be the absolute favorite. This book is a serious and qualified attempt to challenge this
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel □
301
ISBN 0 © 1997 John Wiley & Sons, Inc.
unfortunate situation. Moreover, the lattice structure, based on bars and nodes in the simple rigid triangular configuration, has been considered as the only structural archetype. This defines the triangulated members of the regular polyhedrathe tetrahedron, octahedron, and icosahedron as the only inherently rigid ones, leaving the nontriangulatedthe cube and the dodecahedronas incomplete and inferior structural configurations.
This chapter will try to bring a satisfactory order to the concept of basic
Figure 11.1
Figure 11.2
BOX 1: Expressions and Definitions
A simple polyhedron is a one-connected polyhedron where all facets are planar and one connected. Connectivity is the maximum number of closed chains required to divide the polyhedron into two separate parts; that is, a ball is one connected, whereas a torus is two connected (Figure 11.1). A facet that has a boundary consisting of only one loop is one connected, whereas a facet with a single hole (i.e., two loops) is two connected (Figure 11.2). A simple polyhedron may be convex or nonconvex.
Basic polyhedra, in the present context, mean polyhedra that might be fixed to the ground, and perhaps with some elements or links removed or added, but geometrically based on one or more simple polyhedra.
Elements are plates (facets) or nodes (points), whereas links (lines) are their connectors (shear lines or bars). Linking is a list of information concerning which elements are finked together. The linking of a node is the information concerning which other nodes the node is connected to (by bars). In the case of plates, linking is the information concerning which of the neighboring plates the plate is connected to (by shear lines). In order to define a plate based on the plane of the plate and its linking, the links must be listed in the required order as when walking around the boundary of the plate.
The valency (Figure 11.3) of an element (plate or node) is its number of links (shear lines or bars). Valency, linking, and connectivity are all topological information. Topological information is information about geometric values that are counted but not measured. Metric
geometry is, on the other hand, information about positions given by coordinates, lengths, angles, and so on, that is, all characteristics that can be measured. Mathematically, topology is described by integers (e.g., 1, 5, 112, etc.) and metric geometry by real numbers (e.g., 4.37, 5.00001, 199.998, etc.).
structures in terms of their relationship to the Platonic polyhedra. In order to understand why this structural order in space has not been described a long time ago, it is necessary to take a brief look at the history of the theory of structures.
Brief History of Polyhedra as Structures
The history of the theory of basic structures related to polyhedra and topology is short and uncomplicated.
The French bridge and road engineer, but primarily mathematician, Augustin-Louis Cauchy (1789) described in 1813* the rigidity of arbitrary convex polyhedra from a purely geometrical viewpoint. This means that he did not consider the equilibrium and the type of forces inherent in their geometry.
A few years later, in 1837, the German professor of astronomy August Ferdinand Mobius (1790), inventor of the famous nonorientable Mobius strip in 1858, made what is probably the first statical description of polyhedra as structural objects. In his textbook on statics,2 Mobius states, probably for the first time ever, the minimal number of bars (BA) required to
BOX 2: Expressions and Definitions
A polyhedral lattice structure is composed of nodes (polyhedral vertices) that are linked by bars (polyhedral edges). The bars are hinged to the nodes; that is, it is not possible to transfer bending moments between bars. The nodes distribute axial forcestension or compression between bars (Figure 11.4).
A polyhedral plate structure is composed of flat, rigid-in-plane plates (polyhedral facets) that are hinged together along shear lines (polyhedral edges) as lines of intersection between plates. The plates distribute the forces between the shear lines. In plate action only shear forces are transferred across the shear lines. A shear force is a pair of oppositely directed parallel forces of equal magnitude and with zero distance between them, acting between two plates that are interconnected by a shear line (Figure 11.5). The plates distribute the forces as shear forces among the shear lines.
In solving the static equilibrium, each of the elements (a node or a plate) represents three equations, whereas every link (a bar or a shear line) represents one unknown.
BOX 3: Expressions and Definitions
Two objects are dual if they are based on the same information, but this information is interpreted in a different way. A dttal transformation implies a switch between the interpretation of data. Further, a dual transformation must preserve all data, and the dual of the dual must be the original. It may be described as a kind of mirror image, two sides of the same thing, and so forth.
Whereas duality is a technical expression, dualism is a philosophical term often used as a contradiction to monism and related to two opposites (good/bad, yin/yang, closed/open, feminine/masculine, day/night, etc.). In the actual context, duality in many ways appears to approach dualism. In three-dimensional geometry dualism is related to the substitution of vertices with planes. After a dual transformation the valency, linking, and connectivity remain the same, but the element type has changed, as nodes and plates are exchanged.
Gaussian curvature: The two principal curvatures at a point on a surface may have either equal signs if the centers of curvature are located on the same side of the surface (Figure 11.6) or opposite signs if the centers of curvature are on different sides of the surface (Figure 11.7). If the signs are equal, then the Gaussian curvature is positive because +(+) = + and -(-) = + and negative if they are different because -(+) = -. Positive Gaussian curvature is also called synclastic, elliptic, or dome shaped, whereas negative Gaussian curvature is called anticlastic, hyperbolic, or saddle shaped. If one or both of the principal curvatures are 0, then the Gaussian curvature is 0 because 0 times anything is 0.
Figure 11.6 Figure 11.7
(Figures courtesy of Ola Wedebrunn.)
stabilize a certain number of nodes (NO) BA = 3NO -6 (this should therefore rightly be called Mobius’ theorem of rigidity). By combining the important theorem of Euler (1707) for polyhedra consisting of vertices, facets, and edges (V+ F = E + 2), Mobius also proved that the number of equations and the number of unknowns are equal (neutral configuration) for any triangulated simple polyhedron regarded as a pure lattice structure. The same neutrality holds for an arbitrary simple polyhedron regarded as a lattice structure supplied with rigid-in-plane plates filling out all facets with more than three edges. In this case rigidity is achieved by means of the transfer of forces parallel to the bars between the plates and the lattice structure. However, it is remarkable and quite surprising that he did not describe the bar-and-node free system: pure plate action and its theorem of rigidity.
Mobius wrote a whole chapter,3 Von der unendlich kleinen Beweglichkeit
BOX 4: Expressions and Definitions
Neutrality (or kinematical neutrality): A structure is neutral if it is just rigid; that is, it has no redundancy. It becomes movable if a single link (bar or shear line) is removed from the structure. A neutral structure is statically and geometrically determinate; that is, it is in equilibrium by static considerations alone and complies with the theorems on the minimum requirements for rigidity and it may be built and determined geometrically with no constraints on the metrical values.
Rigidity, stability: A structure is rigid or stable if it has enough links (bars or shear lines) to fix all elements (nodes or plates) and they are arranged geometrically and topologically in such a way that static equilibrium can be achieved; that is, the static equations can be solved. A rigid or stable structure may be sensitive (see below). In the case of a critical situation, it is called flexible. Stability is used here as a kinematicnot an elastic property.
Movability, flexibility: If a structure has too few links (bars or shear lines) to fix the elements (nodes or plates), it is movable or unstable. If the links in a rigid structure change length or position, the structure may become movable. If the geometry of a rigid structure is changed, it may go into a critical (flexible) or a near-critical (sensitive) form. In these cases the static equations give no solutions or give unreliable solutions.
Sensitivity: If a structure is in a near-critical state, a number of internal forces become very large even for moderate external loadings. Hence the deflections will be large and the structure feels movable. This will often happen under very particular external load combinations, whereas it is perfectly rigid for other loading cases.
Redundancy: If a structure has more links (bars or shear lines) than are needed for rigidity, it is redundant. If a redundant structure has a special geometry and/or a special linking, it may be movable, flexible, or sensitive. The redundancy number indicates the number of linksbut not which specific ones that may be removed without changing the stability situation.
(On the Infinitesimal Movability), where he explains that there are special critical cases where a plane neutral lattice structure (the equation for the plane two-dimensional lattice, BA = 2NO -3, was also first stated by Mobius) is not absolutely rigid. The statical characteristic is that the determinant of the equilibrium equations approaches 0; hence the magnitude of the forces approaches 00. Furthermore, he describes methods to create these critical configurations as follows:
-
Make a plane neutral lattice structure movable by removing one bar.
-
Choose two nodes that can be moved relative to each other.
-
The distance between these two nodes has a maximum and a minimum.
-
Place the previously removed bar (with its new appropriate length) in one of these two extreme positions and the system becomes flexible.
This method also works sometimes for creating flexible three-dimensional structures.
Unfortunately, Mobius’ work on statics has been dormant for many years and he rarely gets credit for his important work. A notable exception is in the classical work by Stephen P. Timoshenko.4 Although Mobius’ theorems were rediscovered several years later by a number of prominent engineers, it appears that, for many years, very few discoveries regarding polyhedral structures were made.
In the field of flexibility, R. Bricard5 constructed, in 1897, flexible but selfintersecting octahedra, and in recent years Robert Connelly6 has, on a purely geometrical basis, found true non-self-intersecting and flexible polyhedraalso based on the octahedron. A very interesting paper by Jorgen Nielsen7 shows unexpected instability, argued on the basis of static equilibrium, for some combined plate and lattice structures that are shaped as step pyramids.
The historical work on polyhedral structures by Mobius has three of the four necessary ingredients for the full description of the basic structural morphology of polyhedra, namely, bars, nodes, and plates, but it lacks shear fines as a unique structural member. Probably because Mobius did not consider plate action as being just as basic as lattice action, the inherent structural activity of polyhedra has ever since been based on bars and nodes only. Accordingly, only three of the five Platonic solids appear inherently rigidnamely, all the triangulated onesthe tetrahedron, octahedron, and icosahedron, whereas the two remaining, the cube and the dodecahedron, are basically movable, that is, incomplete as rigid structures (Figure 11.8). In order to make them rigid, one can either add extra bars or plates or introduce bending stiffness in the bars and nodes.
This cosmology of structural action has been common knowledge and supported very actively by, for instance, R. Buckminster Fuller and many others. Of course, this situation is unsatisfactory, as the five Platonic polyhedra in so many other aspects form an archetypical entirety. This entirety can easily be achieved by using Mobius’ considerations about rigid-in-plane plates by intersecting them directly along what become the shear lines and arranging them as polyhedral structures and importantlyavoiding bar-and-node action similarly to the way that pure lattice polyhedra avoid plate action when
Figure 11.8 The three rigid and the two movable regular polyhedra as pure lattice structures. (Courtesy of Ola Wedebrunn.)
Figure 11.9 The three rigid and the two movable regular polyhedra as pure plate structures. Note that vertices are removed in order to avoid nodal (i.e., lattice) action. (Courtesy of Ola Wedebrunn.)
triangulated. The way of avoiding lattice action, hence isolating plate action in a simple polyhedron, is to require that all vertices are trivalent, which is the dual of the pattern for triangles, equal to trivalent facets. The trivalent vertex is topologically significant for the cube, the dodecahedron, and the tetrahedron but not for the octahedron and the icosahedron, which are unstable as plate structures (Figure 11.9). Note that all vertices are removed in order to avoid lattice action, hence isolating plate action. The stabilizing forces are shear forces transferred along the shear lines.
As Mobius’ theorem for pure lattice structures, when using geometrical symbols, is E = 3 V -6, the corresponding theorem for pure plate action can easily be found8 to be E = 3F -6, which, combined with Euler’s theorem for polyhedra, results in 2E = 3 the geometrical requirement of trivalent vertices for structurally neutral pure plate action for simple polyhedra. It is seen that if V and F are exchanged we shift between the two theorems of rigiditywhich means a shift between geometrical duals, because V and F are interchangeable, whereas E remains unchanged in Euler’s theorem V + F = E + 2. With structural symbols the theorem of rigidity for plate action will therefore be SL = 3 x PL -6, where SL and PL are, respectively, the number of shear fines and plates. This is seen to be the dual to Mobius’ theorem of rigidity for lattice structures: BA = ?>NO - 6.
Now the five Platonic polyhedra are all equally basic as structural objects. They are divided into two groups of three (Figure 11.10), where the tetrahedron is present in both groups, following exacdy the pattern for geometrical duality. The trivalent facet has the same structural impact for lattice action as the trivalent vertex has for plate action. This leads to the principle that topology and rigidity (with reservation for the previously mentioned critical situations) for simple polyhedra are the geometrical and structural expressions of the same thing and, at the same time, they are complementary.
Even though these considerations put statics in a satisfactory connection with polyhedra, their importance would have been very limited if the previously mentioned principles were restricted to the five Platonic solids. Fortunately, these static/geometric principles, based on the replacement of lattice nodes with plates and node-connecting bars with plate-intersecting shear fines, are valid, in general, for any arbitrary polyhedronand any cluster of
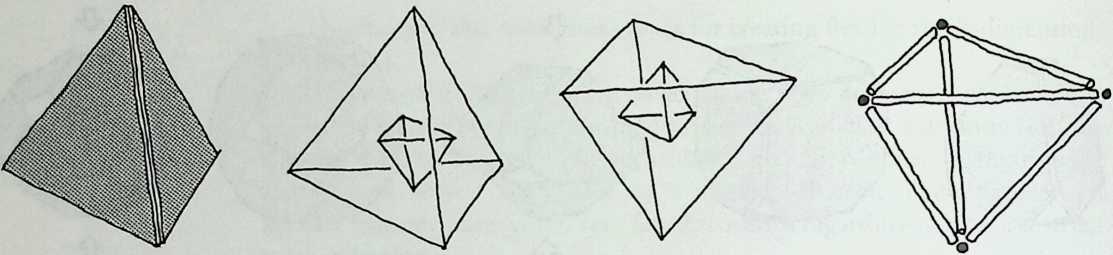
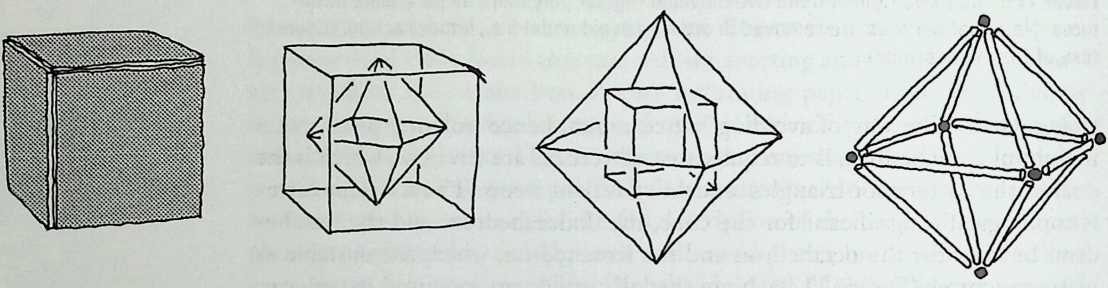
Figure 11.10 The basic structural behavior of the regular polyhedra follows exactly the geometrical duality: One of the dual versions is rigid by plate action, whereas the other is rigid by lattice action. (Courtesy of Ola Wedebrunn.)
polyhedraindependent of connectivity, linking, convexity, and so forth. For any given three-dimensional pure lattice structure, there always exists a dual pure plate structure, and vice versa, but, of course, it may not be suitable as a structure for architectureor anything else.
The trivalent vertex and trivalent facet are geometrical extremes (Figure 11.11) as no plane facet can have fewer edges than three and no vertex in three-dimensional space can have fewer than three adjacent edges. Between these two extremes there are countless possibilities for polyhedra with facets and vertices with different valencies. These not fully trivalent, simple polyhedra are movable either as pure plate structures or as pure lattice structures. They may be regarded as lattice structures stabilized by fill-in plates as considered by Mobius, or they may be regarded as two independent movable structural types (Figure 11.12) stabilized by the transfer of forces between the equally positioned bars and shear fines. I have suggested that these forces that
Figure 11.11 The triva I ent vertex and the equivalent facet are both geometrical extremes and form the geometric pattern synonymous with pure plate and lattice action. (Courtesy of Ola Wedebrunn.)
are working in between the two pure structural types are called buffer forces.9 These considerations give rise to the general theorem for the necessary requirement for rigid, simple polyhedra10
B4+S£+BL/ = 3x(/V0+W)-6
where BA, SL, BU, NO, and PL refer to the number of bars, shear lines, buffer forces, nodes, and plates, respectively. As all three variables on the left-hand side of the equation refer to edges, the equivalence of the general requirement as being identical to Euler’s theorem for polyhedra, E = E+ F -2, is easily rec-
Figure 11.12 The rhombic triacontahedron (left) and its dual, the icosidodecahedron (right), are both unstable as pure lattice and pure plate structures. However, if they are constructed so that both structural actions are possible at the same time and if buffer forces can be transferred between equally positioned bars and shear lines, they then become rigid. Note that trivalent nodes and equivalent plates may be removed without affecting the rigidity. (Courtesy of Ola Wedebrunn.)
ognized. It is also easily seen that the previously stated theorems for pure lattice and plate action will appear if the relevant parameters in the general theorem are required to be 0 (if NO = 0, then BA = 0 and BU = 0, and if PL = 0, then SL = 0 and 517= 0). This interpretation, which equates the level of plate and lattice action, has the advantage of following the concept of geometrical duality. The close topology-rigidity connection between the duals forms a promising basis of a “form-and-force language.” This is because it is possible to set up a number of surprisingly simple and unique rules for the description of the structural action of any three-dimensional configuration that is a combination of planes, vertices, and edges, as explained below.
The duality as described so far works on the level of topology and rigidity. This level of understanding is the most important for the architectural, morphological, and conceptual aspects: choice of structural types, choice of faceting, where to open up the building and where to close it, choice of structural material, and so forth. It does not, however, condition the exact shape, size, and form of facets and so on. However, the dual transformation concept may be extended to the level of metric geometry and statics.
This transformation is based on simple but essential and fundamental considerations:
-
Let the upper left of Figure 11.13 be an w-valent node in a three-dimensional lattice structure. Then Figure 11.13, upper center, shows the force vectors acting on this node and Figure 11.13, right, is the corresponding three-dimensional force vector polygon, which means that the force vectors are arranged unidirected and one after another in correct direction and magnitude. If the vector polygon forms a closed loop, then this is the necessary and sufficient requirement for this node to be in static equilibrium. If all nodes in the lattice structure are in equilibrium, then the whole structure is in equilibrium.
-
Now, let Figure 11.13, lower left, be an *n-*valent plate in a three-dimensional plate structure, and let a point (the origin) be positioned outside the plane of the plate. In this case Figure 11.13, upper center, represents the moment vectors acting on the origin.11 Figure 11.13, right, shows the three-dimensional moment vector polygon derived from the moment vectors acting on the origin. If this is unidirected and forms a closed loop, as before, then this is the necessary and sufficient requirement for this plate to be in static equilibrium. If this is the case for all plates in the plate structure, then the whole structure is in static equilibrium.
-
If a force vector polygon for a node in a lattice structure (Figure 11.13, right) and a moment vector polygon for a plate in a plate structure (also Figure 11.13, right) are identical, then the system of force vectors (Figure 11.13, upper center) is identical to the system of moment vectors (also Figure 11.13, upper center). It is significant that it is not possible to judge from the system of vectors and its polygon if it represents the equilibrium of a plate or a nodethis is up to you. This means that if
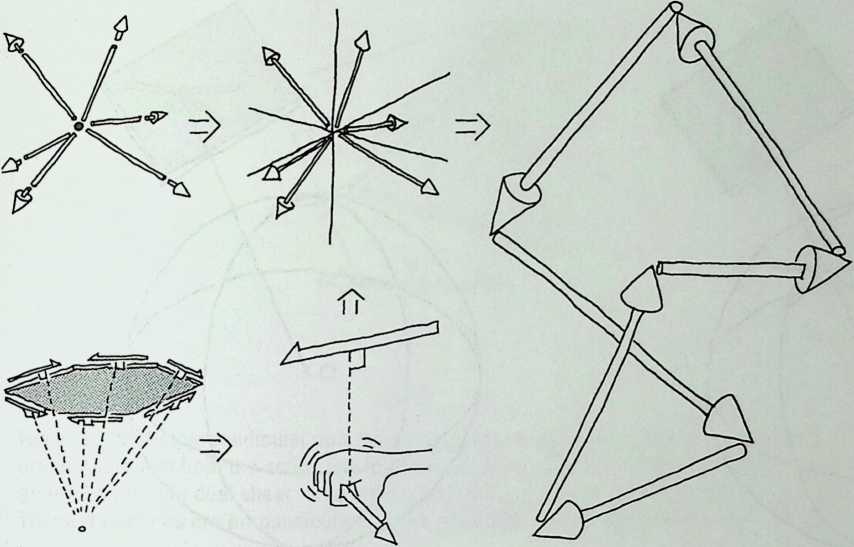
Figure 11.13 The equilibrium offerees on a node and the equilibrium of moments created by forces on a plane plate around a reference point (the origin) can be required to be equal. This forms the basic static requirement for structural duality. (Courtesy of Ola Wedebrunn.)
you do statical calculations on a three-dimensional lattice structure, you calculate a plate structure, of which form you have absolutely no idea, at the same timequite an interesting thought. It is also evident that the two systems cannot be mixed as the equilibrium requires the vector polygon to consist entirely of either force vectors or moment vectors.
-
If there is a transformation method that assures that the force vector and moment vector systems are identical, then we can switch between the two systems.
-
The force vector and moment vector systems can be made identical if the transformation of a node creates a plane plate, if a bar creates a line of intersection between plates (shear line), and if the force vector and the corresponding moment vector are always parallel. These simple requirements are fulfilled if the structures are transformed by the geometrical relation called polar reciprocation as described by Cundy and Rollet.12 A thorough explanation of the particular geometry inherent in polar reciprocation is given by Wenninger, based on his correspondence with Cundy.13
Polar reciprocation relates the location of a vertex and its dual plane simply as follows (Figure 11.14):
-
The method requires a reference point, chosen as the origin for simplicity.
-
The vertex is located on the line from the origin perpendicular to the plane.
-
The distance from the origin to the vertex multiplied by the distance from the origin to the plane is a chosen constant. If this constant is chosen as 1, the two distances are reciprocal.
Figure 11.14 Dual transformation by polar reciprocation. (Courtesy of Ola Wedebrunn.)
Figure 11.15 Direct dual transformation. (Courtesy of Ola Wedebrunn.)
This transforms the metric geometrical information between planes and vertices, whereas the topological information, that is, the linking of the vertices and the planes, respectively, remains unchanged.
A similar transformation, called direct transformation (Figure 11.15), simply changes the interpretation of the geometrical data between nodes and plates, and vice versa. This means that it is identical to polar reciprocation except that the distance between the elements is not reciprocated. Direct transformation maintains the valency of the elements, as does polar reciprocation, but not the statics. Polar reciprocation and direct transformation may be executed repeatedly one after the other, eventually in combination with changes in the position of the origin between the transformations. This combination makes a powerful tool for computerized methods for form finding of structures, not least because they relate architecturally very significant and different geometrieswithout changing the topology.
The polar reciprocation method proves to be as valid as the transformation method for structural duality for the following reasons:
-
It satisfies the requirements of the topological duality as shown in Figure 11.10.
-
There exists a line through the origin that intersects both the line that includes the bar and the line that includes the dual shear line. Furthermore, these three lines are perpendicular to each other (Figure 11.16). This quality implies that the moment vector will always be parallel to the corresponding force vector of the dual structure.
Figure 11.16 The perpendicular dual nature of geometry and forces: The line through the origin intersects both the action line for the axial force (which includes the bar) and the action line for the dual shear force (which includes the edge between the plates). These three lines are perpendicularto each other. (Courtesy of Ola Wedebrunn.)
The transformation factor between the magnitude of the bar force and the corresponding plate force in the dual structure is simply the actual distance d from the origin to the shear tine, because the bar force is required to be equal to the force in the shear line times its distance to the origin. The elastic properties are dually transformed14 by the factor dr. These transformations are very suitable for computers.
The preceding explanation is the extremely simple verification of the existence of structural duality. The static and elastic equations for dual structures are outside the scope of this chapter, but can be studied in the author’s paper.15
The procedure for the creation of dual structures will then be as follows:
-
Move your structure in space so you have the origin where you want it.
-
Perform a polar reciprocation. If the initial structure is a lattice structure, then the definition of which part of the plane should be materialized as a plate is a free choice and does not affect the statics, except that part of all the shear lines connected to this plate must be part of the materialized plate. Of course, the chosen geometry for the plate must enable the plate to be rigid in plane. Often it is practical that the shear lines define the boundaries of the plates.
-
All forces are transformed as explained previously.
A static calculation of a statically determinate plate structure can be executed as follows:
-
Transform the initial plate structure to its dual lattice structure. Any point of origin is possible, so you do not need to move the structure, unless the origin is very close to the plane of one of the plates. If the origin is too close to the plane of the plate, this will result in a computation that includes very small and very large numbers, which may create inaccuracy in the results.
-
Transfer all external loadings to act along the shear lines. For example, loads acting perpendicular to the plates can be transferred to the vertices by bending as in slabs, and these vertex forces can be resolved in the directions of the shear lines.
-
The dual external loads acting along the bars are determined by multiplying the external loads acting along the shear lines by the distance d from the origin to the actual shear line.
-
Compute the internal equilibrium of forces in all bars by a conventional computer program for three-dimensional structural design.
-
Transform the bar forces back to the plate structure as shear forces by dividing the bar forces by the same d used previously.
GEOMETRICAL QUALITIES OF DUAL STRUCTURES
Using the polar reciprocation method, the following qualities of dual structures can be identified:
-
The dual of an w-valent node is an 72-valent plate, and vice versa; see Figure 11.3.
-
There exists a line through the origin that is perpendicular to both a bar and its dual shear line and this bar and shear line are perpendicular to each other (Figure 11.16).
-
There is a certain distance from the origin where a node is part of the dual plane.
-
The origin can never be positioned in between a node and the dual plane.
-
Polar reciprocation cannot be executed if the origin coincides with a node, as the dual plane will be infinitely far away in any direction.
-
Polar reciprocation cannot be executed if the origin is part of the plane of a plate, as the dual node will be infinitely far away in the direction of the axis through the origin and perpendicular to the plane.
-
Polar reciprocation cannot be executed if the origin is part of a bar, as the dual shear line will be infinitely far away and the plates it should connect would be parallel, hence never intersecting.
-
A node close to the origin will, after polar reciprocation, produce a plate far from the origin, and vice versa, as the product of the two distances is a constant; that is, if the initial is very near to the origin, then the dual will be very far from the origin. The near to the for is an inherent dual quality.
-
The sign of Gaussian curvature remains unchanged during polar reciprocation. A saddle shape remains a saddle shape and a dome shape remains a dome shape.
-
Although the facets of a triangulated surface give no information about the sign of the Gaussian curvature for the main shape, the dual facets
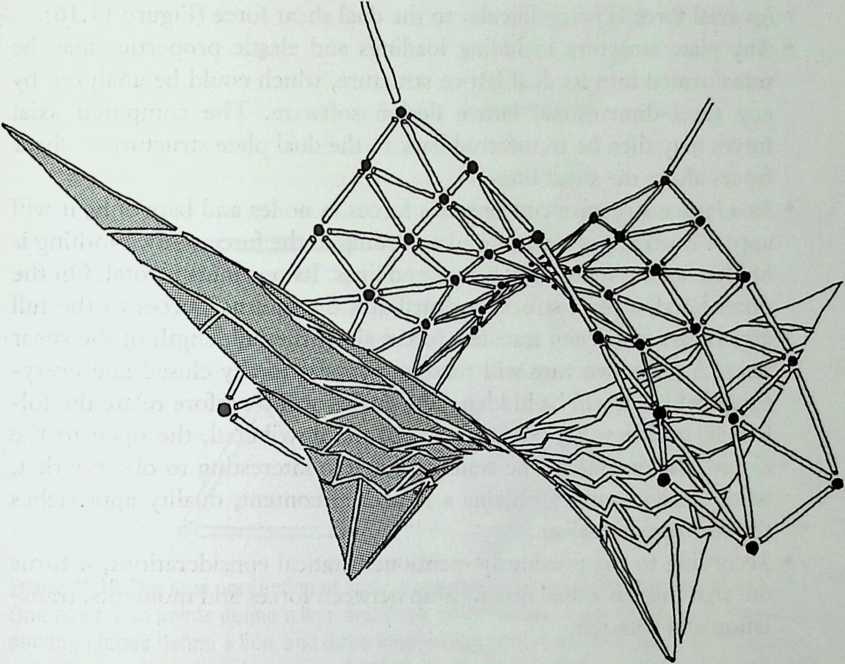
Figure 11.17 Each individual plate in a trivalent polyhedral structure is convex if the Gaussian curvature of the main shape is positive and nonconvex if the curvature is negative. A triangular mesh in a lattice structure does not reveal the sign of the Gaussian curvature. (Courtesy of Ola Wedebrunn.)
turn out to be convex for positive Gaussian curvature and nonconvex for negative curvature; see Figure 11.17. A plate in a pure plate polyhedron may reveal the curvature of the main shape of which it is a part.
STRUCTURAL QUALITIES OF DUALS
-
The bar in a lattice structure connects hinged nodes and transmits axial forces, whereas the dual plate structure transmits shear forces across the hinged intersections between plates.
-
Bars, shear lines, nodes, and plates are basically bending moment free; that is, they are surface-active membrane structures. Bending moments in bars (e.g., beams) and plates (e.g., slabs) are secondary to the lattice and plate action. Bending may be used in transferring and resolving the external loads into the plate-active or lattice-active surface.
-
The statical determinacy (i.e., redundancy) does not change during a dual transformation.
-
All static and elastic information is preserved after a dual transformation.
-
An axial force is perpendicular to the dual shear force (Figure 11.16).
-
Any plate structure including loadings and elastic properties may be transformed into its dual lattice structure, which could be analyzed by any three-dimensional lattice design software. The computed axial forces may then be transferred back to the dual plate structure as shear forces along the shear lines.
-
As a lattice structure concentrates forces in nodes and bars only, it will appear open if it is materialized according to the forces only. Nothing is hidden behind theoretical points and lines. Its openness is total. On the other hand, a plate structure distributes the internal forces to the full area of the plates and transfers forces along the full length of the shear lines. A plate structure will therefore appear totally closed and everything behind it will be hidden. The duality will therefore relate the following qualities: the concentrated to the distributed, the open to the closed, the opaque to the transparent. It is interesting to observe that, when pure geometry obtains a structural content, duality approaches the concept of dualism.
-
According to the previously mentioned statical considerations, it turns out that there is a dual relationship between forces and moments, translation and rotation.
THE STRUCTURAL MORPHOLOGY OF POLYHEDRA AS ARCHITECTURAL OBJECTS
Visually Based Structural Analysis and Design
One of the most fascinating qualities of plate-lattice duality is that it brings a unity to the concept of basic structures. The structural action of polyhedra is so closely and uniquely related to the geometry of polyhedra that they are as one. We have seen that the structural issue of rigidity may be solved either in a purely geometrical or in a statical way, which appear to be complementary. Plate and lattice action seems in this context to be as two sides of the same coin. They form two structural archetypes, which, in an antagonistic way, do not need each other, but together give a full and complementary understanding of basic structures and their interaction with geometry. They indicate that nodes and plates have equal status as main elements in structures, defined in exactly the same metric geometrical way. Bars and shear lines are the connecting links, defined by the topological information of their linking. Just as the geometry of the five Platonic polyhedra can be regarded as two groups with three in each, related by duality, statics fits exactly into the same pattern.
Traditionally, we consider zero-dimensional points as basic geometrical entities and then define the one-dimensional line as a direct connection between any two of them (which do not coincide), while a two-dimensional plane is defined by any three points (which are not collinear). However, in three-dimensional space we may use an alternative definition: We may introduce the two-dimensional plane as the basic geometrical element (a plane may
Figure 11.18 The dual perception of basic geometry (from top to bottom and left to right): One point, two points define a line, and three points define a plane; one plane, two intersecting planes define a line, and three intersecting planes define a point. A set of three coordinates gives the free choice of defining either the position of a point or the position of a plane, by defining the normal to the plane through the origin of the coordinate system. (Courtesy of Ola Wedebrunn.)
be defined, like the point, by three coordinates) and then define a one-dimensional line as an intersecting line between any two of them (which are not parallel) and a one-dimensional point as the intersection between any three planes (which do not have a common line).
For lattice structures the point (node) is the basic element (Figure 11.18, left), and two linked points define a line (bar) whereas three points define a plane, which is a nonactive open mesh. For plate structures the plane (plate) is the basic element (Figure 11.18, right), two linked planes define a line (shear line), and three planes define a vertex, which, if regarded as a node, is nonactive because any trivalent node may be removed from a structure without changing the redundancy of the structure.
A given set of geometrical and topological data can be interpreted in these two different ways, often resulting in very different looking configurations but uniquely tied together by geometrical and structural duality. It appears that all computer software with three-dimensional applications is based on the first interpretation and is therefore not suitable for handling geometrical and structural duality.
Modeling Polyhedral Structures
Physical models seem to be without peer in the study of faceted structures. Pin-jointed bars as connectors between nodes will indicate not only the
architectural appearance of a proposed lattice structure but will often also reveal the structural characteristics of rigidity and sensitivity. Note that the pure lattice structure only uses two of the basic components, the vertex (node) and the edge (bar), not the facet. In a similar way a rigid-in-plane material such as cardboard, which is hinged by bending or gluing along the edges, will be relevant as a simple model for pure plate structures. This type uses two components, the facet (plate) and the edge (shear line), but not the vertex, and as it is important to prevent nodal, that is, lattice action, the vertices should be cut away.
A very good exercise to get a feeling for the characteristics of lattice-and plate-based rigidity is to build models of the five Platonic polyhedra in the two versions and then try to flex them (Figure 11.9). It is indeed important to get a fingertip feeling for the difference between rigidity-movability and strength-failure. The latter quality is connected to the strength and elasticity of the material and connectors and hence irrelevant when investigating the kinematic qualities of such structures. Three of the models turn out to be rigid as pure plate structures, namely, those that have trivalent vertices: the tetrahedron, hexahedron, and dodecahedron; and three are rigid as pure lattice structures, namely, those with trivalent facets: the tetrahedron, octahedron, and icosahedron. It is remarkable that the tetrahedron, with trivalent vertices as well as trivalent facets, is rigid as a pure plate as well as a pure lattice structure. This polyhedron is, in fact, so simple that acting and reacting forces directed along the edges are balancing each other directly and no internal force distribution in the structure is needed.
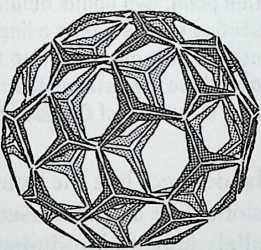
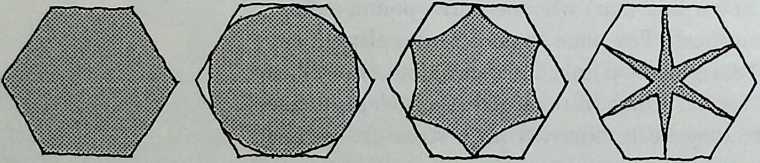
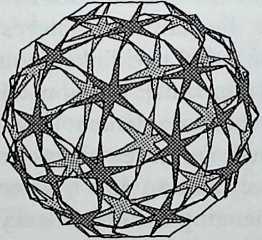
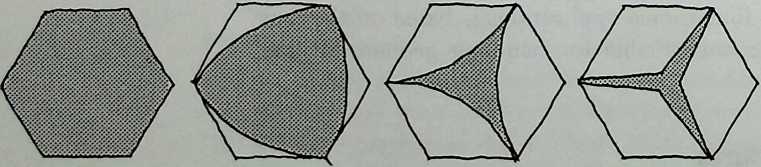
Figure 11.19 Methods of opening up plates without compromising the rigidity. (Courtesy of Ola Wedebrunn.)
Another interesting quality of these rigid structural archetypes is that they are neutral (i.e., statically and geometrically determinate or having zero redundancy), that is, on the edge of rigidity. This may easily be checked by removing one connector: a bar or a shear line.
The unstable versions of the regular polyhedra, for example, the octahedron and icosahedron as plate structures or the cube and dodecahedron as lattice structures, can all be stabilized by adding either bars to the lattice types or shear lines to the plate types.
Physical models are superior to computer models for testing structural qualities, not least because they give answers to much more than what is being asked; for instance, the flexibility or structural sensitivity of any combination of particular loading cases can be determined by physical models, whereas the computer only gives an answer to already specified loading cases. Perhaps virtual-reality technology will be developed in the future that will resolve this issue. Physical models are not often appropriate in the preliminary stages of the creative design process as it is time consuming to build good models. In the process of investigating different geometries, interactive computer modeling is obviously superior to physical models, whereas the latter are superior in investigating structural behavior.
Most of the computer graphics software works with wire frame models that are geometrically similar to lattice structures. These programs are often interactive and the geometry can be easily manipulated. Advanced structural analysis and computer design programs have also implemented interactive and user-friendly shaping features.
Computer modeling is a good deal more complicated for plate structures, but some of the advanced graphics software packages can facilitate the cutting of solids, which can be utilized for shaping plate structures, but the present software is still not efficient enough for this purpose. An adequate program should work like its lattice counterpart, with the difference that the coordinates, instead of defining nodes, should be regarded as the geometrical information for defining planes,16 and the information for linking the plates should be fisted in the correct order as if walking, either way, around the perimeter of the plate. With this information the intersections between a plate and its neighbors can be calculated and the defined plate can be isolated from the rest of the infinite plane of which it is a part. Such software is unfortunately not yet commercially available.17 Plate structures are probably not developed to the same level of complexity and sophistication as lattice structures because of their more complicated and computer-dependent geometry. If plate structures are to be used to their full potential, it is absolutely necessary to add dual transformation and the previously mentioned alternative geometrical interpretation of data to existing software.
Opening Up a Plate
One of the evident advantages of plate action compared to lattice action is that, when the enclosure of a building is designed to resist external load such as wind, snow, and dead load, it usually has an excess of bearing capacity in its own plane so that its utility for plate action is often possible. As the covering material must be there anyway, why not use it to transfer forces in its own plane by plate action? A transformation of a covered lattice structure into a plate structure often makes it possible to eliminate the bars and nodes. The cladding could then be the structure itself. The only extra property that has to be introduced is shear force resistance between adjacent plates.
The dual quality of lattice action, which is concentrating forces in nodes and bars, and plate action, which is distributing forces over the surface, has the effect that lattice structures tend to be constructed from strong material like metal, whereas plate structures may utilize weaker material like wood panels, plywood, plastics, reinforced concrete, and even glass!
That plates are essentially closed elements might be seen as a problem, as buildings usually need openings like windows, doors, and so forth. However, plates may be opened, as long as the essential requirement that they remain rigid in plane and sufficiently strong and stiff to transfer the design forces is maintained. There are essentially two different ways to open up plate structures: either by making holes inside the plates or by removing vertices (Figure 11.19). In both cases the plates develop into frames with bending rigidity in the plane of the plates. The plates become geometrically open but remain structurally closed. Plates with large openings will, of course, need more or stronger material than if they were made without holes. The larger the openings, the more plate structures will approach lattice structures from the point of view of the type of material employed.
PLATE AND LATTICE STRUCTURES IN NATURE
Structure is a major issue in our earthly environment of gravity and other loadings and many living organisms have developed highly sophisticated structural systems over millions of years. Nature’s strategy for improving solutions to structural and other vital challenges, and which has proved to be very creative and efficient, is known as “survival of the fittest.” A major difference from man-made structures is that organisms need to grow. It is vastly more complex to maintain strength and rigidity during a growth process than to erect a safe and rigid building. Just think of the difficulties of many beetles and crabs that have to throw away their external chitin skeleton and become very vulnerable until their new armor has solidified. Other organisms, like the sea urchin, have developed more sophisticated solutions to a similar problem.
It appears that many structures in nature, which can be typified as plate or lattice structures, are very close to being structurally neutral. The shell (also called the test in biological terms) of the sea urchin is one instance (Figure 11.25). Many other echinodermata, the skeleton and armored skin of many vertebrates, the Venus’s-flower-basket (Figure 11.24), the spongy trabecula inside bones (Figure 11.23), different types of spider webs, microscopic plankton such as radiolaria (Figure 11.20), foraminifera (Figure 11.21), coccolithophores (Figure 11.22), and many others are further examples. One of the obvious advantages is that a structure with low redundancy requires less material, which means less dead load, and uses less energy for its construction than a structure with high redundancy. Another advantage is that a neutral or slightly redundant structure develops lower internal stresses during growth and other structural rearrangements than a highly redundant structure. Rearrangements of the structure may therefore be achieved more easily and with less adjusted growth of the total system. Of course, kinematic neutrality is also an obvious disadvantage as the structure tends to become movable if local failure occurs, but often it seems possible to use an alternative structural action if needed. To prevent collapse, the structural action often changes into one that is less stiff than the plate or lattice action, for example, bending. For this softer type of action, the structure is redundantthis is an expansion of our normal conception of the word redundancy in the sense that a failure of the more rigid structure must occur to activate the alternative softer structural type of action. This system can be exemplified by a house in which the main structure has been badly damaged, for example, by an explosion, but has not collapsed because the forces have found alternative rearrangements, (e.g., bending).
The sea urchin may transfer bending moments over the shear lines during the “repair period” of a plate. The trabecula inside our bones and the Venus’s-flower-basket do not have hinged nodes and must therefore also carry loads by the transfer of bending moments between bars if necessary. It is significant that these auxiliary ways of stabilizing are secondary as they produce larger elastic deformations than the very stiff plate and lattice action.
In order to understand the appearance of pure plate structures in nature, it should be noted that a random single-layer configuration of planes will always intersect in trivalent vertices,18 which is the required geometrical pattern for pure plate action in single-layer structures. The same geometry is seen on randomly organized close-packed organic cells or soap bubbles, either on its surface or in cross section. One might conclude that the “creator” has been dealt an incredibly strong hand of cards, when the lowest geometrical order of allthe randomproduces the ideal configuration for pure plate action! The rest is “just” to create rigid-in-plane plates and shear resistant connections in order to introduce plate action to nature. The plate type of structure is very appropriate for faceted structures as the covering surface is at the same time the main structural element, while the more complicated bar-and-node action, which requires higher-strength materials, can be avoided.
Figure 11.20 Radiolaria: Aulosphaera dendrophora (x80) (upper left) and Aulonia hexagonia (x30) (upper right) compared with geodesic polyhedra as a pure lattice structure (lower left) and its dual as a pure plate structure (lower right). (Source: Upper drawings: Ernst Hackel, Challenger Monograph, 1987.)
Figure 11.21 Foraminifera (x450), a multichambered living unit of calcium carbonate polyhedral shells. (Source: Geological Institute, University of Copenhagen.)
Planktonic Organisms
Microscopic plankton floating around in the oceans are subjected to equal loading from all directions. Plankton do not develop up-and-down orientation as many organisms subjected to gravity do. Instead, they often develop nonoriented spherical or polyhedral geometry. The biologist Ernst Hackel19 has been extremely productive in describing comprehensively the siliceous plankton called radiolaria (Figure 11.20), many of which are beautiful images of polyhedral structures. The external skeleton, even when not studied in detail, often shows either a lattice (triangular facets) or a plate (trivalent vertices) configuration or both. Foraminifera (Figure 11.21) are calcitic organisms with similar polyhedral configurations to radiolaria. They often form clusters of polyhedral skeletons with holes producing trivalent vertices. The foraminifer starts out by forming a single chamber with one opening. When the soft organs inside grow too large to fit into the chamber, it bubbles out of the hole and creates a larger chamber, which also has one hole, and so it continues and becomes a cluster of ever-larger polyhedral cells. Coccoliths are another calcitic plankton but with the habit of collaborating to estabfish colonies forming polyhedral shapes called coccolithophores (Figure 11.22). There are several types of connections between the single coccoliths, some of them with a wedge-and-cleft connection and some where the coccoliths are just touching and held close by soft tissue, forming configurations reminiscent of plate structures.
Bone Structures
The classic example of lattice structures in nature is the trabecula inside the enlarged extremities of our tubular bones (Figure 11.23), such as are found in our thigh20 and heel bones. The calcitic trabecular structure is oriented in the optimal structural direction, which is that of the main tension and compres-
Figure 11.22 Coccolithophores: Braarudosphaera bigelowii (x5000), a perfect dodecahedral configuration (left). Pontosphaera discopora (x4000), forming polyhedra from packed ellipses in a trivalent vertex pattern, which indicates rigidity by plate action (right). (Source: Coccolithophores, Amos Winter and William G. Siesser, eds. Courtesy of Cambridge University Press. Photos: S. Nishida.)
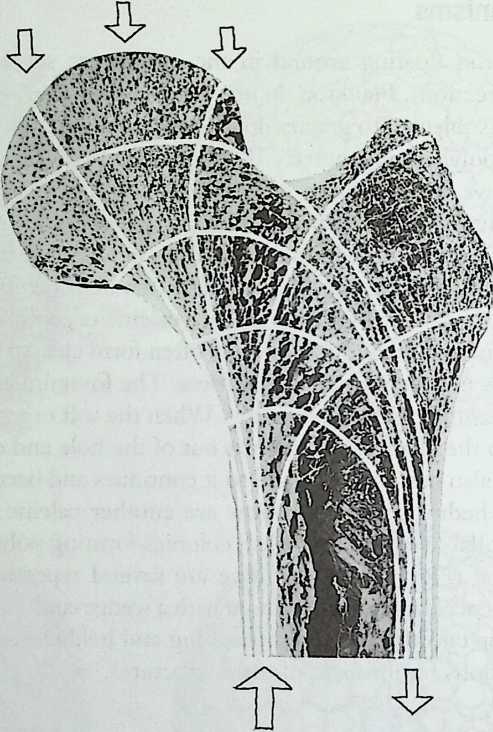
Figure 11.23 The spongious trabecula in the femur follow the stress trajectories for the body weight. The trajectories follow the direction of the principal stresses (shown as a pattern of white lines) in a similar solid structure at any point of the cross section. (Courtesy of Ola Wedebrunn.)
sion forces, the so-called stress trajectories. The trabecula are connected to the compacta, which is the compact bony layer forming the outer surface of the bone. The trajectories, forming a cubic lattice of six-valent nodes, will, together with the compacta, form an ideally shaped three-dimensional structure which, if regarded as a lattice structure, turns out to be close to neutrality, only slightly redundant. Clinical observations of the trabecular pattern of the femur (the upper extended part of the thigh bone) of astronauts and other individuals who have been subjected to unusual loading of these structural parts, show rearrangements of the pattern consistent with the quality of being almost neutral. Hence a configuration of minimum energy consumption and minimum risk of unwanted internal stresses, which might lead to failures during the rearrangement process.
Some of these spongious bone structures are configured as cubic cells with thin cell walls and are therefore more probably stabilized by plate action than by lattice action. It is interesting that if pure plate action is considered for plates forming a cubic matrix configuration, it will have the same kinematically neutral status as the cubic lattice.
Venus’s-Flower-Basket
The Venus’s-flower-basket Euplectella (Figure 11.24) is a deep-sea siliceous glass sponge, consisting of a cylindrical chimney-like structure topped by a
Figure 11.24 Venuss-flower-basket(Z. = 30 cm, D = 3 cm). Total structure and detail.
dome and rooted in the sea bottom with long shiny siliceous fibers. The soft organic tissue is located on the surface of the cylinder. It feeds by filtering small organisms from the sea water sucked through the meshes in the cylinder, pushing the filtered water up and out through the chimney. The meshes of the cylinder are basically squares. Every second mesh, in a chessboard pattern, is cross-braced and forms spiral lines. Half-octahedra are positioned on top of the cross-braced meshes and their upper vertices are interconnected, forming spiral ridges on the outside of the cylinder. If considered as a pure lattice structure, the configuration turns out to be neutral. The nodes are able to resist bending, which means that any local damage does not necessarily lead to total failure. The structure would also be stable if all meshes were braced, but this would interfere with the flow of nutritious water through the surface of the cylinder. Hence, the solution with the ridges appears to be very appropriate.
The Shell of the Sea Urchin
The hard shell of the so-called regular1 sea urchin (Figure 11.25) complies with all the requirements of a perfect plate polyhedron with great functionality in the design of shape, joining, and necessary geometrical openings. In addition to its ability to resist external loading, the polyhedral structure of the
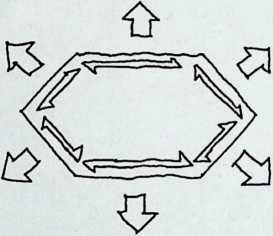
Figure 11.25 Regular sea urchin. Seen from above (upper left) and below (upper right). Note the trivalent vertices on the inside of the shell. Scanning electron microscopy (SEM) (x600) of the toothed link between two plates (middle left) and a drawing showing that the direction of growth and the direction of stabilizing forces are perpendicular, hence uncorrelated (middle right). Lower left and lower right are images of a computer-generated sea urchin subjected to loadings perpendicular to the surface, resembling the action and the appearance of the spines. (Courtesy of Dr. Margit Jensen, Zoological Museum, University of Copenhagen.)
sea urchin must, at the same time, be able to grow. This problem has been solved in a theoretically elegant way.
The regular sea urchin surrounds its soft organs with a protective polyhedral shell of calcite. It consists of an upper almost hemispherical part and a somewhat flattened bottom part. On the outside of this hollow calcite skeleton, a great number of movable sharply pointed or club-shaped spines are arranged, providing efficient protection against attacks from enemies or rough sea. It is probably the spines that transfer the major external forces to the shell.
The shell is basically composed of two types of plates, dividing the surface into five areas and converging at the two poles. Each area consists of two rows of plates, which may be regarded as plane plates, arranged in such a way that all vertices are trivalent. The individual plates are normally connected to between five and seven other plates.
The larger of the two openings appears at the bottom pole where the plates meet a strong and stiff pentagonal frame, on which the highly developed chewing apparatus “Aristotle’s lantern” is mounted. This frame is therefore structurally closed even if it is geometrically open.
The joins between the plates, the shear lines, are distinctly toothed (Figure 11.25). This type of connection is extremely efficient in transferring shear forces, which strongly supports the assumption of plate action. The collagen fibers almost lacing the plates help to keep the plates close together, which will enable the transfer of bending moments from plate to plate. The lacing is important for maintaining sufficient strength and stability during “repair” after a fracture of one or more plates. It is obvious that the plates combined with the collagen fibers enable structural actions other than plate action, for example, bending. The shell may, for example, function as a continuous shell structure. Shell action is very close to plate action because a finely faceted plate polyhedron is nothing but a slightly discontinuous shell, stabilized only by shear forces, acting across the edges.
The sea urchin grows by increasing the number of plates and increasing the size of the single plates as a simple two-dimensional geometrical expansion. By expanding the size of the plate, the direction of growth will be perpendicular to the shear lines (Figure 11.25), hence perpendicular to the direction of the stabilizing shear forces. Growth and transfer of stabilizing forces can therefore be managed concurrently without any interference. Seen as an engineering problem, the combination of growth and maintained rigidity is solved by the sea urchin in a structurally elegant way.
The analysis of the sea urchin as a pure plate structure leads to speculation on the structural nature of other similar configurations. Such configurations are found in the armored skin of reptiles, the shell of the tortoise, the bone structure of the skull, and many other places in nature. Scientists often find it difficult to explain the function of this significant pattern of sutures maybe a part of the answer is given by “rigidity during growth”!
EXAMPLES OF MAN-MADE STRUCTURES
Polyhedral lattice structures appear to be increasingly popular, especially for large spans where the high efficiency of metal lattice structures forms slender, elegant, and extremely lightweight structures. The recent demand for large sports arenas has produced a great number of sophisticated and brilliant lattice structures. There seems to be some chance that these large coverings will influence smaller-scaled buildings such as houses.
Today’s use of plate action is mostly limited to the stabilizing of buildings against horizontal loads such as wind and earthquakes by activating floors, facades, gables, internal walls, walls around staircases, elevators, and so forth. This is a very limited use compared to the vast possibilities of complex spatial plate structures.
As mentioned earlier, most buildings can be characterized as polyhedra or clusters of polyhedra. On the other hand, common buildings are not characterized or analyzed as polyhedra, and polyhedra are usually not on the mind of the architect during the creative process of organizing the building geometry, or on the mind of the structural engineer when making decisions about structural action and design. In fact, almost an entire generation of building designers, such as architects and engineers, are generally unaware of polyhedra and their morphological qualities. I am sure that our architectural landscape, in terms of the shape and structure of our buildings, would become increasingly interesting if architects and engineers were better trained in using the geometrical, topological, and structural archetypes for their buildings.
A very simple example of implementing plate action in buildings is the traditional gable or pitched-roofed house. A view of such a roofscape (Figure 11.26) confirms the frequency of trivalent vertices. This is therefore a configuration where the plate action of facades, gables, roofs, attics, bays, and oriels is obviously a potential that is not realized. Of course, it is necessary that the plates be rigid in plane and that the connections be shear resistant. However, these extra requirements would often be simple additions to the existing construction tradition. An obvious advantage of utilizing the latent plate action would be to increase the structural activity of the building’s surface, hence the possibility to open up the attic space by reducing frames and trusses partially or totally. Another advantage would be that the roofs would tend to be shaped in an appropriate way for efficient plate action or for combined lattice and plate action. Making proper use of this structural potential would lead to more diverse and interesting shapes and structures for roofs as well as for enclosures and interior partitioning.
The Rigidity of Polyhedral Buildings
A major structural difference between a polyhedron and a polyhedral building is that the building is supported by a connection to the ground. To form an idea of the rigidity situation of a supported polyhedron, an unsupported rigid
Figure 11.26 A common roofscape shows many trivalent vertices, indicating potentialbut not utilizedplate action. (Courtesy of Ola Wedebrunn.)
polyhedron is first considered. Such a rigid body has six degrees of freedom22 within which to move and therefore, under the necessary general requirement for the rigidity of unsupported polyhedra, mentioned earlier, the number 6 will be replaced by the number of support conditions (SU):
BA + SL+ BU + SU =3x{N0 + PL)
Note that SU is equivalent to either a bar, a shear line, or a buffer force.
Imagine now any arbitrary closed and rigid simple polyhedron. Make a single cut according to the proposed foundation boundary, which does not necessarily have to be plane but in such a way that the initial polyhedral surface is still triangulated (Figure 11.27). The new polyhedron is now movable because the free edge is an n-gon (for n > 3). The number of extra bars needed to triangulate the hole will be (n -3), which are added. Now the structure has become a simple closed triangulated polyhedron and will therefore again comply with the equation
BA+ SL+ BU = 3x(N0+ PL)-G
which means that the number of support conditions only needs to be 6. As every one of the added bars is equivalent to a support, all the extra bars are equivalent to (n -3) supports. The total number of supports required to stabilize the polyhedron with the free cut edge and no extra bars is therefore 6 + (t2) = 72 + 3. The number of vertices on the formerly free boundary is n. If all these n points are provided with one support condition (e.g., vertical) and three of the boundary edges are provided with one support condition each (e.g., horizontal), the necessary requirement for rigidity is met. If more (e.g., horizontal) support conditions are added, the structure becomes redundant. This means that if all n free comers and all n free edges along the boundary are supported, the structure will have a redundancy of 72 -3. If this is the case, it leads to the
¶ CONCLUSION
that a maximum of (72 -3) bars, shear lines, buffers, or support conditions may be removed from the rest of the structureenabling, for example, larger openingswithout affecting the rigidity. Fol-
Figure 11.27 Stabilizing a part of a polyhedron by adding bars or supports along its periphery. Shown rotated from below. (Courtesy of Ola Wedebrunn.)
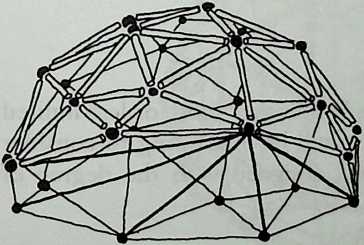
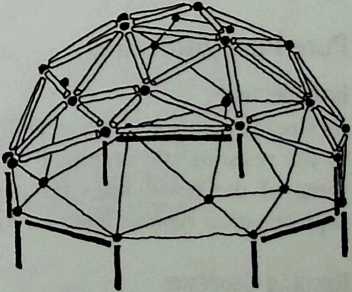
lowing this procedure for removing structural parts, it is very important to investigate for local movability and critical and sensitive situations. The preceding considerations are based on a pure lattice polyhedron, but the same result concerning support requirements is achieved if it is applied to any polyhedron based on plate or combined plate and lattice action.
Pure Lattice Structures
Steel lattice structures were developed by the early pioneering work of engineers during the industrial revolution, mainly in the 18th century. Progressive architects and engineers began to cultivate a significant form-and-force language for the new iron material, based on engineering qualities such as reliability, high strength, and stiffness, coincidental with the architectural qualities of airy delicacy and feathery lightness. We see the results in railway stations, exhibition halls, palm houses, libraries, and so forth.
Structures based on simple spherical polyhedra23 were developed by European engineers with the “father of dome structures,” the German, J. W. Schwedler in the lead. Later in the United States, R. Buckminster Fuller became a legend for developingwith an exceptional energy and originality his thoughts and ideas24 on what he called the geodesic dome. The system had, in fact, already been developed and used by the German engineer Walter Baursfeld for the steel reinforcement of the Jena Planetarium in 1923. Fuller, however, became a kind of guru of the 1960s counterculture, and whole villages25 were built according to Fuller’s thinking, not only on building structures but on his total cosmology. At the other end of the spectrum, Fuller developed, in collaboration with other skilled engineers and architects, larger and fighter dome structures than had ever been erected before.
Polyhedral lattice buildings range from the small “homemade” one-family dwelling to high-tech retractable roofs for large arenas but seem to attract interest, regardless of the scale of the building. They belong to a field where engineers, because of the comprehensive structural content, must put at least as much energy into the creative process of organizing and shaping the building as the architect.
The lattice structure is today so commonly used, so well known, and so well documented that it will not be further dealt with here.
Pure Plate Structures
Introduction
As already mentioned, plate action in today’s buildings is more or less limited to the resisting of horizontal forces, but it would be interesting to consider some of the possibilities for plate structures designed with the degree of sophistication typical of lattice structures.
Regular Geodesics
Because pure plate domes can be created by the simple dual transformation of pure lattice domes (Figure 11.28), it seems obvious to consider the possibili-
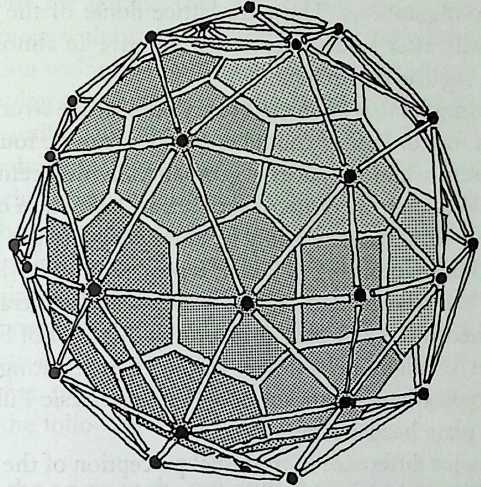
Figure 11.28 Dual configurations are sometimes very easy to match as in this geodesic polyhedral structure with the reference point in the center. (All art on this page courtesy of Ola Wedebrunn.)
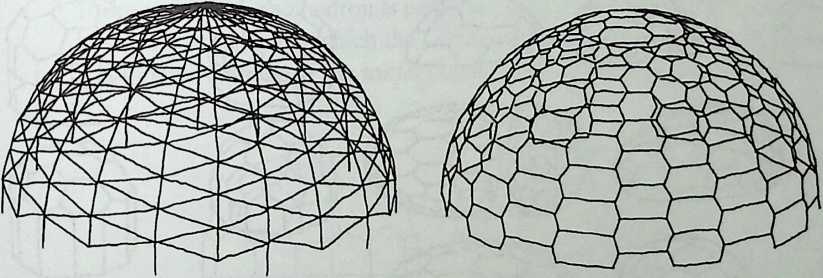
Figure 11.29 The dual (right) of the Schwedlertype of dome (left) is very reminiscent of the sea urchin type of faceting.
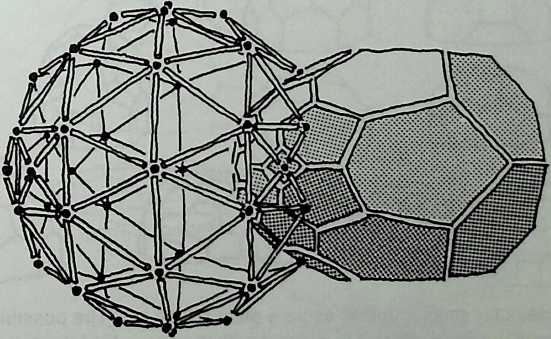
Figure 11.30 Dual configurations for a geodesic polyhedron. The reference point is located at one of the focal points of the ellipsoidal plate structure.
ties for these configurations. The pure lattice dome of the Schwedler type (Figure 11.29) will, after a dual transformation, give an almost perfect model of the shell of a regular sea urchin.
The duality implies that for any arbitrary pure lattice structure a dual plate structure can be found. In fact, countless numbers can be found as each position of the chosen origin produces a geometrically different plate structure (Figure 11.30). Whether the result of such a transformation creates a realistic and constructable form can often only be evaluated after the transformation.
A geodesic dome, according to Fuller, is produced by further triangulation (breakdown) of the triangulated regular polyhedra (the tetrahedron, octahedron, and icosahedron). Dual transformation of this kind of Fuller dome produces structural configurations for a family of interesting geodesic plate domes. As the typical nonsignificant node26 in a geodesic Fuller dome is six-valent, the dual plate becomes hexagonal.
There is a major difference in the visual perception of the lattice and plate dome pattern. Even with small frequencies of breakdown, the lattice dome gives a diffuse and spherical appearance, whereas the dual plate pattern appears as a more obviously faceted form. This is especially pronounced in the
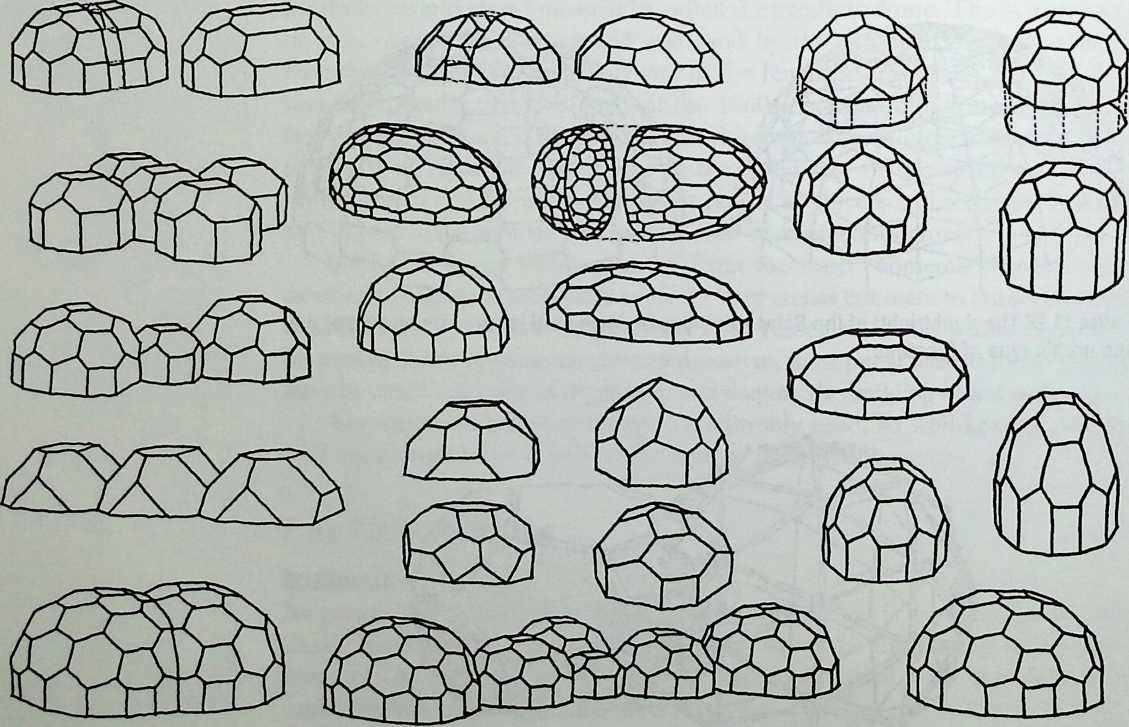
Figure 11.31 Ideas for smaller domes as pure plate structures. The possibility for requiring vertical plates along the perimeter in contact with the ground is latent, and the very simple geometry involved in adding units makes the plate dome in many ways superior to lattice domes. (Courtesy of Ola Wedebrunn.)
lower breakdowns for tetrahedron-and cube-based geodesics. In addition, these strong, almost sculptural plate forms carry a number of possibilities for direct combination with other units or as the basis for further shaping (Figure 11.31). One shaping possibility is zooming, obtained by stretching a sequence of plates with parallel intersection lines. Another possibility is stretching of the dome by applying factors to one or more of the axes, which changes, for example, a spherical shape into an ellipsoidal shape.
A third method for elongation of the shape I have called dual manipulation: Like stretching, this changes the inscribed sphere into an ellipsoid, but whereas stretching maintains the origin at the geometrical center, in dual manipulation the origin is situated at one of the focal points of the inscribed ellipsoid. This transformation changes the size of the plates in an interesting way, in fact so suggestive that the correct construction of a perspective view can be obtained using the following sequence (Figure 11.32):
° Consider the origin in the center of the plate polyhedron.
° Execute a polar reciprocation. This produces a lattice polyhedron.
° Move the origin.
° Execute a polar reciprocation again. This produces a plate polyhedron that is different from the initial one.
° If the new plate polyhedron is projected onto a plane that is perpendicular to the direction in which the origin was moved, this projection shows a perspective image of the initial polyhedron, as will be explained later.
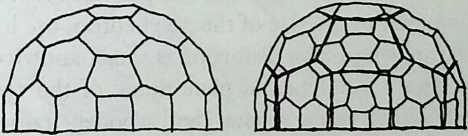
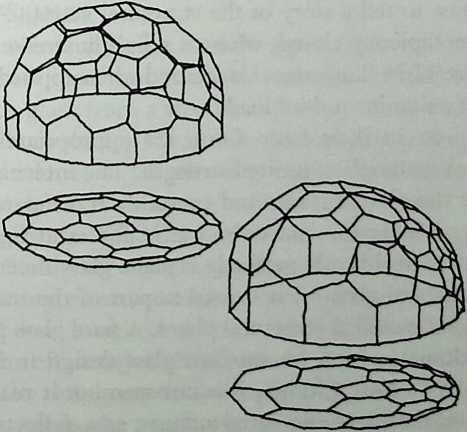
Figure 11.32 A dual manipulation creates not only a family of interesting geometric configurations but also a perfect perspective image of the original: The upper right appears to be a perspective view of the upper left The same configurations are shown lower left and lower right and both are viewed from above from the left (Courtesy of Ola Wedebrunn.)
Figure 11.33 Next to the traditional Danish farmhouse is a pure plate dome with extremely open plates constructed as wooden frames with plywood knees. The open framed plates are bolted together. (The structure was designed by the author in collaboration with the architect Torkild Ebert in 1981.)
Observe now that the size of the plates has changed in such a way that those closer to the origin become smaller and plates farther from the origin become larger. The plates are circumscribing an ellipsoid as mentioned, but because of the different shapes of the plates it gives an illusion of an egg shape. Figure 11.32 shows that if the dual-manipulated polyhedron is projected onto a plane perpendicular to the direction in which the origin was moved, it creates a perfect perspective view of the original polyhedron, where the location of the eye is dual (reciprocal) to the point where the origin was moved. If the origin is moved a little compared to the size of the polyhedron, the location of the eye is far away, hence the perspective distortion is small, and vice versa.
Figure 11.33 shows a polyhedral plate dome of the cube family with a diameter of 12 m. The plates are open rigid wooden frames that are bolted together. Instead of all frame members or holes in the plates being of equal size, they could be adjusted to reflect the magnitude of the internal stresses. This method could be chosen to save material or to open up the roof for daylight, and not least to tell a story of the structural action: A heavily stressed plate would be completely closed, whereas a lightly stressed plate would be wide open. Figure 11.34 illustrates this method when applied to a dome of the cube family with a dominant dead load.
Plate structures, in their basic form, are appropriately made of two- dimensional sheet materials of limited strength. The internal stresses are distributed all over the plate surfaces and smoothly transferred along the connections, hence avoiding the concentration of forces at lines and points. A material that would fit this role perfectly is plane glass sheets. Because of the particular properties of glassif it is used as part of the main structure of a building, it should be used as structural plates. A pure glass plate dome is one answer to the ultimate vision for modern glass design in buildings. Like a “reversed” Emperor’s New Clothes, it is not seen but it really is thereit is only perceived by means of the surroundings, as a reflector of the clouds, skies, neighboring buildings, and so forth.
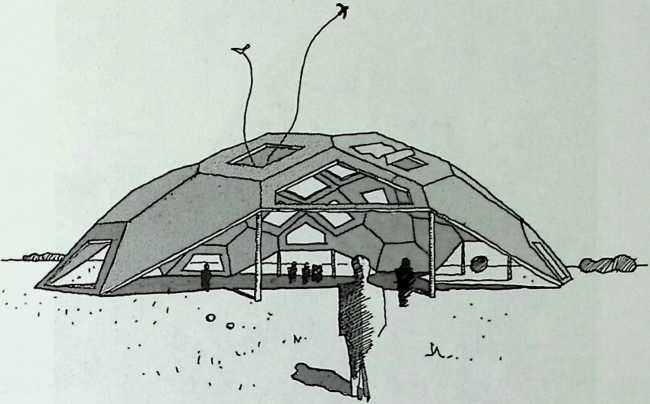
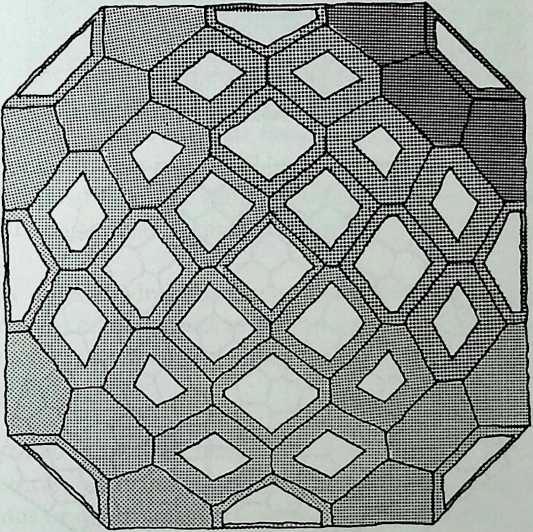
Figure 11.34 A shallow plate-faceted shell where the openings in the plates are adjusted to the magnitude of the internal forces for self-weight. Perspective view and plan. (Courtesy of Ola Wedebrunn.)
Other Polyhedral Shapes
A 3-m-high parabolic sculpture, called Pentagonia (Figure 11.35), was built as a pure plate structure, not from glass but from glazed ceramic tiles, which are basically similar to glass from a structural point of view. Its name is derived from the fact that both the top tile and the ground plan are regular pentagons. The 10-mm thickness of the tiles is greater than is needed from a structural point of view, but it is necessary in order to prevent warping of the tiles during their firing in the kiln. Clay slabs of the required thickness were cut directly from the “fold-out” net generated on the computer by CADual and, after firing and glazing, a sand/cement mortar was used to link the ceramic tile plates. The actual dead load is close to the ideal load for the parabolic shape. This means that the efficiency of the structural shape will be high for the dead load, and as it is the dominant load, the structure and its shape fit perfectly together. In other words, the magnitude of the shear forces to be transferred at the shear fines is minimized.
Figure 11.35 The domeshaped ceramic sculpture, called Pentagonia, circumscribes a paraboloid of revolution, which is a structurally very efficient shape for the dominant selfweight. It forms a 2.5-m-high ceramic pure plate dome. To ensure the transfer of shear forces, the plates are linked with ordinary mortar. The horizontal projection shows a very regular pattern consisting of one pentagon and just two types of hexagons. (Ceramic artists Esben Madsen and Gudrun Rud-jord designed and produced the sculpture in collaboration with the author. It is on display at the Silkeborg Museum in Denmark.)
Polyhedral Clusters
Introducing plate action into traditional cubic building design should be very easy, not only with respect to the roofing, as mentioned earlier, but also for the traditional concrete element building technique. Increasing the strength of the connections between the traditional precast elements might easily enable extensive plate action and increase the architectural and functional possibilities of this building type. Figure 11.36 shows a typical example for a two-level building opened up at the lower level and carrying the loads by activating all horizontal and vertical plates and shear lines. In the same way, it is possible in
Figure 11.36 A simple two-story building structure based on cubic geometry and extensive use of plate action in order to open up the lower level. The building is stabilized for horizontal and vertical loadings by the transfer of shear forces between platesand not by bending. (Courtesy of Ola Wedebrunn.)
a multilevel building to have alternate floors free of internal vertical structural walls. This indicates that it is possible to increase the structural efficiency and architectural possibilities by adding plate action to the conventional precast concrete building system. This is quite similar to the previous considerations for roofs.
Other types of polyhedral clusters are those proposed by J. F. Gabriel.27 These structures are combinations of different simple polyhedra and may be regarded as structures composed of either rigid cells, pure plates, or a combination of plates and lattices.
Combined Lattice and Plate Structures
The pure structures, plate and lattice, have their respective significant qualities, advantageous or disadvantageous, which have been outlined in the previous sections of this chapter. They form opposite poles of the structural world. They may be regarded as geometrical and structural extremes, hence the majority of their possibilities probably fie in between. The statics for the combined plate and lattice action has already been described, and the most interesting architectural potential probably lies in the area of expressing all the basic structural actions such as tension, compression, and shear.
An examination project investigated by engineering students considered a palm house (Figure 11.37), which is a combination of a coarse-meshed steel lattice and a fine-meshed glass plate structure. Both the steel and the glass structure adhere to the same theoretical paraboloid of revolution with the glass plates as tangential planes, whereas the steel nodes touch the same surface at the connection points with the glass plates. The rather complicated geometry, where the horizontal projection of the configuration patterns shows regular triangles (lattice structure), regularly arranged with the regular hexagons (plate structure), is easily generated by dual transformations using CADual.
A common problem when combining faceted spherical forms is the diffi-
Figure 11.37 Palm house project. Physical model and horizontal projection of the steel and glass structure. (The illustration is of a model that was produced as part of a B.S. examination project by P. Ohannessian and N. Grunnet The project, entitled Design of a Glass Plate Dome,\Nas submitted to the Danish Technical University in 1991.)
culty of matching boundaries geometrically but, as the projection of the structural configuration onto the horizontal ground plane has such a strict regularity, the combination of equal types of paraboloids fits perfectly together, as shown in Figure 11.37. Because the fragile glass is part of the structure, it is important that the shape be ideal for the dead load in order to reduce the internal stresses as much as possible. The glass is self-supporting for all loading cases, but, in the case of local fracture, the redundant steel structure will prevent collapse and ensure stability until the broken glass plate is replaced.
Another way of combining lattice and plate action is, as with the non- trivalent simple polyhedra, to achieve strength and rigidity by transferring buffer forces along their common edges. This is exemplified (Figure 11.38) by another student project. The general shape of the highly efficient parabolic structure is the same, but all the facets are now quadrilateral and project into perfect squares on the ground plane. This time the glass is almost unaffected by dead load but plays a structural role for wind loadssimilar to that of many
Figure 11.38 Project for a fruit market covering. Elevation, horizontal projection, and internal view. (The illustration is of a model that was produced as part of an M.S. examination project by P. Ohan-nessian and N. Grunnet The project, entitled Interaction Between Plate and Lattice Structure, was submitted to the Danish Technical University in 1993.)
old palm houses. Both projects prove that the structural performance of glass makes it very suitable for quite large structures and that the problem of brittleness could be dealt with by ensuring sufficient redundancy. The general shape and the faceting are created in a very simple way by dual transformations. At the same time, the surface turns out to be a translation surface.28 As one of the characteristics of these shapes is that the facets are plane parallelograms, which are very simple to produce, they belong to a family of structures appropriate for combined lattice and plate action.
Another example of the combined action is a quite interesting structure (Figure 11.39), where square plates are arranged in a chessboard pattern and hinged at the corners. This structure forms, of course, a highly movable mechanism. One can now crumple it into the desired spatial configuration and brace the open meshes in both directions. If the elements of this double brace do not intersect, then they form edges on a tetrahedron together with the
Figure 11.39 A chessboard pattern plate system, folded in space and braced over both the diagonals of all open meshes, becomes a rigid structure, combining plate and lattice action. The shape is defined by the actual lengths of the bracing bars. (This architectural students project was developed by S. Krohn-Hansen and M. S. Skadborg of the Royal Danish Academy of Fine Arts.)
plate edges. In this case the bracing will not only stabilize the shape, but it will also enable the boundary to be free from stiffening elements, hence producing a slender and beam-free edge. If the configuration is too small or too narrow, it cannot become rigid, but above a certain size it becomes rigid and then more and more redundant as the size increases. To check this, the simplest method is to use the rigidity equations for pure lattice structures and regard the plates as braced lattice squares.
¶ CONCLUSION
It seems quite surprising that these simple relationships between lattice and plate (and combined) structures have beeneven though Mobius came very closeso recently described. They finally have brought a perfect polyhedral order to the concept of basic structural action. On the other hand, it is strikingly difficult to change the firm opinion of many professionals that the lattice is the one and only basic static principle and the triangulated polyhedra are the only inherently rigid configurations.
This chapter introduces the concept that plate and lattice action are equivalent and dual in our “normal” three-dimensional space. This is important, as the static and geometrical rules for pure plate structures or combined lattice and plate structures produce a new and different syntax and vocabulary for shaping spatial structures a structural morphology based on simple algebra and equally simple considerations. This basic concept for what can be called the foundation of a form-and-force language has an impact at several levels: from considerations of the dualistic qualities of basic structures to simple rules for configurational design and analysis of structures, including many biological structures, to operational tools for numerical statical analysis. As can be seen, the theory has not only led to the solution of a number of interesting structural morphological problems but also produced a tool for the design of efficient structures with the possibility of great visual and architectural qualities.
ACKNOWLEDGMENTS
I am greatly indebted to Dr. Emeritus Martyn Cundy and Dr. John Chilton, University of Nottingham, for their valuable comments and suggestions about this chapter, and to my colleague architect Ola Wedebrunn for his advice and graphical art work.
¶ NOTES
-
Augustin-Louis Cauchy, “UMemoire sur les Polygones et les Polyedres,” Journal de PEcole Poly technique, Vol. 26, 1813.
-
August Ferdinand Mobius, Lehrbuch der Statik, Leipzig, 1837, Vol. 2, Chap. 4.
-
Ibid., Chap. 5.
-
Stephen P. Timoshenko, History of Strength of Materials, McGraw-Hill, New York, 1953, Chap. 10.
-
R. Bricard, “Memoire sur la Theorie de 1’Octaedre Articule,” Journal de Mathe-matiques, Vol. 3, 1897, pp. 113.
-
Robert Connelly, “A Flexible Sphere,” The Mathematical Intelligencer, Vol. 1, No. 3, 1978, pp. 130.
-
Jorgen Nielsen, “Some Stability Problems for Shear Wall Structures with Rectangular Plates,” Proceeding? of the IASS Symposium, Copenhagen, 1991, Vol. 2, Kunstakademiets Forlag Arkitektskolen, Copenhagen, pp. 125.
-
See the author’s publication Structural Order in Space The PlateLattice Dualism, Royal Academy of Fine Arts, School of Architecture, Copenhagen, 1983. It was originally stated in a Danish research report of 1976. According to correspondence with Dr. Walter Whiteley, it was found independently by him at approximately the same time.
-
Ibid., p. 26.
-
The equation is deduced in the author’s paper “The Structural Behaviour of Arbitrarily Plane-Facetted Spatial Nets,” Proceedings of the IASS Symposium, Copenhagen 1991, pp. 119.
-
The magnitude of the moment vector is the product of the force and its distance to the origin. The direction of the moment vector is found by the right-handthumb rule: Let the fingers on the right hand bend over the origin with the fingertips in the direction of the force. Then the moment vector will have the direction of the stretched thumb (Figure 11.13, left center), i.e., the perpendicular direction to the force. This moment vector is acting on the origin.
-
H. M. Cundy and A. P. Rollet, Mathematical Models, Tarquin Publications, Norfolk, UK, 1981, p. 78.
-
M. J. Wenninger, Dual Models, Cambridge University Press, 1983, pp. 1.
-
The virtual work done by the force in a bar is required to be equal to the virtual work done by the shear force over the shear line.
-
“The Plate-Lattice Dualism,” Proceedings of the ICSB-IASS Colloquium, Beijing, 1981, Elsevier, London, pp. 321. The dual transformation equations for the elastic properties are also stated in this paper. This enables the statical calculations of redundant dual structures.
-
As described in the polar reciprocation method.
-
A research version called CADual has been developed by the author.
-
Peter S. Stevens writes on page 218 of his classic book Patterns in Nature, Little, Brown, 1974, how a piece of chalk develops facets forming trivalent vertices as it wears against the blackboard. In case a four-valent vertex seems to be found, it is just a question of magnification to separate it into two closely located trivalent vertices.
-
The German biologist and early Darwinist Ernst Heinrich Hackel (1834) described some 3,500 diverse forms or species of radiolaria in his Challenger Monograph (1887). An abridged version of his famous Kunstformen derNatur from 1904 was published in English entitled Art Forms in Nature in 1974 by Dover, New York.
-
The structure is described in the classic work by D’Arcy Thompson, On Growth and Form, abridged edition, Cambridge University Press, 1961.
-
For a thorough description of the regular sea urchin, see R. D. Barnes, Invertebrate Zoology, W. B. Saunders, Philadelphia, 1974.
-
The three independent axes X, Y, and Z enable six independent movements: translation along the three axes and rotation around the same three axes.
-
See the historical article by Z. S. Makowski, ed., in Analysis, Design and Construction of Braced Domes, Granada, London, 1984.
-
Amy C. Edmondson gives an excellent insight into Fuller’s cosmology in A Fuller Explanation: The Synergetic Geometry ofR. Buckminster Fuller, Birkhauser, Boston, 1987.
-
See classics like Dome Cookbook by Steve Baer, Lama Foundation, New Mexico, 1968; Zome Primer by Steve Baer, Zomeworks Corporation, New Mexico, 1970; and Domebook 2 published by Pacific Domes, California, 1971.
-
A significant node is a node that is positioned at one of the vertices at the original regular polyhedron, e.g., a four-valent octahedral or a five-valent icosahedral node. The dual significant plates will therefore become 4-gons or 5-gons, respectively.
-
See Chapter 16.
-
A translation surface is made by two crossing polygonal lines sliding over each other. Such surfaces can easily be created by several CAD programs.
¶ Computer-Aided Processing of Polyhedric Configurations
Hoshyar Nooshin, P. L. Disney, and O. G. Champion
¶ INTRODUCTION
The objective of this chapter is to establish a methodology on which computer-aided techniques for the processing of polyhedric configurations may be based. The term polyhedric configuration is used to refer to any geometric arrangement that is based on polyhedra. In particular, the focus of attention is on polyhedric configurations that are of importance in the architectural and structural engineering fields.
The natural medium for the processing of polyhedric configurations is a programming language that incorporates the concepts of formex algebra. Formian is such a programming language in which the processing of polyhedric configurations can be carried out using the standard elements of the language.1 The term processing of polyhedric configurations in the present context
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
□ 343
simply means the creation and manipulation of polyhedric configurations.
The actual usage of the ideas presented in this chapter is envisaged to be through a programming language such as Formian. However, the main body of the material presented is independent of any particular mathematical system or computer software. The emphasis is on the primary concepts that are fundamental for the processing of polyhedric configurations in any medium.
The approach used in presenting the material is to begin by exploring the basic classes of polyhedric configurations. This is followed by a review of the properties of two families of polyhedra that are of central importance in relation to polyhedric configurations. The rest of the chapter is devoted to describing the basic procedures for processing of polyhedric configurations.
SOME BASIC POLYHEDRA
Polyhedra have been the subject of fascination and interest since ancient times. They have been studied throughout the ages by mathematicians, philosophers, and artists and they play an important role in a number of branches of science and technology.
The interest in polyhedra in this chapter stems from the fact that they provide a basis for the generation of a number of important classes of structural forms. Examples of polyhedra that are of particular interest in the present chapter are shown in Figure 12.1. These are the tetrahedron, octahedron, dodecahedron, icosahedron, and cuboctahedron, where
-
the tetrahedron has four triangular faces,
-
the octahedron has eight triangular faces,
-
the dodecahedron has 12 pentagonal faces,
-
the icosahedron has 20 triangular faces, and
-
the cuboctahedron has eight triangular faces and six square faces.
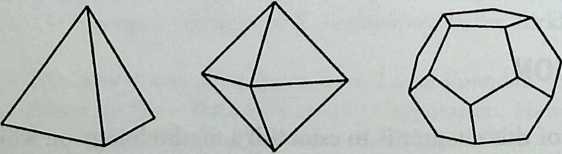
(a) Tetrahedron (b) Octahedron (c) Dodecahedron
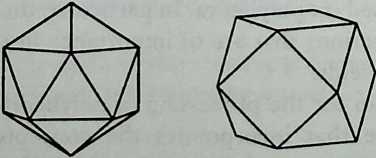
(d) Icosahedron (e) Cuboctahedron
Figure 12.1 Some basic polyhedra.
vavavavA.
▼avavavaWj
3TAVaVaWaVa<.
»kVAVATAVAVAW< 1
▼avavatavavavavAs?
jAVAVAVAVAWAVAVAVA
WavavavaWavavava, ;
▼avavavavavavavavavavJ
(b)
Figure 12.2 Mapping onto faces of an icosahedron.
MAPPING ONTO FACES OF POLYHEDRA
The first class of polyhedric configurations to be considered is obtained by placing objects onto the faces of polyhedra. For example, the configuration shown in Figure 12.24? is a polyhedric configuration that is obtained by placing a triangulated pattern on five faces of an icosahedron. A configuration that is used for mapping onto the faces of a polyhedron is referred to as a face-object. The face-object in the example under consideration is shown in Figure 12*.2a.* Also, the faces of the icosahedron that are to be mapped onto are shown in Figure 12.2b. These faces are shown again in Figure 12.2c, with one of them having the face-object placed onto it. The complete arrangement with the face-object mapped onto all five faces is shown in Figure 12.24?. In the preceding description of the procedure for obtaining a polyhedric configuration, the terms mapping and placing have been used interchangeably. This is appro-
Figure 12.3 Mapping with different face-objects.
priate because mapping in the present context simply means placing.
Another example of a polyhedric configuration is shown in Figure 12.2/ This configuration is obtained using the same procedure as described previously. However, in this case, a different face-object is used for mapping. The new face-object is shown in Figure 12.2e and the boundaries of one of the faces of the icosahedron on which the face-object is mapped are shown by dotted lines in Figure 12.2/
Further examples of polyhedric configurations that are obtained by face mapping are shown in Figure 12.3. The configurations shown in Figures 12.3/zd are obtained by mapping different face-objects onto five faces of an icosahedron. The point illustrated by these configurations is that face-objects are not limited to simple primary patterns and one is free to choose any required pattern for mapping. The polyhedric configuration shown in Figure
12.3c illustrates the fact that a face-object need not necessarily “match” the boundaries of the faces onto which it is mapped. Indeed, in general, a faceobject may only partially “fill” a face or may extend beyond a face. The point illustrated by Figure 12.3 d is that a polyhedric configuration may involve more than one type of face-object. In the configuration of Figure 12.3d, three faces have a face-object with a uniform pattern and two faces have a faceobject with openings that create a “daisy window” effect.
Figure 12.3e shows a polyhedric configuration that is obtained by mapping a face-object onto three neighboring faces of a dodecahedron. These faces are shown by thick lines on a small sketch at the top left comer of the figure. The face-object has a pentagonal boundary with internal hexagonal subdivisions. The polyhedric configuration of Figure 12.3/ is obtained by mapping face-objects onto five faces of a cuboctahedron. These faces are shown by thick lines on a small sketch at the top left comer of the figure. A new situation is encountered here in that the faces are of different types. Namely, there are four triangular faces and one square face. This, however, does not create any problem because one can use different face-objects for different types of faces, as required. The face-objects used for the polyhedric configuration of Figure 12.3/are a square-shaped face-object for the top face and a triangular face-object for the four side faces. It is to be noted, however, that the triangular face-object used does not fill the side faces. This fact is indicated in Figure 12.3/ where the actual boundaries of the side faces are shown by dotted lines.
The polyhedric configurations shown in Figures 12.2 and 12.3 are samples of a wide variety of configurations that may be created by mapping different face-objects onto the faces of polyhedra. These polyhedric configurations constitute an important class of structural forms. In addition, they provide the bases for the creation of geodesic forms, as will be discussed later.
MAPPING ON EDGES OF POLYHEDRA
The constitution of a polyhedron may be perceived in different ways. A tetrahedron, for example, may be regarded as a solid body with four faces, six edges, and four vertices. Alternatively, it may be regarded as a “stick arrangement” consisting of six line segments (sticks) that meet at the vertices. With this new way of visualizing a tetrahedron, one can again recognize four faces, six edges, and four vertices. Another way of perceiving a tetrahedron is to think of it as a basis for mapping. Thus the tetrahedron is regarded as a “geometric jig” that has four faces, six edges, and four vertices and is used for the positioning of mapping objects. This way of perceiving a polyhedron is helpful in visualizing the process of mapping face-objects as described in the previous section. This point of view is also useful for visualizing the mapping of objects on the edges of polyhedra. Mapping on the edges of polyhedra is the production mechanism for a major class of polyhedric configurations. Examples of this kind of configuration are shown in Figure 12.4.
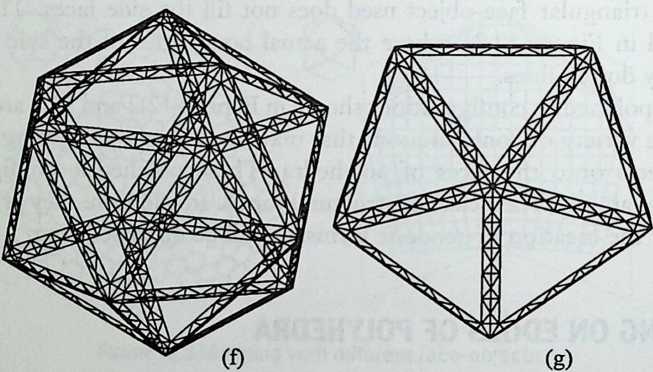
Figure 12.4 Mapping on edges of polyhedra.
Figure 12.4c shows a polyhedric configuration that is obtained by mapping (placing) a space truss configuration on the edges of a tetrahedron. A configuration that is used for mapping on the edges of a polyhedron is referred to as an edge-object. The edge-object in the example under consideration is shown in Figure 12.4/z. Also, the edges of the tetrahedron with the edge-object mapped on one of them is shown in Figure 12.4Z>. In this example the ends of the edgeobject are shaped such that when it is mapped on the edges of the tetrahedron the ends match with one another at the vertices. Figure 12.4// shows a polyhedric configuration that is obtained by mapping a space truss configuration on the edges of an octahedron. The ends of the edge-object are again suitably shaped such that they match with one another after mapping. Figure 12.4e illustrates the fact that the mapping of an edge-object need not necessarily involve all the edges of a polyhedron. In the case of the polyhedric configuration of Figure 12.4e, the edge-object is mapped on eight edges of an octahedron. In Figure 12 Af an icosahedron has been used as the basis for mapping. The edgeobject is again a space truss with its ends suitably shaped. The same edge-object is used to produce the polyhedric configuration of Figure 12.4g. In this case a group of 10 edges of an icosahedron is used for the operation.
The pioneering work of Gabriel involves a number of examples of polyhedric configurations of the type described above.2,3
MAPPING ON VERTICES OF POLYHEDRA
The idea of mapping objects on the vertices of polyhedra is a natural extension of the processes of mapping objects on the faces and edges of polyhedra. Examples of polyhedric configurations that are obtained by mapping objects on the vertices of polyhedra are shown in Figure 12.5.
Figure 12*.5a* shows a polyhedric configuration that is produced by mapping (placing) a star-like object on the vertices of a tetrahedron. In this figure the dotted lines indicate the positions of the edges of the tetrahedron. A configuration that is used for mapping on the vertices of a polyhedron is referred to as a vertex-object. The vertex-object used for the creation of the polyhedric configuration of Figure 12 .Sa is shown in Figure 12.5&. A similar operation is performed to produce the configuration of Figure 12.5 J using an icosahedron as the basis. The vertex-object is shown in Figure 12.5c.
Figure 12.5e shows a polyhedric configuration that is obtained by mapping the vertex-object of Figure 12.5/on the vertices of a tetrahedron. This vertexobject has an interesting effect. Namely, it creates end bases for the edges of the tetrahedron. The facets of the vertex-object that create the end bases are shown shaded in Figure 12.5f and the significance of these end bases becomes clear in relation to the polyhedric configuration of Figure 12.5g. This configuration is obtained by a combination of vertex mapping and edge mapping. To elaborate, a smaller version of the vertex-object of Figure 12.5/is mapped on the vertices of a tetrahedron. This is followed by mapping the space truss configuration of Figure 12.5h on the edges of the tetrahedron. The scale and position of this edge-object are chosen such that the ends of the space trusses fit the triangular bases created by the vertex-object. A similar procedure is followed in producing the polyhedric configuration of Figures 12.Si xn&j. In this case an octahedron has been used as the basis for the operation.
The technique employed to create the polyhedric configurations of Figures 12.5g and/ can be of value in some practical applications. The technique provides an alternative way of dealing with the “end matching” problem. Thus, instead of shaping the ends of the edge-object for matching at the vertices, the vertex-object is designed to act as a connecting medium. This will result in a simpler edge-object because it only requires straightforward ends.
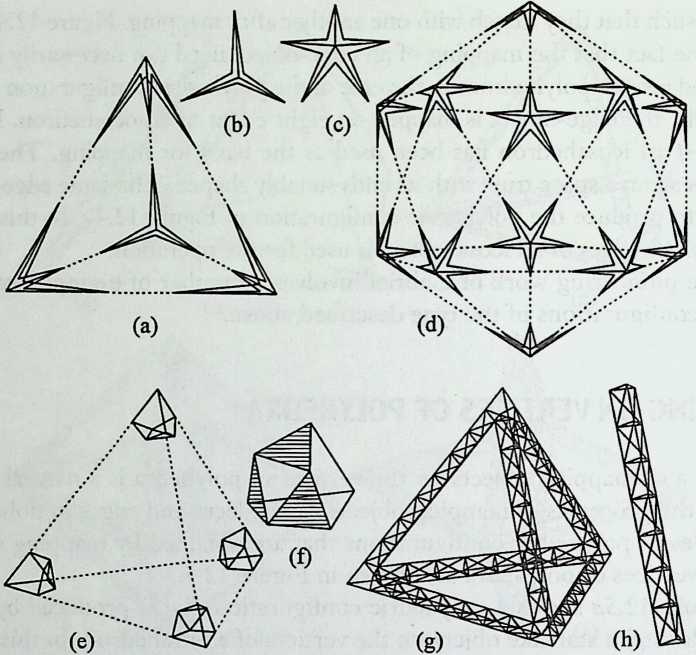
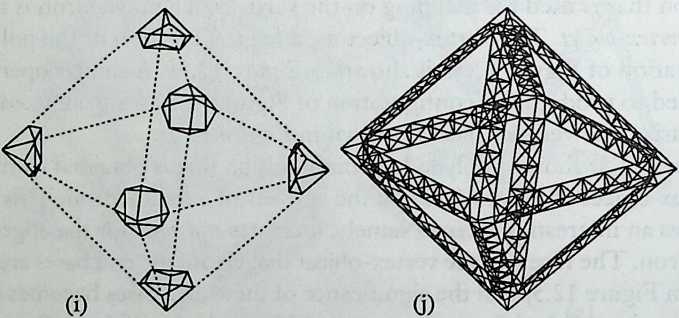
Figure 12.5 Mapping on vertices of polyhedra.
Another point that is illustrated by Figures 12.5g andy is worth highlighting. Namely, a polyhedric configuration may involve a combination of edge and vertex mappings. Indeed, in general, there is no restriction regarding the mixing of different types of mappings and any combination of face, edge, and vertex mappings may be used without any problem.
GEODESIC CONFIGURATIONS
The configuration shown in Figure 12.6a is obtained by projecting the configuration of Figure 12.2 onto the surface of a sphere. The sphere is concentric with the icosahedron on which the configuration of Figure 12*.2d* is based.
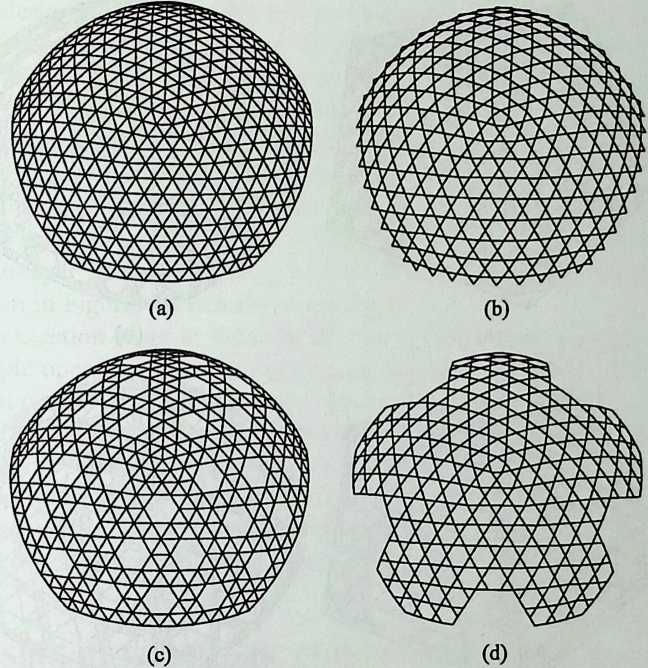
Figure 12.6 Some geodesic forms.
This common center of the sphere and icosahedron is also chosen as the center of projection. A polyhedric configuration of the type shown in Figure 12.6a is referred to as a geodesic form or geodesic configuration. The same procedure is used to produce the geodesic configurations shown in Figures 12.6b-d. These configurations are obtained using the polyhedric configurations of Figures 12.2f and 12.3£ and c as the bases for projection.
The surface on which a geodesic form is produced need not necessarily be spherical. Indeed, a variety of different surfaces such as ellipsoids and paraboloids may be used for the creation of geodesic forms. Also, the type of projection need not necessarily be central and other kinds of projections, such as parallel projection, may be used instead.
Figure 12.6e shows a geodesic form that is obtained by projecting the poly-
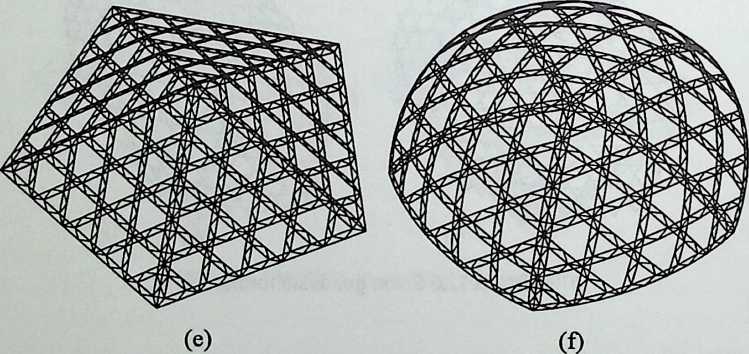
Figure 12.7 Some double-layer polyhedric configurations.
hedric configuration of Figure 12.2/ onto an ellipsoidal surface. A different process is involved in producing the configuration shown in Figure 12.6/ This is obtained by stretching the configuration of Figure 12.6b in one direction.
The configuration shown in Figure 12.6/illustrates a point of general importance. Namely, any polyhedric configuration may be subjected to modifications and alterations to suit a particular application. In other words, there is no “inherent” final stage in the processing of a polyhedric configuration. Like a lump of steel in the hands of a blacksmith, a polyhedric configuration may be worked, in as many stages as required, to turn it into a desired shape.
A geodesic form may involve two or more layers. For example, the geodesic configuration shown in Figure 12 .lb has two layers of elements that are interconnected together by intermediate web elements. This double-layer geodesic form is based on the configuration shown in Figure 12.7/z. This is a polyhedric configuration that is obtained by mapping (placing) a double-layer face-object onto five faces of an icosahedron. The geodesic form of Figure 12.1 b is obtained by projecting the two layers of the configuration of Figure 12.7/z onto two concentric spheres. A similar procedure is used in obtaining the double-layer geodesic forms of Figures 12.Id and/from the configurations shown in Figures 12.7c and e, respectively.
The projection stage in the creation of a geodesic form involves a relatively simple operation. This is true for projection on a single surface as well as projection on two or more surfaces. The reason for the simplicity of operation is that projection is a straightforward concept and can easily be dealt with through a standard computer-based routine.4
An abundance of structures have been constructed all over the world using various forms of geodesic configurations. These begin with the pioneering work of R. Buckminster Fuller and include many impressive examples.5,6
PROCESSING OF POLYHEDRIC CONFIGURATIONS
The processing of polyhedric configurations in precomputer days was an extremely difficult task. In spite of this, a number of gifted designers managed to deal with the problem and create many beautiful structures based on polyhedric configurations. The constraint of the processing difficulties, however, did not allow the designers to take full advantage of the whole spectrum of possibilities and their scope remained rather limited. Even today, the processing of polyhedric configurations is mainly carried out using computer programs that lack generality and have many limitations and shortcomings.
In contrast, the conceptual methodology that will be presented in this chapter, combined with suitable computer software such as Formian, provides a means for dealing with the processing of any kind of polyhedric configuration with relative ease.
One key factor in dealing with the processing of polyhedric configurations is the ability to generate face-objects, edge-objects, and vertex-objects in a convenient manner. The creation of these objects in Formian can be carried out using the concepts of formex algebra. The algebra works through concepts that effect movement, propagation, deformation, and curtailment of forms (Figure 12.8).1,7
PLATONIC AND ARCHIMEDEAN POLYHEDRA
In this chapter the use of polyhedra in the creation of structural forms is discussed in terms of Platonic and Archimedean polyhedra. There are five Platonic polyhedra, whose views are shown in Figure 12.9. These five polyhedra
Formex algebra includes:
concepts that allow movement of forms
G=verad(0,0) E
concepts that allow propagation of forms
G=lamid(5,5/2)E
concepts that allow deformation of forms G=bb(l,3/2)bp(l,9)[E \
Figure 12.8 Basic concepts of formex algebra.
were known to the ancient world before Plato and the designation “Platonic” is due to the fact that Plato paid special attention to these polyhedra.8 Each one of the Platonic polyhedra is a convex body with faces that are congruent regular polygons of the same type.
An Archimedean polyhedron is also a convex body with faces that are regular polygons. However, unlike the Platonic polyhedra, the faces of an Archimedean polyhedron are not all of the same type. There are 15 Archimedean polyhedra, whose views are shown in Figure 12.9. Each of these polyhedra has either two or three different types of faces. Archimedean polyhedra were discovered in ancient Greece and were described by Archimedes. However, the writings of Archimedes in this regard together with the knowledge of these polyhedra were lost and it was not until the Renaissance that they were gradually rediscovered.8
The Platonic and Archimedean polyhedra are closely related and a family tree indicating the relationships between them is shown in Figure 12.10. This
PLATONIC POLYHEDRA
Pl: Tetrahedron P2: Cube P3: Octahedron P4: Dodeca
PS: Icosa
hedron hedron
ARCHIMEDEAN POLYHEDRA
P6: Truncated P7: Cubocta-
Tetrahedron
hedron
P8: Truncated P9: Truncated
Cube Octahedron
PIO: Small Rhombicub-octahedron
Pl 1: Great Rhombicub-octahedron
P12: Icosido-decahedron
P13: Truncated
Dodecahedron
P14: Truncated
Icosahedron
P15: Left
Snub Cube
P16: Right
Snub Cube
P17: Small Rhombicosi-dodecahedron
P18: Great Rhombicosi-dodecahedron
P19:Left Snub Dodecahedron
P20: Right Snub Dodecahedron
Figure 12.9 Platonic and Archimedean polyhedra.
is a modified version of a family tree produced by Motro.5 It is seen from Figure 12.10 that the tetrahedron is the “mother polyhedron” and all the other Platonic and Archimedean polyhedra may be derived from it. This may be done through five basic transformations, which are briefly described in Figure 12.11. These transformations are referred to as truncation, canting, snubbing, duality, and planing. Detailed general descriptions of Platonic and Archimedean polyhedra may be found in many excellent publications.810
POLYHEDRON CODES AND P-NAMES
A numeric code is required for identification of the Platonic and Archimedean polyhedra in computer-based procedures for the processing of polyhedric configurations. This numeric code is chosen to consist of the integer numbers 1 to 20, associated with the Platonic and Archimedean polyhedra in the order
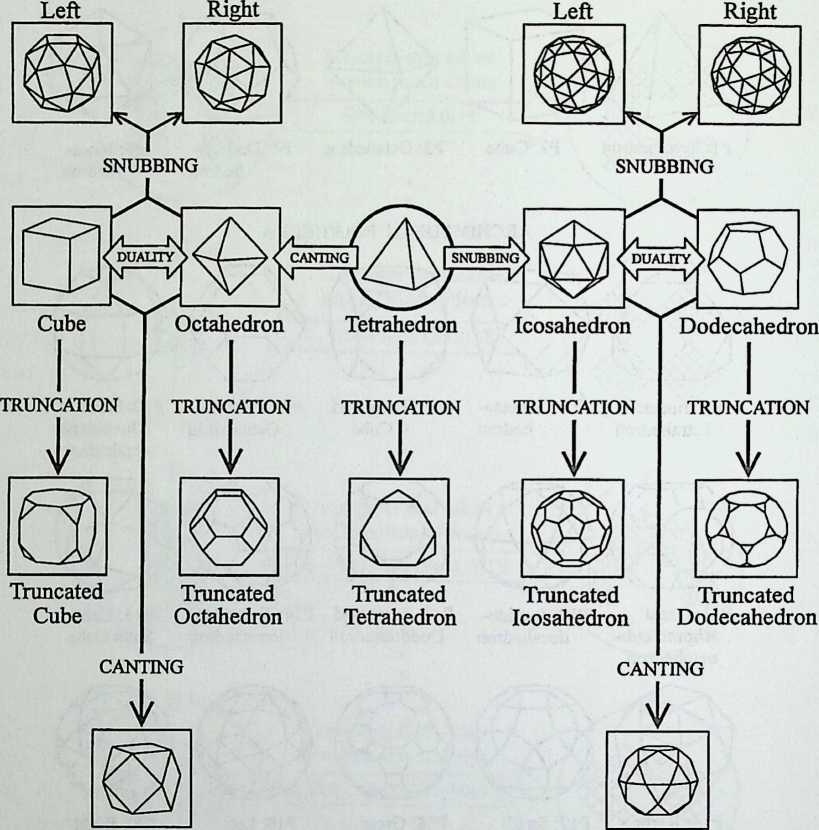
Figure 12.10 Family tree of Platonic and Archimedean polyhedra.
Snub Cubes
Snub Dodecahedra
Cuboctahedron
Icosidodecahedron
Great
CANTING + PLANING
TRUNCATION + PLANING
Small
Rhombicuboctahedron
Great
CANTING + PLANING
TRUNCATION + PLANING
Small
Rhombicosidodecahedron
they appear in Figure 12.9. These identity numbers are referred to as polyhedron codes. For instance, the polyhedron codes for the tetrahedron, cuboctahedron, and icosidodecahedron are 1, 7, and 12, respectively. A polyhedron code, preceded by the letter P, is used as an alternative name for the polyhedron. A name of this form is referred to as a P-name. The P-names of the Platonic and Archimedean polyhedra are shown in Figure 12.9 together with the traditional names of the polyhedra. In the following material the P-names are sometimes used by themselves or together with the traditional names to identify polyhedra.
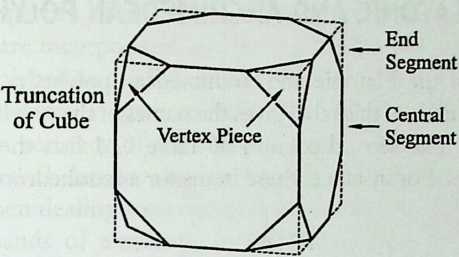
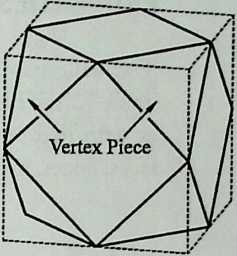
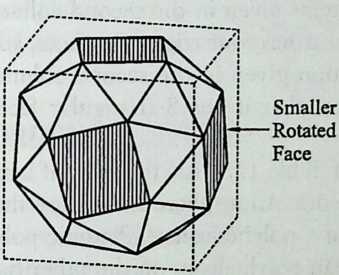
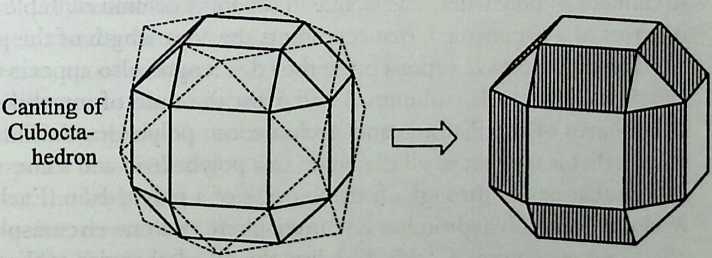
Canting of Cube
Truncation: Each edge is divided into a central segment and two end segments and the vertex pieces obtained by connecting the division points are cut off, as shown.
Canting: Each edge is divided into two equal segments and the vertex pieces obtained by connecting the division points are cut off, as shown.
Snubbing of Cube
Dual of Cube
Snubbing: A smaller rotated version of each face is placed centrally on the face (shown shaded) and the regions between the edges of the new faces are trimmed off by faceting.
Duality: The center of each face is regarded as the vertex of another polyhedron (or each vertex is regarded as the center of a face of a polyhedron).
Planing of Canted Cuboctahedron
Planing: The term ‘planing’ implies ‘planing down’ (scraping off) the surface of a polyhedron. For instance, in producing the small rhombicuboctahedron, a cuboctahedron is subjected to canting, as shown above. This will give rise to a polyhedron that is similar to the small rhombicuboctahedron but in which the faces that are shown shaded are rectangular rather than square. To overcome the problem, the shaded rectangular faces together with the triangular faces are planed down to a depth that equalizes all the edges.
Figure 12.11 Truncation, canting, snubbing, duality, and planing.
PROPERTIES OF PLATONIC AND ARCHIMEDEAN POLYHEDRA
The basic particulars of the Platonic and Archimedean polyhedra are given in Table 12.1. The first column of this table gives the names of the polyhedra together with their P-names. The second column of Table 12.1 fists the numbers of faces, edges, and vertices. For instance, these items for a tetrahedron are given as
F3:4
F:6
I/: 4
Here, the letter F stands for face and the digit that follows F indicates the number of sides of the face. Also, the letter E stands for edge and the letter V stands for vertex. The items given in the second column of Table 12.1 for a tetrahedron indicate that it has four triangular faces, six edges, and four vertices. Also, the information given in the second column of the table for P7 (cuboctahedron) indicates that it has 8 triangular faces, 6 square faces, 24 edges, and 12 vertices.
The third column of Table 12.1 lists the radii of inspheres of the Platonic and Archimedean polyhedra. An insphere is a sphere that is tangent to all the faces of the same type of a polyhedron. A Platonic polyhedron has only one insphere. An Archimedean polyhedron, on the other hand, has either two or three inspheres, depending on whether it has two or three different types of faces. The radius of insphere for an Archimedean polyhedron given in the third column of Table 12.1 corresponds to the smallest insphere, that is, the insphere that is tangent to the largest faces. Also included at the end of Table 12.1 are two general formulas for evaluation of the radii of inspheres for Platonic and Archimedean polyhedra. Each value in the third column of Table 12.1 is given in terms of a parameter L that represents the edge length of the polyhedron.
The parameter L, representing the edge length, also appears in columns 4 and 5 of Table 12.1. Columns 4 and 5 list the radii of interspheres and cir-cumspheres of the Platonic and Archimedean polyhedra. An intersphere is a sphere that is tangent to all the edges of a polyhedron and a circumsphere is a sphere that passes through all the vertices of a polyhedron. Each Platonic or Archimedean polyhedron has one intersphere and one circumsphere.
The last column of Table 12.1 lists the dihedral angles of the Platonic and Archimedean polyhedra. A dihedral angle is the angle between two faces of a polyhedron that share an edge. For any Platonic polyhedron, all the dihedral angles are equal. In contrast, an Archimedean polyhedron may have up to three different dihedral angles, as shown in the last column of Table 12.1. For an Archimedean polyhedron that has more than one dihedral angle, the faces that correspond to each dihedral angle are specified by the numbers of their sides given in square brackets. For example, in the case of P6 (truncated tetrahedron), the first dihedral angle is preceded by [6 indicating that the angle is between two hexagonal faces and the second dihedral angle is preceded by [6 indicating that the angle is between a hexagonal face and a triangular face.
The properties of the Platonic and Archimedean polyhedra, as given in Table 12.1, are incorporated into the part of Formian that deals with the processing of polyhedric configurations. The information is built into Formian in terms of the formulas given in Table 12.1. The use of formulas will allow the full available accuracy of the computer to be utilized. High accuracy of the basic polyhedral data is essential in many situations. This is the case, for instance, when dealing with complex polyhedric configurations that consist of many thousands of elements, in particular, when the generated geometric details are to be used as a basis for other operations, such as structural analysis.
In regard to the accuracy of the entries in Table 12.1, it should be noted that for the snub polyhedra (P15, P16, P19, and P20), the accuracy of the entries for radii of insphere, intersphere, and circumsphere depends on the accuracy of a parameter k. The value of this parameter in Table 12.1 is given accurate to nine decimal places. The values of the dihedral angles for the snub polyhedra in Table 12.1 are also given accurate to nine decimal places.
POLYHEDRAL COORDINATE SYSTEMS
A view of a polyhedric configuration is shown in Figure 12.12/z. The configuration is obtained by mapping a triangulated pattern onto the faces of a tetrahedron. When a computer-aided approach is used in processing such a configuration, the internal computer representation of the configuration will be a numerical model that describes the configuration in terms of the coordinates of its nodal points. It is therefore necessary to have a coordinate system with respect to which the nodal coordinates are specified. The most convenient approach in this regard is to establish a standard coordinate system for the tetrahedron and to use it for all polyhedric configurations that are based on a tetrahedron.
The chosen standard coordinate system for the tetrahedron is the right- handed Cartesian coordinate system that is shown as XYZ in Figure 12.12a. Figure 12.12# illustrates the conventions used in specifying this standard coordinate system. The origin of the coordinate system is at the center of the polyhedron. This point is indicated by a large dot. The points where the X, Y, and Z axes intersect the body of the polyhedron are referred to as the X-point, Y- point, and Z-point, respectively. The X-point is at the center of the circle with an X inside it. The T-point is indicated by a little circle and the Y axis is shown as an arrow emanating from the K-point. Similarly, the Z-point is indicated by a tittle circle and the Z axis is shown as an arrow emanating from the Z-point.
The standard coordinate system for the tetrahedron is shown again in Figure 12.13 together with the standard coordinate systems for all the other Platonic and Archimedean polyhedra. Some of the polyhedra in this figure have additional sketches shown near them. The tetrahedron, for example, has such a sketch. These sketches provide information about the precise positions of the X-points and are included whenever the positions of the X-points are not obvious from the main figures.
A view of a set of cardboard models of Platonic and Archimedean polyhe-
TABLE 12.1 Properties of Platonic and Archimedean Polyhedra
| Polyhedron | Faces, Edges, Vertices |
Radius of Insphere | Radius of Intersphere | Radius of Circumsphere | Dihedral Angle |
| Pl: Tetrahedron | F3:4 E: 6 V:4 |
(0.204124145 Z) | (0.353553390 Z) |
|
/ 1 X acos(y) (70.5287794°) |
| P2: Cube | F4: 6 E: 12 V: 8 |
L 2 | Z ■Ji (0.707106781 Z) |
Z 2 (0.866025403 Z) | ° |
| P3: Octahedron | F3: 8 E: 12 V: 6 |
_L_ JU (0.408248290 L) |
L 2 | Z ■Ji (0.707106781 Z) |
/-lx acos() (109.471221°) |
| P4: Dodecahedron | F5: 12 E: 30 V: 20 |
+1175 2710 (1.11351636 Z) | 3 + 75 T la 4 (1.30901699 Z) | 718 + 65/5 r
|
acos(-) (116.565051°) |
| P5: Icosahedron | F3:20 E: 30 V: 12 |
+ 473 (0.755761314 Z) | l + 75z 4 (0.809016994 Z) |
4 (0.951056516 Z) |
/-75 k acos() (138.189685°) |
P6: Truncated Tetrahedron |
F3:4 F6:4 E: 18 V: 12 | Z 4 (0.612372435 Z) | _ 4 (1.06066017 Z) | 722z 4 (1.17260394 Z) | [6 acos( 1/3) (70.5287794°) [6 acos(-l/3) (109.471221°) |
| P7: Cuboctahedron | F3: 8 F4: 6 E:24 V: 12 |
L ■Ji (0.707106781 Z) |
|
Z | acos(-y) (125.264390°) |
| PS: Truncated Cube | F3: 8 F8: 6 E: 36 V:24 |
l+£ 2 (1.20710678 Z) | 2+-J2 r JL 2 (1.70710678 Z) |
77 + 472 T la 2 (1.77882365 Z) |
[8 90° [8 acos(-1/5/3) (125.264390°) |
| P9: Truncated Octahedron | F4: 6 F6: 8 E: 36 V: 24 |
Z 2 (1.22474487 Z) | 3-l 2 | TiOz 2 (1.58113883 Z) | [6 acos(-l/3) (109.471221°) [6 acos(-1/5/3) (125.264390°) |
PIO: Small
|
F3: 8 F4: 18 E: 48 V: 24 |
i+z 2 (1.20710678 Z) | J1 + 2-J2 r …. ■ 2z 2 (1.30656297 Z) |
75 + 25/2 r
|
[4 135° [4 acos(-5/6/3) (144.735610°) |
| PH: Great Rhombicub-octahedron | F4: 12 F6: 8 F8: 6 E: 72 V: 48 |
1+2 r jlz 2 (1.91421356 Z) | J12 + &J2 r la 2 (2.26303344 Z) | 713 + 65/2 T
|
[8 acos(-l/x/J) (125.264390°) [8 135° [6 acos(-5/6/3) (144.735610°) |
| Pll: Icosido-decahedron | F3: 20 F5: 12 E: 60 V: 30 |
J5+245 t ■Js (1.37638192 Z) | 75+2 T 2 (1.53884177 Z) | + 5Z 2 (1.61803399 Z) |
|
P13: Truncated Dodecahedron |
F3: 20 F10:12 E: 90 V: 60 |
J50 + 22J5 T la 4 (2.48989829 Z) | + 35/5 _
|
774 + 305/5 T
|
[10 acos(-1/5/5) (116.565051°) [10 acos( ) (142.622632°) |
TABLE 12.1 Properties of Platonic and Archimedean Polyhedra (continued)
| Polyhedron | Faces, Edges, Vertices | Radius of Insphere | Radius of Intersphere | Radius of Circumsphere | Dihedral Angle |
| [6 acos(-75/3) | |||||
| + 3£ | +1875 r | (138.189685°) | |||
| (2.42705098 Z) |
|
rrcl (-75+275 \ [6 acos( ) (142.622632°) |
|||
P15: Left Snub Cube P16: Right Snub |
Z 2k (1.14261351 Z) | 71 +A:2 T 2k (1.24722317 Z) |
71 + 2A:2 T 2k (1.34371337 Z) |
[4 142.983430° [3 153.234588° |
|
| Cube | |||||
P17: Small
|
+ 275 275 (2.06457288 Z) |
710 + 475 T ■1 ■“ 2 (2.17625090 Z) |
711 + 475 2 (2.23295051 Z) |
||
/ /5+2 V5 \ [10acos( ) (142.622632°) |
|||||
| P18: Great Rhombicosi-dodecahedron | 725 + 105 r 2 (3.44095480 Z) |
730+1275 r 2 (3.76937713 Z) |
731+1275 T ■“Jj 2 (3.80239450 Z) |
(-710 + 275 1 [10 acos( ) (148.282526°) [6 acos(z<l±)) (159.094843°) |
|
P19: Left Snub Dodecahedron P20: Right Snub |
F3: 80 F5: 12 E: 150 V: 60 |
+ 1175 V 40£2 (1.98091595 Z) |
1 3 + V5+2k2 L V (40) k2 (2.09705384 Z) |
l7 + 3V5 + 8k2J. \(204j5)k2 (2.15583737 Z) |
[5 152.929920° [3 164.175366° |
| Dodecahedron |
Some General Relations
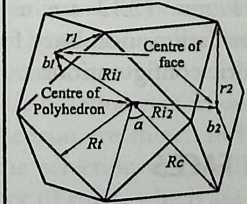(l)Rc=7/?t2+Z2/4 (2)Ri=Rc2-L2/4 Q)Rip=Rc2 -rp2 (4) Rip = yj R12 -bp2 (5) L = 2Jrc2-Ri2 (6) a - 2 asin(Z/2Rc) (7) a = 2 acos(A//7?c) (8) a = 2 atan(Z/2Rt) The above relations are applicable to every Platonic and Archimedean polyhedron, where: ■ Z is the edge length ■ a is the angle subtended by an edge at the center of the polyhedron ■ Rc is the radius of the circumsphere ■ Rt is the radius of the intersphere ■ Rip is the radius of an insphere, that is, a sphere which is tangent to all the faces of type p ■ rp is the distance between the center and a comer of a face of type p ■ bp is the distance between the center and the midpoint of a side of a face of type p ■ The radius of insphere for an Archimedean polyhedron given in the third column of the table corresponds to the smallest insphere, that is, the insphere which is tangent to the largest faces.
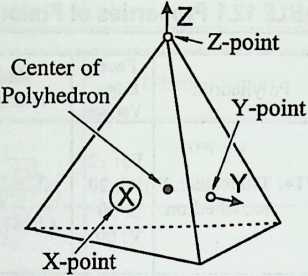
(a) (b)
Figure 12.12 A coordinate system for tetrahedron.
dra is shown in Figure 12.14. The models of the Platonic polyhedra are placed in the front row and those of the Archimedean polyhedra are arranged in the three back rows. The X-point and Z-point for each model are situated at the centers of the circular spots on the model. The darker spot that appears in front of the model indicates the position of the X-point and the lighter spot that appears on the top indicates the position of the Z-point.
From the point of view of compatibility of the coordinate systems, as given in Figure 12.13, the Platonic and Archimedean polyhedra may be divided into three groups. First, there is a group consisting of two polyhedra, namely, the tetrahedron and truncated tetrahedron. These two polyhedra occupy the central part of the family tree in Figure 12.10. The coordinate systems for these polyhedra are compatible with each other. By the term compatible, in this context, it is meant that when a truncated tetrahedron is produced by cutting off the comers of a tetrahedron, then the original coordinate system of the tetrahedron will become the coordinate system for the truncated tetrahedron without any change.
The second family of polyhedra with compatible coordinate systems consists of nine polyhedra. These are the polyhedra that can be derived from the cube or octahedron and appear to the left of the center in the family tree of Figure 12.10. The third family of polyhedra with compatible coordinate systems again has nine members. These are the polyhedra that can be derived from the dodecahedron or icosahedron and appear to the right of the center in the family tree of Figure 12.10.
The standard coordinate systems shown in Figure 12.13 are used in Formian as the basis for formulation of the transformations necessary for the creation of numerical models representing polyhedric configurations.
IDENTITY NUMBERS AND BASELINES FOR FACES OF POLYHEDRA
Figure 12.15e shows a polyhedric configuration that is obtained by mapping the face-object of Figure 12.15a onto the top five faces of an icosahedron. If the face-object for mapping onto the faces is chosen to be that of Figure 12.15b, then the result will be the polyhedric configuration shown in Figure 12.15/ In the case of the polyhedric configuration of Figure 12.15g, the faceobject of Figure 12.15/7 is mapped onto one of the top faces of an icosahedron and the face-object of Figure 12.15c is mapped onto the remaining four faces. The polyhedric configuration of Figure 12.15b is obtained by a similar procedure using the face-objects shown in Figures 12.15b and d.
The point that is meant to be illustrated by the above examples is that in most practical cases a face-object is mapped onto a selected number of the faces rather than all the faces of a polyhedron. In the examples of Figures 12.15 e-h, the top five faces of an icosahedron have been selected for mapping. Furthermore, in the examples of Figures 12.15g and b, one of the faces has been selected for mapping of a face-object and the other four faces have been selected for mapping of a different face-object. In order to select faces, it is necessary to have a means of identifying the faces of a polyhedron. This is achieved by associating an identity number with each face of a polyhedron, as will be described later.
Another problem that has to be addressed is illustrated in terms of the polyhedric configurations shown in Figures 12.15/ and/. Figure 12.15/ shows a polyhedric configuration that is obtained by mapping the face-object of Figure 12.15c onto the top five faces of an icosahedron. However, the orientation of the face-object as mapped onto the faces in Figure 12.15/ is different from the orientation of the face-object as it appears in Figure 12.15c. The polyhedric configuration shown in Figure 12.15/ has the face-object of Figure 12.15/7 mapped onto three of the faces and the face-object of Figure 12.15c mapped onto two of the faces with different orientations. These examples show that, in addition to the requirement of an identity number for each face of a polyhedron, it is also necessary to associate a frame of reference with the face. This would then allow the required position of a face-object for mapping onto the face to be specified unambiguously.
A frame of reference for a face of a polyhedron is established by assigning the status of baseline to one of the sides of the face and by associating the letters A and B to the end points of this baseline, as shown in Figures 12.16a and b. The end of the baseline that is associated with the letter A is referred to as the 4-end and the end that is associated with the letter B is referred to as the 2?-end. The baseline of a face is indicated by a vector. The vector is placed near the baseline with its arrowhead showing the direction from the A-end to the 5-end. In addition, the identity number of each face is placed near the baseline vector.
The baseline vectors and the face identity numbers for the top part of an icosahedron are shown in Figure 12.16a. The allocation of identity numbers and the selection of baselines for the faces of polyhedra are governed by a number of rules, which are described in the Appendix. Also, the face identity numbers together with the baselines for a group of six polyhedra are shown in Figure 12.17. This group contains all the Platonic polyhedra and one Archimedean polyhedron, namely, the cuboctahedron.
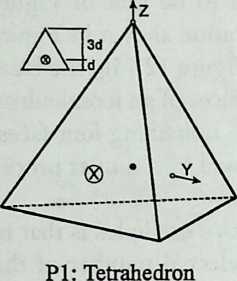
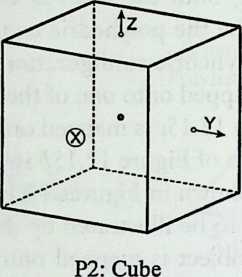
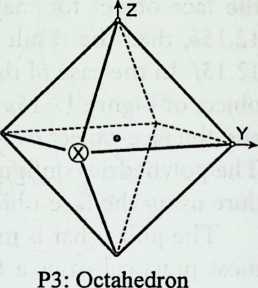
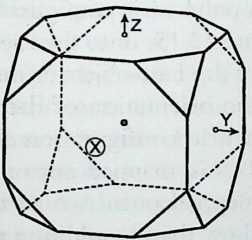
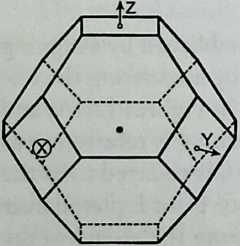
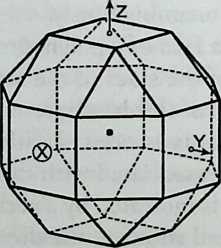
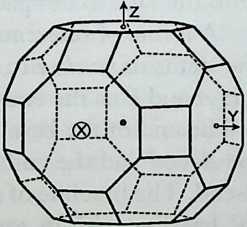
P4: Dodecahedron
P5:Icosahedron
P6: Truncated
Tetrahedron
P8: Truncated Cube
P9: Truncated
Octahedron
PIO: Small Rhombi-cuboctahedron
Pl 1: Great Rhombi-cuboctahedron
Figure 12.13 (part 1) Coordinate systems of Platonic and Archimedean polyhedra.
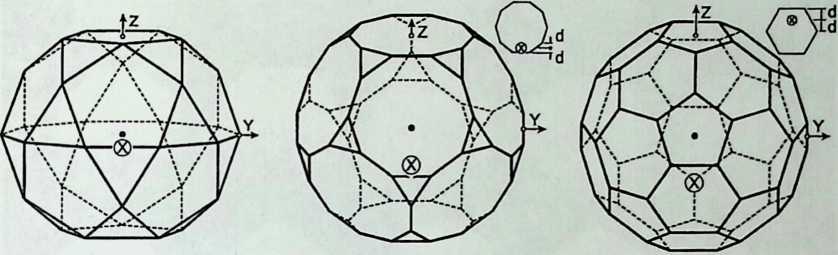
P12: Icosido-Pl3: Truncated Pl4: Truncated
decahedron Dodecahedron Icosahedron
Pl5: Left Snub Cube
Pl6: Right Snub Cube
Pl7: Small Rhomb-
icosidodecahedron
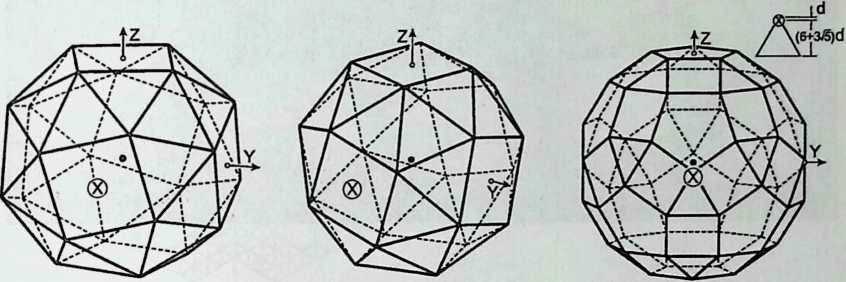
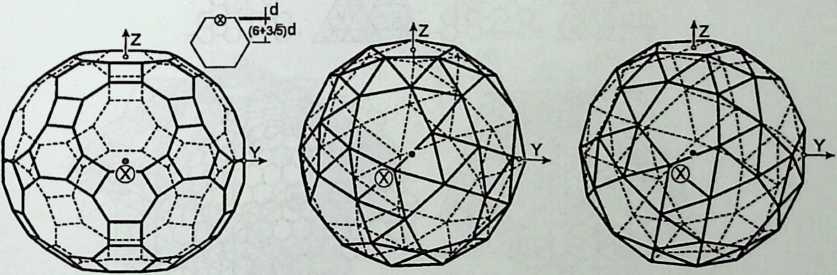
Pl8: Great Rhomb-icosidodecahedron
Pl9: Left Snub Dodecahedron
P20: Right Snub Dodecahedron
e is parallel to the Y
axis and f is parallel to the Z axis.
e = 0.192893711 L f= 0.144866867 L
Position of X-pointforP19
Position of X-point for P20
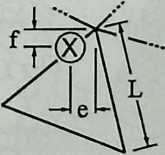
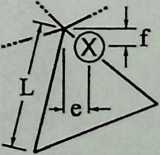
Figure 12.13 (part 2) Coordinate systems of Platonic and Archimedean polyhedra.
Figure 12.14 Models of Platonic and Archimedean polyhedra with the darker front spots indicating the X-points and the lighter top spots indicating the Z-points.
Figure 12.15 Examples of face mapping.
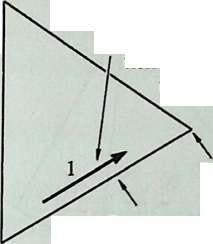
B-end
Baseline
A-end
(b)
Vector indicating the baseline
of face No 1 with the arrow-
head showing the direc-
tion from the A-end
to B-end
Z (upward)
WaTaWaV HtatatatA HtatataTaTO.Atatatatatat ▼atatatatatjM »rAVAVJ«rAVAW Wava /avaVa VAVAVA_yAVAVA7/
Face-object
A-point (To be placed at the A-end of the baseline)
B-point (To be placed at the B-end of the baseline)
(d)
Z (upward)
VatatataI
KotaTaTO_
.JATATATATATATAW fcrAVATATATATA ▼AlVMWrATj
WaVaVaX MW
IAVAVASkTAVA F. VaVavavavavav/
Face-object
B-point (To be placed at the B-end of the baseline)
A-point (To be placed at the A-end of the baseline)
(f)
Figure 12.16 Face-mapping process.
MAPPING OF FACE-OBJECTS
The process of mapping a face-object onto a face of a polyhedron involves the following steps:
-
A face-object is specified by a formex relative to the standard X-Y-Z coordinate system of the polyhedron.
-
Two points of the face-object are specified by their X-Y-Z coordinates. These points are referred to as the A -point and B-point. The role of the /(-point and B-point is to provide information regarding the required
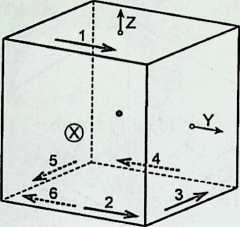
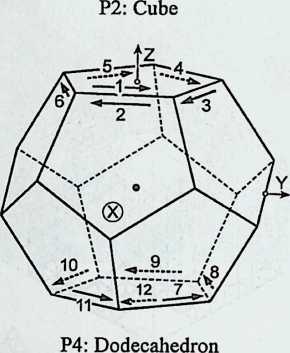
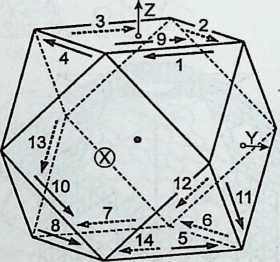
Figure 12.17 Identity numbers and baselines for the faces of a selection of polyhedra.
position, orientation, and size of the face-object in its final mapped position on the face of the polyhedron, as exemplified in Figures 12.16c-f.
-
The face-object is scaled such that the distance between the A-point and 5-point is equal to the edge length of the polyhedron. In this scaling process, the same scale factor is used in the X, Y, and Z directions.
-
The mapping plane is determined. This is the plane of the face-object that is to coincide with the face of the polyhedron. If the line containing the A-point and B-point of the face-object is parallel to (or coincident with) the X axis, then the mapping plane is the plane that contains the A-point and 5-point and is parallel to (or coincident with) the X-Y plane. This simple case is applicable in most practical situations and is the only case considered here.
-
The face-object is subjected to a sequence of rigid-body movements (translations and rotations) such that the following conditions are satisfied:
-
The //-point of the face-object is coincident with the ?/-end of the baseline of the face.
-
The B-point of the face-object is coincident with the B-end of the baseline of the face.
-
The mapping plane is coincident with the face.
° The direction that was initially the positive Z direction of the faceobject is pointing to the outside of the polyhedron.
Two examples of the face-mapping process are shown in Figure 12.16. Figure 12.16c shows the top part of an icosahedron with a face-object mapped onto five faces. The boundaries of these faces are shown by dotted lines. The face-object is shown in Figure 12.16d with the line that passes through the-point and B-point being parallel to the X axis. The mapping is achieved by suitably scaling the face-object and then placing it on each face in a position where the /(-point coincides with the /(-end of the basefine of the face and the B-point coincides with the B-end of the baseline of the face.
It is important to note that the //-point and B-point of the face-object need not necessarily be actual points of the face-object. For example, in the case of the face-object in Figure 12.16d, the //-point and B-point are outside the face-object altogether. The dotted lines here are included to indicate the positions of the y4-point and B-point. These dotted lines are not supposed to be part of the face-object.
A second example of face mapping is shown in Figures 12.16e and/ The face-object in this example is the same as that of the previous one. The only difference is in the positions of the //-point and B-point. To be specific, the positions of the /(-point and B-point have crossed over as well as being shifted. Consequently, the face-object has been turned around for mapping.
IDENTITY NUMBERS AND DIRECTIONS FOR EDGES OF POLYHEDRA
The upper part of Figure 12.18/z shows a polyhedric configuration that is obtained by mapping a truss configuration on the edges of an octahedron. The edge-object is shown in the lower part of Figure 12.18a with the //-point and B-point being assumed to be on the X axis. The mapping is carried out by placing a suitably scaled version of the edge-object on the edges of the octahedron. For each edge, the edge-object is positioned such that the end points of the top chord of the truss coincide with the end points of the edge and the plane of the truss passes through the center of the octahedron. The angle of the inclined sides of the truss is chosen such that, after mapping on the edges of the octahedron, the ends of the bottom chords of the trusses meet without any gaps. The term miter angle is used to refer to the angle that will allow the ends of the trusses to match after mapping. Figure 12.18b shows the result of
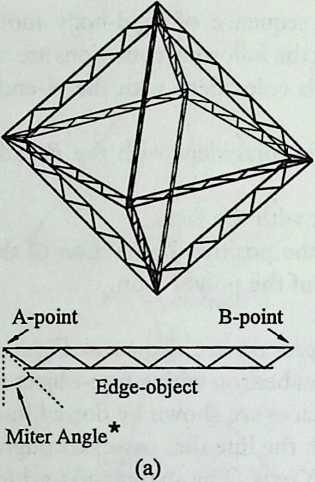
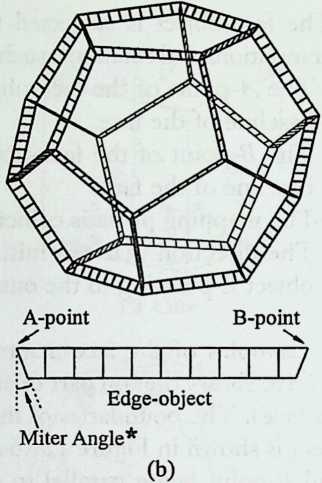
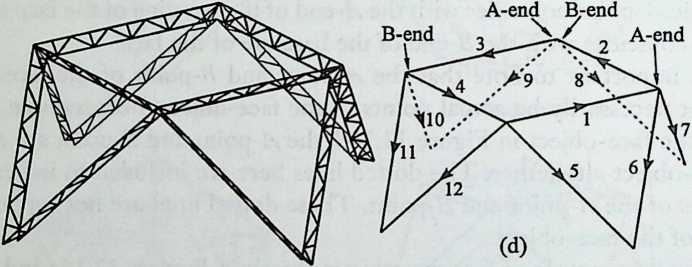
where L is the edge length of the polyhedron and Rc is the radius of its circumsphere.
* The ‘mitre angle’ is given by: asin(L/2Rc)
Edge-object
Miter Angle
(c)
Figure 12.18 Examples of edge mapping.
mapping a Vierendeel-girder-type configuration on the edges of a dodecahedron. Also, the result of mapping a truss-like configuration on the upper half of a cuboctahedron is shown in Figure 12.18c.
If the edge-object consists of a plane configuration and if this is to be mapped on the edges of a Platonic or Archimedean polyhedron, then the miter angle may be obtained from the general formula given at the right bottom corner of Figure 12.18.
In order to carry out the mapping of an object on an edge of a polyhedron, it is necessary to identify the edge on which the object is to be mapped and to estabfish a way of specifying the position, orientation, and size of the object at its final mapped form. The identification of the edges of a polyhedron is achieved by allocating an identity number to each edge, as exemplified in Figure 12.18d for the upper half of a cuboctahedron. Also, each end of an edge is
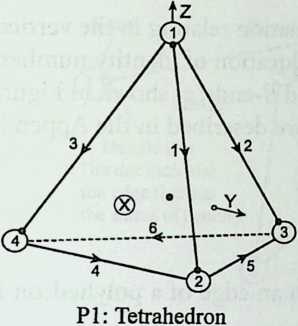
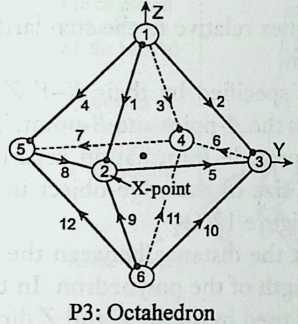
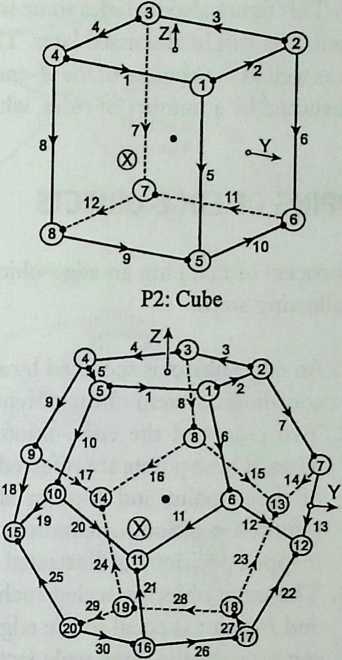
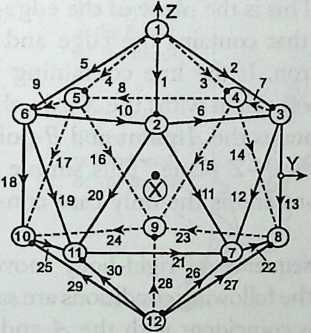
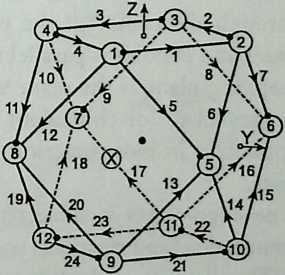
P4: Dodecahedron
P5:Icosahedron
Figure 12.19 Identity numbers, directions, and handles for edges and vertices of a selection of polyhedra.
P7: Cuboctahedron
associated with a letter. One end is associated with the letter A and is referred to as the /4-end and the other end is associated with the letter B and is referred to as the 5-end. The /Tends and 5-ends for two of the edges of a cuboctahedron are shown in Figure 12.18d. The convention is adopted that the positions of the /Tend and 5-end of an edge are indicated by placing an arrowhead on the edge pointing from the /Tend to the 2?-end, as shown in Figure 12.18*7. Thus the /Tend and 5-end effectively establish a “direction” for the edge.
The identity numbers of the edges together with the arrowheads indicating the /Tends and 5-ends for the Platonic polyhedra and a sample of an Archimedean polyhedron (namely, a cuboctahedron) are shown in Figure 12.19. This figure also includes some information relating to the vertices of the polyhedra, as will be discussed later. The allocation of identity numbers to the edges as well as the choices of the/(-ends and 5-ends, as shown in Figure 12.19, are governed by a number of rules, which are described in the Appendix.
MAPPING OF EDGE-OBJECTS
The process of mapping an edge-object on an edge of a polyhedron involves the following steps:
-
An edge-object is specified by a formex relative to the standard X-Y-Z coordinate system of the polyhedron.
-
Two points of the edge-object are specified by their X-Y-Z coordinates. These points are referred to as the A -point and 5-point. The role of the /(-point and 5-point is to provide information regarding the required position, orientation, and size of the edge-object in its final mapped position, as illustrated in Figure 12.18.
-
The edge-object is scaled such that the distance between the 24-point and 5-point is equal to the edge length of the polyhedron. In this scaling process, the same scale factor is used in the X, Y, and Z directions.
-
The mapping plane is determined. This is the plane of the edge-object that is to coincide with the plane that contains the edge and passes through the center of the polyhedron. If the fine containing the A- point and B-point is parallel to (or coincident with) the X axis, then the mapping plane is the plane that contains the /(-point and 5-point and is parallel to (or coincident with) the X-Z plane. This simple case is applicable in most practical situations and is the only case considered here.
-
The edge-object is subjected to a sequence of rigid-body movements (translations and rotations) such that the following conditions are satisfied:
-
The /(-point of the edge-object is coincident with the /(-end of the edge.
-
The 5-point of the edge-object is coincident with the 5-end of the edge.
-
The mapping plane is coincident with the plane that contains the edge and passes through the center of the polyhedron.
-
The direction that was initially the positive Z direction of the edgeobject is pointing to the outside of the polyhedron.
IDENTITY NUMBERS AND HANDLES FOR VERTICES
OF POLYHEDRA
Examples of mapping of objects on the vertices of polyhedra are shown in Figure 12.20. lb begin with, as for the faces and edges, it is necessary to allocate an identity number and a frame of reference to each vertex of a polyhedron.
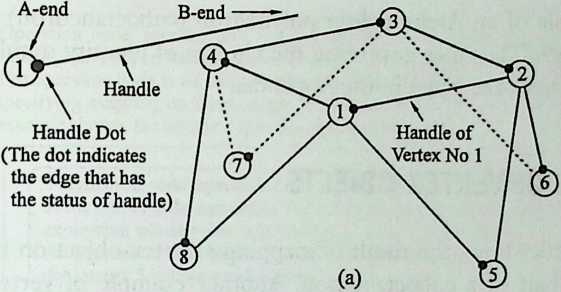
B-point -(To be placed at the B-end of the handle)
Vertex-object
A-point (To be placed at the A-end of the handle)
(b)
Vertex-object
(To be placed at the B-end of the handle)
A-point (To be placed at the A-end of the handle)
(c)
Figure 12.20 Examples of vertex mapping.
Identity numbers for vertices in the upper half of a cuboctahedron are shown in Figure 12.20a. The convention is adopted that a vertex identity number is shown in a circle placed at the vertex. The frame of reference for a vertex is provided by selecting one of its edges to become a base with respect to which vertex-objects may be mapped on the vertex. This edge is referred to as the handle of the vertex. Also, the vertex end of the handle is referred to as the A- end and the other end is referred to as the 5-end. The convention is adopted that the handle of a vertex is indicated by placing a dot (referred to as a handle dot) at its Af-end, as shown in Figure 12.20#.
The vertex identity numbers and handles for all the Platonic polyhedra and a sample of an Archimedean polyhedron (cuboctahedron) are shown in Figure 12.19. The rules governing the choices of identity numbers and handles for vertices are given in the Appendix.
MAPPING OF VERTEX-OBJECTS
Figure 12.20£ shows the result of mapping a vertex-object on the vertices of the upper half of a cuboctahedron. Another example of vertex mapping is shown in Figure 12.20c, where a vertex-object is mapped on the vertices of a dodecahedron.
With one important difference, which will be discussed below, the process of mapping a vertex-object is identical to the procedure for mapping an edgeobject. To elaborate, if a vertex-object is to be mapped on a vertex of a polyhedron, then the procedure followed will be as though the vertex-object is an edge-object that is to be mapped on the edge which is the handle of the vertex.
The important difference between vertex mapping as compared with edge mapping (and face mapping) is that, in some cases, a vertex-object is to be subjected to reflection in the mapping process. To elaborate, the mapping of a face-object or an edge-object is always carried out through a sequence of rigid-body movements (translations and rotations) and simple scaling. This fact remains true for a vertex-object in most cases. However, for two Archimedean polyhedra the process of mapping a vertex-object may require an additional operation of reflection. These two polyhedra are Pll (great rhombicuboctahedron) and P18 (great rhombicosidodecahedron) and the reason for the need for reflection in these cases is discussed in the Appendix.
POLYMATION FUNCTION
The processes involved in mapping objects on the faces, edges, and vertices of polyhedra are discussed in the previous sections. In Formian, these processes are carried out through the polymation function. For example, a Formian instruction that creates a formex representing the polyhedric configuration of Figure 12.20c may be written as
G = pol(3, 4, all], 1, [0,0; 1,01)1 E
where
-
E is a formex representing the vertex-object.
-
G is a formex representing the polyhedric configuration of Figure 12.20c.
-
pol is an abbreviation for the name of the function, that is, polymation.
-
The first item in parentheses is the operation code specifying the type of mapping to be performed, where the integer 3 indicates mapping on vertices.
-
The second item in parentheses is the polyhedron code specifying the
Operation code specifies the type of operation to be performed, namely, mapping on faces, mapping on edges or mapping on vertices. The operation code is an integer expression whose value is 1, 2 or 3 specifying mapping on faces, edges or vertices, respectively. In the example shown, the integer 2 specifies mapping on edges.
Polyhedron code specifies the type of polyhedron to be used as the basis for the operation. The polyhedron code is an integer expression whose value is in the range 1 to 20 specifying one of the Platonic or Archimedean polyhedra. In the example shown, the integer 7 indicates cuboctahedron.
Radius specifier1 determines the size of the polyhedron by specifying the radius of its circumsphere. The radius specifier is a numeric expression whose value is a nonzero positive number. In the example shown, the radius is given as 10. It is possible to specify different radii for different layers of the object to be used for mapping. In this case, the radii are specified in terms of a formex expression.
T
Entity list gives the list of face, edge or vertex numbers on which mapping is to be performed. The entity list is a string expression whose value is a list of items separated by commas. The items in the example shown are 1, 11 and 12, where 1 is equivalent to 1, 2, 3,4, 5, 6 and 7. It is possible to use all as an item implying all the faces, edges or vertices, as appropriate, listed in the ascending order. An item may also be a negative integer, like -8, or a negative parenthesised list, like -(6,12,9). A negative item has a cancelling effect
Locator1 is a formex expression whose value specifies the coordinates of the A-point and B-point of the object to be used for mapping. In the example shown, 0,0 and 1,0 are the coordinates of the A-point and B-point of the object respectively.
Figure 1221 Polymation function.
polyhedron to be used as the basis for mapping. The polyhedron code is the integer that follows the letter P in the P-name of a polyhedron. The integer 4 in the example implies a dodecahedron.
The third item in parentheses is the entity list specifying the vertices on which mapping is to be performed. The entity list as given in the example indicates all the vertices.
The fourth item in parentheses is the radius specifier, which determines the size of the polyhedron by specifying the radius of the circumsphere of the polyhedron.
The last item in parentheses is the locator specifying the yl-point and B- point of the vertex-object. In general, the /{-point and 5-point are to be specified by giving their X, Y, and Z coordinates. However, if the third coordinates are not given, then it will be assumed that the Z coordinates are equal to 0. In the example, the X and Y coordinates of the /4-point are given as 0,0 and those of the B-point are given as 1,0. The Z coordinates will then be assumed to be equal to 0.
The items within parentheses provide information about the manner in which the mapping is required to be carried out. Further details about these items are given in Figure 12.21. Information about the locations of all the faces, edges, and vertices of Platonic and Archimedean polyhedra, in terms of their identity numbers, is incorporated into Formian. This information is used by the polymation function for determining the locations of the faces, edges, or vertices specified by the entity list (third item in parentheses in Figure 12.21). Also, Formian incorporates complete information about the baselines of faces, directions of edges, and handles of vertices for the Platonic and Archimedean polyhedra. This information is used by the polymation function for the correct positioning of the objects to be mapped.
The argument of the polymation function in Figure 12.21 is represented by E and is separated from the function by the symbol I. Normally, this argument is a formex variable that represents the object to be used for mapping. Examples of formex formulations for the creation of formex variables representing the mapping objects are shown in Figure 12.22. Figure 12*.22a* shows a face-object together with its formex formulation, which is shown in a box. This formex formulation gives rise to a formex variable F that represents the face-object. The face-object has a pattern similar to the one used for the poly-
AvavA
AvavavA
AvavavavA
/avavaVaVavA
/AVaVaVaVaVaVA
AvaTaVaVaVaVavA
/AvavavavaVavavavaX ‘
/WAVaVVaVaVaVA
AvaVavaVaWaVaVaVavA
AvaVaVAVZVVaVaVaVaS’-
. AvaVaVaVaVALJaVaVaVavA .
. AvavaVav/-w/vyataW3
AvavavavaWaWaWaVaVaVavA I
AvaVavaVaVAavAWavayavavJMM
/A AVaVAVAVaVaVaVaVaVAVAVaVaVaVaVaVA
AvaVaVAVaVaVaVaVaVaVaVaVaVaVaVaVaVavA
F=bb(l,sqrt 13) lux(genid(4,M,2,2,-l) [15,5]) genid(21,21,2,1,1,-!)
(a)
E=pan(2,0) (rin(l,20,l) [0,0;l,0]#rin(l,10,2) lam(l,l) [0,0;l,-2]#rin(l,18,l) [l,-2;2z-2]#rin(l,19,l) [l,0;l,-2]) s /
(b)
a=-0.15; b=0.25; c=-a*tan asin (0.5/1.40125854) V=iosax(0,0,0:,0,a,12D) {[0,0,0;b,0,0],[0,0,0;c,0,a],[c,0,a;
Figure 12.22 Formex formulations for a face-object, an edge-object, and a vertex-object.
b,0,a/2],[c,0,a;b/2,0,0j,[b/2,0,0;b,0,a/2],[b,0,0;b,0,a/2])
(c)
hedric configuration of Figure 12.3zz. A truss-like edge-object together with its formex formulation is shown in Figure 12.22k Also, a vertex-object with its formex formulation is shown in Figure 12.22r. This is the vertex-object used for the polyhedric configuration of Figure 12.20c.
A reader who is familiar with the concepts of formex algebra will be able to follow the formex formulations of Figure 12.22. However, a reader who is unfamiliar with formex algebra should not worry about the details of the formulations at this point. In the present discussion the main aim is to describe the basics of the processes that are involved in the creation of polyhedric configurations. The formex formulations in this context may then be seen as “boxes of instructions” that imply the given configurations.
SHAPING AND COMPOSING POLYHEDRA
The polymation function may be employed to create a variety of different kinds of polyhedric configurations, some of which are outside the categories of configurations discussed so far. Two such classes of polyhedric configurations are discussed next.
The configurations shown in Figure 12.23 are obtained by cutting away
G=pex pol(l,l,all],l,[0A0;l,0,0]) rosad(l/2,sqrt 13/6,
3,120) {[0.4,0,0;0.6,0,0],[0.4,0,0;0.2,sqrt 13/5,0])
GoKl/faUJMJO.OAlAOJJIAOltfpol/ig-lMlO,)], l,[0,0,0;l,0,0D dil(3,05) tranix(05,0.5,0.5) poipA’, sqrt 13/2,[0,0,0;!,0,0]) [0,0,0;l,0,0]
G=pol(l,2,l],l,[0,0,0;2,0,0]) rosad(l,l) [0,l,0;l,0,0]#rosad(0,0)
pol(l,2,2],l,[0,0,0;2,0,0]) {[0,0,0;2,0,0],[2,0,0;1,2,0],[1,2,0;0,0,0]}
k. /
(b)
G=rosad(0,0) pex lam(3,0) pol(lAir/l,[0,0,0;4,0,0])
G=pol(25,aU],1/sqrt 12,[0,0,0;l,0,0]) [0,0,0;l,0,0]#pol(l ,3,,[1,7], 1/sqrt 12,[0,0,0;l,0,0]) ver(2,1,0,0) tranix(-cos 130/3,0.5, 1/sqrt 124) pol(2,l,l-3],sqrt 16/4,[0,0,0;l,0,0J) [0,0,0;l,0,0]
G=pex lam(3xos (2*asin (05/0.951056516)))
pol(25,l-10],l,[0,0,0;l,0,0]) [0,0,0;1,0,0]
(c)
(c)
Figure 12.23 Examples of polyhedron shaping.
Figure 12.24 Examples of polyhedral compositions.
parts of three polyhedra, where the original polyhedra are shown by thin lines and the resulting configurations are shown by thick lines. All three configurations are obtained using the polymation function and the formex formulation for each case is given enclosed in a box.
The configuration shown by thick lines in Figure 12.23# is similar to a P6 (truncated tetrahedron), but its proportions are different from those of a P6. The configuration shown by thick lines in Figure 12.23£ is a decahedron (a polyhedron with 10 faces), which is obtained by cutting away parts of a cube, and the configuration shown in Figure 12.23c is again a decahedron, which is obtained by cutting away the top and bottom corners of an octahedron.
Examples of another class of polyhedric configuration are shown in Figure 12.24. Here, the polymation function has been used to create polyhedric configurations involving a combination of polyhedra or their parts. The formex formulations for these configurations are shown enclosed in boxes.
Figure 12.24/z shows a configuration that is obtained by placing half-cubes on four faces of a cuboctahedron. Figure 12.24Z* shows a configuration that is obtained by placing two tetrahedra on two opposite faces of an octahedron. Figure 12.24c shows a configuration that is obtained by taking the top part of an icosahedron and combining it with its own reflection.
PROCESSING OF MULTILAYER POLYHEDRIC CONFIGURATIONS
An example of a double-layer polyhedric configuration is shown in Figure 12.25#. Here, a Vierendeel-girder-type edge-object is mapped on a number of edges of a dodecahedron and a formex formulation for the operation is shown enclosed in a box. The approach employed in handling the process is the same as that described for the example of Figure 12.18A
Figure 12.25b shows a different approach in dealing with the problem. Here, the mapping of both the top layer and bottom layer of the edge-object is controlled by the polymation function. Thus there are two /l-points and two B-points with additional fourth coordinates for layer identification. A formex formulation for the operation is shown in a box in Figure 12.25 b. Also, the setup of the polymation function for the problem is given in Figure 12.26. The procedure followed in this approach is more elaborate than that used in relation to Figure 12.25#. The main advantage in the second approach is that the problem of mitering is sorted out automatically.
The approach employed in creating the polyhedric configuration of Figure 12.25b may also be applied in cases when there are more than two layers and in cases involving multilayer face or vertex mapping.
It should be noted that the polyhedric configurations of Figures 12.25# and b are not completely identical. The difference is in the orientations of the web elements. To be specific, the web elements in Figure 12.25# remain perpendicular to the top and bottom chords, whereas the web elements in Figure 12.25b are along radial lines emanating from the center, as indicated by the dotted lines in the figure. However, this particular feature of the configuration of Figure 12.25b should not be considered as a necessary consequence of the second
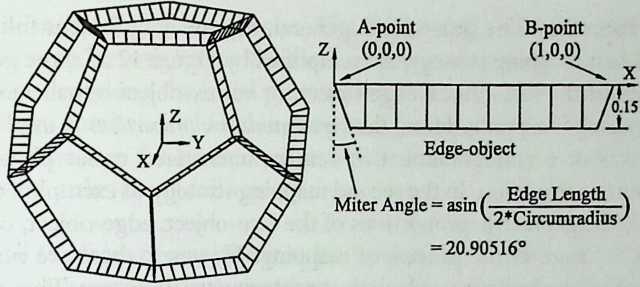
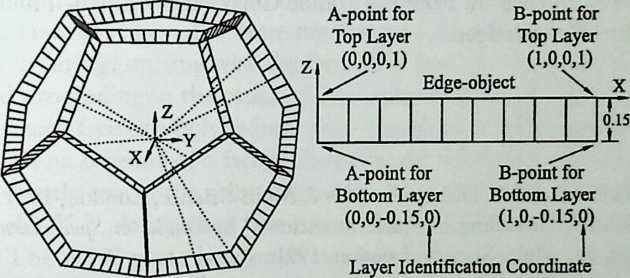
rc=1.40125854; a=-0.15; b=l/9; c=-a*tan asin (0.5/rc) E=lam(l,0.5) {[0z0z0;cz0za],[cz0za;bz0za]}#lux([lz0za]) rin(lz9zb) {[0z0z0;bz0z0]z[bz0z0;bz0za]z[bz0za;2*bz0za]}
G=poI(2z4zl-13z-8z18z-(23)z30]zrcz[0z0z0;lz0z0]) E
(a)
rc=l .40125854; a=-0.15; b=l/9; d=-a/cos asin (0.5/rc)
E=rin(l,9zb) [0z0z0zl;bz0z0zl]#rin(lz9zb) [0z0zaz0;bz0zaz0]#rin(lz10,b) [0z0z0zl;0z0,az0]
G=poI(2z4zl-13z-8z18z-(23)z30],z[2z4;lzrc;0zrc-d]z [0z0z0;lz0z0]z[0z0,a;lz0za]) E
(b)
Figure 12.25 Double-layer mapping.
Number of Layers Operation Code Entity List
Polyhedron Code
Position of Layer Identification Coordinate
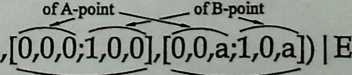G=pol(2,4,’[1,-8,18,-(23),30],
X-Y-Z Coordinates X-Y-Z Coordinates
Locator for
Locator for
Bottom Layer
Radius Specifier
[2,4;l,rc;0,rc-d]
Value of Layer Identification Coordinate and the
Corresponding Circumradius Top Layer
Figure 12.26 Polymation function for double-layer mapping. mapping approach. The situation, in general, may be described as follows.
In the first mapping strategy, as exemplified by Figure 12.25#, the geometric proportions of the face-object, edge-object, or vertex-object remain unchanged in the process of mapping. Here, the term geometric proportions is used to mean those aspects of a configuration that remain unchanged under photographic enlargement or reduction. In the second mapping strategy, as exemplified by Figure 12.2 Sb, the geometric proportions of the face-object, edge-object, or vertexobject may change in the process of mapping. However, there are no general rules regarding the manner in which the proportions may change. These changes are governed by the choices of the H-points and 5-points.
ACKNOWLEDGMENTS
The work presented in this chapter has been supported by NASA Grant NAGW-4132 and a grant from the Tomoe Corporation, Japan. Their support is gratefully acknowledged.
¶ NOTES
-
H. Nooshin and P. L. Disney, Permian 2, Multi-Science, London, 1997.
-
J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science, London, 1991.
-
J. F. Gabriel, “Space Frames: An Alternative to Architectural Cube,” International Journal of Space Structures (Special Issue on the Architecture of Space Frames), Vol. 6, No. 4, 1991.
-
H. Nooshin and D. Tzourmaldiotou, “An Approach for Generation of Geodesic Forms,” Proceedings of the Fourth International Conference on Space Structures, G. A. R. Parke and C. M. Howard, eds., Thomas Telford, London, 1993.
-
R. Motro, “Review of the Development of Geodesic Domes,” in Analysis, Design and Construction of Braced Domes, Z. S. Makowski, ed., Granada, London, 1984.
-
D. L. Richter, “Developments in Temcor Aluminium Domes,” in Analysis, Design and Construction of Braced Domes, V. S. Makowski, ed., Granada, London, 1984.
-
H. Nooshin, Formex Configuration Processing in Structural Engineering, Elsevier, London, 1984.
-
A. Pugh, Polyhedra: A Visual Approach, University of California Press, 1976.
-
H. M. Cundy and A. P. Rollett, Mathematical Models, 2nd ed., Oxford University Press, 1961.
-
A Gheorghiu and V Dragomir, Geometry of Structural Forms, Elsevier, London, 1978.
APPENDIX
Ordering Rules
This appendix contains a collection of rules for ordering the faces, edges, and vertices of a Platonic or Archimedean polyhedron, where the term ordering is
used to mean putting in a sequence. The sequencing would then allow identity numbers to be assigned to the faces, edges, and vertices of a polyhedron. This is done by taking the serial position number of an entity in the sequence as its identity number. Included in the appendix are also rules that govern the choices of baselines for faces, /4-ends and E-ends for edges, and handles for vertices. The rules are as follows:
- If all the faces of a polyhedron have the same number of sides, then the faces are ordered with respect to the ascending values of the angular spherical coordinates r and t of the centers of the faces, where the value of t is considered first and the value of s is considered only if the centers of the faces compared have the same value of t. The disposition of the r and t spherical coordinates together with the X-Y-Z global coordinate system in relation to a polyhedron (cuboctahedron) is shown in Figure Al2.1.
If the faces of a polyhedron have different numbers of sides, then all the faces that have the same number of sides are considered together for ordering, starting with the faces that have the least number of sides and proceeding in the order of increasing number of sides.
- For each face of a polyhedron, one of its sides is designated as the baseline. The baseline of a face is chosen in the following manner:
-
If only one of the sides of the face is parallel to the r=90° plane (i.e., the X-Y plane), then this side is chosen as the baseline of the face. The ?=90° plane is referred to as the equatorial plane or the E-plane (Figure A12.1).
-
If only two of the sides of the face are parallel to the E-plane, then, of these two sides, the one that is nearer to the E-plane is chosen as the baseline, and if the sides are equidistant from the E-plane, then the “southern” side is chosen as the baseline.
-
If the face is parallel to the E-plane and one of its sides intersects the r=0° semiplane, then this side is chosen as the baseline of the face. The r=0° semiplane is referred to as the Greenwich plane or the G-
Figure A12.1 Cartesian and spherical coordinate systems for a polyhedron.
plane. This is the part of the X-Z plane for which X > 0 (Figure A12.1).
-
If the face is parallel to the E-plane and the G-plane passes through a corner of the face, then, of the two sides that are connected to this comer, the one whose midpoint has the smaller r coordinate is chosen as the baseline of the face.
-
If the face does not have a side that is parallel to the E-plane, then the face is imagined to be subjected to a rotation in the “right-handed screw direction” and, as the angle of rotation increases, the first side that assumes a position satisfying either condition (a) or (b) is chosen as the baseline of the face. To describe the term right-handed screw direction, imagine a right-handed screw whose head is at the center of the polyhedron and is pointing toward the center of a face. The direction of rotation that causes the screw to move toward the face is referred to as the right-handed screw direction or the RS-direction.
-
Each end of the baseline of a face of a polyhedron has an associated letter. To elaborate, one end is associated with the letter A and is referred to as the /Tend and the other end is associated with the letter B and is referred to as the 5-end. The allocation of the letters A and B to the ends is made such that movement from A to B is in the .RS-direction.
-
The edges of a polyhedron are ordered with respect to the ascending values of the angular spherical coordinates r and t of their midpoints, where the value of t is considered first and the value of r is considered only if the midpoints of the edges compared have the same value of t.
-
Each end of an edge of a polyhedron has an associated letter. To elaborate, one end is associated with the letter A and is referred to as the A- end and the other end is associated with the letter B and is referred to as the 5-end. The allocation of the letters A and B to the ends is made in the following manner:
-
If the edge is parallel to the E-plane, then the /1-end and 5-end of the edge are chosen such that movement from A to B is in the positive r direction (Figure A12.1).
-
If the edge is not parallel to the E-plane, then the /1-end and 5-end of the edge are chosen such that
-
if the midpoint of the edge is in the E-plane or if its midpoint is in the northern hemisphere, then movement from A to B is southward and
-
if the midpoint of the edge is in the southern hemisphere, then movement from A to B is northward.
-
The vertices of a polyhedron are ordered with respect to the ascending values of their angular spherical coordinates r and t, where the value of t is considered first and the value of r is considered only if the vertices compared have the same value of t.
-
For each vertex one of the edges that is connected to it is designated as the handle. The handle of the first vertex of a polyhedron (i.e., vertex no. 1) is the edge that connects it to vertex no. 2. The handle of any other vertex is obtained by mapping the configuration of the first vertex onto the configuration of that vertex and selecting the edge that corresponds to the handle of the first vertex. The configuration of a vertex of a polyhedron can, in most cases, be mapped onto the configuration of any other vertex of the same polyhedron by simple rigid motion (by translation and rotation). However, in some cases, the mapping of the configuration of a vertex onto that of another vertex cannot be achieved unless an additional reflectional operation is performed. To elaborate, with two exceptions, for every Platonic or Archimedean polyhedron, all the vertices of the polyhedron are directly congruent. That is, the configuration of each vertex of the polyhedron may be mapped onto that of every other vertex of the polyhedron by simple rigid motion of the configuration. The exceptions are Pl 1 (great rhom-bicuboctahedron) and Pl8 (great rhombicosidodecahedron). For each of these two polyhedra, some vertices are directly congruent to the first vertex of the polyhedron and the other vertices are oppositely congruent to the first vertex. The term oppositely congruent is used to refer to two configurations that cannot be mapped onto one another without reflection (in addition to rigid motion). The need for reflection in vertex mapping for Pl 1 and Pl8 arises as a consequence of the shapes of their vertex figures, as shown in Table Al 2.1 (a vertex figure is a poly-
TABLE A12.1 Vertex Figures of Platonic and Archimedean Polyhedra
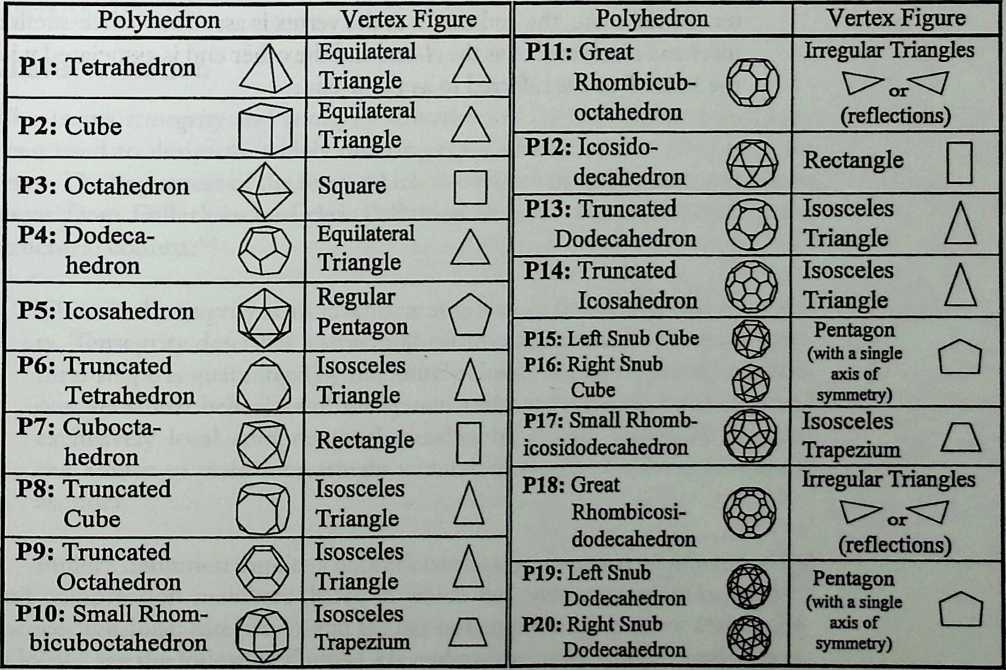
gon obtained by connecting the midpoints of the edges that meet at a vertex). From Table Al2.1 it may be seen that every Platonic or Archimedean polyhedron, other than Pl 1 and Pl8, has only one vertex figure. On the other hand, in the case of Pl 1 or Pl 8, there are two vertex figures that cannot be mapped onto one another without reflection.
The vertex-mapping procedure described above will allow the handles to be “uniquely” determined for all the vertices in all the cases except for P12 (icosidodecahedron), P7 (cuboctahedron), and the Platonic polyhedra. For each of these seven polyhedra, the mapping of the configuration of the first vertex onto that of another vertex can be done in more than one way. This is a consequence of the shapes of the vertex figures of these seven polyhedra. To elaborate, it may be seen from Table Al2.1 that the vertex figure of each of these polyhedra can map onto itself in more than one way. In the case of these polyhedra, the handles of vertices are chosen using the following rules:
-
For a “ring” of vertices, that is, for a circularly disposed set of vertices that lie in a plane parallel to the E-plane, the handles are chosen such that they constitute a cyclically symmetric configuration.
-
The disposition of the handles for a southern ring of vertices is obtained by “turning over” the corresponding northern ring (and rotating it, if necessary).
-
If there is a vertex whose handle is not uniquely determined by the above rules, then, among different possible handles, the one that has the smallest vertex number at the other end is chosen.
- Each end of the handle of a vertex of a polyhedron has an associated letter. To elaborate, the end that is at the vertex is associated with the letter A and is referred to as the/l-end and the other end is associated with the letter 5 and is referred to as the S-end.
13
□ 385
¶ Tensegrity: Theory and Application
Ariel Hanaor
¶ INTRODUCTION
Characterization
The terms tensegrity and tensegrity structures are not well defined, and have been used to designate widely differing types of structures in different contexts. The vagueness of the term, which was coined by R. Buckminster Fuller, stems from Fuller’s lack of clear definition in either the geometrical or the structural context:1
The word tensegrity is an invention: it is a contraction of tensional integrity. Tensegrity describes a structural-relationship principle in which structural shape is guaranteed by the finitely closed, comprehensively continuous, tensional behaviors of the system and not by the discontinuous and exclusively local compressional member behaviors. Tensegrity provides the ability to yield increasingly without ultimately breaking or coming asunder.4
Fuller’s definition implies a network consisting of tension members (cables) and compression members (bars), in which the cable network is continuous (hence “tensional integrity”), and the bar system presumably is not (“exclusively local,” see the following figures). He endows the concept with mystical qual-
Beyond the Cube: The Architecture of Space Frames and Polybedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
ities: “All structures, properly understood, from the solar system to the atom, are tensegrity structures. Universe is omnitensional integrity.” Such a sweeping generalization renders the definition useless. Fuller goes on to equate tensegrity and pneumatic structures (“Tensegrity structures are pure pneumatic structures…”), when, in fact, these are totally different structural systems. Following are some of the more precise definitions used in the literature.
The widest definition of tensegrity structures, from the geometric point of view, is sometimes used by mathematicians in the field of discrete geometry. They define tensegrity structure as a pin-jointed network consisting of any combination of bars, struts, and tendons. Bars are straight members of fixed length and can sustain either compression or tension. Struts are straight members with a lower bound on length. They cannot contract but they can extend indefinitely in a “telescoping” fashion and therefore cannot support tension. Tendons are straight “cables”members with an upper bound on length. They cannot extend but can contract freely and therefore cannot sustain compression.
This definition covers the whole range of pin-jointed structures, including trusses and cable networks. The narrowest definition of tensegrity structures, in the geometrical context, is: a network consisting of tendons and bars (or struts), such that any one bar is connected only to cables but to no other bar (except, perhaps, at the boundary). Thus the bar system, under this narrow definition, is completely disjointed. Such a system can be called “pure tensegrity.”
A more general definition, in the structural context, is: an internally prestressed cable network. The “tensile integrity” aspect is covered by the well-defined term cable network, whereas the presence of bars is implied by the term intent ally prestressed, which indicates that the network does not require an external anchoring system, like conventional cable networks, but is prestressed internally by means of compression members (bars), which form part of the network. Emmerich5 calls them “self-tensioned structures,” but because any prestressed structure is “self-tensioned,” this is not appropriate. The concept of internal prestress is the key concept in tensegrity, because it is precisely this feature that distinguishes this type of structure from conventional cable networks and from pneumatic structures. This definition is generally adopted in the present work, but most of the discussion is limited to the more restricted class of “pure” tensegrity networks, in which bars are not mutually in contact.
One type of structure encountered in the literature under the “tensegrity” caption is a certain class of dome (e.g., the Georgia Dome in Atlanta), consisting of cables prestressed against a disjointed system of bars, but requiring a compression ring in the perimeter. This type of dome is clearly excluded from the preceding definition of tensegrity networks, because it is externally prestressed, incorporating an external anchorage system (the compression ring). Cable dome would be a more appropriate term for this type of structure.
Background
Few, if any, engineered structures of substantial scale exist that can fit the preceding definition of tensegrity structures. The London Zoo aviary (Figure 13.1) contains elements of tensegrity in the form of disjointed tetrahedra used
Figure 13.1 The London Zoo aviary.
in prestressing the cable network, but it also involves external anchoring (to the ground). A number of tensegrity sculptures exist, most notably by the artist Kenneth Snelson (Figure 13.2). These are ornamental objects of quite striking appearance located in various public places, mostly in the United States (Figures 13.3 and 13.4). The simplest object that can be perceived as a tensegrity structure, under the definition in force, is the kite. It probably served as the inspiration and starting point for more complex objects such as Snelson’s “sculptures.”
The first to conceive of tensegrity as a building structure was probably Fuller, arguably as a result of his collaboration with Snelson. His first patent for “Tensile-Integrity Structures” was filed in 1959.6 It is a dome of spherical surface consisting of struts and tendons such that struts are connected only to tendons at their ends and at the midpoints (Figure 13.5a and £)• In the patent application Fuller claims that the invention “has special application to structures of vast proportions such as free-span domes capable of roofing a stadium or housing an entire village or city,.. .”7 This vastly exaggerated claim is based on the misconception that in very large domes the struts themselves can be constructed as tensegrity structures (Figure 13.5c), thus progressively reducing the relative length (or volume) of struts and generating an almost purely tensile structure, like a balloon. In the words of Fuller:
Every time we can see a separate strut and can devise means for making a tensegrity strut of that overall size, we can substitute it for a previously “solid” strut. By such a process of progressive substitutions in diminishing order of sizes, leading eventually via sub-sub-sub-miniaturizing tensegri-ties to …a minimum “solid state” strut diameter, which corresponds exactly with two diameters of the atoms of which it is constructed…. The atom is a tensegrity, and there are no “solids” left in the entire structural system…. ”8
Figure 13.2 Kenneth Snelson in his studio in lower Manhattan (1990).
Figure 13.3 Snelsons sculpture in front of the Maryland Science Museum, Baltimore.
Figure 13.4 Snelsons “Needle Tower” at the Hirshhorn Museum of Modern Art, Washington, DC: (a) general view, (b) view from below.
Since the miracle of a purely tensile, freestanding structure has been achieved (“no solids”), there is practically no limit to achievable spans. The basic theoretical principle involved in this reasoning is that of material dilution. This principle, which applies to all structures, involves increasing structural depth without adding material (and therefore weight) in order to achieve larger spans. In tensegrity structures, as in all structures, the application of the principle is limited by practical constraints. The concept of tensegrity in general, and Fuller’s version of it in particular, suffers from other drawbacks, which will be discussed later.
Nevertheless, the credit goes to Fuller for opening the field of tensegrity structures for research and invention. Several other patents have followed over the years, including Fuller’s,9 but these appear to have produced no actual structures. The sections that follow review some of the main research topics and results. The research falls into two general areas. Most of the work is concerned with geometric configuration. Some limited research has been carried out into the actual load response of this type of structure, but a lot more is needed. The last section is a critical evaluation of the concept and its prospects for implementation.
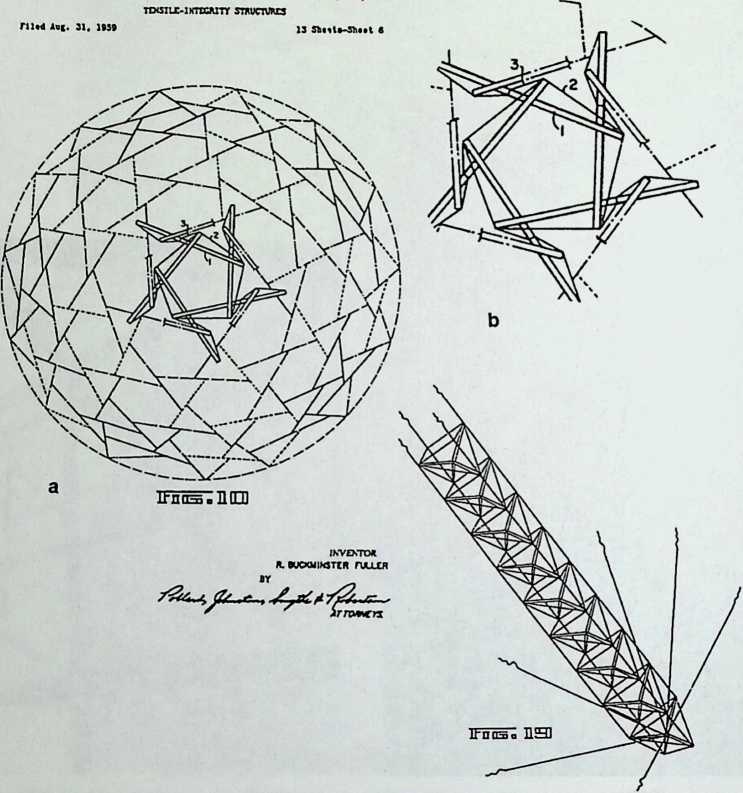
Figure 13.5 Fullers tensegrity dome of his 1962 patent (a) plan, (b) detail, fc) tensegrity strut (Source: R. B. Fuller, “Tensile-Integrity Structures,” U.S. Patent 3,053,521, Nov. 13, 1962.)
Not. 13, 1962 r. b. fuller 3,063,521
GEOMETRY
Polyhedra
The simplest three-dimensional tensegrity object is the tensegrtty prism (T prism), the simplest of which is the triangular prism, sometimes termed simplex. A tensegrity prism is a skew prism formed by cables along the edges of the prisms, with bars along the diagonals of the side faces in a consistent sense. Figure 13.6 shows a number of these prisms. The two bases of the prism are rotated relative to each other by an angle that is dictated by the requirement for stability of the shape.10 For regular prisms (i.e., having regular base polygons), this angle is half the base polygon angle (30° for a triangular prism, 45° for a square prism, etc.). Right-handed and left-handed configurations can be distinguished, in accordance with the sense of rotation of the two bases. It is possible to add cables along diagonals of skew prism faces the diagonals not occupied by barsto obtain a reinforced prism. Figure 13.6e shows a triangular rein-
Figure 13.6Tensegrity prisms: (a) triangular, 6Wsquare, (c) pentagonal, *(d)*hexagonal, (e) triangular, reinforced.
forced prism, which has the property of geometric rigidity (see the following discussion under Load Response). The relative base rotation of reinforced prisms is no longer predetermined but can be varied in a range between the simple prism value, as a lower bound, and double that value, as an upper bound (at the upper bound the bars intersect at the centroid of the prism).
Higher polyhedra can be constructed. Figure 13.7 shows some relatively simple polyhedra, but any polyhedron can be constructed as a tensegrity.11,12 Emmerich shows a systematic way of deriving tensegrities from a range of Platonic and Archimedean polyhedra.13 Some of these polyhedra are shown in Figure 13.8. Fuller’s dome (Figure 13.5) is, in effect, a high-order tensegrity polyhedron obtained by geodesic subdivision of the sphere. It can be termed a geodesic tensegrity dome and is closely related to Fuller’s geodesic dome. It is
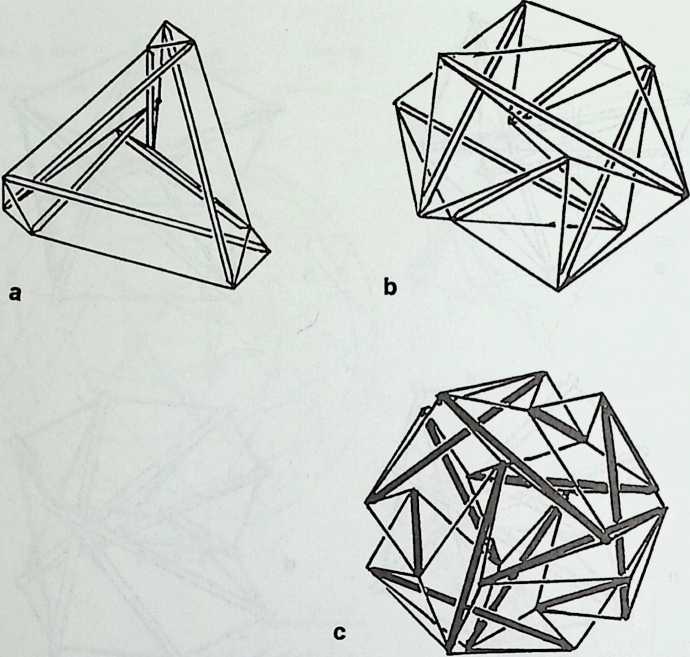
Figure 13.8 Some of Emmerichs Archimedean polyhedra: /a/truncated dodecahedron, /"truncated icosahedron, (c) great rhombicosidodeca-hedron, (d) small rhombi-cosidodecahedron. (Source: D. G. Emmerich, “Self-Tensioning Spherical Structures: Single and Double Layer Spheroids,” International Journal of Space Structures (Special Issue on Geodesic Forms), T. Tarnai, ed., Vol. 5, No. 3/4, 1990, pp. 353. Courtesy of Multi-Science Publishing.)
interesting to note that although the geodesic dome concept found widespread application, the tensegrity concept has so far found none.
Figure 13.7 Tensegrity polyhedra: (a) truncated tetrahedron, (b) octahedron, (c) cuboctahedron.
Networks
Whereas tensegrity polyhedra enclose a finite space, networks consist of repetitive patterns of bar-cable connections covering surfaces or filling space. Vilnay conceived single-layer infinite networks, a sample of which is shown in Figure 13.9.14 As a planar surface, these networks are not stable. They require curvature to produce shell-like surfaces. Double-layer networks can be produced by joining together tensegrity prisms. Some ways of joining such prisms to generate double-layer tensegrity grids (DLTGs) are shown in Figure 13.10.15 Figure 13.11 shows grids generated by these methods (only prism top and bottom bases are shown, for clarity). While the patterns are quite intricate, the lines joining the centroids of individual prisms form quite regular grids, termed the arch-grids. Figure 13.12 shows some simple models. A different way of joining T prisms to generate DLTGs is due to Motro and is shown in Figure 13.13.16 It differs from other networks in that it contains bar-bar connections at the joints, but it has certain advantages, such as continuity of cables and simplicity of geometry.
More complex network geometries can be generated by joining polyhedra of higher order. Emmerich produced some rather complex surface-covering and
Figure 13.9 Some of Vil-nays single-layer tensegrity networks.
Figure 13.10 Methods of forming double-layer tensegrity networks from tensegrity prisms. (Source: A. Hanaor, “Double Layer Tensegrity Grids,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, 1991.)
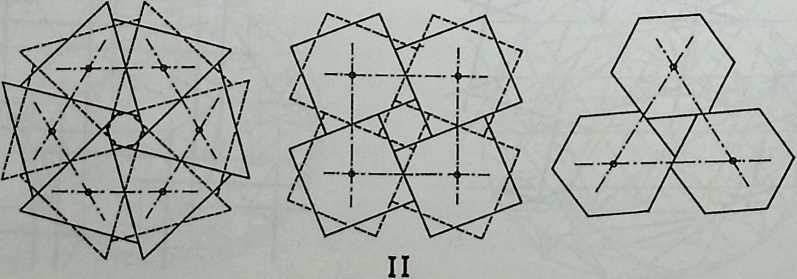
Figure 13.11 Double-layer tensegrity grids formed by the method of Figure 13.10. Top and bottom cable layers only are shown. Dash-dot line indicates arch-grid.
Figure 13.12 Models of double-layer tensegrity grids: (a) triangular type la, /d) square type II, (c) triangular type II.
space-filling configurations.17 Fuller and Grip developed a different type of space-filling network, a sample of which is shown in Figure 13.14.18,19
Structural Forms
Single-layer domes or domical surfaces can be formed on the basis of tensegrity polyhedra and geodesic spherical subdivision, such as Fuller’s dome (Figure 13.5). The use of polyhedra without face subdivision is limited to relatively small spans, as faces become impractically large with increasing spans. Single-
Figure 13.13 Metros double-layer tensegrity grid using square prisms or truncated pyramids connected at vertices. (Source: R. Motro, “Tensegrity Systems and Geodesic Domes,” International Journal of Space Structures (Special Issue on Geodesic Forms), T. Tarnai, ed.. Vol. 5, No. 3/4,1990, pp. 341. Courtesy of Multi-Science Publishing.)
Figure 13.14 Some of Grips multilayer and space-filling tensegrity grids. (Source: R. Grip, “The Correspondence Between Convex Polyhedra and Tensegrity Systems: A Classification System,” International Journal of Space Structures (Special Issue on Tensegrity Systems), R. Motro, ed., Vol. 7, No. 2,1992, pp. 3115. Courtesy of Multi-Science
Publishing.)
layer curved surfaces of any shape can be generated from single-layer networks. Figure 13.15 shows a dome based on Vilnay’s network.20 This dome differs significantly from Fuller’s dome. In Fuller’s dome, as spans increase and curvature decreases, bars quickly come into contact with one another if module size is to be kept to a reasonable value. This is avoided in Vilnay’s concept but at the cost of increased bar lengths.
Emmerich developed double-layer domes based on hyper-polyhedra, in which the polyhedron face is replaced with a tensegrity truncated pyramid (T pyramid).21 This is, in fact, a T prism with base polygons of similar geometry but different sizes. Figure 13.16 shows one such hyper-polyhedron. The comment on the span limitation of domes based on polyhedra also applies to this concept, but the concept can be extended to include geodesic subdivision and to avoid both bar contact and excessive bar lengths. Bars are laced between two parallel cable surfaces and these surfaces can be kept wide enough apart to prevent bar contact.
Figure 13.15 Vilnays tensegrity dome based on single-layer tensegrity grid. (Source: 0. Vil-nay, Cable Nets and Tensegric Shells, Analysis and Design Applications, Ellis Norwood, New York, 1990.)
Figure 13.16 Emmerichs double-layer hyper-polyhedron and its derivation (from truncated icosahedron). (Source: D. G. Emmerich, “Self-Tensioning Spherical Structures: Single and Double Layer Spheroids,” International Journal of Space Structures (Special Issue on Geodesic Forms), T. Tanai, ed., Vol. 5, No. 3/4,1990, pp. 353. Courtesy of Multi-Science Publishing.)
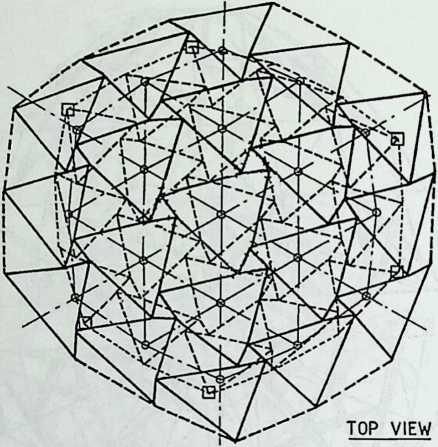
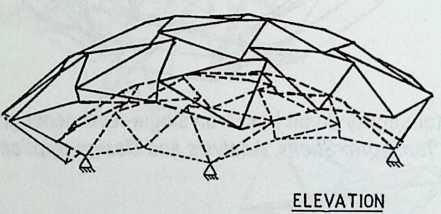
Figure 13.17 Double-layer tensegrity dome constructed using type la connection triangular truncated pyramids (only top and bottom cable layers shown). The dash-dot line represents the arch-grid, which is a geodesic subdivision of a hexagonal pyramid. (Source: A. Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids,” International Journal of Space Structures,\ lo\ 9, No. 4,1994, pp. 227.)
Double-layer surfaces of any shape, including flat surfaces, can be generated from double-layer networks based on T prisms or pyramids, as shown in Figures 13.10 to 13.13. Figure 13.17 shows a DLTG dome based on the triangular grid type la of Figure 13.11 (only top and bottom cable layers are shown).22 Although the pattern appears complex, the arch-grid forms a simple geodesic subdivision of a hexagonal pyramid. The arch-grid nodes indicate the locations of the centroids of the T pyramids constituting the dome. Figure 13.18 shows a model of part of a dome constructed on this basis.
Figure 13.18 Scale model of double-layer tensegrity dome segment using triangular truncated pyramids in type la connection.
LOAD RESPONSE
Geometric Rigidity
Referring back to the definition of tensegrity structures, tensegrity structures are prestressed cable networks, from the structural point of view. This implies that they are in most cases geometrically deformable. The terms geometric deformability and geometric rigidity require some explanation, as there is considerable confusion in terminology concerning this topic. The essence of the concepts is best explained by the simple prestressed cable structures shown in Figure 13.19. Figure 13.19/z shows a geometrically deformable prestressed cable. The deformability is expressed by the fact that the system cannot maintain equilibrium with the applied load in its original geometry. It must deform and change its shape in order to develop internal force components to balance the external load. The magnitude of the deformation depends primarily on the load and on the level of prestressthe tension force in the cable. It can be quite large, even for small load values. By comparison, the planar cable “network” of Figure 13.19£ (the cables are loaded in their plane) can maintain equilibrium in its original geometry, and its deformation is a result of elastic deformations (elongation and shortening) of the cables alone. These deformations are small in comparison to the geometric deformations of the cable of Figure 13.19a.
Some sources refer to geometrically deformable structures as “unstable,” but this is clearly a misnomer, because they are perfecdy capable of sustaining load, albeit at large deflections, compared with geometrically rigid structures such as trusses. Other sources refer to them as kinematically indeterminate, referring to the fact that the geometry changes depend on the load. A more rigorous discussion of this topic can be found in Pellegrino and Calladine.23
Most cable networks are geometrically deformable, including all tensegrity
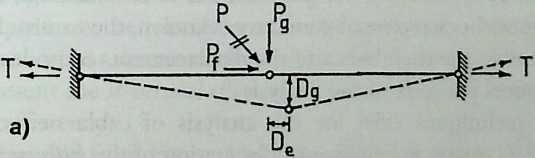
Figure 13.19 Illustration of geometric rigidity: (a) geometrically deformable prestressed cable, (b) geometrically rigid cable configuration.
configurations discussed up to this point, with the exception of the reinforced prism of Figure 13.6e. Geometrically rigid structures do not require prestress to maintain a reasonable stiffness. Some degree of prestress is nonetheless applied in cable networks, in order to ensure the tautness of cables. A geometrically rigid DLTG is described and discussed later (Figure 13.20#). Geometrically deformable networks are insensitive to inaccuracies in cable lengths. Tension in all cables is easy to maintain either by the shortening of a relatively small number of cables or by the elongation of bars. The inaccuracies in member lengths translate into deviations in the overall geometry. Geometrically rigid structures, on the other hand, are statically indeterminate. They can maintain equilibrium with the prestress force in the original geometry and do not adapt their geometry to compensate for changes in member lengths. Consequently, inaccuracy in bar or cable lengths may result in some slack cables. This tolerance sensitivity is a price that has to be paid for enhanced stiffness.
Features of Structural Analysis
A detailed discussion of structural analysis techniques for cable networks is beyond the scope of this chapter, but some general comments are warranted on the problems involved in analysis and design. Owing to the large deflections associated with geometrically deformable structures, nonlinear computational methods are needed, which are considerably more complex than the analysis of stiff, geometrically rigid structures such as trusses. Typically, the analysis of cable networks requires two phases. Phase I is a shape-finding procedure aimed at determining the equilibrium geometry of the network under prestress. Except in some special cases (such as tensegrity prisms and simple polyhedra), the initial geometry is not known, as it depends on the prestress. An initial geometry is assumed close to the desired final shape, prestress is then applied, and the new geometry is found in an iterative procedure. If this geometry is not satisfactory, the prestress has to be modified, and the process resumed. Once the prestressed geometry is known, the external load is applied and the forces in the members and the displacements of nodes are computed. This constitutes phase H of the analysis.
Several techniques exist for the analysis of cable networks. Levy and Spillers give a concise yet rigorous presentation of the stiffness method for geometrically nonlinear structures, including cable networks (computer programs implementing the algorithms are also presented).24 Barnes presents the principles of the dynamic relaxation method, developed specifically for tension structures (cable and membrane structures).25 This method is more powerful in dealing with highly nonlinear problems than the stiffness method, which may have convergence problems when the assumed initial geometry is greatly in error.
Characteristics of Load Response
As mentioned previously, very few studiesanalytical and experimental have been carried out on real-scale prototypes. Such studies are essential for the assessment of the concept of tensegrity structures and of the range of its feasible or practical applications. Two such studies are presented in the following sections, illustrating both the strengths and the weaknesses inherent in the concept of tensegrity.
Analytical Study
The study by Hanaor involves the full design, including nonlinear analysis (using the stiffness method), of several types of DLTGs of the triangular type la geometry (Figures 13.10 and 13.11).26 To facilitate the assessment of tensegrity structures in comparison with “conventional” space structures, a space truss of similar dimensions is also designed. The truss is a square-on-square offset double-layer grid (DLG). Figure 13.20/z shows the dimensions and layout of the DLTGs. Only the arch-grids are shown for clarity. Figure 13*.20b* depicts the layout of the DLG. Both types cover an area roughly circular in plan, with a diameter of approximately 27 m.
The four configurations of DLTGs included in the study are: planar (flat), geometrically deformable; planar, geometrically rigid; geometrically deformable dome; and geometrically rigid dome. It should be noted that in order to obtain a geometrically rigid DLTG, it is not sufficient to join together reinforced T prisms (Figure 13.6e); the units have to be laced together by the diagonal cables forming the prism side edges. A detail of the lacing is shown in Figure 13.20/z. Full details of the study are given in Hanaor.27
Results of the study are given in Figure 13.21 as normalized load (uniformly distributed) versus deflection of the central node. The abbreviations used in Figure 13.21 to denote the four DLTG configurations consist of two letters. The first letter denotes the geometry: Pplanar (flat); Ddome. The second letter denotes the geometric rigidity: Rrigid; Fdeformable (flexible). The curves represent the stiffness of the structure. The stiffness of deformable DLTGs depends on the level of prestress. The average level of prestress in bars was assumed as approximately half the capacity of the bar (initially assuming constant bar cross section).
Table 13.1 presents the relative unit weight (weight per unit surface area) of the structure, without the covering, with the DLG serving as control. This value may represent the structural efficiency of the system (the lower the value, the higher the efficiency).
It can be observed from Figure 13.21 and Table 13.1 that all DLTG configurations are considerably less stiff than the truss, and that all but the configuration marked with an asterisk have lower structural efficiency. The reason for the low structural efficiency is the length of the bars, as compared to the length of the bars in the truss (maximum forces are of the same order). The configuration marked with an asterisk relates to the rigid dome, with bars restrained against buckling at their midlength (e.g., by joining them together at this point). It can be seen that this has dramatic influence on structural efficiency.
Relatively long bars (compared with the length of cables) is a feature of all tensegrity structures encountered in the literaturerefer to all figures. Unless this problem is addressed, it appears that structural inefficiency’ is inherent in tensegrity structures, at least those with no bar-bar connections. It is not a trivial matter, for instance, to restrain midpoints of bars in the DR*
CROSS-SECTION OUTLINES DETAIL OF
RIGID CONNECTION
Figure 13.20 Grids for analysis/design study: (a) double-layer tensegrity grid configurations, (b) double-layer grid space truss.(Source: A. Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids,” International Journal of Space Structures, Vol. 9, No. 4, 1994, pp. 227.)
b
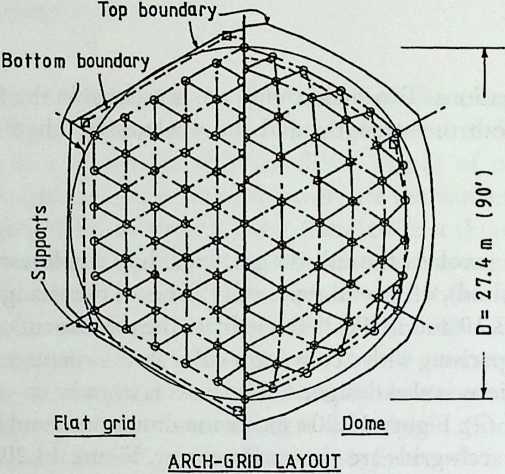
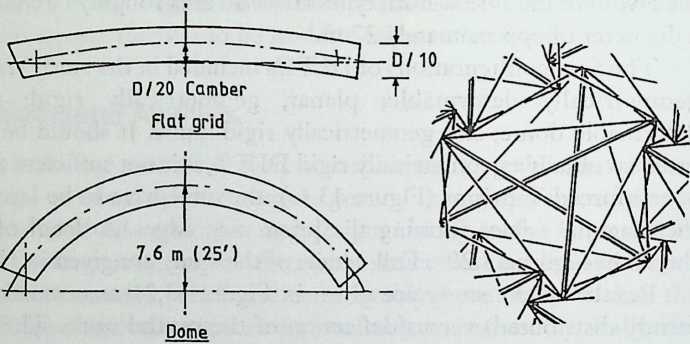
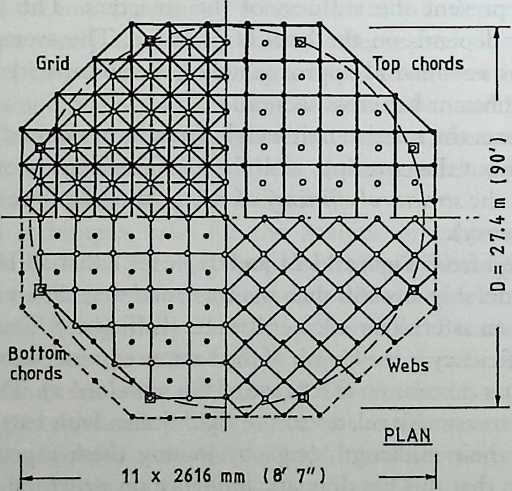
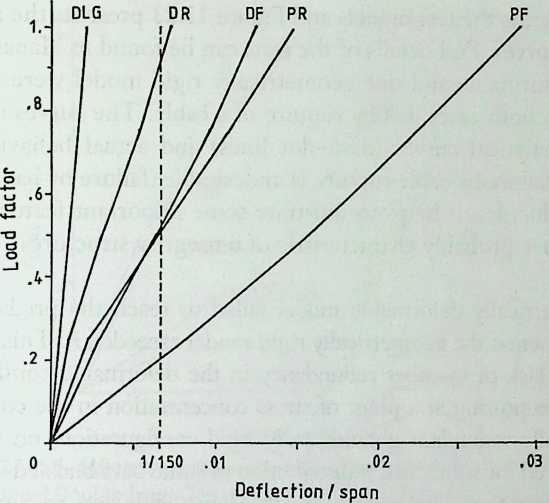
Figure 13.21 Normalized load-deflection curves of grids in design study. (Source: A. Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids,” International Journal of Space Structures, Vol. 9, No. 4,1994, pp. 227.)
configuration, without actually joining the bars. In all fairness it should be noted, however, that the comparison between space truss and tensegrity structures may be somewhat misleading. For a start, it does not include the roofing weight, which in tensegrity structures is expected to be a fight membrane, nor does it include the walls and other nonstructural elements absent in the dome configuration. In addition, the range of overlapping applications for the two types of structures (where a selection has to be made) is expected to be narrow. A more appropriate comparison might be with “conventional” cable and membrane structures, where the weight of anchoring systems has to be included. A discussion of the merits, limitations, and range of applications of tensegrity structures forms the substance of the last section.
Experimental Study
No load tests of large-scale tensegrity structures have been performed to date. Tests on some small-scale models are presented in Figures 13.22 and 13.23.28
TABLE 13.1 Relative Unit Weights of Grids
| Grid Type | Unit Weight (%) |
| Space truss (DLG) | |
| Flat deformable DLTG (PF) | |
| Flat rigid DLTG (PR) | |
| Deformable dome (DF) | |
| Rigid dome (DR) | |
| Rigid dome* (DR*) |
* Bars restrained at midlength.
Figure 13.22 presents the test models and Figure 13.23 presents the results as load-deflection curves. Full details of the tests can be found in Hanaor.29 One geometrically deformable and one geometrically rigid model were tested to failure. Failure in both cases was by rupture of a cable. The curves of Figure 13.23 present analytical curves (dash-dot lines) and actual behavior (solid lines). Although failure by cable rupture is undesirable (failure by bar buckling would be more ductile), it helps to illustrate some important features of the behavior, which are probably characteristic of tensegrity structures:
-
The geometrically deformable model failed to reach the predicted load capacity, whereas the geometrically rigid model exceeded it. This is probably due to lack of member redundancy in the deformable configuration, with cable rupturing at a point of stress concentration in the connection. The statically redundant geometrically rigid configuration, on the other hand, allowed for some load redistribution as some bars buckled elastically.
-
Both configurations, but particularly the deformable one, regained a substantial portion of their load-bearing capacity following cable rupture, even though this rupture amounted to the loss of a whole unit, representing one-seventh of the members in the structure. This feature is due to the way in which the structure is constructed of individual tensegrity units, with the rupture of one not affecting the integrity of others. In the geometrically rigid structure, this unit separation is somewhat compromised by the interlacing of units. This characteristic is an expression of
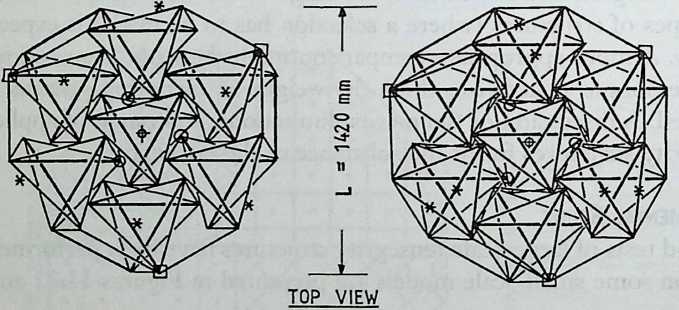
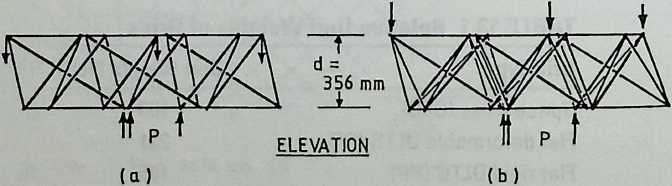
□ Support O Load point * Critical member
Figure 13.Z2 Double-layer tensegrity grids for load testing. (Source: A. Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids,” International Journal of Space Structures, Vol. 9, No. 4, 1994, pp. 227.)
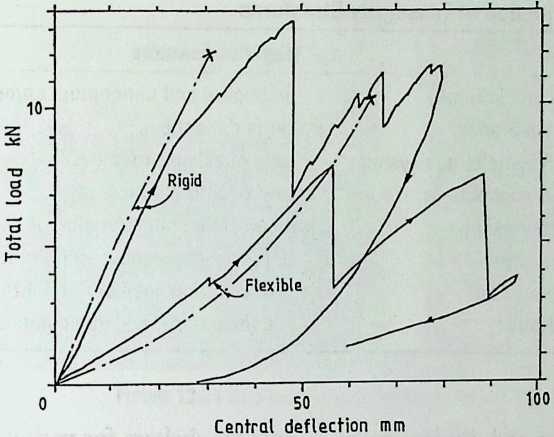
Figure 13.23 Load-deflection curves of tested tensegrity grids. (Source: A. Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids,” International Journal of Space Structures, Vol. 9, No. 4,1994, pp. 227.)
structural redundancy (as distinct from static redundancy or indeterminacy), which is a major factor in avoiding progressive collapse.
ASSESSMENT
Evaluation
Table 13.2 presents an evaluation of tensegrity structures, in terms of positive and negative features, based on current knowledge and understanding. There is no attempt at assigning weight or significance to these features. The negative features probably constitute a major factor in the nonimplementation of the concept to date, but psychological and other nontechnical factors probably play a role as well.
Applications
In view of their peculiar features, both positive and negative, it is not expected that tensegrity structures will find widespread application, replacing more familiar structural systems. Implementation of the concept is expected to be limited to applications of unusual or exotic nature. Following are some applications where it is thought that tensegrity structures could provide a viable and effective solution:
-
Large open spaces with light or translucent coverings, such as swimming pools, conservatories, covered “outdoor” cafes, and other public spaces.
-
Temporary, dismountable structures, such as exhibition halls, temporary storage facilities, and hangars.
-
Deployable (i.e., folding/unfolding) structures, such as mobile reusable
| Positive Features | Negative Features |
Geometric variety and intricacy Light, intriguing appearance Absence of massive anchorage systems Simple (bar-cable) connections High structural redundancy Low tolerance sensitivity (connections in tension) Convenient deployability |
Geometric and conceptual complexity Large deflections Long buckling-prone bars Low structural efficiency Incomplete understanding of behavior
|
exhibition and display spaces; temporary shelters for various functions (celebrations, festivals, etc.); shelters in inaccessible places; and deployable structures in space.
-
Additional, emergency support for air-supported structures to allow for unusual loading, such as asymmetrical snow loads, loss of pressure, and rupture.
-
Exotic architectural features where dramatic visual effects are sought.
Implementation
Two of the negative features of tensegrity structures mentioned in Table 13.2 are a lack of complete understanding and some unresolved questions. Some of these questions have to be resolved and practical solutions provided for implementation in actual, functional structures. Following are a few of the more immediate requirements that come to mind:
-
There has been very little work done on the roofing/surfacing material for the structures. It is recognized that in most cases the surfacing has to be fabric or other flexible material, yet most of the surfaces of structures proposed to date consist of planar facets. Such facets are unsuitable for fabric covering, which requires surfaces of negative Gaussian curvature (saddle shaped). How such surfaces are to be achieved is a question that requires thorough investigation and may fundamentally affect the geometric design of these structures.
-
The incorporation of surfacing material affects other topics such as loading and structural analysis. It also offers the challenge of trying to use the fabric in a system to stabilize bars against buckling. Bar buckling is another major problem requiring a solution that will not detract from any of the concept’s main assets, such as its eerie “floating bars” appearance.
-
Deployability is another topic that has received little attention. It may yet prove to be one of the main, if not the principal, assets of the concept, yet very little thorough research has been done into its theory and technology. Figure 13.24 presents a small deployable model.30 The
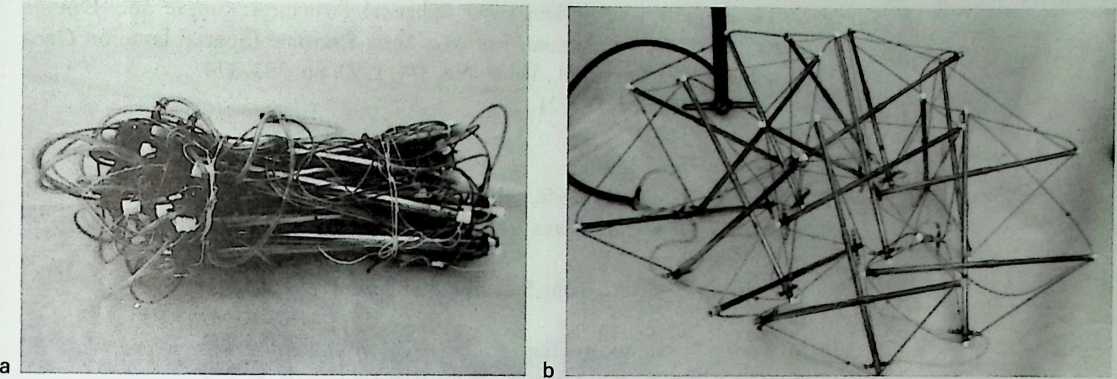
Figure 13.24 Deployable tensegrity dome model: (ajfolded, *(b)*deployed.
model was constructed under primitive conditions, yet it proved to be quite efficient. It consists of telescoping bars with O-ring seals. When bars are contracted, all cables are slack and the structure collapses into a bundle (Figure 13.24/?). Deployment is by means of air pressure (supplied by a bicycle pump in this case) applied into the bars’ outer tubes by means of thin flexible tubes laced between them. Deployment was quite smooth with the flexible bars easily compensating for any inaccuracies in construction.
• Although such simple models demonstrate the inherent deployability of the concept, there are many technical problems to be overcome. The effect of scale is of critical importance in mechanical devices in general. A major advantage of the present device is that it is self-adjusting and free of the problem of accumulating “free-play,” which plagues bar-folding structures. Nevertheless, means of adjusting the final geometry and providing adequate prestress are needed. The possibility of cable entanglement and its prevention also needs investigation. Another scale problem is the effect of cable stiffness and joint dimensions. Incorporation of roof covering adds another level of complexity to the deployment problem.
With these and other questions in mind, it can be said that the concept is long overdue for its first full-scale implementation in a highly visible prestigious architectural project.
¶ NOTES
-
R. B. Fuller, Synergetics, Explorations in the Geometry of Thinking, Macmillan, New York, 1975.
-
R. B. Fuller, “Tensile-Integrity Structures,” U.S. Patent 3,053,521, Nov. 13,1962.
-
R. B. Fuller, “Non-Symmetrical Tension-Integrity Structures,” U.S. Patent 3,866,366, Feb. 18, 1975.
-
Fuller, Synergetics, p. 372.
-
D. G. Emmerich, “Self-Tensioning Spherical Structures: Single and Double Layer Spheroids,” International Journal of Space Structures (Special Issue on Geodesic Forms), T. Tamai, ed., Vol. 5, No. 3/4, 1990, pp. 353.
-
Fuller, U.S. Patent 3,053,521.
-
Ibid.
-
Fuller, Synergetics, p. 408.
-
Fuller, U.S. Patent 3,866,366.
-
H. Kenner, Geodesic Math and How to Use It, University of California Press, 1976.
-
Fuller, Synergetics.
-
Emmerich, “Self-Tensioning Spherical Styructures.”
-
Ibid.
-
O. Vilnay, “Determinate Tensegric Shells,” Architectural Science Revue, Vol. 22, No. 2, June 1979, pp. 39.
-
A. Hanaor, “Double Layer Tensegrity Grids,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science, Brentwood, 1991.
-
R. Motro, “Tensegrity Systems and Geodesic Domes,” International Journal of Space Structures (Special Issue on Geodesic Forms), T. Tamai, ed., Vol. 5, No. 3/4, 1990, pp. 341.
-
D. G. Emmerich, “Absolute Minimal Self-Tensioning Configurations,” Space Structures 4, G. A. R. Parke and C. M. Howard, eds., Proceedings of the Fourth International Conference on Space Structures, University of Surrey, England, Thomas Telford, London, 1993, pp. 998.
-
Fuller, Synergetics.
-
R. Grip, “The Correspondence Between Convex Polyhedra and Tensegrity Systems: A Classification System,” International Journal of Space Structures (Special Issue on Tensegrity Systems), R. Motro, ed., Vol. 7, No. 2, 1992, pp. 3115.
-
O. Vilnay, Cable Nets and Tensegric Shells, Analysis and Design Applications, Ellis Horwood, New York, 1990.
-
Emmerich, “Self-Tensioning Spherical Structures.”
-
A. Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids,” International Journal of Space Structures, Vol. 9, No. 4, 1994, pp. 227.
-
S. Pellegrino and C. R. Calladine, “Matrix Analysis of Statically and Kinematically Indeterminate Frameworks,” International Journal of Solids and Structures, Vol.
22, 1986, pp. 409.
-
R. Levy and W. R. Spillers, Analysis of Geometrically Nonlinear Structures, Chapman and Hall, New York, 1995.
-
M. R. Barnes, “Forms and Stress Engineering of Tension Structures,” Structural Engineering Review (Special Issue on Tension Structures), M. R. Barnes and B. H. V Topping, eds., Vol.6, No.3/4, 1994, pp. 175.
-
Hanaor, “Geometrically Rigid Double-Layer Tensegrity Grids.”
-
Ibid.
-
Ibid.
-
Ibid.
-
A. Hanaor, “Double-Layer Tensegrity Grids as Deployable Structures,” International Journal of Space Structures (Special Issue on Deployable Space Structures), S. Pellegrino, ed., Vol. 8, No. 1/2, 1993, pp. 135.
¶ Visual Morphology of Space Labyrinths: A Source for Architecture and Design
Haresh Lalvani
¶ INTRODUCTION
The spatial and visual appeal of morphological images is inescapable for architects, designers, and engineers willing to explore new geometries and structures for architectural space making and the fundamental order of space underlying structures across the disciplines. Such an order imposes itself upon every architect who experiments with geometry as a device for shaping and structuring space, and upon every engineer who searches for a morphologic basis of improved structural performance. Basic morphological principles are embodied at varying levels of complexity in architecture and in the design process itself. The knowledge of such principles is essential for architects willing to “create” lasting works that integrate the art with the science of architecture.
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
□ 409
This pictorial essay is put together to show a small fragment of the vast design resources offered by the study of morphology and design science. The examples shown here demonstrate the limitless scope of this new design field, which is in need of a comprehensive visual encyclopedia of morphology. An atlas of form and structure, noticeably absent in the field of architecture and design, can serve as a standard reference for architects, artists, designers, engineers, scientists, and mathematicians. Morphology provides the underpinnings of a taxonomy for such an atlas. Our work in the development of a unified morphological system of space structures provides a candidate model for such a taxonomy.
In this chapter we illustrate excerpts from our morphological system by focusing on an interesting class of structures called space labyrinths, based on the author’s ongoing research on these particular structures.
SPACE LABYRINTHS
Reminiscent of the Cretan legend where the labyrinth designed by Daedalus was a single “sequential” linear space, the space labyrinths described here are “distributed” spaces in three or more dimensions. These labyrinths are spatial structures composed of a continuous surface (called a manifold) that divides space into two parts, one on the “inside” and the other on the “outside.” Seen as surfaces, these configurations are not unlike the commonly used boxshaped rooms in architecture or the familiar donut shape, with the essential difference that these space labyrinths are surfaces that are “open” and can be extended finitely as well as infinitely, whereas the box is a finite “closed” region of space. Three such structures were known to mathematicians in 193 71 and the concept was extended independently by Burt et al.,2 Pearce,3 and Schoen,4 and additional examples were developed by Lalvani.5 This catalog shows some of these and several interesting cases from new classes of labyrinths already mentioned in the author’s previous works. These include nonperiodic space labyrinths,6 -dimensional space labyrinths termed hyperlabyrinths) •” and hyperbolic labyrinths.9
Space labyrinths are inherently interesting for architecture because of their continuously winding three-dimensional space. The first example of a built space labyrinth with curved surfaces is provided by Pearce’s structure for the Brooklyn Children’s Museum. Burt has suggested novel applications for very large span building structures.10 Our new periodic, nonperiodic, and higher-dimensional labyrinths provide alternative geometries for such large structural spans. In aquatic environments, the “outside” space of the labyrinth can accommodate the water displaced by the “inside” space, thereby providing a natural marriage of geometry with Archimedes’ buoyancy principle. Transformational labyrinths provide candidates for deployable and adaptable architecture, which changes its size and shape with changing needs.
The study of space labyrinths is an active area in the sciences, especially in certain classes of biological structures, and it also provides new directions in crystallography. In macroscopic biological structures, the trabeculae of bones are among the common examples of irregular curved-faced labyrinths. The use of labyrinths at a micro level in nature is found in the structure of zeolites, which act as molecular sieves. Such sieves are filters that remove or trap undesirable substances. Recent applications to car filters, and spin-off applications to surfaces and “openings” of smart buildings that “breathe” or otherwise maintain homeostasis through a labyrinth membrane, are promising applications of micro space labyrinths to architecture.
SYSTEMATIC METAMORPHOLOGY
We have adopted Anne Tyng’s term metamorphology to define our approach to the systematic morphological classification and generation of form. We use the concept of higher-dimensional (72-dimensional) periodic tables, or hypertables. Our method permits an exhaustive classification, indexing, generation, as well as transformation, of a wide variety of space structures.11 Here, we show the use of this technique for the generation of labyrinths, both known and new. The chapter is, in most part, restricted to labyrinths that have a single type of vertex only. All vertices of such structures are identical, with each vertex having the same number of polygons and edges meeting at it in the same sequence. This restriction offers a convenient starting point for exploring the fundamental order of space and is, in addition, significant for modular building systems where identical components translate into economy in construction. For the purposes of illustration, we show structures composed of plane regular polygons, but the method extends to all of its topologic variants: curved-space labyrinths composed of curved polygons, nonperiodic labyrinths, labyrinths projected from higher dimensions, and labyrinths in non-Euclidean space. Some examples of these different types of labyrinths, most of them new, are shown toward the end of the chapter.
Regular Structures
The concept of hypertables is briefly recapitulated from our previous work and is followed by its application to space labyrinths. For 72-dimensional regular structures, characterized by the Schlafli symbol \p,q,r,s,… ,u,v,ru)}, the hypertable is a hypercubic lattice of dimension 72-I, where each distinct regular structure occupies a different vertex of this lattice; for details, see Lalvam.12 In this space the structures are indexed by corresponding higher-dimensional Cartesian coordinates (p,q,r,s,…;u,v,u)). Three-dimensional structures {p,q}, comprising polyhedra, plane and hyperbolic tessellations, and characterized by/2-sided polygonal faces, q of which meet at every vertex, are indexed (p,q) and are arranged in a two-dimensional lattice with the integer p varying along one axis and the integer q along the other. Four-dimensional structures [p,q,r}, comprising four-dimensional polytopes, which are composed of cells {p,q} and vertex figures {q,r}, are indexed (p,q,r) and are arranged in a three-
{3,3,5} 600-cell |
{4,3,5} | {5,3,5} |
{3,3,4} 16-cell |
{4,3,4}*
|
{5,3,4} |
| {3,3,3} | {4,3,3} | {5,3,3} |
| -cell | -cell | -cell |
Figure 14.1 A portion of a three-dimensional lattice of four-dimensional polytopes designated by the Schlafli symbol {p, q, /}.
dimensional cubic lattice defined by the integer variables p, q, and r. And so on for higher-dimensional structures.
Figure 14.1 shows a portion of a square lattice extracted from the three-dimensional cubic lattice of polytopes. This figure includes nine four-dimensional polytopes, which are indicated by their Schlafli symbol. Of these nine, five are finite structures in Euclidean space and include the simplex {3,3,3} (or 5-cell), the four-dimensional cube {4,3,3} (or 8-cell) and its dual {3,3,4} (or 16-cell), and the 120-cell {5,3,3} and its dual {3,3,5} (or 600-cell). The structure {4,3,4} is the simple cubic lattice, a degenerate four-dimensional structure, and the remaining three are structures in hyperbolic space. The computer-animated film Not Knot by Charles Gunn and Delle Maxwell and based on William Thurston’s work,13 shows the transformation of the structures in the last column on the right. Clearly, our hypertable system provides a basis for a multitude of such intertransformations between these and other structures within the hypertable.
Semiregular Structures
Semiregular structures, composed of more than one type of regular polygon meeting identically at each vertex of the structure, can be mapped in an extended hypertable. Each vertex of the hypertable of regular structures splits into n additional directions to accommodate 2” semi-regular structures; for details, see Lalvani.12 The extended hypertable is composed of regular and semi-regular structures and provides a starting point for generating space labyrinths. The structures in this space are indexed in binary combinations of 0’s and l’s or 0’s and X’s, where X is any integer for the number of stages (frames in an animation) in the transformation process between labyrinths. The index gives the location of each structure within the hypercubic lattice.
Figure 14.2 shows the tetrahedral fundamental region PQRO of a fourdimensional polytope {p,q,r}. It is composed of six edges, which join the centers of a cell, a face, an edge, and a vertex to each other. The fines radiating from the cell center 0, the “radial” edges, are coded in three primary colors,
Figure 14.2 The tetrahedral fundamental region of a fourdimensional polytope in six edge colors orthree pairs of complementary colors.
Figure 14.3 Six planes meeting at one vertex within the fundamental region; each plane is perpendicular to one of the six edges of Figure 14.2 and colored correspondingly.
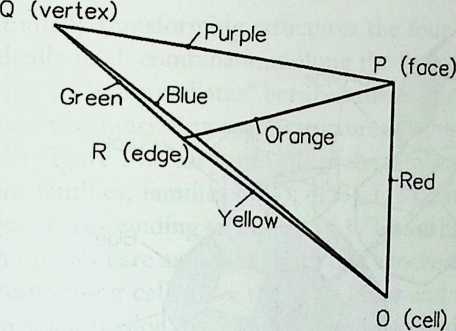
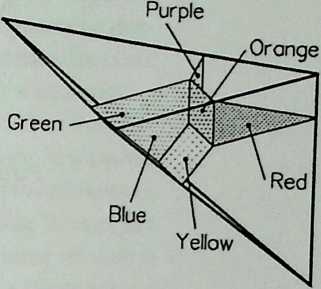
and the “circumferential” edges are coded in three secondary colors with the complementary colors coding the opposite edges.
Figure 14.3 shows portions of six dual planes (faces) meeting at a vertex within the fundamental region. The faces are defined by four different edges, each perpendicular to the face of the fundamental region. Each face plane is perpendicular to one of the six axes and colored accordingly; that is, a red plane is perpendicular to the red axis, and so on. Alternatively, a pair of complementary colors could be used to illustrate the line-plane duality. The six planes define the faces of a semi-regular polytope 1111 composed of four different cells. This is one of a family of 16 four-dimensional polytopes obtained by different combinations of the four different edges, with each edge corresponding to a different dimension of the hypertable. Within the fundamental region of each structure, the vertex occupies a distinct position different from the others. In fact, only 16 distinct positions are possible and hence 16 structures. Details of this organization have been described elsewhere for one family of structures corresponding to the simple cubic lattice {4,3,4} and referred to as family (43 4).7 The left-handed and right-handed “snub” structures require the introduction of two additional dimensions to the hypertable, one for left-handedness and the other for right-handedness.
The six planes defining the structure corresponding to Figure 14.3, and belonging to the cubic family (434), are shown in Figure 14.4. Its associated
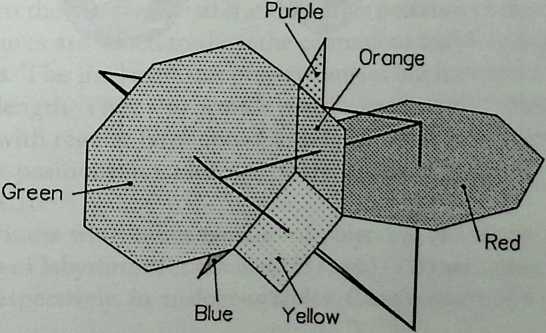
Figure 14.4 Six planes at a vertex located within the fundamental region of the simple cubic lattice {4,3, 4}, a degenerate fourdimensional polytope. The structure obtained this way is indexed 1111.
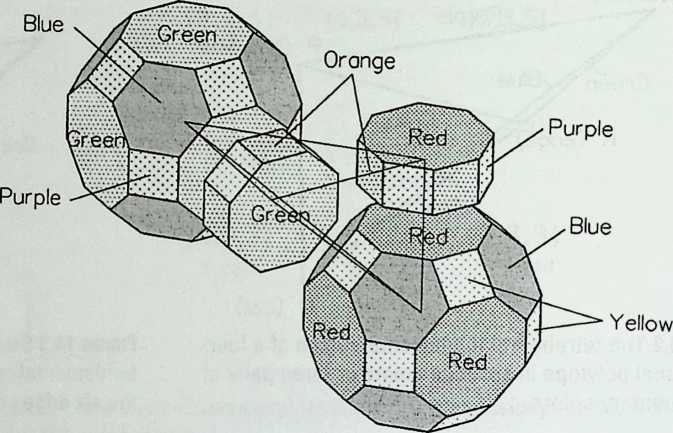
Figure 14.5 Four cells corresponding to the six planes of Figure 14.4, shown here in an exploded view.
four cells are shown in an exploded view in Figure 14.5. The entire set of regular and semi-regular structures of this family comprises a total of 16 structures and is illustrated in Color Art 6 in a four-dimensional hypertable; only four cells associated with a fundamental region are shown in an exploded view. This fundamental region, when repeated by symmetry operations, generates the complete structure which, in the example shown, is space filling. A portion of this space filling for each of the 16 structures is shown in Color Art 7. In
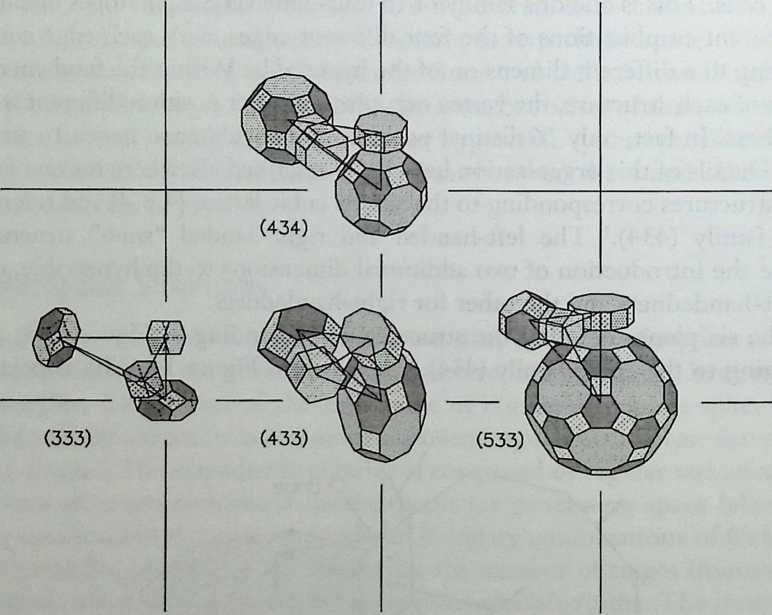
q=3
Figure 14.6 Structures 1111 of four families of polytopes corresponding to Figure 14.1 and arranged in a corresponding three-dimensional lattice; only a two-dimensional portion of this lattice is shown.
continually transforming structures the four edges “implode” and “explode” gradually in all combinations along the four directions of the hypertable generating all “intermediates” between these 16 structures. The intermediates are themselves interesting space structures as shown later with a few examples.
In Figure 14.6 the four cells of the semi-regular polytopes 1111 of four different families, families (333), (433), (533), and (434), are shown in a square lattice corresponding to Figure 14.1. The cells are shown in exploded views in each case and are analogous with one another. The corresponding faces of the corresponding cells have the same color and in each case the same six colors are needed. Color Art 7 and Figure 14.6 combined are part of a larger sevendimensional table that maps all the regular and semi-regular four-dimensional structures in one space.
LABYRINTH GENERATION
Families of space labyrinths, which divide space into two parts, can be derived from the families of regular and semi-regular structures by removing all faces in complementary colors. In fact, the removal of complementary colors is a convenient selection because any single color, or any combination of colors, could be removed to provide space structures composed of cells with different types of openings. This aspect of systematic face removal by color was addressed by Lalvani.11 Clearly, labyrinths, where only two complementary-colored faces are removed, are special cases in such an extended family of space structures produced from each source family.
Cells of one family of labyrinths belonging to the cubic family (434) are shown in Color Art 8 in an exploded view. Here, red and green faces are removed from the cells of structures in Color Art 6. Several “degenerate” labyrinths, composed of isolated closed cells, are produced in the process. Of the 16 structures generated this way, 9 are “legitimate” labyrinths having a continuous interior space. The cells of these are shown in Figure 14.7 in a portion of the hypertable. The same nine structures are shown as cubic portions of a space-filling array in Color Art 9; in this illustration the continuous surfaces of the labyrinths can be better appreciated.
One of the four two-dimensional tables, each defined by a different face of the hypertable and embedded in Color Art 9, is shown in Color Art 10. In addition to the structures lying at the vertex positions of the table, intermediate structures are added to show the continuous transformations between the labyrinths. The intermediates preserve angles but have more than one different edge length. They also provide visually and spatially interesting variants of the ones with regular faces only. Close-up views of three labyrinths located at the vertex positions in Color Art 10 are shown in exploded views in Figures 14.8 to 14.10.
Labyrinths from other families of polytopes can be derived in a similar way. Cells of labyrinths for families (433) and (533) are shown in Color Art 11 and 13, respectively, in analogous tables. Continuous transformations within
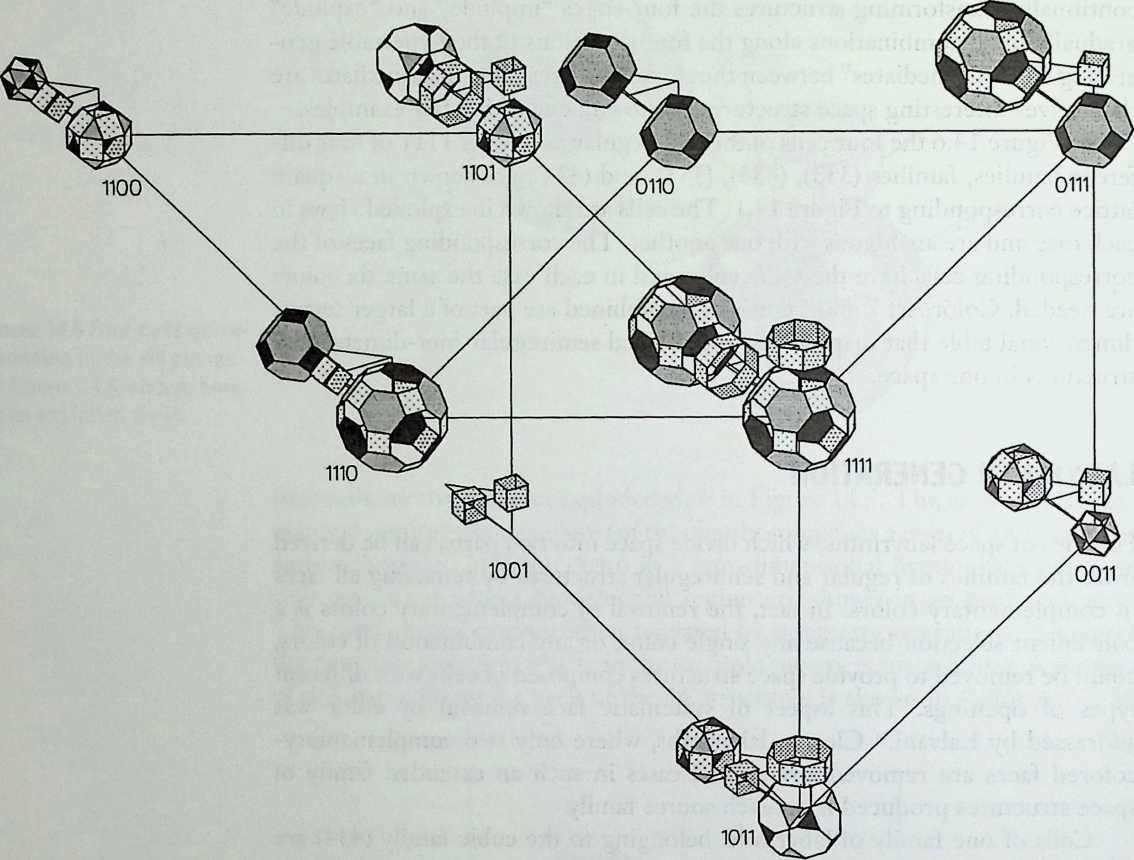
Figure 14.7 Basic cells of labyrinths of family (434) in exploded view.
each table are suggested by the structures shown in Color Art 12 and 14. Compared with the cubic family (434), these labyrinths are more legitimate four-dimensional labyrinths and can be built in three-dimensional space as “projections.” The cells, as well as the labyrinths composed of these cells, are completely analogous to one another between all the families. These structures are part of a larger table of labyrinths obtained by interconnecting the families. The complete larger table includes all four-dimensional labyrinths, finite as well as infinite, and Euclidean as well as hyperbolic, -dimensional labyrinths (w>4) are similarly included in a larger, more inclusive hypertable.
Additional labyrinths for each family are obtained by removing the remaining pairs of complementary-colored faces, namely, blue and orange and yellow and violet. The legitimate labyrinths in these cases are much fewer. Cells of such labyrinths having blue and orange faces removed are shown in Figure 14.11 in a portion of an extended table for four families (333), (433), (533), and (434). In Figure 14.12, cells of labyrinths having yellow and violet faces removed from the structures 1111 of the same families are shown; compare this illustration with Figure 14.6.
Figure 14.8 A detailed view of the labyrinth 1111 in an exploded view (compare with Color Art 9).
Figure 14.10 A detailed view of the labyrinth 1101 in an exploded view (compare with Color Art 9).
Figure 14.9 A detailed view of the labyrinth 1011 in an exploded view (compare with Color Art 9).
Figure 14.11 Cells of labyrinths of families (333), (433), (533), and (434) having blue and orange faces removed.
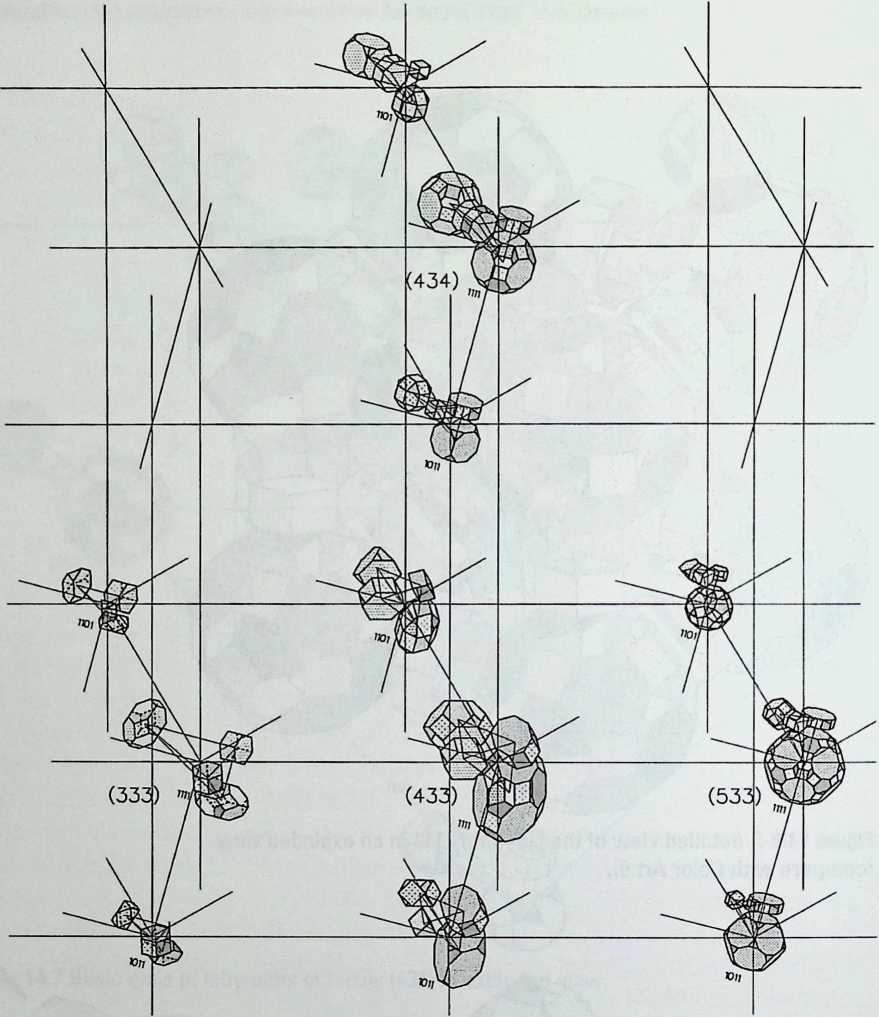
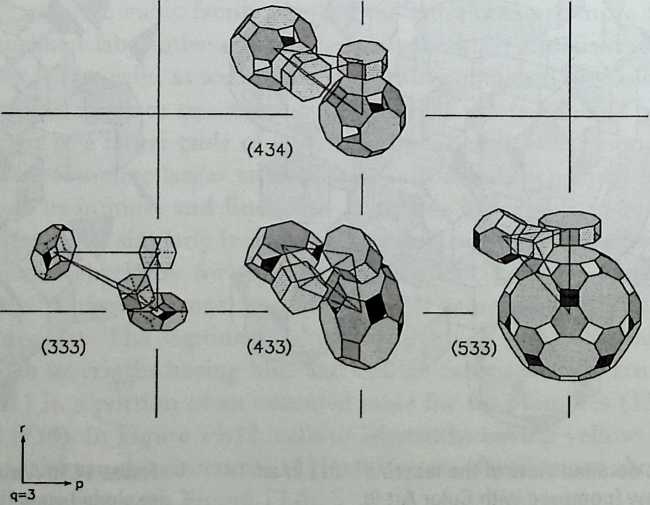
Figure 14.12 Cells of labyrinths 1111 of families (333), (433), (533), and (434) having yellow and violet faces removed.
CURVED VARIANTS AND OTHER DERIVATIVES
A large variety of labyrinths and related structures can be derived from the regular and semi-regular labyrinths described in the previous sections. Nonperiodic space labyrinths related to the new class of quasicrystals, curved labyrinths having curved edges and faces, and periodic as well as nonperiodic labyrinths in non-Euclidean space are interesting examples. Other possibilities include “curved space” labyrinths, which are in non-Euclidean space, as opposed to “curved surface” labyrinths like Pearce’s and Burt’s, which are in Euclidean space.
An assortment of examples is shown in the illustrations that follow. Figures 14.13 to 14.20 show examples of a variety of nonperiodic labyrinths projected from higher dimensions. These are embedded in spaces defined by hypercubes and hypercubic lattices and are analogs of the ones derived from the simple cubic lattice shown in the earlier sections. They can be built as three-dimensional projections of the hyperlabyrinths.
Figure 14.13 shows a portion of a nonperiodic space labyrinth embedded in an array of six-dimensional cubes. The cells (in their three-dimensional states) are tilted rhombicuboctahedra and the labyrinth is the higher-dimensional analog of the structure 0011 in the simple cubic family of Color Art 9. Similar structures can be built for other dimensions. Figure 14.14 shows another example of a nonperiodic labyrinth composed of tilted truncated octa-hedra and analogous to the cubic labyrinth 0110 of Color Art 9 and Figure 14.7 and belonging to the six-dimensional cubic family. Similarly, the nonpe-
Figure 14.13 Portion of the nonperiodic labyrinth having tilted rhombicuboctahedral cells and embedded in a six-cubic lattice (compare with labyrinth 0011 of Color Art 9).
Figure 14.14 Portion of the nonperiodic labyrinth having tilted truncated octahedral cells and embedded in a six-cubic lattice (compare with labyrinth 0110 of Color Art 9).
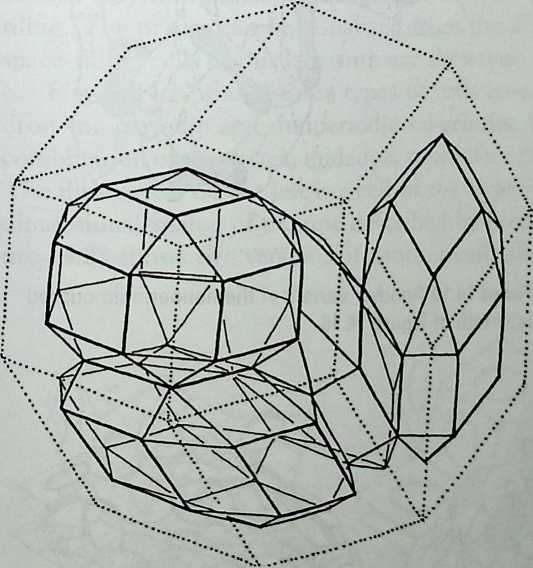
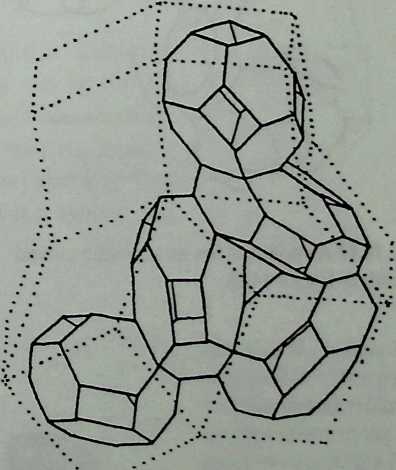
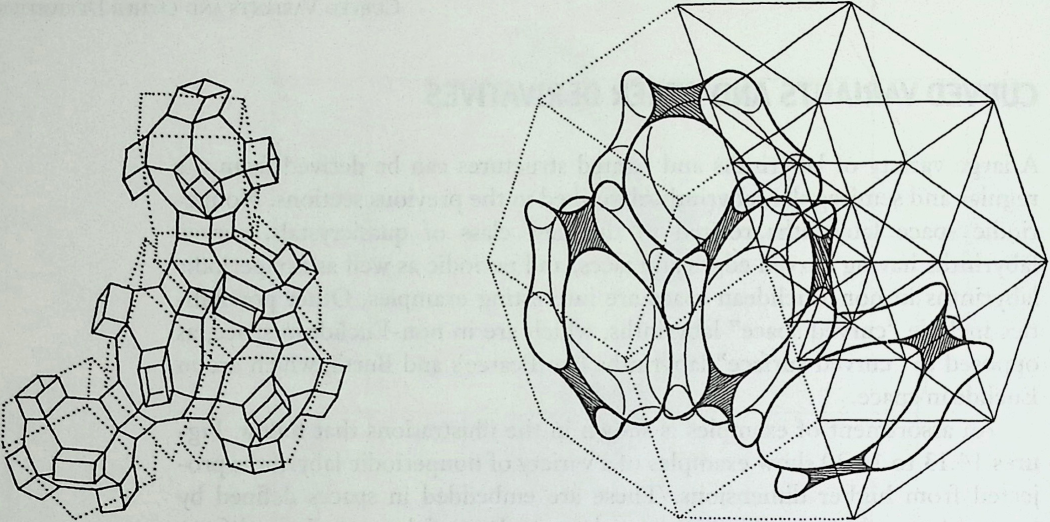
Figure 14.16 Portion of the nonperiodic curved surface labyrinth having tilted truncated octahedral cells and embedded in a six-cubic lattice (compare with labyrinth 0110 of Color Art 9).
Figure 14.15 Portion of the nonperiodic labyrinth having tilted truncated octahedral cells connected by parallelepipeds and embedded in a six-cubic lattice (compare with labyrinth 1110 of Color Art 9).
Figure 14.17 A variant of the nonperiodic curved labyrinth of Figure 14.16.
Figure 14.18 Another variant of the nonperiodic curved labyrinth of Figure 14.16.
Figure 14.19 Schwarz-type cells of dimensions 3,4, and 5 for periodic and nonperiodic labyrinths based on zonohedra.
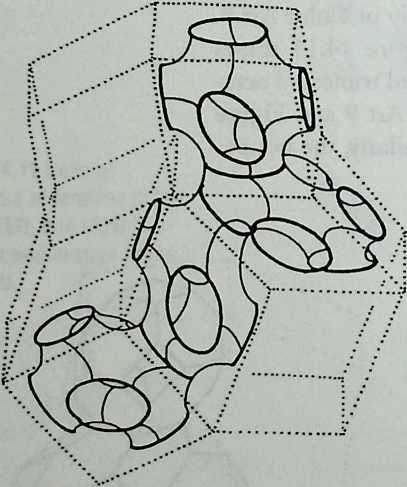
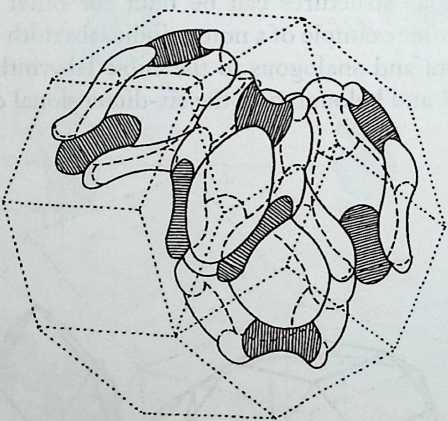
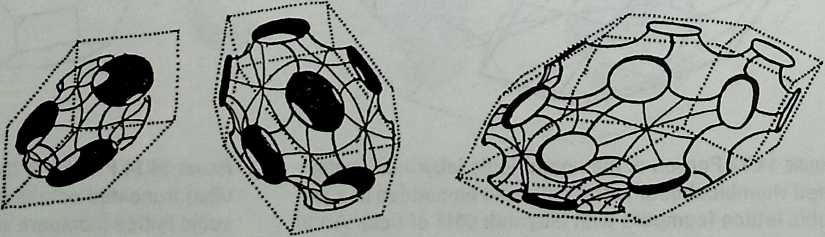
Figure 14.20 Alternative geometries for cells of dimensions 3,4, and 5 for labyrinths.
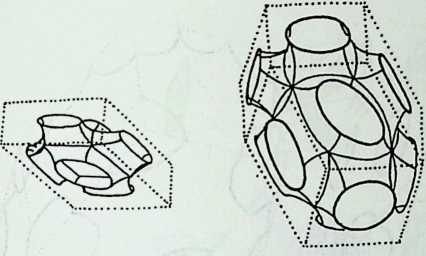
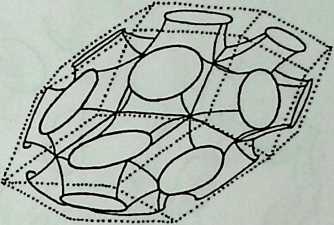
riodic labyrinth in Figure 14.15, which is similar to the one in Figure 14.14 but has, in addition, parallelepipeds that connect the truncated octahedra, is a higher-dimensional version of the structure 1110 of Color Art 9.
Figures 14.16 to 14.18 show curved variants of the hyperlabyrinth of Figure 14.14; the edges are curved inwards or outwards along the plane of the rhombic faces of the hidden hypercubic lattice. These three examples are embedded in the curved variants of the hyper-Schwarz surface. The Schwarz surface is the three-dimensional case first described by Schwarz over 100 years ago,14 and the first example of a hyper-Schwarz surface was developed by Brisson.15 The nonperiodic labyrinth embedded in the hyper-Schwarz surface was first described by Lalvani.6
Figure 14.19 shows Schwarz-type cells based on zonohedra (outer shells of hypercubes or zonotopes) of dimensions 3,4, and 5. These cells can be used in various combinations to generate periodic and nonperiodic labyrinths. Figure 14.20 shows variations of the cells in Figure 14.19.
Figure 14.21 shows a single layer (on the left) from a nonperiodic curved-surface labyrinth based on the upright or tilted prism version of the Penrose tiling. The prisms can be visualized from the illustration in the middle. The space-filling cells of this labyrinth are shown on the right.
Figure 14.22 shows three types of cells based on the rhombic dodecahedron for periodic and nonperiodic labyrinths; the openings can lie on any combination of the vertex, midedge, or midface of the rhombic dodecahedron. The illustration on the left is a cell of the hyper-Neovius surface, the higherdimensional analog of the one described by Neovius over 100 years ago. Figure 14.23 shows two versions of another cell, illustrated with connectors, and
Figure 14.21 A single-layered portion of the nonperiodic curved labyrinth corresponding to the prism version of the Penrose tiling. The two small illustrations on the right show cells of multilayered versions of the labyrinth shown on the left
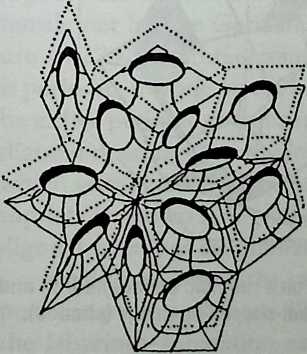
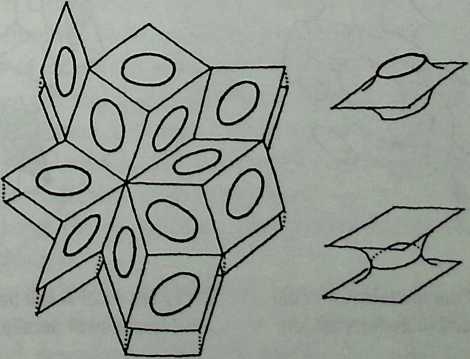
Figure 14.22 Cells of labyrinths based on rhombic dodecahedra. The cell on the left is a higherdimensional version of the cells in the labyrinth discovered by Neovius.
Figure 14.25 A cell based on a rhombic dodecahedron and composed of parallelogram-shaped openings (shaded).
Figure 14.23 Two variations of a cell of a labyrinth based on the rhombic dodecahedron shown here with connector prisms.
Figure 14.24 A periodic array of curved labyrinth composed of cells based on the rhombic dodecahedron.
Figure 1426 A variety of cells for periodic and nonperiodic labyrinths having digonal openings.
also based on the rhombic dodecahedron. Figure 14.24 shows a periodic array of a curved-surface labyrinth composed of cells based on the rhombic dodecahedron. Figure 14.25 shows a cell with parallelogram-shaped openings and also based on the rhombic dodecahedron.
Figure 14.26 shows a variety of cells for periodic and nonperiodic labyrinths with digons (two-sided and two-vertexed polygons) as openings. Architecturally, digons (as well as monogons) provide natural shapes of openings for tensile membranes. Frei Otto termed the monogons as “eyes” in his tensile net for the German Pavilion at the Montreal Expo held in 1967. Figure 14.27 shows three examples of labyrinths with digons; the one on the top is periodic, the one on the bottom left is nonperiodic, and the remaining could be either periodic or nonperiodic. Figure 14.28 shows two different cells with digonal openings (on the left), each based on the truncated tetrahedron from which tetrahedral connectors protrude. A periodic array using the cell on the top left is shown alongside. A large variety of other structures composed of digonal openings are similarly possible.
Additional labyrinths can be derived from other layered and nonlayered periodic plane and space fillings, and having plane or curved faces, following the labyrinth-generation method described previously. Interesting cases are
Figure 14.27 Portions of periodic and nonperiodic curved labyrinths composed of cells with digonal openings.
Figure 14.28 Two types of truncated tetrahedral cells with digonal openings and curved tetrahedral connectors with digonal ends; a periodic labyrinth based on one of the cells (on top left) is also shown.
the multilayered labyrinths composed of hyperbolic prisms in multilayered versions of Poincare’s hyperbolic disk space. This concept was mentioned by Lalvani9 and one example is shown in Figure 14.29. Other hyperbolic space labyrinths follow and are arranged in families in analogous hypertables. Spherical, ellipsoidal, cylindrical, saddle-shaped, toroidal, and other curved-space labyrinths in non-Euclidean curved space are similarly possible. The spherical and cylindrical cases, based on periodic subdivisions of the sphere and the cylinder, were first mentioned by Burt.10 A portion of a nonperiodic spherical labyrinth is shown in Figure 14.30. Several possibilities are suggested in different parts of the illustration, and the concept extends to all hypergeodesic surfaces developed by the author.16 Interesting cases are fractal labyrinths where the surface of the labyrinth is itself a labyrinth, a process that can be used recursively as well as self-similarly or randomly. One example is shown in Figure 14.31, where a saddle face of a Schwarz-type surface is composed of Schwarz-type modules.
Space labyrinths expand the repertoire of spaces and structures available to the architect. Many of the labyrinths presented here, and elsewhere in the author’s work, are mathematically new and await imaginative use as architectural space enclosures and alternatives to building systems. These are presented here to display the exploratory and open-ended nature of morphology, which can continually provide new possibilities for design.
Author’s Note
Last year (summer of 1995), while curating the Buckminster Fuller Centennial Exhibit, the author received two models of four-dimensional space labyrinths related to the 120-cell from Koji Miyazaki. These models were displayed in the exhibition. In the same exhibition we also displayed the author’s independent work on four-dimensional labyrinths.5,7,8 These hyperlabyrinths, including those derived from the 120-cell, were included in the computer drawing of our higher-dimensional periodic table of space structures, also shown in the exhibition.
Figure 1429 One example from a large family of single-, double-, and multilayered hyperbolic labyrinths composed of hyperbolic prisms.
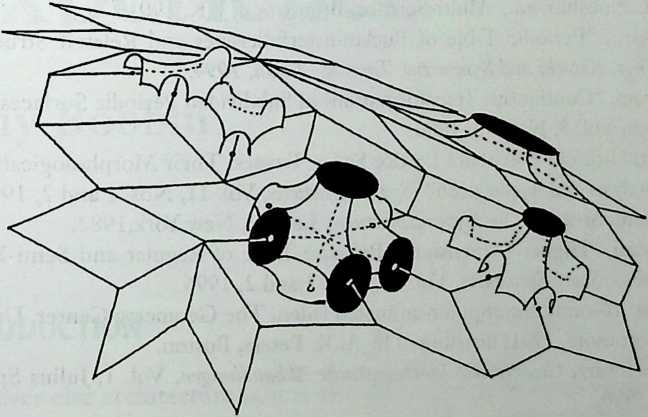
Figure 14.30 A portion of a nonperiodic spherical labyrinth; several alternatives are shown.
Figure 14.31 A saddle face of a fractal labyrinth where the face is itself a labyrinth surface.
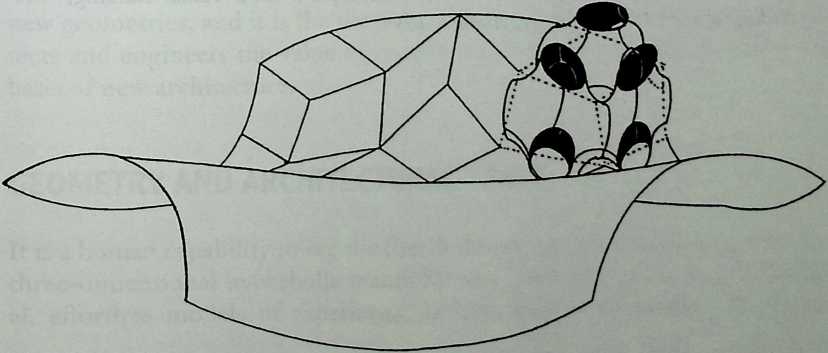
ACKNOWLEDGMENTS
The author wishes to thank Neil Katz of Skidmore, Owings and Merrill, New York, for all computer-generated drawings in this chapter.
¶ NOTES
-
H. S. M. Coxeter, Twelve Geometric Essays, Southern Illinois University Press, Carbondale, 1968.
-
M. Burt, M. Kleinman, and A. Wachman, Infinite Polyhedra, Technion, Haifa, Israel, 1974.
-
P. Pearce, Structure in Nature Is a Strategy for Design, MIT Press, Cambridge, MA, 1978.
-
A. Schoen, “Infinite Periodic Minimal Surfaces Without Self-Intersections,” NASA Technical Note D-5541, May 1970.
-
H. Lalvani, “Families of Multi-Directional Periodic Space Labyrinths,” Structural Topology, Vol. 21, 1995.
-
H. Lalvani, “Non-periodic Space-Fillings of Golden Polyhedra,” Proceedings of the First International Conference on Lightweight Structures in Architecture, University of New South Wales, Sydney, 1986.
-
H. Lalvani, “Morphological Aspects of Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science, Brentwood, UK, 1991.
-
H. Lalvani, “Periodic Table of Buckminsterfullerenes and Related Structures,” Proceedings, Katachi and Symmetry, Tsukuba, Japan, 1994.
-
H. Lalvani, “Continuous Transformations of Subdivided Periodic Surfaces,” Space Structures, Vol. 5, No. 3/4, 1990.
-
M. Burt, “Infinite Polyhedra Lattice Space Trusses: Their Morphological Evolution, Analysis and Application,” Space Structures, Vol. 11, Nos. 1 and 2, 1996.
-
H. Lalvani, Structures on Hyper-Structures, Lalvani, New York, 1982.
-
H. Lalvani, “Higher-Dimensional Periodic Table of Regular and Semi-Regular Polytopes,” Space Structures, Vol. 11, Nos. 1 and 2, 1996.
-
Not Knot, 16-minute computer-animated video, The Geometry Center, University of Minnesota, 1991; distributed by A. K. Peters, Boston.
-
H. A. Schwarz, Gesammelte Mathematische Abhandlungen, Vol. 1, Julius Springer, Berlin, 1890.
-
D. Brisson, The Hyper-Schwarz-Surface, Brisson, Rehoboth, MA, 1976.
-
H. Lalvani, “Hyper-Geodesic Structures, Excerpts from a Visual Catalog,” Proceedings of the IASS Conference, Atlanta, 1994.
¶ Quasicrystal Architecture: The Space of Experience
Tony Robbin
¶ INTRODUCTION
Whatever else architecture is, it is also geometry. If the geometrical concepts of a designer are old-fashioned, then no matter how elegant a building is in its details, it cannot help but look a bit recycled. We live in an era of marvelous new geometries, and it is the purpose of this chapter to demonstrate to architects and engineers the value of considering these modem geometries as the basis of new architecture.
GEOMETRY AND ARCHITECTURAL SPACE
It is a human capability to see the fourth dimension; exotic geometries such as three-dimensional hyperbolic manifolds and quasicrystals can become natural, effortless models of experience. Indeed, they must become so because
Beyond the Cube: The Architecture of Space Frames and Polyhedra, edited by J. Francois Gabriel ISBN 0 © 1997 John Wiley & Sons, Inc.
human experience at the turn of the 21st century is far too complex and omni-attentive to fit comfortably in an old-fashioned model of three-dimensional rectilinear space. We designers of spaces that people inhabitartists, architects, and engineersowe it to our audience to make spaces that enhance our capability to visualize the four-dimensional, hyperbolic, fractal, and quasicrystalline world that we are really living in.
Consider engineers first. Most engineers would reject such a directive; their duty is not to make mathematical spaces visible and comprehensible but primarily to be efficient and only secondarily to be artistic, a goal considered to have nothing to do with esoteric geometries. (It goes without saying that public safety is the foremost duty of engineers and architects.) However, do engineers really act as though efficiency is more important than aesthetics? As Ariel Hanaor has pointed out, space frames, tensegrity systems, and other popular engineering concepts are not necessarily the most efficient solutions in either labor or materials.1 Membrane combinations can easily cost more than $100 a square foot of installed coverage; some nodes of the tensegrity roof in Atlanta weigh two tons; and free-form shells require troublesome single-use formwork. Is it possible that engineers select options on the basis of aesthetics first and efficiency second? From my experience talking with many of the world’s great engineers at engineering conferences in Copenhagen, Surrey, and Atlanta, I am convinced that tastes drive engineering as surely as the science of new materials and new engineering systems drive architecture. Therefore, it is important for engineers to understand that a great source of new aesthetics, I believe it is the only true source, is the idea of space found in contemporary mathematics (including morphology studies) and physics. Designers should feel permitted to explore the aesthetics of mathematical space, how the subjective space of experience and the objective space of contemporary physics and mathematics mutually reinforce each other, and substitute this sophisticated understanding for the knee-jerk minimalist aesthetic still popular among engineers but abandoned by almost everyone else.
Architects and artists also resist such a directive. They fear that to explore the intellectual world of mathematics and physics is to submerge sensibility; or (they might say) that to submit to the rigors of geometry is to resign one’s creations to a boring repetitive simplicity that is totally out of character with the self-referential, ironic, and mock-heroic styles now in fashion. These assumptions are false. The new geometries are not repetitive, nor rectilinear, nor simplistically grasped by the mind. Instead, they promote a sensual involvement, an intriguing, intuitive relationship with space. Furthermore, the mock-heroic may be fun at first, but a building is an expensive way to tell a joke and most jokes do not bear revisiting. Architects love theory; they should perceive new geometries as the liberating theories they are, rather than the constraining rectilinear boxes they most certainly are not.
Two examples from history may demonstrate that space in art, space in architecture, and coeval space in mathematics are alike. Alberti’s St. Andrea in Mantua, built in 1470, was an astoundingly original building, capturing the imagination of patrons and architects for centuries, and becoming the model for such divergent buildings as St. Peter’s in Rome and Grand Central Station
Figure 15.1 With St Andrea in Mantua, Alberti revolutionized architecture by using the conception of space created by the mathematics and science of his time.
in New York. The concept that so excited onlookers was that both mass and void could be sculpted: Both building and air had substance, both were plastic elements that could be manipulated, interlocked. This was very different from the planar and linear Gothic architecture where tracery planes prop each other up. In both Gothic and Renaissance architecture, the detailing of the walls and facade reinforce the concept of space; the flat patterns of the stained glass or colored marble of the Gothic contrast with the blocks and hollows of the Renaissance. Alberti formed his new building space when ideas of space, in general, were changing. Masaccio’s paintings put humans in space, in the same space as gods, and Leonardo (a few years later) first studied air as material capable of filtering light. Space was no longer the zero-density symbol and body of a god, but earth-bound stuff under human control, defined by the very new, human-oriented, instantaneously fixed projective geometry, also pioneered by Alberti.
The Eiffel lower (1889), too, was a work of mathematical space as much as a work of iron. Eiffel depended on new calculation techniques to sum over the forces of so many members in so many directions in three-dimensional space, but more than that, mathematics and physics presented Eiffel with a concept of space as a force field that he could use in a more conceptual way. Maxwell’s field equations of 1864, made part of popular culture in the famous 11th edition of the Encyclopedia Britannica (1875), demonstrated how small local forces could aggregate to effect action at a distance, like metal filings on a sheet of paper over a magnet. Indeed, it was suggested that all the space of the world was filled with field: an active multidirectional ether capable of inducing powerful forces on test particles: “…that there is an ethereal medium filling space and permeating bodies, capable of being set in motion and of transmitting that motion….”4 To build his tower to the sky, Eiffel had only to select and stack elements of this force-field space, confident that a solid core to the top of the tower would not be necessary.
In his paintings of the period, van Gogh abandoned the delicate atmospheric perspective of the French naturalists and even the more robust atmospherics of the impressionists to construct instead a space packed with texture, color, and brush strokes freed from their role of describing objects, free to act on their own and influence one another. His Night Cafe (1888) presents space as a pressure chamber with tilted-up floor and pressed-in walls, thick with radiation powerful enough to overwhelm the inhabitants. Thus the space-as-field that was created by science at the end of the 19th century became the space of both architecture and painting.
The “two cultures” hypothesis is incorrect: Even if art and science no longer study each other directly, reciprocal influences and the sharing of basic paradigms are inevitable. Practitioners often think they are in a private tradition: Mathematics comes out of mathematics; architects work from the example of other architects. However, mathematicians and architects are both in culture, liberated and constrained by the same cultural constructs; it never happens that Gothic architecture is developed in a culture also working on the physics of relativity.
THE FOURTH DIMENSION
To begin the study of space in our culture, we must first realize that the fourth dimension is not time; it is another dimension just like the other ones. On a pool table the third dimension is time. On a map the second dimension is north. We must not confuse the applications of geometry with the geometry itself. Think not of space-time, but of four mutually perpendicular fines intersecting at a point, the axes of a grid on which space and time dimensions could be plotted, or on which any other four scalar variables could be plotted. Points in the four-dimensional grid can be connected to make regular geometric figures, analogous to the Platonic solids: As the square begets the cube, the cube begets the hypercube; as the triangle begets the tetrahedron, the tetrahedron begets the four-simplex. For over a hundred years, mathematicians have studied these four-dimensional figures, the four-dimensional polytopes, and have been stimulated by efforts to visualize them.
Now the effort is far more manageable. Computers can show us the projections, the shadows, of the four-dimensional polytopes and show us how the projections deform when the polytopes are rotated in four-dimensional space. Henri Poincare repeatedly suggested that successive models of the projections of four-dimensional figures when seen in sequence could lead to a vision of the fourth dimension, a geometry no more or less true or sacrosanct than any other “convenient” geometry. Since the late 1960s, numerous researchers have written computer graphics programs that carry out Poincare’s suggestion, some in real-time motion and with binocular vision (including one such useful program written by the author). As a result, this once arcane branch of
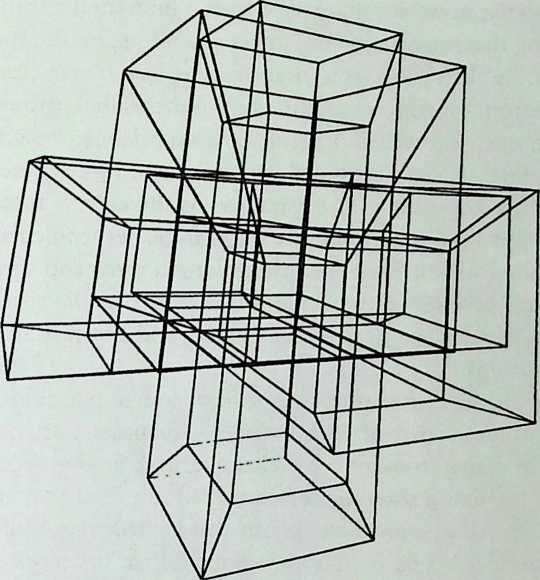Figure 152 Eight hypercubes are stacked around a central hypercube and drawn in perspective. All the cells of all the hypercubes are the same size and shape; those farthest away are shown to be
smaller.
mathematics is accessible to all. Often misunderstood and filled with romance and mysticism, the idea of the fourth dimension has inspired artists, writers, and philosophers since the early part of this century. Now that nonmathematicians can know the realthe geometricfourth dimension, much more profound inspirations await us.
It is important to realize how pervasive four-dimensional geometry is in contemporary mathematics and physics. Relativity, cosmology, and quantum physics take place in varieties of four-dimensional space. Few problems in modern geometry, such as linear programming or three-dimensional topology, can avoid reference to a higher-dimensional space. Like calculus, higherdimensional geometry is part of the basic conceptual tools of mathematics, part of the furniture. I suppose individuals differ in the degree to which they take these higher-dimensional spaces to be literal spaces as opposed to abstract bookkeeping devices, but to be efficient, to gain an intuitive and insightful mastery, some sense of the reality, the objecthood, of these higher-dimensional structures and spaces is necessary and inevitable.
SEEING THE FOURTH DIMENSION
For the last 25 years, my painting and sculpture have been dedicated to the principle that four-dimensional geometry can be and should be the operating model of the space of our experience. In Fourfield, a 27-foot wall relief completed in 1981,1 used two-dimensional and three-dimensional elements working together to provide the visual information of four spatial dimensions, the space defined by four mutually perpendicular lines.
It is true that we possess no biological organ capable of seeing the fourth dimension directly; however, that is not such a limitation as one might imagine, considering that we have no organ capable of seeing the third dimension directly either. By the time that a three-dimensional object reaches our eyes, it is a flat wavefront of light, a changing two-dimensional pattern that we nevertheless experience as three dimensional, an experience primarily due to cultural conditioning. Two-dimensional projections of three-dimensional structures, say a lattice cube, are full of paradox. As the cube is rotated, the shadows swim through each other; lines we know to be perpendicular to two other lines instead bisect them; lines of constant length grow and shrink; lines hide whole faces. It is precisely these paradoxes that give us the visual information that we are seeing a three-dimensional object and not just an intricate two-dimensional pattern.
Changing characteristic projections from four-dimensional space are as effectively communicative of four-space as are projections of three-space. However, only planar rotations are characteristic in this way: A plane can rotate around a point; a three-dimensional cell can rotate around a line; only an object in four-dimensional space can rotate around a plane, a particular action best revealed to us by Thomas Banchoff in his pioneering film The Hypercube, Projections and Slicings (1979). It is precisely this planar rotation that I have captured with the simple formal device of using welded steel rods the same color and dimension as painted lines that are made with half round skeins of thick paint. As one passes by Fourfield, the three-dimensional elements parallax, but the painted lines do not, yet both are perceived to be part of the same rigid object. All the paradoxes of planar projection and rotation are present in Fourfield. Parts of rigid three-dimensional objects move relative to one another and pass through each other without interference (two objects are in the same place at the same time); cells grow, shrink, and disappear altogether, hidden behind lines. It is precisely these paradoxes that prove that we are witnessing a four-dimensional experience and not merely an intricate three-dimensional one. With practice, that four-dimensional visual experience
Figure 15.3 Fourfield, based on four-dimensional geometry, replicates the experience of a four-dimensional planar rotation as the viewer walks by. (Acrylic on canvas with welded rods, 8.5x27x1.5 feet. Collection: The General Electric Company, Fairfield.)
Figure 15.4 A detail of Fourfield shows that the image is composed of three-dimensional elements, welded steel rods, and two-dimensional elements, painted lines, that work in concert
can become as natural, as automatic, as the seeing of three-dimensional space.5 In my light pieces of the late 1980s, I have pushed the same formal strategy a step further. Because both the three-dimensional elements and the two-dimensional elements of the rod/canvas pieces are shadows from the fourth dimension, it is elegant to have the two-dimensional elements be the actual cast shadows of the three-dimensional elements. We still walk around the three-dimensional welded steel rods, and still the two-dimensional elements are unaffected by our movement, being a function of the fixed fights and the fixed rods. However, now, two lights, one red and one blue, illuminate the piece, and where they shine together they make white light, and where a rod blocks the red light, a blue line is created, and vice versa. The different colored lights are each filtered separately by assorted Plexiglas plates. The simple piece is filled with various colored planes and colored lines, two-thirds of which are only lighta painting of light. Three-dimensional glasses can be worn, and the two-dimensional elements of red-and-blue shadows fuse to become a three-dimensional structure more present and closer to the viewer than the welded steel boxes; the paradoxes of planar rotation are dramatically and unmistakably created.6
A QUASICRYSTAL FOR DENMARK’S COAST
As Haresh Lalvani and Koji Miyazaki have separately pointed out, quasicrystals are the three-dimensional projections of higher-dimensional objects. In fact, they are regular and rational in their original space and only take on quasicrystalline properties as a result of their projection to three-dimensional
Figure 15.5 In the light pieces the two-dimensional components of the image are the colored cast shadows of the three-dimensional elements. The shadows are colored because the work is lit by strongly colored blue and red lights. (Untitled #1,1986, welded steel, acrylic, and colored light, 35 inch diameter.)
space.7 All the visual richness of four-dimensional geometry is here: multiple objects in the same place at the same time, objects appearing and disappearing by rotation, objects passing through one another without interference. Thus quasicrystals can be seen as an application of four-dimensional geometry, and, for us three-dimensional beings, a way to experience and communicate a greater awareness of four-dimensional space.
In 1993 I made a large sculpture based on quasicrystal geometry for the Center of Art Science and Technology at Denmark’s Technical University. This new geometry is only 15 years old and has four interesting properties that make it fundamentally different from all previous patternings. First, a quasicrystal is nonrepeating; although it fills space with standard elements, it confounds our expectations by repeating elements only at irregular intervals. Second, it has simultaneous fivefold, threefold, and twofold symmetry, which means that sometimes it appears to be made up of right angles, other times of triangles, and from still other vantage points it appears to be made up of star pentagons. This multiplicity of image results, in part, from using dodecahedra for nodes, as Steve Baer first did in the early 1970s, followed soon after by Miyazaki. Third, a quasicrystal is assembled from intermediate groupings; the four golden zonohedra (a skewed cube, a rhombic dodecahedron, a rhombic icosahedron, and a rhombic triacontahedron, all with faces whose diagonals are in the golden ratio). These geometric solids float in the quasicrystal. Finally, the components of a quasicrystal subdivide into smaller self-similar elements, something like a fractal foliation. There are two such deflations in the sculpture: one with the golden ratio, 1:t, and another l:r3.
The three-story atrium of the Danish Technical University is an ideal set
ting for such a quasicrystal sculpture. Open stairs and two bridges allow the viewer to pass under, over, around, and through the work, and to happen upon the many and unexpected occurrences of fivefold, threefold, and twofold symmetry. In winter, sunlight is caught by mirrored plates and reflected down into the room and into the sculpture. Half mirrors on the bottom of the work reflect crisp moving colored light paintings onto the walls and the ceiling of the space. In summer, direct sunlight passes over the sculpture, casting direct shadows onto the floor that transform from fivefold to threefold to twofold images as the sun passes overhead. Finally, on cloudy days, six strong artificial lights illuminate the morning, noon, and afternoon patterns.
The sculpture is in four parts, each of which illuminates one of the special qualities of the quasicrystal. First is the dome: From above the fivefold symmetry of this structure is apparent, but from below we see the near chaos that is inside. A large pinwheel shape is opposite the dome. There are 15 ways that a rhombic dodecahedron can be oriented in a quasiciystal, and this spiral pinwheel is composed of those 15 dodecahedra. The snake is a curvaceous, linear section that connects the dome and the pinwheel. It is based on three five-petal flower shapes, and from above it presents a perfect Penrose pattern.10 Finally, there is the large-scale section, based on the 1:t5 deflation discovered by the Japanese physicist T. Ogawa. Like a fugue, the geometry breaks apart and appears to run wild, only to converge again at key nodes.
Imagine a quasicrystal architecture. When approaching the structure from the east, squares and cubes are seen; when the car passes by to the north, the structure has the fivefold symmetry of a Penrose pattern with star pentagons; moments later looking back from the northwest, the structure is not only a different overall shape but appears to be made up of triangles, hexagons, and 60° parallelograms. The structure as kaleidoscope is never more apparent than when the sun casts shadows through the structure; truss systems make triangular nets that slide across the floors and walls, while quasicrystals transmute to an astounding variety of shapes all through the day. This kaleidoscope is the protean space of our experience of the world, suggested to us by our understanding of the objective world, reinforced in us by the multiplicity of images and media imploding on us. Why insist on a mechanistic, repetitive structur-
Figure 15.6 A computer drawing of a quasicrystal dome shows the patterns of the dome on the floor as they change from morning, to noon, to afternoon.
Figure 15.7 Shadows at noon from a model of a quasicrystal space frame make a two-dimensional quasicrystalline patternsometimes called a Penrose pattern.
al pattern? Why nudge toward this vision with little, ironic architectural gambits when the tools are at hand to master such a vision.11,12
Because engineers make design decisions on the basis of their aesthetics, they owe it to us all to become more conscious of their aesthetic choices. Because architects live in culture, they owe it to us all to help us experience the spaces we mentally inhabit. Problems arise when the idea of beauty is anachronistic; if the public feels that its built environment is less vital than its conceptual environment, then buildings become a drag on consciousness. It is as if the engineers of France were to present the people of the United States with a full-scale replica of the Statue of Liberty, only one made with inflated
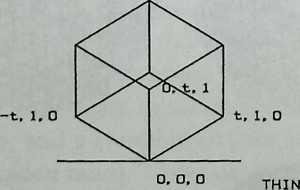
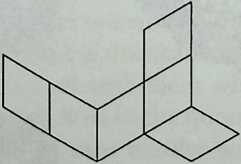
Figure 15.8 The plans for the two cells that make up all three-dimensional quasicrystals. By photocopying, cutting, and folding the patterns to the right, the reader can begin to build quasicrystals.
Figure 15.9 Quasicrystal at COAST. A view of the dome and snake from the first floor. (Aluminum and acrylic, 17 x 10 x 8 m, 1993. Collection: COAST at the Danish Technical University. Photo: Poul lb Henriksen.)
Figure 15.10 View from the back of the large-scale section of the COAST sculpture. (Photo:
Poul lb Henriksen.)
plastic sheeting. A technological marvel perhaps, but one that mocks history and mocks the current audience. Such a joke would not be funny for long; but what would linger is a sense of the abdication of designers to make culture new. Three-dimensional geometric space frames of the Eiffel Tower variety are a similar abdication; they come from another time and were fresh in a context long past. We have our own discoveries of space to make, based on the mathematics and physics of our own time.
Figure 15.11 A detail of the dodecahedral nodes and standard-length rods that make up the nonrepeating patterns in quasicrystal space frames.
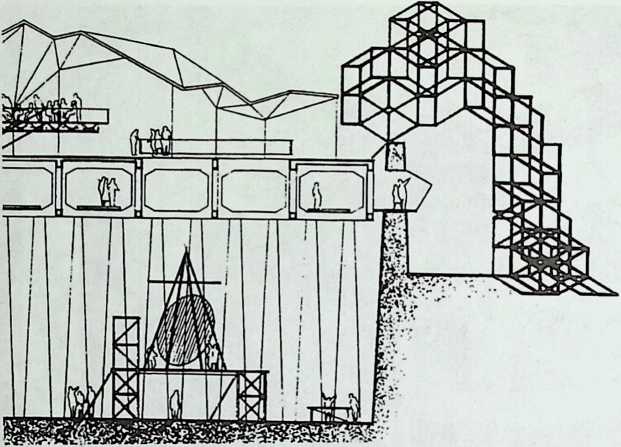
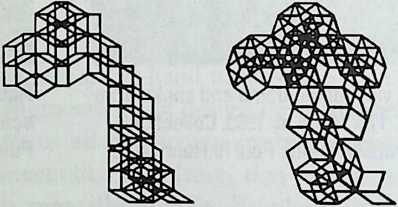
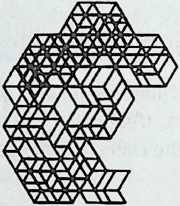
Figure 15.12 The first proposal for COAST was an exterior structure, a canopy that appeared to change its shape as one passed by.
northwest
¶ NOTES
-
Ariel Hanaor, “Engineering Properties of Double-Layer Tensegrity Grids,” Proceedings of the IASS, Copenhagen, 1991.
-
Ariel Hanaor, “Aspect of Design of Double Layer Tensegrity Domes,” Journal of Space Structures, Vol. 7, No. 2, 1992.
-
Ariel Hanaor, private communication.
-
James Clerk Maxwell, “A Dynamical Theory of the Electromagnetic Field,” Philosophical Transactions, Vol. 155, 1865, p. 459.
-
Tony Robbin, Fou?field: Computer, Art and the Fourth Dimension, Bulfinch/Little Brown, Boston, 1992, Chap. 1.
-
Ibid., Chap. 3.
-
Haresh Lalvani, “Non Periodic Space Structures,” Space Structures, Vol. 2, No. 2, 1986.
-
Haresh Lalvani, “Hyper-Geodesic Structures: Excerpts from a Visual Catalog,” Proceedings of the IASS, Atlanta, 1994.
-
Koji Miyazaki, An Adventure in Multidimensional Space, Wiley, New York, 1986.
-
Roger Penrose, The Emperor’s New Mind, Oxford University Press, New York, 1989.
-
Tony Robbin, “A Quasicrystal for Denmark’s COAST,” Proceedings of the IASS, Atlanta, 1994.
-
Tony Robbin, Engineering, New Architecture, Yale University Press, New Haven; 1996, Chap. 7. See also Architectural Body having a Quasicrystal Structure, U.S. Patent 5.,603,188, Feb. 18, 1997.
¶ Are Space Frames Habitable?
J. Francois Gabriel
¶ INTRODUCTION
The preceding chapters offer good arguments in favor of an architecture of polyhedra. The purpose of this chapter is to look at the spaces within, the spaces we would be living in. Are they practical, comfortable, pleasant? Are they varied as well as versatile? Can they be flooded with sunlight? Can they accommodate our furniture, our tools, the equipment on which we depend? In other words, are they as good as our conventional rooms?
Most of us live and work in rooms whose shape approximates a cube. Since we spend a lifetime in variations on the cubic theme, we have come to take it for granted that a cube, or a near-cube, is the best shape for a room, in fact the only possible shape for it. We know that generations of other cultures have dwelt successfully in yurts, tepees, and igloos, but few of us would seriously entertain the possibility of living our present lifestyle in one of these. Is it possible to take a rational look at our conventional, “square” dwellings and learn to distinguish between the features that respond to our real needs, practical or emotional, and what is around us thoughtlessly, simply by force of habit?
As you can probably see by looking around you from where you are sitting right now, a conventional room is characterized by a horizontal floor and a number of vertical planes: walls, partitions, doors, and windows. There is a logic to that, as gravity makes us stand vertically for balance, and it is easier for the average person to evolve on a horizontal floor than on a slanting one. It also feels good to be surrounded by a modicum of vertical surfaces, for reference or for reassurance. What is not necessary at all is a horizontal ceiling. In fact, the best architecture is more often than not distinguished by shapely roofs or vaults. And what is even more unnecessary is that all the walls meet one another at right angles. We need to orient ourselves easily and to know where we are, and therefore we need an orderly environment, but many orderly environments can, and have been, designed that do not rely on rectangular plans.
It is true that we, the people (for whom architecture is made), have a front, a back, and two sides. When life used to be structured around the sun cycles and when religion was unquestioned, to build a room on a square plan was a meaningful, indeed a sacred act. For better or for worse, neither the sun nor religion controls modern life today. The survival of rectangular rooms and buildings is just that: a survival. This is not to say that rectangular spaces are fundamentally wrong. Superb architecture has been generated on a rectangular basis and will undoubtedly continue to be. The points I am trying to make are simply that there are many other avenues to explore in the making of architectural space, and that we deprive ourselves of rewarding experiences when we fail to explore and experiment. Furthermore, many aggregates of polyhedra, in particular, all those discussed in this chapter, do fit in an orthogonal axial system and accept bilateral symmetry as naturally as any buildings conceived on rectangular plans.
An important issue to consider when discussing the essential aspects of a room is its height. Ideally, the height of a room should not be considered independently from the shape of its roof. However, most buildings consist of several stories piled up on top of one another and, for reasons of economy, the floor of a room will often be the ceiling of the room underneath. The minimal height is determined by the necessity for even tall individuals to stand up, move about, and wave their arms around without hitting the enclosures. Eight feet in America and 2.5 m in Europe are the standard heights, although some architects are unhappy with such rigid constraints. Frank Lloyd Wright, for instance, ordered a ceiling height of 6 feet, 4 inches in the vestibule of his marvelous design for the famous house Fallingwater.
However, there is no upper limit to the height of a room, not only because some of them must contain large objects, but because others might be tall to express an ideal: Have you ever heard anybody complain that the 40-m-high nave of a Gothic cathedral is too high? Probably not. Indeed, the art of architecture does not consist in packing the most in the smallest possible amount of space. It is rather the art of wasting space wisely.
¶ INSIDE POLYHEDRA
In this chapter polyhedra will be discussed from an architectural standpoint, an important part of which concerns, naturally, their habitability. There are so many polyhedra and combinations of polyhedra with architectural possibilities that a selection had to be made for our case study. Only two polyhedra were retained: the tetrahedron and the octahedron. In fact, a further restriction proved necessary: Our two polyhedra will be examined with their position remaining constant with regard to the ground. What we learn from these two will increase our understanding of any other polyhedral combination.
There are several reasons for selecting the tetrahedron and the octahedron. One is that they are the simplest of all polyhedra. Another is that they can together organize space, something that neither one can do individually. If a tetrahedron is placed on each face of an octahedron, clones of the octahedron will fit perfectly against the exposed faces of the tetrahedra. The process can be repeated indefinitely, producing what is called an infinite structure (Figure 16.1).
What may appear to be a digression will be useful here. The names given to polyhedra indicate the number of their faces. Thus we know from their names that a tetrahedron has four faces and an octahedron has eight. However, if all the faces were removed and only their edges remained, the three-dimensional configuration would be essentially the same. Only our perception changes. What we understood as an aggregate of solids is now a space lattice.
Figure 16.1 Octahedra and tetrahedra can organize space without gaps or overlap when the faces of the octahedra are in contact with the faces of the tetrahedra. In this top view, polyhedra are pulled apart to show that an octahedron (0) is surrounded by six tetrahedra, three of them straight side up and the others (T) upside down.
Both are infinite structures; in fact, they are the same. (The reader who is not familiar with this space lattice will probably experience difficulties at this point. Alan Holden would recommend the making of a model. As he says: “The best way to learn about these objects is to make them, next best to handle them.”11 would recommend the use of wooden toothpicks, the round sort that are tapered at both ends. Assemble them with a good glue and keep in mind that accuracy is important.)
We are interested in the spaces found within our tetrahedron-octahedron space lattice. They are our “rooms.” What shapes are they? The answer depends on the position of the space lattice with regard to the ground. When the struts found in horizontal planes meet at right angles, the space lattice is called a two-way space frame, and all the rooms are in the shape of cubes.2 When the horizontal struts form triangles, the space lattice is called a three-way space frame, and all the rooms are in the shape of hexagonal prisms (Figure 16.2).
Most people are already familiar with the cube, and the object of this book
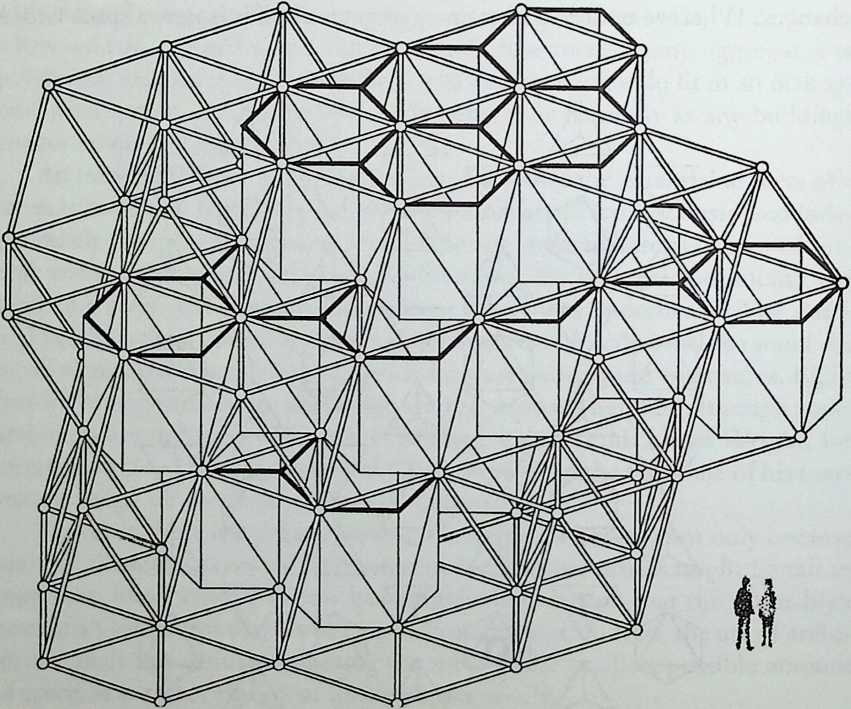
Figure 16.2 A three-story aggregate of octahedra and tetrahedra with faces deleted. Only edges remain, in the form of struts, to form a space lattice, or space frame. Because the horizontal struts are arranged in triangles, this is called a three-way space frame. A honeycomb pattern of hexagonal rooms is obtained by the addition of vertical planes against the diagonals, which are the struts connecting one floor to the next. (Source: J. F. Gabriel, “Three-Dimensional Suburbs,” Proceedings of the IASS World Congress on Space Enclosures, P. Fazio, G. Haider, and A. Biron, eds., 1976, pp. 89, Fig. 3. Reprinted with permission of the Centre for Building Studies, Concordia University, Montreal.)
is to present other, lesser known spaces, waiting for discovery inside polyhedra. We will therefore abandon the two-way space frame and its cubic spaces to focus our attention exclusively on the three-way space frame. How exactly are the hexagonal spaces seen in Figure 16.2 obtained? Simply by applying a vertical surface (wall panel or cladding) to the struts that connect one floor to the next. These struts are called diagonals, and the floor structures they connect are referred to as chords. Spatially, we have gone from an aggregate of octahedra and tetrahedra to a honeycomb pattern: Each octahedron has increased in size and volume by absorbing, as it were, a third of the volume of six adjacent tetrahedra.
The natural place for doorways is where diagonals form “A-frames,” that is, where three diagonals are joined by their upper extremities. Three doorways can be found in each hexagonal room, in alternate comers, and each doorway gives access to two other rooms (Figures 16.2 and 16.3).
For my studies I have usually adopted a regular octahedron with an edge length of 4 m. A standard octahedral frame of that size would provide a rather small but adequate room within. The corresponding floor-to-floor height will be 3,266 m. Headroom will be ample regardless of the depth of the floor structure itself, which depends on many factors such as building materials, building program, size and shape of the overall structure, climate, and so forth. The width of the room, measured between parallel walls, is 4 m and, measured diagonally, 4.62 m.
In many cases it will be possible to give hexagonal rooms what might be a more pleasant height-to-width ratio by decreasing their height. The angle between a diagonal and the floor plane is 54° 44 8". Reducing this angle to 45° might improve the proportions of the space within and have the advantage of squaring off the vertical faces of hexagonal prisms.
With this said, it should be clear that a space frame of appropriate depth meets the basic requirements for habitability. Horizontal floors, headroom,
Figure 16.3 Three diagonals meeting overhead provide the space for doorways. This occurs in alternate corners of each hexagonal room, that is, three times per room. Thus each room can have access to six others.
vertical walls, accessibility are necessary in buildings, but are these conditions enough? Can a space frame accommodate vertical shafts, or wells, of varied cross section wherever they are needed? We will address the problem of fitting stairs, elevators, and flues, without which buildings are not viable, in the next section of this chapter.
At this point, a word of clarification is in order. This chapter is written by an architect and is about architecture, not structure. Of course, structural considerations should never be ignored altogether, especially since they are an important argument for the increased use of space frames, but here they are looked at in their broadest general aspects. Space frames are attractive to me, as an architect, because their geometry makes them essentially indeformable. They are lightweight structural frameworks made versatile by their structural redundancy. They lend themselves to the design of large buildings, the form of which could not be obtained otherwise, and they can provide the answer to many difficult urban problems. They are modular and therefore orderly. They can be produced industrially, and they can be designed for reuse.
¶
CUMBERSOME CHORDS
Unlike the conventional post-and-beam system, which is three directional, our space lattice is a six-directional system. Seen from above, a multistory, three-way space frame presents an intricate mesh. The introduction of vertical shafts would be very difficult, for it would require the elimination of considerable portions of the space frame. It would also lead to a breakdown of the system because chords and diagonals would not be lined up (Figure 16.4).
Figure 16.4 Top view of a multilayer, three-way space frame. Although the chords are all made of the same triangular pattern, they shift with the diagonals from floor to floor with the end result a complicated, obtrusive mesh. The insertion of vertical shafts is difficult. Many structural members would have to be removed, opening up irregular spaces that do not coincide with the vertical surfaces of shafts.
With the reader’s permission, I would like to make a recommendation. Visualization of the six-directional space lattice is not easy to achieve for one who is not thoroughly familiar with the morphology of noncubic configurations. It requires patience. To avoid fatigue and discouragement, I would suggest that the reader go over the drawings with color pencils and tracing paper until the spatial relationships described in this chapter become clear and familiar.
The next drawing represents the same configuration as Figure 16.4, also seen from above, but with the chords deleted. Only diagonals are shown, up
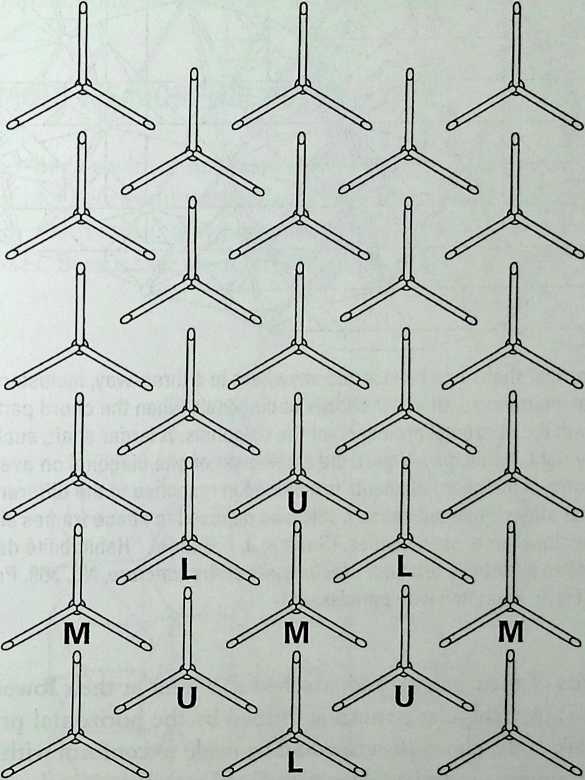
Figure 16.5 Top view of the same configuration as in Figure 16.4, with the chords deleted. Diagonals are shown up to two-thirds of their height and attached to a joint at their lower extremity. Instead of identifying consecutive floors with numbers such as 1,2, and 3,1 prefer to use the letters L, M, and U, referring to lower, median, and upper levels. One sees that the L-M-U sequence is complete and will repeat itself again and again as the structure goes up. The honeycomb pattern formed by the diagonals on every floor can be clearly seen. The triangular pattern resulting from the horizontal projection of the diagonals indicates that vertical shafts could be found anywhere, as long as the chords are not allowed to interfere. Chords can indeed be modified in order to superimpose exactly with the diagonals. As long as the floor joints continue to be connected by a triangular grid, no weakening of the structure will ensue. (Source: J. F. Gabriel, “Three-Dimensional Suburbs,” Proceedings of the IASS World Congress on Space Enclosures, P. Fazio, R Haider, and G. Biron, eds., 1976, pp. 89, Fig. 11. Reprinted with permission of the Centre for Building Studies, Concordia University, Montreal.)
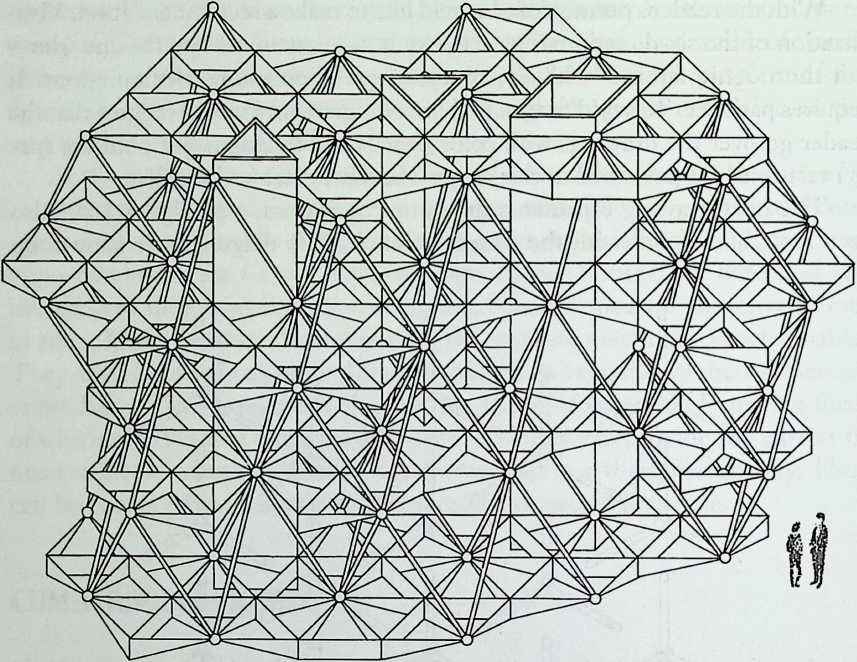
Figure 16.6 Vertical shafts can be inserted anywhere in a three-way, multistory space frame without interfering with either chords or diagonals when the chord pattern is made to conform with the horizontal projection of the diagonals. A larger shaft, such as is shown on the right, would only require the elimination of one diagonal on every third story. The profile of the chord elements is modified in response to the different loading conditions that affect inhabited space frames, as opposed to space frames simply used to cover or enclose large, open spaces. (Source: J. F. Gabriel, “Habitabilite des structures tridimensionelles a Iechelle urbaine,” Techniques et Architecture, No. 309, Paris, 1976, pp. 110, Fig. 6. Reprinted with permission.).
to two-thirds of their height, and attached to a joint at their lower extremity (Figure 16.5). A triangular pattern is formed by the horizontal projection of the diagonals. If the chord pattern could be made to conform with that of the diagonals, triangular wells could be introduced anywhere in a three-way space frame and this without interference from either chord members or diagonals. It so happens that this can be achieved quite easily: Chords -will superimpose precisely with the diagonals when they are rotated 30° in their own plane, which is, of course, the horizontal plane (Figure 16.6).
Triangular shafts obtained from this simple operation measure 2.31 m on the side. A large elevator could fit comfortably in a shaft of this size, and any number of shafts can be created anywhere, either in bundles or scattered throughout the structure. It should be underlined that triangular elevator cabins are more efficient than rectangular cabins, for they fill up and empty faster.
For stairs, larger wells can be made by opening up several triangular shafts onto each other. This requires the elimination of some diagonals, but remaining chords and diagonals will always coincide with the “walls” of the shafts, whether their shape is a triangle, a hexagon, or a parallelogram.
We are interested in lived-in space frames and polyhedra, where loading conditions are quite different from those in single-or double-layer space frames used to cover large, column-free spaces, such as sports arenas or convention centers. Our new floor structure reflects this difference in a new, tapered profile. The floor structure itself is fully triangulated in all directions. Its configuration is of the space frame type, and the elimination of certain portions of it would not compromise its geometric rigidity.
The tapering of the floor structural elements, added to the minor modification performed on the chords, open up a number of architectural and structural possibilities, some of which are described in the following sections.
¶ THE HEXMOD: ITS MORPHOLOGY
This chapter began with a description of the space frame considered as an aggregate of octahedra and tetrahedra. These shapes are also called geometric solids and, for that reason, they are unfortunately perceived not as spaces but as solid masses. Because we are interested in them as voids, it will be useful to
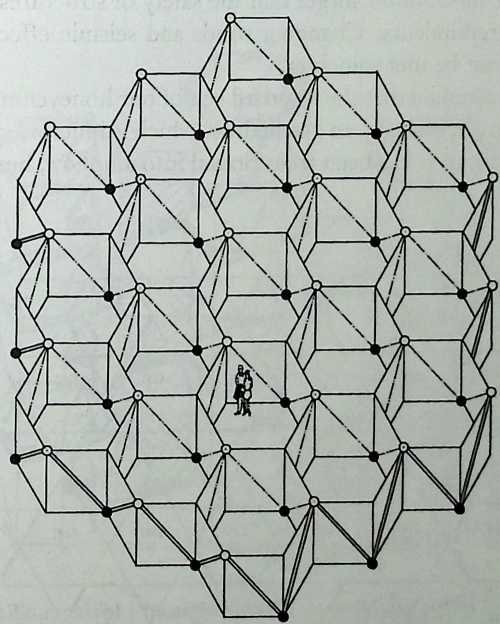
Figure 16.7 Originally, the diagonals represented the edges of octahedra and tetrahedra, but that reading has been replaced by a new one. When vertical planes are placed along the diagonals, a honeycomb pattern is created. Doorways find their place where diagonals meet on an upper joint. Each doorway gives access to two other hexagonal rooms. Because there are three doorways in each room, each room has access to the six rooms that surround it. (Source: J. E Gabriel, "Space Frames: The Space Within-A Guided Tour,” International Journal of Space Structures, Vol. 1, No. 1, 1985, pp. 3, Fig. 3. Reprinted with permission of Elsevier Science Ltd, The Boulevard, Langford Lane, Kidlington 0X5 1GB, UK.)
think of a space frame as an infinite structure of hollow “geometric solids.” I have already dispelled the myth that the spaces within must of necessity be in the shape of either a tetrahedron or an octahedron. This was done by showing that a space frame can form a honeycomb (Figure 16.7).
Now, a honeycomb may satisfy the crudest needs for shelter, but it can hardly be expected that a honeycomb will have the malleability required by the complexity and the variety of our building programs. All the rooms cannot be the same shape and the same size.3
Is it possible to “open up,” as it were, the honeycomb pattern and not lose the structural strength of the space frame, which is one of the main reasons for our interest in them? One of the major differences between the post-and-beam structural system and the three-way space frame is this: Whereas there can only be one vertical column in one place in the former, there are normally three diagonals in the latter. This may be redundant under certain conditions, but it must be remembered that diagonals do more than carry loads; they ensure the rigidity of the structural framework. It is conceptually possible to eliminate in a systematic way some of the diagonals from the framework without compromising its geometric rigidity.
Once again, this chapter is concerned with concepts and speculation, and one should, of course, never forget that the safety of structures depends precisely on their redundancy. Changing winds and seismic effects create load reversals that must be met somehow.
What if we assumed that the standard cell of our honeycomb is a building block? It is, after all, basically an octahedron, which is indeformable. From the antiprism that it was, it has been transformed into a hollow, hexagonal prism.
Figure 16.8 The framework of a hexagonal room can be considered as a building block called a hexmod. Instead of remaining tightly packed, the building blocks are here separated by a distance equal to their width, that is, 4 m. This redistribution lets architectural space flow around freestanding hex-mods. The lower left area of the drawing shows where the eliminated diagonals used to be. The new, open pattern uses only one-half of the original number of diagonals.
However, it is still a geometrically rigid frame. We call it a hexmod because it is a module and it has a hexagonal plan. What if we distributed hexmods on a horizontal base, 4 m apart (which is also their width) and on a repeating pattern of hexagons and triangles? The spatial transformation is radical and can be appreciated by imagining ourselves standing between “building blocks” and looking around: We can see between building blocks and our line of vision is uninterrupted in six directions (Figure 16.8). An axonometric drawing of one story will help us to better understand the relationship between all the elements of the structure. Three joints of the upper floor, out of four, are still supported, but instead of each joint being supported by three diagonals, it is now supported by two. This means that half the diagonals can be eliminated. A hexmod sits on three others, situated on the floor below, and shares one of its three lower joints with each. Likewise, a hexmod shares its three upper joints with three hexmods situated on the floor above, helping to support them (Figure 16.9).
A hexmod consists of six diagonals connecting two very similar hexagonal frames, one forming the floor of the hexmod and the other forming its roof. These frames are called, respectively, the lower cap and the upper cap of the hex-mod, or LC and UC (Figure 16.10).
Figure 16.9 The six diagonals of a hexmod connect three lower joints to three upper joints. In a regular, multilayer space frame, a joint would receive six diagonals, three underneath and three above the joint In the new pattern, a joint receives only two diagonals from above and two from below. For greater visual clarity, the tops of the hexmods are deleted on both upper and lower floors. (Source: J. F. Gabriel and J. Mandel, “A Space Frame Building System for Housing,” Proceedings of the Third International Conference on Space Structures, H. Nooshin, ed., Elsevier, London, 1984, p. 1054, Fig. 5. Reprinted with permission of Chapman and Hall, Cheriton House, North Way, Andover, HANTS, SP10 5BE, UK.)
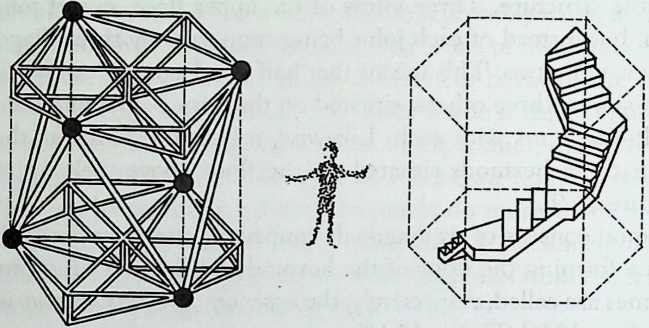
Figure 16.10 A building system based on the hexmod building block requires an inventory of only two components, the hexmod itself and a hexagonal subassembly, called a complementary cap, that is used to connect hexmods with one another. It is called CC, while the upper and lower caps of the hexmod itself are called DC and LC, respectively. The drawing also shows a stairs component. Although not structural, it is an indispensable element of the building system. It fits within a hexmod and does not require the elimination of any diagonals to be functional. (Source: J. F. Gabriel and J. Mandel, “The Application of Lightweight Modular Structures to Housing,” in Housing, the Impact of Economy and Technology, 0. Ural and R. Krapfenbauer, eds., Pergamon Press, 1981, p. 65, Fig. 1.)
Another subassembly contributes to the building system. It is also hexagonal and it is called the complementary cap, or CC. It is an essential component for two reasons. It makes floors continuous by filling the gaps between hex-mods. Its three-dimensional design makes it a geometrically rigid unit and, theoretically at least, this renders a number of diagonals structurally redundant. In the original space frame, six diagonals would have met at the joint that is now at the center of a CC. Because of its geometrically rigid shape, the CC should no longer require support at its center. Presumably, the six diagonals that would have met at the center of the CCthree above and three belowcan be deleted. Spanning, vertical load transfer, and resistance to lateral stresses can all be theoretically handled by hexmods and CCs.
Whereas these two modules constitute the complete inventory of parts, another component must be added to make the building system complete and viable: a stair module. The proposed helicoidal design fits comfortably within a hexmod and can also be used between hexmods. The clear space between handrails is 1 m or even wider.
Returning to Figure 16.8 for a moment, we see that LCs and UCs form two out of three hexagons of the floor structure, on this and any other story.
The hexagons marked CC, for complementary cap, complete the pattern of hexagons of the floor structure. Each CC is connected with six caps by its corners; three of them are UCs and the others are LCs. This relationship can also be seen in Figure 16.13.
To finish our description of the spatial relationships that exist between hexmods and between hexmods and CCs, one more remark will be useful: In a vertical sequence, a hexmod is always found on an intermediate floor, between two superimposed CCs (Figure 16.11). The next drawing shows the structural connection between subassemblies: Six diagonals carrying a CC belong to three distinct hexmods. Likewise, six diagonals belonging to another set of three hexmods carry the hexmod directly above a CC (Figure 16.12).
The trade-off caused by the eventual elimination of half of the diagonals would be total structural interdependency between the hexmod and CC com-
Figure 16.11 Hexmods and CCs always alternate in a vertical sequence of several stories. The joint at the center of the CC is not connected with diagonals, as it would be in the original space frame. (Source: J. F. Gabriel and J. Mandel, “The Application of Lightweight Modular Structures to Housing,” in Housing, the Impact of Economy and Technology, 0. Ural and R. Krapfenbauer, eds., Perg- amon Press, 1981, pp. 64, Fig. 2© J. F. Gabriel and J. Mandel.).
Figure 16.12 This figure shows the same relationship as Figure 16.11 does, but here all the diagonals are shown. A hexmod is carried by three hexmods underneath. Vertical planes placed against the diagonals make the location of these hexmods explicit A CC is also carried by three hexmods.
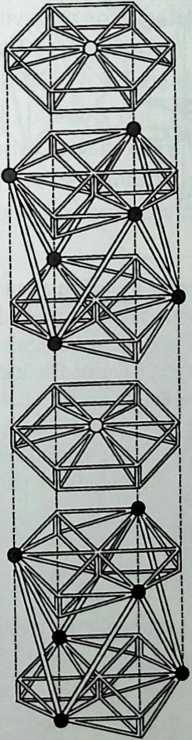
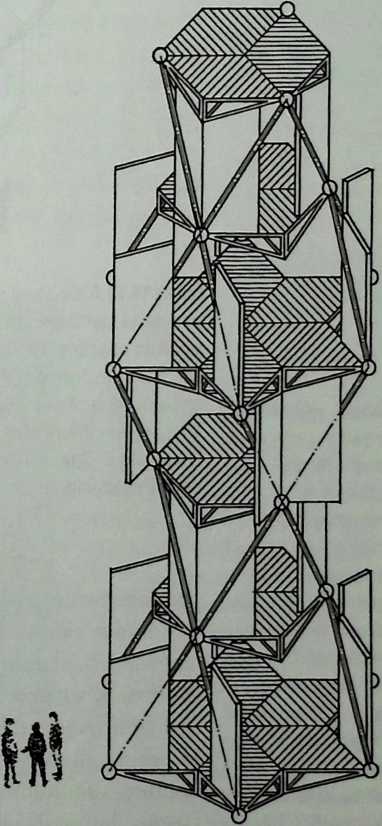
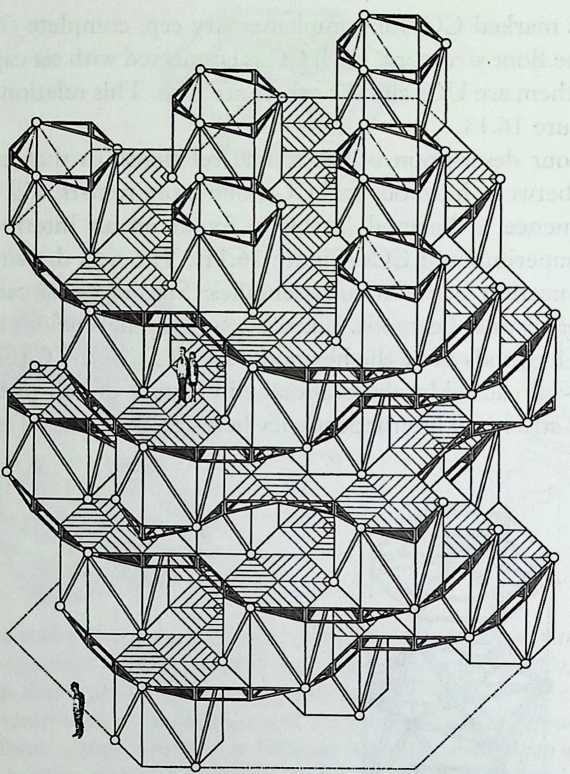
Figure 16.13 A six-story structure may be too ambitious for a building system that relies on structural members, presumably made of steel, the cross sections of which should be as small as possible. The intent of this drawing is merely to confirm the three-dimensional relationships described in the text Although not representing a finished building, the drawing gives an idea of how such a building might appear. Except for the six hexmods on the upper floor, all the others play a structural part in a configuration like this. (Source: J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 7. Reprinted with permission.)
ponents. Structural interdependency exists to a point in any building technology, and it cannot be regarded as a serious hindrance to design. As with any language, be it verbal or visual, the discipline of a syntax is only an obstacle to expression when it is not mastered. Without a language, complete with rules and limitations, nothing can be expressed, nothing can be communicated. However, there is no single building technology capable of satisfying all the building requirements of our time. Like all systems, the hexmod has its limitations, but it also has its special merits (Figure 16.13).
If I described in some detail the interrelationships of all the components, it is because they are essential to an understanding of the structural concept as a whole and to an overview of the architectural horizons it opens. A good part of the rest of this chapter will discuss formal variations on the same theme. We will see designs that the hexmod system cannot handle alone but which can be built with other combinations of the same parts.
THE HEXMOD: A BUILDING SYSTEM
My fascination with space frames stems in part from the multiplicity of stable configurations that can be obtained from the six-directional space lattice. For this reason, it would be of questionable interest to choose a space frame as the matrix for a low, ground-hugging building. On the other hand, fire safety imposes limitations on the height of a structure relying on thin structural members. Hexmods are adequate for buildings three or four stories high.4
It is obvious that stairs are vital in walk-up buildings. The hexmod system can accept a great number of different stair designs. One approach is to confine stairs to an enclosed vertical shaft, and certain building codes do indeed require such a solution for emergencies. This conventional design can be accommodated within a hexmod framework because, as we have seen, vertical shafts of varied size and shape can be inserted anywhere (Figure 16.6).
Instead of being confined into a sort of rigid, vertical “tube,” the stair modules could overlap and, in doing so, engage the user in a spatial experience that calls to mind Le Corbusier’s architectural promenade. Perhaps this point should be elaborated. It is true that the shortest distance between two points is a straight line, but it is not necessarily true that a straight path will always feel shorter. A boring walk will seem longer to the user, or at least to the user who is aware of his/her environment, whereas an interesting or pleasant walk will seem shorter. An architect must know how to make the distinction. By
Figure 16.14 In a three-way, multilayer space frame, octahedra overlap by one-third, as do the bee cells of a honeycomb. A modular stair, 1 m wide, can fit in a hex-mod (see Figure 16.10). Hexmods containing stairs must be rotated by 120° when they are superimposed, in order to achieve these objectives: No diagonals need be removed to create headroom in the stairs. Landings will consist of two-thirds of the floor of a hexmod. Two doorways on every landing will give access to the rest of the floor. The configuration of hexmods will approximate a helix, completing a revolution in three stories. (Source: J. F. Gabriel, La Poutre-etoile,” Techniques et Architecture, No. 320, Paris, 1978, pp. 70. Reprinted with permission. J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 22. Reprinted with permission.)
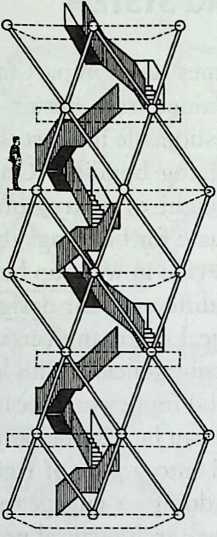
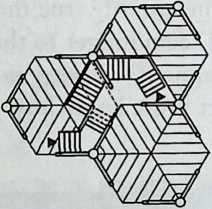Figure 16.15 Plan and elevation of the configuration shown in Figure 16.14. (Source: J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 20. Reprinted with permission.)
engaging users in the stories through which they travel, stairs can enhance the quality of life in certain types of buildings.
Interesting designs like these can make use of modular stairs that actually fit within hexmods (Figure 16.10). These can even be inserted in a “saturated” space frame, which is one from which no diagonal has been deleted (Figures 16.14 and 16.15). The same helicoidal module can be oriented in one of three directions. If the modules were rotated 120° from floor to floor, they would generate a helicoidal path that would repeat every three stories. Another pattern can be obtained from assembling the same stair modules in a straight line parallel to one set of diagonals (Figure 16.16).
For the helicoidal module to fit inside a hexmod, the width of the stairs can barely exceed 1 m. Domestic programs do not normally require wider stairs than that. Wherever wider stairs are needed, however, they too can be accommodated within the hexmod system. Of course, more space must be cleared for them. Stairs as wide as 2 m, or even 4 mthe equivalent of a hex-mod’s widthshould satisfy the circulation requirements of any building (Figure 16.17). The drawings actually suggest several design solutions for varying widths, all of them fitting in a vertical shaft 2 or 4 m wide.
This brief survey of possible stair designs is not exhaustive, and the hex-
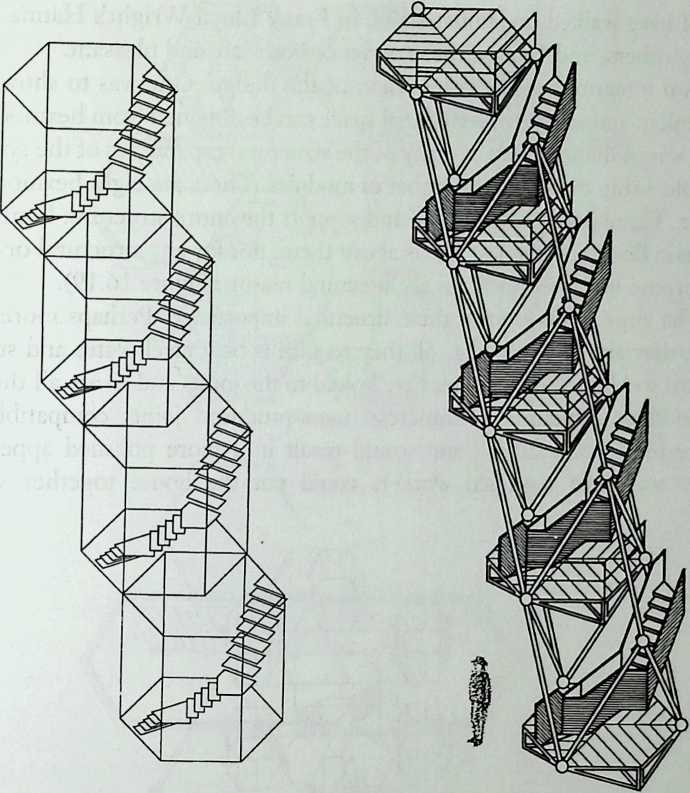Figure 16.16 Instead of being rotated on every floor, the orientation of the stairs can remain constant Instead of a helix, the new pattern will move in the direction of one set of diagonals. (Source: J. E Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 19. Reprinted with permission.)
mod system can accept many others. Indeed, this structural framework is not restrictive at all.
To illustrate the architectural possibilities of the hexmod building system, I would like to present a design for a small building: a two-bedroom residence (Figure 16.18). The main rooms are all on the second level. A central living space with openings in three directions is extended by two outdoor decks. The kitchen and dining zone is at one end of the living space, the sitting area at the other end. There is a private study and, opposite to it, the two bedrooms, sharing a bathroom. The study and the bedrooms, which are in greater need of privacy, occupy three of the hexmods on the main floor. The fourth hex-mod houses the stairs. As for the single hexmod on the roof, it does nothing more than enhance the dynamics of the space. Its lower cap has been removed, and the opening in the plane of the roof stretches the verticality of the enclosed space for the viewer. As one prepares to ascend the stairs and looks up, one is silently invited to move upwards.
Entering the house is done under the shelter of the main floor, which is cantilevered. One end of the hall can be closed off to serve as a utility room, a workshop, a garden room, a powder room, or storage. Access to the main floor is gained by a stair of a design we have not yet seen. The steps form a 30° angle with the stringers, to be consistent with the hexagonal/triangular
plan. I have walked on similar stairs, in Frank Lloyd Wright’s Hanna House among others, and I found the experience both safe and pleasant.
Two intentions were at the origin of the design. One was to show that a convenient and attractive residential space can be obtained from hexmods. The other was to demonstrate as many of the structural capabilities of the system as possible, using the smallest number of modules. There are eight hexmods altogether. Three rest on the ground and support the entire structure. Four are on the main floor, and the last one is above them, not for any structural or practical purpose but for a poetic or architectural reason (Figure 16.19).
The large joints express their structural importance. Perhaps more to the point, they are easy to make. All they require is bent steel plates and straightforward welding. The diagonals are bolted to the joints and so are all the struts of the floor structure. Commercial mass-produced joints compatible with square tubes are available and would result in a more polished appearance. Either way, two unskilled workers could put the house together without
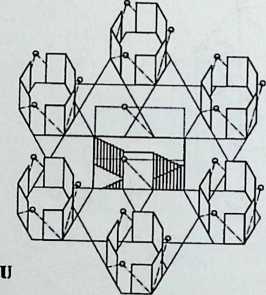
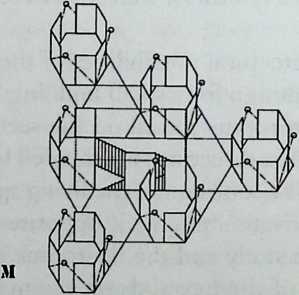
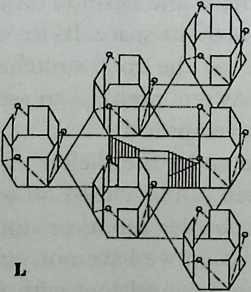
Figure 16.17 Although they demand much more space, stairs up to 4 m in width only require the deletion of a few diagonals on every floor. Nowhere must a complete hexmod be removed to accommodate the stairs. (Source: J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 23. Reprinted with permission.).
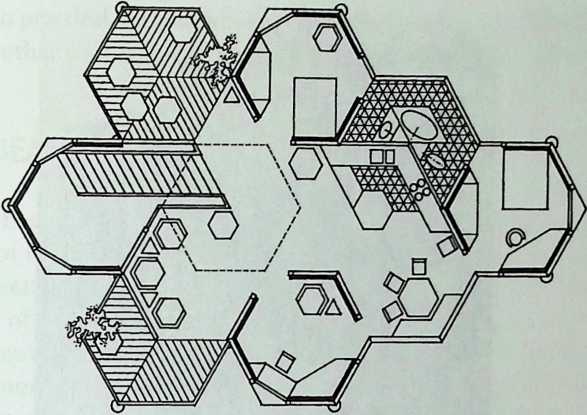
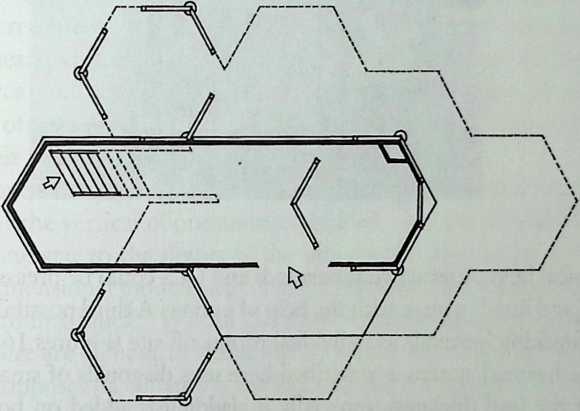
Figure 16.18 Plans of the ground level and of the main floor of a two-bedroom house. Three hex-mods are in contact with the ground and carry the entire structure. (Source: J. F. Gabriel and J. A. Mandel, “A Space Frame Building System for Housing,” Proceedings of the Third International Conference on Space Structures, H. Nooshin, ed., Elsevier, London, 1984, p. 1052, Fig. 8. Reprinted with permission of Chapman and Hall, Cheriton House, North Way, Andover, HANTS, AP10 5BE, UK.)
Figure 16.19 Scale model of the house shown in Figure 16.18. Only the hex-mods are shown with enclosures.
Figure 16.20 Quarter-scale model of several hexmods. Partial view. (Source: J. F. Gabriel and J. A. Mandel, “A Space Frame Building System for Housing,” Proceedings of the Third International Conference on Space Structures, H. Nooshin, ed., Elsevier, London, 1984, p. 1057, Fig. 11. Reprinted with permission of Chapman and Hall, Cheriton House, North Way, Andover, HANTS, AP10 5BE, UK.)
mechanical help. Alternatively, hexmods and CCs could be preassembled on the ground and lifted in place with the help of a crane. A third possibility would consist of finishing hexmods as individual rooms off site (Figures 16.20 and 16.21).
The hexmod system as described here uses diagonals of small cross section to limit the wall thickness, especially if cladding is added on both sides of the diagonals, interior and exterior. This restriction to the size of diagonals makes the
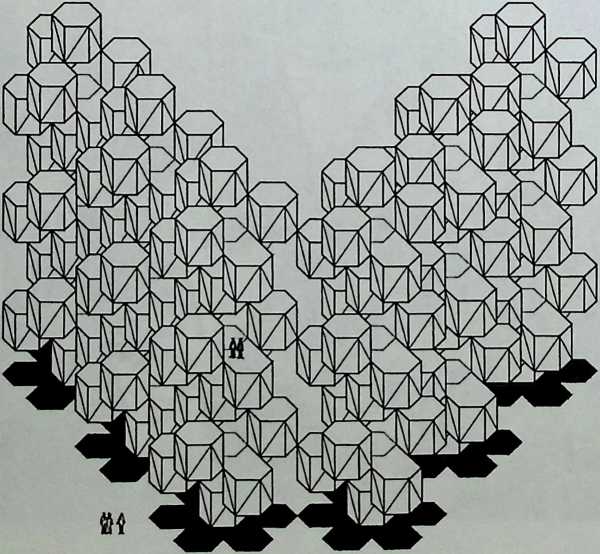
Figure 16.21 Simplified drawing of a large assemblage of hexmods. Most CCs are deleted to show the points of contact between hexmods. This is only a diagram, not a realistic design. A building of this size would have to rely on a complementary structural framework.
hexmod system practical only for buildings of limited height We will see later on that there are other ways to use its space-making potential in very tall buildings.
THE star beam
Although the hexmod building system makes possible the conception and the construction of many building forms, it has limitations. All building systems do. We could retain the same floor structure, with all its advantages, and select a different set of diagonals between floors. The building blocks could be dispensed with but would the structural framework remain stable? Could we create different, more open architectural spaces? Might these possibly lend themselves to architectural programs that hexmods could not accommodate?
In a hexmod framework, the floor structure is made of hexagonal subassemblies interconnected by their comers. The triangles formed in the intervals between hexagons can give each CC, UC, or LC the shape of a six-pointed star (Figures 16.8 and 16.9). We could describe the floor structure as entirely made of star shapes centered on CCs and connected laterally to one another by their points.
Consider one of these stars and the corresponding one on the floor above. They are not at the vertical of one another. Indeed, they are shifted. Connect the points of one star to the points of the other with diagonals and you will have a three-dimensional module, a geometrically rigid configuration that will be our new “building block.” We call this a star module because of the shape of the chords. There are eight faces altogether to what amounts to a convex polyhedron. What opposes its collapse is the fact that the ten diagonals form eight triangular frames situated in four different planes (Figure 16.22).
The star module is interesting in spatial terms. The diagonals divide themselves into two groups of five, symmetrically distributed on either side of the long axis. They frame a single space between them, 8 m wide. This space
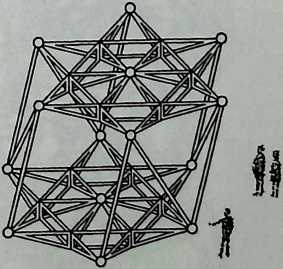
Figure 16.22 A star is a CC extended by six triangles. The star module consists of two star shapes located on consecutive floors and connected to each other. Ten diagonals connect the points of one star to the points of the other. The triangular frames formed by the diagonals and the different planes in which these triangles are found add up to an inde-formable configuration. (Source: J. F. Gabriel and J. A. Mandel, “The Star Beam,” in Shell and Spatial Structures Engineering, F.L.LB. Carneiro, A. J. Ferrante, R. C. Batista, and R.
L. Palanco, eds., Pentech Press, London, 1984, p. 14, Fig. 2.)
can be entered from both ends through rectangular bays that measure 4 m across. The space within then widens from 4 m at one end, to 8 m in the middle, and narrows down again to 4 m at the other end.
Let us see how this module combines with others, first vertically, then horizontally, then in all directions. It is a directional shape, in the sense that the stars that form its floor and its roof are shifted in the direction of the six diagonals that are parallel to one another. Matching points of the two stars are found at the top and at the bottom of a diagonal. Because there are three sets of diagonals, each leaning in a different direction, star modules can be rotated 120° one at a time, as they are piled up on top of one another. The result is an elegant configuration approximating a helicoid and as close to the vertical as can be obtained from star modules (Figure 16.23).
A major difference between the hexmod system and the star system is this: Hexmods enclose portions of space and they mold the spaces between them into other shapes. The star module creates only one space. It is a “space filler” by itself, meaning that it can organize all space without gaps or overlaps. Therefore, minimal towers like the one just described can be juxtaposed to
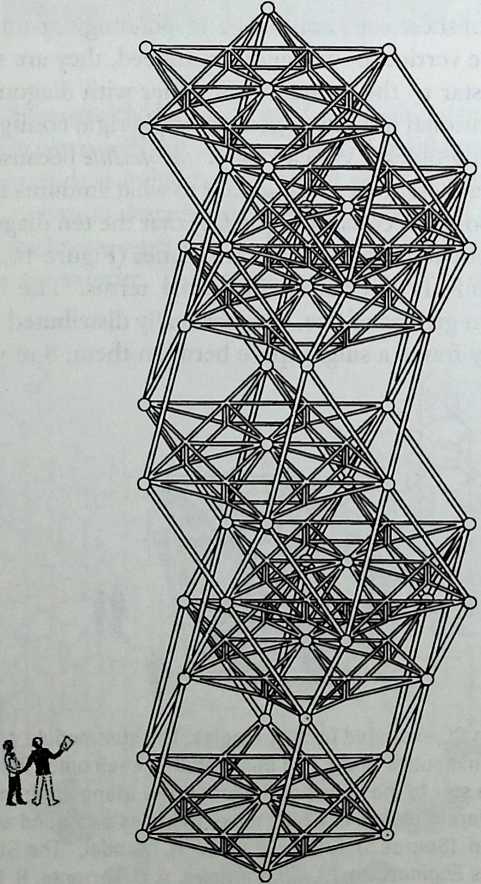
Figure 16.23 This minimal tower is made of star modules, each one rotated by 120° in relation to the one immediately below. Because the imaginary line connecting the centers of the stars is parallel to one set of diagonals, there are only three orientations possible for a star module. Consequently, the fourth module has the same orientation as the first one and the two share precisely the same vertical projection. (Source: J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 6. Reprinted with permission.).
one another, as many times and in any direction as desired, if what the designer wants is a structural matrix approaching the vertical. The following configurations that are derived from the star module are mostly space fillers (an unfortunate term, because the modules organize space but do not fill it).
Superimposing star modules without changing their orientation results in leaning towers, or pods. This suggests that they should, perhaps, lean against one another and form pyramidal/tetrahedral constructions (Figures 16.24 and 16.33).
There are several possible ways to assemble star modules horizontally. The most obvious is to line up their larger openings in order to form a throzigh-truss (Figures 16.25 and 16.26). The space within is entered at one end through a 4-m-wide bay, then the space swells to 8 m, to return to 4 m, and so on, until the user reaches the other end and leaves through a last 4-m-wide bay.
As with hexmods, space is defined laterally by vertical planes applied against the diagonals. And, as in hexmods, natural passageways are also found wherever two diagonals form an A by meeting overhead. Needless to say, windows could be installed where doors are not wanted (Figures 16.27 and 16.28).
We have seen that star modules can be superimposed in two different
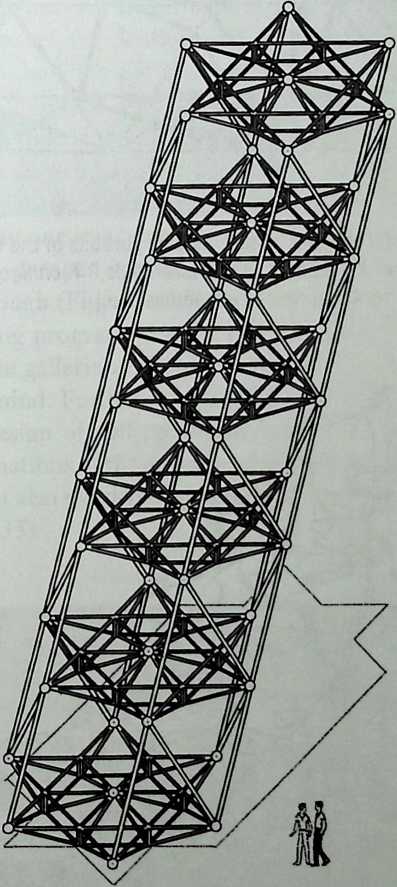
Figure 16.24 Here, the star modules all face the same direction. They are superimposed to form a rectilinear tower that leans at an angle of 54° 6, which is the angle formed between a diagonal and the ground. (Source: J. F. Gabriel, “Space Frames: The Space WithinA Guided Tour," International Journal of Space Structures, Vol. 1, No. 1,1985, p. 9, Fig. 10. Reprinted with permission of Elsevier Science Ltd, The Boulevard, Langford Lane, Kidlington 0X5 1GB, UK.)
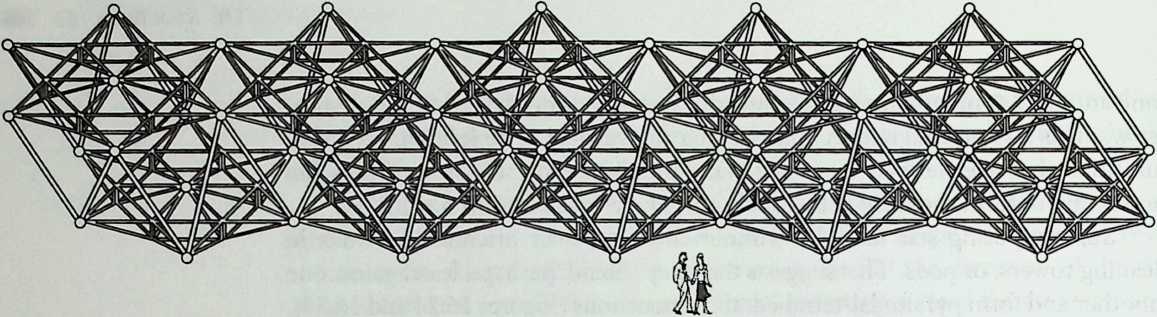
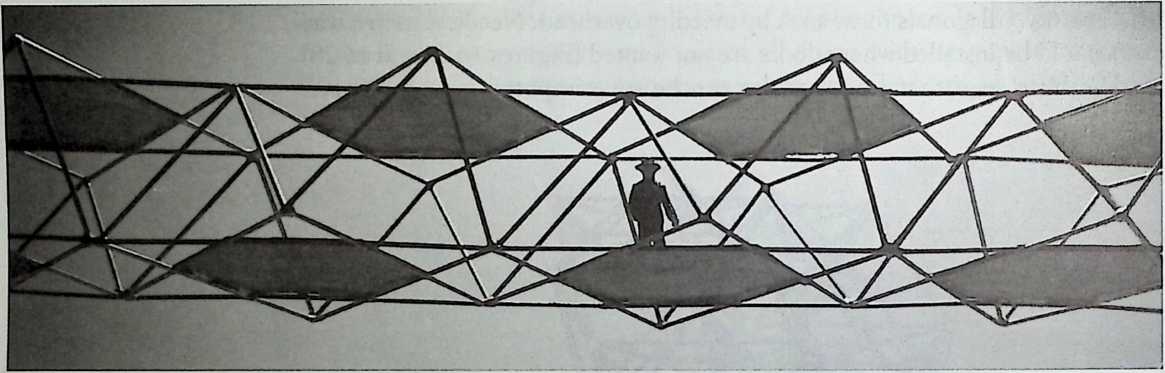Figure 16.27 This figure shows the space within a five-unit star beam. The roof has been deleted, but the stars are clearly visible on the floor. Vertical cladding coincides with diagonals and lateral openings are found where diagonals form A-frames. Depending on the location of a star beam within a larger structural context, these openings would frame doors or windows. The floor structure has been expanded laterally. Otherwise, this structure is identical to that shown in Figure 16.25. (Source: J. F. Gabriel, “La Poutre-Etoile," Techniques et Architecture, No. 320, Paris, 1978, p. 70, Fig.
Figure 16.25 The star beam is, in fact, a hollow, or “through," truss. The width of the open space within alternates between 4 and 8 m. There are five star modules here, connected in such a way that their large openings coincide. This configuration is geometrically rigid (Source: J. F. Gabriel, “From Space Lattice to Architecture,” Bulletin of the International Association for Shell and Spatial Structures, Vol. 20, No. 2,1979, pp. 19, Fig. 12. Reprinted with permission.)
Figure 16.26 Schematic model of a star beam. The only portions of the floor planes to be shown are the CCs. (Source: J. F. Gabriel, “La Poutre-Etoile," Techniques et Architecture, No. 320, Paris, 1978, p. 70, Fig. 4. Reprinted with permission.)
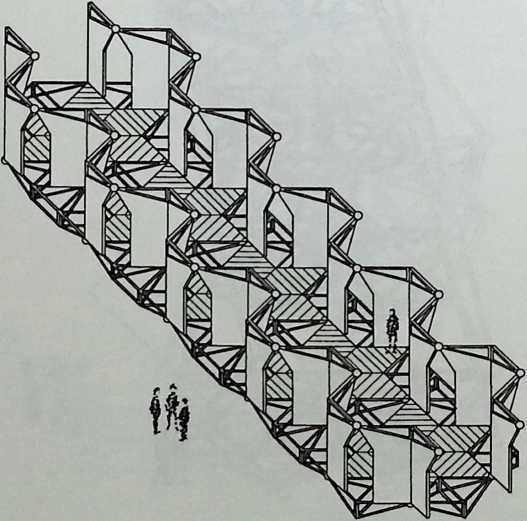3. Reprinted with permission.)
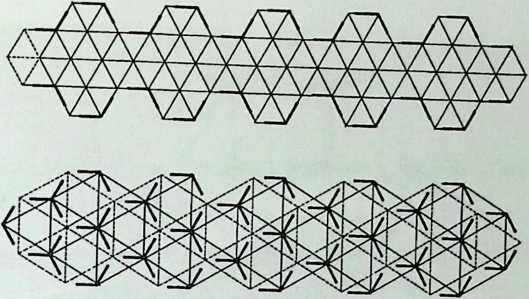
Figure 16.28 Top: Simplified plan of a five-unit star beam. Diagonals and chords coincide, as described in the first part of the chapter. Bottom: A similar configuration based on the conventional three-way space frame. Chords and diagonals do not coincide. (Source: J. F. Gabriel and J. A. Mandel, “The Star Beam,” in Shell and Spatial Structures Engineering, F. L. L. B. Carneiro, A. J. Ferrante, R. C. Batista, and R. Palanco, eds., Pentech Press, London, 1984, p. 16, Fig. 4.)
ways: They can be joined horizontally to form through-trusses, and they can also be juxtaposed laterally to partition all space. In all these formal arrangements, interior spaces are identical, and one might think that the only difference between one building and another would come from their overall shape. This impression would be true if the spanning capabilities of the star beam were overlooked. Indeed, combinations of star modules are endless and so is the variety of spaces generated by these combinations. There is an especially interesting one because it is simplicity itself, and I find the yield spectacular. It consists of using one star beam to cover the space between two others. This results in 8-m-wide open spaces, alternating with 12-m-wide spaces as one walks in and through (Figures 16.29 to 16.32).
Many building programs require galleries lined up with rooms wider or narrower than the galleries. Schools, museums, shopping centers, offices, and hotels come to mind. Furthermore, applications of star modules need not be limited to the design of stiff rectilinear buildings. Hexagonal and Y-shaped plans and combinations of these can be made (Figures 16.33 and 16.34). Finally, star beams can also overlap in such a way as to form large pyramidal structures (Figure 16.35).
Figure 16.29 The width of the space within a star beam varies from 4 to 8 m. When a star beam is used to span the interval between two more star beams, the width of the space between these reaches 12 m, with a minimum of 8 m at its narrowest.
Figure 16.30 The purpose of this diagram is to show how star beams can create wider spaces than the spaces they contain. (Source: J. F. Gabriel and J. A. Mandel, “The Star Beam,” in Shell and Spatial Structures Engineering, F. L. L B. Carneiro, A. J. Ferrante, R.
C. Batista, and R. L. Palanco, eds., Pentech Press, London, 1984, p. 18, Fig. 7.)
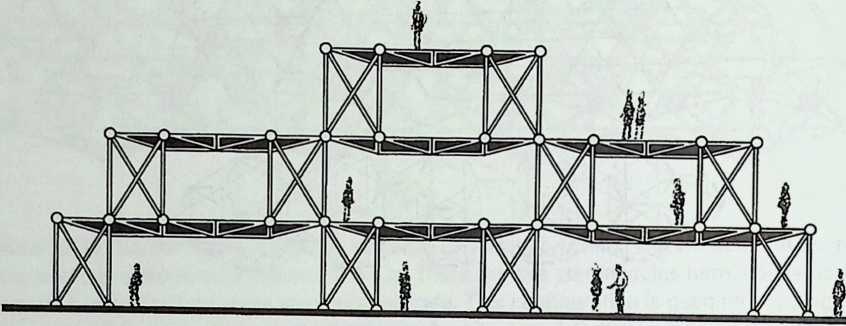
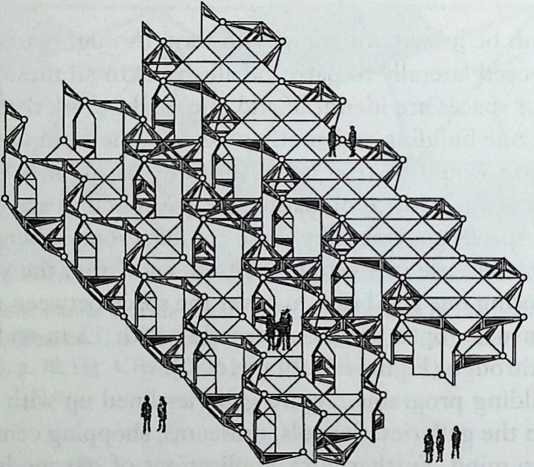
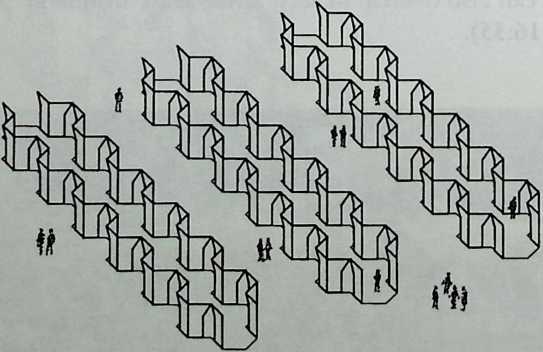
Figure 16.31 Detail of the configuration shown in Figure 16.29. The roof of the lower star beam is deleted so that the space within can be seen. (Source: J. F. Gabriel and J. A. Mandel, “The Star Beam,” in Shell and Spatial Structures Engineering, F. L. L. B. Carneiro, A. J. Ferrante, R. C. Batista, and R. L. Palanco, eds., Pentech Press, London, 1984, p. 20, Fig. 11.)
Figure 16.32 If star beams are used to cover the interval between other star beams, this is how the spaces on the lower level will be, within the star beams and between them. (Source: J. E Gabriel and J. A. Mandel, “The Star Beam,” in Shell and Spatial Structures Engineering, F. L. L. B. Carneiro, A. J. Ferrante, R. C. Batista, and R. L Palanco, eds., Pentech Press, London, 1984, p. 19, Fig. 9.)
Figure 16.33 Schematic model of a star beam supported by a leaning tower of the type shown in Figure 16.24. It is worth observing that the space molded by the star beam is not interrupted, or even modified, by the presence of the tower. It continues right through it, totally unaffected in its shape. (Source: J. F. Gabriel, “La Poutre-Etoile,” Techniques et Architecture, No. 320, Paris, 1978, p. 70, Fig. 5. Reprinted with permission.)
Figure 16.34 Although essentially rectilinear, star beams can generate rich and varied building forms, as this diagram shows. The dotted line indicates the outline of the floor above. (Source: J. F. Gabriel and J. A. Mandel, “The Star Beam,” in Shell and Spatial Structures Engineering, F. L. L. B. Carneiro, A. J. Ferrante, R. C. Batista, and R. L Palanco, eds., Pentech Press, London, 1984, p. 21, Fig. 12.)
Figure 16.35 Another relationship between star beams, where one of them would cover most of the one immediately below. Although there is little difference in structural continuity between this configuration and the one shown in Figure 16.31, the architectural results are fundamentally dissimilar. This drawing does not represent a finished building; it only shows different construction stages of a building. (Source: J. F. Gabriel, “From Space Lattice to Architecture,” Bulletin of the International Association for Shell and Spatial Structures, Vol. 20, No. 2,1979, p. 23, Fig. 14.)
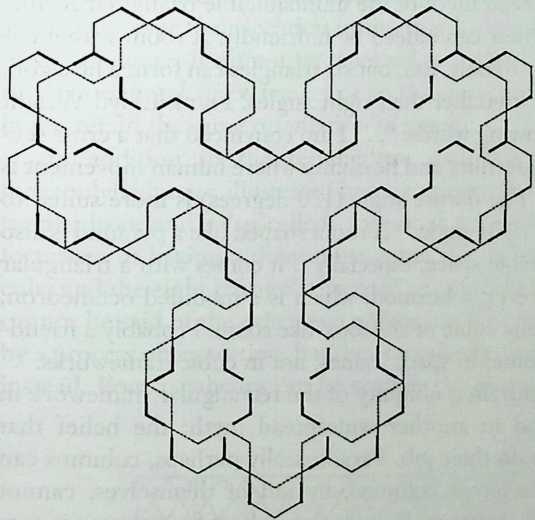
SPACE TRUSSES AND MEGAPOLYHEDRA
Should space frames also be used for very tall buildings? Yes, of course, for the taller the building, the more critical the stresses. A triangulated structure is not necessary for small buildings such as houses, where stresses are minimal. Square frames will do. However, when in 1889 Gustave Eiffel conceived and built “la tour de 300 metres,” he designed a triangulated structure. So did the engineer Fazlur Khan in 1967 for the John Hancock Tower in Chicago, which, at the time, was the tallest building in the world. And so did I. M. Pei and Partners at the Bank of China building in Hong Kong more recently.5
It is malicious to say that architects dream up a building form and turn to a structural engineer to do whatever is necessary to make it stand up. This is a caricature of the architect. It is also a myth to give credit to engineers for always thinking rationally. However, why is it that so many architects and engineers conceive tall structures as aggregates of cubes? A cubic frame is not a sound structural unit until cross-bracing is added to it, as an afterthought. And a cubic volume does not necessarily make a good room. Would it not make more sense to approach the design of tall buildings from a structural frame with integrated triangulation in mind? One suspects that reluctance to do so is based on the widespread myth of the uninhabitable triangular form.
Buildings with sharp comers can indeed be unfriendly. A room with a triangular plan is likely to be unfriendly, too, but six triangles can form a hexagon, with 120° angles, which are friendlier than right angles. Frank Lloyd Wright remarked on that in the following words: “…I am convinced that a cross section of honeycomb has more fertility and flexibility where human movement is concerned than the square. The obtuse angle (120 degrees) is more suited to human “to and fro” than the right angle.”6 A room shaped Eke a pyramid is also likely to make an uncomfortable space, especially if it comes with a triangular base, as tetrahedra do. However, a hexmod, which is a modified octahedron, makes as friendly a room as any cubic or shoebox-like room. Probably a friendlier one. And hexmods are found in space frames, not in cubic frameworks.
Another reason for the puzzling ubiquity of the rectangular framework in tall buildings may be found in another widespread myth: the belief that columns must be vertical to do their job. Paradoxically perhaps, columns can be replaced by diagonals, whereas columns, in and of themselves, cannot ensure the wind-bracing of a structure. Even at the scale of furniture, it is easy to see that four sticks under a board do not make a table, unless the connections are made rigid. However, rigid connections have their price, which is excess material and inelegant structural workings.
What, then, if we conceived very large space frames? What sort of buildings would we be able to create? Would they be beautiful, practical, and lasting? Would they possibly have a potential not found in conventional buildings? Might they open up possibilities we do not dare to dream of because we do not know we have the means to realize them?7
The concept of gigantic space frames is not new. Louis Kahn (with Anne Tyng), Buckminster Fuller, Yona Friedman, and Peter Cook are among the best known to have explored the idea.8 What is new here is the systematic use °f a 4-m octahedron as a conceptual building block containing enough space for a small room. Eight such octahedra, joined in a straight line to one another by a shared edgehere a strutconstitute our next module, which we will call the space truss. Tetrahedral shapes fit in the interstices between the octahedra and make the space truss rigid. Each one of our modular space trusses, 32 m long, comprises eight octahedra and 14 tetrahedra. Why eight octahedra? Because this is the number of 4-m octahedra that will make possible the erection of regular megapolyhedra with a standard space truss. It is also the largest preassembled module that can be moved to a construction site and raised without too much difficulty. Finally, shorter space trusses would be redundant and cumbersome (Figures 16.36 and 16.40).
The terms space truss and space frame are often given the same meaning. As there is no consensus among architects, engineers, morphologists, and historians, I hope the reader will bear with me and, for now, understand them in the sense I have intended them.
Eight-story octahedra and tetrahedra can be erected with the modular space truss, which is to say that mega-space frames can be erected with it. Whatever the orientation of a space truss in spaceand six of them are possible as well as necessarythe orientation of all the 4-m octahedra remains the same, wherever their location in the structure. Although this is generally true in space frames, it cannot be repeated too often. Whether they belong to the three horizontal space trusses or to the three oblique ones, all the 4-m octahedra retain the same orientation in space.
In addition to the tetrahedron and the octahedron, three possible megapolyhedra are illustrated here: a cuboctahedron, a (so-called) truncated tetrahedron, and a (so-called) truncated octahedron. The cuboctahedron is fortunate in having a descriptive name, for it has the four square faces of a cube and the eight triangular faces of an octahedron (Figure 16.37). The same cannot be said of the other two polyhedra. They could, it is true, be obtained by a process of truncation, but they can also be the result of an additive process instead. Four octahedra can be seen in the drawing as entering into the for-
Figure 16.36 Top view, elevation, and side view of a space truss. Eight 4-m octahedra are joined together edge to edge. Interstitial spaces are filled by tetrahedra. (Source: J. F. Gabriel, “Multi-Layer Space Frames and Architecture,” Proceedings of the International Conference on Lightweight Structures in Architecture, Sydney, 1986, V. Sedlak, ed., Vol. 1, 1986, pp. 104, Fig. 2. Reprinted with permission).
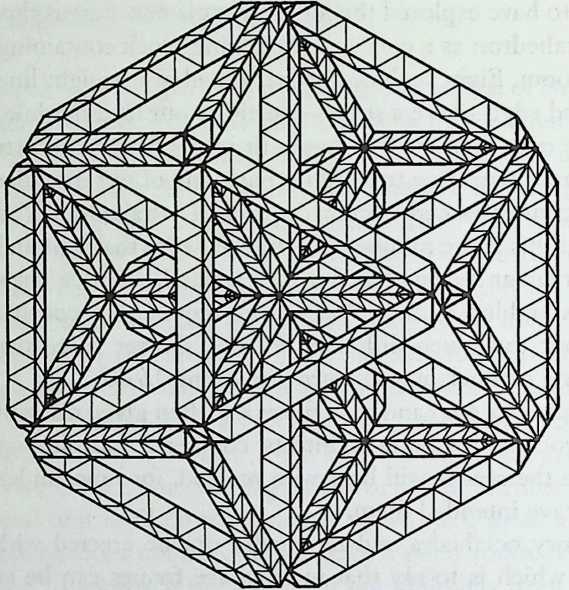
Figure 16.37 Top view of a cuboctahedron made of 36 interconnected space trusses. Six horizontal and six oblique space trusses meet at the center, which can be clearly seen. This is a 19-story structure. In addition to the 16 stories corresponding to two superimposed sets of oblique space trusses, there are three sets of horizontal space trusses, each a story high. In this and the following drawings, the physical connections between space trusses are not shown in their entirety. They would only obscure the picture. The shape of the connections is worth describing, even if it is difficult to describe clearly. In the case of 12 converging space trusses, a gap appears, the shape of which is a stellated octahedron, or Stella octangula. Each space truss is in contact with four others, but none can touch the space truss opposite. Converging space trusses generate an additional octahedron between them, each space truss contributing one of the 12 edges. Eight tetrahedra fill the interstices between the butts of the space trusses and the additional octahedron. (Source: J. F. Gabriel, “Megapolyhedra,” Proceedings of the IASS Symposium on Spatial Structures at the Turn of the Millennium, Copenhagen, 1991, T. Wester, S. J. Medwadowski, and I. Mogensen, eds., 1991, pp. 35, Fig. 7A.)
mation of the truncated tetrahedron. They are nestled among seven tetrahedra (Figure 16.38).
As for the truncated octahedron, it includes half-octahedra in addition to complete octahedra and tetrahedra. The cuboctahedron has eight tetrahedra but comprises no complete octahedra, only six halves (Figure 16.39).
The cuboctahedron shown here has 19 stories; the truncated tetrahedron also. The truncated octahedron would have 28 stories. Included in this count are the stories contributed by the horizontal space trusses.
I am not recommending that buildings should adopt the shape of these megapolyhedra. I am showing them in the hope that they might open up new horizons in architecture and urban design. We are accustomed to buildings sitting squarely on the ground. We also expect buildings to fill up the totality of the space occupied by their structure. I am suggesting that, if we take advantage of the most efficient structural configuration available to us, which
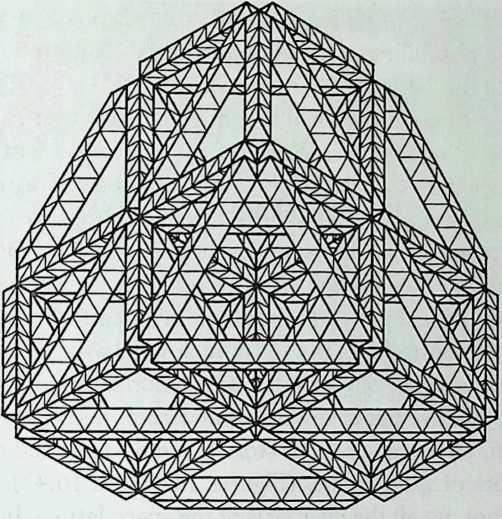Figure 16.38 Top view of a truncated tetrahedron obtained by the aggregation of fourmegaoctahedra and seven megatetrahedra.This also is a 19-story structure. (Source: J. F. Gabriel, “Megapolyhedra,” Proceedings of the IASS Symposium on Spatial Structures at the Turn of the Millennium, Copenhagen, 1991, T. Wester, S. J. Medwadowski, and I. Mogensen, eds., 1991, pp. 35, Fig. 8.)
is that of the space frame, we could conceive structural frameworks at the urban scale rather than at the scale of individual buildings, and buildings could be hovering over the ground where necessary.
I would like to point out that our three polyhedra can be combined to form varied infinite structures. One pattern can be formed by using them all. Another pattern can be obtained from the exclusive use of truncated octahedra, and a third pattern is possible with octahedra and cuboctahedra. This is in addition to the octahedron-tetrahedron pattern. These infinite structures are compatible with one another and, naturally, with the underlying six-directional space lattice that originated them all. If I add that large open spaces can alternate with enclosed spaces without a breakdown in geometric continuity, it becomes clear
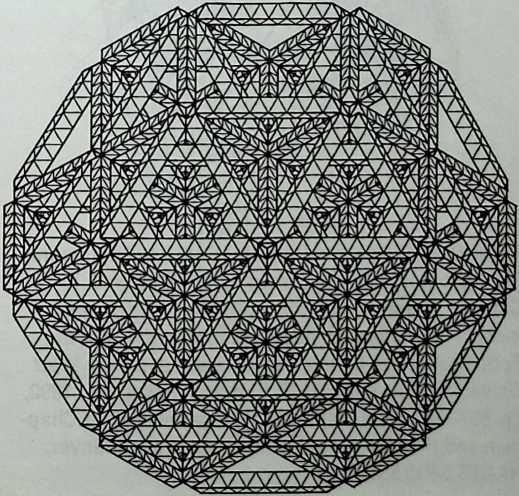Figure 16.39 Top view of a truncated octahedron. Four of the eight hexagonal faces and three of the six square faces can be recognized. This structure has 28 stories. Three sets of oblique space trusses correspond to 24 stories and four sets of horizontal space trusses correspond to four stories. (Source: J. F. Gabriel, “Megapolyhedra,’ Proceedings of the IASS Symposium on Spatial Structures at the Turn of the Millennium, Copenhagen, 1991, T. Wester, S. J. Medwadowski, and I. Mogensen, eds., 1991, pp. 35, Fig. 9.)
that we have a mind-boggling number of design options at our disposal for a truly spatial urbanism. All these possibilities depend on the prefabrication of a noncombustible space truss that can be securely attached to others.9
So far, so good. We have a three-dimensional urban framework that can accommodate buildings. The next question is: What sort of buildings? Consider one of the simplest forms within the urban space frame: an octahedron. It is an eight-story space defined by space trusses (Figure 16.40). What structural system should be used to organize that space in architectural terms? Obviously, the answer is a system based on the same geometry as the space trusses; more precisely, a six-directional network of thin members attached to the space trusses. This network reintroduces the hexmod system with a fanfare: The thin members, stretched from one space truss to another, can now work more efficiently because they are put in tension. The structural capabilities of the hexmod system, limited to three or four stories, can be extended to eight stories within a framework of space trusses (Figures 16.41 and 16.42).
The hexmod system does not use all the diagonals of the space lattice, but the diagonals it uses are continuous from one end of the building to the other. Some will be attached to space trusses and others will not, but none will have to be in compression for more than three consecutive stories.
igure 16.40 Twelve space trusses frame an eight-story Dctahedron. Next to it, on the ground, is a 4-m octahedron. It is the basic, conceptual "building block” of space truss and hexmod alike. (Source: J. F. Gabriel, “Skyscrapers or Space Towns,” in Developments in Structural Engineering, Proceedings of the Forth Rail Bridge Centenary Conference, He riot-Watt University, Edinburgh, 1990, B. H. V. Topping, ed., 1990, pp. 657, fig. 3. Reprinted with permission of Chapman and Hall, Cheriton House, North Way, Andover, HANTS SP10 5BE, UK.)
Figure 16.41 The hexmod system is used to implement the eight-story building shown here. (Source: J. F. Gabriel, “Skyscrapers or Space Towns,” in Developments in Structural Engineering, Proceedings of the Forth Rail Bridge Centenary Conference, Heriot-Watt University, Edinburgh, 1990, B. H. V. Topping, ed., 1990, pp. 657, Fig. 3. Reprinted with permission of Chapman and Hall, Cheriton House, North Way, Andover, HANTS SP10 5BE, UK.)
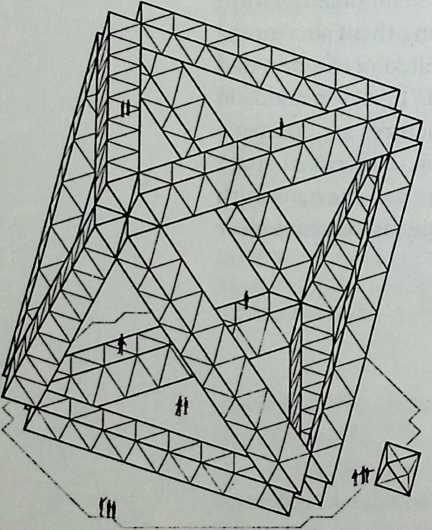
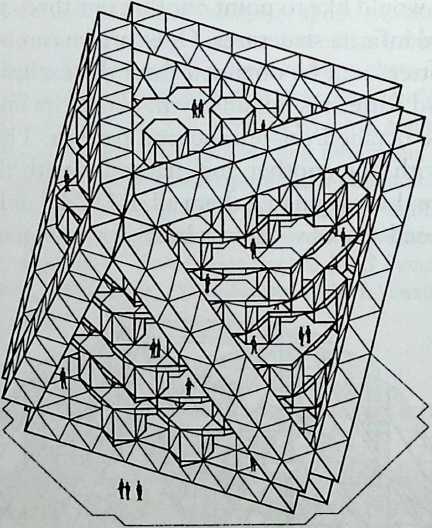
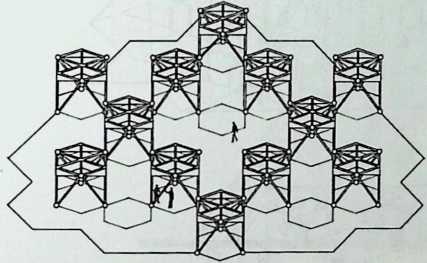
Figure 16.42 Model of the megaoctahedron with the lower two stories partially built with hexmods. (Source: J. F. Gabriel, “Space Frames: The Space WithinA Guided Tour,” International Journal of Space Structures, Vol. 6, No. 4,1991, pp. 287, Fig. 15. Reprinted with permission of Multi-Science Publishing, Brentwood, UK. Model by John Tanzi.)
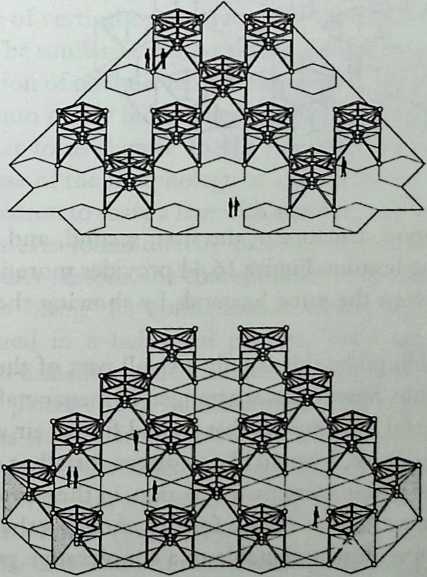Figure 16.43 The bottom three stories of the building shown in Figure 16.41 are represented sequentially here, from the bottom up. The drawings convey an airiness that is not apparent in Figure 16.41. Careful experimentation showed that the elimination of certain hexmods is possible. Three hexmods on the first floor, three on the second floor, and one on the third floor were deleted, opening up large, column-free spaces. Upper caps show part of the floor structure. Attentive examination of the drawings will allow the reader to verify the continuity of diagonals from one floor to the next Hexagons shown on the floor of the upper two stories indicate the location of the hexmods underneath. The presence of space trusses interferes with six hexmods on the first floor. These hex-mods are deleted in Figure 16.41. (Source: J. F. Gabriel, “Megapolyhedra,” Proceedings of the IASS Symposium on Spatial Structures at the Turn of the Millennium, Copenhagen, 1991, T. Wester, S. J. Medwadowski, and I. Mogensen, eds., 1991, pp. 35, Fig. 5A. Reprinted with permission of T. Robbin, Engineering a New Architecture, Yale University Press, 1996, p. 94, fig. 7.17.)
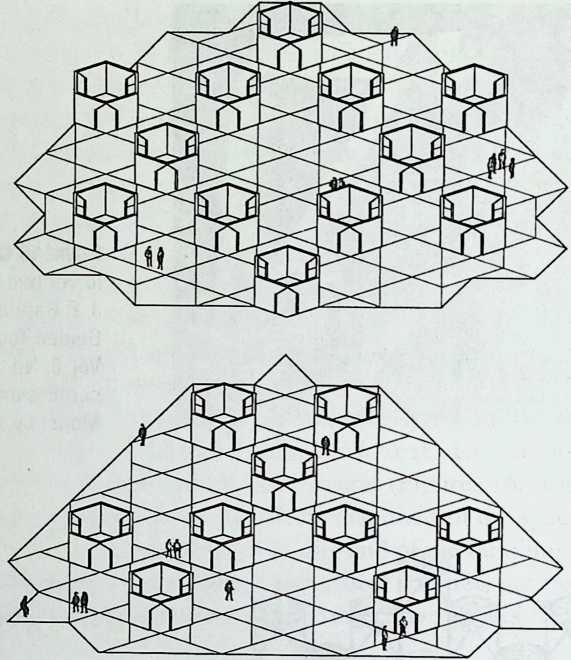
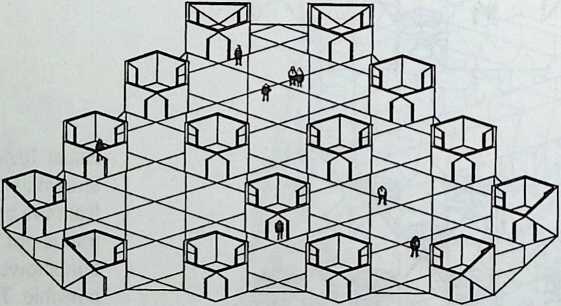
Figure 16.43 shows the hexmod structure of the first, second, and third stories, with the lower story at the bottom. Figure 16.44 provides more information on the relationships between the same hexmods by showing them as enclosed rooms.
However, an eight-story building like this is only a small part of the sort of urban ensembles that are feasible. Space trusses arranged in megaoctahedra and megatetrahedra create powerful frameworks that should find their applications in vast structures. As an example, I would like to discuss briefly a study for a 135-story structure. It is a relatively conservative design, in the sense that it resembles a skyscraper in some ways. The reason for this choice is that elevators that run in vertical shafts are more acceptable to a conservative public. Also, vertical shafts occupy less space than oblique shafts. Settlements nor-
Figure 16.44 Whereas the hexmods were drawn as structural elements in Figure 16.43, they are shown here as rooms, with enclosures. (Source: J. F. Gabriel, “Space Frames: The Space WithinA Guided Tour,” International Journal of Space Structures, Vol. 6, No. 4,1991, pp. 287, Fig. 14. Reprinted with permission of Multi-Science Publishing, Brentwood, UK.)
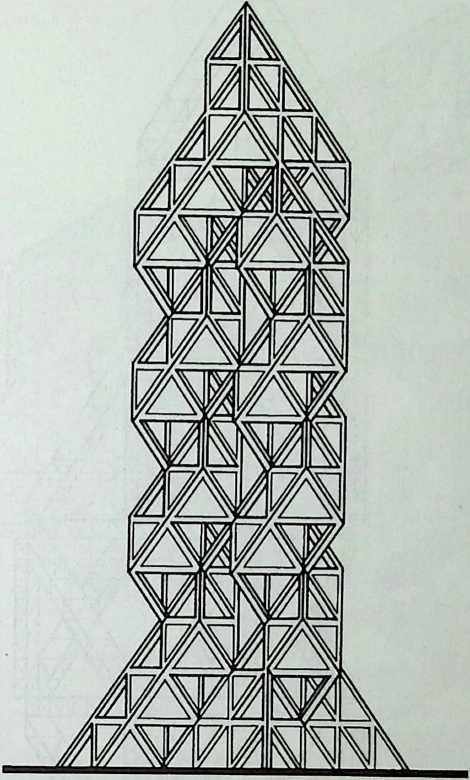
Figure 16.45 Space trusses can be assembled in multilayer frameworks of vast dimensions. Here is 3135-story structure composed of megaoctahedra and megatetrahedra arranged vertically in three identical helicoids. (Source: J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 18. Reprinted with permission.)
mally occur along roads, and elevators are modem roads. They determine the shape of vertical configurations (Figures 16.45 and 16.50).
The similarities with a skyscraper end here. The greatest difference after the adoption of oblique, rather than vertical, supports is the division of the building bulk into nearly independent units. Each unit is an eight-story module, already familiar to us (Figure 16.41), fitted into an octahedral frame of space trusses. Because of the morphology of a space frame, which makes it impossible for an octahedron to share a face with another, each unit is practically freestanding. No unit is ever found directly above or below another; it is always offset. For this and other reasons, the concept is not so much of a building as of a space town.10
To bring the configuration closer to the vertical, megaoctahedra are arranged in a helicoidal pattern. They are connected to one another by megatetrahedra, which render the whole rigid. The description of an unfamiliar pattern often sounds complicated but, more often than not, the pattern itself is simple: In the present case, it consists of one tetrahedron above and one under the octahedron. Together, the three polyhedra add up to a simple, six-sided geometric solid (called an oblate rhombohedron) resembling an elongated cube (Figure 16.46).
The entire structure is made of three helicoids attached to one another for stability, surrounding an open space for elevators. Every ninth floor, a platform
Figure 16.46 A detail of one of the helicoids. There is a tetrahedron above, and another one under each octahedron. The resulting form, which has six rhombic faces, is an oblate rhombohedron. The drawing shows four of these, connected by their faces. The uppermost oblate rhombohedron is in contact, tip to tip, with the one at the very bottom. (Source: J. F. Gabriel, “Dwelling in Space Structures,” in Studies in Space Structures, H. Nooshin, ed., Multi-Science Publishing, Brentwood, UK, 1991, pp. 69, Fig. 17. Reprinted with permission.)
connects the helicoids. This is where the main elevators discharge their passengers, who will find other, smaller elevators within the eight-story unit where they five, work, or do other business. The platform functions as a fire barrier: The horizontal space trusses are linked by two reinforced concrete slabs that would prevent an eventual fire from spreading. People escaping from the building will reach safety by moving on to the next helicoid (Figure 16.47).
A space town has certain advantages over a conventional building. Depending on functional needs and/or climatic conditions, the large tetrahedral space adjacent to each eight-story unit can be made into a garden or an “atrinm.” This space can also be used for expansion of the eight-story unit if it becomes too small (Figures 16.48 to 16.50).
Figure 16.47 Top view of three helicoids forming a space town. Hexmods are used in the building units, which occupy the octahedral spaces framed by space trusses. Glass walls enclose building units. The hexagon at the center outlines the elevators and stairs zone.
Figure 16.48 In the helicoids a tetrahedron is adjacent to every octahedron. The building unit housed in the octahedron can expand in the tetrahedral space if necessary. An alternative use for that space is an open garden or an enclosed greenhouse.
Figure 16.49 Two stages of the construction of a building unit. From the bottom up, construction of the fourth, fifth, and sixth stories. Hexmods push out the glass enclosure where it interferes with their formal integrity. (Source. J. E Gabriel, “Megapolyhedra,” Proceedings of the IASS Symposium on Spatial Structures at the Turn of the Millennium, Copenhagen, 1991, T. Wester, S. J. Medwad-owski, and I. Mogensen, eds., 1991, PP-35, Fig. 4A, B, C. Reprinted with permission.)
Figure 16.50 Model of the three helicoids forming the bare bones of the space town. The structure shown here has 89 stories. A few eight-story buildings are already inserted in the upper part. The central space reserved for the elevators can be better seen in the top view (see Figure 16.47). Figure 16.45 shows a similar configuration at a more advanced design stage, with the special needs of the base and the top taken into consideration. (Source: J. F. Gabriel, “Skyscrapers or Space Towns,” in Developments in Structural Engineering, Proceedings of the Forth Rail Bridge Centenary Conference, Edinburgh, 1990, B. H. V. Topping, ed„ 1990, pp. 657, Fig. 1. Reprinted with permission of Chapman and Hall, Cheriton House, North Way, Andover, HANTS SP10 5BE, UK.)
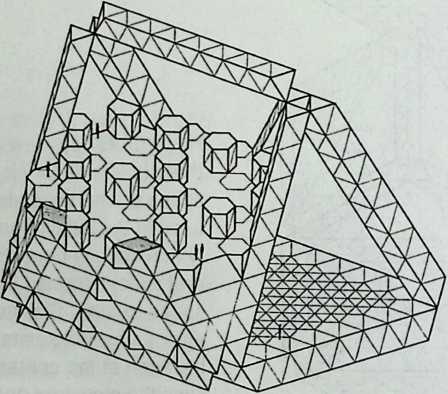
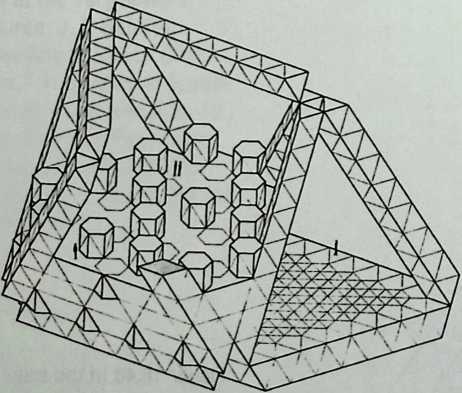
SPACE FRAMES AND POLYHEDRA
This chapter begins with a study of the space within two polyhedra that are closely related to the cube: the octahedron and the tetrahedron. These are the modules that form space frames. They are most habitable when their faces are deleted and only their edges remain as the integral part of a space lattice structure. Vertical enclosures and partitions can then be introduced to create a rather conservative architectural environment.
Although the process yields simple, honeycomb-like clusters of rooms, further investigation reveals that richer patterns are also possible. Hexmods, star beams, and megapolyhedra describe some of these patterns. They are variations on a single theme, which is the transformation of an octahedron into a hexagonal, prismatic space.
Although intimately related, the hexmod and the octahedron bear little resemblance to one another. From an architectural point of view, the most distinctive feature of polyhedra is their oblique walls. To some critics, this appears to be their most disturbing attribute. Regardless of whether one likes or dislikes oblique walls, it could be argued that the substitution of vertical planes for oblique ones is a betrayal of the fundamental nature of polyhedra. But what of livability? What of the mental and physical comfort of the dweller? Do oblique walls make a space impossible to live in? Certainly not. But how serious an impediment are they to livability? The question must be examined closely.
From studies conducted over several years with students from various universities, including Syracuse, Harvard, and MIT, I learned that many polyhedra are not only habitable but they also have a rich architectural potential when used as the modules of infinite structures. They all cannot be dealt with here, but the following list may be a starting point for readers interested in doing research on their own. This is certainly not an exhaustive list, and it is not presented in any particular order, but it includes useful clues concerning viable positions of polyhedra in space. By “viable,” I mean that the orientation of the polyhedra relative to the ground is such that the interior spaces meet essential architectural requirements. For ease of visualization, orientation is indicated by the words “resting” or “poised” and should not be taken literally.11
-
Cubes, resting on a face or poised on an edge or a node.
-
Truncated octahedra, resting on a square face, a hexagonal face, or an edge shared by hexagons.
-
Truncated octahedra in combination with cubes and great rhom- bicuboctahedra, resting on an octahedral face or on a square one.
-
Truncated cubes in combination with great rhombicuboctahedra and truncated tetrahedra, resting on a hexagonal or an octagonal face.
-
Truncated octahedra in combination with cuboctahedra and truncated tetrahedra, resting on a square face or on a hexagonal one.
-
Octahedra in combination with truncated cubes, resting on an octahedral or a triangular face.
-
Octahedra in combination with cuboctahedra, resting on a square face or on a triangular one.
-
Octahedra and tetrahedra, resting on a face (three-way space frame) or poised on a node (two-way space frame) or poised on an edge.
-
Small rhombicuboctahedra in combination with cubes and tetrahedra, resting on a square face or poised on a node.
-
Small rhombicuboctahedra in combination with cubes and cuboctahedra, poised on a node or resting on a square or a triangular face.
-
Rhombic dodecahedra resting on a face or poised on a node (nodes are either at the intersection of three or four faces).
What system of polyhedra shall we choose to investigate? Although spatially and formally different from one another, most polyhedra have common characteristics, and one of them is oblique walls. Because we normally stand upright and are accustomed to having vertical walls around us, these provide a useful reference. It can be argued, however, that not all the walls surrounding us need be vertical. Only a few are useful for reference. Most habits dull the senses, and the vertical-wall habit is no exception: In many cases vertical walls fail to interest us because they are all around us. If, on the other hand, the actual enclosure of a space is made of oblique walls, our awareness of being sheltered will be enhanced. And so will be our sense of being in a specific place, with all its implications, including an increased sense of identity for ourselves. Knowing where we are goes a long way toward telling us who we are.12
One of the most commonly heard arguments against oblique walls is that they waste space. If a wall leans inward, it will be said to interfere with headroom. If a wall leans outward, it will be presumed to be unusable in itself and to generate an unusable space in front of it. Yet a look at traditional building plans shows that a considerable amount of floor space is taken up by closets and other storage spaces. This is wasteful, and it is a consequence of the exclusive use of vertical walls: In conventional buildings, that is, “cubic” buildings, closets must occupy floor space because there is no other place for them. On the contrary, walls that lean out make room for storage without taking up any floor space. A vertical plane, placed in front of the oblique wall, supplies both the space for storage and the wanted vertical surface for reference. Many other ingenious uses have been proposed for spaces found near oblique walls.13
Almost any single polyhedral form can be used to explore the advantages or disadvantages of oblique wallsbut only to a certain point. A better, more comprehensive picture is obtained from polyhedra in clusters. Because I have looked more closely at combinations of truncated octahedra, cuboctahedra, and truncated tetrahedra than at any other infinite structure, I propose this system for our case study (Figures 16.51 and 16.52).
As already mentioned, the names of both the truncated octahedron and the truncated tetrahedron are somewhat misleading. Although it is true that these forms could result from a subtractive process of truncation, it is more significant for us to consider them as compound forms, obtained from the addition of tetrahedra to octahedra. That their names are misleading cannot be helped, but that the same names are cumbersome can be remedied: From
Figure 16.51 Design study for a kindergarten by Hans Graf. The formal components are the truncated tetrahedron, the cuboctahedron, and the truncated octahedron (TT, CO, and TO). The implicit layering of these polyhedra made it possible to introduce two simultaneous scales: Rooms are successfully planned for little human beings whose height is approximately half that of the others. (Source: J. E Gabriel, “The Architectural Potential of Polyhedra,” in Space Structures, G. A. R. Parke and C. M. Howard, eds., Thomas Telford, London, 1993, pp. 2025, Fig. 6. Reprinted with permission. Photo: J. F. Gabriel.)
here on, we will call the truncated octahedron TO, the cuboctahedron, CO, and the truncated tetrahedron, TT.
If the octahedra used to form TOs, COs, and TTs are the size of hexmods, the TO will be a three-story unit, whereas both the CO and the TT will be two-story units (Figure 16.53).
Ideally, a building matrix should accommodate both large and small habitable spaces. The TO, the CO, and the TT can contain and determine the shape of large rooms, which will be as wide as they themselves are. As for their height, it can be one to three stories. For the space within these rooms to be entirely free of structural elements, the octahedra and tetrahedra that were originally used to shape it would have to remain purely conceptual (Figures 16.54 to 16.57).
If the structural system used in the building is a multilayer space frame, it will have to be external to the larger rooms. For this to be possible, a choice must be made between TOs, COs, and TTs. Where will the large, open spaces be created? The structural space frame cannot be eliminated from all polyhedral spaces at the same time. Many options are available. For instance, TOs can be “hollowed out,” leaving COs and TTs to carry the structural framework or, conversely, the TOs will consist of three stories of space frames and the open spaces will be in COs and TTs. The choice will be made on the basis of programmatic and functional needs. As to the smaller rooms, they can be found within the space frame itself, most likely in the shape of hexmods. Visually as well as spatially, the result of this conceptual approach will be buildings combining the form language of the hexmod systeman aggregate of hexagonal prismsand that of polyhedra retaining their oblique faces.14
Figure 16.52 The six layers of this configuration, clearly visible, suggest a six-story structure. This is the scale adopted for the rest of this discussion. A TO divides itself spontaneously into three layers, whereas a CO and a TT divide themselves into two. COs always share their triangular faces with TTs in this pattern. The large space at the core is a TO. Each of its six square faces is shared with a CO. Its eight hexagonal faces can only be shared with TTs. There are four TTs in the model, all straight side up. (Source: J. F. Gabriel, “Space Frames and Polyhe-dra,” in Spatial, Lattice and Tension Structures, Proceedings of the IASS-ASCE International Symposium, J. Abel, J. Leonard, and C. Penalba, eds., 1994, pp. 1037, Fig. 1. Reprinted with permission of the ASCE.)
Figure 16.53 The relationship between the polyhedra of an infinite structure is fixed. A vertical sequence reveals this relationship: From the bottom up, four elements complete the inventory: a CO, a TT, a TO, and a TT again. On top of that, another CO signals the beginning of a new cycle. The TT appears twice, in upright position above and inverted below. In this drawing proportions were changed for experimental purposes, but the topology of the system is not affected. (Source: J. F. Gabriel, “Polyhedra: Skin and Structure,” Application of Structural Morphology to Architecture, Proceedings of the Second International Seminar on Structural Morphology, R. Holler, J. Hennicke, and F. Klenk, eds., 1994, pp. 37, Fig. 2. Reprinted with permission of Institute for Lightweight Structures, University of Stuttgart)
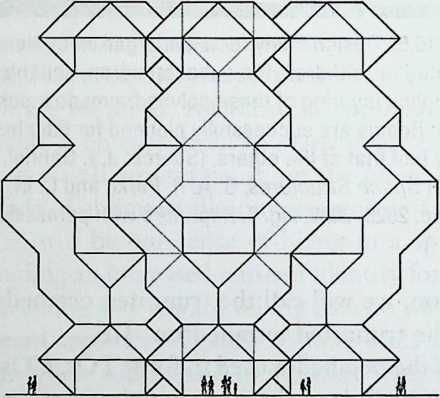
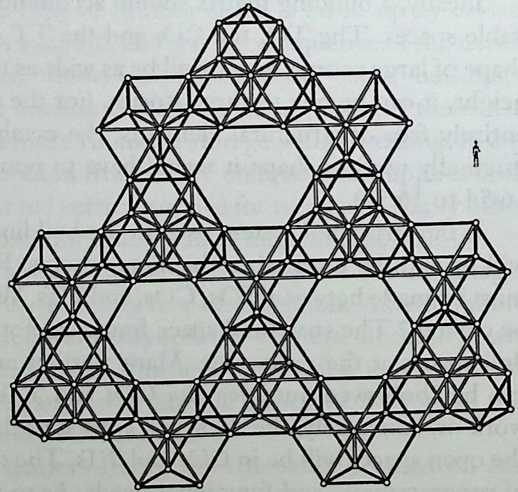Figure 16.54 Horizontal sections engage all the polyhedra of the system and reveal their relationships. Here, a CO, at the center is connected with three TTs by their triangular faces. These TTs are “upside down,” and the level involved is the upper one. The TTs, in turn, are connected with six CO S, and so on. There is a total of seven COs and six TTs in the configuration represented. There are also three TOs, with their interiors free of structural members: Their outer form is defined by the continuous space frame found in adjacent TTs and COs. The larger rooms required in most building programs would be accommodated in the TOs. The space frame would accommodate the smaller rooms and also assume a structural function. Structural members that indicate the outline of polyhedral fragments are shown in black. The space frame is completed with structural members shown white. On this story, passing directly from a CO to a TT is impossible. To solve this problem, hexmods should replace the octahedra of the space frame. (Source: J. F. Gabriel, “Polyhedra in Architecture,” International Journal of Space Structures (Special Issue on Morphology and Architecture), H. Lalvani, ed., 1996, Fig. 8. Reprinted with permission of Multi-Science Publishing, Brentwood, UK.)
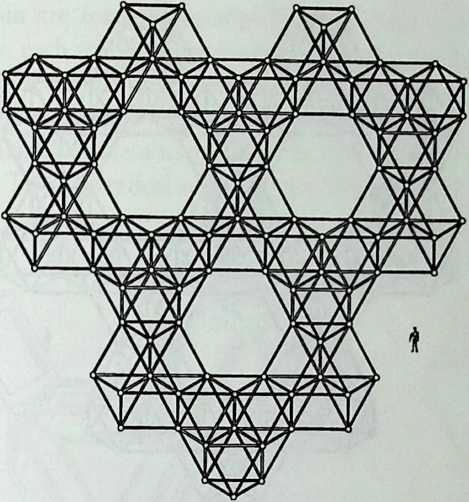
Figure 16.55 This horizontal section shows the story directly above that of Figure 16.54. The upper half of a CO can be recognized at the center. It is connected with three other TTs, but these are “straight side up,” and they are located above TOs. There are also three TOs, located above the “upside-down” TTs. (Source: J. F. Gabriel, “Polyhedra in Architecture,” International Journal of Space Structures (Special Issue on Morphology and Architecture), H. Lalvani, ed., 1996, Fig. 5. Reprinted with permission of Multi-Science Publishing, Brentwood, UK.)
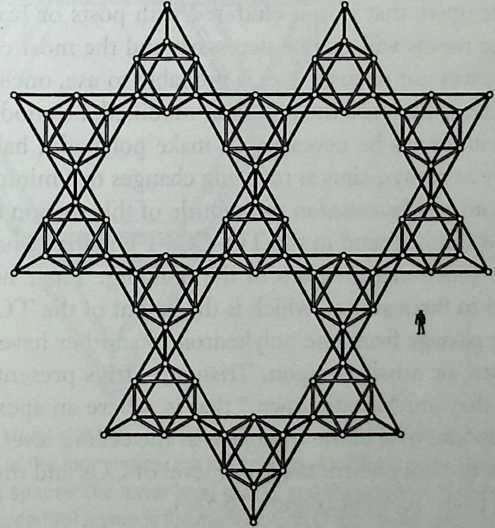
Figure 16.56 On this plan, located directly above that of Figure 16.55, we find the median story of three TOs. No structural member is allowed inside. The space frame surrounding the TOs belongs to the upper level of three “straight-side-up” TTs and to the lower level of three “upside-down” TTs. This story does not carry any COs. (Source: J. F. Gabriel, “Polyhedra in Architecture," International Journal of Space Structures (Special Issue on Morphology and Architecture), H. Lalvani, ed., 1996, Fig. 2. Reprinted with permission of Multi-Science Publishing, Brentwood, UK.)
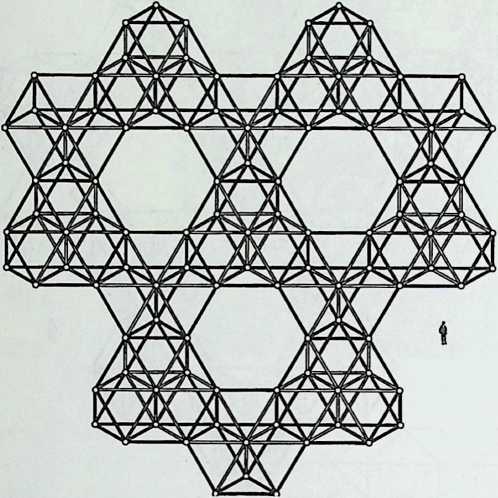
Figure 16.57 This story, directly above that of Figure 16.56, repeats the pattern shown in Figure 16.54, three stories below, and would appear again three stories above. Although identical, repeating patterns such as these are not superimposed: It is only every ninth story that identical patterns share vertical projections.
UNADULTERATED POLYHEDRA
The problem is different if the structural system used to build the TO-CO-TT matrix is not a space frame. Consider a monolithic structure of the shell or folded-plate type, such as shown in Figure 16.52. There, presumably, the space within all the TOs, all the COs, and all the TTs could theoretically be wide open, that is, not cluttered with posts or braces. As in any building, smaller rooms will also be necessary, and the most coherent means to make small spaces out of large ones is probably to use, once again, octahe-dra and tetrahedra, and to use them in their modified, hexmod version. Some modifications will always be necessary to make polyhedra habitable but my main effort, here as always, aims at reducing changes to a minimum. Thus the choice of the word unadulterated in the subtitle of this section (Figure 16.58).
Large rooms can be found in the TO-CO-TT matrix whenever they are required by the functional program of the building. Their height will normally be limited to three stories, which is the height of the TO. Observe that bays permitting passage from one polyhedron to another have the shape of a triangle, a square, or a half-hexagon. Triangular bays present an occasional obstacle where they are “upside-down,” that is, where an apex is at the floor level and the opposite base of the triangle is at the ceiling level. This situation is only found on the story where the lower level of COs and the upper level of upside-down TTs are adjacent (Figure 16.58£).
Because the conditions of habitability within unadulterated polyhedra cannot all be reviewed together, we will look at all basic spaces separately. We already know that the TO is a three-story volume and the TT and the CO are two-story volumes. In the infinite structure of which these polyhedra are the modules, only the TT is found in two different positions, that is, either resting on a hexagon or resting on a triangle. Depending on their relative position, the
four spaces within are totally dissimilar. Consequently, it is a series of nine spaces altogether, each with its own distinct shape, that we must examine.
The three-dimensional relationship between the polyhedra obeys rigorous rules. Hexagonal faces always separateand also unite, for that matter TOs and TTs. Triangles are always shared by COs and TTs. Finally, squares connect COs to TOs. A vertical sequence will then always consist of a CO, a
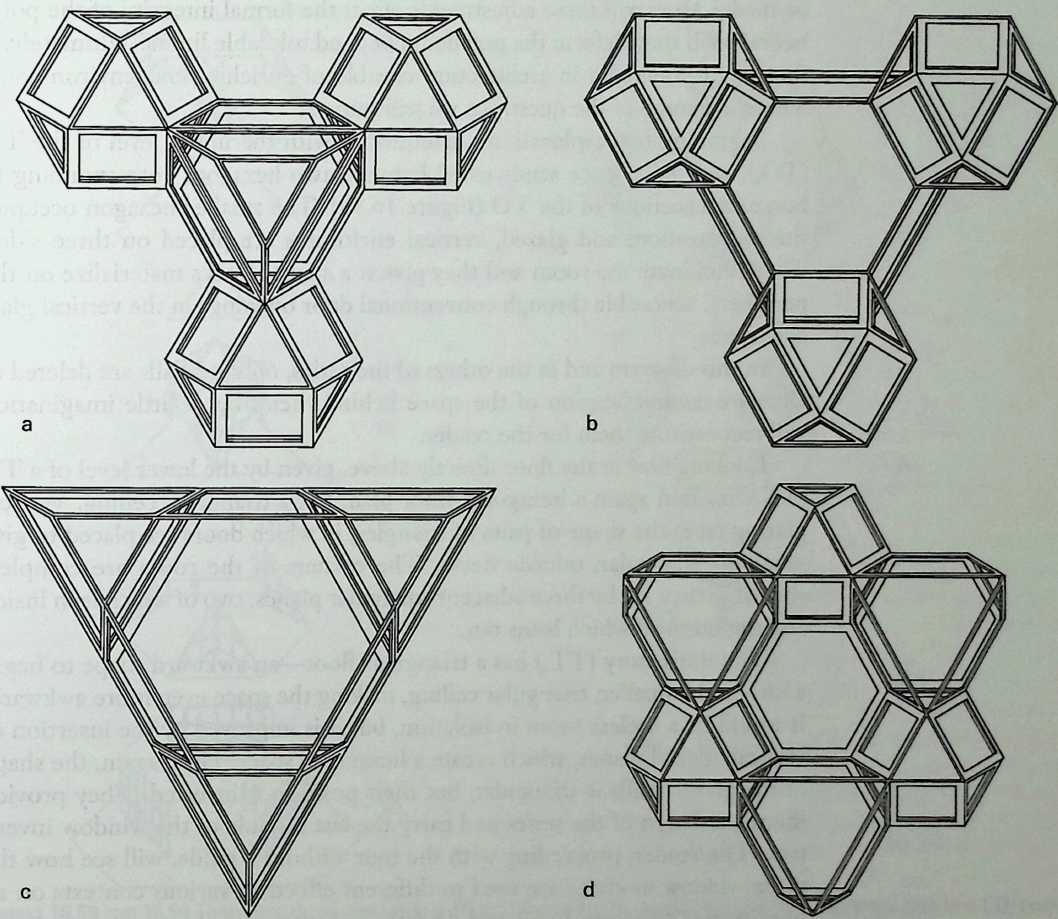
Figure 16.58 The nature of the spaces within is shown in a selection of four horizontal sections, one above the other. Beginning with the first of the four stories, the lower level of a TO occupies the center of the cluster (d). Surrounding it are two sets of alternating spaces: the lower level of a TT and the upper level of a CO, each repeated three times. On the story directly above, the central space is the median level of the TO, surrounded by the upper level of aTT, repeated three times (c). The spaces that would be found above the COs of the story below are deleted. The reader is invited to identify them and, in the process, become familiar with the complete three-dimensional pattern. The third story, with the upper level of the TO at the center, is surrounded by the lower level of another set of COs (b). Here again, three peripheral spaces are missing: What are they? On the fourth story, last of the sequence, the lower level of aTT is at the center of the cluster (a). The upper level of three COs is shown around it What are the spaces that would nestle in the interstices? As a reminder that spaces can be higher than one story, floors are deleted from all the drawings. In (a)the upper level of the TT is shown as well as the lower level. (Source: J. F. Gabriel, “The Architectural Potential of Polyhedra,” in Space Structures, G. A. R. Parke and C. M. Howard, eds., Thomas Telford, London, 1993, pp. 2025, Figs. 2,3. Reprinted with permission.)
TT, a TO, and another TT, after which this order is repeated again. Only the TT appears twice in the sequence, because of its inverted position in space (Figure 16.53).
As stated previously, there are nine basic spaces in the matrix. Before we set out to visit them, I would like to clarify my point of view once again: It is that of an architect in search of the essential conditions of habitability. What are these conditions? They consist of enclosures, horizontal floors, doors, and windows. Do our polyhedra meet these conditions? What adjustments must be made? How will these adjustments affect the formal integrity of the poly-hedra? Will they deform the polyhedra beyond tolerable limits? Ultimately, is the use of polyhedra in architecture capable of enriching our environment? Those are some of the questions we will pursue.
Beginning our explorationarbitrarilywith the upper level of the TO (TOU), we find a space sandwiched between two hexagons corresponding to horizontal sections of the TO (Figure 16.59). The smaller hexagon occupies the top position, and glazed, vertical enclosures are placed on three sides. They illuminate the room and they give it a shape. Decks materialize on the periphery, accessible through conventional door openings in the vertical glass enclosures.
In this diagram and in the others of the series, oblique walls are deleted to facilitate comprehension of the space behind them, but a little imagination will reconstitute them for the reader.
Looking now at the floor directly above, given by the lower level of a TT (TTi), we find again a hexagonal floor plan, but a triangular ceiling. Vertical glazing takes the shape of pairs of triangles, in which doors are placed to give access to triangular, outside decks. The corners of the room are complex, shaped as they are by three adjacent triangular planes, two of which lean inside and the other of which leans out.
The third story (TTU) has a triangular flooran awkward shape to begin withand a smaller, triangular ceiling, making the space even more awkward. It would be a useless room in isolation, but it is improved by the insertion of vertical, glazed planes, which create a hexagonal space. Here again, the shape of the glazed walls is triangular, but their position is inverted. They provide the third design of the series and carry the last module of the window inventory. The reader, proceeding with the tour without a guide, will see how the three window modules are used to different effects in various contexts on all nine stories (Figures 16.59 and 16.60). The shape of the next story (COi) appears to be even more awkward and wasteful than the third one, but in context, it plays an important role as a space connecting others (Figure 16.61a).
What led me to this particular design of glazed walls? In part, the necessity to draw something: If I am to make a case for architectural polyhedra, I must be able to represent them. To do so, a basic formal vocabulary must be chosen. In addition to the needs already mentioned for enclosures and openings, doors and windows, two considerations influenced the design of the glazed walls. One was the desire to accommodate conventional doors, which can only be done with vertical walls. The other was a wish to respect the for-
mal integrity of polyhedral forms, and this led to glazed walls, which, except in one case, do not project outside the faces of polyhedra. If this rule had not been observed, the polyhedra would have been transformed into monsters. After all, polyhedra do not exist simply for the enjoyment of architects. If they are to become building forms, the process of adaptation should be handled with sensitivity. In other words, my goals were truthfulness, simplicity, and consistency. The search for a personal style was not a consideration.
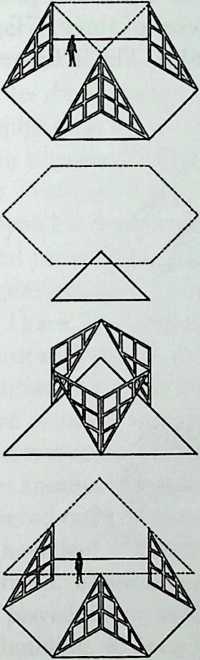
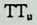
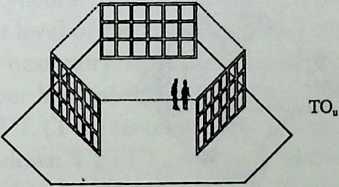
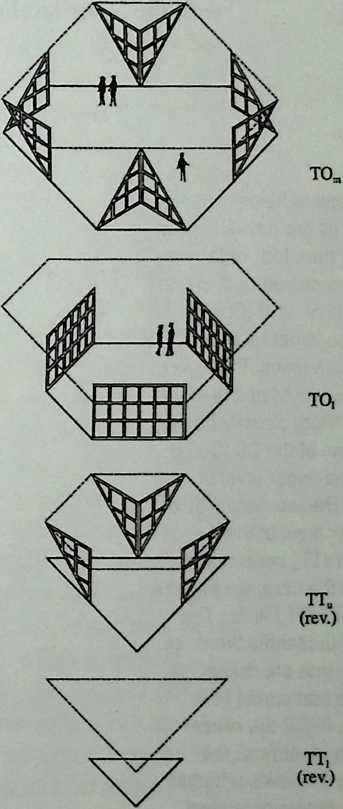
coo
CO!
Figures 16.59 and 16.60 There are three stories in a TO and therefore three distinct spaces. There are two in a CO, two in a TT, and another two in an “upside-down” TT. Going down, for instance, from the upper level of a CO (Figure 16.59, top), we can examine all nine different spaces in a sequential order that never varies. After reaching TO,, at the bottom of Figure 16.59, we continue the visit with T0ra, at the top of Figure 16.60. The last space of the complete series is TT, (reversed), at the bottom of Figure 16.60, but the sequence can be repeated, starting with C0u, which would be found directly under TTt (reversed) already seen at the top of Figure 16.59. It is unlikely that any of these spaces would be freestanding, but looking at them in isolation is a good preliminary to understanding them when grouped in clusters. Vertical glazing replaces certain faces of the polyhedra, and conventional doors can be installed. The complete inventory of glazed, modular parts consists of a total of three designs. (Source: J. F. Gabriel, “Polyhedra: Skin and Structure,” Application of Structural Morphology to Architecture, Proceedings of the Second International Seminar on Structural Morphology, R. Holler, J. Hennicke, and F. Klenk, eds., 1994, pp. 37, Figs. 3,4. Reprinted with permission of Institute for Lightweight Structures, University of Stuttgart.)
The formal vocabulary used here is not the only possible one. Far from it. The imaginative reader will quickly discover many other design possibilities and derive a great deal of satisfaction from trying them out. A wealth of design possibilities is one important aspect of the field and perhaps the least understood of all.
Having looked individually at the nine basic spaces found in a vertical sequence, we are now ready to look at them in context (Figure 16.61). As a consequence of the threefold symmetry that rules the pattern, each basic space is surrounded by six others, divided into two sets of three. For instance, the upper level of a CO is adjacent to the lower level of three TTs, alternating with the lower level of three TOs (Figure 16.61a). The TTs are shown, but
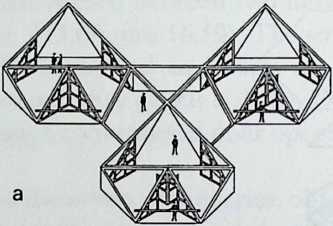
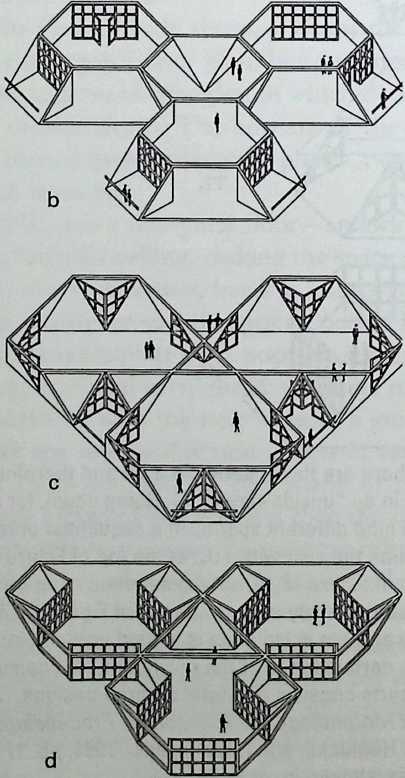Figure 16.61 Instead of being isolated, some basic spaces are now shown in clusters. We see here four of the nine stories that form a complete cycle. In (a)the upper level of a CO (COJ is surrounded by the lower level of a TT (TT) repeated three times. The lower level of three TOs would nestle in the intervals. On the story directly below /&),the lower level of the CO (CO,) is surrounded by the upper level of three TOs (TOJ. The intervals would receive the upper level of three upside-down TTs (TT„, reversed). Below the CO at the core, we find the upper level of a TT (TTJ in (c). The reader is invited to identify the three adjacent spaces that are drawn, as well as the three that would fit in between. Finally, in (d),the reader should be able to identify all the spaces found on this level, whether they are entirely drawn or implied. The faces that would affect the legibility of the interior spaces are deleted in these drawings. All the “edges,” however, are retained. (Source: J. F. Gabriel, “Habitability Studies of Certain Polyhedra,” Spatial Structures: Heritage, Present and Future, Proceedings of the IASS International Symposium, Milan, 1995, G. C. Giuliani, ed„ Vol. 1, 1995, pp. 165, Figs. 2,3, 4,5. Reprinted with permission of SGEditoriali, Padova, Italy.) the TOs are not. For a more thorough representation of our spaces, a rotation of 60° has been implemented between the series shown in Figures 16.59 and 16.60 and the series shown in Figure 16.61.
Polyhedral spaces are fundamentally changed when placed at the core of a cluster and opening onto adjacent polyhedra. The differences can be observed when comparing, for instance, the TT, at the center of Figure 16.61J with the same space shown by itself in Figure 16.59. Portions of the faces that have been replaced with glazing in one case are kept solid in the other. Rectangular bays now appear where a complex assemblage of triangular planes existed. Beyond observations like these, an adequate description of the spaces and of the transformations that occur is difficult and probably pointless.
The reader should keep in mind that these are only diagrams, not complete designs. It might not be necessary to eliminate an entire face to create a passage between adjacent polyhedra. It will be observed that all edges are retained on all floors. What edge refers to here is a structural member placed where two or three polyhedral faces would intersect. Also note that in Figure 16.61 additional vertical planes close the gaps between vertical and oblique enclosures.
Of the nine stories forming a complete sequence, four are shown in Figure 16.61. These four stories include seven of the nine basic spaces. As I already mentioned, one of them appears in relation to two sets of polyhedra: It is TTb shown once surrounded by three TOs (Figure 16.61d) and again when its turn comes to cluster around a CO (Figure 16.61a).
The next two series of diagrams include all the polyhedra that can be clustered around another one at the core (Figures 16.62 and 16.63). The three stories, represented once in axonometric views and once in plan views, are those that would have had a TO on center, but for which stairs and elevators have been substituted. Elevator shafts take over the structural role that the TO would have played. Stairs and elevator shafts belong to the public zone, at the core of the building, whereas the more private spaces are found in the peripheral polyhedra. They are distributed as follows: On the lower story, that is, at the first level of the truncated octahedron (TOi), a TTj alternates with a COU. On the next story, which corresponds with the median level of the TO (TOm), the upper level of the TT (TTU) alternates with the lower level of an upsidedown TT (TTi, reversed). On the third story (TOU), the upper level of the upside-down TT (TTU, reversed) alternates with the lower level of a CO (COi).
Further horizontal subdivision may be necessary, depending on the programmatic needs of the building. This can be done by means of vertical planes disposed on a hexagonal grid. The reader will recognize the hexmod system in this approach, for the form and the location of the dividers are consistent with the octahedra that implicitly “fill” the larger polyhedra. The vertical elements may also contribute added rigidity and support to the whole structure.
Readers who still question the title of this section, Unadulterated Polyhedra, are begged to remember that polyhedra must be modified to some degree when we use them in the design of buildings. Nor should this be regretted because polyhedra are pure abstractionsconcepts of the mind whereas construction is a physical reality. Polyhedra should be modified and lose some
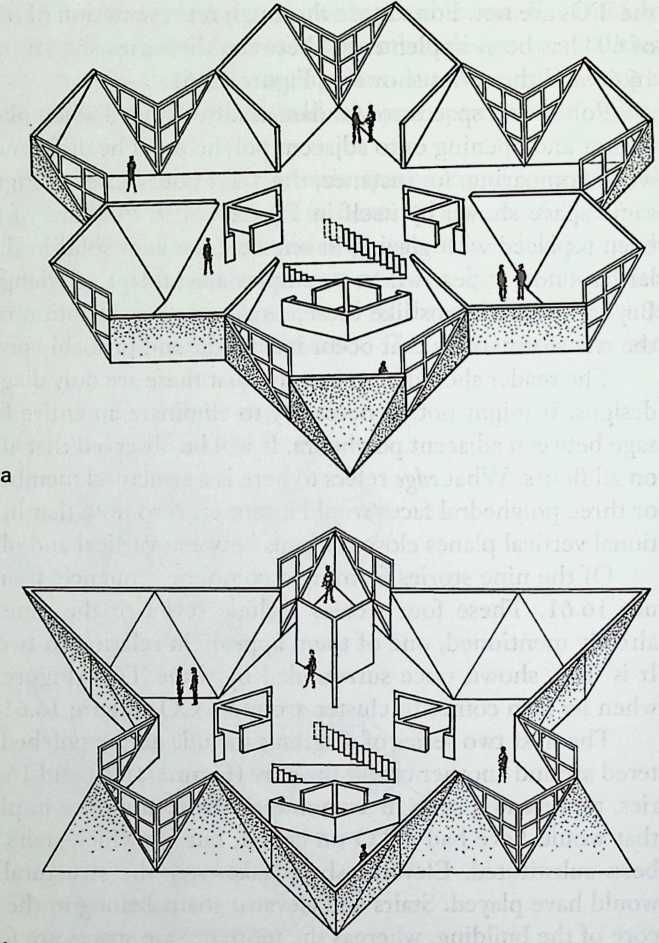
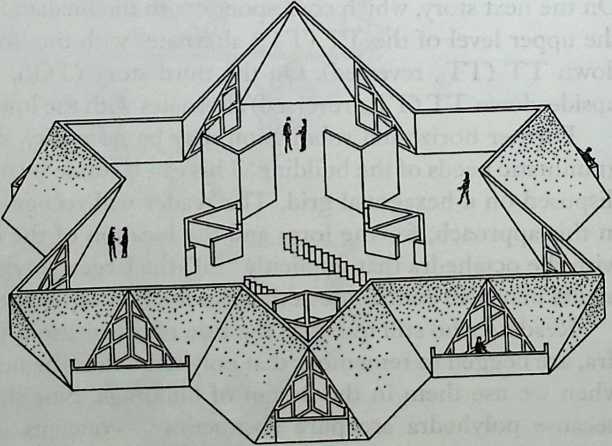Figure 16.62 Three more stories of the cycle, with a TO at the core. All six polyhedra, or portions thereof, surrounding its three levels are shown. In (a) the lower level of a CO alternates with the upper level of an upsidedown TT. Stairs and elevator shafts are fitted in the space conceptually occupied by the TO, whose form is no longer recognizable. The shafts can accommodate up to six elevators or they can house services; they are drawn shorter than they are so as not to interfere with our perception of the main spaces. On the story immediately below (b) which corresponds to the median level of the TO, the lower level of three upsidedown TTs alternates with the upper level of three straight-side-up TTs. The reader who makes the effort to identify the spaces shown on the next story (c) will be rewarded with an understanding of a three-dimensional pattern rich in architectural possibilities. Whatever the use of the building, its functional organization will probably require further subdivision of the space within. In (a)the triangular faces shared by COs and TTs suggest a possible means of subdivision. Another method, shown in (b) and (c), consists of using vertical dividers derived from the hexmod pattern. In either case, the dividing elements can also contribute to the structural framework, if necessary.
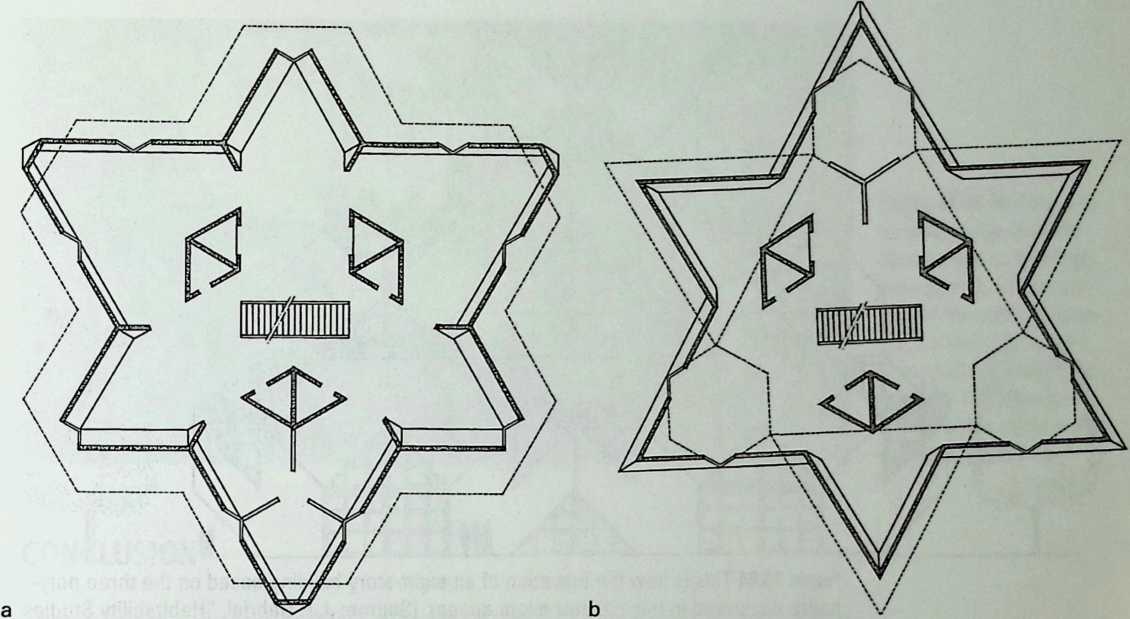
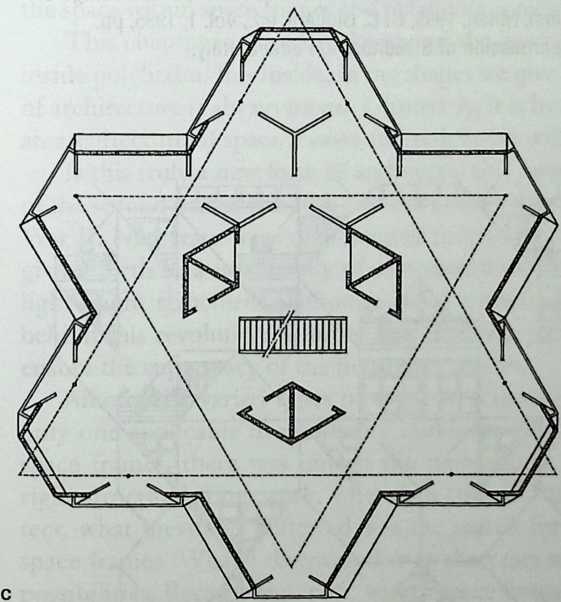Figure 16.63 These three floor plans match the diagrams of Figure 16.62. The only variations between the two sets of drawings concern some of the dividers.
of their geometric perfection in the process of becoming architecture. I chose that title simply because, in the last section of this chapter, my intention was to keep polyhedra and infinite structures as close to their ideal states as possible (Figures 16.64 to 16.66).
We have seen, on the contrary, that when a three-way, multilayer space frame is transformed into the hexmod system, it undergoes such changes that an observer might find it difficult to recognize the kinship of one with the other.
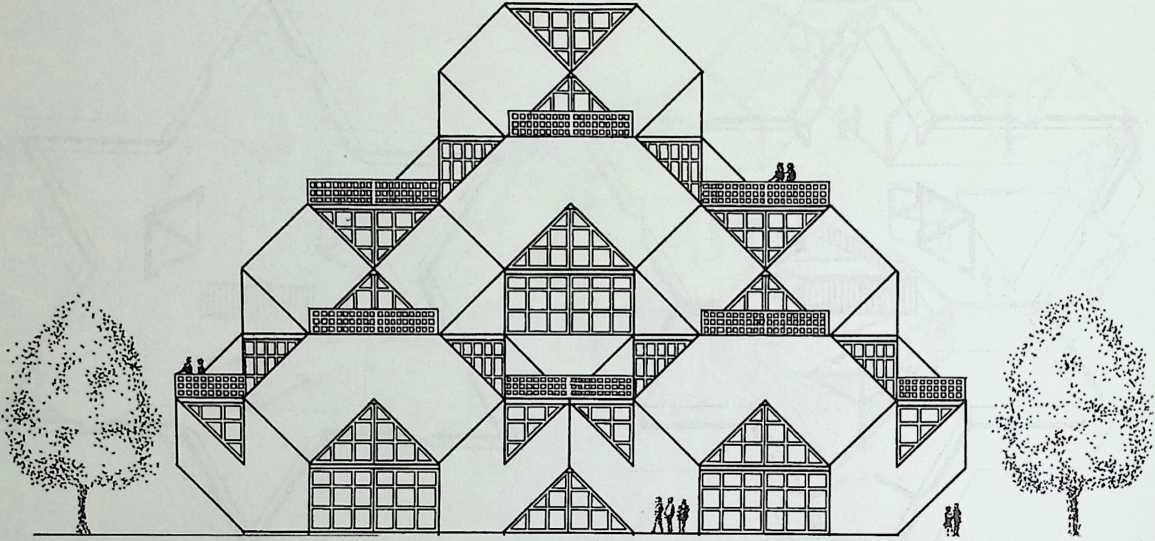
Figure 16.64 This is how the elevation of an eight-story building based on the three poly-hedra discussed in this chapter might appear. {Source: J. F. Gabriel, “Habitability Studies of Certain Polyhedra,” Spatial Structures: Heritage, Present and Future, Proceedings of the IASS International Symposium, Milan, 1995, G. C. Giuliani, ed., Vol. 1,1995, pp. 165, Fig. 6. Reprinted with permission of SGEditoriali, Padova, Italy.)
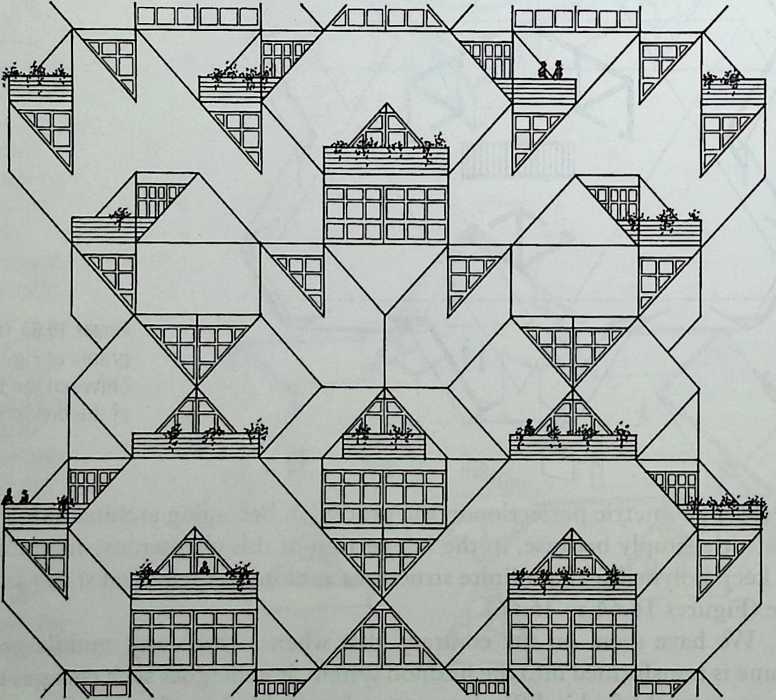
Figure 16.65 Shown here in elevation is the complete cycle of all nine possible spatial patterns discussed in this chapter. The three basic polyhedra are arranged in superimposed rings of six, with a seventh one at the core. Although the relationship between the polyhedra is always the same, all nine floor plans are different, as are their spatial characteristics.
Figure 16.66 Models give an idea of the possible appearance of buildings based on an infinite pattern of truncated octahedra, cuboctahedra, and truncated tetrahedra. As in Figure 16.65, the nine stories of the cycle are included.
¶ CONCLUSION
I hope this last chapter makes a substantial contribution to the argument that the space within space frames and polyhedra is habitable, versatile, and pleasant.
This chapter is placed at the end of the book because in it we take a look inside polyhedra. It is inside, in the shapes we give our rooms, that the essence of architecture is always found: Ultimately, it is by the quality of its spaces that an architecture of space frames and polyhedra will be judged.
Is this truly a new form of architecture? The major structural innovations of the second half of the 20th century occurred in the decade following World War II. New ways were then devised to span larger spaces with less material, giving birth to a new family of structural systems called space structures, or lightweight structures. Although economy was certainly a motivating force behind this revolution, a loftier way of looking at it is as one more effort to ensure the supremacy of the mind over matter.
Among the varied types of space structures, the space frame is still the only one applicable in multistory buildings. At the origin of my interest in space frames, there was indeed the recognition that a tetrahedron made a rigid structural framework, whereas a cube did not. Because I am an architect, what inevitably followed was the search for architectural space within space frames. What I discovered over the years were countless architectural possibilities. Because the space within space frames yields all sorts of perfectly habitable shapes, it seems to me that space frames should be more commonly employed in multistory buildings than conventional post-and-beam, or post-and-slab, systems.
Octahedra and tetrahedra, being the basic structural units of a space frame, can be used as “building blocks.” They can also be used at the conceptual level to generate other, larger, polyhedral forms and spaces, the construction of which would rely not on steel but on different materialsreinforced concrete most likelyand different structural principles, such as shells or folded plates.
Polyhedra that have more faces than the cube have a better ratio between the area of their envelope and their volume than the cube. These polyhedra would presumably use less material to build and suffer less heat loss than a cubic box. Motivations like these are valid, but there are others, just as legitimate. The intrinsic beauty of polyhedra is one. The visual and spatial order of infinite structures is another. The necessity to simply explore new avenues is yet another.
While I was engaged in my voyage of discovery among polyhedra, fashion in architecture tended more and more to turn its back on logic, clarity, and order. Imagination, is of course, crucial in architectural design and fantasy is by no means unwelcome, but, in the last few decades, arbitrary new building forms have been sprouting at an alarming rate. The license to do anything that fancy suggests can result in aberrations and, eventually, chaos. I hope the time has come for a turnaround. Design is the search for order, not irresponsible self-expression. A structuralist approach, combined with the discipline of geometry, would provide a renewed logic and a sound philosophical basis for architectural design. The application of a consistent formal language, with its many rules and restrictions, has never inhibited creativity. On the contrary, it always liberates it.
In this chapter I have tried to show the architectural potential of a limited number of configurations derived from the 12-connected network. There are many more configurations, waiting to be discovered by the curious mind, that could be applied in the design of buildings by imaginative architects and engineers. I believe that infinite structuresspace frames and polyhedracould be the means toward a sensible and dynamic architecture, one that could contribute to the visual and spatial expression of an organized and democratic society. As one would drive or walk around one of these structures, its appearance would slowly change, but always return to the reassurance of symmetry. Inside, one would experience a variety of spaces, some of them unexpected, but all devoid of the unbearable boredom of the modern bare box effect.
¶ NOTES
-
A. Holden, Shapes, Space, and Symmetry, Columbia University Press, 1971.
-
J. F. Gabriel, “Three-Dimensional Suburbs,” Proceedings of the IASS World Congress on Space Enclosures, Montreal, 1916, Building Research Centre, Concordia University.
-
J. F. Gabriel, “Living in a Space Frame,” Proceedings of the Second International Conference on Space Structures, University of Surrey, Guildford, 1975.
-
J. F. Gabriel and J. A. Mandel, “A Space Frame Building System for Housing,” Proceedings of the Third International Conference on Space Structures, University of Surrey, Guildford, 1984, Elsevier, London, 1984.
-
David P. Billington, The Tower and the Bridge, The New Art of Engineering, Basic Books, New York, 1983.
-
The Architectural Forum, Jan. 1938, p. 68.
-
J. F. Gabriel, “Metamorphic Architecture and Space Towns,” Proceedings of the IASS International Conference, Alma-Ata, 1977.
-
J. Dahinden, Urban Structures for the Future, Pall Mall Press, London, 1972.
-
J. F. Gabriel, “Megapolyhedra, Spatial Structures at the Turn of the Millennium, Vol. H, Structural Form,” Proceedings of the IASS Symposium, Copenhagen, 1991.
-
J. F. Gabriel, “Skyscrapers or Spacetowns, Developments in Structural Engineering,” Proceedings of the Forth Rail Bridge Centenary Conference, Edinburgh, 1990.
-
J. E Gabriel, “Polyhedra in Architecture,” Proceedings of the International Conference on the Design and Construction ofNon-Conventional Structures, London, 1981.
-
J. F. Gabriel, “Infinite Structures in Architecture,” Proceedings of the First International Seminar on Structural Morphology, Montpellier, France, 1992. Reprinted in the IASS Bulletin, Vol. 34, No. 3, 1993.
-
C. Dumitrescu, Arhitectura Formelor Poliedrate, Bucharest, 1993.
-
J. F. Gabriel, “Clusters of Polyhedra in Architecture,” International Journal of Space Structures (Special Issue on Morphology and Architecture), 1996.
¶ BIBLIOGRAPHY
Baldwin, J.: Bucky Works, Buckminster Fuller’s Ideas for Today, Wiley, New York, 1996.
Banham, R.: “A Clip-on Architecture,” Design Quarterly, Vol. 63, 1965.
Borrego, J.: Space Grid Structures, MIT Press, Cambridge, MA, 1968.
Bragdon, C.: The Beautiful Necessity, A Quest Book, 1978.
Burt, M.: “Periodic Hyperbolic Surfaces as Modular Membrane Structures,” International Symposium, Weitgespannte Flachentragwerke, University of Stuttgart, 1985.
Burt, M.: “Low Density I.P.L. Space Frames for Wide-Span and High Rise Structures,” IASS International Conference, Madrid, 1989.
Burt, M.: The Periodic Table of the Polyhedral Universe, Technion, Israel Institute of Technology, Haifa, 1996.
Condit, C.: “The Wind Bracing of Buildings,” Scientific American, Vol. 230; No. 2, 1974.
Cook, P.: Architecture: Action and Plan, Reinhold/Studio Vista, 1967.
Crapo, H.: “The Tetrahedral-Octahedral Truss,” Structural Topology, No. 8, 1983.
Critchlow, K.: Order in Space, Viking, New York, 1965.
Crosbie, M.: “Desert Shield,” Architecture, May 1991.
Dixon, J. M.: “Campus City Continued,” The Architectural Forum, Vol. 129, No. 5,1968.
Du Chateau, S.: Structures Spatiales, Brussels, 1967.
Du Chateau, S.: “Structures spatiales, Phenomene d’Ideation en Architecture,” Third International Conference on Space Structures, University of Surrey, 1984, Elsevier.
Edmondson, A.: A Fuller Explanation, The Synergetic Geometry ofR Buckminster Fuller, Van Nostrand Reinhold, New York, 1992.
Eekhout, M.: Architecture in Space Structures, Vitgeverij Olo, Rotterdam, 1989.
Emmerich, D. G.: Exercices de Geometric Constructive, Travaux d’Etudiants, Ecole Nationale Superieure des Beaux-Arts, Paris, 1970.
Friedman, Y: Une utopie realisee, Catalogue de 1’Exposition, Musee d’Art Modeme de la Ville de Paris, 1975.
Friedman, Y.: “Space Frames and Span-Over Buildings,” International Journal of Space Structures, Vol. 6, No. 4, 1991.
Fuller, R. B.: “Conceptuality of Fundamental Structures,” in G. Kepes, ed., Structure in Art and in Science, Braziller, New York, 1965.
Fuller, R. B.: “Design Science-Engineering, an Economic Success of All Humanity,” Zodiac, Vol. 19, 1969.
Fuller, R. B., and Marks, R.: The Dymaxion World of Buckminster Fuller, Anchor Books, 1973.
Hanaor, A.: “Prefabricated Spatial Frame Systems,” International Journal of Space Structures, Vol. 10, No. 3, 1995.
Ishii, K., ed.: Membrane Structures in Japan, SPS Publishing, Tokyo, 1996.
Kappraff, J.: “A Course in the Mathematics of Design,” Structural Topology, No. 8, 1983.
Kihlstedt, F. T: “The Crystal Palace,” Scientific American, Vol. 251, No. 4, 1984.
Kuhn, W: “Cubic Structures with Elements Obtained by the Concretization of Geometrical Reticulations,” Zodiac, Vol. 19, 1969.
Lalvani, H.: Transpolyhedra, Dual Transformations by Explosion-Implosion, New York, 1977.
Lalvani, H.: “Spatial Concepts for Non-Periodic Architecture, A Selection from 8 Patents Focusing on Non-Periodic Geometries for a New Generation of Architectural Space Structures and Space-Defining Systems,” 1991.
Lalvani, H., and Collins, T: “Comparative Morphology of Configurations with Reduced Part Count Derived from the Octahedral-Tetrahedral Truss,” NASA Technical Memorandum 102768, 1991.
Le Ricolais, R.: Interviews with Le Ricolais, Structures Implicit and Explicit, Graduate School of Fine Arts, University of Pennsylvania, Philadelphia, 1973.
Makowski, Z. S.: “Space Structures of Today and Tomorrow,” Proceedings of the Third International Conference on Space Structures, University of Surrey, 1984.
Makowski, Z. S.: “New trends in Spatial Structures,” Bulletin of the International Association for Shell and Spatial Structures, Vol. 27, No. 1, 1986.
Makowski, Z. S.: “Space StructuresA Review of the Developments Within the Last Decade,” Space Structures, 1993.
Medwadowski, S. J.: “Space Frames and Architecture,” Bulletin of the International Association for Shell and Spatial Structures, Vol. 14, No. 3, 1983.
Mengeringhausen, M.: Komposition i?n Raum, Wurzburg, 1983.
Nervi, P. L.: “Is Architecture Moving Toward Unchangeable Forms?” Structure in Art and in Science, G. Kepes, ed., Braziller, New York, 1965.
Neumann, A.: “Architecture as Ornament,” Zodiac, Vol. 19, 1969.
Pauling, L.: The Nature of the Chemical Bond, Cornell University Press, 1939.
Pearce, P.: Structure in Nature Is a Strategy for Design, MIT Press, Cambridge, MA.
Popko, E.: Geodesics, University of Detroit Press, 1968.
Rebielak, J.: “Space StructuresProposal for Shaping,” International Journal of Space Structures, Vol. 7, No. 3, 1992.
Safdie, M.: “New Environmental Requirements for Urban Building,” Zodiac, Vol. 19, 1969.
Salvadori, M.: Why Buildings Stand Up, W. W. Norton, 1980.
Samuely, F. J.: “Space Frame Defined,” Architectural Forum, Feb. 1953.
Satterwhite, R. G.: “A Space-Frame as a Home,” International Journal of Space Structures, Vol. 6, No. 4, 1991.
Sloane, N.J. A.: “The Packing of Spheres,” Scientific American, Vol. 250, No. 1, 1984.
Stewart, D.: “Skyscraping,” Discover, Vol. 1, No. 9, 1988.
Stuart, D. R.: “Space-Filling Ortho-Surfaces and Their Duals,” International Journal of Space Structures, Vol. 6, No. 4, 1991.
Thompson, D. W.: On Growth and Form, Cambridge University Press, 1969.
Tbrroja, E.: The Structures of Eduardo Torroja, F. W. Dodge Corporation, New York, 1958.
Tucker, J. B.: “Superskyscrapers: Aiming for 200 Stories,” High Technology, Vol. 5, No. 1, 1985.
Tyng, A. G.: “Synthesis of a Traditional House with a Space-Frame,” International Journal of Space Structures, Vol. 6, No. 4, 1991.
Wachsmann, K: The Turning Point of Building, Reinhold, 1961.
0 ontributors
IRENE E. AYAD was bom in Germany and partially raised in England, where she completed her secondary education. After a brief stay in Egypt, she came to the United States, where she studied art history at Empire State College in Buffalo, New York While an undergraduate student there, she was also a regular contributor to a broadcast program on cultural affairs. The program was offered weekly by an affiliate station of National Public Radio and focused on art, architecture, and urban issues. This gave Irene Ayad the impetus for earning her graduate degree in urban planning at the State University of New York at Buffalo. It is there that she became interested in the work of Louis Kahn and went on to pursue further graduate studies at Cornell University. She received her Ph.D. in architectural and urban history with a thesis on Louis Kahn.
Dr. Ayad has taught at Cornell University, the University of Tennessee at Knoxville, and Roger Williams University. She is currently working on a book about Louis Kahn’s neighborhood and housing projects.
LAWRENCE DAVIS, a registered architect, grew up in the Midwest and earned a Bachelor of Architecture degree (magna cum laude) from the University of Cincinnati, and a master’s degree from Columbia University, New York. He studied under Kenneth Frampton and Steven Holl, and he was teaching assistant and occasional employee of the latter. He worked for three years in the office of James Stewart Polshek and Partners, most notably on the Yerba Buena Theater in San Francisco. He opened his own practice in Cincinnati in 1991, at the same time teaching and pursuing his research interests.
Since 1994, Lawrence Davis has been an assistant professor at the Syracuse University School of Architecture, New York, where he teaches architectural design and the history and theory of the suburban environment in America.
J. FRANCOIS GABRIEL was bom and raised in Paris where he studied art and architecture. He received a classical training at the Ecole des Beaux-Arts and practiced architecture in Paris and the United States. While a student he was invited by Le Corbusier to join CIAMZAscoral.
For many years, J. Francois Gabriel has investigated the architectural potential of space frames and advocated their use. He has published and lectured on the subject in many countries. He belongs to the International Association for Shell and Spatial Structures (IASS) and is co-founder of its Structural Morphology Working Group. He is also a member of the editorial board of the International Journal of Space Structures.
J. Francois Gabriel has taught at several universities, including the Massachusetts Institute of Technology and Syracuse University, New York, where he currently teaches courses on the design of classical buildings, space structures, and the architecture of space frames.
ARIEL HANAOR earned a Bachelor of Science degree and a master’s degree in civil engineering from the Technion in Haifa. In 1980, he received a Doctorate of Philosophy in civil engineering from the University of Melbourne, Australia. He worked as a consulting engineer in Israel from 1965 to 1972, and in Australia from 1973 to 1979.
His doctoral research at the University of Melbourne focused on space trusses, and he did postdoctoral research at the Imperial College in London on concrete technology, and at Rutgers University in New Jersey on structural analysis, space structures, tensegrity systems, and concrete technology. Since 1980, he has been a senior research fellow at the National Building Research Institute, the Technion, working primarily on steel structures.
Dr. Hanaor is a member of the International Association for Shell and Spatial Structures (IASS), and of the editorial board of the International Journal of Space Structures.
PIETER HUYBERS was bom in the Netherlands and studied architecture at the Faculty of Building Engineering of the Technical University of Delft. He received a doctorate degree in 1972.
He worked in an architectural office and his designs were built in the Netherlands, Mali, and England. In research, he concentrates on the potential of construction materials such as GRP, cardboard, plastics, membranes, thin roundwood, and on the potential of polyhedra in building. He is the head of a research group on building technology at the Civil Engineering Faculty of Delft University.
Dr. Huybers is a member of the International Association for Shell and Spatial Structures (IASS) and one of the founding members of the IASS working group on structural morphology.
HARESH LALVANI is a professor of architecture at the Pratt Institute and Design Scientistin-Residence at the Cathedral of St. John the Divine in New York.
He has been involved with morphological research for nearly three decades and has exhibited and published widely, presenting his work at leading forums on art, morphology, architecture, engineering, mathematics, space structures, and computer graphics. He has authored two books, Transpolyhedra in 1977 and Structures on Hyper-Structures in 1982.
He contributed to the 1988 U.S. government report on research strategy for computer-aided productivity and, between 1989 and 1990, he spent a sabbatical year at the NASA-Langley Research Center, Hampton, Virginia. He was curator of the Buckminster Fuller Centennial Exhibition Contemporary Developments in Design Science, which opened at the Cathedral of St. John the Divine in 1995, continued at the Pratt Institute, and moved to Mimar Sinan University in conjunction with the United Nations’s Habitat II Conference, held in Istanbul in 1996.
Professor Lalvani received grants from the Graham Foundation for Advanced Studies in the Fine Arts, the National Endowment for the Arts, and the National Institute for Architectural Education. He is affiliated with the International Society for the Interdisciplinary Study of Symmetry (ISIS), the Japan Institute for Hyper-Space Science, and the Structural Morphology Working Group, and he serves on the editorial boards of the International Journal of Space Structures and Structural Topology. He is the guest editor of the special issue of Space Structures on Morphology and Architecture.
MATTHYS LEVY was bom in Switzerland and graduated from the City College of New York. He earned a Master’s of Science degree and a civil engineering degree from Columbia University.
He was the principal designer of the Javits Exhibition and Conference Center in New York, the Georgia Dome in Atlanta, the Banque Lambert building in Brussels, among many other buildings, for example, in Boston, London, and Korea.
Matthys Levy taught at Columbia University and the Pratt Institute in New York and has lectured at universities around the world. In addition to numerous professional publications on structures, computer analysis, aesthetics, and building systems design, he is co-author of the books Why Buildings Fall Down, Structural Design in Architecture, and Why the Earth Quakes. He is a member of the National Academy of Engineering and many professional societies, and he has served as director of several corporations. He is the recipient of many awards, including the American Society of Civil Engineers (ASCE) Innovation in Civil Engineering Award and the IASS Tsuboi Award.
He is the inventor of the Tenstar Dome structure, a tensegrity dome used to cover large spaces.
ARTHUR L. LOEB was bom in Amsterdam, where he received his primary and secondary education. He earned a Bachelor of Science degree in chemistry from the University of Pennsylvania, and a master’s degree in physics and a Doctorate of Philosophy in chemical physics from Harvard University.
Arthur Loeb’s publications include Introduction to Wave Mechanics, with Louis Harris (McGraw-Hill), Color and Symmetry (Wiley/Krieger), Space Structures (Addison-Wesley/Birkhaiiser), Concepts and Images (Birkhaiiser), and contributions to Gyorgy Kepes’s Vision and Value series, Buckminster Fuller’s Synergetics, Hargittai’s Symmetry, and Clifford Pickover’s Future of Fractals. His articles have been published in Acta Crystallo-graphica, Leonardo, International Journal of Space Structures, Physical Review, and other periodicals.
He is the editor of the Design Science Collection for Birkhaiiser, vice-president of the International Society for the Interdisciplinary Study of Symmetry, member of the Advisory Board of the Buckminster Fuller Institute, and a life fellow of the American Institute of Chemistry and the Royal Society of Arts of London.
Professor Loeb is also an artist and a professional singer. He is the founder of the Collegium losquinum in Boston.
A former Master and Honorary Associate of Dudley House at Harvard University, he is currently a senior lecturer and honorary associate in visual and environmental studies and a member of the faculty of the Graduate School of Education. He teaches design science and visual mathematics.
RENE MOTRO is a civil engineer and, since 1983, a doctor of state of the University of Montpellier in France. He has assumed the scientific leadership of two research teams on lightweight structures, one of which is established at the School of Architecture of the University of Montpellier. He is engaged in the study of initially stressed systems applied to tensegrity systems and form-finding of cable nets and membrane structures.
Professor Motto’s interest in spatial structures led him to study the geometry of poly-hedra with a view toward geometric optimization. He has become simultaneously involved with the symbolism of polyhedra, a topic on which he has lectured and published a number of studies.
A member of the executive council of the International Association for Shell and Spatial Structures (IASS) and co-founder of its working group on structural morphology, in 1992 he organized the First International Seminar on that topic.
HOSHYAR NOOSHIN was bom in Tehran and received his first degree in civil engineering from the University of Tehran. He subsequently earned a Ph.D. from the University of London.
He is currently a professor of space structures in the Department of Civil Engineering at the University of Surrey, where he is also the director of the Space Structures Research Centre.
Professor Nooshin is the chief editor of the International Journal of Space Structures and a fellow of the Institution of Civil Engineers. He is the originator of the concept of formex algebra.
ROLLAND RISTINE is an architect who studied under Bruce Goff at the University of Oklahoma.
He has worked with several architectural firms in Chicago, then in New York, notably with Edgar Tafel, Conklin and Rossant, Stephen B. Jacobs, and Robert E. Meadows. He has taught courses on the history of architecture at the Manhattan Center of the New York Institute of Technology. His practice, based in Brooklyn, now concentrates on the making of architectural renderings.
Rolland Risdne is the editor of Network News, the newsletter of the Friends of Keb-yar, an organization comprising the friends, clients, and former students of Frank Lloyd Wright, Bruce Goff, and their followers.
TONY ROBBIN is an artist who lives in New York. He has had over 20 solo exhibitions and participated in 150 group exhibitions in the United States and abroad.
He is the author of two books, Fourfield: Computers, Art and the Fourth Dimension, published in 1992 (Bulfinch, Little Brown), and Engineering a New Architecture, published in 1996 (Yale University Press). He was the recipient of grants from the Graham Foundation for Advanced Studies in the Arts, the National Science Foundation, and the National Endowment for the Arts. He has lectured extensively to university audiences and professional organizations of artists, mathematicians, computer scientists, architects, and engineers.
For the past 10 years, Tony Robbin has pioneered and advocated the use of quasicrystal geometry in architecture.
MASAO SAITOH is a graduate of the Department of Architecture of Nihon University, where he currently is a professor of structural engineering. Active in research on space structures and their applications, he has developed hybrid tension systems such as beam string structures, “Skelsion,” and complex string domes.
He contributed to the design of many notable structures, including the Suntory Pavilion at Tsukuba Expo ‘85, the Multi-Sports Complex Amagi Dome, the Iwase Sports Dome, both of 1991, and the Izumo Dome Stadium of 1992. In 1986, he received the Architectural Institute of Japan Award.
Professor Saitoh is a member of the executive council of the International Association for Shell and Spatial Structures (IASS) and vice-chairman of its working group on tension structures.
JOSTOMLOW is a Dutch engineer who studied architecture at Delft University. Early on, he developed an interest in the structural and mathematical aspects of architecture and he became one of the co-founders of the Gaudf Research Delft Group, directed by Jan Mole-ma. In 1986, he received a doctoral degree from Stuttgart University. His thesis was about Gaudi’s hanging model, which was reconstituted on a large scale by a German-Dutch team.
Jos Ibmlow was inspired by Frei Otto’s influence to work at the Institute of Lightweight Structures. There, he assisted Rainer Graefe and Ekkehard Ramm in their studies on the history of structural design. This is one area investigated by the research group SFB 230: Natural Structures-Lightweight Structures in Architecture and Nature.
Since 1995, Professor Tomlow has been teaching art and architectural history in the Building Department of the Hochschule fur Technik, Wirtschaft und Sozialwesen Zit-tau/Gbrlitz in Germany.
TURE WESTER graduated from the Danish Engineering Academy and worked on form-finding and the design of spatial structures with several consulting engineering companies before joining the School of Architecture at the Royal Danish Academy of Fine Arts as a lecturer and research assistant. He is currently associate professor and head of the Laboratory for Plate Structures, which is supported by the Danish Technical Research Foundation and the Danish Ministry of Culture.
Structural morphology, structures in nature, force and form language, and the structural behavior and optimal shaping of plate structures are among Tire Wester’s main research topics. He is the originator of the concept of structural duality and the author of Structural Order in Space. He has published numerous research papers in international journals and conference proceedings.
Professor Wester is a member of the board of the International Society for the Interdisciplinary Study of Symmetry (ISIS), the executive council of the International Association for Shell and Spatial Structures (IASS), chairman of the IASS working group on structural morphology, and a member of the editorial board of the International Journal of Space Structures. He was also co-editor of several conference proceedings.
¶ Index
Abu Ali al-Hasan (Alhazen), 9
Adams (John Quincy) House (Vinita, Oklahoma, Goff), 69
Adath Jeshurun Synagogue and School Building (Elkins Park, Pennsylvania, Kahn), 136
Amman, Jost, 16, 18
Antiprisms:
construction polyhedra, 262, 264
polyhedra, 253, 256, 259
Applewhite, E. J., 156, 157
Arabic world, polyhedra, 9, 154
Arch-grids, tensegrity, 393
Archimedes, 6
Archimedian polyhedra, computer-aided processing, 353.
See also Computer-aided processing Architecture:
geometry and, 427. See also Geometry
habitability, 439. See also Habitability
Augmentation, construction polyhedra, 276
August of Saxony, 23
Ayad, Irene, ix
Baer, Steve, 434
Banchoff, Thomas, 432
Bank of China (Hong Kong, Pei), 466
Barbari, Jacopo de’, 12
Barbaro, Daniele, 11
Barbarossa Chandelier (Aachen Cathedral), 6
Bartlett, Jennifer, 183
Bartman (Irma) House (Triaero, Fem
Creek, Kentucky, Goff), 64, 68 Basic polyhedra. See also Computer-aided processing computer-aided processing, 344 defined, 302
Bass (William H.) House (Tulsa, Oklahoma, Goff), 59
Baursfeld, Walter, 330
Bell, Alexander Graham, viii, 28
Bernini, Gian, 168
Birkerts, Gunnar, 176
Black Bear Motor Lodge (Jackson
Hole, Wyoming, Goff), 71
Body ornaments, polyhedra, 2
Bone structure, 321, 323
Boullee, E.-L., 177
Bragdon, Claude, 38
Brahe, Tycho, 21
Briar Associates Projects (Bartlesville,
Oklahoma, Goff), 71
Bricard, R., 306
Brown, Denise Scott, 184
Bruckner, Max, 28, 250
Buckminsterfullerene, 158
Buffer forces, structural morphology, 309
Burgee, John, Crystal Cathedral
(Orange County, California, Johnson & Burgee), 161. See also
Crystal Cathedral (Orange County, California, Johnson 8c Burgee) Brut, M., 410, 419
Calladine, C. R., 399
Canting, computer-aided processing, 357
Case Study Movement, 176
Cauchy, Augustin-Louis, 303
Champion, O. C., xi
Choisy, Auguste, 132
Chorbachi, Wasma’a, 154 Chords. See Lattice structures Churchill, Winston, 58
City lower (Philadelphia, Pennsylvania,
Kahn), 130, 138
Civic Center-Forum (Philadelphia, Pennsylvania, Kahn), 141
Close packings, construction polyhedra, 262,263
COAST (Technical University, Denmark, Robbin), 437
Coccolithophores, 321, 323
Cole, Thomas, 181, 182
Collapse analysis, Javits Center (New
York City, Freed), 206 Complementary cap, hexmods, 450 Component tests, Javits Center (New
York City, Freed), 204
Computer-aided processing, 343 architectural objects, structural morphology, 319 basic polyhedra, 344 codes and P-names, 355 coordinate systems, 359, 362 face identity numbers and baselines, 362
generally, 353 geodesic configurations, 350 Goff, Bruce and, 40
identity numbers and directions for edges, 369
identity numbers and handles for vertices, 372
mapping
of edge-objects, 372 on edges, 347 of face-objects, 367 on faces, 345 of vertex-objects, 374 on vertices, 349
multi-layer configurations, 378 ordering rules, 380 overview, 343
Platonic and Archimedian polyhedra, 353
polyhedric configurations, 353 polymation function, 374 properties, 358, 360 shaping and composing, 377
Connectivity, defined, 302 Connelly, Robert, 306
Construction polyhedra, 260 augmentation, 276 close packings, 262, 263 hemispherical structures, 265 prismatic and antiprismatic forms, 262, 264
prisms, 260
reciprocal sphere subdivisions, 272 solitary applications, 260
Cook, Peter, 467
Coordinate systems, computer-aided processing, 359, 362
Coxeter, H. S. M., 37,153,157,158, 281 Cret, Paul Philippe, 132 Critchlow, K., 9, 281, 297
Crystal Cathedral (Orange County, California, Johnson & Burgee), 161. See also Johnson, Philip contemporary pasture, 181 evangelism and, 163 glass chain, 171 morality, 167 nature and, 180 overview, 161, 185 postmodern context, 177
Crystal Chapel (Norman, Oklahoma, Goff), 90
Crystals. See Natural crystals Cube deconstruction, 229 cuboctahedron, 231, 234 duals, 239 overview, 229, 239 regular tetrahedron and octahedron, 230
rhombic dodecahedron, 237 Stella octangula, 233, 234, 235 truncated octahedron, 233, 235, 236, 237
Cubic form, 36 instability of, x, 466 prevalence of, vii proportion, 291
Cuboctahedron, 36 computer-aided processing, 344 cube deconstruction, 231, 234 described, 149 Fuller and, 153 Goff and, 92 habitability, 479, 481. See also Habitability
megapolyhedra, 468, 470 vector equilibrium, 153
Curved variants, space labyrinths, 419
Debussy, Claude, 40 Decks, habitability, 483
De Long, David, 43, 48, 56, 61, 89, 112
“Devil’s work ball” (Chinese), polyhe-dra, 25
Dipyramid (octahedron), 36, 69. See also Octahedron
Direct transformation, structural morphology, 312
Disney, P. L., xi
Dodecahedron, 36
computer-aided processing, 344 cube and, proportion, 291 history, 12, 13
icosahedron and, proportion, 293 octahedron and, proportion, 292 rhombic, cube deconstruction, 237
tetrahedron and, proportion, 292 Doors, habitability, 443, 483 Doppelmayr, J. G., 23
Double-layer tensegrity grids, 393, 398, 400, 401. See also Tensegrity
Dualism, defined, 304
Duality:
computer-aided processing, 357 defined, 304
Dual objects:
cube deconstruction, 239 defined, 304
Dual structures:
geometrical qualities of, 314 structural qualities of, 315
Dual transformation, defined, 304 Diirer, Albrecht, 11, 14, 16 Dynamic relaxation method, tensegrity, load response, 400
Eames, Charles, 176
Eames, Ray, 176
Echinodermata, 321, 326
Edmondson, Amy, 157
Eiffel, Gustave, 466
Elements, defined, 302
Elevators, hexmods, 446,475
Emmerich, D. G., 277, 386, 391,396, 397
Equilibrium forces, structural morphology, 310
Escher, M. C., 154, 155 Euclid, 1, 3, 5, 9, 14, 16, 25 Euler, L., 304
Evangelism, 163
Face mapping. See Mapping Faust, Robert, 65, 67, 68 Fire safety, hexmods, 453, 475 First National Bank (Independence, Missouri, Goff), 77
Flexibility, defined, 305
Floor plans:
habitability, 486 tessellated, 48
Floors, habitability, 484
Floral Hills Temple of Rest (Las Vegas Nevada, Goff), 51
Foraminifera (plankton), 321, 322 Ford, Henry, vii
Formalism, rejection of, 43
Formex algebra, computer-aided processing, 343
Foster, Norman, 176
Fourth dimension, geometry, 430 Frampton, Kenneth, 171, 176
Freed, James Ingo, 189. See also Javits Convention and Exhibition Center (NYC, Pei, Cobb, and Freed)
Frustum, 36
Fuller, Anne Hewlett, 157
Fuller, Margaret, 156
Fuller, R. Buckminster, ix, xi, 37, 46, 80, 101, 104, 127, 129, 130, 133, 147, 232, 306, 330, 332, 385, 391, 396, 467
Gabriel, J. Frangois, 31, 337
Garden Grove Community Chapel. See Crystal Cathedral (Orange County, California, Johnson & Burgee)
Gaudf, Antonio, 31, 37, 39, 98
Gaussian curvature:
defined, 304
dual structures, geometrical qualities of, 314
Gehry, Frank, 40
Geodesic configurations, computer-aided processing, 350
Geodesic domes, 36, 46, 391. See also
Tensegrity
Geometric rigidity, tensegrity, load response, 399
Geometry, 427
architectural space and, 427 fourth dimension, 430 quasicrystals, 433
tensegrity, 390. See also Tensegrity
Ghyka, M. C., 281, 284
Gillespie, John Burkes, 97
Glass chain, Crystal Cathedral (Orange
County, California, Johnson &
Burgee), 171
Goff, Bruce, viii, 35
architectural history and, 38
computer and, 40
geometry and, 40, 44
legacy of, 118
monumentality, 42
overview, 35
polyhedra and, 36, 44, 48
psychology and symbolism, 42 spatial experience and, 43 works, 50
Adams (John Quincy) House (Vinita, Oklahoma), 69
Bartman (Irma) House (Triaero, Fem Creek, Kentucky), 64, 68
Bass (William H.) House (Tulsa, Oklahoma), 59
Black Bear Motor Lodge (Jackson Hole, Wyoming), 71
Briar Associates Projects (Bartlesville, Oklahoma), 71
Crystal Chapel (Norman, Oklahoma), 90
First National Bank (Independence, Missouri), 77
Floral Hills Temple of Rest (Las Vegas Nevada), 51
Gutman (Emil) House (Gulfport, Mississippi), 65
Hyde/Lane (Lawrence and Scott) House (Kansas City, Missouri), 50
Jones (Howard) House (Bartlesville, Oklahoma), 81
MacBryde (W. R.) House (Kansas City, Kansas), 73
Nicol (Mr. and Mrs. James) House (Kansas City, Missouri), 51
Phi Beta Delta Fraternity House (Norman, Oklahoma), 75
Phi Sigma Epsilon Fraternity House (Talequah, Oklahoma), 73
Pi Lambda Phi Fraternity House (Norman, Oklahoma), 75
Pollock/Warriner (Donald, John, and Laura) House (Oklahoma City, Oklahoma), 111
Price (Joe) Studio and Residence (Bartlesville, Oklahoma), 82
Rudd (Vernon E.) House (San Mateo, California, 102
Snyder (Russell B.) House, 47 Unseth/Newman (Helen and
Sheldon) House (Park Ridge, Illinois), 70
Wilson (James D.) House (Pensacola, Florida), 105 Golden proportion, 43, 282 Graham, Billy, 165, 166, 169 Grantham, Larry Wayne, 44, 80, 81, 86, 110
Greek antiquity: polygons, 3 polyhedra, 5
Greene, Herb, 35, 40 Grip, R., 396
Gropius, Walter, 135
Gunn, Charles, 412
Gutman (Emil) House (Gulfport, Mississippi, Goff), 65
Habitability, 439
hexmods, 447
building system, 453
generally, 447
lattice structures, 444 overview, 439, 490 polyhedra interiors, 440
space frames and polyhedra, 476
space trusses and megapolyhedra, 466
star beam, 459
unadulterated polyhedra, 481
Haeckel, E. H.P.A., 31
Hanaor, Ariel, xii
Harrison, Wallace, 95
Harvey, David, 170, 171, 173
Haughton, Eric, 155
Hayden, Hans, 18
Heath, James, 97
Helicoidal module, hexmods, 454, 473, 474, 475
Hemispherical structures, construction polyhedra, 265
Hexagon, habitability, 466
Hexmods, 447
building system, 453
generally, 447
habitability, 466
large buildings, 473
star beam compared, 459, 460
Hilbert, D., 281
Hockney, David, 183
Holden, Alan, 442
Honeycomb pattern, 448, 466
Huybers, Pieter, x
Hyde/Lane (Lawrence and Scott)
House (Kansas City, Missouri, Goff), 50
Hyper-polyhedra, tensegrity, 396
Icosahedron, 36 computer-aided processing, 344 dodecahedron and, proportion, 293
Icosidodecahedron, 36, 309
Imperfect polyhedra, 37
Inness, George, 181
International Plaza of PORTOPIA’81 (Kobe, Japan). See PORTOPIA’81 (Kobe, Japan)
Islam. See Arabic world
Jamnitzer, Wenzel, 16
Javits Convention and Exhibition Center (NYC, Pei, Cobb, and Freed), x, 189
assembly, 197
collapse analysis, 206 component tests, 204
fabrication and construction, 201 geometry and structural form, 190
jointing, 194 overview, 189 politics and, 189 risk models, 204
structural analysis, 199 ultimate load capacity, 206
Jeanneret, Pierre, 167
Jewish Community Center/Day Camp (Trenton, New Jersey, Kahn), 138
John Hancock Tower (Chicago, Illinois, Khan), 466
Johnson, Philip, ix-x, 40, 101, 102, 161. See also Crystal Cathedral (Orange County, California, Johnson & Burgee)
Jointing, Javits Center (NYC, Pei, Cobb, and Freed), 194
Jones (Howard) House (Bartlesville, Oklahoma, Goft), 81
Kahn, Louis I., ix, 127, 175, 467 Adath Jeshurun Synagogue and
School Building (Elkins Park, Pennsylvania), 136
City Tower (Philadelphia, Pennsylvania), 130, 138
Civic Center-Forum (Philadelphia, Pennsylvania), 141
Jewish Community Center/Day
Camp (Trenton, New Jersey), 138 overview, 127
Yale University Art Gallery (New Haven, Connecticut), 128, 135
Kent, George, 175
Kepes, Gyorgy, 157
Kepes, Juliette, 157
Kepler, Johannes, 4, 9, 12, 21, 257, 301
Khan, Fazlur, 466
Kindi, A1-, 9
Kites, polyhedra and, 28
Knoppe, Hugo, 24, 25
Koller, Christof, 24
Laban, Rudolf von, 229
Lalvani, Haresh, xii, 281, 298, 410, 421,424,433
Langer, Suzanne, K., 42
Large buildings, space trusses and megapolyhedra, 466
Lattice structures:
combined lattice and plate structures, structural morphology, 337
defined, 303
habitability, 442, 444. See also
Habitability
structural morphology, man-made structures, 330
tetrahedron, history of, 28
Lautner, John, 102
Lawlor, R., 281
Le Corbusier, ix, 43, 75, 83, 142, 167, 168,281,453
Ledoux, C.-N., 177
Lencker, Hans, 18, 20, 24
Le Ricolais, Robert, 127, 133, 134 Levy, Matthys, x
Levy, R., 400
Lichtenstein, Roy, 180
Links and linking, defined, 302
Livability. See Habitability
Load response, tensegrity, 399.
See also Tensegrity
Lobenigk, Egidius, 24
Loeb, Arthur L., x, 147
London Zoo aviary, 386, 387
Lower cap, hexmods, 449, 450
Lyotard, Jean-Frangois, 173
MacBryde (W. R.) House (Kansas City,
Kansas, Goff), 73
Maggiore, Giovanni Ambrogio, 24
Mainestone, R., 13
Malkevitch, J., 6
Mapping:
of edge-objects, computer-aided processing, 372
on edges, computer-aided processing, 347
of face-objects, computer-aided processing, 367
on faces, computer-aided processing, 345
of vertex-objects, computer-aided processing, 374
on vertices, computer-aided processing, 349
Marx, Leo, 180
Maxwell, Delle, 412
Mazzocchio (hat), 9
Medieval forms, polyhedra, 6
Megapolyhedra, habitability, 466
Metamorphology, systematic, space labyrinths, 411
Meton, 282
Metric geometry, defined, 302
Meurant, R. C., 281
Michelangelo, 13
Mies vander Rohe, Ludwig, ix, 43, 83, 140, 142, 167, 171
Miyazaki, Koji, 424, 433, 434
Mobius, August Ferdinand, 303, 304, 306, 308, 340
Mobius strip, 303
Mobius’ theorem, 304, 307
Modeling, architectural objects, structural morphology, 317
Monumental! ty, polyhedra, 42
Moody, D. L., 165, 166
Morality, Crystal Cathedral (Orange
County, California, Johnson & Burgee), 167
Morris, William, 181
Motro, Rene, xi, 355, 395
Movability, defined, 305
Muller, John, 173, 175
Multicell regular polyhedra, Goff, Bruce, 46, 48
Multi-layer configurations, computer-aided processing, 378
Natural crystals: ordering of, 151 polyhedra, 1, 36
X-ray diffraction patterns, 158
Natural plate and lattice structures, 320
bone structures, 321, 323 generally, 320
planktonic organisms, 321, 322, 323 sea urchin, 325
Venus’s-flower-basket, 321, 324
Nature, Crystal Cathedral (Orange County, California, Johnson & Burgee), 180
Networks, tensegrity, 393
Neudorfer, Johann, 16
Neufchatel, Nicolas, 16
Neutra, Richard, 169, 176, 179
Neutrality, defined, 305
Nicol (Mr. and Mrs. James) House (Kansas City, Missouri, Goff), 51
Nielsen, J., 306
Nonregular polyhedra, Goff, Bruce, 45
Nooshin, Hoshyar, xi
Oblique walls, habitability, 476, 483 Octagons, Goff, Bruce, 52, 81 Octahedral stelladon, Goff, Bruce, 95
Octahedron, 36
computer-aided processing, 344 dodecahedron and, proportion, 292 Goff, Bruce, 69
interiors of, habitability, 441. See also
Habitability megapolyhedra, 468, 469 natural crystals, 151 regular, cube deconstruction, 230 truncated, cube deconstruction, 233, 235,236,237
Ogawa, T., 435
Oldenberg, Claes, 180
Otto, Frei, 423
Pacioli, Luca, 11, 28, 281, 290, 298 Paper models, polyhedra, 28, 29 Pappus, 6
Parabola, pure plate structures, structural morphology, 335
Parallelpiped architectural spaces, ubiquity of, 43
Park, Ben Allan, 38
Pastoral metaphor, Crystal Cathedral
(Orange County, California, Johnson & Burgee), 180
Paxton, Joseph, 97, 176
Pearce, Peter, 156, 298, 410, 419 Pei, Cobb, and Freed, x
Pei, I. M., 102, 466
Pellegrino, S., 399
Pelli, Cesar, 176
Pentagon, golden proportion, 282 Pentagonal geometry, Goff, Bruce, 61 Perspective projection, polyhedra, 27 Pfinzing, Paulus, 18
Phi Beta Delta Fraternity House (Norman, Oklahoma, Goff), 75
Phidias of Cercio, 13
Phi Sigma Epsilon Fraternity House (Talequah, Oklahoma, Goff), 73
Phisterer, Henry A., 128
Piero della Francesca, 11, 12
Pi Lambda Phi Fraternity House (Norman, Oklahoma, Goff), 75
Planing, computer-aided processing, 357
Planktonic organisms, 321, 322, 323
Plate structures:
combined lattice and plate structures, structural
morphology, 337 defined, 303
structural morphology, man-made structures, 330
Plato, xi, 5, 6, 281, 289, 290, 295, 296, 301
Platonic polyhedra, computer-aided processing, 353. See also Computer-aided processing
Poincare, J.-H., 424, 430
Polar reciprocation, structural morphology, 311
Politics, Javits Center (NYC, Pei, Cobb, and Freed), 189
Pollock/Warriner (Donald, John, and Laura) House (Oklahoma City, Oklahoma, Goff), 111
Polo, Marco, 25
Polygonal subdivisions, construction polyhedra, 268
Polygons:
Arabic world, 9
Greek antiquity, 3
Polyhedra, 243
classes of, 36
computer-aided processing, 343.
See also Computer-aided processing construction, 260. See also Con
struction polyhedra
definitions, 36, 245, 302, 303, 304, 305
Goff, Bruce, 35. See also Goff, Bruce
golden mean ratio, 43 history of, 1
Arabic contributions, 9 Bell, Alexander Graham, 28 body ornaments, 2 Bruckner, Max, 28
Chinese “devil’s work ball,” 25 Diirer, Albrecht, 14 Greek antiquity, 3 Jamnitzer, Wenzel, 16 Kepler, Johannes, 21 Medieval forms, 6 natural crystals, 1 Neudorfer, Johann, 16 Pacioli, Luca, 11 Piero della Francesca, 11 Taylor, Brook, 27 Uccello, Paolo, 9 Vinci, Leonardo da, 13 Zick, Lorenz, 22
imperfect, 37 interiors of, habitability, 440.
See also Habitability monumentality, 42 overview, 243 prisms and antiprisms, 253, 256, 259
proportion and, 282. See also Proportion
psychology and symbolism, 42 reciprocal faces, 250, 252, 254, 255
reciprocals, 250 regular forms, 36 stellated (Kepler-Poinsot) polyhedra, 257, 260
structural morphology, 301. See also Structural morphology symbolism, 294
essence of, 295 generally, 294 Plato’s cosmogony, 296 tensegrity, 390. See also Tensegrity types of, 245 vertex situations, 249
Polyhedral sphere subdivisions, construction polyhedra, 267
Polyhedric configuration: computer-aided processing, 353 defined, 343
Polymation function, computer-aided processing, 374
PORTOPIA’81 (Kobe, Japan), 211 construction, 223, 226 overview, 211, 225, 227 space truss shell numerical analysis, 221
structural design, 222 structural outline, 213 structural planning, 215
curved surface transition, 218 form, 216
member arrangement, 219 Postmodern context, Crystal Cathedral
(Orange County, California, Johnson & Burgee), 177
Price, Joe, 40
Price (Joe) Studio and Residence (Bartlesville, Oklahoma, Gofi), 82
Prisms, 36 construction polyhedra, 260, 262, 264
Goff, Bruce, 45 polyhedra, 253, 256, 259 skew prism, tensegrity, 390
Proportion, 282 golden, 282 overview, 281, 282 polyhedra, 288 dodecahedron and cube, 291 dodecahedron and icosahedron, 293 dodecahedron and octahedron, 292 dodecahedron and tetrahedron, 292 generally, 288 spheres, 293
Proust, Marcel, 43
Psychology, polyhedra, 42
Pure lattice structures, structural morphology, man-made structures, 330
Pure plate structures, structural morphology, man-made structures, 330
Pyramidization, construction polyhedra, 265
Pyramids, 36, 78 Pythagoras, viii, 1, 3
Quarter-tetrahedron, cube deconstruction, 238, 239
Quasicrystals, 158, 433. See also Geometry
Radiolaria (plankton), 321, 322
Reciprocal faces, polyhedra, 250, 252, 254, 255
Reciprocals, polyhedra, 250
Reciprocal sphere subdivisions, construction polyhedra, 272
Redundancy, defined, 305
Regular octahedron, cube deconstruction, 230
Regular polyhedra, described, 36
Regular tetrahedron, cube deconstruction, 230
Renaissance, polyhedra, 9, 11, 14, 16
Revivalism, Crystal Cathedral (Orange
County, California, Johnson & Burgee), 163
Rhombic dodecahedron, cube deconstruction, 237
Rhombic hexahedron, Goff, Bruce, 96
Rhombic triacontahedron, structural morphology, 309
Rhombicuboctahedron, history, 12 Rigidity:
defined, 305
geometric, tensegrity, load response, 399
man-made structures, 328
Risk models, Javits Center (New York City, Freed), 204
Ristine, Rollie, viii
Robbins, Tony, xii
Roche, Kevin, 176
Rodgers, Richard, 176
Room height, habitability, 440
Rowe, Peter, 166, 180, 181, 182, 183 Rudd (Vernon E.) House (San Mateo,
California, Goff), 102
Ruskin, John, 181
Saarinen, Eero, 176
Sadao, Shoji, 101, 154
Safdie, Moshe, 102, 158
Saitoh, Masao, x
Satie, Erik, 40
Scheerbart, Paul, 171
Schindler, Rudolf, 176
Schoen, A., 410
Schuller, Robert, 165, 166, 167, 168,
169, 170, 171, 173, 179
Schwedler, J. W., 330, 332
Sea urchin, 321, 325
Sensitivity, defined, 305
Sergeant, John, 64
Shear force, defined, 303
Simple polyhedra, defined, 302 Single-cell regular polyhedra, Goff,
Bruce, 46
Single-layer tensegrity grids, 395 Skew prism, tensegrity, 390 Skidmore, Owings, and Merrill, 99 Skinner, B. E, 155
Slack, Rex, 110
Snelson, Kenneth, 387, 388, 389
Snubbing, computer-aided processing, 357
Snyder (Russell B.) House (Goff), 47 Space frames, polyhedra and, habitabil
ity, 476
Space labyrinths, 409
curved variants and derivatives, 419
generation, 415
overview, 409
systematic metamorphology, 411 Space lattice. See Lattice structures Space trusses, habitability, 466 Space truss shell numerical analysis,
PORTOPIA’81 (Kobe, Japan), 221
Spheres, proportion, 293
Spider webs, 321
Spillers, W. R., 400
Spinel, 147
Stability, defined, 305
Staircase:
hexmods, 453
lattice structures, 446
Star beam, habitability, 459
Stella octangula, cube deconstruction, 233,234,235
Stellated (Kepler-Poinsot) polyhedra, 257, 260
Stevin, Simon, 277
Stiffness method, tensegrity, load response, 400
Stone, Barton Warren, 166
Storer, Lorenz, 18, 21
Structural analysis, Javits Center (New York City, Freed), 199
Structural design, PORTOPIA’81 (Kobe, Japan), 222
Structural morphology, 301 architectural objects, 316 modeling structures, 317 plate action, 320 visually-based analysis and design, 316
definitions, 302, 303, 304, 305 dual structures
geometrical qualities of, 314 structural qualities of, 315 historical perspective, 303 man-made structures, 327
combined lattice and plate structures, 337
generally, 327 pure lattice structures, 330 pure plate structures, 330 rigidity, 328
natural plate and lattice structures, 320
bone structures, 321, 323 generally, 320
planktonic organisms, 321, 322, 323
sea urchin, 325
Venus’s-flower-basket, 321, 324
overview, 301, 340 Structural outline, PORTOPIA’81
(Kobe, Japan), 213. See also
PORTOPIA’81 (Kobe, Japan) Structural planning, PORTOPIA’81
(Kobe, Japan), 215. See also
PORTOPIA’81 (Kobe, Japan)
Sullivan, Louis, 48
Sunday, Billy, 165, 166
Symbolism, 294
essence of, 295 generally, 294
Plato’s cosmogony, 296 polyhedra, 42
Systematic metamorphology, space
labyrinths, 411
Tafiiri, Manfredo, 179
Tall buildings, space trusses and megapolyhedra, 466
Tatlin, Vladimir, 167
Taut, Bruno, 97, 171
Taut, Max, 97
Taylor, Brook, 27
Technology:
Crystal Cathedral (Orange County, California, Johnson & Burgee), 177, 179
hexmods, 452
Tensegrity, xi-xii, 385
assessment, 405
definitions, 385
geometry, 390
networks, 393
polyhedra, 390
structural forms, 395 historical perspective, 386 load response, 399
characteristics of, 400 geometric rigidity, 399 structural analysis, 400
Tessellated floor plan, 48
Tetrahedron, 36 computer-aided processing, 344 dodecahedron and, proportion, 292 Goff, Bruce, 71, 92 history of, 28, 30
interiors of, habitability, 441. See also Habitability
Kahn, Louis L, 128 megapolyhedra, 468 natural crystals, 151 quarter-tetrahedron, cube deconstruction, 238, 239
regular, cube deconstruction, 230 Thomson, D’Arcy Wentworth, 131 Thurston, William, 412
Timaeus, 5, 289
Timoshenko, Stephen P., 306
Tomlow, Jos, viii
Topological information, defined, 302
Transformation, structural morphology, 312
Triacontahedron, rhombic, structural morphology, 309
Triaero (Irma Bartman House, Fem Creek, Kentucky, Goff), 64, 68
Triangular design, Goff, Bruce, 65 Truncated octahedron:
cube deconstruction, 233, 235, 236, 237
habitability, 479, 481. See also Habitability
megapolyhedra, 468, 469
Truncated tetrahedron: habitability, 479, 481. See also Habitability
megapolyhedra, 468, 469, 470
Truncation:
computer-aided processing, 357 construction polyhedra, 275
Tyng, Anne Griswold, ix, 127, 129, 130, 131, 133, 138, 140, 411,467
Uccello, Paolo, 9
Ultimate load capacity, Javits Center (New York City, Freed), 206
Unit cell, 148
Unseth/Newman (Helen and Sheldon) House (Park Ridge, Illinois, Goff), 70
Upper cap, hexmods, 449, 450
Valency, defined, 302 van der Ende, Gerrit, 277 van Gogh, Vincent, 430 Varney, William, 153
Vasari, Giorgio, 9, 13
Vector equilibrium, 149, 153, 232
Venturi, Robert, 184 Venus’s-flower-basket, 321, 324 Vertex situations, polyhedra, 249 Vieus, M., 295
Vilnay, O., 396, 397
Vinci, Leonardo da, 12, 13
Viollet-Le-Duc, Emmanuel, 132, 167 Virtual polyhedra, Goff, Bruce, 44 Visual morphology, of space labyrinths, 409. See also Space labyrinths
Wainwright, William, 152
Walls:
glazed, habitability, 484 oblique, habitability, 476, 483
Warhol, Andy, 180
Wecker, Georg, 24
Wester, Ture, xi
Wilson (James D.) House (Pensacola, Florida, Goff), 105
Windows, habitability, 483, 484 Wood, Robert, 166
Wright, Frank Lloyd, ix, 37, 45, 68, 75, 76, 78, 82, 83, 86, 87, 98, 99, 108, 118, 142,440, 456, 466
Yale University Art Gallery (New Haven, Connecticut, Kahn), 128, 135
Zick, Lorenz, 22, 26
¶ Source Scans
¶ eBook Formats
It has a high degree of applicability to a shape with a free-form curved surface. ↩︎
Stiffness and stress can be controlled by regulating the depth between the upper and lower layers. ↩︎
The bending moment is larger in stage 1 than in stage 3 and the deflec ↩︎
tion in stage 1 is smaller than in stage 3. ↩︎