¶ 900.00 Modelability
¶ 900.01 Definition: Modelability
¶ 900.10 Modelability
[900.11]{style="color: purple3"} []{#ver:900.11 label="ver:900.11"} Modelability is topologically conceptual in generalized principle independent of size and time: ergo, conceptual modelability is metaphysical.
[900.12]{style="color: purple3"} []{#ver:900.12 label="ver:900.12"} Conceptual formulation is inherently empirical and as such is always special case sizing and always discloses all the physical characteristics of existence in time.
¶ 900.20 Synergetics
[900.21]{style="color: purple3"} []{#ver:900.21 label="ver:900.21"} Synergetics is a book about models: humanly conceptual models; lucidly conceptual models; primitively simple models; rationally intertransforming models; and the primitively simple numbers uniquely and holistically identifying those models and their intertransformative, generalized and special case, number-value accountings.
¶ 900.30 Model vs. Form
[900.31]{style="color: purple3"} []{#ver:900.31 label="ver:900.31"} Model is generalization; form is special case.
[900.32]{style="color: purple3"} []{#ver:900.32 label="ver:900.32"} The brain in its coordination of the sensing of each special case experience apprehends forms. Forms are special case. Models are generalizations of interrelationships. Models are inherently systemic. Forms are special case systems. Mind can conceptualize models. Brains can apprehend forms.
[900.33]{style="color: purple3"} []{#ver:900.33 label="ver:900.33"} Forms have size. Models are sizeless, representing conceptuality independent of size.
¶ 901.00 Basic Disequilibrium Triangle
¶ 901.01 Definition
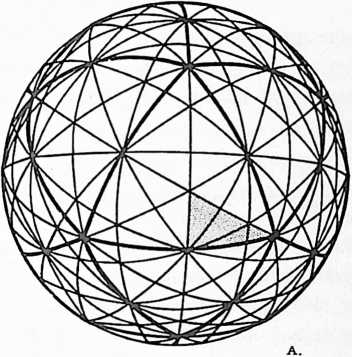
[901.02]{style="color: purple3"} []{#ver:901.02 label="ver:901.02"} The Basic Disequilibrium 120 Spherical Triangle of synergetics is derived from the 15-great-circle, symmetric, three-way grid of the spherical icosahedron. It is the lowest common denominator of a sphere’s surface, being precisely Vi2oth of that surface as described by the icosahedron’s 15 great circles. The trigonometric data for the Basic Disequilibrium Triangle includes the data for the entire sphere and is the basis of all geodesic dome calculations.
[901.03]{style="color: purple3"} []{#ver:901.03 label="ver:901.03"} As seen in Sec. 610.20 there are only three basic structural systems in Universe: the tetrahedron, octahedron, and icosahedron. The largest number of equilateral triangles in a sphere is 20: the spherical icosahedron. Each of those 20 equiangular spherical triangles may be subdivided equally into six right triangles by the perpendicular bisectors of those equiangular triangles. The utmost number of geometrically similar subdivisions is 120 triangles, because further spherical-triangular subdivisions are no longer similar. The largest number of similar triangles in a sphere that spheric unity will accommodate is 120: 60 positive and 60 negative. Being spherical, they are positive and negative, having only common arc edges which, being curved, cannot hinge with one another; when their corresponding angle-and-edge patterns are vertex-mated, one bellies away from the other: concave or convex. When one is concave, the other is convex. (See Illus. 901.03 and drawings section.)
[901.04]{style="color: purple3"} []{#ver:901.04 label="ver:901.04"} We cannot further subdivide the spherical icosahedron’s equiangular triangles into similar, half-size, equiangular triangles, but we can in the planar icosahedron. When the sides of the triangle in the planar icosahedron are bisected, four similar half-size triangles result, and the process can be continued indefinitely. But in the spherical icosahedron, the smaller the triangle, the less the spherical excess; so the series of triangles will not be similar. Each corner of the icosahedron’s equiangular triangles is 72 degrees; whereas the corners of its mid-edge-connecting triangle are each approximately 63 degrees.
¶ 901.10 Geodesic Dome Calculations
[901.11]{style="color: purple3"} []{#ver:901.11 label="ver:901.11"} When two great-circle geodesic lines cross, they form two sets of similar angles, any one of which, paired with the other, will always add to 180. (This we also learned in plane geometry.) When any one great circle enters into or exits froma spherical triangle, it will form the two sets of similar angles as it crosses the enclosing great-circle-edge-lines of that triangle.
[901.12]{style="color: purple3"} []{#ver:901.12 label="ver:901.12"} As in billiards or in electromagnetics, when a ball or a photon caroms off a wall it bounces off at an angle similar to that at which it impinged.
[901.13]{style="color: purple3"} []{#ver:901.13 label="ver:901.13"} If a great-circle-describing, inexhaustibly re-energized, satellite ball that was sufficiently resilient to remain corporeally integral, were suddenly to encounter a vertical, great-circle wall just newly mounted from its parent planet’s sphere, it would bounce inwardly off that wall at the same angle that it would have traversed the same great-circle line had the wall not been there. And had two other great-circle walls forming a right spherical triangle with the first wall been erected just as the resilient ball satellite was hitting the first great-circle wall, then the satellite ball would be trapped inside the spherical-triangle-walled enclosure, and it would bounce angularly off the successively encountered walls in the similar-triangle manner unless it became aimed either at a corner vertex of the triangular wall trap, or exactly perpendicularly to the wall, in either of which cases it would be able to escape into the next spherical area lying 180 ahead outside the first triangle’s walls.
[901.14]{style="color: purple3"} []{#ver:901.14 label="ver:901.14"} If, before the satellite bouncingly earned either a vertexial or perpendicular exit from the first-described spherical triangle (which happened to be dimensioned as one of the 120 right triangles of the spherical icosahedron) great-circle walls representing the icosahedron’s 15 complete great circles, were erectthus constructing a uniform, spherical, wall patterning of 120 (60 positive, 60 negative) similar spherical, right triangleswe would find the satellite sphere bouncing around within one such spherical triangle at exactly the same interior or exiting angles as those at which it would have crossed, entered into, and exited, each of those great-circle boundaries of those 120 triangles had the wall not been so suddenly erected.
[901.15]{style="color: purple3"} []{#ver:901.15 label="ver:901.15"} For this reason the great-circle interior mapping of the symmetrically superimposed other sets of 10 and 6 great circles, each of which together with the 15 original great circles of the icosahedronproduces the 31 great circles of the spherical icosahedron’s total number of symmetrical spinnabilities in respect to its 30 mid-edge, 20 mid-face, and 12 vertexial poles of half-as-many-each axes of spin. (See Sec. 457.00.) These symmetrically superimposed, 10- and 6-great-circles subdivide each of the disequilibrious 120 triangles into four lesser right spherical triangles. The exact trigonometric patterning of any other great circles orbiting the 120-LCD-triangled sphere may thus be exactly plotted within any one of these triangles.
[901.16]{style="color: purple3"} []{#ver:901.16 label="ver:901.16"} It was for this reason, plus the discovery of the fact that the icosahedronamong all the three-and-only prime structural systems of Universe (see Sec. 610.20)required the least energetic, vectorial, structural investment per volume of enclosed local Universe, that led to the development of the Basic Disequilibrium 120 Spherical Triangle and its multifrequenced triangular subdivisioning as the basis for calculating all high-frequency, triangulated, spherical structures and structural subportions of spheres; for within only one disequilibrious triangle were to be found all the spherical chord-factor constants for any desired radius of omnisubtriangulated spherical structure.
[901.17]{style="color: purple3"} []{#ver:901.17 label="ver:901.17"} In the same way it was discovered that local, chord-compression struts could be islanded from one another, and could be only tensionally and non-inter-shearingly connected to produce stable and predictably efficient enclosures for any local energetic environment valving uses whatsoever by virtue of the approximately unlimited range of frequency-and-angle, subtrianglestructuring modulatability.
[901.18]{style="color: purple3"} []{#ver:901.18 label="ver:901.18"} Because the 120 basic disequilibrious triangles of the icosahedron have 2\sfrac{1}{2} times less spherical excess than do the 48 basic equilibrious triangles of the vector equilibrium, and because all physical realizations are always disequilibrious, the Basic Disequilibrium 120 Spherical Triangles become most realizably basic of all general systems’ mathematical control matrixes.
[901.19]{style="color: purple3"} []{#ver:901.19 label="ver:901.19"} Omnirational Control Matrix: Commensurability of Vector Equilibrium and Icosahedron The great-circle subdivisioning of the 48 basic equilibrious triangles of the vector equilibrium may be representationally drawn within the 120 basic disequilibrious triangles of the icosahedron, thus defining all the aberrationsand their magnitudesexisting between the equilibrious and disequilibrious states, and providing an omnirational control matrix for all topological, trigonometric, physical, and chemical accounting.
¶ 902.00 Properties of Basic Triangle
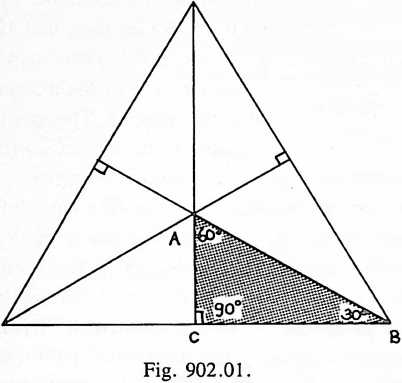
[902.01]{style="color: purple3"} []{#ver:902.01 label="ver:902.01"} Subdivision of Equilateral Triangle: Both the spherical and planar equilateral triangles may be subdivided into six equal and congruent parts by describing perpendiculars from each vertex of the opposite face. This is demonstrated in Fig. 902.01, where one of the six equal triangles is labeled to correspond with the Basic Triangle in the planar condition.
[902.10]{style="color: purple3"} []{#ver:902.10 label="ver:902.10"} Positive and Negative Alternation: The six equal subdivision triangles of the planar equilateral triangle are hingeable on all of their adjacent lines and foldable into congruent overlays. Although they are all the same, their dispositions alternate in a positive and negative manner, either clockwise or counterclockwise.
[902.20]{style="color: purple3"} []{#ver:902.20 label="ver:902.20"} Spherical Right Triangles: The edges of all spherical triangles are arcs of great circles of a sphere, and those arc edges are measured in terms of their central angles (i.e., from the center of the sphere). But plane surface triangles have no inherent central angles, and their edges are measured in relative lengths of one of themselves or in special-case linear increments. Spherical triangles have three surface (corner) angles and three central (edge) angles. The basic data for the central angles provided below are accurate to \sfrac{1}{1,000} of a second of arc. On Earth
1 nautical mile = 1 minute of arc
1 nautical mile = approximately 6,000 feet
1 second of arc = approximately 100 feet
\sfrac{1}{1,000}second of arc = approximately \sfrac{1}{10} foot
\sfrac{1}{1,000} second of arc = approximately 1 inch
These calculations are therefore accurate to one inch of Earth’s arc.
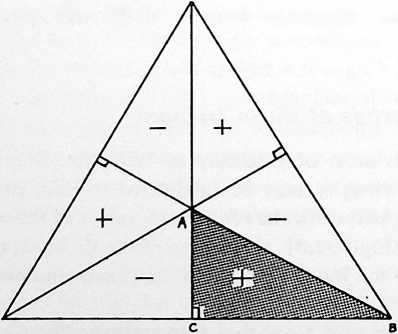
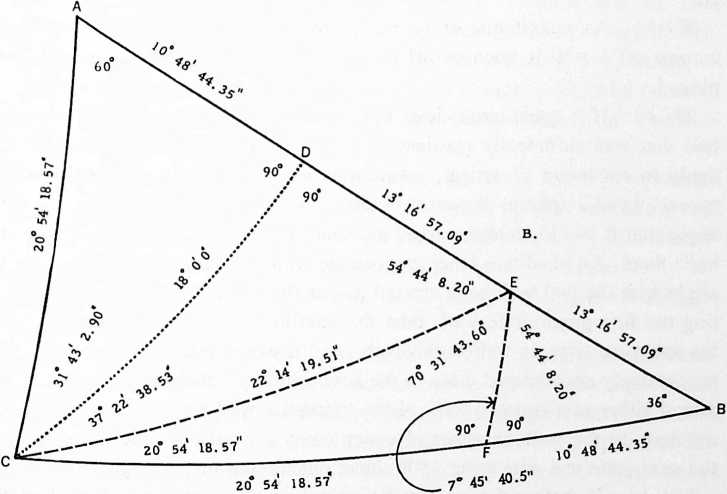
[902.21]{style="color: purple3"} []{#ver:902.21 label="ver:902.21"} The arc edges of the Basic Disequilibrium 120 Triangle as measured by their central angles add up to 90as do also three internal surface angles of the triangle’s corner:
[902.22]{style="color: purple3"} []{#ver:902.22 label="ver:902.22"} The spherical surface angle is exactly equal to two of the arc edges of the Basic Disequilibrium 120 Triangle measured by their central angle. .
[902.30]{style="color: purple3"} []{#ver:902.30 label="ver:902.30"} Surface Angles and Central Angles: The Basic Triangle can be folded on the lines and and . We may then bring to coincide with and fold BEF down to close the tetrahedron, with congruent with because the arc Then the tetrahedron’s corner will fit exactly down into the central angles , and . (See Illus. 901.03 and 902.30.)
[902.31]{style="color: purple3"} []{#ver:902.31 label="ver:902.31"} As you go from one sphere-foldable great-circle set to another in the hierarchy of spinnable symmetries (the 3-, 4-, 6-, 12-sets of the vector equilibrium’s 25-great-circle group and the 6-, 10-, 15-sets of the icosahedron’s 31-great-circle group), the central angles of one often become the surface angles of the next-higher-numbered, more complex, great-circle set while simultaneously some (but not all) of the surface angles become the respective next sphere’s central angles. triangle on the surface of the icosahedron folds itself up, becomes a tetrahedron, and plunges deeply down into the congruent central angles’ void of the icosahedron (see Sec. 905.47).
[902.32]{style="color: purple3"} []{#ver:902.32 label="ver:902.32"} There is only one noncongruence: the last would-be hinge, is an external arc and cannot fold as a straight line; and the spherical surface angle is 36 degrees whereas a planar 30 degrees is called for if the surface is cast off or the arc subsides chordally to fit the 90-60-30 right plane triangle.
[902.33]{style="color: purple3"} []{#ver:902.33 label="ver:902.33"} The 6 degrees of spherical excess is a beautiful whole, rational number excess. The 90-degree and 60-degree corners seem to force all the excess into one corner, which is not the way spherical triangles subside. All the angles lose excess in proportion to their interfunctional values. This particular condition means that the 90 degrees would shrink and the 60 degrees would shrink. I converted all the three corners into seconds and began a proportional decrease study, and it was there that I began to encounter a ratio that seemed rational and had the number 31 in one corner. This seemed valid as all the conditions were adding up to 180 degrees or 90 degrees as rational wholes even in both spherical and planar conditions despite certain complementary transformations. This led to the intuitive identification of the Basic Disequilibrium 120 Triangle’s foldability (and its fall-in-ability into its own tetra-void) with the Quanta Module, as discussed in Sec. 910.00, which follows.
¶ 905.00 Equilibrium and Disequilibrium Modelability
[905.01]{style="color: purple3"} []{#ver:905.01 label="ver:905.01"} Tetrahedron as Model: Synergetics is the geometry of thinking. How we think is epistemology, and epistemology is modelable; which is to say that knowledge organizes itself geometrically, i.e., with models.
[905.02]{style="color: purple3"} []{#ver:905.02 label="ver:905.02"} Unity as two is inherent in life and the resulting model is tetrahedral, the conceptuality of which derives as follows:
-
life’s inherent unity is two;
-
no otherness = no awareness;
-
life’s awareness begins with otherness;
-
otherness is twoness;
-
this moment’s awareness is different from previous awareness;
-
differentiations of time are observed directionally;
-
directions introduce vectors (lines);
-
two time lines demonstrate the observer and the observed;
-
the interconnection of two lines results in a tetrahedron;
-
sixfold interrelatedness is conceptual;
¶ 905.10 Doubleness of Unity
[905.11]{style="color: purple3"} []{#ver:905.11 label="ver:905.11"} The prime number twoness of the octahedron always occurs in structuring doubled together as fouri.e., a fourness which is also doubleness of unity. Unity is plural and, at minimum, is two. The unity volume 1 of the tetrahedron is, in structural verity, two, being both the outwardly displayed convex tetrahedron and the inwardly contained concave tetrahedron. (See Chart 223.64, columns 2, 12, and 15)
[905.12]{style="color: purple3"} []{#ver:905.12 label="ver:905.12"} The three-great-circle model of the spherical octahedron only “seems” to be three; it is in fact “double”; it is only foldably produceable in unbroken (whole) great-circle sheets by edge-combining six hemicircularly folded whole great circles (see Sec. 850). Thus it is seen that the octahedron as in Iceland spar crystalsoccurs only doubly, i.e., omnicongruent with itself, which is “quadrivalent.”
[905.13]{style="color: purple3"} []{#ver:905.13 label="ver:905.13"} Among the three possible omnisymmetrical prime structural systems the tetrahedron, octahedron, and icosahedrononly the tetrahedron has each of its vertexes diametrically opposite a triangular opening. (See Illus. 610.20.) In the octahedron and icosahedron, each vertex is opposite another vertex; and each of their vertexes is diametrically blocked against articulating a self-inside-outing transformation. In both the octahedron and the icosahedron, each of the vertexes is tense-vector-restrained from escaping outwardly by the convergent vectorial strength of the system’s other immediately surrounding at minimum threevertexial event neighbors. But contrariwise, each of the octahedron’s and icosahedron’s vertex events are constrainingly impulsed inwardly in an exact central-system direction and thence impelled toward diametric exit and inside-outing transformation; and their vertex events would do so were it not for their diametrically opposed vertexes, which are surroundingly tense-vector-restrained from permitting such outward egress.
[905.14]{style="color: purple3"} []{#ver:905.14 label="ver:905.14"} As a consequence of its uniquely unopposed diametric vertexing ergo permitteddiametric exit, only the tetrahedron among all the symmetric polyhedra can turn itself pulsatingly inside-out, and can do so in eight different ways (see Sec. 624); and in each instance, as it does so, one- half of its combined concave-convex unity “twoness” is always inherently invisible.
[905.15]{style="color: purple3"} []{#ver:905.15 label="ver:905.15"} The octahedron, however, restrainingly vector-blocked as described, can only infold itself pulsatingly to a condition of hemispherical congruence like a deflated basketball. Thus the octahedron’s concave-convex, unity-twoness state remains plurally obvious. You can see the concave infolded hemisphere nested into the as-yet outfolded convex hemisphere. Verifying the octahedron’s fourness as being an evolutionary transformation of the tetrahedron’s unity-twoness, we may take the four triangles of the tetrahedron which were edge-hinged together (bivalently) and reassemble them univalently (that is, corner-to-corner) and produce the octahedron, four of whose faces are triangular (ergo structurally stable) voids. This, incidentally, introduces the structural stability of the triangle as a visualizable yet physical nothingness.
[905.16]{style="color: purple3"} []{#ver:905.16 label="ver:905.16"} The triangle is structure. Structure is spontaneous pattern stabilization of a complex of six individual events. Structure is an integral of six events. Structure is a pattern integrity. Pattern integrity is conceptual relationship independent of size. The integrity of the nuclear structuring of the atoms is conceptually thinkable, as are the associability and disassociability proclivities of chemistry, virology, biology, and all nonbiological structuring and mechanics.
[905.17]{style="color: purple3"} []{#ver:905.17 label="ver:905.17"} Any and all of the icosahedron’s vertexes pulsate individually and independently from the convex to concave state only in the form of local dimpling, because each only-from-outward-motion-restrained vertex being free to articulate inwardly toward its system center, and having done so becomes abruptly five-vector-restrained by its immediate neighboring vertexial event convergences; and the abrupt halting of its inward travel occurs before it reaches the system center. This means that one vertex cannot pulse inwardly more deeply than a local dimple similar to the popping in of a derby hat.
[905.18]{style="color: purple3"} []{#ver:905.18 label="ver:905.18"} Both the coexisting concave and convex aspects of the icosahedron like those of the octahedron, but unlike those of the unique case of the tetrahedron are always visually obvious on the inside and outside of the only locally dimpled-in, or nested-in, vertex. In both the octahedron and the icosahedron, the concave-convex, only inwardly pulsative self-transforming always produces visually asymmetrical transforming; whereas the tetrahedron’s permitted inside-outing pulsatively results only in a visible symmetry, the quasiasymmetry being invisibly polarized with the remainder of Universe outside the tetrahedron, which, being omniradially outward, is inferentiallybut not visuallysymmetrical; the only asymmetrical consideration of the tetrahedron’s inside-outing being that of an initial direction of vertexial exiting. Once exited, the visible remaining symmetrical tetrahedron is in verity the inside-outness of its previously visible aspects.
[905.19]{style="color: purple3"} []{#ver:905.19 label="ver:905.19"} In either of the two sets of four each as alternatively described, one of the polar states is always visible and the other complementarily invisible. This is a dynamic relationship. Dynamically, all four of each of the two sets of the tetrahedral potential are co-occurrently permitted and are required by omni-action-reaction-resultant synergetics. The seeming significance of the separately considered asymmetries are cancelled by the omnidirectional symmetry.
[905.20]{style="color: purple3"} []{#ver:905.20 label="ver:905.20"} The vertexes are the unique, individual, ergo in-time events; and the nonvertex voids are the outdividual, ergo out, timeless, sizeless non-events. The both outwardly and inwardly escaping nonevents complement the embryo, local-in-time, special-case, convergent-event, systemic pattern fixation of individual intercomplementary event identities.
[905.21]{style="color: purple3"} []{#ver:905.21 label="ver:905.21"} is unidirectional, pointable. Out is omnidirectional, unpointablego out, to-go-out, or go-in-to-go-out on the other side. Any direction from here is out; only one direction from here is in. Go either temporarily in to go diametrically out on the other side of the individually identical local in, or go anydirectionally out …to the complete, eternal, unidentifiable, non-ness, noneness of the a priori mysterious, integrally regenerative, inherently complex Universe.
[905.22]{style="color: purple3"} []{#ver:905.22 label="ver:905.22"} So-called edges and vectors are inherently only convergent or divergent interrelationships between multiply-identifiable, point-to-able, vertex fixes.
[905.23]{style="color: purple3"} []{#ver:905.23 label="ver:905.23"} Because each tetrahedron has both four vertexes and four subtending nonvertex voids, we can identify those four diametrically complementary sets of all minimal cosmic structural systems as the four visible vertexes and the four nonvisible nonvertexes, i.e., the triangularly symmetrical, peripheral voids. The tetrahedron thus introduces experientially the cosmic principle of the visible and invisible pairs or couples; with the nonvisible vertex as the inside-out vertex, which nonvertex is a nonconvergence of events; whereas the vertexes are visible event convergences.
¶ 905.30 Hierarchy of Pulsating Tetrahedral Arrays
[905.31]{style="color: purple3"} []{#ver:905.31 label="ver:905.31"} Among the exclusively, three and only, prime cosmic structural systems the tetra, octa, and icosaonly the tetrahedron’s pulsative transforming does not alter its overall, visually witnessable symmetry, as in the case of the “cheese tetrahedron”, (see Sec. 623). It is important to comprehend that any one of the two sets of four each potential vertexial inside-outing pulsatabilities of the tetrahedronconsidered only by themselvesconstitutes polarized, but only invisible, asymmetry. In one of the two sets of four each potential inside-outings we have three-of-each-to-three-of-the-other (i.e., tri-valent, triangular, base-to-base) vertexial bonding together of the visible and invisible, polarized pair of tetrahedra. In the other of the two sets of four each potential inside-outings we have one-vertex-to-one-vertex (i.e., univalent, apex-to-apex) interbonding of the visible and invisible polarized pair of tetrahedra.
[905.32]{style="color: purple3"} []{#ver:905.32 label="ver:905.32"} Because each simplest, ergo prime, structural system tetrahedron has at minimum four vertexes (point-to-able, systemic, event-patterned fixes), and their four complementary system exit-outs, are symmetrically identified at mid-void equidistance between the three other convergent event identity vertexes; and because each of the two sets of these four half-visible/half-in-visible, polar-paired tetrahedra have both three-vertex-to-three-vertex as well as single-vertex-to-single-vertex inside-out pulsatabilities; there are eight possible inside-outing pulsatabilities. We have learned (see Sec. 440) that the vector equilibrium is the nuclear-embracing phase of all eight “empty state” tetrahedra, all with common, central, single-vertex-to-single-vertex congruency, as well as with their mutual outward-radius-ends’ vertexial congruency; ergo the vector equilibrium is bivalent.
[905.33]{style="color: purple3"} []{#ver:905.33 label="ver:905.33"} The same vector equilibrium’s eight, nuclear-embracing, bivalent tetrahedra’s eight nuclear congruent vertexes may be simultaneously outwardly pulsed through their radially-opposite, outward, triangular exits to form eight externally pointing tetrahedra, which thus become only univalently, i.e., only-single-vertex interlinked, and altogether symmetrically arrayed around the vector equilibrium’s eight outward “faces.” The thus-formed, eight-pointed star system consisting of the vector equilibrium’s volume of 20 (tetrahedral unity), plus the eight star-point-arrayed tetrahedra, total volumetrically to 28. This number, 28, introduces the prime number seven factored exclusively with the prime number two, as already discovered in the unity-twoness of the tetrahedron’s always and only, co-occurring, concave-convex inherently disparate, behavioral duality. This phenomenon may be compared with the 28-ness in the Coupler accounting (see Sec. 954.72).
[905.34]{style="color: purple3"} []{#ver:905.34 label="ver:905.34"} We have also learned in the vector equilibrium jitterbugging that the vector equilibrium contracts symmetrically into the octahedral state, and we thus witness in the octahedron the eight tetrahedrathree-vertex-to-three- vertex (face-to-face, trivalent, triple-interbonded)which condition elucidates the octahedron’s having a volumetric four in respect to the tetrahedron’s dual unity. Whereas the octahedron’s prime number is two in respect to the tetrahedron’s prime number one, it is experientially evidenced that the octahedron always occurs as both the double phase and the fourfold phase of the tetrahedron; i.e., as (a) the tetrahedral invisible/visible, (No-Yes), concave/convex; as well as (b) the octahedral visible/visible, (Yes-Yes), concave/convex: two different twoness manifestations. The tetrahedron has a unity-two duality in both its generalized dynamic potential and kinetic states, having always both the cosmic macro-tetrahedron and the cosmic micro-tetrahedron, both embracingly and inclusively defined by the four convergent event fixes of the minimum structural system of Universe. There is also the fundamental twoness of the tetrahedron’s three sets of two-each, opposed, 90-degree-oriented edge-vectors whose respective four ends are always most economically omni-inter-connected by the four other vectors of the tetrahedron’s total of six edge-vectors.
[905.35]{style="color: purple3"} []{#ver:905.35 label="ver:905.35"} The jitterbug shows that the bivalent vector equilibrium contracts to the octahedral trivalent phase, going from a twentyness of volume to a fourness of volume, , i.e., a contraction, which introduces the prime number five into the exclusively tetrahedrally evolved prime structural system intertransformabilities. We also witness that the octahedron state of the jitterbug transforms contractively even further with the 60-degree rotation of one of its triangular faces in respect to its nonrotating opposite triangular face wherewith the octahedron collapses into one, flattened-out, two-vector-length, equiedged triangle, which in turn consists of four one-vector-edged, equiangled triangles, each of which in turn consists of two congruent, one-vector-long, equiedged triangles. All eight triangles lie together as two congruent sets of four small, one-vector-long, equiedged triangles. This centrally congruent axial force in turn plunges the two centrally congruent triangles through the inertia of the three sets of two congruent, edge-hinged triangles on the three sides of the congruent pair of central triangles which fold the big triangle’s corners around the central triangle in the manner of the three petals folding into edge congruence with one another to produce a tetrahedrally shaped flower bud. Thus is produced one tetrahedron consisting of four quad-rivalently congruent tetrahedra, with each of its six edges consisting of four congruent vectors. The tetrahedron thus formed, pulsatively reacts by turning itself inside-out to produce, in turn, another quadrivalent, four-tetrahedra congruence; which visible-to-visible, quadrivalent tetrahedral inside-outing/outside-inning is pulsatively regenerative. (See Illus. 461.08.)
[905.36]{style="color: purple3"} []{#ver:905.36 label="ver:905.36"} Herewith we witness both visible and heretofore invisible phases of each of the single tetrahedra thus pulsatively involved. The univalent, apex-to-apex-bonded, four tetrahedra and the three-point-to-three-point, trivalent, base-bonded, four tetrahedra are both now made visible, because what was visible to the point-to-point four was invisible to the three-point-to-three-point four, and vice versa.
[905.37]{style="color: purple3"} []{#ver:905.37 label="ver:905.37"} In the two extreme limit cases of jitterbug contractionboth the positive-negative and the negative-positive phasesthe two cases become alternately visible, which results in the invisible phase of either case becoming congruent with the other’s invisible phase: ergo rendering both states visible.
[905.38]{style="color: purple3"} []{#ver:905.38 label="ver:905.38"} This pulsating congruence of both the alternately quadrivalent visible phases of the limit case contractions of the vector equilibrium results in an octavalent tetrahedron; i.e., with all the tetrahedron’s eight pulsative intertransformabilities simultaneously realized and congruently oriented.
[905.39]{style="color: purple3"} []{#ver:905.39 label="ver:905.39"} This hierarchy of events represents a 28-fold volumetric contraction from the extreme limit of univalently coherent expandability of the ever-integrally-unit system of the eight potential pulsative phases of self-intertransformability of the tetrahedron as the minimum structural system of all Universe. In summary we have:
-
the 28-volume univalent;
-
the 20-volume bivalent;
-
the 8-volume quadrivalent;
-
the two sets of 1-volume quadrivalent; and finally,
-
the complex limit congruence of the 1-volume octavalent tetrahedron.
[905.40]{style="color: purple3"} []{#ver:905.40 label="ver:905.40"} As we jitterbuggingly transform contractively and symmetrically from the 20-volume bivalent vector equilibrium phase to the 8-volume quadrivalent octahedral phase, we pass through the icosahedral phase, which is nonselfstabilizing and may be stabilized only by the insertion of six additional external vector connectors between the 12 external vertexes of the vector equilibrium travelling toward convergence as the six vertexes of the trivalent 4-volume octahedron. These six vectors represent the edge-vectors of one tetrahedron.
[905.41]{style="color: purple3"} []{#ver:905.41 label="ver:905.41"} The 28-volume, univalent, nucleus-embracing, tetrahedral array extends its outer vertexes beyond the bounds of the nucleus-embracing, closest-packed, omnisymmetrical domain of the 24-volume cube formed by superimposing eight Eighth-Octahedra, asymmetrical, equiangle-based, three-convergent-90-degree-angle-apexed tetrahedra upon the eight outward equiangular triangle facets of the vector equilibrium. We find that the 28-ness of free-space expandability of the univalent, octahedral, nucleus embracement must lose a volume of 4 (i.e., four tetrahedra) when subjected to omni-closest-packing conditions. This means that the dynamic potential of omniinterconnected tetrahedral pulsation system’s volumetric embracement capability of 28, upon being subjected to closest-packed domain conditions, will release an elsewhere-structurally-investable volume of 4. Ergo, under closest-packed conditions, each nuclear array of tetrahedra (each of which is identifiable energetically with one energy quantum) may lend out four quanta of energy for whatever tasks may employ them.
[905.42]{style="color: purple3"} []{#ver:905.42 label="ver:905.42"} The dynamic vs. kinetic difference is the same difference as that of the generalized, sizeless, metaphysically abstract, eternal, constant sixness-of-edge, fourness-of-vertex, and fourness-of-void of the only-by-mind-conceptual tetrahedron vs. the only-in-time-sized, special-case, brain-sensed tetrahedron. This generalized quality of being dynamic, as being one of a plurality of inherent systemic conditions and potentials, parts of a whole set of eternally co-occurring, complex interaccommodations in pure, weightless, mathematical principle spontaneously producing the minimum structural systems, is indeed the prime governing epistemology of wave quantum physics.
[905.43]{style="color: purple3"} []{#ver:905.43 label="ver:905.43"} In consideration of the tetrahedron’s quantum intertransformabilities, we have thus far observed only the expandable-contractable, variablebonding-permitted consequences. We will now consider other dynamical potentials, such as, for instance, the axial rotatabilities of the respective tetras, octas, and icosas.
[905.44]{style="color: purple3"} []{#ver:905.44 label="ver:905.44"} By internally interconnecting its six vertexes with three polar axes: and , and rotating the octahedron successively upon those three axes, three planes are internally generated that symmetrically subdivide the octahedron into eight uniformly equal, equiangle-triangle-based, asymmetrical tetrahedra, with three convergent, 90-degree-angle-surrounded apexes, each of whose volume is one-eighth of the volume of one octahedron: this is called the Eighth-Octahedron. (See also Sec. 912.) The octahedron, having a volume of four tetrahedra, allows each Eighth-Octahedron to have a volume of one-half of one tetrahedron. If we apply the equiangled-triangular base of one each of these eight Eighth-Octahedra to each of the vector equilibrium’s eight equiangle-triangle facets, with the Eighth-Octahedra’s three-90-degree-angle-surrounded vertexes pointing outwardly, they will exactly and symmetrically produce the 24-volume, nucleus-embracing cube symmetrically surrounding the 20-volume vector equilibrium; thus with 8 \times \sfrac{1}{2}= 4 being added to the 20-volume vector equilibrium producing a 24-volume total.
[905.45]{style="color: purple3"} []{#ver:905.45 label="ver:905.45"} non-nucleus-embracing 3-volume cube may be produced by applying four of the Eighth-Octahedra to the four equiangled triangular facets of the tetrahedron. (See Illus. 950.30.) Thus we find the tetrahedral evolvement of the prime number three as identified with the cube. Ergo all the prime numbers of the octave wave enumeration system, with its zero-nineness, are now clearly demonstrated as evolutionarily consequent upon tetrahedral intertransformabilities.
[905.46]{style="color: purple3"} []{#ver:905.46 label="ver:905.46"} Since the tetrahedron becomes systematically subdivided into 24 uniformly dimensioned Quanta Modules (one half of which are positive and the other half of which are negatively inside-out of the other); and since both the positive and negative Quanta Modules may be folded from one whole triangle; and since, as will be shown in Sec. 905.62, the flattened-out triangle of the Quanta Module corresponds with each of the 120 disequilibrious triangles, it is evidenced that five tetrahedra of 24 Quanta Modules each, may have their sum-total of 120 Modules all unfolded, and that they may be edge-bonded to produce an icosahedral spherical array; and that 2\sfrac{1}{2} tetrahedra’s 60 Quanta Modules could be unfolded and univalently (single-bondedly) arrayed to produce the same spheric icosahedral polyhedron with 60 visible triangles and 60 invisible triangular voids of identical dimension.
[905.47]{style="color: purple3"} []{#ver:905.47 label="ver:905.47"} Conversely, 60 positive and 60 negative Quanta Modules could be folded from the 120 Module triangles and, with their “sharpest” point pointed inward, could be admitted radially into the 60-positive-60-negative tetrahedral voids of the icosahedron. Thus we discover that the icosahedron, consisting of Quanta Modules (each of which is \sfrac{1}{24}th of a tetrahedron) has a volume of \sfrac{120}{24}= 5. The icosahedron volume is 5 when the tetrahedron is 1; the octahedron ; the cube 3; and the star-pointed, univalent, eight-tetrahedra nuclear embracement is 28, which is ; 28 also being the maximum number of interrelationships of eight entities:
[905.48]{style="color: purple3"} []{#ver:905.48 label="ver:905.48"} The three surrounding angles of the interior sharpest point of the Quanta Module tetrahedron are each a fraction less than the three corresponding central angles of the icosahedron: being approximately one-half of a degree in the first case; one whole degree in the second case; and one and three-quarters of a degree in the third case. This loose-fit, volumetric-debit differential of the Quanta Module volume is offset by its being slightly longer in radius than that of the icosahedron, the Module’s radial depth being that of the vector equilibrium’s, which is greater than that of the icosahedron, as caused by the reduction in the radius of the 12 balls closest-packed around one nuclear ball of the vector equilibrium (which is eliminated from within the same closest-radially-packed 12 balls to reduce them to closest surface-packing, as well as by eliminating the nuclear ball and thereby mildly reducing the system radius). The plus volume of the fractionally protruded portion of the Quanta Module beyond the icosahedron’s surface may exactly equal the interior minus volume difference. The balancing out of the small plus and minus volumes is suggested as a possibility in view of the exact congruence of 15 of the 120 spherical icosahedra triangles with each of the spherical octahedron’s eight spherical equiangle faces, as well as by the exact congruence of the octahedron and the vector equilibrium themselves. As the icosahedron’s radius shortens, the central angles become enlarged.
[905.49]{style="color: purple3"} []{#ver:905.49 label="ver:905.49"} This completes the polyhedral progression of the omni-phase-bond-integrated hierarchies ofsymmetrically expanded and symmetrically subdivided tetrahedra; from the -tetrahedron (12 positive and 12 negative Quanta Modules); through its octavalent 8-in-1 superficial volume-1; expanded progressively through the quadrivalent tetrahedron; to the quadrivalent octahedron; to the bivalent vector equilibrium; to the univalent, 28-volume, radiant, symmetrical, nucleus-embracing stage; and thence exploded through the volumeless, flatout-outfolded, double-bonded (edge-bonded), 120--Quanta-Module-triangular array remotely and symmetrically surrounding the nuclear volumetric group; to final dichotomizing into two such flatout half (positive triangular) film and half (negative triangular) void arrays, single-bonded (corner-bonded), icosahedrally shaped, symmetrically nuclear-surrounding systems.
¶ 905.50 Repeatability and Split Personality of Tetrahedron
[905.51]{style="color: purple3"} []{#ver:905.51 label="ver:905.51"} Having completed the expansive-contractive, could-be, quantum jumps, we will now consider the rotatability of the tetrahedron’s six-edge axes generation of both the two spherical tetrahedra and the spherical cube whose “split personality’s”, four-triangle-defining edges also perpendicularly bisect all of both of the spherical tetrahedron’s four equiangled, equiedged triangles in a three-way grid, which converts each of the four equiangled triangles into six right-angle spherical trianglesfor a total of 24, which are split again by the spherical octahedron’s three great circles to produce 48 spherical triangles, which constitute the 48 equilibrious Basic Triangles of omni-equilibrious eventless eternity (see Sec. 453).
[905.52]{style="color: purple3"} []{#ver:905.52 label="ver:905.52"} The spherical octahedron’s eight faces become skew-subdivided by the icosahedron’s 15 great circles’ self-splitting of its 20 equiangular faces into six-each, right spherical triangles, for an spherical triangle total of 120, of which 15 such right triangles occupy each of the spherical octahedron’s eight equiangular facesfor a total of 120which are the same 120 as the icosahedron’s 15 great circles.
[905.53]{style="color: purple3"} []{#ver:905.53 label="ver:905.53"} The disequilibrious 120 triangle = the equilibrious 48 triangle \times 2\sfrac{1}{2}. This 2\sfrac{1}{2}+ 2\sfrac{1}{2}= 5; which represents the icosahedron’s basic fiveness as split-generated into 2\sfrac{1}{2} by their perpendicular, mid-edge-bisecting 15 great circles. Recalling the six edge vectors of the tetrahedron as one quantum, we note that is $1
- 1 + \sfrac{1}{2}= 2\sfrac{1}{2}$; and that 2\sfrac{1}{2}\times 6 = 15 great circles. (This half-positive and half negative dichotomization of systems is discussed further at Sec. 1053.30ff.)
[905.54]{style="color: purple3"} []{#ver:905.54 label="ver:905.54"} We find that the split personality of the icosahedron’s 15-great- circle splittings of its own 20 triangles into 120, discloses a basic asymmetry caused by the incompleteness of the 2\sfrac{1}{2}, where it is to be seen in the superimposition of the spherical icosahedron upon the spherical vector equilibrium. In this arrangement the fundamental prime number fiveness of the icosahedron is always split two ways: 2\sfrac{1}{2} positive phase and 2\sfrac{1}{2} negative phase. This half-fiving induces an alternate combining of the half quantum on one side or the other: going to first three on one side and two on the other, and vice versa.
[905.55]{style="color: purple3"} []{#ver:905.55 label="ver:905.55"} This half-one-side/half-on-the-other induces an oscillatory alternating 120-degree-arc, partial rotation of eight of the spherical tetrahedron’s 20 equiangled triangles within the spherical octahedron’s eight triangles: 8 \times 2\sfrac{1}{2}= 20. We also recall that the vector equilibrium has 24 internal radii (doubled together as 12 radii by the congruence of the four-great-circle’s hexagonal radii) and 24 separate internal vector chords. These 24 external vector chords represent four quanta of six vectors each. When the vector equilibrium jitterbuggingly contracts toward the octahedral edge-vector doubling stage, it passes through the unstable icosahedral stage, which is unstable because it requires six more edge-vectors to hold fixed the short diagonal of the six diamond-shaped openings between the eight triangles. These six equilength vectors necessary to stabilize the icosahedron constitute one additional quantum which, when provided, adds 1 to the 4 of the vector equilibrium to equal 5, the basic quantum number of the icosahedron.
¶ 905.60 The Disequilibrium 120 Triangle
[905.61]{style="color: purple3"} []{#ver:905.61 label="ver:905.61"} The icosahedral spherical great-circle system displays:
12 vertexes surrounded by 10 converging angles;
20 vertexes surrounded by 6 converging angles;
30 vertexes surrounded by 4 converging angles
12 x 10 = 120
20x6 =120
30x4 =120
360 converging angle sinuses.
[905.62]{style="color: purple3"} []{#ver:905.62 label="ver:905.62"} According to the Principle of Angular Topology (see Sec. 224), the 360 converging angle sinuses must share a 720-degree reduction from an absolute sphere to a chorded sphere: \sfrac{72O\degree}{360\degree}= 2\degree. An average of 2 degrees angular reduction for each corner means a 6 degrees angular reduction for each triangle. Therefore, as we see in each of the icosahedron’s disequilibrious 120 triangles, the well-known architects and engineers’ 30triangle has been spherically opened to 36 a “spherical excess,” as the Geodetic Survey calls it, of 6 degrees. All this spherical excess of 6 degrees has been massaged by the irreducibility of the 90-degree and 60-degree corners into the littlest corner. Therefore, 30 > 36 in each of the spherical icosahedron’s 120 surface triangles.
[905.63]{style="color: purple3"} []{#ver:905.63 label="ver:905.63"} In subsiding the 120 spherical triangles generated by the 15 great circles of the icosahedron from an omnispherical condition to a neospheric 120-planar-faceted polyhedron, we produce a condition where all the vertexes are equidistant from the same center and all of the edges are chords of the same spherical triangle, each edge having been shrunk from its previous arc length to the chord lengths without changing the central angles. In this condition the spherical excess of 6 degrees could be shared proportionately by the 90, 60, 30 flat triangle relationship which factors exactly to . Since 6= 1/ao of 180, the 30 quanta of six each in flatout triangles or in the 120 LCD spherical triangles’ 186 degrees, means one additional quantum crowded in, producing 31 quanta.
[905.64]{style="color: purple3"} []{#ver:905.64 label="ver:905.64"} Alternatively, the spherical excess of 6 degrees (one quantum) may be apportioned totally to the biggest and littlest corners of the triangle, leaving the 60-degree, vector equilibrium, neutral corner undisturbed. As we have discovered in the isotropic vector matrix nature coordinates crystallographically in 60 degrees and not in 90 degrees. Sixty degrees is the vector equilibrium neutral angle relative to which life-in-time aberrates.
Basic Draftsman’s Triangle (Flat) (minus 5) = 30
Flatout >1 Quanta
*Module Triangle *
*35
60
[84
]{.underline}180
(unchanged) = 60
(plus 5) = [90]
180
[905.65]{style="color: purple3"} []{#ver:905.65 label="ver:905.65"} By freezing the 60-degree center of the icosahedral triangle, and by sharing the 6-degree, spherical-planar, excess reduction between the 36-degree and 90-degree corners, we will find that the Quanta Modules are exactly congruent with the 120 internal angles of the icosahedron. The minus 5 closely approximates the one quantum 6+ of spherical excess apparent at the surface, with a comparable nuclear deficiency of 5. (See Table 905.65.)
Table 905.65
[905.66]{style="color: purple3"} []{#ver:905.66 label="ver:905.66"} The Earth crust-fault angles, steel plate fractionation angles, and ship’s bow waves all are roughly the same, reading approximately 70-degree and 110-degree complementation.
Dihedral angle of octahedron = 109= 2 x 54
Dihedral angle of tetrahedron = 70
180
54
5
x 2–60
10
+ 54
109
If 5= unity; 54= 60- 1 quantum; and 70= 60+ 2 quanta.
Obviously, the 70and 109relate to the “twinkle angle” differential from 60(cosmic neutral) and to the 109central angle of the spherical tetrahedron. (See also Sec. 1051.20.)
¶ 950.70 Summary: Wave Propagation Model
[905.71]{style="color: purple3"} []{#ver:905.71 label="ver:905.71"} Both in the spherical vector equilibrium and in the disequilibrious icosahedral spherical system, the prime number five is produced by the fundamental allspace-filling complementarity of the 1-volume tetrahedron and the 4-volume octahedron.
Symmetrical:
Asymmetrical:
The effect is symmetrical when the tetrahedron’s four vertexes simultaneously pulse outwardly through their opposite void triangles to produce the “star tetrahedron,” one outwardly-pointing tetrahedron superimposed on each of the four faces of a nuclear tetrahedron: i.e., 1+4 = 5. The effect is asymmetrical when one outwardly-pointing tetrahedron is superimposed on one face of one octahedron: i.e., .
[905.72]{style="color: purple3"} []{#ver:905.72 label="ver:905.72"} We now understand how the equilibrious 48 basic triangles transform into the 120 disequilibrious basic triangles. The 120 (60 positive and 60 negative) spherical triangles’ central (or nuclear) angles are unaltered as we transform their eternal systemic patterning symmetry from (a) the octahedral form of \sfrac{120}{8}= 15 A Quanta Modules per each octa triangle; to (b) the icosahedron’s \sfrac{120}{20}= 6 A Quanta Modules per each icosa triangle; to (c) the dodecahedron’s \sfrac{120}{12}= 10 A Quanta Modules per each pentagon. This transformational progression demonstrates the experientially witnessable, waveproducing surface-askewing caused by the 120-degree, alternating rotation of the icosahedron’s triangles inside of the octahedron’s triangles. Concomitant with this alternating rotation we witness the shuttling of the spherical vector equilibrium’s 12 vertexial positions in a successive shifting-back-and-forth between the spherical icosahedron’s 12 vertexial positions; as well as the wave-propagating symmetrical, polyhedral alterations of the inward-outward pulsations which generate surface undulations consequent to the radial contractions, at any one time, of only a fractional number of all the exterior vertexes, while a symmetrical set of vertexes remains unaltered.
[905.73]{style="color: purple3"} []{#ver:905.73 label="ver:905.73"} This elucidates the fundamental, electromagnetic, inward-outward, and complex great-circling-around type of wave propagation, as does also the model of spheres becoming voids and all the voids becoming spheres, and their omniradiant wave propagation (see Sec. 1032).
[905.74]{style="color: purple3"} []{#ver:905.74 label="ver:905.74"} There are also the approximately unlimited ranges of frequency modulatabilities occasioned by the symmetrical subdivisioning of all the prime, equiangled, surface triangles of the tetrahedron, octahedron, and icosahedron. This additionally permitted wave undulation of surface pattern shifting is directly identified with the appearance of photons as spherically clustered and radiantly emittable tetrahedra (see Sec. 541.30).
¶ 910.00 and Quanta Modules
[910.01]{style="color: purple3"} []{#ver:910.01 label="ver:910.01"} All omni-closest-packed, complex, structural phenomena are omnisymmetrically componented only by tetrahedra and octahedra. Icosahedra, though symmetrical in themselves, will not close-pack with one another or with any other symmetrical polyhedra; icosahedra will, however, face-bond together to form open-network octahedra.
[910.02]{style="color: purple3"} []{#ver:910.02 label="ver:910.02"} In an isotropic vector matrix, it will be discovered that there are only two omnisymmetrical polyhedra universally described by the configuration of the interacting vector lines: these two polyhedra are the regular tetrahedron and the regular octahedron.
¶ Rational Fraction Elements
[910.11]{style="color: purple3"} []{#ver:910.11 label="ver:910.11"} All other regular, omnisymmetric, uniform-edged, -angled, and -faceted, as well as several semisymmetric, and all other asymmetric polyhedra other than the icosahedron and the pentagonal dodecahedron, are described repetitiously by compounding rational fraction elements of the tetrahedron and octahedron. These elements are known in synergetics as the and Quanta Modules. They each have volume of \sfrac{1}{24}th of a tetrahedron.
¶ 911.00 Division of Tetrahedron
[911.01]{style="color: purple3"} []{#ver:911.01 label="ver:911.01"} The regular tetrahedron may be divided volumetrically into four identical Quarter-Tetrahedra, with all their respective apexes at the center of volume of the regular unit tetrahedron. (See Illus. 913.01.) The Quarter-Tetrahedra are irregular pyramids formed upon each of the four triangular faces of the original unit tetrahedra, with their four interior apexes congruent at the regular tetrahedron’s volumetric center; and they each have a volume of one quarter of the regular tetrahedron’s volume-1.
[911.02]{style="color: purple3"} []{#ver:911.02 label="ver:911.02"} Any of the Quarter-Tetrahedra may be further uniformly subdivided into six identical irregular tetrahedra by describing lines that are perpendicular bisectors from each vertex to their opposite edge of the QuarterTetrahedron. The three perpendicular bisectors cut each Quarter-Tetrahedron into six similar tetrahedral pieces of pie. Each one of the six uniformly symmetrical components must be \sfrac{1}{6}th of One Quarter, which is \sfrac{1}{24}th of a regular tetrahedron, which is the volume and description of the Quanta Module. (See Illus. 913.01B.)
¶ 912.00 Division of Octahedron
[912.01]{style="color: purple3"} []{#ver:912.01 label="ver:912.01"} The regular octahedron has a volume equivalent to that of four unit tetrahedra. The octahedron may be subdivided symmetrically into eight equal parts, as Eighth-Octahedra, by planes going through the three axes connecting its six vertexes. (See Illus. 916.01.)
[912.02]{style="color: purple3"} []{#ver:912.02 label="ver:912.02"} The Quarter-Tetrahedron and the Eighth-Octahedron each have an equilateral triangular base, and each of the base edges is identical in length. With their equiangular-triangle bases congruent we can superimpose the Eighth-Octahedron over the Quarter-Tetrahedron because the volume of the Eighth-Octahedron is \sfrac{1}{2} and the volume of the Quarter-Tetrahedron is \sfrac{1}{4}. The volume of the Eighth-Octahedron is twice that of the QuarterTetrahedron; therefore, the Eighth-Octahedron must have twice the altitude because it has the same base and its volume is twice as great.
¶ 913.00 Quanta Module
[913.01]{style="color: purple3"} []{#ver:913.01 label="ver:913.01"} The Quanta Module is \sfrac{1}{6}th of a Quarter-Tetrahedron. The six asymmetrical components of the Quarter-Tetrahedron each have a volume of \sfrac
{1}{24}th of the unit tetrahedron. They are identical in volume and dimension, but three of them are positive and three of them are negative. (See Illus. 913.01.)
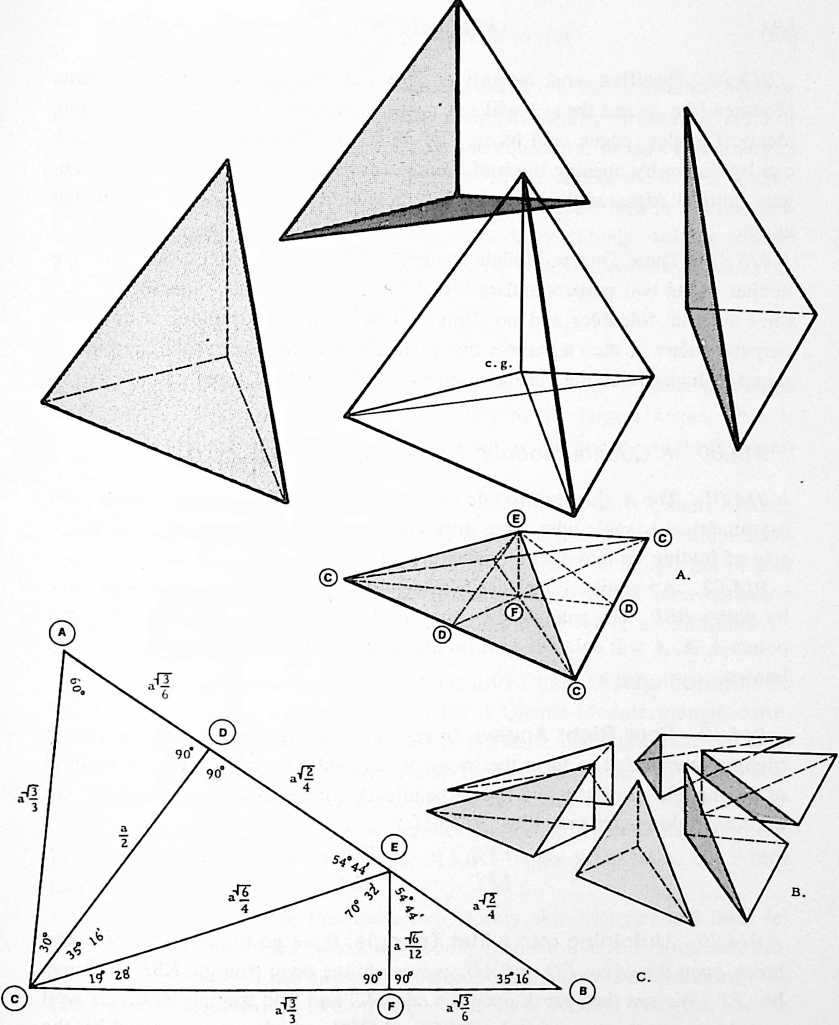
A Quanta Module:
-
The regular tetrahedron is divided volumetrically into four identical quarters.
-
The quarter-tetrahedron is divided ino six identical irregular tetrahedra, which appear as three right-hand and three left-hand volumetric units each equal in volume to \sfrac{1}{2}th of the original tetrahedron. This unit is called the Module.
-
The plane net which will fold into either left or right modules is shown. Vertex is at the vertex of the regular tetrahedron. Vertex is at the center of gravity of the tetrahedron. Vertex is at the mid-edge of the tetrahedron. Vertex is at the center of the tetrahedron face. Note that , and .
-
Positive and Negative: The positive and negative Quanta Modules (the + and the) will not nest in one another congruently despite identical angles, edges, and faces. The pluses are inside-out minuses, which can be shown by opening three of their six edges and folding the three triangles’ hinged edges in the opposite direction until their edges come together again.
-
The/ Quanta Module triangle is possibly a unique scalene in that neither of its two perpendiculars bisect the edges that they intersect. It has three internal foldables and no “internally contained” triangle. It drops its perpendiculars in such a manner that there are only three external edge increments, which divide the perimeter into six increments of three pairs.
¶ 914.00 Quanta Module: Foldability
[914.01]{style="color: purple3"} []{#ver:914.01 label="ver:914.01"} The Quanta Module can be unfolded into a planar triangle, an asymmetrical triangle with three different edge sizes, yet with the rare property of folding up into a whole irregular tetrahedron.
[914.02]{style="color: purple3"} []{#ver:914.02 label="ver:914.02"} An equilateral planar triangle /// may be bisected in each edge by points BBB. The triangle may be folded on lines and points will coincide to form the regular tetrahedron. This is very well known.
[914.10]{style="color: purple3"} []{#ver:914.10 label="ver:914.10"} Four Right Angles: In respect to the / Quanta Module flatout triangle or infolded to form the irregular tetrahedron, we find by the method of the module’s construction (by perpendicular planes carving apart) that there are four right angles (see Illus. 913.01C):
EFB EDC
EFC ADC
[914.20]{style="color: purple3"} []{#ver:914.20 label="ver:914.20"} Unfolding into a Flat Triangle: If we go to the vertex at and break open the edges and , we can hinge open triangle on hinge line . We can then break open the edge and fold triangle , as well as folding out the two triangles and , which are connected by the hinge , so that now the whole asymmetric / Quanta Module is stretched out flat as a triangle.
[914.21]{style="color: purple3"} []{#ver:914.21 label="ver:914.21"} The Quanta Module unfolds into a scalene triangle; that is, all of its non-90-degree angles are different, and all are less than 90 degrees. Two of the folds are perpendicular to the triangle’s sides, thus producing the four right angles. The Quanta Module triangle may be the only triangle fulfilling all the above stated conditions.
[914.30]{style="color: purple3"} []{#ver:914.30 label="ver:914.30"} Spiral Foldability: The foldability of the Quanta Module planar triangle differs from the inter-mid-edge foldability of the equilateral or isosceles triangle. All the mid-edge-foldable equilateral or isosceles triangles can all form tetrahedra, regular or irregular. In the case of the folded equilateral or isosceles triangle, the three triangle corners meet together at one vertex: like petals of a flower. In the case of the inter-mid-edge-folding scalene triangle, the three corners fail to meet at one vertex to form a tetrahedron.
¶ 915.00 Twinkle Angle
[915.01]{style="color: purple3"} []{#ver:915.01 label="ver:915.01"} The faces of an Quanta Module unfold to form a triangle with 84(30+ 35+ 19) as its largest angle. This is 5less than a right angle, and is known as the twinkle angle in synergetics (see Illus. 913.01C).
[915.02]{style="color: purple3"} []{#ver:915.02 label="ver:915.02"} There is a unique 5-ness relationship of the Quanta Module to the symmetry of the tetrahedron-octahedron allspace-filling complementation and other aspects of the vector equilibrium that is seemingly out of gear with the disequilibrious icosahedron. It has a plus-or-minus incrementation quality in relation to the angular laws common to the vector equilibrium.
[915.10]{style="color: purple3"} []{#ver:915.10 label="ver:915.10"} Quanta Module Triangle and Basic Disequilibrium 120 Triangle: The angles of fold of the Quanta Module triangle correspond in patterning to the angles of fold of the Basic Disequilibrium 120 Triangle, the \sfrac{1}{120}th of a sphere whose fundamental great circles of basic symmetry subdivide it in the same way. The angles are the same proportionally when the spherical excess subsides proportionally in all three corners. For instance, the angle in Illus. 913.01C is not 90 degrees, but a little less.
[915.11]{style="color: purple3"} []{#ver:915.11 label="ver:915.11"} It is probable that these two closely akin triangles and their respective folded tetrahedra, whose Module Quantum phase is a rational subdivider function of all the hierarchy of atomic triangulated substructuring, the 120 Basic Disequilibrium triangles and the Module triangles, are the same quanta reoccurrent in their most powerful wave-angle oscillating, intertransformable extremes.
[915.20]{style="color: purple3"} []{#ver:915.20 label="ver:915.20"} Probability of Equimagnitude Phases: The 6spherical excess of the Basic Disequilibrium 120 Triangle, the 5“twinkle angle” of the Quanta Module triangle, and the 7“unzipping angle” of birth, as in the DNA tetrahelix, together may in time disclose many equimagnitude phases occurring between complementary intertransforming structures.
¶ 916.00 Quanta Module
[916.01]{style="color: purple3"} []{#ver:916.01 label="ver:916.01"} The Quanta Module is \sfrac{1}{6}th of the fractional unit described by subtracting a Quarter-Tetrahedron from an Eighth-Octahedron. The six asymmetrical components of the fractional unit so described each have a volume of \sfrac{1}{24}th of the unit tetrahedron. They are identical in volume and dimensioning, but three of them are positive and three of them are negative. (See Illus. 916.01.)
[916.02]{style="color: purple3"} []{#ver:916.02 label="ver:916.02"} When the Eighth-Octahedron is superimposed on the QuarterTetrahedron, the top half of the Eighth-Octahedron is a fractional unit, like a concave lid, with a volume and weight equal to that of the QuarterTetrahedron below it. We can slice the fractional unit by three planes perpendicular to its equilateral triangular base and passing through the apex of the Quarter-Tetrahedron, through the vertexes of the triangular base, and through the mid-points of their respective opposite edges, separating it into six equidimensional, equivolume parts. These are Quanta Modules.
[916.03]{style="color: purple3"} []{#ver:916.03 label="ver:916.03"} Quanta Modules are identical irregular tetrahedra that appear as three positive (outside-out) and three negative (outside-in) units. Each of the Quanta Modules can be unfolded into a planar, multitriangled polygon. (See Illus. 916.O1F.)
¶ 920.00 Functions of and Modules
[920.01]{style="color: purple3"} []{#ver:920.01 label="ver:920.01"} The and Quanta Modules may possibly quantize our total experience. It is a phenomenal matter to discover asymmetrical polyhedral units of geometry that are reorientably compositable to occupy one asymmetrical polyhedral space; it is equally unique that, despite disparate asymmetric polyhedral form, both have the same volume; and both associate in different kinds of simplex and complex, symmetrical and asymmetrical, coherent systems. While they consist, in their positive and negative aspects, of four different asymmetrical shapes, their unit volume and energy quanta values provide a geometry elucidating both fundamental structuring and fundamental and complex intertransformings, both gravitational and radiational.
¶ 921.00 Energy Deployment in and Quanta Modules
[921.01]{style="color: purple3"} []{#ver:921.01 label="ver:921.01"} By virtue of their properties as described in Secs. 920, 921.20, and 921.30, the centers of energy in the and Quanta Modules can be locally reoriented within the same space without disturbing contiguously surrounding configurations of closest-packed geometry; these local reorientations can either concentrate and hold or deploy and distribute the energies of the respective and Quanta Modules, in the first case concentrating the centers of energy inwardly, and in the second case deploying the centers of energy outwardly.
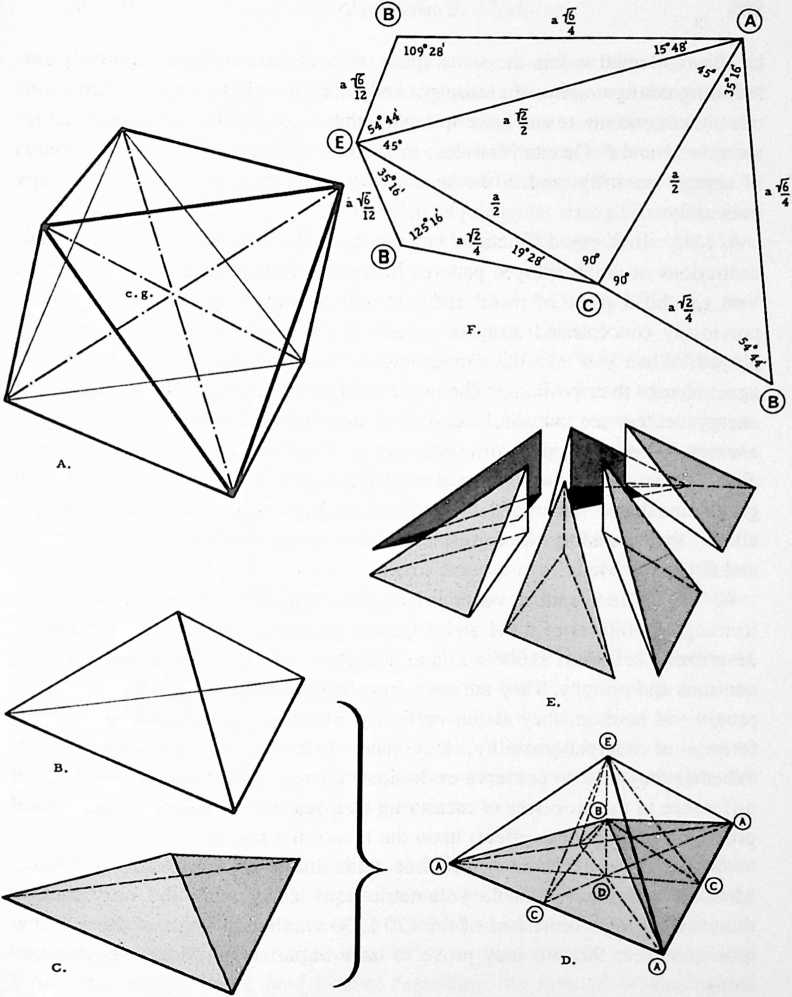
Fig. 916.01 Division of Eighth-Octahedron into Six Parts: Quanta Module: The regular octahedron (A) is divided into eight identical units (B) equaling of the volume of the octahedron. The quarter tetrahedron as defined by six Modules (C) is subtracted from the ‘/s-octahedron (D). This fractional unit is then subdivided into six identical irregular tetrahedra that appear as three right-hand and three left-hand units and are referred to as Modules. They are equal in volume to the Modules and are consequently also ’/21th of the regular tetrahedron. In (F) is shown the plane net which will fold into either the right or left Module. Vertex is at the vertex of the octahedron. Vertex is at the mid-edge of the octahedron. Vertex is at the center of gravity of the octahedron.
[921.02]{style="color: purple3"} []{#ver:921.02 label="ver:921.02"} In X-ray diffraction, you can see just such alternate energy concentrations of omnideployed patterns in successive heat treatments of metals. You can hit a piece of metal and you will find by X-ray diffraction that a previously concentrated array of centers of energy have been elegantly deployed. When you take the temper out of the metal, the energy centers will again change their positions. The metal’s coherence strength is lessened as the energy centers are outwardly deployed into diffused remoteness from one another. When the centers of energy are arranged closer to one another, they either attract or repulse one another at the exponentially increasing rates of gravitational and radiational law. When we heat-treat or anneal metals and alloys, they transform in correspondence with the reorientabilities of the and Quanta Modules.
[921.03]{style="color: purple3"} []{#ver:921.03 label="ver:921.03"} The identical volumes and the uniquely different energy-transforming capabilities of the and Quanta Modules and their mathematically describable behaviors () hint at correspondence with the behaviors of neutrons and protons. They are not mirror images of one another, yet, like the proton and neutron, they are energetically intertransformable and, due to difference of interpatternability, they have difference in mass relationship. Whether they tend to conserve or dissipate energy might impose a behavioral difference in the processes of measuring their respective masses. behavioral proclivity must impose effects upon the measuring process.
[921.04]{style="color: purple3"} []{#ver:921.04 label="ver:921.04"} The exact energy-volume relationship of the and Quanta Modules and their probable volumetric equivalence with the only meager dimensional transformations of the 120 tetrahedral voids of the icosahedron (see Sec. 905.60) may prove to have important physical behavior kinships.
[921.10]{style="color: purple3"} []{#ver:921.10 label="ver:921.10"} Energy Behavior in Tetrahedra: tetrahedron that can be folded out of a single foldable triangle has the strange property of holding energy in varying degrees. Energy will bounce around inside the tetrahedron’s four internal triangles as we described its bouncing within one triangle (see Sec. 901). Many bounce patterns are cyclically accomplished without tendency to bounce out of tetrahedrons, whether regular or irregular, symmetrical or asymmetrical.
[921.11]{style="color: purple3"} []{#ver:921.11 label="ver:921.11"} The equiangled, omni-sixty-degreed, regular tetrahedron can be opened along any three edges converging at any one of its vertexes with its edge-separated vertexial group of three triangles appearing as a three-petaled flower bud about to open. By deliberately opening the three triangular petals, by rotating them outward from one another around their three unsevered baseedge hinges, all three may be laid out flat around the central base triangle to appear as a two-frequency, edge-moduled, equiangular triangle consisting of four internal triangles. Energy tends by geodesical economy and angular law to be bounce-confined by the tetrahedron.
[921.12]{style="color: purple3"} []{#ver:921.12 label="ver:921.12"} The irregular, asymmetrical, tetrahedral Quanta Module’s four triangular facets unfold spirally into one asymmetrical triangle.
[921.13]{style="color: purple3"} []{#ver:921.13 label="ver:921.13"} But the triangular facets of the Quanta Module unfold inherently into four mutually dissimilar but interhinged 90-degree triangles.
[921.14]{style="color: purple3"} []{#ver:921.14 label="ver:921.14"} All the interior edges of the triangles, like the edges of a triangular billiard table, will provide unique internal, bouncing, corner-pocket-seek- ing patterns. An equilateral, equiangled triangle will hold the bouncing with the least tendency to exit at the pocketed corners. The more asymmetrical the triangular billiard table, the more swiftly the angular progression to exit it at a corner pocket. The various bounce patterns prior to exit induce time-differentiated lags in the rate of energy release from one tetrahedron into the other tetrahedron.
[921.15]{style="color: purple3"} []{#ver:921.15 label="ver:921.15"} Energy bounces around in triangles working toward the narrowest vertex, where the impossibility of more than one line going through any one point at any one time imposes a twist vertex exit at the corners of all polyhedra. Therefore, all triangles and tetrahedra “leak” energy, but when doing so between two similar corresponding vertexes-interconnected tetrahedra, the leaks from one become the filling of the other.
[921.20]{style="color: purple3"} []{#ver:921.20 label="ver:921.20"} Energy Characteristics of Quanta Module: The/ Quanta Modules can hold energy and tend to conserve it. They do so by combining with one another in three unique ways, each of which combine as one regular tetrahedron; the regular tetrahedron being a fundamental energy-holding formthe energy being held bounce-describing the internal octahedron of every tetrahedron.
[921.21]{style="color: purple3"} []{#ver:921.21 label="ver:921.21"} The Quanta Modules can also combine with theB Quanta Modules in seven ways, each of which result in single whole tetrahedra, which, as noted, hold their energy within their inherent octahedral centers.
[921.30]{style="color: purple3"} []{#ver:921.30 label="ver:921.30"} Energy Characteristics of Quanta Module: TheB Quanta Modules can vertex-combinedly hold energy but tend to release it.
[921.31]{style="color: purple3"} []{#ver:921.31 label="ver:921.31"} While all the single triangles will hold swift-motion energies only for relatively short periods of time, the four very asymmetrical and dissimilar triangles of the Quanta Module will release energy four times faster than any one of their asymmetrical tetrahedral kin.
[921.32]{style="color: purple3"} []{#ver:921.32 label="ver:921.32"} The Quanta Modules do not retain energy, and they cannot combine with one another to form a single tetrahedron with energy-introverting and -conserving proclivities.
[921.40]{style="color: purple3"} []{#ver:921.40 label="ver:921.40"} Summary: Though of equal energy potential or latent content, the/s and the s are two different systems of unique energy-behavior containment. One is circumferentially embracing, energy-impounding, integratively finite, and nucleation-conserving. The other is definitively distintegrative and nuclearly exportive. is outside-inwardly introvertive. is outside-outwardly extrovertive. (See Illus. 924.20.)
¶ 922.00 Conceptual Description and Contrast
[922.01]{style="color: purple3"} []{#ver:922.01 label="ver:922.01"} The Quanta Module is all of the nonconsidered, nonconceptual, finite, equilibrious, not-now-tuned-in Universe.
[922.02]{style="color: purple3"} []{#ver:922.02 label="ver:922.02"} The Quanta Module is the only momentarily extant considered subdividsion of disequilibrious Universe, i.e., the attention-preoccupying, special-case local system. The Quanta Module is always the real live “baby”; it is most asymmetrical.
¶ 923.00 Constant Volume
[923.10]{style="color: purple3"} []{#ver:923.10 label="ver:923.10"} Precession of Two Module Edges: There are six edges of a tetrahedron, and each edge precesses the opposite edge toward a 90-degrees-maximum of attitudinal difference of orientation. Any two discrete, opposite edges can be represented by two aluminum tubes, and (see Illus. 923.10 D), which can move longitudinally anywhere along their respective axes while the volume of the irregular tetrahedra remains constant. They may shuttle along on these lines and produce all kinds of asymmetrical tetrahedra, whose volumes will always remain unit by virtue of their developed tetrahedra’s constant base areas and identical altitudes. The two tubes’ four ends produce the other four interconnecting edges of the tetrahedron, which vary as required without altering the constantly uniform volume.
[923.15]{style="color: purple3"} []{#ver:923.15 label="ver:923.15"} One Tetra Edge Constant: Using a constant-volume, vectorially edged tetrahedron with six edges and with only one of those six edge lengths holding a constant length AB, all five of the tetrahedron’s other edge lengths may covary as the tetrahedron rotates around the fixed edge length AB, which acts as an axis of rotation. While the axis is precessionally tilted within its celestial theater, it is experientially demonstrable thatwithout changing the tetrahedron’s volume or its constant-length vector ABits two other corners and may interconnect the /15-fixed??-length-axis points with any other two points in Universe no matter how remote from one another. This is the reason why electromagnetic waves can interlink any points in Universe in response to a given constant wavelength AB. (Compare Secs. 426.40, 530.11, 960.08, and 961.10-40.)
[923.20]{style="color: purple3"} []{#ver:923.20 label="ver:923.20"} Constant Volume: comparison of the end views of the and Quanta Modules shows that they have equal volumes as a result of their equal base areas and identical altitudes.
[923.21]{style="color: purple3"} []{#ver:923.21 label="ver:923.21"} line can be projected from its origin at the center of area of the triangular base of a regular tetrahedron, outward through the opposite apex of the tetrahedron to any desired distance. When subdivided into increments equal to the distance between its triangular-base center and its apex, and when each of these equilinear increments outward beyond the apex is interconnected by three lines leading to each of the three corners of the base triangle, then each of the successive volumetric additions will be of identical volume to that of the original tetrahedra, and the overall form will be that of a tetrahedron which become progressively longer and sharp-pointed with each addition. (See Illus. 923.10 A, B, and C.) As the ever-sharpening and elongating tetrahedron approaches infinity, the three elongating edges tend to parallelism; i.e., toward what is known as parallax in astronomy. The modules will tend to congruence with the parallaxing lines. Each full-line-long length model of these congruent lines will have the same volume as the original module.
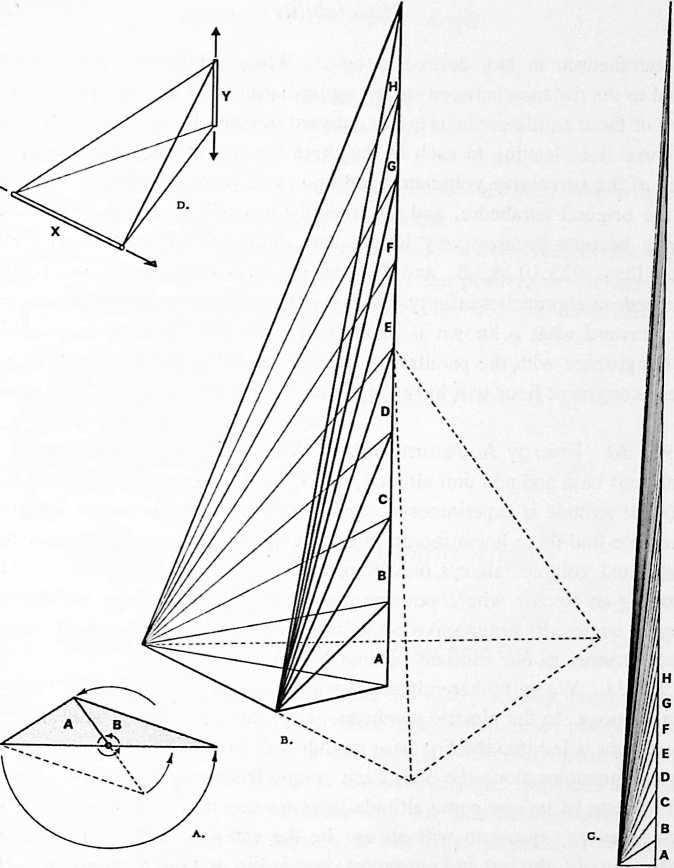
Fig. 923.10 Constant Volume of and Quanta Modules:
-
comparison of the end views of the and Quanta Modules shows that they have equal volumes by virtue of the fact that they have equal base areas and identical altitudes.
-
It follows from this that if a line, originating at the center of area of the triangular base of a regular tetrahedron, is projected through the apex of the tetrahedron to infinity, is subdivided into equal increments, it will give rise to additional Modules to infinity. Each additional Module will have the same volume as the original or Module, and as the incremental line approaches infinity the Modules will tend to become lines, but lines still having the same volume as the original A or B Module.
-
End view shows .Modules beyond the Module shown in (B).
-
The two discrete members and can move anywhere along their respective axes and the volume of the irregular tetrahedron remains constant. The other four edges vary as required.
[923.30]{style="color: purple3"} []{#ver:923.30 label="ver:923.30"} Energy Accommodation: The and Quanta Modules start with unit base and add unit altitude, and so forth, but as each additional altitude is superimposed, the volume remains the same: a volume of one. We find these linear incrementation assemblies getting longer, with their additional volumes always one. Suppose we think about this progression as forming an electric-wire conductor and divide its circular base into three 120-degree angles. Its progressive conic increments could grow and operate in the same manner as our constant-volume, tetrahedral modules.
[923.31]{style="color: purple3"} []{#ver:923.31 label="ver:923.31"} We will inherently superimpose progressive base-to-apex attenuating sections. In the electric conductor wire, this means that whatever energy increment is fed into the first base module will tend to be conducted at various unit frequencies along the line. Each unique frequency introduced at the base will create its unique conic altitude incrementation. The outermost, line-long cone’s energy quantum will always be the same as that of the initial base cone. Finally, the last and outermost cone is just as long as the wire itselfso there is an outside charge on the wire tending to fluoresce a precessional broadcasting of the initial inputs at 90 degrees; i.e., perpendicularly away from the wire. This may elucidate antenna behaviors as well as long-distance, high- voltage, electric energy conductions which tend to broadcast their conducted energy. (For further elaboration of the constant-volume, tetrahedral models, see Secs. 961.10, 20, 30, 40 and 50.)
¶ 924.00 Congruence of Centers
[924.10]{style="color: purple3"} []{#ver:924.10 label="ver:924.10"} Congruence of and Quanta Module Centers: Within either the or Quanta Modules the
centers of effort;
centers of energy;
centers of gravity;
centers of radiation;
centers of volume; and
centers of field
are congruent, i.e., identical. The same centers are involved. We will call their six congruent centers their synergetic centers.
[924.11]{style="color: purple3"} []{#ver:924.11 label="ver:924.11"} But the (+) and (), and (+) and ( ) respective volumetric centers are never congruent. However, the positive or the negative aggregates (these are the “Mites.” See Sec. 953.10) have identical volumetric centers.
[924.20]{style="color: purple3"} []{#ver:924.20 label="ver:924.20"} Table of Tetrahedral Functions of and Quanta Modules: See page 514.
¶ 930.00 Tetrahelix: Unzipping Angle
¶ Continuous Pattern Strip: “Come and Go”
[930.11]{style="color: purple3"} []{#ver:930.11 label="ver:930.11"} Exploring the multiramifications of spontaneously regenerative reangulations and triangulations, we introduce upon a continuous ribbon a 60-degree-patterned, progressively alternating, angular bounce-off inwards from first one side and then the other side of the ribbon, which produces a wave pattern whose length is the interval along any one side between successive bounce-offs which, being at 60 degrees in this case, produces a series of equiangular triangles along the strip. As seen from one side, the equiangular triangles are alternately oriented as peak away, then base away, then peak away again, etc. This is the patterning of the only equilibrious, never realized, angular field state, in contradistinction to its sine-curve wave, periodic realizations of progressively accumulative, disequilibrious aberrations, whose peaks and valleys may also be patterned between the same length wave intervals along the sides of the ribbon as that of the equilibrious periodicity. (See Illus. 930.11.)
[930.20]{style="color: purple3"} []{#ver:930.20 label="ver:930.20"} Pattern Strips Aggregate Wrapabilities: The equilibrious state’s 60-degree rise-and-fall lines may also become successive cross-ribbon fold-lines, which, when successively partially folded, will produce alternatively a tetrahedral- or an octahedral- or an icosahedral-shaped spool or reel upon which to roll-mount itself repeatedly: the tetrahedral spool having four successive equiangular triangular facets around its equatorial girth, with no additional triangles at its polar extremities; while in the case of the octahedral reel, it wraps closed only six of the eight triangular facets of the octahedron, which six lie around the octahedron’s equatorial girth with two additional triangles left unwrapped, one each triangularly surrounding each of its poles; while in the case of the icosahedron, the equiangle-triangulated and folded ribbon wraps up only 10 of the icosahedron’s 20 triangles, those 10 being the 10 that lie around the icosahedron’s equatorial girth, leaving five triangles uncovered around each of its polar vertexes. (See Illus. 930.20.)
Table 924.20 Tetrahedral Functions of and Quanta Modules.
Fig. 930.11: This continuous triangulation pattern strip is a 60, angular, “come and go” alternation of very-high-frequency energy events of unit wavelength. This strip folded back on itself becomes a series of octahedra. The octahedra strips then combine to form a space-filling array of octahedra and tetrahedra, with all lines or vectors being of identical length and all the triangles equilateral and all the vertexes being omnidirectionally evenly spaced from one another. This is the pattern of “closest packing” of spheres.
[930.21]{style="color: purple3"} []{#ver:930.21 label="ver:930.21"} The two uncovered triangles of the octahedron may be covered by wrapping only one more triangularly folded ribbon whose axis of wraparound is one of the symmetrical axes of the octahedron.
[930.22]{style="color: purple3"} []{#ver:930.22 label="ver:930.22"} Complete wrap-up of the two sets of five triangles occurring around each of the two polar zones of the icosahedron, after its equatorial zone triangles are completely enclosed by one ribbon-wrapping, can be accomplished by employing only two more such alternating, triangulated ribbon-wrappings.
[930.23]{style="color: purple3"} []{#ver:930.23 label="ver:930.23"} The tetrahedron requires only one wrap-up ribbon; the octahedron two; and the icosahedron three, to cover all their respective numbers of triangular facets. Though all their faces are covered, there are, however, alternate and asymmetrically arrayed, open and closed edges of the tetra, octa, and icosa, to close all of which in an even-number of layers of ribbon coverage per each facet and per each edge of the three-and-only prime structural systems of Universe, requires three, triangulated, ribbon-strip wrappings for the tetrahedron; six for the octahedron; and nine for the icosahedron.
[930.24]{style="color: purple3"} []{#ver:930.24 label="ver:930.24"} If each of the ribbon-strips used to wrap-up, completely and symmetrically, the tetra, octa, and icosa, consists of transparent tape; and those tapes have been divided by a set of equidistantly interspaced lines running parallel to the ribbon’s edges; and three of these ribbons wrap the tetrahedron, six wrap the octahedron, and nine the icosahedron; then all the four equiangular triangular facets of the tetrahedron, eight of the octahedron, and 20 of the icosahedron, will be seen to be symmetrically subdivided into smaller equiangle triangles whose total number will be , the second power of the number of spaces between the ribbon’s parallel lines.
[930.25]{style="color: purple3"} []{#ver:930.25 label="ver:930.25"} All of the vertexes of the intercrossings of the three-, six-, nine- ribbons’ internal parallel lines and edges identify the centers of spheres closest-packed into tetrahedra, octahedra, and icosahedra of a frequency corresponding to the number of parallel intervals of the ribbons. These numbers (as we know from Sec. 223.21) are:
for the tetrahedron;
for the octahedron; and
for the icosahedron (or vector equilibrium).
[930.26]{style="color: purple3"} []{#ver:930.26 label="ver:930.26"} Thus we learn sum-totally how a ribbon (band) wave, a waveband, can self-interfere periodically to produce in-shuntingly all the three prime structures of Universe and a complex isotropic vector matrix of successively shuttle-woven tetrahedra and octahedra. It also illustrates how energy may be wave-shuntingly self-knotted or self-interfered with (see Sec. 506), and their energies impounded in local, high-frequency systems which we misidentify as only-seemingly-static matter.
¶ 931.00 Chemical Bonds
[931.10]{style="color: purple3"} []{#ver:931.10 label="ver:931.10"} Omnicongruence: When two or more systems are joined vertex to vertex, edge to edge, or in omnicongruencein single, double, triple, or quadruple bonding, then the topological accounting must take cognizance of the congruent vectorial build in growth. (See Illus. 931.10.)
[931.20]{style="color: purple3"} []{#ver:931.20 label="ver:931.20"} Single Bond: In a single-bonded or univalent aggregate, all the tetrahedra are joined to one another by only one vertex. The connection is like an electromagnetic universal joint or like a structural engineering pin joint; it can rotate in any direction around the joint. The mutability of behavior of single bonds elucidates the compressible and load-distributing behavior of gases.
[931.30]{style="color: purple3"} []{#ver:931.30 label="ver:931.30"} Double Bond: If two vertexes of the tetrahedra touch one another, it is called double-bonding. The systems are joined like an engineering hinge; it can rotate only perpendicularly about an axis. Double-bonding characterizes the load-distributing but noncompressible behavior of liquids. This is edge-bonding.
[931.40]{style="color: purple3"} []{#ver:931.40 label="ver:931.40"} Triple Bond: When three vertexes come together, it is called a fixed bond, a three-point landing. It is like an engineering fixed joint; it is rigid. Triple-bonding elucidates both the formational and continuing behaviors of crystalline substances. This also is face-bonding.
-
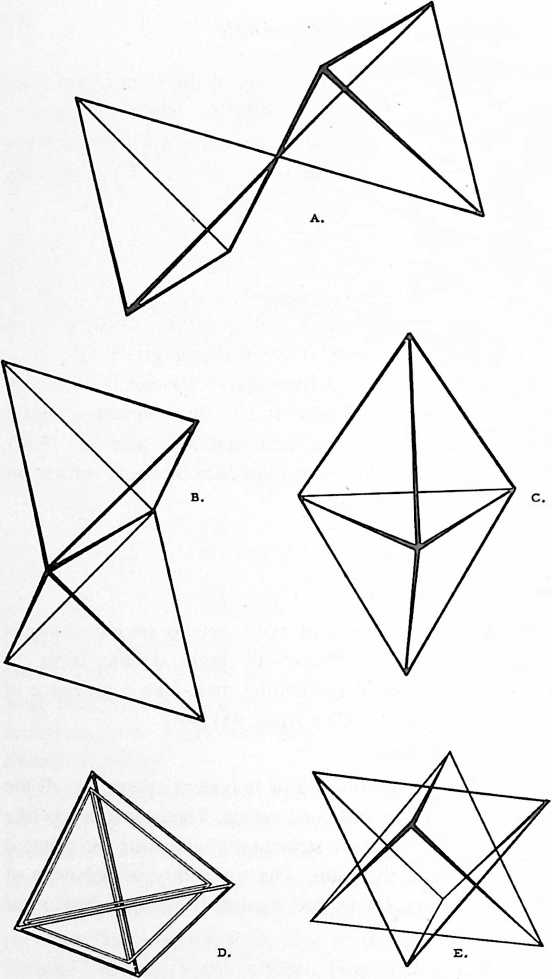
The single-bonded tetrahedron system is like an engineering pin joint: it can move in any direction. It characterizes the behavior of gases.
-
The double-bonded tetrahedron system is like an engineering hinge joint: it can rotate about an axis. It characterizes the behavior of liquids.
-
The triple-bonded tetrahedron system is like an engineering fixed joint: it is rigid. It demonstrates the behavior of crystalline substances.
D & E. The quadri-bond and mid-edge-coordinate tetrahedron systems demonstrate the super strength of substances such as diamond and the metals.
F. The tetrahelix: a helical array of triple-bonded tetrahedra.
[931.50]{style="color: purple3"} []{#ver:931.50 label="ver:931.50"} Quadruple Bond: When four vertexes are congruent, we have quadruple-bonded densification. The relationship is quadrivalent. Quadri-bond and mid-edge coordinate tetrahedron systems demonstrate the super-strengths of substances such as diamonds and metals. This is the way carbon suddenly becomes very dense, as in a diamond. This is multiple self-congruence.
[931.51]{style="color: purple3"} []{#ver:931.51 label="ver:931.51"} The behavioral hierarchy of bondings is integrated four-dimensionally with the synergies of mass-interattractions and precession.
[931.60]{style="color: purple3"} []{#ver:931.60 label="ver:931.60"} Quadrivalence of Energy Structures Closer-Than-Sphere Packing: In 1885, van’t Hoff showed that all organic chemical structuring is tetrahedrally configured and interaccounted in vertexial linkage. constellation of tetrahedra linked together entirely by such single-bonded universal jointing uses lots of space, which is the openmost condition of flexibility and mutability characterizing the behavior of gases. The medium-packed condition of a double-bonded, hinged arrangement is still flexible, but sum-totally as an aggregate, allspace-filling complex is noncompressible as are liquids. The closest-packing, triple-bonded, fixed-end arrangement corresponds with rigid-structure molecular compounds.
[931.61]{style="color: purple3"} []{#ver:931.61 label="ver:931.61"} The closest-packing concept was developed in respect to spherical aggregates with the convex and concave octahedra and vector equilibria spaces between the spheres. Spherical closest packing overlooks a much closer packed condition of energy structures, which, however, had been comprehended by organic chemistry extemdash that of quadrivalent and fourfold bonding, which corresponds to outright congruence of the octahedra or tetrahedra themselves. When carbon transforms from its soft, pressed-cake, carbon black powder (or charcoal) arrangement to its diamond arrangement, it converts from the so-called closest arrangement of triple bonding to quadrivalence. We call this self-congruence packing, as a single tetrahedron arrangement in contradistinction to closest packing as a neighboring-group arrangement of spheres.
[931.62]{style="color: purple3"} []{#ver:931.62 label="ver:931.62"} Linus Pauling’s X-ray diffraction analyses revealed that all metals are tetrahedrally organized in configurations interlinking the gravitational centers of the compounded atoms. It is characteristic of metals that an alloy is stronger when the different metals’ unique, atomic, constellation symmetries have congruent centers of gravity, providing mid-edge, mid-face, and other coordinate, interspatial accommodation of the elements’ various symmetric systems.
[931.63]{style="color: purple3"} []{#ver:931.63 label="ver:931.63"} In omnitetrahedral structuring, a triple-bonded linear, tetrahedral array may coincide, probably significantly, with the DNA helix. The four unique quanta corners of the tetrahedron may explain DNA’s unzipping dichotomy as well as T-A; G-Cpatterning control of all reproductions of all biological species.
¶ 932.00 Viral Steerability
[932.01]{style="color: purple3"} []{#ver:932.01 label="ver:932.01"} The four chemical compounds guanidine, cytosine, thiamine, and adenine, whose first letters are , and of which DNA always consists in various paired code pattern sequences, such as , , , , , , in which and are always paired as are and . The pattern controls effected by DNA in all biological structures can be demonstrated by equivalent variations of the four individually unique spherical radii of two unique pairs of spheres which may be centered in any variation of series that will result in the viral steerability of the shaping of the DNA tetrahelix prototypes. (See Sec. 1050.00 et. seq.)
[932.02]{style="color: purple3"} []{#ver:932.02 label="ver:932.02"} One of the main characteristics of DNA is that we have in its helix a structural patterning instruction, all four-dimensional patterning being controlled only by frequency and angle modulatability. The coding of the four principal chemical compounds, GCTA, contains all the instructions for the designing of all the patterns known to biological life. These four letters govern the coding of the life structures. With new life, there is a parent-child code controls unzipping. There is a dichotomy and the new life breaks off from the old with a perfect imprint and control, wherewith in turn to produce and design others.
¶ 933.00 Tetra helix
[933.01]{style="color: purple3"} []{#ver:933.01 label="ver:933.01"} The tetrahelix is a helical array of triple-bonded tetrahedra. (See Illus. 933.01.) We have a column of tetrahedra with straight edges, but when face-bonded to one another, and the tetrahedra’s edges are interconnected, they altogether form a hyperbolic-parabolic, helical column. The column spirals around to make the helix, and it takes just ten tetrahedra to complete one cycle of the helix.
[933.02]{style="color: purple3"} []{#ver:933.02 label="ver:933.02"} This tetrahelix column can be equiangle-triangular, triple-ribbon-wave produced as in the methodology of Secs. 930.10 and 930.20 by taking a ribbon three-panels wide instead of one-panel wide as in Sec. 930.10. With this triple panel folded along both of its interior lines running parallel to the three-band-wide ribbon’s outer edges, and with each of the three bands interiorly scribed and folded on the lines of the equiangle-triangular wave pattern, it will be found that what might at first seem to promise to be a straight, prismatic, three-edged, triangular-based columnupon matching the next-nearest above, wave interval, outer edges of the three panels together (and taping them together)will form the same tetrahelix column as that which is produced by taking separate equiedged tetrahedra and face-bonding them together. There is no distinguishable difference, as shown in the illustration.
Fig. 933.01: These helical columns of tetrahedra, which we call the tetrahelix, explain the structuring of DNA models of the control of the fundamental patterning of nature’s biological structuring as contained within the virus nucleus. It takes just 10 triplebonded tetrahedra to make a helix cycle, which is a molecular compounding characteristic also of the Watson-Crick model of the DNA. When we address two or more positive (or two or more negative) tetrahelixes together, they nestle their angling forms into one another. When so nestled the tetrahedra are grouped in local clusters of five tetrahedra around a transverse axis in the tetrahelix nestling columns. Because the dihedral angles of five tetrahedra are 7short of 360, this 7is sprung-closed by the helix structure’s spring contraction. This backed-up spring tries constantly to unzip one nestling tetrahedron from the other, or others, of which it is a true replica. These are direct (theoretical) explanations of otherwise as yet unexplained behavior of the DNA.
[933.03]{style="color: purple3"} []{#ver:933.03 label="ver:933.03"} The tetrahelix column may be made positive (like the right-hand- threaded screw) or negative (like the left-hand-threaded screw) by matching the next-nearest-below wave interval of the triple-band, triangular wave’s outer edges together, or by starting the triple-bonding of separate tetrahedra by bonding in the only alternate manner provided by the two possible triangular faces of the first tetrahedron furthest away from the starting edge; for such columns always start and end with a tetrahedron’s edge and not with its face.
[933.04]{style="color: purple3"} []{#ver:933.04 label="ver:933.04"} Such tetrahelical columns may be made with regular or irregular tetrahedral components because the sum of the angles of a tetrahedron’s face will always be 720 degrees, whether regular or asymmetric. If we employed asymmetric tetrahedra they would have six different edge lengths, as would be the case if we had four different diametric balls and we paired them tangentially, with , and with , and we then nested them together (as in Sec. 623.12 ), and by continuing the columns in any different combinations of these pairs we would be able to modulate the rate of angular changes to design approximately any form.
[933.05]{style="color: purple3"} []{#ver:933.05 label="ver:933.05"} This synergetics’ tetrahelix is capable of demonstrating the molecular-compounding characteristic of the Watson-Crick model of the DNA, that of the deoxyribonucleic acid. When Drs. Watson, Wilkins, and Crick made their famous model of the DNA, they made a chemist’s reconstruct from the information they were receiving, but not as a microscopic photograph taken through a camera. It was simply a schematic reconstruction of the data they were receiving regarding the relevant chemical associating and the disassociating. They found that a helix was developing.
[933.06]{style="color: purple3"} []{#ver:933.06 label="ver:933.06"} They found there were 36 rotational degrees of arc accomplished by each increment of the helix and the 36 degrees aggregated as 10 arc increments in every complete helical cycle of 360 degrees. Although there has been no identification of the tetrahelix column of synergetics with the Watson-Crick model, the numbers of the increments are the same. Other molecular biologists also have found a correspondence of the tetrahelix with the structure used by some of the humans’ muscle fibers.
[933.07]{style="color: purple3"} []{#ver:933.07 label="ver:933.07"} When we address two or more positive or two or more negative tetrahelixes together, the positives nestle their angling forms into one another, as the negatives nestle likewise into one another’s forms.
[933.08]{style="color: purple3"} []{#ver:933.08 label="ver:933.08"} Closest Packing of Different-sized Balls: It could be that the tetrahelix derives from the closest packing of different-sized balls. The Mites and Sytes (see Sec. 953) could be the tetrahedra of the because they are both positive-negative and allspace filling.
¶ 934.00 Unzipping Angle
[934.01]{style="color: purple3"} []{#ver:934.01 label="ver:934.01"} If we take three columns of tetrahelixes and nest them into one another, we see that they also apparently internest neatly as with a three-part rope twist; but upon pressing them together to close the last narrow gap between them we discover that they are stubbornly resisting the final closure because the core pattern they make is one in which five tetrahedra are triple-bonded around a common edge axiswhich angular gap is impossible to close.
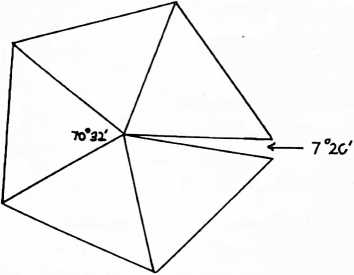
[934.02]{style="color: purple3"} []{#ver:934.02 label="ver:934.02"} Five tetrahedra triple-bonded to one another around a common edge axis leave an angular sinus[^30] of 7as the birth unzipping angle of DNA-RNA behaviors. This gap could be shared 10 ways, i.e., by two faces each of the five circle-closing tetrahedra, and only 44 minutes of circular arc per each tetra face, each of whose two faces might be only alternatingly edge-bonded, or hinged, to the next, which almost-closed, face-toward-face, hinge condition would mechanically accommodate the spanned coherence of this humanly-invisible, 44-minutes-of-circular-arc, distance of interadherence. Making such a tetrahelix column could be exactly accomplished by only hinging one edge of each tetrahedron to the next, always making the next hinge with one of the two-out-of-three edges not employed in the previous hinge. Whatever the method of interlinkage, this birth dichotomy is apparently both accommodated by and caused by this invisible, molecular biologist’s 1per tetra and 7per helical-cycle hinge opening.
703&
35Z
36tf oo
-352 40
7 -ZU Unzipping angle
Fig. 934.02.
[934.03]{style="color: purple3"} []{#ver:934.03 label="ver:934.03"} Unzipping occurs as the birth dichotomy and the new life breaks off from the old pattern with a perfect imprint and repeats the other’s growth pattern. These helixes have the ability to nest by virtue of the hinge-spring linkage by which one is being imprinted on the other. Positive columns nest with and imprint only upon positive helix columns and negative helix columns nest with and imprint their code pattern only with and upon negative helix columns. Therefore, when a column comes off, i.e., unzips, it is a replica of the original column.
[934.04]{style="color: purple3"} []{#ver:934.04 label="ver:934.04"} We know that the edge angle of a tetrahedron is 70, and five times that is 352, which is 7 less than 360. In other words, five tetrahedra around a common edge axis do not close up and make 360 degrees, because the dihedral angles are 7 short. But when they are brought together in a helixdue to the fact that a hinged helix is a coil springthe columns will twist enough to permit the progressive gaps to be closed. No matter how long the tetrahelix columns are, their sets of coil springs will contract enough to bring them together. The backed-up spring tries constantly to unzip one nesting tetrahedron from the others of which it is a true replica. These are only synergetical conjectures as to the theoretical explanations of otherwise as yet unexplained behaviors of the DNA.
¶ 935.00 Octahedron as Conservation and Annihilation Model
* [935.00-938.16 Annihilation Scenario]
¶ 935.10 Energy Flow and Discontinuity
[935.11]{style="color: purple3"} []{#ver:935.11 label="ver:935.11"} Though classic science at the opening of the 18 th century had achieved many remarkably accurate observations and calculations regarding the behaviors of light, individual scientists and their formal societieswith one notable exceptionremained unaware that light (and radiation in general) has a speed. Ole Roemer (1644–1710), both Royal Astronomer and Royal Mathematician of Denmark, was that exception. Roemer’s observations of the reflected light of the revolving moons of the planet Jupiter made him surmise that light has a speed. His calculations from the observed data very closely approximated the figure for that speed as meticulously measured in vacuo two centuries later, in the Michelson-Morley experiment of 1887. Though Roemer was well accredited by the scientists and scientific societies of Europe, this hypothesis of his seemed to escape their cosmological considerations. Being overlooked, the concept did not enter into any of the cosmological formulations (either academic or general) of humanity until the 20th century.
[935.12]{style="color: purple3"} []{#ver:935.12 label="ver:935.12"} Until the 20th century scientists in general assumed the light of all the stars to be instantaneously and simultaneously extant. Universe was an instantaneous and simultaneous system. The mid-19th-century development of thermodynamics, and in particular its second law, introduced the concept that all systems always lose energy and do so in ever-increasingly disorderly and expansive ways. The academicians spontaneously interpreted the instantaneity and simultaneity of Universe as requiring that the Universe too must be categorized as a system; the academicians assumed that as a system Universe itself must be losing energy in increasingly expansive and disorderly ways. Any expenditure of energy by humans on Earth to whom the stars in the heavens were just so much romantic scenery; no more, no lesswould hasten the end of the Universe. This concept was the foundation of classical conservatismeconomic, political, and philosophical. Those who “spent” energy were abhorred.
[935.13]{style="color: purple3"} []{#ver:935.13 label="ver:935.13"} This viewpoint was fortified by the hundred-years-earlier concept of classical science’s giant, Isaac Newton, who in his first law of motion stated that all bodies persist in a state of rest, or in a line of motion, except as affected by other bodies. This law posits a cosmic norm of at rest: change is abnormal. This viewpoint as yet persists in all the graphic-chart coordinates used by society today for plotting performance magnitudes against a time background wherein the baseline of “no change” is the norm. Change is taken spontaneously as being inherently abnormal and is as yet interpreted by many as being cause for fundamental social concern.
[935.14]{style="color: purple3"} []{#ver:935.14 label="ver:935.14"} With the accurate measurement, in 1887, of the speed of light in vacuo, science had comprehensively new, experimentally redemonstrable challenges to its cosmogony and cosmology. Inspired by the combined discoveries of the Brownian movement, black body radiation, and the photon of light, Einstein, Planck, and others recognized that energy-as-radiation has a top speedergo, is finitely terminaledbut among them, Einstein seems to have convinced himself that his own cosmological deliberations should assume Boltzmann’s concept to be validergo, always to be included in his own exploratory thoughts. There being no experimental evidence of energy ever being created or lost, universal energy is apparently conserved. Wherefore Boltzmann had hypothesized that energy progressively and broadcastingly exported from various localities in Universe must be progressively imported and reassembled at other localities in Universe.
[935.15]{style="color: purple3"} []{#ver:935.15 label="ver:935.15"} Boltzmann’s concept was analogous to that upon which was developed the theory and practice of the 20th-century meteorological weather forecasting, which recognizes that our terrestrial atmosphere’s plurality of high-pressure areas are being progressively exhausted at different rates by a plurality of neighboring low-pressure areas, which accumulate atmospheric molecules and energy until they in turn become new high-pressure areas, which are next to be progressively exhausted by other newly initiated low-pressure areas. The interpatterning of the various importing-exporting centers always changes kaleidoscopically because of varying speeds of moisture formation or precipitation, speeds and directions of travel, and local thermal conditions.
[935.16]{style="color: purple3"} []{#ver:935.16 label="ver:935.16"} Though they did not say it that way, the 20th-century leaders of scientific thinking inferred that physical Universe is apparently eternally regenerative.
[935.17]{style="color: purple3"} []{#ver:935.17 label="ver:935.17"} Einstein assumed hypothetically that energies given off omnidirectionally with the ever-increasing disorder of entropy by all the stars were being antientropically imported, sorted, and accumulated in various other elsewheres. He showed that when radiant energy interferes with itself, it can, and probably does, tie itself precessionally into local and orderly knots. Einstein must have noted that on Earth children do not disintegrate entropically but multiply their hydrocarbon molecules in an orderly fashion; little saplings grow in an orderly way to become big trees. Einstein assumed Earthian biology to be reverse entropy. (This account does not presume to recapitulate the actual thought processes of Einstein at any given point in the development of his philosophy; rather it attempts to illustrate some of the invitable conclusions that derive from his premises.)
[935.18]{style="color: purple3"} []{#ver:935.18 label="ver:935.18"} What made it difficult for scientists, cosmologists, and cosmogonists to comprehend about Boltzmann’s conceptor Einstein’s implicit espousal of itwas the inherent discontinuity of energy events implicit in the photon as a closed-system package of energy. What happened to the energy when it disappeared? For disappear it did. How could it reappear elsewhere in a discontinuous system?
¶ 935.20 Precessional Transformation in Quantum Model
[935.21]{style="color: purple3"} []{#ver:935.21 label="ver:935.21"} One quantum of energy always consists of six energy vectors, each being a combined push-pull, positive-negative force. (See Secs. 600.02 through 612.01 and Fig. 620.06.) Twelve unique forces: six plus and six minus. Six vectors break into two sets of three each. Classical engineers assumed that each action had its equal and opposite reaction at 180 degrees; but since the discovery of the speed of light and the understanding of nonsimultaneity, we find that every action has not only a reaction but also a resultant. Neither the reaction nor the resultant are angularly “opposite” in 180-degree azimuth from the direction of action. The “equal and opposite” of classical engineering meant that both action and reaction occurred in opposite directions in the same straight line in the same geometrical plane. But since the recognition of nonsimultaneity and the speed of light, it has been seen that action, reaction, and resultant vectors react omnidirectionally and precessionally at angles other than 180 degrees. (See Fig. 511.20.)
[935.22]{style="color: purple3"} []{#ver:935.22 label="ver:935.22"} As we enter the last quarter of the 20th century, it is recognized in quantum mechanics and astrophysics that there could never have existed the traditionally assumed, a priori universal chaos, a chaos from which it was also assumed that Universe had escaped only by the workings of chance and the long-odds-against mathematical probability of a sequence of myriad-illions of coincidences, which altogether produced a universal complex of orderly evolutionary events. This nonsense was forsaken by the astrophysicists only a score of years ago, and only because science has learned in the last few decades that both the proton and the neutron always and only coexist in a most orderly interrelationship. They do not have the same mass, and yet the one can be transformed into the other by employing both of their respective two energy side effects; i.e., those of both the proton and the neutron. Both the proton and the neutron have their respective and unique two-angle-forming patterns of three interlinked lines, each representing their action, reaction, and resultant vectors.
[935.221]{style="color: purple3"} []{#ver:935.221 label="ver:935.221"} Coming-Apart Phase: Coming-Apart Limit: The astrophysicists say that no matter how far things come apart, fundamentally they never come farther apart than proton and neutron, which always and only coexist.
[935.23]{style="color: purple3"} []{#ver:935.23 label="ver:935.23"} The names of the players, the positions they play, and the identifying letters they wear on the three-vector teams of proton and neutron, respectively, are identified as follows. The proton’s three-vector team consists of:
-
the action vector, played by its captain, the proton, wearing the letters BD;
-
the reaction vector, played by the electron, wearing the letters AD; and
-
the resultant vector, played by the antineutrino, wearing the letters BC.
The neutron’s three-vector team consists of:
-
the action vector, played by its captain, the neutron, wearing the letters AC;
-
the reaction vector, played by the positron, wearing the letters CD; and
-
the resultant vector, played by the neutrino, wearing the letters AB.
Either one of these two teams of three-vector events is identified in quantum mechanics as being a half-quantum (or one-half spin or one-half Planck’s constant). When two half-quanta associate, they produce one unit of quantum. (See Sec. 240.65.) These two sets of three vectors each combine to produce the six vector edges of the tetrahedron, which is the minimum structural system of Universe: one quantum of energy thus becomes structurally and systematically conceptual. (See Fig. 935.23.) One quantum of energy equals one tetrahedron. Humanist writers and broadcasters take notice that science has regained conceptuality. Science’s intertransformabilities and intercomplementarities are modelably demonstrable. The century-long chasm that has separated science and the humanities has vanished.
[935.24]{style="color: purple3"} []{#ver:935.24 label="ver:935.24"} The tetrahedral model of the quantum as the minimum structural system of Universe is a prime component in producing the conceptual bridge to span the vast chasm identified by C. P. Snow as having for so long existed between the one percent of the world people who are scientists and the 99 percent of humanity comprehendingly communicated with by the writers in literature and the humanities. This chasm has been inadvertently sustained by the use of an exclusively mathematical language of abstract equations on the part of scientists, thus utterly frustrating the comprehension of the scientists’ work by the 99 percent of humanity that does not communicate mathematically. This book, Synergetics, contains the conceptualizing adequate to the chasmbridging task, and it does so in vectorially structured geometry and in exclusively low-order prime numbers in rational whole-number accounting.
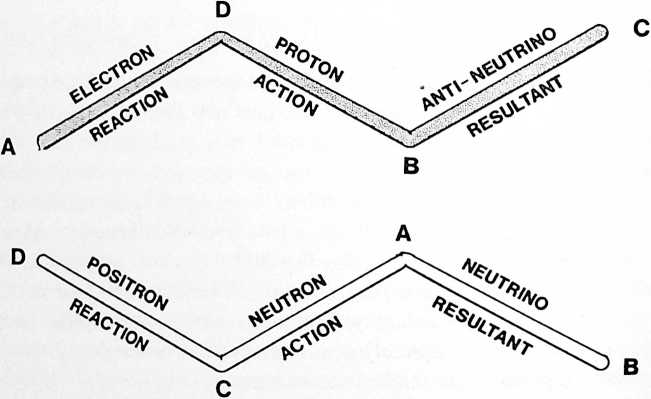
[935.25]{style="color: purple3"} []{#ver:935.25 label="ver:935.25"} As an instance of chasm-spanning between science and the humanities by conceptually transformative energy-quanta accounting, synergetics conceptually elucidates the Boltzmann import-export, entropy-syntropy transaction and the elegant manner in which nature accommodates the “hidden ball” play of now-you-see-it-now-you-don’t energy transference.
¶ 936.00 Volumetric Variability with Topological Constancy
[936.10]{style="color: purple3"} []{#ver:936.10 label="ver:936.10"} Symmetrical and Asymmetrical Contraction
[936.11]{style="color: purple3"} []{#ver:936.11 label="ver:936.11"} An octahedron consists of 12 vector edges and two units of quantum and has a volume of four when the tetrahedron is taken as unity. (See Table 223.64.) Pulling two ends of a rope in opposite directions makes the rope’s girth contract precessionally in a plane at 90 degrees to the axis of purposeful tensing. (Sec. 1054.61.) Or if we push together the opposite sides of a gelatinous mass or a pneumatic pillow, the gelatinous mass or the pneumatic pillow swells tensively outward in a plane at 90 degrees to the line of our purposeful compressing. This 90-degree reaction or resultant is characteristic of precession. Precession is the effect of bodies in motion upon other bodies in motion. The gravitational pull of the Sun on the Earth makes the Earth go around the Sun in an orbit at 90 degrees to the line of the Earth-Sun gravitational interattraction. The effect of the Earth on the Moon or of the nucleus of the atom upon its electron is to make these interattractively dependent bodies travel in orbits at 90 degrees to their mass-interattraction force lines.
[936.12]{style="color: purple3"} []{#ver:936.12 label="ver:936.12"} The octahedron represents the most commonly occurring crystallographic conformation in nature. (See Figs. 931.10 and 1054.40.) It is the most typical association of energy-as-matter; it is at the heart of such association. Any focused emphasis in the gravitational pull of the rest of the Universe upon the octahedron’s symmetry precesses it into asymmetrical deformation in a plane at 90 degrees to the axis of exaggerated pulling. This forces one of the 12 edge vectors of the octahedron to rotate at 90 degrees. If we think of the octahedron’s three axes and its six vertexes, oriented in such a manner that is the north pole and is the south pole, the other four vertexes all occur in the plane of, and define, the octahedron’s equator. The effect of gravitational pull upon the octahedron will make one of the four equatorial vectors disengage from its two adjacent equatorial vertexes, thereafter to rotate 90 degrees and then rejoin its two ends with the north pole and south pole vertexes. (See Fig. 936.12 and color plate 6.)
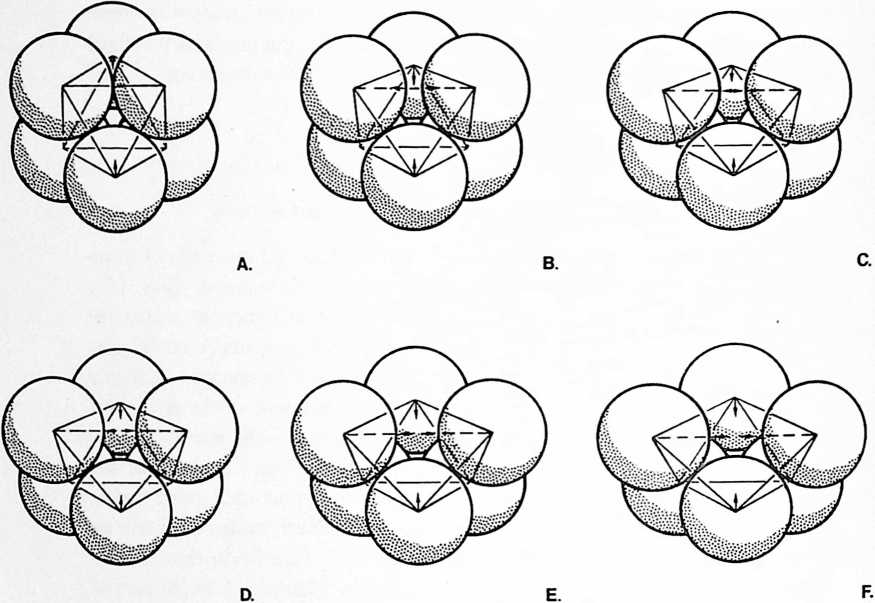
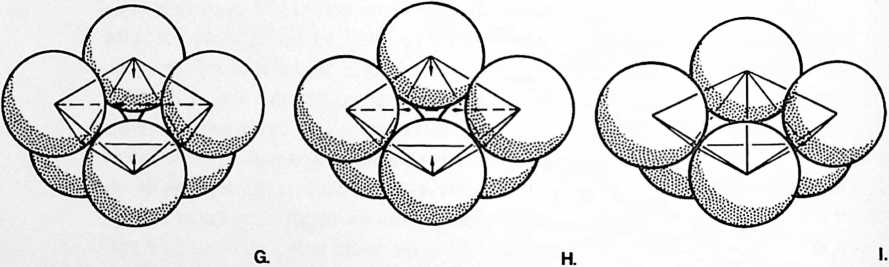
[936.13]{style="color: purple3"} []{#ver:936.13 label="ver:936.13"} When this precessional transformation is complete, we have the same topological inventories of six vertexes, eight exterior triangular faces, and 12 vector edges as we had before in the symmetrical octahedron; but in the process the symmetrical, four-tetrahedra-quanta-volume octahedron has been transformed into three tetrahedra (three-quanta volume) arranged in an arc section of an electromagnetic wave conformation with each of the two end tetrahedra being face bonded to the center tetrahedron. (See Sec. 982.73.)
[936.14]{style="color: purple3"} []{#ver:936.14 label="ver:936.14"} The precessional effect has been to rearrange the energy vectors themselves in such a way that we have gone from the volume-four quanta of the symmetrical octahedron to the volume-three quanta of the asymmetric tetra-arc-array segment of an electromagnetic wave pattern. Symmetric matter has been entropically transformed into asymmetrical and directionally focused radiation: one quantum of energy has seemingly disappeared. When the radiation impinges interferingly with any other energy event in Universe, precession recurs and the three-quantum electromagnetic wave retransforms syntropically into the four-quantum octahedron of energy-as-matter. And vice versa. Q.E.D. (See Fig. 936.14.)
[936.15]{style="color: purple3"} []{#ver:936.15 label="ver:936.15"} The octahedron goes from a volume of four to a volume of three as one tensor is precessed at 90 degrees. This is a demonstration in terms of tension and compression of how energy can disappear and reappear. The process is reversible, like Boltzmann’s law and like the operation of syntropy and entropy. The lost tetrahedron can reappear and become symmetrical in its optimum form as a ball-bearing-sphere octahedron. There are six great circles doubled up in the octahedron. Compression is radiational: it reappears. Out of the fundamental fourness of all systems we have a model of how four can become three in the octahedron conservation and annihilation model.
[936.16]{style="color: purple3"} []{#ver:936.16 label="ver:936.16"} See the Iceland spar crystals for the octahedron’s double vector-edge image.
[936.17]{style="color: purple3"} []{#ver:936.17 label="ver:936.17"} The interior volume of the concave-vector-equilibrium-shaped space occurring interiorly between the six uniradius octahedral collection of closest-packed spheres is greater than is the concave-octahedrally-shaped space occurring interiorly between the four uniradius tetrahedral collection of closest-packed spheres, which tetrahedral collection constitutes the minimum structural system in Universe, and its interior space is the minimum interior space producible within the interstices of closest-packed uniradius spheres.
[936.18]{style="color: purple3"} []{#ver:936.18 label="ver:936.18"} Thus the larger interior space within the omnitriangularly stable, six-vertex-ball, 12-vector-edge octahedron is subject to volumetric compressibility. Because its interior space is not minimal, as the octahedron is omniembracingly tensed gravitationally between any two or more bodies, its six balls will tend precessionally to yield transformingly to produce three closest-packed, uniradius, sphere-vertex-defined, face-bonded tetrahedra.
[936.19]{style="color: purple3"} []{#ver:936.19 label="ver:936.19"} As we tense the octahedron, it strains until one vector (actually a double, or unity-as-two, vector) yields its end bondings and precesses at 90 degrees to transform the system into three double-bonded (face-bonded) tetrahedra in linear arc form. This tetra-arc, embryonic, electromagnetic wave is in neutral phase. The seemingly annihilated but in fact only separated-out-quantum is now invisible because vectorless. It now becomes invisibly face-bonded as one invisible tetrahedron. The separated-out quantum is face-bonded to one of the furthermost outward triangular faces occurring at either end of the tetra-arc array of three (consisting of one tetra at the middle with each of the two adjacent tetra face-bonded to it); the fourth invisible tetrahedron is face-bonded to one or the other of the two alternatively vacant, alternatively available furthermost end faces of the tetra-arc group. With this fourth, invisible tetrahedral addition the overall triple-bonded tetrahedral array becomes either rightwardly or leftwardly spiraled to produce a four-tetrahedron tetrahelix, which is a potential, event embryo, electromagnetic-circuitry gap closer. Transmission may thereafter be activated as a connected chain of the inherently four-membered, individual-link continuity. This may explain the dilemma of the wave vs the particle. (See Sec. 973.30, Fig. 936.19, and color plates 6 and 7.)
¶ 936.20 Conceptual Conservation and Annihilation
[936.21]{style="color: purple3"} []{#ver:936.21 label="ver:936.21"} The octahedron as the conservation and annihilation model provides an experiential and conceptual accounting for the question: What happens to entropically vanishing quanta of energy that have never been identified as discretely lost when new quanta appeared elsewhere and elsewhen? Were these appearing and disappearing quanta being encountered for the first time as we became capable of penetrating exploration of ever vaster ranges of Universe?
[936.22]{style="color: purple3"} []{#ver:936.22 label="ver:936.22"} Boltzmann hypothesized and Einstein supported his working assumption stated in the conceptual language of synergetics that there can be no a priori stars to radiate entropically and visibly to the information-importing, naked eyes of Earthian humans (or to telescopes or phototelescopy or electromagnetic antennae) if there were not also invisible cosmic importing centers. The importing centers are invisible because they are not radiantly exporting; they are in varying stages of progressive retrieving, accumulating, sorting, storing, and compressing energies. The cosmic abundance of the myriads of such importing centers and their cosmic disposition in Scenario Universe exactly balances and conserves the integrity of eternally regenerative Universe.
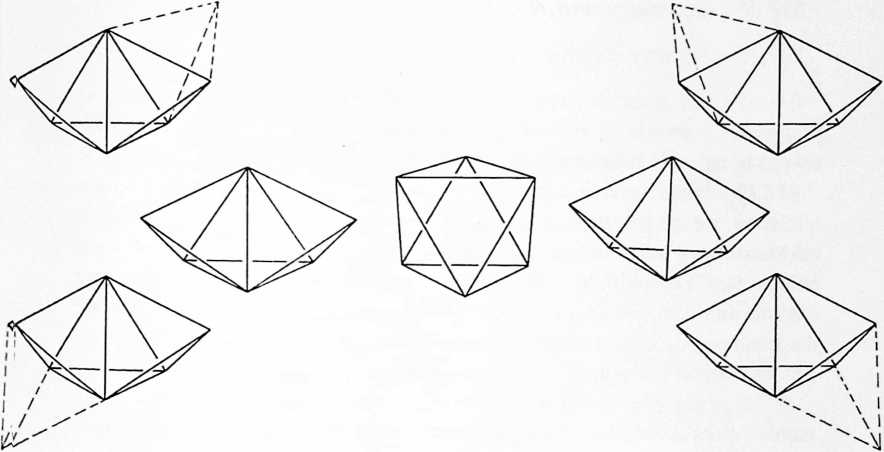
[936.23]{style="color: purple3"} []{#ver:936.23 label="ver:936.23"} In Scenario Universe (in contrast to a spherically-structured, normally-at-rest, celestially-concentric, single-frame-picture Universe) the episodes consist only of such frequencies as are tune-in-able by the limited frequency-range set of the viewer.
[936.24]{style="color: purple3"} []{#ver:936.24 label="ver:936.24"} There is no such phenomenon as space: there is only the at-present-tuned-in set of relationships and the untuned intervailing. Points are twilight-border-line, only amplitude-tuned-in (AM), directionally oriented, static squeaks or pips that, when frequency-tuned (FM), become differentially discrete and conceptually resolvable as topological systems having withinness and withoutness ergo, at minimum having four corner-defining yet subtunable system pips or point-to-able corner loci. In systemic cosmic topology Euler’s vertexes (points) are then always only twilight energy-event loci whose discrete frequencies are untunable at the frequency range of the reception set of the observer.
¶ 937.00 Geometry and Number Share the Same Model
¶ 937.10 Midway Between Limits
[937.11]{style="color: purple3"} []{#ver:937.11 label="ver:937.11"} The grand strategy of quantum mechanics may be described as progressive, numerically rational fractionating of the limit of total energy involved in eternally regenerative Universe.
[937.12]{style="color: purple3"} []{#ver:937.12 label="ver:937.12"} When seeking a model for energy quanta conservation and annihilation, we are not surprised to find it in the middle ranges of the geometrical hierarchy of prime structural systemstetrahedron, octahedron, and icosahedron (see Sec. 610.20). The tetrahedron and icosahedron are the two extreme and opposite limit cases of symmetrical structural systems: they are the minimum-maximum cosmic limits of such prime structures of Universe. The octahedron ranks in the neutral area, midway between the extremes.
[937.13]{style="color: purple3"} []{#ver:937.13 label="ver:937.13"} The prime number characteristic of the tetrahedron is 1; the prime number characteristic of the icosahedron is 5. Both of these prime numbers and 5are odd numbers, in contradistinction to the prime number characteristic of the middle-case structural-system octahedron, which is 2, an even number and the only even numbered prime number. Again, we are not surprised to find that the octahedron is the most common crystal conformation in nature.
[937.14]{style="color: purple3"} []{#ver:937.14 label="ver:937.14"} The tetrahedron has three triangles around each vertex; the octahedron has four; and the icosahedron has five. The extreme-limit cases of structural systems are vertexially locked by odd numbers of triangular gears, while the vertexes of the octahedron at the middle range have an even number of reciprocating triangular gears. This shows that the octahedron’s three great circles are congruent pairsi.e., six circles that may seem to appear as only three, which quadrivalent doubling with itself is clearly shown in the jitterbug model, where the 24 vector edges double up at the octahedron phase to produce 12 double-congruent vector edges and thus two congruent octahedra. (See Fig. 460.08D.)
[937.15]{style="color: purple3"} []{#ver:937.15 label="ver:937.15"} The octahedron is doubled-up in the middle range of the vector equilibrium’s jitterbug model; thus it demonstrates conceptually the exact middle between the macro-micro limits of the sequence of intertransformative events. The octahedron in the middle of the structural-system hierarchy provides us with a clear demonstration of how a unit quantum of energy seemingly disappearsi.e., becomes annihilatedand vice versa.
¶ 937.20 Doubleness of Octahedron
[937.21]{style="color: purple3"} []{#ver:937.21 label="ver:937.21"} The octahedron always exhibits the quality of doubleness. When the octahedron first appears in the symmetrical contraction of the vector equilibrium jitterbug system, it appears with all of its vectors doubled (see Fig. 460.08D). It also takes two sets of three great circles each to fold the octahedron. You might think you could do it with one set of three great circles, but the foldability of the octahedron requires two sets of three great circles each. (See Secs. 835 and 836.) There are always six great circles doubled up in the octahedron to reappear only as three. (See Fig. 937.20.)
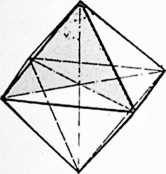
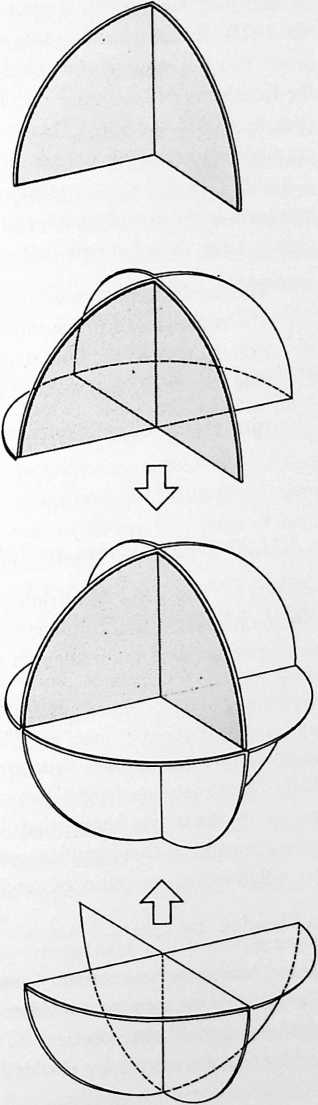
[937.22]{style="color: purple3"} []{#ver:937.22 label="ver:937.22"} And we also recall that the octahedron appears as the prime number 2 in the geometrical hierarchy, while its volume is 4 when the tetrahedron is taken as volumetric units (see Table 223.64).
The tetrahedron’s prime number identity is 1
The octahedron’s prime number identity is 2
Both cubes and rhombic dodecahedra are 3
And icosahedra and vector equilibria are 5
They first occur volumetrically, respectively, as
1, 4, 3, 6, 18.51, and 20.
¶ 937.30 Octahedron as Sphere of Compression
[937.31]{style="color: purple3"} []{#ver:937.31 label="ver:937.31"} The slenderness ratio in gravitationally tensed functioning has no minimum overall limit of its structural-system length, as compared to the diameter of the system’s midlength cross section; ergo,
In crystalline compression structures the column length minimum limit ratio is . There may be a length/diameter compression-system-limit in hydraulics, but we do not as yet know what it is. The far more slender column/diameter ratio attainable with hydraulics permits the growth of a palm tree to approach the column/diameter ratio of steel columns. We recognize the spherethe ball bearing, the spherical island constituting the optimal, crystailine, compressive-continuity, structural-system model. (See Fig. 641.01.) The octahedron may be considered to be the optimum crystalline structural representation of the spherical islands of compression because it is double-bonded and its vectors are doubled.
¶ 938.00 Jitterbug Transformation and Annihilation
¶ 938.10 Positive and Negative Tetrahedra
[938.11]{style="color: purple3"} []{#ver:938.11 label="ver:938.11"} The tetrahedron is the minimum-limit-case structural system of Universe (see Secs. 402 and 620). The tetrahedron consists of two congruent tetrahedra: one concave, one convex. The tetrahedron divides all of Universe into all the tetrahedral nothingness of all the cosmic outsideness and all the tetrahedral nothingness of all the cosmic insideness of any structurally conceived or sensorially experienced, special case, uniquely considered, four-starry-vertex-constellared, tetrahedral system somethingness of human experience, cognition, or thinkability.
[938.12]{style="color: purple3"} []{#ver:938.12 label="ver:938.12"} The tetrahedron always consists of four concave-inward hedra triangles and of four convex-outward hedra triangles: that is eight hedra triangles in all. (Compare Fig. 453.02.) These are the same eightmaximally deployed from one anotherequiangular triangular hedra or facets of the vector equilibrium that converge to differential inscrutability or conceptual zero, while the eight original triangular planes coalesce as the four pairs of congruent planes of the zero-volume vector equilibrium, wherein the eight exterior planes of the original eight edge-bonded tetrahedra reach zero-volume, eightfold congruence at the center point of the four-great-circle system. (Compare Fig. 453.02.)
[938.13]{style="color: purple3"} []{#ver:938.13 label="ver:938.13"} The originalonly vertexially single-bonded, vectorially structured triangles of the vector-equilibrium jitterbug transform by symmetrical contraction from its openmost vector-equilibrium state, through the (unstable-without-six-additional-vector inserts; i.e., one vectorial quantum unit) icosahedral stage only as accommodated by the nuclear sphere’s annihilation, which vanished central sphere reappears transformedly in the 30-vector-edged icosahedron as the six additional external vectors added to the vector equilibrium to structurally stabilize its six “square” faces, which six vectors constitute one quantum package. (See Fig. 938.13.)
[938.14]{style="color: purple3"} []{#ver:938.14 label="ver:938.14"} Next the icosahedron contracts symmetrically to the congruently vectored octahedron stage, where symmetrical contraction ceases and processional torque reduces the system to the quadrivalent tetrahedron’s congruent four positive and four negative tetrahedra. These congruent eight tetrahedra further precess into eight congruent zero-altitude tetrahedral triangles in planar congruence as one, having accomplished this contraction from volume 20 of the vector equilibrium to volume 0 while progressively reversing the vector edges by congruence, reducing the original 30 vector edges (five quanta) to zero quanta volume with only three vector edges, each consisting of eight congruent vectors in visible evidence in the zero-altitude tetrahedron. And all this is accomplished without ever severing the exterior, gravitational-embracing bond integrity of the system. (See Figs. 461.08 and 1013.42.)
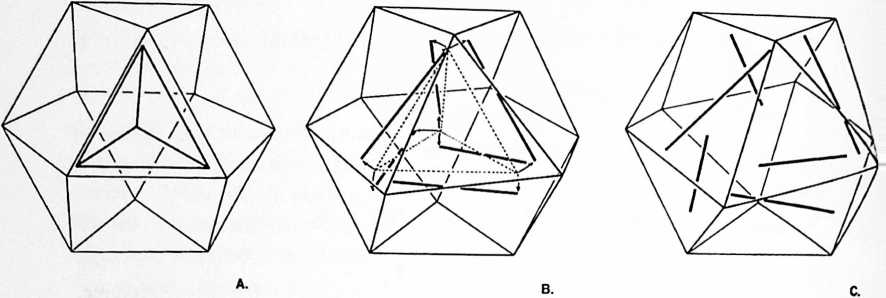
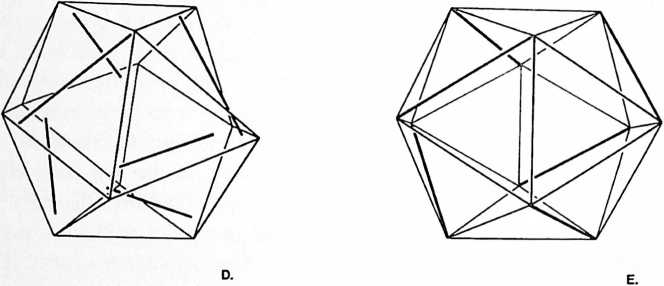
[938.15]{style="color: purple3"} []{#ver:938.15 label="ver:938.15"} The octahedron is produced by one positive and one negative tetrahedron. This is done by opening one vertex of each of the tetrahedra, as the petals of a flower are opened around its bud’s vertex, and taking the two open-flowered tetrahedra, each with three triangular petals surrounding a triangular base, precessing in a positive-negative way so that the open triangular petals of each tetrahedron approach the open spaces between the petals of the other tetrahedron, converging them to produce the eight edge-bonded triangular faces of the octahedron. (See Fig. 938.15.)
[938.16]{style="color: purple3"} []{#ver:938.16 label="ver:938.16"} Because the octahedron can be produced by one positive and one negative tetrahedron, it can also be produced by one positive tetrahedron alone. It can be produced by the four edge-bonded triangular faces of one positive tetrahedron, each being unbonded and precessed 60 degrees to become only vertex-interbonded, one with the other. This produces an octahedron of four positive triangular facets interspersed symmetrically with four empty triangular windows. (See Fig. 938.16.)
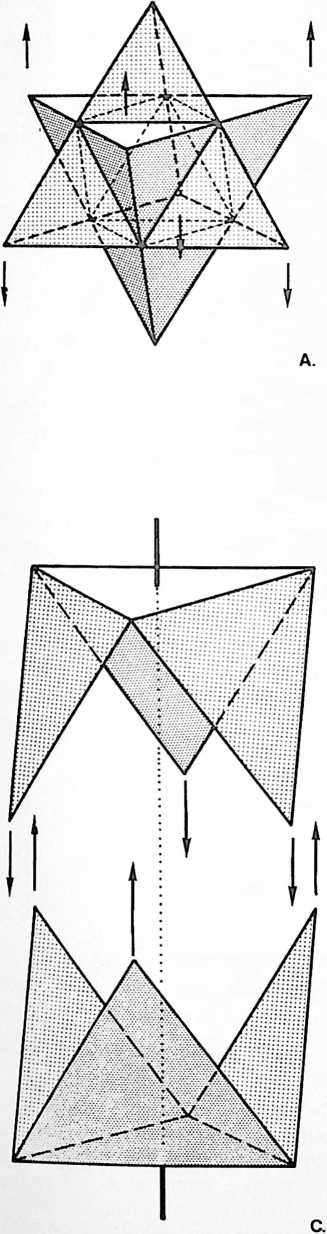
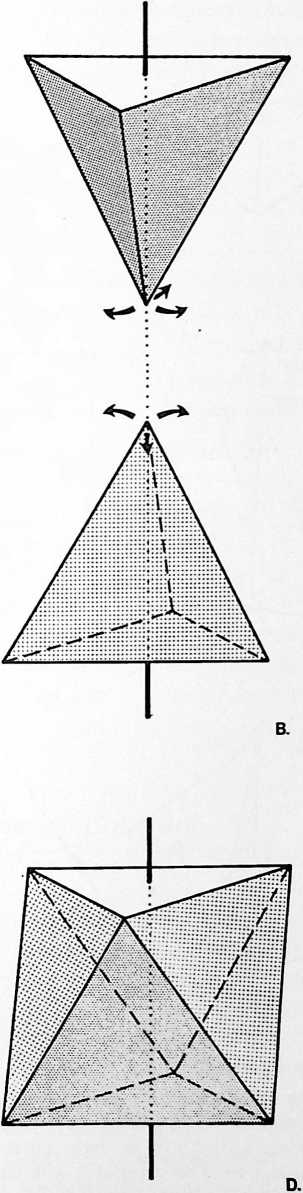
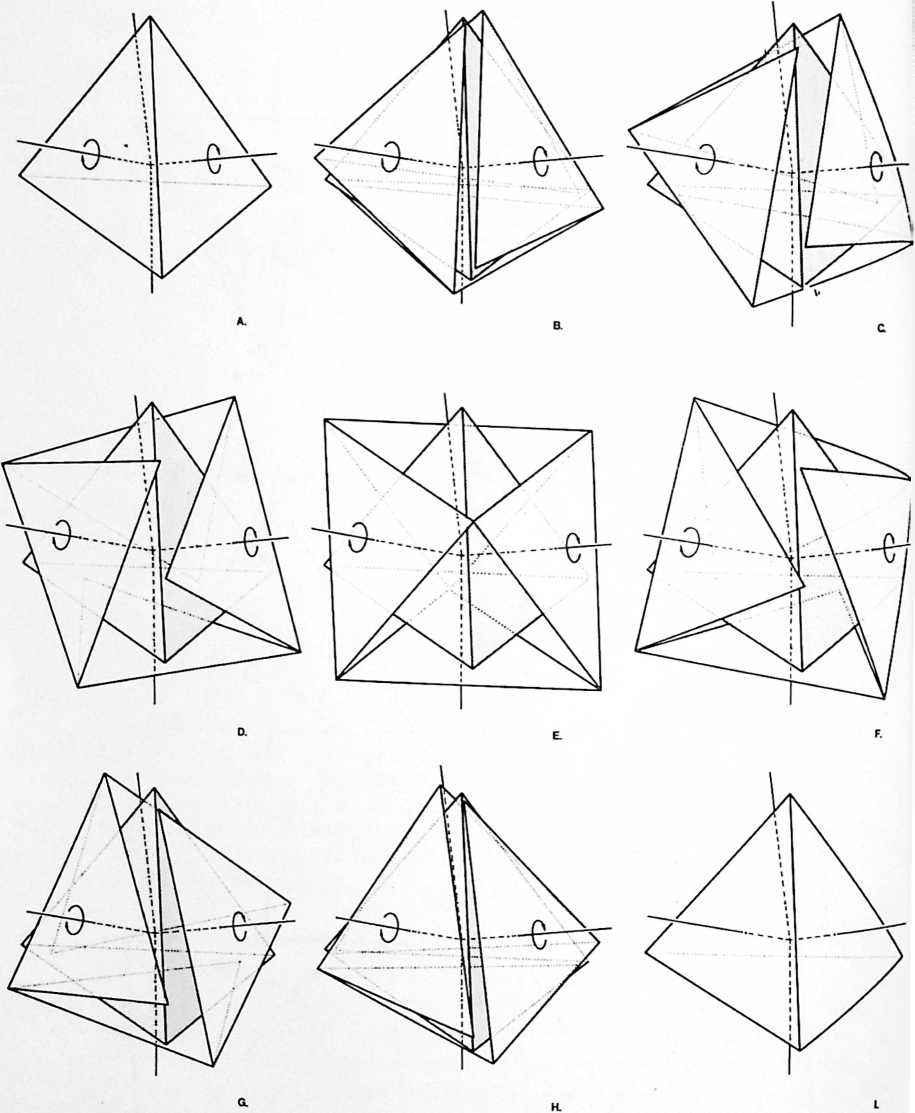
¶ 940.00 Hierarchy of Quanta Module Orientations
[940.10]{style="color: purple3"} []{#ver:940.10 label="ver:940.10"} Blue Modules and Red Modules
[940.11]{style="color: purple3"} []{#ver:940.11 label="ver:940.11"} Modules: We color them blue because the s are energy conservers, being folded out of only one triangle.
[940.12]{style="color: purple3"} []{#ver:940.12 label="ver:940.12"} Modules: We color them red because the are energy distributors, not being foldable out of only one triangle.
[940.13]{style="color: purple3"} []{#ver:940.13 label="ver:940.13"} This coloring will provide quick comprehension of the energy behaviors unique to the various geometrical systems and their transformations for instance, in the outermost module layer shell of the vector equilibrium, all the triangular faces will be blue and all the square faces will be red, indicating that the eight tetrahedra of the vector equilibrium are conserving the system’s structural integrity and will permit export of energy from the square faces of the system without jeopardizing the system’s structural integrity.
¶ 941.00 Relation of Quanta Modules to Closest-Packed Sphere Centers
[941.01]{style="color: purple3"} []{#ver:941.01 label="ver:941.01"} Illustrations of the and Quanta Modules may be made with spherical segment arcs of unit radius scribed on each of their three triangular faces having a common vertex at the sphere’s center. The common center of those circular arcs lies in their respectively most acute angle vertexes; thus, when assembled, those vertexes will lie in the centers of the closest-packed spheres of which each and Quanta Module embraces a part, Vi44th of a sphere, as well as its proportional part of the space between the closest-packed spheres.
¶ 942.00 Progression of Geometries in Closest Packing
[942.01]{style="color: purple3"} []{#ver:942.01 label="ver:942.01"} Two balls of equal radius are closest packed when tangent to one another, forming a linear array with no ball at its center. Three balls are closest packed when a third ball is nested into the valley of tangency of the first two, whereby each becomes tangent to both of the other two, thus forming a triangle with no ball at its center. Four balls are closest packed when a fourth ball is nested in the triangular valley formed atop the closest-packed first three; this fourth-ball addition occasions each of the four balls becoming tangent to all three of the other balls, as altogether they form a tetrahedron, which is an omnidirectional, symmetrical array with no ball at its center but with one ball at each of its four corners. (See Sec. 411.)
[942.02]{style="color: purple3"} []{#ver:942.02 label="ver:942.02"} Four additional balls can be symmetrically closest packed into the four nests of the closest-packed tetrahedral group, making eight balls altogether and forming the star tetrahedron, with no ball at its center.
[942.03]{style="color: purple3"} []{#ver:942.03 label="ver:942.03"} Five balls are closest packed when a fifth ball is nested into the triangular valley on the reverse side of the original triangular group’s side within whose triangular valley the fourth ball had been nested. The five form a polar-symmetry system with no ball at its center.
[942.04]{style="color: purple3"} []{#ver:942.04 label="ver:942.04"} Six balls are closest packed when two closest-packed triangular groups are joined in such a manner that the three balls of one triangular group are nested in the three perimeter valleys of the other triangular group, and vice versa. This group of six balls is symmetrically associated, and it constitutes the six corners of the regular octahedron, with no ball at its center.
[942.05]{style="color: purple3"} []{#ver:942.05 label="ver:942.05"} Eight additional balls can be mounted in the eight triangular nests of the octahedron’s eight triangular faces to produce the star octahedron, a symmetrical group of 14 balls with no ball at the group’s center.
[942.10]{style="color: purple3"} []{#ver:942.10 label="ver:942.10"} Tetrahedron: The tetrahedron is composed exclusively of Modules (blue), 24 in all, of which 12 are positive and 12 are negative. All 24 are asymmetrical, tetrahedral energy conservers[^31]. All the tetrahedron’s 24 blue Modules are situate in its only one-module-deep outer layer. The tetrahedron is all blue: all energy-conserving.
[942.11]{style="color: purple3"} []{#ver:942.11 label="ver:942.11"} Since a tetrahedron is formed by four mutually tangent spheres with no sphere at its center, the Modules each contain a portion of that sphere whose center is congruent with the Module’s most acute corner.
[942.12]{style="color: purple3"} []{#ver:942.12 label="ver:942.12"} The tetrahedron is defined by the lines connecting the centers of the tetrahedron’s four corner spheres. The leak in the tetrahedron’s corners elucidates entropy as occasioned by the only-critical-proximity but non-touching of the tetrahedron’s corners-defining lines. We always have the twistingthe vectorial near-miss at the corners of the tetrahedron because not more than one line can go through the same point at the same time. The construction lines with which geometrical entities are structured come into the critical structural proximity only, but do not yield to spontaneous mass attraction, having relative Moon-Earth-like gaps between their energy-event-defining entities of realization.
[942.13]{style="color: purple3"} []{#ver:942.13 label="ver:942.13"} The tetrahedron has the minimum leak, but it does leak. That is one reason why Universe will never be confined within one tetrahedron, or one anything.
[942.15]{style="color: purple3"} []{#ver:942.15 label="ver:942.15"} Quarter-Tetrahedra: Quarter-Tetrahedra have vector-edged, equiangled, triangular bases that are congruent with the faces of the regular tetrahedron. But the apex of the Quarter-Tetrahedron occurs at the center of volume of the regular tetrahedron.
[942.16]{style="color: purple3"} []{#ver:942.16 label="ver:942.16"} The Quarter-Tetrahedra are composed of three positive Quanta Modules and three negative/ Quanta Modules, all of which are asymmetrical tetrahedra. We identify them as six energy quanta modules. These six energy quanta modules result when vertical planes running from the three vertexes to their three opposite mid-edges cut the Quarter-Tetrahedron into six parts, three of which are positive and three of which are negative.
[942.17]{style="color: purple3"} []{#ver:942.17 label="ver:942.17"} The triangular conformation of the Quarter-Tetrahedron can be produced by nesting one uniradius ball in the center valley of a five-ball-edged, closest-packed, uniradius ball triangle. (See Illus. 415.55C.) The four vertexes of the Quarter-Tetrahedron are congruent with the volumetric centers of four uniradius balls, three of which are at the corners and one of which is nested in the valley at the center of area of a five-ball-edged, equiangle triangle.
[942.18]{style="color: purple3"} []{#ver:942.18 label="ver:942.18"} The Quarter-Tetrahedron’s six edges are congruent with the six lines of sight connecting the volumetric centers of the base triangle’s three uniradius corner balls, with one uniradius ball nested atop at the triangle’s center of area serving as the apex of the Quarter-Tetrahedron.
[942.20]{style="color: purple3"} []{#ver:942.20 label="ver:942.20"} Isosceles Dodecahedron: The isosceles dodecahedron consists of the regular tetrahedron with four Quarter-Tetrahedra extroverted on each of the regular tetrahedron’s four triangular faces, with the extroverted Quarter-Tetrahedra’s volumetric centers occurring outside the regular tetrahedron’s four triangular faces, whereas the central nuclear tetrahedron’s four Quarter-Tetrahedra are introverted with their volumetric centers situate inwardly of its four outer, regular, equiangled, triangular faces.
[942.21]{style="color: purple3"} []{#ver:942.21 label="ver:942.21"} The isosceles dodecahedron is composed of 48 blue Modules, 24 of which are introverted; that is, they have their centers of volume inside the faces of the central, regular tetrahedron and constitute the nuclear layer of the isosceles dodecahedron. An additional 24 extroverted Modules, with their volumetric centers occurring outside the four triangular faces of the central tetrahedron, form the outermost shell of the isosceles dodecahedron. The isosceles dodecahedron is all blue both inside and outside.
[942.30]{style="color: purple3"} []{#ver:942.30 label="ver:942.30"} Octahedron: The octahedron or “Octa” is composed of 96 energy quanta modules of which 48 are red Quanta Modules and 48 blue Quanta Modules. It has two module layers, with the inner, or nuclear, aggregate being the 48 red s and the outer layer comprised of the 48 blue s. The octahedron is all blue outside with a red nucleus.
[942.31]{style="color: purple3"} []{#ver:942.31 label="ver:942.31"} The octahedron has distributive energies occurring at its nucleus, but they are locked up by the outer layer of Modules. Thus the tendency of the 48 red Module energy distributors is effectively contained and conserved by the 48 blue Module conservators.
[942.40]{style="color: purple3"} []{#ver:942.40 label="ver:942.40"} Cube: The cube is composed of a total of 72 energy quanta modules, of which there are 48 blue Modules and 24 red Modules. The cube is produced by superimposing four Eighth-Octahedra upon the four equiangle triangular faces of the regular tetrahedron.
[942.41]{style="color: purple3"} []{#ver:942.41 label="ver:942.41"} The cube is three module layers deep, and the layering occurs around each of its eight corners. All of the cube’s nuclear and outer-shell modules three-layer edges are seen to surface congruently along the six diagonal seams of the cube’s six faces. The inner nucleus of the cube consists of the blue introverted tetrahedron with its 24 Modules. This introverted tetrahedron is next enshelled by the 24 blue Modules extroverted on the introvert nuclear tetrahedron’s four faces to form the isosceles dodecahedron. The third and outer layer of the cube consists of the 24 red Modules mounted outward of the isosceles dodecahedron’s 24 extroverted Modules.
[942.42]{style="color: purple3"} []{#ver:942.42 label="ver:942.42"} Thus, as it is seen from outside, the cube is an all-red tetrahedron, but its energy-distributive surface layer of 24 red Modules is tensively overpowered two-to-one and cohered as a cube by its 48 nuclear modules. The distributors are on the outside. This may elucidate the usual occurrence of cubes in crystals with one or more of their corners truncated.
[942.43]{style="color: purple3"} []{#ver:942.43 label="ver:942.43"} The minimum cube that can be formed by closest packing of spheres (which are inherently stable, structurally speaking) is produced by nesting four balls in the triangular mid-face nests of the four faces of a three-layer, ten-ball tetrahedron, with no ball at its volumetric center. This produces an eight-ball-cornered symmetry, which consists of 14 balls in all, with no ball at its center. This complex cube has a total of 576 and Modules, in contradistinction to the simplest tetra-octa-produced cube constituted of 72 and Modules.
[942.50]{style="color: purple3"} []{#ver:942.50 label="ver:942.50"} Rhombic Dodecahedron: The rhombic dodecahedron is composed of 144 energy quanta modules. Like the cube, the rhombic dodecahedron is a three-module layered nuclear assembly, with the two-layered octahedron and its exclusively red Moduled nucleus (of 48 s) enveloped with 48 exclusively blue/ Modules, which in turn are now enclosed in a third shell of 48 blue / Modules. Thus we find the rhombic dodecahedron and the cube co-occurring as the first three-layered, nuclearly centered symmetrieswith the cube having its one layer of 24 red Modules on the outside of its two blue layers of 24 Modules each; conversely, the rhombic dodecahedron has its two blue layers of 48 Modules each on the outside enclosing its one nuclear layer of 48 red Modules.
[942.51]{style="color: purple3"} []{#ver:942.51 label="ver:942.51"} The most simply logical arrangement of the blue and red Modules is one wherein their \sfrac{1}{144}th-sphere-containing, most acute corners are all pointed inward and join to form one whole sphere completely contained within the rhombic dodecahedron, with the contained-sphere’s surface symmetrically tangent to the 12 mid-diamond facets of the rhombic dodecahedron, those 12 tangent points exactly coinciding with the points of tangency of the 12 spheres closest-packed around the one sphere. (For a discussion of the rhombic dodecahedron at the heart of the vector equilibrium, see Sec. 955.50.)
[942.60]{style="color: purple3"} []{#ver:942.60 label="ver:942.60"} Vector Equilibrium: The vector equilibrium is composed of 336 blue Modules and 144 red Modules for a total of 480 energy quanta modules: . The eight tetrahedra of the vector equilibrium consist entirely of blue Modules, with a total of 48 such blue Modules lying in the exterior shell. The six square faces of the vector equilibrium are the six half-octahedra, each composed of 24 blue s and 24 red Bs, from which inventory the six squares expose 48 red Modules on the exterior shell. An even number of 48 s and 48 s provide an equilibrious exterior shell for the vector equilibrium: what an elegance! The distributors and the conservators balance. The six square areas’ energies of the vector equilibrium equal the triangles’ areas’ energies. The distributors evacuate the half-octahedra faces and the basic triangular structure survives.
[942.61]{style="color: purple3"} []{#ver:942.61 label="ver:942.61"} The vector equilibrium’s inherently symmetrical, closest-packed-sphere aggregate has one complete sphere occurring at its volumetric center for the first time in the hierarchy of completely symmetrical, closest-packed sets. In our multilayered, omniunique patterning of symmetrical nuclear assemblies, the vector equilibrium’s inner layer has four energy quanta modules in both its eight tetrahedral domains and its six half-octahedra domains, each of which domains constitutes exactly one volumetric twentieth of the vector equilibrium’s total volume.
[942.62]{style="color: purple3"} []{#ver:942.62 label="ver:942.62"} The blue Modules and the red Modules of the vector equilibrium are distributed in four layers as follows:
Layer
Tetrahedral Octahedral Octahedral Total
ris $As$ $Bs$
1st innermost layer
2nd middle layer
3rd middle layer
4th outermost layer
Total: 336
Modules Modules Quanta
Modules
[942.63]{style="color: purple3"} []{#ver:942.63 label="ver:942.63"} In both of the innermost layers of the vector equilibrium, the energy-conserving introvert Modules outnumber the Modules by a ratio of two-to-one. In the third layer, the ratio is two-to-zero. In the fourth layer, the ratio of s to s is in exact balance.
[942.64]{style="color: purple3"} []{#ver:942.64 label="ver:942.64"} Atoms borrow electrons when they combine. The open and unstable square faces of the vector equilibrium provide a model for the lending and borrowing operations. When the frequency is three, we can lend four balls from each square. Four is the greatest number of electrons that can be lent: here is a limit condition with the three-frequency and the four-ball edge. All the borrowing and lending operates in the squares. The triangles do not get jeopardized by virtue of lending. lending and borrowing vector equilibrium is maintained without losing the structural integrity of Universe.
[942.70]{style="color: purple3"} []{#ver:942.70 label="ver:942.70"} Tetrakaidecahedron: The tetrakaidecahedronLord Kelvin’s “Solid” is the most nearly spherical of the regular conventional polyhedra; ergo, it provides the most volume for the least surface and the most unobstructed surface for the rollability of least effort into the shallowest nests of closest-packed, most securely self-cohering, allspace-filling, symmetrical, nuclear system agglomerations with the minimum complexity of inherently concentric shell layers around a nuclear center. The more evenly faceted and the more uniform the radii of the respective polygonal members of the hierarchy of symmetrical polyhedra, the more closely they approach rollable sphericity. The four-facet tetrahedron, the six-faceted cube, and the eight-faceted octahedron are not very rollable, but the 12-faceted, one-sphere-containing rhombic dodecahedron, the 14-faceted vector equilibrium, and the 14-faceted tetrakaidecahedron are easily rollable.
[942.71]{style="color: purple3"} []{#ver:942.71 label="ver:942.71"} The tetrakaidecahedron develops from a progression of closest-sphere-packing symmetric morphations at the exact maximum limit of one nuclear sphere center’s unique influence, just before another nuclear center develops an equal magnitude inventory of originally unique local behaviors to that of the earliest nuclear agglomeration.
[942.72]{style="color: purple3"} []{#ver:942.72 label="ver:942.72"} The first possible closest-packed formulation of a tetrakaidecahedron occurs with a three-frequency vector equilibrium as its core, with an additional six truncated, square-bottomed, and three-frequency-based and two-frequency-plateaued units superimposed on the six square faces of the three-frequency, vector-equilibrium nuclear core. The three-frequency vector equilibrium consists of a shell of 92 unit radius spheres closest packed symmetrically around 42 spheres of the same unit radius, which in turn closest-pack enclose 12 spheres of the same unit radius, which are closest packed around one nuclear sphere of the same unit radius, with each closest-packed-sphere shell enclosure producing a 14-faceted, symmetrical polyhedron of eight triangular and six square equiedged facets. The tetrakaidecahedron’s six additional square nodes are produced by adding nine spheres to each of the six square faces of the three-frequency vector equilibrium’s outermost 92-sphere layer. Each of these additional new spheres is placed on each of the six square facets of the vector equilibrium by nesting nine balls in closest packing in the nine possible ball matrix nests of the three-frequency vector equilibrium’s square facets; which adds 54 balls to the
1
12
42
[92]{.underline}
146 surrounding the nuclear ball to produce a grand total of 200 balls symmetrically surrounding one ball in an all-closest-packed, omnidirectional matrix.
[942.73]{style="color: purple3"} []{#ver:942.73 label="ver:942.73"} The tetrakaidecahedron consists of 18,432 energy quanta modules, of which 12,672 are s and 5,760 are s; there are 1,008 s and only 192 s in the outermost layer, which ratio of conservancy dominance of s over distributive s is approximately two-to-one interiorly and better than five-to-one in the outermost layer.
¶ 943.00 Table: Synergetics Quanta Module Hierarchy
(see also drawings section)
[943.01]{style="color: purple3"} []{#ver:943.01 label="ver:943.01"} The orderly elegance of progressive numbers of concentric shells, starting with one as a discrete arithmetical progression, as well as the pattern of energy quanta modules growth rate, and their respective layer-transformation pairings of positive and negative arrangements of and Quanta Modules, of which there are always an even number of (+) or (-) s or s, is revealed in the synergetic quanta module hierarchy of topological characteristics.
¶ 950.00 Allspace Filling
[950.01]{style="color: purple3"} []{#ver:950.01 label="ver:950.01"} The regular tetrahedron will not associate with other regular tetra- hedra to fill allspace. (See Sec. 780.10 for a conceptual definition of allspace.) If we try to fill allspace with tetrahedra, we are frustrated because the tetrahedron will not fill all the voids above the triangular-based grid pattern. (See Illus. 950.31.) If we take an equilateral triangle and bisect its edges and interconnect the mid-points, we will have a “chessboard” of four equiangular triangles. If we then put three tetrahedra chessmen on the three corner triangles of the original triangle, and put a fourth tetrahedron chessman in the center triangle, we find that there is not enough room for other regular tetrahedra to be inserted in the too-steep valleys lying between the peaks of the tetrahedra.
[950.02]{style="color: purple3"} []{#ver:950.02 label="ver:950.02"} If we remove the one tetrahedral chessman from the center triangle of the four-triangle chessboard and leave the three tetra-chessmen standing on the three corner triangles, we will find that one octahedral chessman (of edges equal to the tetra) exactly fits into the valley lying between the first three tetrahedra; but this is not allspace-filling exclusively with tetrahedra.
¶ Self-Packing Allspace-Filling Geometries
[950.10]{style="color: purple3"} []{#ver:950.10 label="ver:950.10"} There are a variety of self-packing allspace-filling geometries. Any one of them can be amplified upon in unlimited degree by high-frequency permitted aberrations. For instance, the cube can reoccur in high-frequency multiples with fundamental rectilinear aspectswith a cubical node on the positive face and a corresponding cubical void dimple on the negative face which will fill allspace simply because it is a complex of cubes.
[954.10A]{style="color: purple3"} []{#ver:954.10A label="ver:954.10A"} Allspace-filling Hierarchy as Rationally Quantifiable in Whole Volume Units of or Modules (Revised)
+:---------------------+:---------+:----------------+:--------------------+
| Synergetics’ | Quanta | Type | Symmetrical or |
| | | | |
| | Module | | |
+----------------------+----------+-----------------+---------------------+
| Name | Volume | Polyhedron | Asymmetrical |
+----------------------+----------+-----------------+---------------------+
| Mite | | Tetrahedron | Asymmetrical |
+----------------------+----------+-----------------+---------------------+
| Syte (3 types) | | Tetrahedron | Asymmetrical |
| | | | |
| Bite | | | |
+----------------------+----------+-----------------+---------------------+
| Rite | | Tetrahedron | Asymmetrical |
+----------------------+----------+-----------------+---------------------+
| Lite | | Hexahedron | Asymmetrical |
+----------------------+----------+-----------------+---------------------+
| Coupler | | Octahedron | Asymmetrical |
+----------------------+----------+-----------------+---------------------+
| Cube | | Hexahedron | Simple Symmetrical |
+----------------------+----------+-----------------+---------------------+
| Rhombic dodecahedron | | Dodecahedron | Simple Symmetrical |
+----------------------+----------+-----------------+---------------------+
| Tetrakaidecahedron | ,432 | Tetradecahedron | Complex Symmetrical |
+----------------------+----------+-----------------+---------------------+
Table 943.00 Synergetics Quanta Module Hierarchy
Sun only; no satellites
k Sun+12 partial sphere satellites
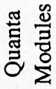
[950.12]{style="color: purple3"} []{#ver:950.12 label="ver:950.12"} There are eight familiar self-packing allspace-fillers:
-
The cube. (6 faces) Discoverer unknown.
-
The rhombic dodecahedron. (12 faces) Discoverer unknown. This allspace filler is the one that occurs most frequently in nature. Rhombic dodecahedron crystals are frequently found in the floor of mineral-rich deserts.
-
Lord Kelvin’s tetrakaidecahedron. (14 faces)
-
Keith Critchlow’s snub-cornered tetrahedron. (16 faces)
-
The truncated octahedron. (14 faces)
-
The trirectangular tetrahedron. (4 faces) Described by Coxeter, “Regular Polytopes,” p. 71. (See Illus. 950.12 B.)
-
The tetragonal disphenoid. (4 faces) Described by Coxeter, “Regular Polytopes,” p. 71. (See Illus. 950.12 C.)
-
The irregular tetrahedron (Mite). (4 faces) Discovered and described by Fuller. (See Illus. 950.12 A.)
¶ 950.20 Cubical Coordination
[950.21]{style="color: purple3"} []{#ver:950.21 label="ver:950.21"} Because the cube is the basic, prime-number-three-elucidating volume, and because the cube’s prime volume is three, if we assess space volumetrically in terms of the cube as volumetric unity, we will exploit three times as much space as would be required by the tetrahedron employed as volumetric unity. Employing the extreme, minimum, limit case, ergo the prime structural system of Universe, the tetrahedron (see Sec. 610.20), as prime measure of efficiency in allspace filling, the arithmetical-geometrical volume assessment of relative space occupancy of the whole hierarchy of geometrical phenomena evaluated in terms of cubes is threefold inefficient, for we are always dealing with physical experience and structural systems whose edges consist of events whose actions, reactions, and resultants comprise one basic energy vector. The cube, therefore, requires threefold the energy to structure it as compared with the tetrahedron. We thus understand why nature uses the tetrahedron as the prime unit of energy, as its energy quantum, because it is three times as efficient in every energetic aspect as its nearest symmetrical, volumetric competitor, the cube. All the physicists’ experiments show that nature always employs the most energy-economical strategies.
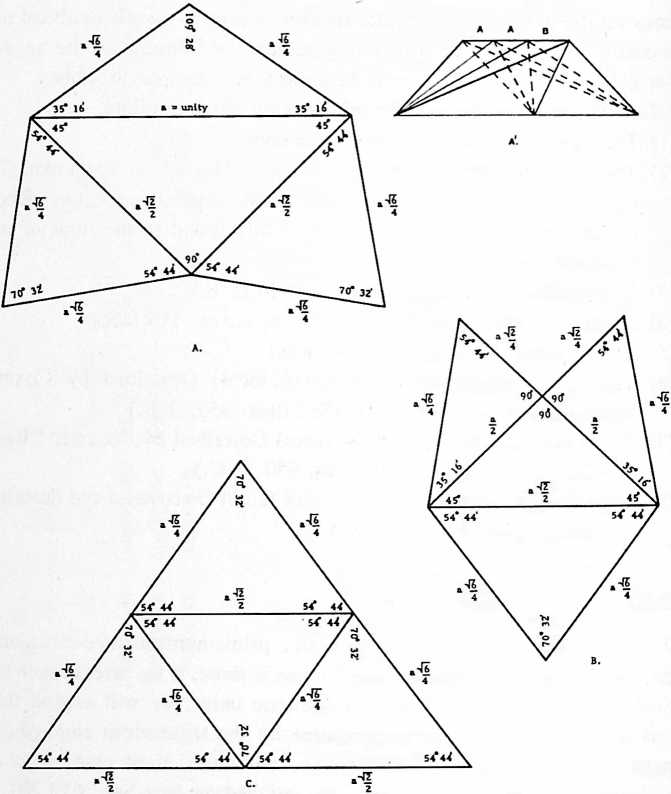
¶ Tetrahedron and Octahedron as Complementary Allspace Fillers: and Quanta Modules
[950.31]{style="color: purple3"} []{#ver:950.31 label="ver:950.31"} We may ask: What can we do to negotiate allspace filling with tetrahedra? In an isotropic vector matrix, it will be discovered that there are only two polyhedra described internally by the configuration of the interacting lines: the regular tetrahedron and the regular octahedron. (See Illus. 950.31.)
[950.32]{style="color: purple3"} []{#ver:950.32 label="ver:950.32"} All the other regular symmetric polyhedra known are also describable repetitiously by compounding rational fraction elements of the tetrahedron and octahedron: the and Quanta Modules, each having the volume of 1/2-ith of a tetrahedron.
[950.33]{style="color: purple3"} []{#ver:950.33 label="ver:950.33"} It will be discovered also that all the polygons formed by the interacting vectors consist entirely of equilateral triangles and squares, the latter occurring as the cross sections of the octahedra, and the triangles occurring as the external facets of both the tetrahedra and octahedra.
[950.34]{style="color: purple3"} []{#ver:950.34 label="ver:950.34"} The tetrahedra and octahedra complement one another as space fillers. This is not very satisfactory if you are looking for a monological explanation: the “building block” of the Universe, the “key,” the ego’s wished-for monopolizer. But if you are willing to go along with the physicists, recognizing complementarity, then you will see that tetrahedra plus octahedra and their common constituents, the unit-volume, and Quanta Modulesprovide a satisfactory way for both physical and metaphysical, generalized cosmic accounting of all human experience. Everything comes out rationally.
¶ 951.00 Allspace-Filling Tetrahedra
[951.01]{style="color: purple3"} []{#ver:951.01 label="ver:951.01"} The tetrahedra that fill allspace by themselves are all asymmetrical. They are dynamic reality only-for-each-moment. Reality is always asymmetrical.
[951.10]{style="color: purple3"} []{#ver:951.10 label="ver:951.10"} Synergetic Allspace-Filling Tetrahedron: Synergetic geometry has one cosmically minimal, allspace-filling tetrahedron consisting of only four Quanta Modules and two Quanta Modulessix modules in all whereas the regular tetrahedron consists of 24 such modules and the cube consists of 72. (See Illus. 950.12.)
¶ 953.00 Mites and Sytes: Minimum Tetrahedra as Three-Module Allspace Fillers
[953.10]{style="color: purple3"} []{#ver:953.10 label="ver:953.10"} Minimum Tetrahedron: Mite: Two Quanta Modules and one Quanta Module may be associated to define the allspace-filling positive and negative sets of three geometrically dissimilar, asymmetric, but unit volume energy quanta modules which join the volumetric center hearts of the octahedron and tetrahedron. For economy of discourse, we will give this minimum allspace-filling complex three-quanta module’s asymmetrical tetrahedron the name of Mite (as a contraction of Minimum Tetrahedron, allspace filler). (See drawings section.)
[953.20]{style="color: purple3"} []{#ver:953.20 label="ver:953.20"} Positive or Negative: Mites can fill allspace. They can be either positive (+) or negative (-), affording a beautiful confirmation of negative Universe. Each one can fill allspace, but with quite different energy consequences. Both the positive and negative Mite Tetrahedra are comprised, respectively, of two Quanta Modules and one Quanta Module. In each Mite, one of the two s is positive and one is negative; the must be positive when the Mite is positive and negative when the Mite is negative. The middle Quanta Module of the wedge-shaped sandwich is positive when the Mite and its Quanta Module are negative. The Mite and its Quanta Module have like signs. The Mite and its middle Quanta Module have unlike signs.
[953.21]{style="color: purple3"} []{#ver:953.21 label="ver:953.21"} If there were only positive Universe, there would be only Sytes (see Sec. 953.40). But Mites can be either plus or minus; they accommodate both Universes, the positive and the negative, as well as the half-positive and half-negative, as manifestations of fundamental complementarity. They are true rights and lefts, not mirror images; they are inside out and asymmetrical.
[953.22]{style="color: purple3"} []{#ver:953.22 label="ver:953.22"} There is a noncongruent, ergo mutually exclusive, tripartiteness (i.e., two, s and one in a wedge sandwich) respectively unique to either the positive or the negative world. The positive model provides for the interchange between the spheres and the spaces[^32]. But the Mite permits the same kind of exchange in negative Universe.
[953.23]{style="color: purple3"} []{#ver:953.23 label="ver:953.23"} The cube as an allspace filler requires only a positive world. The inside-out cube is congruent with the outside-out cube. Whereas the inside-out and outside-out Mites are not congruent and refuse congruency.
[953.24]{style="color: purple3"} []{#ver:953.24 label="ver:953.24"} Neither the tetrahedron, the octahedron, nor the cube can be put together with Mites. But the allspace-filling rhombic dodecahedron and the allspace-filling tetrakaidecahedron can be exactly assembled with Mites. Their entire componentation exclusively by Mites tells us that either or both the rhombic dodecahedron and the tetrakaidecahedron can function in either the positive or the negative Universe.
[953.25]{style="color: purple3"} []{#ver:953.25 label="ver:953.25"} The allspace-filling functions of the (+) or () three-module Mite combines can operate either positively or negatively. We can take a collection of the positives or a collection of the negatives. If there were only positive outside-out Universe, it would require only one of the three alternate six-module, allspace-filling tetrahedra (see Sec. 953.40) combined of two (+), two (-), one (+), and one () to fill allspace symmetrically and complementarily. But with both inside-out and outside-out worlds, we can fill all the outside-out world’s space positively and all the inside-out world’s space negatively, accommodating the inherent complementarity symmetry requirements of the macro-micro cosmic law of convex world and concave world, while remembering all the time that among all polyhedra only the tetrahedron can turn itself inside out.
[953.30]{style="color: purple3"} []{#ver:953.30 label="ver:953.30"} Tetrahedron as Three-Petaled Flower Bud: Positive or negative means that one is the inside-out of the other. To understand the insideouting of tetrahedra, think of the tetrahedron’s four outside faces as being blue and the four inside faces as being red. If we split open any three edges leading to any one of the tetrahedron’s vertexes, the tetrahedron will appear as a three-petaled flower bud, just opening, with the triangular petals hinging open around the common triangular base. The opening of the outside-blue-in-side-red tetrahedron and the hinging of all its blue bud’s petals outwardly and downwardly until they meet one another’s edges below the base, will result in the whole tetrahedron’s appearing to be red while its hidden interior is blue. All the other geometrical characteristics remain the same. If it is a regular tetrahedron, all the parts of the outside-red or the outside-blue regular tetrahedron will register in absolute congruence.
[953.40]{style="color: purple3"} []{#ver:953.40 label="ver:953.40"} Symmetrical Tetrahedron: Syte: Two of the allspacefilling, three-quanta module, asymmetric tetrahedra, the Mitesone positive and one negativemay be joined together to form the six-quanta-module, semisymmetrical, allspace-filling Sytes. The Sytes can be assembled in three different ways to produce three morphologically different, allspace-filling, asymmetrical tetrahedra: the Kites, Lites, and Bites, but all of the same six-module volume. This is done in each by making congruent matching sets of their three, alternately matchable, right-triangle facets, one of which is dissimilar to the other two, while those other two are both positive-negative mirror images of one another. Each of the three pairings produces one six-quanta module consisting of two A(+), two (-), one (+), and one (-).
[953.50]{style="color: purple3"} []{#ver:953.50 label="ver:953.50"} Geometrical Combinations: All of the well-known Platonic, Archimedean, Keplerian, and Coxeter types of radially symmetric polyhedra may be directly produced or indirectly transformed from the whole unitary combining of Mites without any fractionation and in whole, rational number increments of the or B Quanta Module volumes. This prospect may bring us within sight of a plenitudinous complex of conceptually discrete, energy-importing, -retaining, and -exporting capabilities of nuclear assemblage components, which has great significance as a specific closed-system complex with unique energy-behavior-elucidating phenomena. In due course, its unique behaviors may be identified with, and explain discretely, the inventory of high-energy physics’ present prolific production of an equal variety of strange small-energy “particles,” which are being brought into split-second existence and observation by the ultrahigh-voltage accelerator’s bombardments.
[953.60]{style="color: purple3"} []{#ver:953.60 label="ver:953.60"} Prime Minimum System: Since the asymmetrical tetrahedron formed by compounding two Quanta Modules and one Quanta Module, the Mite, will compound with multiples of itself to fill allspace and may be turned inside out to form its noncongruent negative complement, which may also be compounded with multiples of itself to fill allspace, this minimum asymmetric systemwhich accommodates both positive or negative space and whose volume is exactly \sfrac{1}{8}th that of the tetrahedron, exactly \sfrac{1}{32}nd that of the octahedron, exactly \sfrac{1}{160}th that of the vector equilibrium of zero frequency, and exactly \sfrac{1}{1280}th of the vector equilibrium of initial frequency , this Mite constitutes the generalized nuclear geometric limit of rational differentiation and is most suitably to be identified as the prime minimum system; it may also be identified as the prime, minimum, rationally volumed and rationally associable, structural system.
¶ 954.00 Mite as the Coupler s Asymmetrical Octant Zone Filler
(see drawings section)
[954.01]{style="color: purple3"} []{#ver:954.01 label="ver:954.01"} The Coupler is the asymmetric octahedron to be elucidated in Secs. 954.20 through 954.70. The Coupler has one of the most profound integral functionings in metaphysical Universe, and probably so in physical Universe, because its integral complexities consist entirely of integral rearrangeability within the same space of the same plus and/or minus Mites. We will now inspect the characteristics and properties of those Mites as they function in the Coupler. Three disparately conformed, nonequitriangular, polarized half-octahedra, each consisting of the same four equivolumetric octant zones occur around the three half-octants’ common volumetric center. These eight octant zones are all occupied, in three possible different system arrangements, by identical asymmetrical tetrahedra, which are Mites, each consisting of the three Modules.
[954.02]{style="color: purple3"} []{#ver:954.02 label="ver:954.02"} Each of these \sfrac{1}{8} octant-zone-filling tetrahedral Mite’s respective surfaces consists of four triangles, , , and , two of which, and , are dissimilar isosceles triangles and two of which, and EFG2, are right triangles. (See Illus. 953. 10.) Each of the dissimilar isosceles triangles have one mutual edge, and BB, which is the base respectively of both the isosceles triangles whose respective symmetrical apexes, and , are at different distances from that mutual baseline.
[954.03]{style="color: purple3"} []{#ver:954.03 label="ver:954.03"} The smaller of the mutually based isosceles triangle’s apex is a right angle, . If we consider the right-angle-apexed isosceles triangle to be the horizontal base of a unique octant-zone-filling tetrahedron, we find the sixth edge of the tetrahedron rising perpendicularly from the right-angle apex, , of the base to , which perpendicular produces two additional right triangles, and , vertically adjoining and thus surrounding the isosceles base triangle’s right-angled apex, . This perpendicular connects at its top with the apex of the larger isosceles triangle whose baseline, , is symmetrically opposite that apex and congruent with the baseline, , of the right-angle-apexed isosceles base triangle, , of our unique octant-filling tetrahedral Mite, .
[954.04]{style="color: purple3"} []{#ver:954.04 label="ver:954.04"} The two vertical right triangles running between the equilateral edges of the large and small isosceles triangles are identical right triangles, EFG1 and EFG2, whose largest (top) angles are each 54and whose smaller angles are 35each.
90
54
[35]
180
[954.05]{style="color: purple3"} []{#ver:954.05 label="ver:954.05"} As a tetrahedron, the Mite has four triangular faces: BBD, AAC, EFG1, and EFG2. Two of the faces are dissimilar isosceles triangles, and/L4C; ergo, they have only two sets of two different face angles eachB, D, A, and one of which, D, is a right angle.
[954.06]{style="color: purple3"} []{#ver:954.06 label="ver:954.06"} The other two tetrahedral faces of the Mites are similar right triangles, EFG, which introduce only two more unique angles, and F, to the Mite’s surface inventory of unique angles.
[954.07]{style="color: purple3"} []{#ver:954.07 label="ver:954.07"} The inventory of the Mite’s twelve corner angles reveals only five different angles. There are two s and two Fs, all of which are 54each, while there are three right angles consisting of oneZ> and two Gs. There are two s of 45each, two s of 35 each, and one of 70. (See drawings section.)
[954.08]{style="color: purple3"} []{#ver:954.08 label="ver:954.08"} Any of these eight interior octant, double-isosceles, three-right-angled-tetrahedral domainsMites(which are so arrayed around the center of volume of the asymmetrical octahedron) can be either a positively or a negatively composited allspace-filling tetrahedron.
[954.09]{style="color: purple3"} []{#ver:954.09 label="ver:954.09"} We find the Mite tetrahedron, AACD, to be the smallest, simplest, geometrically possible (volume, field, or charge), allspace-filling module of the isotropic vector matrix of Universe. Because it is a tetrahedron, it also qualifies as a structural system. Its volume is exactly Vsth that of its regular tetrahedral counterpart in their common magnitude isotropic vector matrix; within this matrix, it is also only \sfrac{1}{24}th the volume of its corresponding allspace-filling cube, \sfrac{1}{48}th the volume of its corresponding allspace-filling rhombic dodecahedron, and \sfrac{1}{6144}th the volume of its one other known unique, omnidirectional, symmetrically aggregatable, nonpolarized-assemblage, unit-magnitude, isotropic-vector-matrix counterpart, the allspace-filling tetrakaidecahedron.
[954.10]{style="color: purple3"} []{#ver:954.10 label="ver:954.10"} Allspace-Filling Hierarchy as Rationally Quantifiable in Whole Volume Units of or Quanta Modules
*Quanta*
Synergetics’ Module Type Symmetrical or
Name Volume Polyhedron Asymmetrical
Mite Tetrahedron Asymmetrical
Syte (3 types) Tetrahedron Asymmetrical
Kites
Lites
Bites
Coupler Octahedron Asymmetrical
Cube Cube Simple Symmetrical
Rhombic Rhombic
Dodecahedron Dodecahedron Complex Symmetrical
Tetrakaidecahedron ,432 Tetrakaidecahedron Complex Symmetrical
[954.20]{style="color: purple3"} []{#ver:954.20 label="ver:954.20"} Coupler: The basic complementarity of our octahedron and tetrahedron, which always share the disparate numbers 1 and 4 in our topological analysis (despite its being double or 4 in relation to tetra = 1), is explained by the uniquely asymmetrical octahedron, the Coupler, that is always constituted by the many different admixtures of Quanta Modules; the Mites, the Sytes, the cube (72 s and Bs), and the rhombic dodecahedron (144 s and Bs).
[954.21]{style="color: purple3"} []{#ver:954.21 label="ver:954.21"} There are always 24 s or sin our uniquely asymmetrical octahedron (the same as one tetra), which we will name the Coupler because it occurs between the respective volumetric centers of any two of the adjacently matching diamond faces of all the symmetrical, allspace-filling rhombic dodecahedra (or 144 s and Bs). The rhombic dodecahedron is the most-faceted, identical-faceted (diamond) polyhedron and accounts, congruently and symmetrically, for all the unique domains of all the isotropic-vector-matrix vertexes. (Each of the isotropic-vector-matrix vertexes is surrounded symmetrically either by the spheres or the intervening spaces-between-spheres of the closest-packed sphere aggregates.) Each rhombic dodecahedron’s diamond face is at the long-axis center of each Coupler (vol. = 1) asymmetric octahedron. Each of the 12 rhombic dodecahedra is completely and symmetrically omnisurrounded byand diamond-face-bonded with other such rhombic dodecahedra, each representing one closest-packed sphere and that sphere’s unique, cosmic, intersphere-space domain lying exactly between the center of the nuclear rhombic dodecahedron and the centers of their 12 surrounding rhombic dodecahedrathe Couplers of those closest-packed-sphere domains having obviously unique cosmic functioning.
[954.22]{style="color: purple3"} []{#ver:954.22 label="ver:954.22"} variety of energy effects of the and Quanta Module associabilities are contained uniquely and are properties of the Couplers, one of whose unique characteristics is that the Coupler’s topological volume is the exact prime number one of our synergetics’ tetrahedron (24 s) accounting system. It is the asymmetry of the s(of identical volume to the s) that provides the variety of other than plusness and minusness of the all-A-constellated tetrahedra. Now we see the octahedra that are allspace filling and of the same volume as the s in complementation. We see proton and neutron complementation and non-mirror-imaging interchangeability and intertransformability with 24 subparticle differentiabilities and 2, 3, 4, 6, combinationsenough to account for all the isotopal variations and all the nuclear substructurings in omnirational quantation.
[954.30]{style="color: purple3"} []{#ver:954.30 label="ver:954.30"} Nuclear Asymmetric Octahedra: There are eight additional asymmetric octahedra Couplers surrounding each face of each Coupler. It is probable that these eight asymmetric nuclear octahedra and the large variety of each of their respective constituent plus and minus Mite mix may account for all the varieties of intercomplex complexity required for the permutations of the 92 regenerative chemical elements. These eight variables alone provide for a fantastic number of rearrangements and reorientations of the and Quanta Modules within exactly the same geometric domain volume.
[954.31]{style="color: purple3"} []{#ver:954.31 label="ver:954.31"} It is possible that there are no other fundamental complex varieties than those accounted for by the eight nuclear Coupler-surrounding asymmetrical octahedra. There is a mathematical limit of variationwith our friend octave coming in as before. The Coupler may well be what we have been looking for when we have been talking about “number one.” It is quite possibly one nucleon, which can be either neutron or proton, depending on how you rearrange the modules in the same space.
[954.32]{style="color: purple3"} []{#ver:954.32 label="ver:954.32"} There are enough coincidences of data to suggest that the bombardment-produced energy entities may be identified with the three energy quanta modulestwo Quanta Modules and one Quanta Module allspace-filler complexities of associability, all occurring entirely within one uniquely proportioned, polarized, asymmetrical, nonequilateral, eighttriangle-faceted polyhedronthe Couplerwithin whose interior only they may be allspace-fillingly rearranged in a large variety of ways without altering the external conformation of the asymmetrical, octahedral container.
[954.40]{style="color: purple3"} []{#ver:954.40 label="ver:954.40"} Functions of the Coupler: In their cosmic roles as the basic allspace-filling complementarity pair, our regular tetrahedron and regular octahedron are also always identified respectively by the disparate numbers 1 and 4 in the column of relative volumes on our comprehensive chart of the topological hierarchies. (See Chart 223.64.) The volume value 4being 22 extemdash also identifies the prime number 2 as always being topologically unique to the symmetrical octahedron while, on the same topological hierarchy chart, the uniquely asymmetrical allspace-filling octahedron, the Coupler, has a volume of 1, which volume-1-identity is otherwise, topologically, Uniquely identified only with the non-allspace-filling regular symmetrical tetrahedron.
[954.41]{style="color: purple3"} []{#ver:954.41 label="ver:954.41"} The uniquely asymmetrical octahedron has three axes and a center of volume, K. Its and axes are equal in length, while theZ axis is shorter than the other two. The uniquely asymmetrical octahedron is always polarly symmetrical around its short Z axis, whose spin equatorial plane is a square whose diagonals are the equilengthed and axes. The equatorially spun planes of both theX and axes are similar diamonds, the short diagonal of each of these diamonds being the Z axis of the uniquely asymmetrical octahedron, while the long diagonal of the two similar diamonds are theX and axes, respectively, of the uniquely asymmetrical octahedron.
[954.42]{style="color: purple3"} []{#ver:954.42 label="ver:954.42"} The uniquely asymmetrical octahedron could also be named the polarly symmetrical octahedron. There is much that is unique about it. To begin with the “heart,” or center of volume of the asymmetrical octahedron (knowable also as the polarly symmetrical octahedron, of geometrical volume 1), is identified by the capital letter because is always the kissing or tangency point between each and every sphere in all closest-packed unit radius sphere aggregates; and it is only through those 12 kissing (tangency) points symmetrically embracing every closest-packed sphere that each and all of the 25 unique great circles of fundamental crystallographic symmetry must passthose 25 great circles being generated as the 3, 4, 6, 12 = 25 great circle equators of spin of the only-four-possible axes of symmetry of the vector equilibrium. Therefore it is only through those volumetric heart points of the uniquely asymmetrical octahedra that energy can travel electromagnetically, wavelinearly, from here to there throughout Universe over the shortest convex paths which they always follow.
[954.43]{style="color: purple3"} []{#ver:954.43 label="ver:954.43"} The uniquely asymmetrical octahedron is always uniformly composed of exactly eight asymmetrical, allspace-filling, double-isosceles tetrahedra, the Mites, which in turn consist of three-quanta modules each. Though outwardly conformed identically with one another, the Mites are always either positively or negatively biased internally in respect to their energy valving (amplifying, choking, cutting off, and holding) proclivities, which are only “potential” when separately considered, but operationally effective as interassociated within the allspace-filling, uniquely asymmetrical octahedron, and even then muted (i.e., with action suspended as in a holding pattern) until complexes of such allspace-filling and regeneratively circuited energy transactions are initiated.
[954.44]{style="color: purple3"} []{#ver:954.44 label="ver:954.44"} The cosmically minimal, allspace-filling Mites’ inherent bias results from their having always one + and one triple-bonded (i.e., face-bonded) to constitute a symmetrical isosceles (two-module) but non-allspacefilling tetrahedron to either one of the two external faces, of which either one + or one B can be added to provide the allspace-filling, semisymmetrical double-isosceles, triple right-angled, three-moduled Mite, with its positive and negative bias sublimatingly obscured by the fact that either the positive or the negative quantum biasing add together to produce the same overall geometrical space-filling tetrahedral form, despite its quanta-biased composition. This obscurity accounts for its heretofore unbeknownstness to science and with that unbeknownstness its significance as the conceptual link between the heretofore remote humanists and the scientists’ cerebrating, while with its discovery comes lucidly conceptual comprehension of the arithmetical and geometrical formings of the whole inventory of the isotopes of all the atoms as explained by the allspace-filling variety of internal and external associabilities and reorientings permitted within and without the respective local octantfilling of the, also in-tum, omni-space-filling, uniquely asymmetrical octahedron, the Coupler.
[954.45]{style="color: purple3"} []{#ver:954.45 label="ver:954.45"} As learned in Sections 953 and 954, one plus-biased Mite and one minus-biased Mite can be face-bonded with one another in three different allspace-filling ways, yet always producing one energy-proclivity-balanced, six-quanta-moduled, double-isosceles, allspace-filling, asymmetrical tetrahedron: the Syte. The asymmetric octahedron can also be composed of four such balanced-bias Sytes (4 s+ , 2 and 2 Bs1 + , 1). Since there are eight always one-way-or-the-other-biased Mites in each uniquely asymmetrical octahedron, the latter could consist of eight positively biased or eight negatively biased Mites, or any omnigeometrically permitted mixed combination of those cases.
[954.46]{style="color: purple3"} []{#ver:954.46 label="ver:954.46"} There are always 24 modules (16 and 8 of which eighths are always positive and the eight other Xs are always negative, while the eight consist of any of the eight possible combinations of positives and negatives) * in our uniquely asymmetrical octahedron. It is important to note that this 24 is the same 24-module count as that of the 24-/1-moduled regular tetrahedron. We have named the uniquely asymmetrical octahedron the Coupler.
[954.47]{style="color: purple3"} []{#ver:954.47 label="ver:954.47"} We give it the name the Coupler because it always occurs between the adjacently matching diamond faces of all the symmetrical allspacefilling rhombic dodecahedra, the “spherics” (of 96 s and 48 Bs). The rhombic dodecahedron has the maximum number (12) of identical (diamond) faces of all the allspace-filling, unit edge length, symmetrical polyhedra. That is, it most nearly approaches sphericity, i.e., the shortest-radiused, symmetrical, structural, polyhedral system. And each rhombic dodecahedron exactly embraces within its own sphere each of all the closest-packed unit radius spheres of Universe, and each rhombic dodecahedron’s volumetric center is congruent with the volumetric center of its enclosed sphere, while the rhombic dodecahedron also embracingly accounts, both congruently and symmetrically, for all the isotropic-vector-matrix vertexes in closest-packed and all their “between spaces.” The rhombic dodecahedra are the unique cosmic domains of their respectively embraced unit radius closest-packed spheres. The center of area, K, of each of the 12 external diamond faces of each rhombic dodecahedron is always congruent with the internal center of volume (tangent sphere’s kissing points), K, of all the allspace-filling uniquely asymmetrical octahedra.
[954.48]{style="color: purple3"} []{#ver:954.48 label="ver:954.48"} Thus the uniquely asymmetrical octahedra serve most economically to join, or couple, the centers of volume of each of the 12 unit radius spheres tangentially closest packed around every closest packed sphere in Universe, with the center of volume of that omnisurrounded, ergo nuclear, sphere. However the asymmetrical, octahedral coupler has three axes (Y, Y, M), and only its axis is involved in the most economical intercoupling of the energy potentials centered within all the closest-packed unit radius spheres. The and axes also couple two alternative sets of isotropic-vector-matrix centers. The axis coupling the centers of volume of the concave vector equilibria shaped between closest-packed sphere spaces, and the axis interconnecting all the concave octahedral between spaces of unit-radius closest-packed sphere aggregates, both of which concave between-sphere spaces become spheres as all the spheresas convex vector equilibria or convex octahedratransform uniformly, sumtotally, and coincidentally into concave-between-unit-radius-sphere spaces. The alternate energy transmitting orientations of the locally contained and Quanta Modules contained within the 12 couplers of each nuclear set accommodate all the atomic isotope formulations and all their concomitant side effects.
+--------------+--------------+--------------+
| ::: minipage | ::: minipage | ::: minipage |
| ::: | 8 all plus | 0 minus |
| | ::: | ::: |
+:=============+:=============+:=============+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
| | plus | minus |
+--------------+--------------+--------------+
These combinations accommodate the same bow-tie wave
patterns of the Indigs (see Sec. 1223).
This eight-digited manifold is congruent with the Indig bow-tie wave another instance of the congruence of number and geometry in synergetics. Because of the prime quanta functioning of the allspace-filling Mites, we observe an elegant confirmation of the omniembracing and omnipermeative pattern integrities of synergetics.
[954.49]{style="color: purple3"} []{#ver:954.49 label="ver:954.49"} We also call it the Coupler because its volume = 1 regular tetrahedron = 24 modules. The Couplers uniquely bind together each rhombic dodecahedron’s center of volume with the centers of volume of all its 12 omniadjacent, omniembracing, rhombic dodecahedral “spherics.”
[954.50]{style="color: purple3"} []{#ver:954.50 label="ver:954.50"} But it must be remembered that the centers of volume of the rhombic dodecahedral spherics are also the centers of each of all the closest-packed spheres of unit radius, and their volumetric centers are also omnicongruent with all the vertexes of all isotropic vector matrixes. The Couplers literally couple “everything,” while alternatively permitting all the varieties of realizable events experienced by humans as the sensation of “free will.”
[954.51]{style="color: purple3"} []{#ver:954.51 label="ver:954.51"} We see that the full variety of energy effects made by the variety of uniquely permitted -and-B-Module rearrangeabilities and reassociabilities within the unique volumetric domain of the Coupler manifest a startling uniqueness in the properties of the Coupler. One of the Coupler’s other unique characteristics is that its volume is also the exact prime number 1, which volumetric oneness characterizes only one other polyhedron in the isotropic-vector-matrix hierarchy, and that one other prime-number-one-volumed polyhedron of our quantum system is the symmetric, initial-and-minimal-structural system of Universe: the 24-module regular tetrahedron. Here we may be identifying the cosmic bridge between the equilibrious prime number one of metaphysics and the disequilibrious prime number one of realizable physical reality.
[954.52]{style="color: purple3"} []{#ver:954.52 label="ver:954.52"} It is also evidenced that the half-population ratio asymmetry of the Modules (of identical volume to the Modules) in respect to the population of the Modules, provides the intramural variety of rearrangements other than the 1/i plus-and-minusnessof the all-A-Module-constellated regular tetrahedron.
[954.53]{style="color: purple3"} []{#ver:954.53 label="ver:954.53"} The Coupler octahedron is allspace-filling and of the same 24- module volume as the regular tetrahedron, which is not allspace-filling. We go on to identify them with the proton’s and neutron’s non-mirror-imaged complementation and intertransformability, because one consists of 24 blue Modules while the other consists of sixteen blue s and eight redBs, which renders them not only dissimilar in fundamental geometric conformation, but behaviorally different in that the s are energy-inhibiting and theBs are either energy-inhibiting or energy-dissipating in respect to their intramural rearrangeabilities, which latter can accommodate the many isotopal differentiations while staying strictly within the same quanta magnitude units.
[954.54]{style="color: purple3"} []{#ver:954.54 label="ver:954.54"} When we consider that each of the eight couplers which surround each nuclear coupler may consist of any of 36 different intramural orientations, we comprehend that the number of potentially unique nucleus and nuclear-shell interpatternings is adequate to account for all chemical element isotopal variations, as well as accommodation in situ for all the nuclear substructurings, while doing so by omnirational quantation and without any external manifestation of the internal energy kinetics. All that can be observed is a superficially static, omniequivectorial and omnidirectional geometric matrix.
[954.55]{style="color: purple3"} []{#ver:954.55 label="ver:954.55"} Again reviewing for recall momentum, we note that the unique asymmetrical Coupler octahedron nests elegantly into the diamond-faceted valley on each of the 12 sides of the rhombic dodecahedron (called spheric because each rhombic dodecahedron constitutes the unique allspace-filling domain of each and every unit radius sphere of all closest-packed, unit-radius sphere aggregates of Universe, the sphere centers of which, as well as the congruent rhombic dodecahedra centers of which, are also congruent with all the vertexes of all isotropic vector matrixes of Universe).
[954.56]{style="color: purple3"} []{#ver:954.56 label="ver:954.56"} Neatly seated in the diamond-rimmed valley of the rhombic dodecahedron, the unique asymmetrical octahedron’s Z axis is congruent with the short diagonal, and its axis is congruent with the long diagonal of the diamond-rimmed valley in the rhombic dodecahedron’s face into which it is seated. This leaves the axis of the uniquely asymmetrical octahedron running perpendicular to the diamond face of the diamond-rimmed valley in which it so neatly sits; and its axis runs perpendicularly through the point, to join together most economically and directly the adjacent hearts (volumetric centers) of all adjacently closest-packed, unit radius spheres of Universe. That is, the axes connect each nuclear sphere heart with the hearts of the 12 spheres closest-packed around it, while the axis, running perpendicularly to theX axis, most economically joins the hearts (volumetric centers) of the only circumferentially adjacent spheres surrounding the nuclear sphere at the heart of the rhombic dodecahedron, but not interconnecting with those nuclear spheres’ hearts. Thus the axes interlink an omnisymmetrical network of tangential, unit-radius spheres in such a manner that each sphere’s heart is interconnected with the hearts of only six symmetrically interarrayed tangentially adjacent spheres. This alternate interlinkage package of each-with-six, instead of six-with-twelve, other adjacent spheres, leaves every other space in a closest-packed, isotropic-vector-matrixed Universe centrally unconnected from its heart with adjacent hearts, a condition which, discussed elsewhere, operates in Universe in such a way as to permit two of the very important phenomena of Universe to occur: (1) electromagnetic wave propagations, and (2) the ability of objects to move through or penetrate inherently noncompressible fluid mediums. This phenomenon also operates in such a manner that, in respect to the vertexes of isotropic vector matrixes, only every other one becomes the center of a sphere, and every other vertex becomes the center of a nonsphere of the space interspersing the spheres in closest packing, whereby those spaces resolve themselves into two typesconcave vector equilibria and concave octahedra. And, whenever a force is applied to such a matrix every sphere becomes a space and every space becomes a sphere, which swift intertransforming repeats itself as the force encounters another sphere, whereby the sphere vanishes and the resulting space is penetrated.
[954.57]{style="color: purple3"} []{#ver:954.57 label="ver:954.57"} We now understand why the points are the kinetic switch-off- and-on points of Universe.
[954.58]{style="color: purple3"} []{#ver:954.58 label="ver:954.58"} When we discover the many rearrangements within the uniquely asymmetric Coupler octahedra of volume one permitted by the unique self-interorientability of the and Modules without any manifest of external conformation alteration, we find that under some arrangements they are abetting the axis interconnectings between nuclear spheres and their 12 closest-packed, adjacently-surrounding spheres, or the axis interconnectings between only every other sphere of closest-packed systems.
[954.59]{style="color: purple3"} []{#ver:954.59 label="ver:954.59"} We also find that the and Module rearrangeabilities can vary the intensity of interconnecting in four magnitudes of intensity or of zero intensity, and can also interconnect the three and and systems simultaneously in either balanced or unbalanced manners. The unique asymmetric octahedra are in fact so unique as to constitute the actual visual spin variable mechanisms of Dirac’s quantum mechanics, which have heretofore been considered utterly abstract and nonvisualizable.
[954.70]{style="color: purple3"} []{#ver:954.70 label="ver:954.70"} The Coupler: Illustrations: The following paragraphs illustrate, inventory, sort out, and enumerate the systematic complex parameters of interior and exterior relationships of the 12 Couplers that surround every unit-radius sphere and every vertexial point fix in omni-closest-packed Universe, i.e., every vertexial point in isotropic vector matrixes.
[954.71]{style="color: purple3"} []{#ver:954.71 label="ver:954.71"} Since the Coupler is an asymmetric octahedron, its eight positive or negative Mite (AAB module), filled-octant domains introduce both a positive and a negative set of fundamental relationships in unique system sets of eight as always predicted by the number-of-system-relationships formula: N2 N , which with the system number eight has 28 relationships.
[954.72]{style="color: purple3"} []{#ver:954.72 label="ver:954.72"} There being three axestheX, Y, andAf sets of obverse-reverse, polar-viewed systems of eighteach eight has 28 relationships, which makes a total of three times 28 = 84 integral axially regenerated, and 8 face-to-face regenerated K-\.o-K couplings, for a total of 92 relationships per Coupler. However, as the inspection and enumeration shows, each of the three sets of 28, and one set of 8 unique, hold-or-transmit potentials subgroup themselves into geometrical conditions in which some provide energy intertransmitting facilities at four different capacity (quantum) magnitudes: 0, 1, 2, 4 (note: 4 = 22), and in three axial directions. The XX axis transmits between or interconnectsevery spheric center with one of its 12 tangentially adjacent closest-packed spheres.
[954.73]{style="color: purple3"} []{#ver:954.73 label="ver:954.73"} The YY axis transmits between or interconnectsany two adjacent of the six octahedrally and symmetrically interarrayed, concave vector equilibria conformed, ‘tween-space, volumetric centers symmetrically surrounding every unit-radius, closest-packed sphere.
[954.74]{style="color: purple3"} []{#ver:954.74 label="ver:954.74"} The MM axis interlinks, but does not transmit between, any two of the cubically and symmetrically interarrayed eight concave octahedra conformed sets of ‘tween-space, concave, empty, volumetric centers symmetrically surrounding every unit-radius, closest-packed sphere in every isotropic vector matrix of Universe.
[954.75]{style="color: purple3"} []{#ver:954.75 label="ver:954.75"} The eight X-to-X, face-to-face, couplings are energizingly interconnected by one Mite each, for a total of eight additional interconnections of the Coupler.
[954.76]{style="color: purple3"} []{#ver:954.76 label="ver:954.76"} These interconnections are significant because of the fact that the six concave vector equilibria, YY axis-connected ’tween-spaces, together with the eight concave octahedral ‘tween-spaces interconnected by theMM axis, are precisely the set of spaces that transform into spheres (or convex vector equilibria) as every sphere in closest-packed, unit-radius, sphere aggregates transforms concurrently into either concave vector equilibria ‘tweenspaces or concave octahedra ‘tween-sphere spaces.
[954.77]{style="color: purple3"} []{#ver:954.77 label="ver:954.77"} This omni-intertransformation of spheres into spaces and spaces into spheres occurs when any single force impinges upon any closest-packed liquid, gaseous, or plasmically closest-packed sphere aggregations.
[954.78]{style="color: purple3"} []{#ver:954.78 label="ver:954.78"} The further subdivision of the Modules into two subtetrahedra and the subdividing of the Modules into three subtetrahedra provide every positive Mite and every negative Mite with seven plus-or-minus subtetrahedra of five different varieties. Ergo possible combinations, suggesting their identification with the chemical element isotopes.
¶ 955.00 Modular Nuclear Development of Allspace-Filling Spherical Domains
[955.01]{style="color: purple3"} []{#ver:955.01 label="ver:955.01"} The 144 and Quanta Modules of the rhombic dodecahedron exactly embrace one whole sphere, and only one whole sphere of closest-packed spheres as well as all the unique closest-packed spatial domains of that one sphere. The universal versatility of the and Quanta Modules permits the omni-invertibility of those same 144 Modules within the exact same polyhedral shell space of the same size rhombic dodecahedron, with the omni-inversion resulting in six Veth spheres symmetrically and intertangentially deployed around one concave, octahedral space center.
[955.02]{style="color: purple3"} []{#ver:955.02 label="ver:955.02"} On the other hand, the vector equilibrium is the one and only unique symmetric polyhedron inherently recurring as a uniformly angled, centrially triangulated, complex collection of tetrahedra and half-octahedra, while also constituting the simplest and first order of nuclear, isotropically defined, uniformly modulated, inward-outward-and-around, vector-tensor structuring, whereby the vector equilibrium of initial frequency, i.e., “plus and minus one” equilibrium, is sometimes identified only as “potential,” whose uniform-length 24 external chords and 12 internal radii, together with its 12 external vertexes and one central vertex, accommodates a galaxy of 12 equiradiused spheres closest packed around one nuclear sphere, with the 13 spheres’ respective centers omnicongruent with the vector equilibrium’s 12 external and one internal vertex.
[955.03]{style="color: purple3"} []{#ver:955.03 label="ver:955.03"} Twelve rhombic dodecahedra close-pack symmetrically around one rhombic dodecahedron, with each embracing exactly one whole sphere and the respective total domains uniquely surrounding each of those 13 spheres. Such a 12-around-one, closest symmetrical packing of rhombic dodecahedra produces a 12-knobbed, 14-valleyed complex polyhedral aggregate and not a single simplex polyhedron.
[955.04]{style="color: purple3"} []{#ver:955.04 label="ver:955.04"} Since each rhombic dodecahedron consists of 144 modules, 13 X 144=1,872 modules.
[955.05]{style="color: purple3"} []{#ver:955.05 label="ver:955.05"} Each of the 12 knobs consists of 116 extra modules added to the initial frequency vector equilibrium’s 12 corners. Only 28 of each of the 12 spheres’ respective 144 modules are contained inside the initial frequency vector equilibrium, and 12 sets of 28 modules each are 7/36ths embracements of the full 12 spheres closest packed around the nuclear sphere.
[955.06]{style="color: purple3"} []{#ver:955.06 label="ver:955.06"} In this arrangement, all of the 12 external surrounding spheres have a major portion, i.e., \sfrac{29}{36}ths, of their geometrical domain volumes protruding outside the surface of the vector equilibrium, while the one complete nuclear sphere is entirely contained inside the initial frequency vector equilibrium, and each of its 12 tangent spheres have Vseths of one spherical domain inside the initial frequency vector equilibrium. For example, 12x7 = [84/3g]{.smallcaps} = 2J/s + 1 = 3V3 spheric domains inside the vector equilibrium of 480 quanta modules, compared with 144x3.333 rhombic dodecahedron spherics = 479.5 + modules, which approaches 480 modules.
[955.07]{style="color: purple3"} []{#ver:955.07 label="ver:955.07"} The vector equilibrium, unlike the rhombic dodecahedron or the cube or the tetrakaidecahedron, does not fill allspace. In order to use the vector equilibrium in filling allspace, it must be complemented by eight Eighth-Octahedra, with the latter’s single, equiangular, triangular faces situated congruently with the eight external triangular facets of the vector equilibrium.
[955.08]{style="color: purple3"} []{#ver:955.08 label="ver:955.08"} Each eighth-octahedron consists of six and six Quanta Modules. Applying the eight 12-moduled, 90-degree-apexed, or “cornered,” eighth-octahedra to the vector equilibrium’s eight triangular facets produces an allspace-filling cube consisting of 516 modules: one octahedron = 8 x 12 modules = 96 modules. 96 + 480 modules = 576 modules. With the 576-module cube completed, the 12 (potential) vertexial spheres of the vector equilibrium are, as yet, only partially enclosed.
[955.09]{style="color: purple3"} []{#ver:955.09 label="ver:955.09"} If, instead of applying the eight eighth-octahedra with 90-degree corners to the vector equilibrium’s eight triangular facets, we had added six half-octahedra “pyramids” to the vector equilibrium’s six square faces, it would have produced a two-frequency octahedron with a volume of 768 modules: = an octahedron of 768 modules.
[955.10]{style="color: purple3"} []{#ver:955.10 label="ver:955.10"} Mexican Star: If we add both of the set of six half-octahedra made up out of 48 modules each to the vector equilibrium’s six square faces, and then add the set of eight Eighth-Octahedra consisting of 12 modules each to the vector equilibrium’s eight triangular facets, we have not yet completely enclosed the 12 spheres occurring at the vector equilibrium’s 12 vertexes. The form we have developed, known as the “Mexican 14-Pointed Star,” has six square-based points and eight triangular-based points. The volume of the Mexican 14-Pointed Star is 96 + 288 + 480 = 864 modules.
[955.11]{style="color: purple3"} []{#ver:955.11 label="ver:955.11"} Not until we complete the two-frequency vector equilibrium have we finally enclosed all the original 12 spheres surrounding the singlesphere nucleus in one single polyhedral system. However, this second vector equilibrium shell also encloses the inward portions of 42 more embryo spheres tangentially surrounding and constituting a second closest-packed concentric sphere shell embracing the first 12, which in turn embrace the nuclear sphere; and because all but the corner 12 of this second closest-packed sphere shell nest mildly into the outer interstices of the inner sphere shell’s 12 spheres, we cannot intrude external planes parallel to the vector equilibrium’s 14 faces without cutting away the internesting portions of the sphere shells.
[955.12]{style="color: purple3"} []{#ver:955.12 label="ver:955.12"} On the other hand, when we complete the second vector equilibrium shell, we add 3,360 modules to the vector equilibrium’s initial integral inventory of 480 modules, which makes a total of 3,840 modules present. This means that whereas only 1,872 modules are necessary to entirely enclose 12 spheres closest packed around one sphere, by using 12 rhombic dodecahedra closest packed around one rhombic dodecahedron, these 13 rhombic dodecahedra altogether produce a knobby, 14-valleyed, polyhedral star complex.
[955.13]{style="color: purple3"} []{#ver:955.13 label="ver:955.13"} The 3,840 modules of the two-frequency vector equilibrium entirely enclosing 13 whole nuclear spheres, plus fractions of the 42 embryo spheres of the next concentric sphere shell, minus the rhombic dodecahedron’s 1,872 modules, equals 1,968 extra modules distributable to the 42 embryo spheres of the two-frequency vector equilibrium’s outer shell’s 42 fractional sphere aggregates omnioutwardly tangent to the first 12 spheres tangentially surrounding the nuclear sphere. Thus we learn that 1,968 octahedron.
[955.14]{style="color: purple3"} []{#ver:955.14 label="ver:955.14"} Each symmetrical increase of the vector-equilibrium system “frequency” produces a shell that contains further fractional spheres of the next enclosing shell. Fortunately, our and Quanta Modules make possible an exact domain accounting, in whole rational numbersas, for instance, with the addition of the first extra shell of the two-frequency vector equilibrium we have the 3,360 additional modules, of which only 1,872 are necessary to complete the first 12 spheres, symmetrically and embryonically arrayed around the originally exclusively enclosed nucleus. Of the vector equilibrium’s 480 modules, 144 modules went into the nuclear sphere set and 336 modules are left over.
[955.20]{style="color: purple3"} []{#ver:955.20 label="ver:955.20"} Modular Development of Omnisymmetric, Spherical Growth Rate Around One Nuclear Sphere of Closest-Packed, Uniradius Spheres: The subtraction of the 144 modules of the nuclear sphere set from the 480-module inventory of the vector equilibrium at initial frequency, leaves 336 additional modules, which can only compound as sphere fractions. Since there are 12 equal fractional spheres around each corner, with 336 modules we have 336/12ths. 336/12ths = 28 modules at each corner out of the 144 modules needed at each corner to complete the first shell of nuclear self-embracement by additional closest-packed spheres and their space-sharing domains.
[955.21]{style="color: purple3"} []{#ver:955.21 label="ver:955.21"} The above produces 28/144ths = 7/36ths present, and 116/144ths = 29/36ths per each needed.
[955.30]{style="color: purple3"} []{#ver:955.30 label="ver:955.30"} Possible Relevance to Periodic Table of the Elements: These are interesting numbers because the 28/144ths and the 116/144ths, reduced to their least common denominator, disclose two prime numbers, i.e., seven and twenty-nine, which, together with the prime numbers 1, 2, 3, 5, and 13, are already manifest in the rational structural evolvement with the modules’ discovered relationships of unique nuclear events. This rational emergence of the prime numbers 1, 3, 5, 7, 13, and 29 by whole structural increments of whole unit volume modules has interesting synergetic relevance to the rational interaccommodation of all the interrelationship permutation possibilities involved in the periodic table of the 92 regenerative chemical elements, as well as in all the number evolvements of all the spherical trigonometric function intercalculations necessary to define rationally all the unique nuclear vectorequilibrium intertransformabilities and their intersymmetric-phase maximum aberration and asymmetric pulsations. (See Sec. 1238.11 for the Scheherazade Number accommodating these permutations.)
[955.40]{style="color: purple3"} []{#ver:955.40 label="ver:955.40"} Table: Hierarchy of and Quanta Module Development of Omni-Closest-Packed, Symmetric, Spherical, and Polyhedral, Common Concentric Growth Rates Around One Nuclear Sphere, and Those Spheres’ Respective Polyhedral, Allspace-Filling, Unique Geometrical Domains (Short Title: Concentric Domain Growth Rates)
+:---------------------+:--------------------------------------+:------------+
| | and B Quanta Module Inventory | Spherical |
| | | |
| | | Domains |
+----------------------+---------------------------------------+-------------+
| Rhombic Dodecahedron | = 144 modules | = 1 |
| | | |
| Initial-Frequency | | |
+----------------------+---------------------------------------+-------------+
| Vector Equilibrium | = 480 modules | = 3 Vs |
+----------------------+---------------------------------------+-------------+
| Octahedron | = 96 modules | 2/3 |
+----------------------+---------------------------------------+-------------+
| Cube | = 72 modules | V« |
+----------------------+---------------------------------------+-------------+
| Tetrahedron | = 24 modules | Vs |
+----------------------+---------------------------------------+-------------+
[955.41]{style="color: purple3"} []{#ver:955.41 label="ver:955.41"} Table: Spherical Growth Rate Sequence
-
Modular Development of Omnisymmetric Spherical Growth Rate Around One Nuclear Sphere.
-
Nuclear Set of Rhombic Dodecahedron:
144 modules 1 sphere
- Vector Equilibrium, Initial Frequency:
480 modulesItself and 2Vs additional spheres
- CubeInitial Frequency:
576 modules 4 spheres
- Octahedron, Two-Frequency:
768 modules 5Vs spheres
- Mexican 14-Point Star:
864 modules 6 spheres
- Rhombic Dodecahedron, 12-Knobbed Star:
1,872 modules 13 spheres
- Vector Equilibrium, Two-Frequency:
3,840 modules 26Vo spheres
[955.50]{style="color: purple3"} []{#ver:955.50 label="ver:955.50"} Rhombic Dodecahedron at Heart of Vector Equilibrium: Nature always starts every ever freshly with the equilibrious isotropic-vector-matrix field. Energy is not lost; it is just not yet realized. It can be realized only disequilibriously.
[955.51]{style="color: purple3"} []{#ver:955.51 label="ver:955.51"} At the heart of the vector equilibrium is the ball in the center of the rhombic dodecahedron.
[955.52]{style="color: purple3"} []{#ver:955.52 label="ver:955.52"} Look at the picture which shows one-half of the rhombic dodecahedron. (See Illus. 955.52.) Of all the polyhedra, nothing falls so readily into a closest-packed group of its own kind as does the rhombic dodecahedron, the most common polyhedron found in nature.
¶ 960.00 Powers and Dimensions
¶ 960.01 The Coordination of Number Powers and Geometrical Dimensions
[960.02]{style="color: purple3"} []{#ver:960.02 label="ver:960.02"} Powering means the multiplication of a number by itself.
[960.03]{style="color: purple3"} []{#ver:960.03 label="ver:960.03"} Number powers refer to the numbers of times any given number is multiplied by itself. While empty set numbers may be theorized as multipli- able by themselves, so long as there is time to do so, all experimental demonstrability of science is inherently time limited. Time is size and size is time. Time is the only dimension. In synergetics time-size is expressible as frequency.
[960.04]{style="color: purple3"} []{#ver:960.04 label="ver:960.04"} Recalling our discovery that angles, tetrahedra, and topological characteristics are system constants independent of size, the limit of experimentally demonstrable powering involves a constant vector equilibrium and an isotropic vector matrix whose omnisymmetrically interparalleled planes and electable omniuniform frequency reoccurrences accommodate in time-sizing everywhere and anywhere regenerative (symmetrically indestruct, tetrahedral, four-dimensional, zerophase, i.e., the vector equilibrium) rebirths of a constant, unit-angle, structural system of convergent gravitation and divergent radiation resonatability, whose developed frequencies are the specific, specialcase, time-size dimensionings.
Fig. 955.52 Basic Joint for Isotropic Vector Equilibrium Matrix.
[960.05]{style="color: purple3"} []{#ver:960.05 label="ver:960.05"} Dimensional growth is not occasioned by an increase in exponential powers. It is brought about by increasing subdivision of the constant whole of Universe to isolate a locally considerable increment. For instance, says that the amount of energy involved in the isolated “mass” as a local event complex of Universe under consideration in this particular instance is to be determined by reference to the constant amount of cosmic energy involved in the constant rate of growth of a spherical, electromagnetic, wave surface, which constant is . Because the potential energy is in vector equilibrium packages, the centers of energy rebirth are accommodated by the isotropic vector matrix. The constant power is the frequency , which accommodates all the exportive-importive, entropic-syntropic, regeneration patterning of Universe.
[960.06]{style="color: purple3"} []{#ver:960.06 label="ver:960.06"} The only dimension is time, the time dimension being the radial dimension outward from or inward toward any regenerative center, which may always be anywhere, yet characterized by always being at the center of system regeneration.
[960.07]{style="color: purple3"} []{#ver:960.07 label="ver:960.07"} The time dimension is frequency.
[960.08]{style="color: purple3"} []{#ver:960.08 label="ver:960.08"} Any point can tune in any other point in Universe. All that is necessary is that they both employ the same frequency, the same resonance, the same system, center to center.
[960.09]{style="color: purple3"} []{#ver:960.09 label="ver:960.09"} The total nothingness involved is accounted by . The third power accounts both the untuned nothingness and the finitely tuned some-thingness. The 20 is both Einstein’s empty set and all the other untuned non- of Universe. The is the total Universe momentarily all at one time or timeless center. Eternity is 1No frequency . The 20 is eternally constant. The rate of wave growth corresponding to Einstein’s .
[960.10]{style="color: purple3"} []{#ver:960.10 label="ver:960.10"} Thus the isotropic vector matrix of synergetics’ convergence and divergence accommodates elegantly and exactly both Einstein’s and Newton’s radiation and gravitation formulations, both of which are adequately accounted only in second-powered terms.
[960.11]{style="color: purple3"} []{#ver:960.11 label="ver:960.11"} Distance is time. Distance is only frequency-accountable.
[960.12]{style="color: purple3"} []{#ver:960.12 label="ver:960.12"} Newton’s intermass attraction increases at the second power as the time-distance between is halved. Newton deals only with mass and frequency to the second power. Einstein deals only with mass and frequency to the second power. Their masses are relatively variable. In one, mass is acceleratingly expended; in the other, mass is acceleratingly collected.
[960.13]{style="color: purple3"} []{#ver:960.13 label="ver:960.13"} In synergetics, the total mass somethingness to be acceleratingly expended is , with always a bonus spin-aroundable-polar-axis 2: Me and the Otherness. In synergetics, the total nothingness and somethingness involved in both inbound and outbound field is . (Nothing =10. Something = 10. Both = 20.) The multiplicative twoness of me and the otherness. The vector equilibrium and the icosahedron are the prime number five polyhedra; the multiplicative, concave-convex twoness: 2x5 = 10. F3 = Unexpected nothingness F1 x Expected somethingness F2 =F3.
¶ 961.00 Unitary Quantation of Tetrahedron
[961.01]{style="color: purple3"} []{#ver:961.01 label="ver:961.01"} The area of a triangle is arrived at by multiplying the length of the baseline by one-half of the triangle’s apex altitude.
[961.02]{style="color: purple3"} []{#ver:961.02 label="ver:961.02"} The volume of a tetrahedron is the product of the area of the base and one-third of its altitude.
[961.03]{style="color: purple3"} []{#ver:961.03 label="ver:961.03"} minimum garland of “granteds” combines only synergetically to disclose the following:
[961.10]{style="color: purple3"} []{#ver:961.10 label="ver:961.10"} Granted: Slidable Model of Constant Volume: Granted any point that is movable limitlessly anywhere within one of two planes parallel to one another at a given perpendicular distance from one another, and, cogliding anywhere within the other parallel plane, two parallel lines lying at a given perpendicular distance from one another, and a point that is slidable anywhere along one of the parallel lines, along the other line of which (two parallel lines) is a slidable pair of points, and D, always slidable only at a constant and given distance Z from one another; it will be found that the vast variety of tetrahedra to be formed by interconnecting these four points (two independently variable and two only covariable) will always enclose the same volume. (See Sec. 923 and Illus. 923.10D.)
[961.11]{style="color: purple3"} []{#ver:961.11 label="ver:961.11"} Provided the relationship between X, Y, and Z remain constant as described, and the distances and in respect to the “constructed” distance are always such that
T=VZ2-(1/2 Z)2
and
X = VZ2 - (2/3 Y)2
then, by varying Z to correspond with the distance between two experiential event foci, all the other vertexial positions of all the tetrahedra of equal volume can be described by revolution of the constantly cohered tetrahedral system around the axial line running through the two points andZ). This axial line may itself be angularly reoriented to aim the tetrahedral system by combining and interconnecting circuitry closing in any direction, thereby to reach any other two points in Universe to be tetrahedrally inteijoined in unitary quantation.
[961.12]{style="color: purple3"} []{#ver:961.12 label="ver:961.12"} With the observer-articulator’s experientially initiated and interpositioned two control points and D, these uniformly quantated observer-articulator variable initial “tunings,” accomplished exclusively by frequency and angle modulations, may “bring in” subjectively-objectively, receivingly-and-transmittingly, omnicosmic events occurring remotely in nonsimultaneously evolving and only otherness-generated self-awareness and deliberately thinkable self-conceptioning of progressively omnicomprehending embracements and penetrations. This in turn enables the conscious designing capabilities to be realized by these omnicosmic reaching tetrahedral coordinations (which are resolvable into generalized, quantum-regularized sets, consisting of only two human individual mentalities’ predeterminable variables consisting exclusively of frequency and angle modulations identified only with the self-and-other, C- and Z)-defined, selectable wavelength Z and theZ axis’ angular aiming and reorientation regulatability of the Z axis’ ever-constant reorientations of itsX-and /-dependent coordinates in exclusively angle-and frequency-determined invariant relationship), all of whose synergetic integrities’ intersignificance realizations are eternally interaccommodated by the tetrahedral structural system’s prime conceptual initiations.
[961.20]{style="color: purple3"} []{#ver:961.20 label="ver:961.20"} Granted: Model of Comprehensive Covariability: Granted that a tetrahedron of given altitude X, with a base triangle of given altitude and given baseline edge length Z, is volumetrically constant independent of the omnivariable interangling of its four vertexes, and five variable-length edges, and four variable triangular faces, whose comprehensive covariability can altogether accommodate any symmetric or asymmetric aspect transformability to correspond exactly in all its interangular face relationships and relative edge lengths with any tetrahedron to be formed by interconnecting any four points in Universe, provided the relative values of and in respect to Z (which is the only experientially known distance) are always such that:
y=VZ2-C/2Z)2
and,
X= [Vz2-(2/3 /)2]
As the values only of Z are altered, the respective value of the uniformly volumed tetrahedra will vary at a rate of the third power of Z’s linear change.
[961.30]{style="color: purple3"} []{#ver:961.30 label="ver:961.30"} Granted: Model for Third-Power Rate of Variation: Granted that there is then in respect to any two points in Universe a tetrahedron that can be given any symmetrical or asymmetrical tetrahedral shape, any of whose volumes will remain uniform or will vary uniformly at a third-power rate in respect to any alteration of the distance between the two initial control points on the axial control line; then, any four points in Universe, provided one is not in the plane of the other three, can be interconnected by varying the angular orientation of the control-line axis and the distance between the two central control points.
[961.31]{style="color: purple3"} []{#ver:961.31 label="ver:961.31"} Being generalized, these three relative distance-control coordinates X, Y, and Z are, of course, also present in the special-case, omnirectilinear XYZc.g,.s. coordinate system. That the most economical time distances between the two parallel planes and two parallel lines are coincident with perpendiculars to those parallel planes and lines does not impose any rectilinear profiling or structuring of the tetrahedron, which is a unique, four-planes-of-symmetry, self-structuring system, as the three-plane-defined cube of basic reference is not.
[961.40]{style="color: purple3"} []{#ver:961.40 label="ver:961.40"} Granted: Model for Six Degrees of Freedom: Granted the area of a triangle is base times one-half the altitude, with one given length of line marked on a flat plane and another infinitely extensible line number two lying in the same plane as short line AB, with line two parallel to AB; then connecting any point on line two with both and will produce a constant-area triangle ABC. Holding fixed and moving only in any direction on line two, the shape of triangle will change, but its area will be constant. If we move along line two in one direction the three edges will approach congruence with one another, appearing only as a line but being, in fact, a constant-area triangle.
[961.41]{style="color: purple3"} []{#ver:961.41 label="ver:961.41"} Granted the volume of a tetrahedron is its base area times one-third of its altitude, we can now take the permitted, special condition discussed in Sec. 961.40 whereby on line two is equidistant from both of line one’s terminal-defining points and B. We may next take a fourth point D, lying in an infinitely extensible second plane which is parallel to the first infinitely extensible plane defined by points ABC. With/) equidistant from .4, B, and C, the volume of the regular tetrahedron will not be altered by letting travel to any point in plane two while point travels to any point on line two. Thus we learn that constant-volume tetrahedron might become so distended as to appear to be a line of no volume. Since there could be no volumeless line produced operationally, we may assume that all visible lines must be at minimum extended tetrahedra.
[961.42]{style="color: purple3"} []{#ver:961.42 label="ver:961.42"} These variabilities of the constant-volume tetrahedron and its constant-area faces will permit congruence of the four vertexes of the tetrahedron with any four points of Universe by simply taking the initial distance to suit the task. This unit linear adjustment is a familiar wavelength tuning function. Here we have the six cosmic degrees of freedom (see Sec. 537.10); whereby we are free to choose the length of only one line to be held constant, while allowing the other five edge-lines of the tetrahedron to take any size. We can connect any four points in Universe and produce a tetrahedron that is matchable with whole, unit, rational-number, volume increments of the and Quanta Modules.
[961.43]{style="color: purple3"} []{#ver:961.43 label="ver:961.43"} With large, clear plexiglass Models of the and Quanta Modules, we can easily see their clearly defined centers of volume. The centers of area of the triangular faces are arrived at by bisecting the edges and connecting the opposite angle. The center of volume of the tetrahedron is arrived at by interconnecting the four centers of triangular area with their opposite vertexes. These four lines constructed with fine, taut wires will converge to tangency atand then diverge away fromthe tetrahedron’s center of volume.
[961.44]{style="color: purple3"} []{#ver:961.44 label="ver:961.44"} The lines defining the center of four triangles and the center of volume inherently divide the modules into 24 equal parts. The same progressive subdivisions of the last 24 can be continued indefinitely, but each time we do so the rational bits become more and more asymmetrical. They get thinner and thinner and become more and more like glass splinters. By varying the frequency we can make any shape tetrahedron from the regular to the most asymmetric.
[961.45]{style="color: purple3"} []{#ver:961.45 label="ver:961.45"} The modules make all the geometriesall the crystallography. Any probabilities can be dealt with. With the two of Euler: and Gibbs the Me-and-Other-Awarenessthe beginning of time, if there is time. … It starts testing the special cases that have time. They are absolutely quantized. The s are blue and the sare red. The blues and reds intertransform. Every sphere becomes a space, and every space becomes a sphere, palpitating in the wire model of electromagnetic wave action.
[961.46]{style="color: purple3"} []{#ver:961.46 label="ver:961.46"} The and Quanta Modules become linear, as did the progression of concentric, common-base, uniform, linear, frequencied, electric-impulse conductors (see Sec. 923.21); and as also did the concentric, annually-frequencied, common-base-into-cone-rotated tetrahedra (see Sec. 541.30); the free energy put in at the base electronically, when you close the circuit at the beginning of the wireyou get the same package out at the other end, the same quanta. The longer the wire gets or the tree growsas it approaches parallelism, the more the energy packages begin to precess and to branch out at right angles.
[961.47]{style="color: purple3"} []{#ver:961.47 label="ver:961.47"} Fluorescing occurs until all the juice is finally dissipated off the wire or until all of this year’s additional frequency’s growth is realized in new branches, twigs, leaves and tetrahedrally-precessed buds. Birth: buds: and Modules; three-, four-, five-, and six-petallings: tetra, octa, icosa, rhombic-dodeca bud petals. The original inputthe six Quanta Modules of the original base tetrahedronbecomes distributive at 90 degrees. Coaxial cables tend to divert the precessional distributives inwardly to reduce the loss.
[961.48]{style="color: purple3"} []{#ver:961.48 label="ver:961.48"} When great electrostatic charges built into clouds become dischargingly grounded (to Earth) by the excellently-conducting water of rain, and lightning occurs; we see the Earthward, precessionally-branching lightning. In grounding with Earth, lightning often closes its circuit through the tree’s branches, whose liquid, water-filled, cell fibers are the most efficient conductors available in conducting the great electric charges inward to Earth through the trunk and the precessionally-distributive roots’ branchings. Lines are tetrahedra. Lines can wave-bounce in ribbons and beams: tetra, octa, and icosa energy lock-up systems. . All tetra and only tetra are volumetric, i.e., quanta-immune to any and all transformation.
¶ 962.00 Powering in the Synergetics Coordinate System
[962.01]{style="color: purple3"} []{#ver:962.01 label="ver:962.01"} In the operational conventions of the XYZc.g.s. coordinate system of mathematics, physics, and chemistry, exponential powering meant the development of dimensions that require the introduction of successively new perpendiculars to planes not yet acquired by the system.
[962.02]{style="color: purple3"} []{#ver:962.02 label="ver:962.02"} In synergetics, powering means only the frequency modulation of the system; i.e., subdivision of the system. In synergetics, we have only two directions: radial and circumferential.
[962.03]{style="color: purple3"} []{#ver:962.03 label="ver:962.03"} In the system, three planes interact at 90 degrees (three dimensions). In synergetics, four planes interact at 60 degrees (four dimensions).
[962.04]{style="color: purple3"} []{#ver:962.04 label="ver:962.04"} In synergetics there are four axial systems: ABCD. There is a maximum set of four planes nonparallel to one another but omnisymmetrically mutually intercepting. These are the four sets of the unique planes always comprising the isotropic vector matrix. The four planes of the tetrahedron can never be parallel to one another. The synergetics *AB CD-*four-dimensional and the conventional *XYZ-*three-dimensional systems are symmetrically intercoordinate. coordinate systems cannot rationally accommodate and directly articulate angular acceleration; and they can only awkwardly, rectilinearly articulate linear acceleration events.
[962.05]{style="color: purple3"} []{#ver:962.05 label="ver:962.05"} Synergetic geometry discloses the rational fourth- and fifth-powering modelability of nature’s coordinate transformings as referenced to the 60-degree equiangular isotropic-vector equilibrium.
[962.06]{style="color: purple3"} []{#ver:962.06 label="ver:962.06"} XYZ volumetric coordination requires three times more volume to accommodate its dimensional results than does the 60-degree coordination calculating; therefore, 90-degree coordination cannot accommodate the fourth and fifth powers in its experimental demonstrability, i.e., modelability.
[962.07]{style="color: purple3"} []{#ver:962.07 label="ver:962.07"} In the coordinate vectorial topology of synergetics, exponential powers and physical model dimensioning are identified with the number of vectors that may intercept the system at a constant angle, while avoiding parallelism or congruence with any other of the uniquely convergent vectors of the system.
[962.10]{style="color: purple3"} []{#ver:962.10 label="ver:962.10"} Angular and Linear Accelerations: Synergetics accommodates the direct expression of both angular and linear accelerations of physical Universe. The frequency of the synergetics coordinate system, synchrosystem, simultaneously and directly expresses both the angular and linear accelerations of nature.
[962.11]{style="color: purple3"} []{#ver:962.11 label="ver:962.11"} The Mass is the consequence of the angular accelerations, c2 or G2 of linear acceleration of the same unit inventory of forever regeneratively finite physical Universe, ever intertransforming and transacting in association (angular) or disassociation (linear) interaccelerations.
[962.12]{style="color: purple3"} []{#ver:962.12 label="ver:962.12"} The “three-dimensional” XYZc.gt.s.** system of coordination presently employed by world-around science can only express directly the linear accelerations and evolve therefrom its angular accelerations in awkward mathematics involving irrational, non-exactly-resolvable constants. c.gt.s. per second, is cubistically awkwardized into calculatively tattering irrationality.
[962.20]{style="color: purple3"} []{#ver:962.20 label="ver:962.20"} Convergence: In the topology of synergetics, powering is identifiable only with the uniangular vectorial convergences. The number of superficial, radiantly regenerated, vertex convergences of the system are identified with second powering, and not with anything we call “areas,” that is, not with surfaces or with any experimentally demonstrable continuums.
[962.30]{style="color: purple3"} []{#ver:962.30 label="ver:962.30"} Calculation of Local Events: All local events of Universe may be calculatively anticipated in synergetics by inaugurating calculation with a local vector-equilibrium frame and identifying the disturbance initiating point, direction, and energy of relative asymmetric pulsing of the introduced resonance and intertransformative event. (Synergetics Corollary, see Sec. 240.39.)
[962.40]{style="color: purple3"} []{#ver:962.40 label="ver:962.40"} Time and Dimension: Synergetic geometry embraces all the qualities of experience, all aspects of being. Measurements of width, breadth, and height are awkward, inadequate descriptions that are only parts of the picture. Without weight, you do not exist physically; nor do you exist without a specific temperature. You can convert the velocity-times-mass into heat. Vectors are not abstractions, they are resolutions. Time and heat and length and weight are inherent in every dimension. Ergo, time is no more the fourth dimension than it is the first, second, or third dimension.
[962.41]{style="color: purple3"} []{#ver:962.41 label="ver:962.41"} No time: No dimension. Time is dimension.
[962.42]{style="color: purple3"} []{#ver:962.42 label="ver:962.42"} Time is in synergetic dimensioning because our geometry is vectorial. Every vector = mass x velocity, and time is a function of velocity. The velocity can be inward, outward, or around, and the arounding will always be chordal and exactly equated with the inwardness and outwardness time expendabilities. The Euclidian-derived coordinate geometry cannot express time equi-economically around, but only time in and time out. Synergetics inherently has time equanimity: it deals with anything that exists always in time coordination.
[962.50]{style="color: purple3"} []{#ver:962.50 label="ver:962.50"} Omnidirectional Regeneration: The coordinate systems of synergetics are omnidirectionally regenerative by both lines and planes parallel to the original converging set. The omnidirectional regeneration of synergetic coordination may always be expressed in always balanced equivalence terms either of radial or circumferential frequency increments.
¶ 963.00 First Power: One Dimension
[963.01]{style="color: purple3"} []{#ver:963.01 label="ver:963.01"} In conventional coordination, one-dimensionality is identified geometrically with linear pointal frequency. The linear measure is the first power, or the edge of the square face of a cube.
[963.02]{style="color: purple3"} []{#ver:963.02 label="ver:963.02"} In synergetics, the first-power linear measure is the radius of the sphere.
[963.10]{style="color: purple3"} []{#ver:963.10 label="ver:963.10"} Synergetics Constant: The synergetics constant was evolved to convert third-power, volumetric evaluation from a cubical to a tetrahedral base and to employ the -four-dimensional system’s vector as the linear computational input. In the case of the cube this is the diagonal of the cube’s square face. Other power values are shown in Table 963.10. We have to find the total vector powers involved in the calculation. In synergetics we are always dealing in energy content: when vector edges double together in quadrivalence or octavalence, the energy content doubles and fourfolds, respectively. When the vector edges are half-doubled together, as in the icosahedron phase of the jitterbug halfway between the vector equilibrium 20 and the octahedron compression to fourfold and fivefold contraction with the vectors only doubled, we can understand that the volume of energy in the icosahedron (which is probably the same 20 as that of the vector equilibrium) is just compressed. (See Secs. 982.45 and 982.54.)
[963.11]{style="color: purple3"} []{#ver:963.11 label="ver:963.11"} In Einstein’s E =Mc2, M is volume-to-spherical-wave ratio of the system considered. Mass is the integration of relative weight and volume. What Einstein saw was that the weight in the weight-to-volume ratio, i.e., the Mass, could be reduced and still be interpreted as the latent energy-per-volume ratio. Einstein’s is partly identified with volume and partly with relative energy compactment within that spherical wave’s volume. There are then relative energy-of-reality concentration-modifiers of the volumes arrived at by third powering.
[963.12]{style="color: purple3"} []{#ver:963.12 label="ver:963.12"} All of the frozen volumetric and superficial area mensuration of the past has been derived exclusively from the external linear dimensions. Synergetics starts system mensuration at the system center and, employing omni-60-degree angular coordinates, expresses the omni-equal, radial and chordal, modular linear subdivisions in “frequency” of module subdivisioning of those radii and chords, which method of mensuration exactly accommodates both gravitational (coherence) and radiational (expansion) calculations. As the length of the vectors represents given mass-times-velocity, the energy involvements are inherent in the isotropic vector matrix.
SYNERGETICS CONSTANT
E
L??L?? o
-7?
g
0
ill
[q]{.smallcaps} _c
01= §
-8-* .2-= o S
TETRAXIDECAHEDRON
(Tetraxidec. 1)
Lord Kelvins all-space solid. 8 square, V=cdgc <Rational
8 hexagonal faces. Dymaxion+1% 96.0000
Octa “total 1J4 Dy maxion.
rag
>8Si
!§
Ills
z
o
C5
Q
W 3
5 g
M &
Q 3
QL??i
ei
Table 963.10 Dymaxion Energetic Geometry, 1950
[963.13]{style="color: purple3"} []{#ver:963.13 label="ver:963.13"} Synergetics is a priori nuclear; it begins at the center, the center of the always centrally observing observer. The centrally observing observer asks progressively, “What goes on around here?”
¶ 964.00 Second Power: Two Dimensions
[964.01]{style="color: purple3"} []{#ver:964.01 label="ver:964.01"} In conventional coordination, two-dimensionality is identified with areal pointal frequency.
[964.02]{style="color: purple3"} []{#ver:964.02 label="ver:964.02"} In synergetics, second poweringpoint aggregate quanta = area. In synergetics, second powering represents the rate of system surface growth.
[964.10]{style="color: purple3"} []{#ver:964.10 label="ver:964.10"} Spherical Growth Rate: In a radiational or gravitational wave system, second powering is identified with the point population of the concentrically embracing arrays of any given radius, stated in terms of frequency of modular subdivisions of either the radial or chordal circumference of the system. (From Synergetics Corollary, see Sec. 240.44.)
[964.20]{style="color: purple3"} []{#ver:964.20 label="ver:964.20"} Vertexial Topology: Second powering does not refer to “squaring” or to surface amplification, but to the number of the system’s external vertexes in which equating the second power and the radial or circumferential modular subdivisions of the system (multiplied by the prime number one, if a tetrahedral system; by the prime number two, if an octahedral system; by the prime number three, if a triangulated cubical system; and by the prime number five, if an icosahedral system), each multiplied by two, and added to by two, will accurately predict the number of superficial points of the system.
[964.30]{style="color: purple3"} []{#ver:964.30 label="ver:964.30"} Shell Accounting: Second power has been identified uniquely with surface area, and it is still the “surface,” or shell. But what physics shows is very interesting: there are no continuous shells, there are only energy-event foci and quanta. They can be considered as points or “little spheres.” The second-power numbers represent the number of energy packages or points in the outer shell of the system. The second-power number is derived by multiplying the frequency of wave divisions of the radius of the system, i.e., = frequency to the second power.
[964.31]{style="color: purple3"} []{#ver:964.31 label="ver:964.31"} In the quantum and wave phenomena, we deal with individual packages. We do not have continuous surfaces. In synergetics, we find the familiar practice of second powering displaying a congruence with the points, or separate little energy packages of the shell arrays. Electromagnetic frequencies of systems are sometimes complex, but they always exist in complementation of gravitational forces and together with them provide prime rational integer characteristics in all physical systems. Little energy actions, little separate stars: this is what we mean by quantum. Synergetics provides geometrical conceptuality in respect to energy quanta.
¶ 965.00 Third Power: Three Dimensions
[965.01]{style="color: purple3"} []{#ver:965.01 label="ver:965.01"} In a radiational or gravitational wave system, third powering is synergetically identified with the total point population involvement of all the successively propagated, successively outward bound in omniradial direction, wave layers of the system. Since the original point was a tetrahedron and already a priori volumetric, the third powering is in fact sixth powering: [N3xN3=N&.]{.smallcaps}
[965.02]{style="color: purple3"} []{#ver:965.02 label="ver:965.02"} Third powering = total volumetric involvementas, for instance, total molecular population of a body of water through which successive waves pass outwardly from a splash-propagated initial circle. As the circle grows larger, the number of molecules being locally displaced grows exponentially.
[965.03]{style="color: purple3"} []{#ver:965.03 label="ver:965.03"} Third powering identifies with a symmetric swarm of points around, and in addition to, the neutral axial line of points. To find the total number of points collectively in all of a system’s layers, it is necessary to multiply an initial quantity of one of the first four prime numbers (times two) by the third power of the wave frequency.
[965.04]{style="color: purple3"} []{#ver:965.04 label="ver:965.04"} Perpendicularity (90-degreeness) uniquely characterizes the limit of three-dimensionality. Equiangularity (60-degreeness) uniquely characterizes the limits of four-dimensional systems.
¶ 966.00 Fourth Power: Four Dimensions
[966.01]{style="color: purple3"} []{#ver:966.01 label="ver:966.01"} In a radiational or gravitational wave system, fourth powering is identified with the interpointal domain volumes.
[966.02]{style="color: purple3"} []{#ver:966.02 label="ver:966.02"} It is not possible to demonstrate the fourth dimension with 90-degree models. The regular tetrahedron has four unique, omnisymmetrically interacting face planesergo, four unique perpendiculars to the four planes.
[966.03]{style="color: purple3"} []{#ver:966.03 label="ver:966.03"} Four-dimensionality evolves in omnisymmetric equality of radial and chordal rates of convergence and divergence, as well as in all symmetrically interparalleled dimensions. All of synergetics’ isotropic-vector-matrix field lines are geodesic and weave both four-dimensionally and omnisymmetrically amongst one another, for all available cosmic time, without anywhere touching one another.
[966.04]{style="color: purple3"} []{#ver:966.04 label="ver:966.04"} The vector-equilibrium model displays four-dimensional hexagonal central cross section.
[966.05]{style="color: purple3"} []{#ver:966.05 label="ver:966.05"} Arithmetical fourth-power energy evolution order has been manifest time and again in experimental physics, but could not be modelably accommodated by the c.g.s. system. That the fourth dimension can be modelably accommodated by synergetics is the result of complex local intertransformabilities because the vector equilibrium has, at initial frequency zero, an inherent volume of 20. Only eight cubes can be closest packed in omnidirectional embracement of any one point in the system: in the third powering of two, which is eight, all point-surrounding space has been occupied. In synergetics, third powering is allspace-fillingly accounted in tetrahedral volume increments; 20 unit volume tetrahedra close-pack around one point, which point surrounding reoccurs isotropically in the centers of the vector equilibria. When the volume around one is 20, the frequency of the system is at one. When the system modular frequency is at one, the cube volume is one, while in the vector-equilibrium synergetic system, the initial volume is 20. When the frequency of modular subdivision of cubes reads two, the volume is eight. When the vector equilibria’s module reads two, the volume is tetrahedral volumes thus demonstrating the use of conceptual models for fourth- and fifth-powering volumetric growth rates. With the initial frequency of one and the volume of the vector equilibrium at 20, it also has 24 x 20 and Quanta Modules; ergo is inherently initially 480 quanta modules. . With frequency of two the vector equilibrium is quanta modules. . (See Illus. 966.05.)
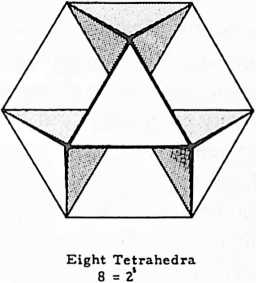
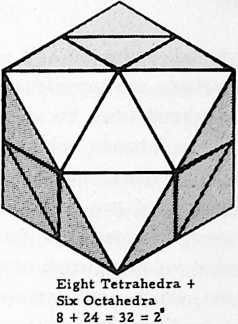
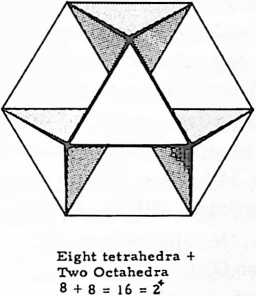
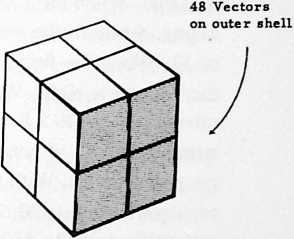
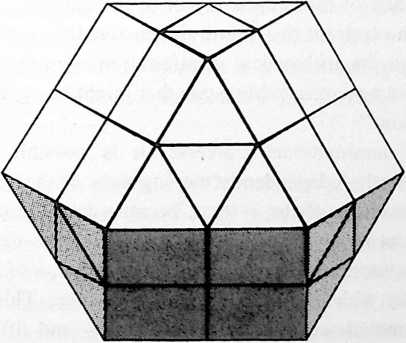
Tetrahedron “unity” Volume = 1
Octahedron
4 = /
Eight cubes is maximum around a single point.
8=2*
Fig. 966.05 Tetrahedral Modelability of 2nd, 3rd, 4th, and 5th Power Relationships:
-
Polyhedral assemblies around a single point having volumes that are integral powers of two when referred to tetrahedron as unity volume.
-
Two-frequency vector equilibrium: 5,25=160.
[966.06]{style="color: purple3"} []{#ver:966.06 label="ver:966.06"} Because the volume of one cube equals the volume of three regular tetrahedra, it is now clear that it was only the threefold overstuffing which precluded its capability of providing conceptual modelability of fourth powering. It was the failure of the exclusively three-dimensional coordination that gave rise to the concept that fourth-dimensionality is experimentally undemonstrableergo, its arithmetical manifestation even in physics must be a mysterious, because nonconceivable, state that might be spoken of casually as the “time dimension.”
[966.07]{style="color: purple3"} []{#ver:966.07 label="ver:966.07"} In an omnimotional Universe, it is possible to join or lock together two previously independently moving parts of the system without immobilizing the remainder of the system, because four-dimensionality allows local fixities without in any way locking or blocking the rest of the system’s omnimotioning or intertransforming. This independence of local formulation corresponds exactly with life experiences in Universe. This omnifreedom is calculatively accommodated by synergetics’ fourth- and fifth-power transformabilities. (See Sec. 465, “Rotation of Wheels or Cams in Vector Equilibrium.”) (See Illus. 465.01.)
[966.08]{style="color: purple3"} []{#ver:966.08 label="ver:966.08"} In three-dimensional, omni-intermeshed, unclutchable, mechanical systems, if any gear is blocked, the whole gear train is locked. In a four-dimensional unclutchable gear system, a plurality of local gears may be locked, while the remainder of the system interarticulates freely. Odd numbers of individual gears (not gear teeth) lock and block while even numbers reciprocate freely in mechanical gear trains.
[966.10]{style="color: purple3"} []{#ver:966.10 label="ver:966.10"} Fourth Power in Physical Universe: While nature oscillates and palpitates asymmetrically in respect to the omnirational vector-equilibrium field, the plus and minus magnitudes of asymmetry are rational fractions of the omnirationality of the equilibrious state, ergo, omnirationally commensurable to the fourth power, volumetrically, which order of powering embraces all experimentally disclosed physical volumetric behavior.
[966.11]{style="color: purple3"} []{#ver:966.11 label="ver:966.11"} The minimum set of events providing macro-micro differentiation of Universe is a set of four local event foci. These four “stars” have an inherent sixness of relationship. This four-foci, six-relationship set is definable as the tetrahedron and coincides with quantum mechanics’ requirements of four unique quanta per each considerable “particle.”
[966.12]{style="color: purple3"} []{#ver:966.12 label="ver:966.12"} In synergetics, all experience is identified as, a priori, unalterably four-dimensional. We do not have to explain how Universe began converting chaos to a “building block” and therefrom simplex to complex. In synergetics Universe is eternal. Universe is a complex of omni-interaccommodative principles. Universe is a priori orderly and complexedly integral. We do not need imaginary, nonexistent, inconceivable points, lines, and planes, out of which non-sensible nothingness to inventively build reality. Reality is a priori Universe. What we speak of geometrically as having been vaguely identified in early experience as “specks” or dots or points has no reality. point in synergetics is a tetrahedron in its vector-equilibrium, zero-volume state, but too small for visible recognition of its conformation. line is a tetrahedron of macro altitude and micro base. A plane is a tetrahedron of macro base and micro altitude. Points are real, conceptual, experienceable visually and mentally, as are lines and planes.
[966.20]{style="color: purple3"} []{#ver:966.20 label="ver:966.20"} Tetrahedron as Fourth-Dimension Model: Since the outset of humanity’s preoccupation exclusively with the coordinate system, mathematicians have been accustomed to figuring the area of a triangle as a product of the base and one-half its perpendicular altitude. And the volume of the tetrahedron is arrived at by multiplying the area of the base triangle by one-third of its perpendicular altitude. But the tetrahedron has four uniquely symmetrical enclosing planes, and its dimensions may be arrived at by the use of perpendicular heights above any one of its four possible bases. That’s what the fourth-dimension system is: it is produced by the angular and size data arrived at by measuring the four perpendicular distances between the tetrahedral centers of volume and the centers of area of the four faces of the tetrahedron.
[966.21]{style="color: purple3"} []{#ver:966.21 label="ver:966.21"} As in the calculation of the area of a triangle, its altitude is taken as that of the triangle’s apex above the triangular baseline (or its extensions); so with the tetrahedron, its altitude is taken as that of the perpendicular height of the tetrahedron’s vertex above the plane of its base triangle (or that plane’s extension outside the tetrahedron’s triangular base). The four obtuse central angles of convergence of the four perpendiculars to the four triangular midfaces of the regular tetrahedron pass convergently through the center of tetrahedral volume at 109.
¶ 970.00 First- and Third-Power Progressions of Vector Equilibria
[970.01]{style="color: purple3"} []{#ver:970.01 label="ver:970.01"} Operational Note: In making models or drawing the concentric growth of closest-packed sphere-shells, we are illustrating with great-circle cross sections through the center of the vector equilibrium; i.e., on one of its symmetrically oriented four planes of tetrahedral symmetry; i.e., with the hexagonally cross-section, concentric shells of half-KEs.
[970.02]{style="color: purple3"} []{#ver:970.02 label="ver:970.02"} Your eye tends quickly to wander as you try to draw the closest- packed spheres’ equatorial circles. You have to keep your eye fixed on the mid-points of the intertriangulated vectorial lines in the matrix, the mid-points where the half-radiuses meet tangentially.
[970.03]{style="color: purple3"} []{#ver:970.03 label="ver:970.03"} In the model of , the green area, the space occupied by the sphere per se, is really two adjacent shells that contain the insideness of the outer shell and the outsideness of the inner shell. These combine to produce tangentially paired shellsergo, two layers.
[970.10]{style="color: purple3"} []{#ver:970.10 label="ver:970.10"} Rationality of Planar Domains and Interstices: There is a omniplanar-bound, volumetric-domain marriage with the strictly spherical shell accounting. (See tables at Sec. 955.40 and at Sec. 971.00.)
[970.11]{style="color: purple3"} []{#ver:970.11 label="ver:970.11"} Both the total inventories of spheres and their planar-bound domains of closest-packed sphere shells, along with their interstitial, “concave” faceted, exclusively vector equilibrium or octahedral spaces, are rationally accountable in nonfractional numbers.
[970.12]{style="color: purple3"} []{#ver:970.12 label="ver:970.12"} Synergetics’ isotropic-vector-matrix, omnisymmetric, radiantly expansive or contractive growth rate of interstices that are congruent with closest-packed uniradius spheres or points, is also rational. There is elegant, omniuniversal, metaphysical, rational, whole number equating of both the planar-bound polyhedral volumes and the spheres, which relationships can all be discretely expressed without use of the irrational number (), , always required for such mathematical expression in strictly coordinate mathematics.
[970.13]{style="color: purple3"} []{#ver:970.13 label="ver:970.13"} sphere is a convexly expanded vector equilibrium, and all inter-closest-packed sphere spaces are concavely contracted vector equilibria or octahedra at their most disequilibrious pulsative moments.
[970.20]{style="color: purple3"} []{#ver:970.20 label="ver:970.20"} Spheres and Spaces: The successive layer-shell, planar-bound, tetrahedral volumes embrace only the tangential inner and outer portions of the concentrically closest-packed spheres, each of whose respective complete concentric shell layers always number . The volume of each concentric vector-equilibrium layer is defined and structured by the isotropic vector matrix, or octet truss, occurring between the spherical centers of any two concentric-sphere layers of the vector equilibrium, the inner part of one sphere layer and the outer part of the other, with only the center or nuclear ball being both its inner and outer parts (see drawings section).
[970.21]{style="color: purple3"} []{#ver:970.21 label="ver:970.21"} There is realized herewith a philosophical synergetic sublimity of omnirational, universal, holistic, geometrical accounting of spheres and spaces without recourse to the transcendentally irrational (). (See drawings section.)
¶ 971.00 Table of Basic Vector Equilibrium Shell Volumes
[971.01]{style="color: purple3"} []{#ver:971.01 label="ver:971.01"} Relationships Between First and Third Powers of Correlated to Closest-Packed Triangular Number Progression and Closest-Packed Tetrahedral Number Progression, Modified Both Additively and Multiplicatively in Whole Rhythmically Occurring Increments of Zero, One, Two, Three, Four, Five, Six, Ten, and Twelve, All as Related to the Arithmetical and Geometrical Progressions, Respectively, of Triangularly and Tetrahedrally Closest-Packed Sphere Numbers and Their Successive Respective Volumetric Domains, All Correlated with the Respective Sphere Numbers and Overall Volumetric Domains of Progressively Embracing Concentric Shells of Vector Equilibria: Short Title: Concentric Sphere Shell Growth Rates (see drawings section).
[971.02]{style="color: purple3"} []{#ver:971.02 label="ver:971.02"} The red zigzag between Columns 3 and 4 shows the progressive, additive, triangular-sphere layers accumulating progressively to produce the regular tetrahedra.
[971.03]{style="color: purple3"} []{#ver:971.03 label="ver:971.03"} Column 5 demonstrates the waves of SIX integer additions to the closest-packed tetrahedral progression. The first SIX zeros accumulate until we get a new nucleus. The first two of the zero series are in fact one invisible zero: the positive zero plus its negative phase. Every six layers we gain one new, additional nucleus.
[971.04]{style="color: purple3"} []{#ver:971.04 label="ver:971.04"} Column 6 is the tetrahedral number with the new nucleus.
[971.05]{style="color: purple3"} []{#ver:971.05 label="ver:971.05"} In Column 7, the integer SIX functions as zero in the same manner in which NINE functions innocuously as zero in all arithmetical operations.
[971.06]{style="color: purple3"} []{#ver:971.06 label="ver:971.06"} In Column 7, we multiply Column 6 by a constant SIX, to the product of which we add the six-stage wave-factor growth crest and break of Column 8.
[971.07]{style="color: purple3"} []{#ver:971.07 label="ver:971.07"} Column 8’s SIXness wave synchronizes elegantly the third-power arithmetical progression of N, i.e., with the integer-metered volumetric growth of N. Column 8’s SIXness identifies uniquely with the rhombic dodecahedron’s volume-quantum number. Column 8 tells us that the third powers are most fundamentally identified with the one central, holistic, nuclear-sphere-containing, or six-tangented-together, one-sixth sphere of the six vertexes of the 144 A and B Moduled rhombic dodecahedra.
[971.08]{style="color: purple3"} []{#ver:971.08 label="ver:971.08"} Columns 7 and 8 show the five-sixths cosmic geometry’s sphere/space relationship, which is also relevant to:
icosa’s basic sphere surface triangles as the outer faces of the icosahedron’s 120 centrally convergent similar tetrahedra, which 120 modules of icosahedral unity correspond in respect to the radially centralized, or circumferentially embracing 144 modules uniquely constituting and exclusively defining the rhombic dodecahedron sphere;
as 120 is to 144;
the icosahedron is to spherical unity as 5 is to 6;
as is also any one shell of the vector equilibrium’s concentric closest-packed sphere count to its corresponding concentric omnispace volume count, i.e., as 10 is to 12.
[971.09]{style="color: purple3"} []{#ver:971.09 label="ver:971.09"} Column 10 lists the cumulative, planar-bound, tetrahedral volumes of the arithmetical progression of third powers of the successive frequencies of whole vector equilibria. The vector equilibrium’s initial non-frequencied tetra-volume, i.e., its quantum value, is 20. The formula for obtaining the frequency-progressed volumes of vector equilibrium is:
Volume of EE = 20F3.
[971.10]{style="color: purple3"} []{#ver:971.10 label="ver:971.10"} In Column 11, we subtract the previous frequency-vector equilibrium’s cumulative volume from the new one-frequency-greater vector equilibrium’s cumulative volume, which yields the tetrahedral volume of the outermost shell. The outer vector equilibrium’s volume is found always to be:
[971.11]{style="color: purple3"} []{#ver:971.11 label="ver:971.11"} Incidentally, the part of the formula is inherent in the formula-, which determines the exact number of unique relationships always existing between any number of items.
[971.20]{style="color: purple3"} []{#ver:971.20 label="ver:971.20"} Pulsation Between Icosahedron and Vector Equilibrium: There is manifest in the icosahedral fiveness, in contradistinction to the vector equilibrium’s sixness, the seemingly ever annihilatable and ever-re-creatable integer, eternally propagating the complex of unique frequencies of the 92 inherently regenerative chemical elements as well as all the other unique resonances and frequencies of the electromagnetic, protoplasmic, pneumatic-hydraulic, and crystallographic spectrums, whose omnidirectional yes-no pulsativeness occasions the omniexperienceable, exclusively wavilinear, optically or instrumentally tunable, allness of time-accommodated human experience.
¶ 972.00 Universal Integrity Model
[972.01]{style="color: purple3"} []{#ver:972.01 label="ver:972.01"} Gravitational-Radiational: In its introvert mode, the rhombic dodecahedron interconnects six \sfrac{1}{5}th spheres and manifests gravity. In its extrovert mode, the rhombic dodecahedron comprises one whole sphere at its center with no other spheres implied; these are the spheres that together fill allspace. The extrovert mode of the rhombic dodecahedron manifests radiation.
[972.02]{style="color: purple3"} []{#ver:972.02 label="ver:972.02"} The rhombic dodecahedron is the integrated sphere (syntropic) OR the disintegrated sphere (entropic). (See color section.)
¶ 973.00 Basic Tetrahedra as Volumetric Modules
[973.01]{style="color: purple3"} []{#ver:973.01 label="ver:973.01"} Basic Tetrahedron: Each Basic Tetrahedron (Mite)[^33] is semi-symmetric, four of its six edges consisting always of two pairs of equal-length edges and only two being of odd lengths. The Mite itself consists of six entirely asymmetric Modules, four of which are dissimilar to the other two:
-
2 positive Modules
-
2 negative Modules
-
1 positive Module
-
1 negative Module
[973.10]{style="color: purple3"} []{#ver:973.10 label="ver:973.10"} Regular Tetrahedron: The Plato-identified “regular” (i.e., omnisymmetric) tetrahedron is comprised entirely of Modules: 12 positive s and 12 negatives, but the symmetric, “regular,” Platonic, equiangled, equi-edged tetrahedron cannot by itself fill allspace as could the cube, the rhombic dodecahedron, and the tetrakaidecahedronnone of which allspacefilling forms have self-stabilizing structural-conformation integrity, not being comprised of triangles, which alone can stabilize pattern.
[973.11]{style="color: purple3"} []{#ver:973.11 label="ver:973.11"} The “regular” Platonic tetrahedron may be combined with the octahedron to fill allspace.
[973.12]{style="color: purple3"} []{#ver:973.12 label="ver:973.12"} The volumes of all the symmetrical Platonic polyhedra, except the icosahedron and its pentagonal dodecahedron, are whole, low-order-number multiples of the “regular” Platonic tetrahedron, consisting itself of 24 modules, making that tetrahedron seemingly the “basic unit of measure” of all polyhedra. The inability of that “regular” tetrahedron to fill all cosmic space turns our comprehensive, cosmic-coordinate-system exploration to the consideration of the least common divisor aggregates of the and Modules.
[973.20]{style="color: purple3"} []{#ver:973.20 label="ver:973.20"} Functions of and Quanta Modules and Sytes: The/ and Quanta Modules are omnitriangulated and individually asymmetric but not maximally asymmetric. The Quanta Module has three of its 12 total angles at 90 degrees, and the Quanta Module has two 90-degree angles. The/ Quanta Module has a 30-degree and a 60-degree angle. TheB Quanta Module has two 45-degree angles.
[973.21]{style="color: purple3"} []{#ver:973.21 label="ver:973.21"} These angles all represent low-order whole fractions of unity: \sfrac
{1}{4}, \sfrac{1}{6}, \sfrac{1}{8}, \sfrac{1}{12}, and \sfrac{1}{16} of unity in a planar circle; all the other angles of the/ and Quanta Modules are unit and symmetric central angles of the tetrahedron and octahedron.
[973.22]{style="color: purple3"} []{#ver:973.22 label="ver:973.22"} The variety of their mixability produces what need be only momentary bewilderment and only an illusion of “disorder” occasioned initially by the subtlety and muchness of the unfamiliar.
[973.23]{style="color: purple3"} []{#ver:973.23 label="ver:973.23"} This brings us to consider the only superficially irregular, only semiasymmetric Syte as possibly being the most separately universal structural-system entity.
[973.24]{style="color: purple3"} []{#ver:973.24 label="ver:973.24"} The Syte, consisting of only six modules and filling allspace in a threefold intertransformable manner, is found to be far more universal and “primitive” than the regular tetrahedron. The Mite is the single most universal and versatile structural componentsave for its own subcomponents, the and Quanta Modules, which of unit volume and non-mirror-imaged complementation do indeed initially provide, singly or in complementation, the beginnings of all cosmic structuring.
[973.25]{style="color: purple3"} []{#ver:973.25 label="ver:973.25"} The Syte’s six Modules are always subdivided into two sets of three Modules eachtwo s, one of which two sets of the three Modules each are identically dimensioned both angularly and linearly, but one is inside out of the other. Therefore, one set of three Modules two s, one is positively outside-outed, and the other is negatively inside-outed.
[973.30]{style="color: purple3"} []{#ver:973.30 label="ver:973.30"} Particle and Wave Involvement: Particle Quanta Equation: (Prime numbers 2 and 5)
[973.31]{style="color: purple3"} []{#ver:973.31 label="ver:973.31"} Wave Quanta Equation: (Prime numbers 2, 5, and 3)
[973.32]{style="color: purple3"} []{#ver:973.32 label="ver:973.32"} One is particle involvement; the other is total involvement. Inadvertently, they correlate the sphere and all the other polyhedra rationally.
[973.33]{style="color: purple3"} []{#ver:973.33 label="ver:973.33"} The difference is the difference between using the tetrahedron as volumetric unity, while the physicist has always been using the cubic centimeter of water and then only lifting it in one direction, against gravity, against the imagined plane of the world. On the other hand, synergetics moves omnidirectionally, inwardly, outwardly, and aroundly.
¶ 974.00 Initial Frequency
[974.01]{style="color: purple3"} []{#ver:974.01 label="ver:974.01"} The initially potential-only frequency vector equilibrium has a volume of 20 regular tetrahedra, each of which consists of 24 modules. modules = initial vector equilibrium.
[974.02]{style="color: purple3"} []{#ver:974.02 label="ver:974.02"} The initial-frequency vector equilibrium has alternatively either a radiant rhombic dodecahedron core or a gravitational rhombic dodecahedron core, either of these alternates being of identical overall size and shape. Both consist of 144 modules. From the 480 modules of the vector equilibrium, we subtract the 144 modules of the rhombic dodecahedron, which leaves 366 modules surrounding either the radiant or gravitational rhombic dodecahedron nuclear-sphere-enveloping core. Each module = \sfrac{1}{144}th of our spherical domain. 336/144 = 2\sfrac
{1}{3}; and 480/144 = 3\sfrac{1}{3}; therefore, one nuclear-sphere domain surrounded by the parts of exactly 27s additional spherical-domain-producing modules, distributed symmetrically around the nucleus in exactly 12 groups of 28 modules each. 27s spheres divided by 12 = 73sths of one spherical domain. 273 = 73 = 84/36 spheres = 73eths of a nuclear sphere. We do not produce any complete regular polyhedron by adding 28 modules to each of the 12 rhombic dodecahedron faces. While 28 modules, i.e., 73sths of one spherical domain, may be added to each corner vertex of the vector equilibrium, they do not produce any complete regular polyhedron at initial frequency where = both + 1 and. Each nucleated vector equilibrium = 3 V3 spheres exactly, and not 13 whole spheres as do 12 closest packed around one. They have the centers of 12 fractional spheres (7/36 each) close packed around one whole sphere.
[974.03]{style="color: purple3"} []{#ver:974.03 label="ver:974.03"} Each cube = 3 tetrahedra x 24 modules = 72 modules. 144 modules = 1 sphere. Each initial-frequency cube = V2 a spherical domain. Eight cubes in aF2 cube=four spherical domains. Eight cubes have one whole central nuclear sphere and eight Vsth spheres on the eight outer corners. The eight = 1 cubes combined to = IF = 2 cubes have 8 x 72 = 576 modules.
[974.04]{style="color: purple3"} []{#ver:974.04 label="ver:974.04"} One octahedron has modules = 1/144 = 2/s spherical domain. One vector equilibrium = 3–7s spheres. Therefore, one vector equilibrium plus one octahedron = four spheres = one tetrahedron of four closest-packed spheres. One Eighth-Octahedron = 96 = 12 modules. If we add eight Eighth-Octahedra to each of the vector equilibrium’s eight triangular faces, we produce a cube of 480 + 96 modules = 576 modules, which is the same as the eight-cube cube.
¶ 980.00 Pi and Synergetics Constant
¶ 980.01 Relative Superficial and Volumetric Magnitudes
[980.02]{style="color: purple3"} []{#ver:980.02 label="ver:980.02"} Starting With Just Twoness: Granted a beyond-touch-reach apartness between two initially inter-self-identifying cosmic events of the basic otherness generating the awareness called “life,” the approximate distance between the volumetric centers of the respective event complexes can only be guessed at as observingly informed by a sequence of angular-differentialing of any two fixed-distance-apart, “range-finder” optics, integral to the observer in respect to which some feature of the remote pattern characteristics of the otherness correspond with some self-sensible features integral to the observing self-ness.
[980.03]{style="color: purple3"} []{#ver:980.03 label="ver:980.03"} Self has no clue to what the overall size of the away-from-self otherness may be until the otherness is in tactile contact with integral self, whereby component parts of both self and otherness are contactingly compared, e.g., “palm-to-palm.” Lacking such tactile comparing, self has no clue to the distance the other may be away from self. The principle is manifest by the Moon, whose diameter is approximately one-million times the height of the average human. The Moon often appears to humans as a disc no bigger than their fingernails.
[980.04]{style="color: purple3"} []{#ver:980.04 label="ver:980.04"} Without direct contact knowledge, curiosity-provoked assumptions regarding the approximate distance can be only schematically guessed at relativistically from a series of observationally measured angular relationship changes in the appearance of the observed otherness’s features in respect to experienced time-measured intervals of evolutionary transformation stages of self; such as, for instance, self-contained rhythmic frequencies or self-conceptualizability of angular-integrity relationships independent of size. Relative macro-micro system differentialing of direct-experience-stimulated cosmic conceptuality initiates progressive self-informing effectiveness relative to covarying values integral to any and all self-evolutionarily developing observational history.
[980.05]{style="color: purple3"} []{#ver:980.05 label="ver:980.05"} For instance, it is discoverable that with linear size increase of the tetrahedral structural systems (see Sec. 623.10), the tetrahedral surface enclosure increases as the second power of the linear growth rate, while the volumetric content co-increases at a third-power rate of the linear rate of size increase. Ergo, with a given tensile strength of cross section of material (itself consisting of nebular aggregates of critically proximate, mass-interattracted, behavioral-event integrities), which material is completely invested in the tetrahedral envelope stretched around four events, with one of the events not being in the plane of the other three. The envelope of a given amount of material must be stretched thinner and thinner as the tetrahedron’s four vertexes recede from one another linearly, the rate of the skin material thinning being a second power of the rate of linear retreat from one another of the four vertexial events. All the while the interior volume of the tetrahedron is increasing at a third-power rate and is being fed through one of its vertexes with an aggregate of fluid matter whose atomic population is also increasing at a third-power volumetric rate in respect to the rate of linear gain by symmetrical recession from one another of the four vertexial points.
[980.06]{style="color: purple3"} []{#ver:980.06 label="ver:980.06"} child of eight years jumping barefootedly from rock to rock feels no pain, whereas a grownup experiences not only pain but often punctures the skin of the bottom of the feet because the weight per square inch of skin has been increased three- or fourfold. If humans have not learned by experience that the surface-to-volume relationships are not constant, they may conclude erroneously that they have just grown softer and weaker than they were in childhood, or that they have lost some mystical faculty of childhood. Realizing intuitively or subconsciously with self-evolution-gained information and without direct knowledge regarding the internal kinetics of atoms and molecules in the combined fluid-gaseous aggregate of organisms, we can intuit cogently that naturally interrepellent action-reaction forces are causing the interior gaseous molecules to accelerate only outwardly from one another because the closest-packed limits will not accommodate inwardly, while expansion is ever less opposed and approaches entirely unlimited, entirely unpacked condition. Sensing such relationships without knowing the names of the principles involved, humans can comprehend in principle that being confined only by the ever-thinning films of matter stretched about them on, for instance, a tetrahedron’s surface, the third-power rate of increase of the bursting force of the contained volume of gases against the second-power growth rate of the ever more thinly stretched film, in respect to the first-power growth rate of the system, swiftly approaches parting of the enclosing film without knowing that the subvisible energy events have receded beyond the critical proximity limits of their mutual mass-interattractiveness and its inter-fall-in-ness proclivities, instead of which they interprecess to operate as individually remote cosmic orbitings. All of these principles are comprehensible in effective degree by individuals informed only by repeated self-observation of human saliva’s surface tension behaviors of their lung-expelled, tongue-formed, mouth-blowable air bubbles as they swiftly approach the critical proximity surface-tension conditions and burst.
[980.07]{style="color: purple3"} []{#ver:980.07 label="ver:980.07"} Such information explains to self that the critical dimensional interrelationships are to be expected regarding which their own and others’ experimental measurements may lead them to comprehend in useful degree the complex subvisible organisms existing between the energy states of electromagnetics, crystals, hydraulics, pneumatics, and plasmics. Thus they might learn that the smaller the system, the higher the surface-tension effectiveness in respect to total volumetric-force enclosure and interimpact effects of locally separate system events; if so, they will understand why a grasshopper can spring outward against a system’s gravity to distances many times the greatest height of the grasshopper standing on the system and do so without damaging either its mechanical or structural members; on the other hand, humans are unable to jump or spring outwardly from Earth’s surface more than one module of their own height, and if they were dropped toward the system from many times that height, it would result in the volumetric-contentmass-concentration acceleration bursting their mass intertensioning’s critical limits.
[980.08]{style="color: purple3"} []{#ver:980.08 label="ver:980.08"} Thus locally informed of relative magnitude-event behaviors, the individual could make working assumptions regarding the approximate distances as though, informed of the observed presence of enough event details of the otherness corresponding with those of the within-self-complex, as provided by the relative electromagnetic-frequency color effects that identify substances and their arrangement in the otherness corresponding to the observer’s integral-event complex, the individual has never heard of or thought of the fact that he is not “seeing things” but is tuning in electromagnetic wave programs. The foregoing embraces all the parameters of the generalized principles governing always and only self-inaugurated education and its only secondary augmentability by others.
[980.09]{style="color: purple3"} []{#ver:980.09 label="ver:980.09"} Flying-boat aviators landing in barren-rock- and ice-rimmed waters within whose horizons no living organism may be observed are completely unable to judge the heights of cliffs or valleys and must come in for a landing at a highly controllable glide angle and speed suitable for safe touch-in landing.
[980.10]{style="color: purple3"} []{#ver:980.10 label="ver:980.10"} Once there has been contact of the observer with the otherness, then the approximate distance estimation can be improved by modular approximations, the modules being predicated on heartbeat intervals, linear pacings, or whatever. These do, however, require time intervals. No otherness: No time: No distance. The specific within-self rhythm criterion spontaneously employed for time-distance-interval measurements is inconsequential. Any cycle tunable with the specific-event frequencies will do.
¶ 981.00 Self and Otherness Sequence
[981.01]{style="color: purple3"} []{#ver:981.01 label="ver:981.01"} Coincidentally synchronized with the discovery of self through the discovery of otherness and otherness’s and self’s mutual inter-rolling-around (see Sec. 411), we have self-discovery of the outside me and the inside me, and the self-discovery of the insideness and outsideness of the otherness. The inside me in my tummy is directionally approachable when I stick my finger in my mouth.
[981.02]{style="color: purple3"} []{#ver:981.02 label="ver:981.02"} Now we have the complete coordinate system of self-polarizing in-out-and-aroundness apprehending and comprehending of self experience, which initiates life awareness and regeneratively processes the evoluting agglomeration of individual experiences. Individual experiences are always and only special-case physical manifestations of utterly abstract, cosmically eternal, generalized principles observable at remotely large and small as well as at everyday local middling time ranges, all of which accumulate progressively to provide potential convertibility of the experience inventory from energetic apprehensions into synergetically discovered comprehensions of a slowly increasing inventory of recognized, inherently and eternally a priori generalized principles from which gradually derive the inventory of human advantages gainable through the useful employment of the generalized principles in special-case artifacts and inventions, which are realized and accumulate only through mutually acknowledged self-and-other individual’s omnidirectional observations of the multioverlapped relay of only discontinuously living consciousness’s apprehension-comprehension-awareness evolution of the totally communicated and ever-increasing special-case information and synergetically generalized knowledge environment, all of which integrally evolving overlapped and nonsimultaneously interspliced finite experience awareness aggregate is experientially identified as nonunitarily conceptual, but finitely equatable, Universe.
[981.03]{style="color: purple3"} []{#ver:981.03 label="ver:981.03"} Going beyond the original formulation of the four-sphere-vertexed minimum structural system (Sec. 411), we observe that the addition of a fifth spherical otherness to the four-ball structural system’s symmetry brings about a polarized-system condition. The fifth ball cannot repeat the total mutually intertouching experienced by each of the first four as they joined successively together. The fifth sphere is an oddball, triangularly nested diametrically opposite one of the other four and forming the apex of a second structural-system tetrahedron commonly based by the same three equatorially triangulated spheres. This brings about a condition of two polar-apex spheres and an equatorial set of three. Each of the three at the middle touches not only each other but each of the two poles. While each of the equatorial three touches four others of the fivefold system, each of the two polar spheres touches only three others. Due to this inherent individual differentiability, the fivefoldedness constitutes a self-exciting, pulsation-propagating system. (Compare the atomic time clock, which is just such a five-folded, atomic-structured, mutually based tetrahedral configuration.)
[981.04]{style="color: purple3"} []{#ver:981.04 label="ver:981.04"} This is a second-degree polarization. The first polarization was subsystem when the selfness discovered the otherness and the interrelatedness became an axis of cospinnability, only unobservably accomplished and only intuitively theorized during the initial consciousness of inter-rolling-around anywhere upon one another of the mutually interattracted tangency of self and first otherness, which simultaneous and only theoretically conceivable axial-rotation potential of the self and one other tangential pairing could only be witnessingly apprehended by a secondly-to-be-discovered otherness, as it is mass-attractively drawn toward the first two from the unthinkable nowhere into the somewhere.
[981.05]{style="color: purple3"} []{#ver:981.05 label="ver:981.05"} The whole associated self-and-otherness discloses both in-outing (A) and arounding (B), which are of two subclasses, respectively: (1) the individually coordinate, and (2) the mutually coordinate.
- (1) is individually considered, radial or diametric, inward and outward
exploration of self by self;
(2) is comprehensive expansion or contraction only mutually and systematically accomplishable;
- (1) is individual spinnability;
(2) is orbiting of one by another, which is only mutually accomplishable.
[981.06]{style="color: purple3"} []{#ver:981.06 label="ver:981.06"} The couple may rotate axially, but it has no surrounding environment otherness in respect to which it can observe that it is rotating axially (or be mistaken and egotistically persuaded that the entire Universe is revolving axially around “self”).
[981.07]{style="color: purple3"} []{#ver:981.07 label="ver:981.07"} Not until a sixth otherness appears remotely, approaches, and associates with the fivefold system can the latter learn from the newcorner of its remote witnessing that the fivefold system had indeed been rotating axially. Before that sixth otherness appears, the two polar balls of the fivefold polarized system symmetry attract each other through the hole in their common basethe triangular three-ball equatorand their approach-accelerated, second-power rate of interattraction increases momentum, which wedge-spreads open the equatorial triangle with the three equatorial spheres centrifugally separated by the axial spin, precessionally arranged by dynamic symmetry into a three-ball equatorial array, with the three spheres spaced 120 degrees apart and forming the outer apexes of three mutually edged triangles with the two axially tangent polar spheres constituting the common edge of the three longitudinally arrayed triangles.
[981.08]{style="color: purple3"} []{#ver:981.08 label="ver:981.08"} Then along comes a sixth ball, and once more momentum-produced dynamic symmetry rearranges all six with three uniradius spheres in the northern hemisphere and three in the southern hemisphere: i.e., they form the octahedron, spinning on an axis between the face centers of two of its eight triangular faces, with the other six triangles symmetrically arrayed around its equator. Dynamic symmetry nests the next ball to arrive at the axial and volumetric center occurring between the north and south polar triangular groups, making two tetrahedra joined together with their respective apexes congruent in the center ball and their respective triangular base centers congruent with the north and south poles. Now the mass-interattracted, dynamically symmetried group of seven spheres is centered by their common mid-tetra apex; since the seven-ness is greater than the combined mass of the next six arriving spheres, the latter are dynamically arranged around the system equator and thus complete the vector equilibrium’s 12-around-one, isotropic, closest-packed, omnicontiguous-embracing, nuclear containment.
[981.09]{style="color: purple3"} []{#ver:981.09 label="ver:981.09"} As awareness begins only with awareness of otherness, the mass- interattracted accelerating accelerationat a second-power rate of gain as proximity is progressively halved by the self and otherness interapproachboth generates and locally impounds the peak energy combining at tangency, now articulated only as round-and-about one another’s surfaces rolling.
[981.10]{style="color: purple3"} []{#ver:981.10 label="ver:981.10"} Self has been attracted by the other as much as the other has been attracted by self. This initial manifest of interacceleration force must be continually satisfied. This accumulative force is implicit and is continually accountable either as motion or as structural-system coherence. Four balls manifest structural interstabilization, which combiningly multiplied energy is locked up as potential energy, cohering and stabilizing the structural system, as is manifest in the explosive release of the enormous potential energy locked into the structural binding together of atoms.
[981.11]{style="color: purple3"} []{#ver:981.11 label="ver:981.11"} With all the 12 spherical othernesses around the initial self-oneness sphericity apparently uniformly diametered with self, the positivenegative vectorial relativity of nuclear equilibrium is operationally established. The pattern of this nuclear equilibrium discloses four hexagonal planes symmetrically interacting and symmetrically arrayed (see Sec. 415) around the nuclear center.
[981.12]{style="color: purple3"} []{#ver:981.12 label="ver:981.12"} Awareness of otherness involves mutually intertuned event frequencies. The 12 othernesses around the initially conceiving self-oneness establish both an inward and an outward synchroresonance. Circuit frequency involves a minimum twoness. This initial frequency’s inherent twoness is totally invested as one inward plus one outward wavetwo waves appearing superficially as one, or none.
[981.13]{style="color: purple3"} []{#ver:981.13 label="ver:981.13"} The self extension of the central sphere reproduces itself outwardly around itself until it is completely embraced by self-reproduced otherness, of which there are exactly 12, exact-replica, exactly spherical domains symmetrically filling all the encompassing space outside of the initial sphere’s unique closest-packed cosmic domain, which includes each sphere’s exact portion of space occurring outside and around their 12 points of intertangency. The portion of the intervening space belonging to each closest-packed sphere is that portion of the space nearest to each of the spheres as defined by planes halfway between any two most closely adjacent spheres. There are 12 of these tangent planes symmetrically surrounding each sphere whose 12 similar planes are the 12 diamond-shaped facets of the rhombic dodecahedron. The rhombic dodecahedra are allspace filling. Their allspacefilling centers are exactly congruent with the vertexes of the isotropic vector matrixergo, with the centers of all closest-packed unit radius sphere complexes.
[981.14]{style="color: purple3"} []{#ver:981.14 label="ver:981.14"} This is the self-defining evolution of the sphere and spherical domain as omnisymmetrically surrounded by identical othernesses, with the self-regenerative surroundment radially continuous.
[981.15]{style="color: purple3"} []{#ver:981.15 label="ver:981.15"} We now reencounter the self-frequency-multipliable vector equilibrium regeneratively defined by the volumetric centers of the 12 closest-packed rhombic dodecahedral spheric domains exactly and completely surrounding one such initial and nuclear spheric domain.
[981.16]{style="color: purple3"} []{#ver:981.16 label="ver:981.16"} What seemed to humans to constitute initiation and evolution of dimensional connection seemed to start with his scratching a line on a plane of a flat Earth, in which two sets of parallel lines crossed each other perpendicularly to produce squares on the seemingly flat Earth, from the corners of which, four perpendiculars arose to intersect with a plane parallel to the base plane on flat Earth occurring at a perpendicular distance above Earth equal to the perpendicular distance between the original parallel lines intersecting to form the base square. This defined the cube, which seemed to satisfy humanity’s common conception of dimensional coordination defined by width, breadth, and height. Not knowing that we are on a spherethe sphere, even a round pebble, seems too foreign to the obvious planar simplicity seemingly accommodated by the environment to deserve consideration. But we have learned that Universe consists primarily of spherically generated events. Universe is a priori spherically islanded. The star-energy aggregates are all spherical.
[981.17]{style="color: purple3"} []{#ver:981.17 label="ver:981.17"} If we insist (as humans have) on initiating mensuration of reality with a cube, yet recognize that we are not living on an infinite plane, and that reality requires recognition of the a priori sphericity of our planet, we must commence mensuration with consideration of Earth as a spherical cube. We observe that where three great-circle lines come together at each of the eight corners of the spherical cube, the angles so produced are all 120 degreesand not 90 degrees. If we make concentric squares within squares on each of the six spherical-surface squares symmetrically subdividing our planet, we find by spherical trigonometry that the four corner angles of each of the successively smaller squares are progressively diminishing. When we finally come to the little local square on Earth within which you stand, we find the corner angles reduced from 120 degrees almost to 90 degrees, but never quite reaching true 90-degree corners.
[981.18]{style="color: purple3"} []{#ver:981.18 label="ver:981.18"} Because man is so tiny, he has for all of history deceived himself into popular thinking that all square corners of any size are exactly 90 degrees.
[981.19]{style="color: purple3"} []{#ver:981.19 label="ver:981.19"} Instead of initiating universal mensuration with assumedly straight-lined, square-based cubes firmly packed together on a world plane, we should initiate with operationally verified reality; for instance, the first geometrical forms known to humans, the hemispherical breasts of mother against which the small human spheroidal observatory is nestled. The synergetic initiation of mensuration must start with a sphere directly representing the inherent omnidirectionality of observed experiences. Thus we also start synergetically with wholes instead of parts. Remembering that we have verified the Greek definition of a sphere as experimentally invalidated, we start with a spheric array of events. And the “sphere” has definable insideness and seemingly undefinable outsideness volume. But going on operationally, we find that the sphere becomes operationally omni-intercontiguously embraced by other spheres of the same diameter, and that ever more sphere layers may symmetrically surround each layer by everywhere closest packings of spheres, which altogether always and only produces the isotropic vector matrix. This demonstrates not only the uniformly diametered domains of closest-packed spheres, but also that the domains’ vertexially identified points of the system are the centers of closest-packed spheres, and that the universal symmetric domain of each of the points and spheres of all uniformly frequencied systems is always and only the rhombic dodecahedron.
[981.20]{style="color: purple3"} []{#ver:981.20 label="ver:981.20"} All the well-known Platonic polyhedra, as well as all the symmetrically referenced crystallographic aberrations, are symmetrically generated in respect to the centers of the spheric domains of the isotropic vector matrix and its inherently nucleating radiational and gravitational behavior accommodating by concentrically regenerative, omnirational, frequency and quanta coordination of vector equilibria, which may operate propagatively and coheringly in respect to any special-case event fix in energetically identifiable Universe.
[981.21]{style="color: purple3"} []{#ver:981.21 label="ver:981.21"} The vector equilibrium always and only represents the first omnisymmetric embracement and nucleation of the first-self-discovered-byotherness sphere by the completely self-embracing, twelve-fold, isotropic, continuous otherness.
[981.22]{style="color: purple3"} []{#ver:981.22 label="ver:981.22"} Sphere is prime awareness.
[981.23]{style="color: purple3"} []{#ver:981.23 label="ver:981.23"} Spheric domain is prime volume.
[981.24]{style="color: purple3"} []{#ver:981.24 label="ver:981.24"} Only self-discoverable spheric-system awareness generates all inwardness, outwardness, and aroundness dimensionality.
¶ 982.00 Cubes, Tetrahedra, and Sphere Centers
[982.01]{style="color: purple3"} []{#ver:982.01 label="ver:982.01"} Spheric Domain: As the domain hierarchy chart shows (see “Concentric Domain Growth Rates,” Sec. 955.40), the inherent volume of one prime spheric domain, in relation to the other rational low order number geometric volumes, is exactly sixfold the smallest omnisymmetrical structural system polyhedron: the tetrahedron.
[982.02]{style="color: purple3"} []{#ver:982.02 label="ver:982.02"} The spheric domain consists of 144 modules, while the tetrahedron consists of 24 modules. 24/i44 = [Vg.]
[982.03]{style="color: purple3"} []{#ver:982.03 label="ver:982.03"} The vector equilibrium consists of 480 modules. 24/4so = 1/2o.
[982.04]{style="color: purple3"} []{#ver:982.04 label="ver:982.04"} Within the geometries thus defined, the volume of the cube = 3. The cube consists of 72 modules. [72/24 = 3/i.]{.smallcaps} The initial cube could not contain one sphere because the minimum spheric domain has a volume of six.
[982.05]{style="color: purple3"} []{#ver:982.05 label="ver:982.05"} The initial generated minimum cube is defined by four Vsth spheres occurring close-packingly and symmetrically only at four of the cube’s eight corners; these four corners are congruent with the four corners of the prime tetrahedron, which is also the prime structural system of Universe.
[982.06]{style="color: purple3"} []{#ver:982.06 label="ver:982.06"} We thus discover that the tetrahedron’s six edges are congruent with the six lines connecting the four fractional spheres occurring at four of the eight alternate corners of the cube.
[982.10]{style="color: purple3"} []{#ver:982.10 label="ver:982.10"} Noncongruence of Cube and Sphere Centers: The centers of cubes are not congruent with the sphere centers of the isotropic vector matrix. All the vectors of the isotropic vector matrix define all the centers of the omni-interconnections of self and otherness of omnicontiguously embracing othernesses around the concentrically regenerating, observing self sphere.
[982.11]{style="color: purple3"} []{#ver:982.11 label="ver:982.11"} The vector equilibrium represents self’s initial realization of self both outwardly and inwardly from the beginning of being between-ness.
[982.12]{style="color: purple3"} []{#ver:982.12 label="ver:982.12"} The cube does occur regularly in the isotropic vector matrix, but none of the cubes has more than four of their eight corners occurring in the centers of spheres. The other four corners always occur at the volumetric centers of octahedra, while only the octahedra’s and tetrahedra’s vertexes always occur at the volumetric centers of spheres, which centers are all congruent with all the vertexes of the isotropic vector matrix. None of the always co-occurring cube’s edges is congruent with the vectorial lines (edges) of the isotropic vector matrix. Thus we witness that while the cubes always and only co-occur in the eternal cosmic vector field and are symmetrically oriented within the field, none of the cubes’ edge lines is ever congruent or rationally equatable with the most economical energetic vector formulating, which is always rational of low number or simplicity as manifest in chemistry. Wherefore humanity’s adoption of the cube’s edges as its dimensional coordinate frame of scientific-event reference gave it need to employ a family of irrational constants with which to translate its findings into its unrecognized isotropic-vector-matrix relationships, where all nature’s events are most economically and rationally intercoordinated with omni-sixty-degree, one-, two-, three-, four-, and five-dimensional omnirational frequency modulatability.
[982.13]{style="color: purple3"} []{#ver:982.13 label="ver:982.13"} The most economical force lines (geodesics) in Universe are those connecting the centers of closest-packed unit radius spheres. These geodesics interconnecting the closest-packed unit radius sphere centers constitute the vectors of the isotropic (everywhere the same) vector matrix. The instant cosmic Universe insinuatability of the isotropic vector matrix, with all its lines and angles identical, all and everywhere equiangularly triangulatedergo, with omnistructural integrity but always everywhere structurally double- or hinge-bonded, ergo, everywhere nonredundant and force-fluidis obviously the idealized eternal coordinate economy of nature that operates with such a human-mind-transcending elegance and bounty of omnirational, eternal, optional, freedom-producing resources as to accomplish the eternal regenerative integrity of comprehensively synergetic, nonsimultaneous Universe.
[982.14]{style="color: purple3"} []{#ver:982.14 label="ver:982.14"} The edges of the tetrahedra and octahedra of the isotropic vector matrix are always congruent with one another and with all the vectors of the system’s network of closest-packed unit radius spheres.
[982.15]{style="color: purple3"} []{#ver:982.15 label="ver:982.15"} The whole hierarchy of rationally relative omnisymmetrical geometries’ interdimensional definability is topologically oriented exactly in conformance with the ever cosmically idealizable isotropic vector matrix;
[982.16]{style="color: purple3"} []{#ver:982.16 label="ver:982.16"} Though symmetrically coordinate with the isotropic vector matrix, none of the co-occurring cube’s edges is congruent with the most economical energy-event lines of the isotropic vector matrix; that is, the cube is constantly askew to the most economic energy-control lines of the cosmic-event matrix.
[982.20]{style="color: purple3"} []{#ver:982.20 label="ver:982.20"} Starting With Parts: The Nonradial Line: Since humanity started with parallel lines, planes, and cubes, it also adopted the edge line of the square and cube as the prime unit of mensuration. This inaugurated geomathematical exploration and analysis with a part of the whole, in contradistinction to synergetics’ inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimentally verifiable information. Though life started with whole Universe, humans happened to pick one partthe line, which was so short a section of Earth arc (and the Earth’s diameter so relatively great) that they assumed the Earth-scratched-surface line to be straight. The particular line of geometrical reference humans picked happened not to be the line of most economical interattractive integrity. It was neither the radial line of radiation nor the radial line of gravity of spherical Earth. From this nonradial line of nature’s event field, humans developed their formulas for calculating areas and volumes of the circle and the sphere only in relation to the cube-edge lines, developing empirically the “transcendentally irrational,” ergo incommensurable, number [(),]{.smallcaps} …ad infinitum, which provided practically tolerable approximations of the dimensions of circles and spheres.
[982.21]{style="color: purple3"} []{#ver:982.21 label="ver:982.21"} Synergetics has discovered that the vectorially most economical control line of nature is in the diagonal of the cube’s face and not in its edge; that this diagonal connects two spheres of the isotropic-vector-matrix field; and that those spherical centers are congruent with the two only-diagonally-interconnected corners of the cube. Recognizing that those cube-diagonal-connected spheres are members of the closest packed, allspace-coordinating, unit radius spheres field, whose radii = 1 (unity), we see that the isotropic-vector-matrix’s field-occurring-cube’s diagonal edge has the value of 2, being the line interconnecting the centers of the two spheres, with each half of the line being the radius of one sphere, and each of the whole radii perpendicular to the same points of intersphere tangency.
[982.30]{style="color: purple3"} []{#ver:982.30 label="ver:982.30"} Diagonal of Cube as Control Length: We have learned elsewhere that the sum of the second powers of the two edges of a right triangle equals the second power of the right triangle’s hypotenuse; and since the hypotenuse of the two similar equiedged right triangles formed on the square face of the cube by the sphere-center-connecting diagonal has a value of two, its second power is four; therefore, half of that four is the second power of each of the equi-edges of the right triangle of the cube’s diagonaled face: half of four is two.
[982.31]{style="color: purple3"} []{#ver:982.31 label="ver:982.31"} The square root of , ergo, the length of each of the cube’s edges is 1.414214. The \/~2 happens to be one of those extraordinary relationships of Universe discovered by mathematics. The relationship is: the number one is to the second root of two as the second root of two is to two: 1 : V 2 = V 2 : 2, which, solved, reads out as
[982.32]{style="color: purple3"} []{#ver:982.32 label="ver:982.32"} The cube formed by a uniform width, breadth, and height of V 2 is V 23, which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428.
[982.33]{style="color: purple3"} []{#ver:982.33 label="ver:982.33"} This is exploratorily noteworthy because this cube, when calculated in terms of man’s conventional mensuration techniques, would have had a volume of one, being the first cube to appear in the omni-geometry-coordinate isotropic vector matrix; its edge length would have been identified as the prime dimensional input with an obvious length value of oneergo, its volume would be one: 1X1X1 = 1. Conventionally calculated, this cube with a volume of one, and an edge length of one, would have had a face diagonal length of V 2 , which equals 1.414214. Obviously, the use of the diagonal of the cube’s face as the control length results in a much higher volume than when conventionally evaluated.
[982.40]{style="color: purple3"} []{#ver:982.40 label="ver:982.40"} Tetrahedron and Synergetics Constant: And now comes the big surprise, for we find that the cube as coordinately reoccurring in the isotropic vector matrix as most economically structured by naturehas a volume of three in synergetics’ vector-edged, structural-system-evaluated geometry, wherein the basic structural system of Universe, the tetrahedron, has a volume of one.
[982.41]{style="color: purple3"} []{#ver:982.41 label="ver:982.41"} necklace-edged cube has no structural integrity. tension-linked, edge-strutted cube collapses.
[982.42]{style="color: purple3"} []{#ver:982.42 label="ver:982.42"} To have its cubical conformation structurally (triangulated) guaranteed (see Secs. 615 and 740), the regular equiangled tetrahedron must be inserted into the cube, with the tetrahedron’s six edges congruent with each of the six vacant but omnitriangulatable diagonals of the cube’s six square faces.
[982.43]{style="color: purple3"} []{#ver:982.43 label="ver:982.43"} As we learn elsewhere (Secs. 415.22 and 990), the tetrahedron is not only the basic structural system of Universe, ergo, of synergetic geometry, but it is also the quantum of nuclear physics and is, ipso facto, exclusively identifiable as the unit of volume; ergo, tetrahedron volume equals one. We also learned in the sections referred to above that the volume of the octahedron is exactly four when the volume of the tetrahedron of the unit-vector edges of the isotropic-vector-matrix edge is one, and that four Eighth- Octahedra are asymmetrical tetrahedra with an equiangular triangular base, three apex angles of 90 degrees, and six lower-corner angles of 45 degrees each; each of the 1/8th octahedron’s asymmetric tetrahedra has a volumetric value of one-half unity (the regular tetrahedron). When four of the Eighth-Octahedrons are equiangle-face added to the equiangled, equiedged faces of the tetrahedra, they produce the minimum cube, which, having the tetrahedron at its heart with a volume of one, has in addition four one-half unity volumed Eighth-Octahedra, which add two volumetric units on its corners. Therefore, the volume of the cube. The cube is volume three where the tetrahedron’s volume is one, and the octahedron’s volume is four, and the cube’s diagonally structured faces have a diagonal length of one basic system vector of the isotropic vector matrix. (See Illus. 463.01.)
[982.44]{style="color: purple3"} []{#ver:982.44 label="ver:982.44"} Therefore the edge of the cube = V Va \sfrac{1}{2}.
[982.45]{style="color: purple3"} []{#ver:982.45 label="ver:982.45"} turns out in energetic reality to have a conventionally calculated volume of 2.828428, but this same cube in the relative-energy volume hierarchy of synergetics has a volume of 3.
Humanity’s conventional mensuration cube with a volume of one
3
- =1.06066
2.828428
[982.46]{style="color: purple3"} []{#ver:982.46 label="ver:982.46"} To correct 2.828428 to read 3, we multiply 2.828428 by the synergetics conversion constant . (See Chart 963.10.)
[982.47]{style="color: purple3"} []{#ver:982.47 label="ver:982.47"} Next we discover, as the charts at Secs. 963.10 and 223.64 show, that of the inventory of well-known symmetrical polyhedra of geometry, all but the cube have irrational values as calculated in the rectilinear-coordinate system “cubism” is a convenient termin which the cube’s edge and volume are both given the prime mensuration initiating value of one. When, however, we multiply all these irrational values of the Platonic polyhedra by the synergetic conversion constant, 1.06066, all these values become unitarily or combinedly rational, and their low first-four-prime-number-accommodation values correspond exactly with those of the synergetic hierarchy of geometric polyhedra, based on the tetrahedron as constituting volumetric unity.
[982.48]{style="color: purple3"} []{#ver:982.48 label="ver:982.48"} All but the icosahedron and its “wife,” the pentagonal dodecahedron, prove to be volumetrically rational. However, as the tables show, the icosahedron and the vector-edged cube are combiningly rational and together have the rational value of three to the third power, i.e., 27. We speak of the pentagonal dodecahedron as the icosahedron’s wife because it simply outlines the surface-area domains of the 12 vertexes of the icosahedron by joining together the centers of area of the icosahedron’s 20 faces. When the pentagonal dodecahedron is vectorially constructed with flexible tendon joints connecting its 30 edge struts, it collapses, for, having no triangles, it has no structural integrity. This is the same behavior as that of a cube constructed in the same flexible-tendon-vertex manner. Neither the cube nor the pentagonal dodecahedron is scientifically classifiable as a structure or as a structural system (see Sec. 604).
[982.50]{style="color: purple3"} []{#ver:982.50 label="ver:982.50"} Initial Four-Dimensional Modelability: The modelability of the coordinate system is limited to rectilinear-frame-of-reference definition of all special-case experience patternings, and it is dimensionally sized by arbitrary, e.g., c.gt.s.-system, subdivisioning increments. The initial increments are taken locally along infinitely extensible lines always parallel to the three sets of rectilinearly interrelated edges of the cube. Any one of the cube’s edges may become the one-dimensional module starting reference for initiating the mensuration of experience in the conventional, elementary, energetical[^34] school curriculum.
[982.51]{style="color: purple3"} []{#ver:982.51 label="ver:982.51"} The cube has no initially moduled, vertex-defined nucleus; nor has it any inherent, common, most-economically-distanced, uniform, in-out-and-circumferentially-around, corner-cutting operational interlinkage, uniformly moduled coordinatability. Nor has it any initial, ergo inherent, time-weight-energy-(as mass charge or EMF) expressibility. Nor has it any omni-intertransformability other than that of vari-sized cubism. The exploratory coordination inherently commences differentially, i.e., with partial system consideration. Consider the three-dimensional, weightless, timeless, temperatureless volume often manifest in irrational fraction increments, the general reality impoverishments of which required the marriage of the system with the c.gt.s. system in what resembles more of an added partnership than an integration of the two.
[982.52]{style="color: purple3"} []{#ver:982.52 label="ver:982.52"} The synergetics coordinate system’s initial modelability accommodates four dimensions and is operationally developable by frequency modulation to accommodate fifth- and sixth-dimensional conceptual-model accountability. Synergetics is initially nuclear-vertexed by the vector equilibrium and has initial in-out-and-around, diagonaling, and diametrically opposite, omni-shortest-distance interconnections that accommodate commonly uniform wavilinear vectors. The synergetics system expresses divergent radiational and convergent gravitational, omnidirectional wavelength and frequency propagation in one operational field. As an initial operational vector system, its (mass x velocity) vectors possess all the unique, special-case, time, weight, energy (as mass charge or EMF) expressibilities. Synergetics’ isotropic vector matrix inherently accommodates maximally economic, omniuniform intertransformability.
[982.53]{style="color: purple3"} []{#ver:982.53 label="ver:982.53"} In the synergetics’ four-, five-, and six-dimensionally coordinate system’s operational field the linear increment modulatability and modelability is the isotropic vector matrix’s vector, with which the edges of the co-occurring tetrahedra and octahedra are omnicongruent; while only the face diagonalsand not the edgesof the inherently co-occurring cubes are congruent with the matrix vectors. Synergetics’ exploratory coordination inherently commences integrally, i.e., with whole-systems consideration. Consider the one-dimensional linear values derived from the initially stated whole system, six-dimensional, omnirational unity; any linear value therefrom derived can be holistically attuned by unlimited frequency and one-to-one, coordinated, wavelength modulatability. To convert the system’s cubical values to the synergetics’ values, the mathematical constants are linearly derived from the mathematical ratios existing between the tetrahedron’s edges and the cube’s corner-to-opposite-corner distance relationships; while the planar area relationships are derived from the mathematical ratios existing between cubical-edged square areas and cubical-face-diagonaled-edged triangular areas; and the volumetric value mathematical relationships are derived from ratios existing between (a) the cube-edge-referenced third power of the often odd-fractionededge measurements (metric or inches) of cubically shaped volumes and (b) the cube-face-diagonal-vector-referenced third power of exclusively whole number vector, frequency modulated, tetrahedrally shaped volumes. (See Sec. 463 and 464 for exposition of the diagonal of the cube as a wave-propagation model.)
[982.54]{style="color: purple3"} []{#ver:982.54 label="ver:982.54"} The mathematical constants for conversion of the linear, areal, and volumetric values of the system to those of the synergetics system derive from the synergetics constant (1.060660). (See Sec. 963.10 and Chart 963.12.) The conversion constants are as follows:
-
First Dimension: The first dimensional cube-edge-to-cube-face- diagonal vector conversion constant from to synergetics is as 1:1.060660.
-
Second Dimension: The two-dimensional linear input of vector vs. cube-edged referenced, triangular vs. square area product identity is 1.0606602 = 1.125 = 1 Vath = 9/sths. The second-power value of the vector, 9/s, is in one-to-one correspondence with “congruence in modulo nine” arithmetic (see Secs. 1221.18 and 1221.20); ergo is congruent with wave-quanta modulation (see Secs. 1222 and 1223).
-
Third Dimension: The three-dimensional of the cube-edge vs. vector-edged tetrahedron vs. cube volumetric identity is 1.0606603= 1.192.
[982.55]{style="color: purple3"} []{#ver:982.55 label="ver:982.55"} To establish a numerical value for the sphere, we must employ the synergetics constant for cubical third-power volumetric value conversion of the vector equilibrium with the sphere of radius 1. Taking the vector equilibrium at the initial phase (zero frequency, which is unity-two diameter: ergo unity-one radius) with the sphere of radius 1; i.e., with the external vertexes of the vector equilibrium congruent with the surface of the sphere = Vs pi [(tt)]{.smallcaps} multiplied by the third power of the radius. Radius =1. 13 = 1. 1 x 1.333x3.14159 = 4.188. 4.188 times synergetics third-power constant 1.192 = 5 = volume of the sphere. The volume of the radius 1 vector equilibrium = 2.5. sphere = 2 .
[982.56]{style="color: purple3"} []{#ver:982.56 label="ver:982.56"} We can assume that when the sphere radius is 1 (the same as the nuclear vector equilibrium) the Basic Disequilibrium 120 tetrahedral components of mild off-sizing are also truly of the same volumetric quanta value as the and Quanta Modules; they would be shortened in overall greatest length while being fractionally fattened at their smallest-triangular-face end, i.e., at the outer spherical surface end of the 120 asymmetric tetrahedra. This uniform volume can be maintained (as we have seen in Sec. 961.40).
[982.57]{style="color: purple3"} []{#ver:982.57 label="ver:982.57"} Because of the fundamental 120-module identity of the nuclear sphere of radius 1 (F = 0), we may now identify the spherical icosahedron of radius 1 as five; or as 40 when frequency is 2F2. Since 40 is also the volume of the 2 vector-equilibrium-vertexes-congruent sphere, the unaberrated vector equilibrium F2 = 20 (i.e., 8 x 2V2 nuclear-sphere’s inscribed vector equilibrium). We may thus assume that the spherical icosahedron also subsides by loss of half its volume to a size at which its volume is also 20, as has been manifested by its prime number five, indistinguishable from the vector equilibrium in all of its topological hierarchies characteristics.
[982.58]{style="color: purple3"} []{#ver:982.58 label="ver:982.58"} Neither the planar-faceted exterior edges of the icosahedron nor its radius remain the same as that of the vector equilibrium, which, in transforming from the vector equilibrium conformation to the icosahedral stateas witnessed in the jitterbugging (see Sec. 465)did so by transforming its outer edge lengths as well as its radius. This phenomenon could be analagous the disappearance of the nuclear sphere, which is apparently permitted by the export of its volume equally to the 12 surrounding spheres whose increased diameters would occasion the increased sizing of the icosahedron to maintain the volume 20-ness of the vector equilibrium. This supports the working assumption that the 120 LCD asymmetric tetrahedral volumes are quantitatively equal to the or Quanta Modules, being only a mild variation of shape. This effect is confirmed by the discovery that 15 of the 120 Spherical Triangles equally and interiorly subdivide each of the eight spherical octahedron’s triangular surfaces, which spherical octahedron is described by the three-great-circle set of the 25 great circles of the spherical vector equilibrium. (See drawings section.)
[982.59]{style="color: purple3"} []{#ver:982.59 label="ver:982.59"} We may also assume that the pentagonal-faced dodecahedron, which is developed on exactly the same spherical icosahedron, is also another transformation of the same module quantation as that of the icosahedron’s and the vector equilibrium’s prime number five topological identity.
[982.60]{style="color: purple3"} []{#ver:982.60 label="ver:982.60"} Without any further developmental use of () we may now state in relation to the isotropic vector matrix synergetic system, that:
The volume of the sphere is a priori always quantitatively:
extemdash 5F3 as volumetrically referenced to the regular tetrahedron (as volume = 1); or
120F3 as referenced to the and Quanta Modules.
[982.61]{style="color: purple3"} []{#ver:982.61 label="ver:982.61"} There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres, each of a tetra volume of five; i.e., of 120 and Quanta Modules omniembracing our hierarchy of nuclear event patternings. See Illus. 982.61 in the color section, which depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order whole number, equilibrious state of the micro-macro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially-rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualizable only in its equilibrious state.
[982.61A]{style="color: purple3"} []{#ver:982.61A label="ver:982.61A"} Cosmic Hierarchy of Omnidirectionally-phased Nuclear-centered, Convergently-divergently Intertransformable Systems. There is realized herewith a succession of concentric, 12-around-one, closest packed spheres omniembracing our hierarchy of nuclear event patternings. The synergetics poster in color plate 9 depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order-whole-number, equilib rious state of the macro-micro cosmic limits of nuclearly unique, symmetri cal morphological relativity in their interquantation, intertransformative, inter transactive, expansive-contractive, axially rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualized only in its equilibrious state.
982.62A Table of Concentric, 12-around-one, Closest-packed Spheres Omniembracing Our Hierarchy of Nuclear Event Patternings (Revised):
+:------------------------------+:---------------+:---------------------------+
| Symmetrical Form | Tetravolumes | A and Quanta Modules |
+-------------------------------+----------------+----------------------------+
| F Tetrahedron | | ::: minipage |
| | | > 24 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F Vector equilibrium | | ::: minipage |
| | | > 60 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F Double-Tet cube | | ::: minipage |
| | | > 72 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F Octahedron | | ::: minipage |
| | | > 96 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F Rhombic triacontahedron* | + | ::: minipage |
| | | > 120 + |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F Rhombic dodecahedron | | ::: minipage |
| | | > 144 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F2 Vector equilibrium | | ::: minipage |
| | | > 480 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
| F2 Double-Tet cube | | ::: minipage |
| | | > 576 |
| | | ::: |
+-------------------------------+----------------+----------------------------+
* The spheric spin domain of the rhombic triacontahedron “sphere.”
[982.63]{style="color: purple3"} []{#ver:982.63 label="ver:982.63"} Sphere and Vector Equilibrium: Sphere = vector equilibrium in combined four-dimensional orbit and axial spin. Its 12 vertexes describing six great circles and six axes. All 25 great circles circling while spinning on one axis produce a spin-profiling of a superficially perfect sphere.
[982.64]{style="color: purple3"} []{#ver:982.64 label="ver:982.64"} The vector equilibrium also has 25 great circles (see Sec. 450.10), of which 12 circles have 12 axes of spin, four great circles have four axes of spin, six great circles have six axes of spin, and three great circles have three axes of spin.
[982.65]{style="color: purple3"} []{#ver:982.65 label="ver:982.65"} Vector equilibrium = sphere at equilibrious, ergo zero energized, ergo unorbited and unspun state.
[982.70]{style="color: purple3"} []{#ver:982.70 label="ver:982.70"} Hierarchy of Concentric Symmetrical Geometries: It being experimentally demonstrable that the number of and Quanta Modules per tetrahedron is 24 (see Sec. 942.10); that the number of quanta modules of all the symmetric polyhedra congruently co-occurring within the isotropic vector matrix is always 24 times their whole regular-tetrahedral-volume values; that we find the volume of the nuclear sphere to be five (it has a volumetric equivalence of 120 and Quanta Modules); that the common prime number five topological and quanta-module value identifies both the vector equilibrium and icosahedron (despite their exclusively unique morphologiessee Sec. 905, especially 905.55 ); that the icosahedron is one of the three-and-only prime structural systems of Universe (see Secs. 610.20 and 1011.30) while the vector equilibrium is unstablebecause equilibriousand is not a structure; that their quanta modules are of equal value though dissimilar in shape; and that though the vector equilibrium may be allspace-fillingly associated with tetrahedra and octahedra, the icosahedron can never be allspace-fillingly compounded either with itself nor with any other polyhedron: these considerations all suggest the relationship of the neutron and the proton for, as with the latter, the icosahedron and vector equilibrium are interexchangingly transformable through their common spherical-state omnicongruence, quantitatively as well as morphologically.
[982.71]{style="color: purple3"} []{#ver:982.71 label="ver:982.71"} The significance of this unified field as defining and embracing the minimum-maximum limits of the inherent nuclear domain limits is demonstrated by the nucleus-concentric, symmetrical, geometrical hierarchy wherein the rhombic dodecahedron represents the smallest, omnisymmetrical, selfpacking, allspace-filling, six-tetra-volume, uniquely exclusive, cosmic domain of each and every closest-packed, unit-radius sphere. Any of the closest-packed, unit-radius spheres, when surrounded in closest packing by 12 other such spheres, becomes the nuclear sphere, to become uniquely embraced by four successive layers of surrounding, closest-packed, unit-radius sphereseach of which four layers is uniquely related to that nucleuswith each additional layer beyond four becoming duplicatingly repetitive of the pattern of unique surroundment of the originally unique, first four, concentric-layered, nuclear set. It is impressive that the unique nuclear domain of the rhombic dodecahedron with a volume of six contains within itself and in nuclear concentric array:
the unity-one-radiused sphere of volume five;
the octahedron of volume four;
the cube of volume three;
the prime vector equilibrium of volume 21/z; and
the two regular (positive and negative) tetrahedra of volume one each. This succession of rational volume relationships embraces the first four prime numbers 1, 2, 3, and 5. (See Illus. 982.61 in color section.) The volume-24 (tetra) cube is the largest omni symmetrical self-packing, allspace-filling polyhedron that exactly identifies the unique domain of the original 12-around-one, nuclear-initiating, closest packing of unit-radius spheres. The unit quantum leap of 1going to 2going to 3 going to 4going to 5going to 6, with no step greater than 1, suggests a unique relationship of this set of six with the sixness of degrees of freedom[^35].
[982.72]{style="color: purple3"} []{#ver:982.72 label="ver:982.72"} The domain limits of the hierarchy of concentric, symmetrical geometries also suggests the synergetic surprise of two balls having only one interrelationship; while three balls have threeeasily predictable relationships; whereas the simplest, ergo prime, structural system of Universe defined exclusively by four balls has an unpredictable (based on previous experience) sixness of fundamental interrelationships represented by the six edge vectors of the tetrahedron.
[982.73]{style="color: purple3"} []{#ver:982.73 label="ver:982.73"} The one-quantum “leap” is also manifest when one vector edge of the volume 4 octahedron is rotated 90 degrees by disconnecting two of its ends and reconnecting them with the next set of vertexes occurring at 90 degrees from the previously interconnected-with vertexes, transforming the same unit-length, 12-vector structuring from the octahedron to the first three-triple-bonded-together (face-to-face) tetrahedra of the tetrahelix of the DNA-RNA formulation. One 90-degree vector reorientation in the complex alters the volume from exactly 4 to exactly 3. This relationship of one quantum disappearance coincident to the transformation of the nuclear symmetrical octahedron into the asymmetrical initiation of the DNA-RNA helix is a reminder of the disappearing-quanta behavior of the always integrally end-cohered jitterbugging transformational stages from the 20 tetrahedral volumes of the vector equilibrium to the octahedron’s 4 and thence to the tetrahedron’s 1 volume. All of these stages are rationally concentric in our unified operational field of 12-around-one closest-packed spheres that is only conceptual as equilibrious. We note also that per each sphere space between closest-packed spheres is a volume of exactly one tetrahedron: .
[982.80]{style="color: purple3"} []{#ver:982.80 label="ver:982.80"} Closest Packing of Circles: Because we may now give the dimensions of any sphere as 5 Fn, we have no need for in developing spheres holistically. According to our exploratory strategy, however, we may devise one great circle of one sphere of unit rational value, and, assuming our circle also to be rational and a whole number, we may learn what the mathematical relationship to may belengthwiseof our a priori circle as a whole part of a whole sphere. We know that is the length of a circle as expressed in the diameters of the circle, a relationship that holds always to the transcendentally irrational number 3.14159. But the relationship of volume 5 to the radius of one of our spheres is not altered by the circumference-to-diameter relationship because we commence with the omnidimensional wholeness of reality.
[982.81]{style="color: purple3"} []{#ver:982.81 label="ver:982.81"} We recall also that both Newton and Leibnitz in evolving the calculus thought in terms of a circle as consisting of an infinite number of short chords. We are therefore only modifying their thinking to accommodate the manifest discontinuity of all physical phenomena as described by modem physics when we explore the concept of a circle as an aggregate of short event-vectors tangents (instead of Newtonian short chords) whose tangential overall length must be greater than that of the circumference of the theoretical circle inscribed within those tangent event-vectors-just as Newton’s chords were shorter than the circle encompassing them.
[982.82]{style="color: purple3"} []{#ver:982.82 label="ver:982.82"} If this is logical, experimentally informed thinking, we can also consider the closest-tangential-packing of circles on a plane that produces a non-all-area-filling pattern with concave triangles occurring between the circles. Supposing we allowed the perimeters of the circles to yield bendingly outward from the circular centers and we crowded the circles together while keeping themselves as omni-integrally, symmetrically, and aggregatedly together, interpatterned on the plane with their areal centers always equidistantly apart; we would find then as floor-tile makers learned long agothat when closest packed with perimeters congruent, they would take on any one of three and only three possible polygonal shapes: the hexagon, the square, or the triangleclosest-packed hexagons, whose perimeters are exactly three times their diameters. Hexagons are, of course, cross sections through the vector equilibrium. The hexagon’s six radial vectors exactly equal the six chordal sections of its perimeter.
[982.83]{style="color: purple3"} []{#ver:982.83 label="ver:982.83"} Assuming the vector equilibrium hexagon to be the relaxed, cosmic, neutral, zero energy-events state, we will have the flexible but not stretchable hexagonal perimeter spun rapidly so that all of its chords are centrifugally expelled into arcs and the whole perimeter becomes a circle with its radius necessarily contracted to allow for the bending of the chords. It is this circle with its perimeter equalling six that we will now convert, first into a square of perimeter six and then into a triangle of perimeter six with the following results:
Circle radius 0.954930 perimeter 6
Hexagon radius 1.000000 perimeter 6 (neutral)
Square radius 1.060660 perimeter 6
Triangle radius 1.1546 perimeter 6
(In the case of the square, the radius is taken from the center to the corner, not the edge. In the triangle the radius is taken to the corner, not the edge.) We take particular note that the radius of the square phase of the closest-packed circle is 1.060660, the synergetics constant.
[982.84]{style="color: purple3"} []{#ver:982.84 label="ver:982.84"} In accomplishing these transformations of the uniformly-perimetered symmetrical shapes, it is also of significance that the area of six equiangular, uniform-edged triangles is reduced to four such triangles. Therefore, it would take more equiperimeter triangular tiles or squares to pave a given large floor area than it would using equiperimetered hexagons. We thus discover that the hexagon becomes in fact the densest-packed patterning of the circles; as did the rhombic dodecahedron become the minimal limit case of self-packing allspace-filling in isometric domain form in the synergetical from-whole-to-particular strategy of discovery; while the rhombic dodecahedron is the six-dimensional state of omni-densest-packed, nuclear field domains; as did the two-frequency cube become the maximum subfrequency self-packing, allspace-filling symmetrical domain, nuclear-uniqueness, expandability and omni-intertransformable, intersymmetrical, polyhedral evolvement field; as did the limit-of-nuclear-uniqueness, minimally at three-frequency complexity, self-packing, allspace-filling, semi-asymmetric octahedron of Critchlow; and maximally by the three-frequency, four-dimensional, self-packing, allspace-filling tetrakaidecahedron: these two, together with the cube and the rhombic dodecahedron constitute the only-four-is-the-limit-system set of self-packing, allspace-filling, symmetrical polyhedra. These symmetrical realizations approach a neatness of cosmic order.
¶ 983.00 Spheres and Interstitial Spaces
[983.01]{style="color: purple3"} []{#ver:983.01 label="ver:983.01"} Frequency: In synergetics, =
either, frequency of modular subdivision of one radius;
or, frequency of modular subdivision of one outer chord of a hexagonal equator plane of the vector equilibrium. Thus,F = r, radius; orF Ch, Chord.
[983.02]{style="color: purple3"} []{#ver:983.02 label="ver:983.02"} Sphere Layers: The numbers of separate spheres in each outer layer of concentric spherical layers of the vector equilibrium grows at a rate:
= 10r2 + 2, or .
[983.03]{style="color: purple3"} []{#ver:983.03 label="ver:983.03"} Whereas the space between any two concentrically parallel vector equilibria whose concentric outer planar surfaces are defined by the spheric
* centers of any two concentric sphere layers, is always 10 (2+12 -), or 10 (2+ 122~ F).
[983.04]{style="color: purple3"} []{#ver:983.04 label="ver:983.04"} The difference is the nonsphere interstitial space occurring uniformly between the closest-packed spheres, which is always tetrahedron.
¶ 984.00 Rhombic Dodecahedron
[984.10]{style="color: purple3"} []{#ver:984.10 label="ver:984.10"} The rhombic dodecahedron is symmetrically at the heart of the vector equilibrium. The vector equilibrium is the ever-regenerative, palpitatable heart of all the omniresonant physical-energy hearts of Universe.
¶ 985.00 Synergetics Rational Constant Formulas for Area of a Circle and Area and Volume of a Sphere
[985.01]{style="color: purple3"} []{#ver:985.01 label="ver:985.01"} We employ the synergetics constant, “,” for correcting the cubical coordinate inputs to the tetrahedral inputs of synergetics:
We learn that the sphere of radius 1 has a “cubical” volume of 4.188; corrected for tetrahedral value we have 4.188 X 1.193 =4.996 = 5 tetrahedra= 1 sphere. Applying the to the area of a circle of radius 1, (pi = 3.14159) 3.14159 x 1.125 = 3.534 for the corrected “square” area.
[985.02]{style="color: purple3"} []{#ver:985.02 label="ver:985.02"} We may also employ the to synergetics conversion factors between commonly based squares and equiangled triangles: from a square to a triangle the factor is 2.3094; from a triangle to a square the factor is . The constant ; thus 774 triangles equal the area of a circle of radius 1. Since the circle of a sphere equals exactly four circular areas of the same radius, area of the surface of a sphere of radius 1.
[985.03]{style="color: purple3"} []{#ver:985.03 label="ver:985.03"} The area of a hexagon of radius 1 shows the hexagon with its vertexes lying equidistantly from one another in the circle of radius 1 and since the radii and chords of a hexagon are equal, then the six equilateral triangles in the hexagon plus 1\sfrac{1}{4} such triangles in the arc-chord zones equal the area of the circle: zone arc-chord area. Wherefore the area of a circle of frequency triangles and the surface of a sphere of radius equilateral triangles.
[985.04]{style="color: purple3"} []{#ver:985.04 label="ver:985.04"} For the 120 spherical triangles 5 = 4; =4 for four great-circle areas of the surface of a sphere; therefore for one great-circle area equals exactly one spherical triangle, since 120Ai = 30 spherical triangles vs. 116/4 = 29 equilateral triangles. The disparity of 1 is between a right spherical triangle and a planar equiangular triangle. Each of the 120 spherical triangles has exactly six degrees of spherical excess, their three corners being 90 degrees, 60 degrees and 36 degrees vs. 90 degrees, 60 degrees, 30 degrees of their corresponding planar triangle. Therefore, 6 degrees per each spherical triangle times 120 spherical triangles amounts to a total of 720 degrees spherical excess, which equals exactly one tetrahedron, which exact excessiveness elucidates and elegantly agrees with previous discoveries (see Secs. 224.07, 224.10, and 224.20).
[985.05]{style="color: purple3"} []{#ver:985.05 label="ver:985.05"} The synergetical definition of an operational sphere (vs. that of the Greeks) finds the spheric experience to be operationally always a star-point-vertexed polyhedron, and there is always a 720 degree (one tetrahedron) excess of the Greek’s sphere’s assumption of 360 degrees around each vertex vs. the operational sum of the external angles of any system, whether it be the very highest frequency (seemingly “pure” spherical) regular polyhedral system experience of the high-frequency geodesic spheres, or irregular giraffe’s or crocodile’s chordally-interconnected, outermost-skin-points-defined, polyhedral, surface facets’ corner-angle summation.
[985.06]{style="color: purple3"} []{#ver:985.06 label="ver:985.06"} Thus it become clear that is the difference between the infinite frequency series’ perfect nuclear sphere of volume 5 and 120 quanta modules, and the four-whole-great-circle surface area of 116 equilateral triangles, which has an exact spherical excess of 720 degrees = one tetrahedron, the difference between the 120 spherical triangles and the 120 equilateral triangles of the 120-equiplanar-faceted polyhedron.
[985.07]{style="color: purple3"} []{#ver:985.07 label="ver:985.07"} This is one more case of the one tetrahedron : one quantum jump involved between various stages of nuclear domain intertransformations, all the way from the difference between integral-finite, nonsimultaneous, scenario Universe, which is inherently nonunitarily conceptual, and the maximumminimum, conceptually thinkable, systemic subdivision of Universe into an omnirelevantly frequenced, tunable set which is always one positive tetrahedron (macro) and one negative tetrahedron (micro) less than Universe: the definitive conceptual vs. finite nonunitarily conceptual Universe (see Secs. 501.10 and 620.01).
[985.08]{style="color: purple3"} []{#ver:985.08 label="ver:985.08"} The difference of one between the spheric domain of the rhombic dodecahedron’s six and the nuclear sphere’s five or between the tetra volume of the octahedron and the three-tetra sections of the tetrahelixthese are the prime wave pulsation propagating quanta phenomena that account for local aberrations, twinkle angles, and unzipping angles manifest elsewhere and frequently in this book.
[985.10]{style="color: purple3"} []{#ver:985.10 label="ver:985.10"} Table: Triangular Area of a Circle of Radius 1
F 1 = Zero-one frequency = 774.
Table of whole triangles only with = Even N, which is because Even N = closed wave circuit.
$pN$
Open X
Close X
Open X (63 + 274)
Close X (112 + 4) (also surface of one sphere)
Open X (175 + 674)
Close X (252 + 9)
[985.20]{style="color: purple3"} []{#ver:985.20 label="ver:985.20"} Spheric Experience: Experientially defined, the spheric experience, i.e., a sphere, is an aggregate of critical-proximity event “points.” Points are a multidimensional set of crossings of orbits: traceries, foci, fixes, vertexes coming cometlike almost within intertouchability and vertexing within cosmically remote regions. Each point consists of three or more vectorially convergent events approximately equidistant from one approximately locatable and as yet nondifferentially resolved, point; i.e., three or more visualizable, four-dimensional vectors’ most critical proximity, convergently-divergently interpassing region, local, locus, terminal and macrocosmically the most complex of such point events are the celestial stars; i.e., the highest-speed, high-frequency energy event, importing-exporting exchange centers. Microcosmically the atoms are the inbound terminals of such omniorderly exchange systems.
[985.21]{style="color: purple3"} []{#ver:985.21 label="ver:985.21"} Spheres are further cognizable as vertexial, star-point-defined, polyhedral, constellar systems structurally and locally subdividing Universe into insideness and outsideness, macrocosm-macrocosm.
[985.22]{style="color: purple3"} []{#ver:985.22 label="ver:985.22"} Physically, spheres are high-frequency event arrays whose spheric complexity and polyhedral system unity consist structurally of discontinuously islanded, critical-proximity-event huddles, compressionally convergent events, only tensionally and omni-interattractively cohered. The pattern integrities of all spheres are the high-frequency, traffic-described subdivisionings of either tetrahedral, octahedral, or icosahedral angular interference, intertriangulating structures profiling one, many, or all of their respective great-circle orbiting and spinning event characteristics. All spheres are high-frequency geodesic spheres, i.e., triangular-faceted polyhedra, most frequently icosahedral because the icosasphere is the structurally most economical.
¶ 986.00 and Quanta Modules: Structural Model of : The Discovery that the Quanta Module Is the True, Experimentally Evidenceable Model of E = mc^
*[986.00-986.874 Demass Model Scenario][]
¶ 986.010 Narrative Recapitulation
[986.011]{style="color: purple3"} []{#ver:986.011 label="ver:986.011"} The exposition herein recounts and recapitulates the original surprise and excitement of the progressive, empirically verified conceptionings; the family of relevant experimental-evidence recalls; the modus operandi; the successive, only-evolutionarily-discovered inputs; and the synergetic comprehension of the omniinterresultant cosmic significance of these strategically employable, synergetically critical additions to human knowledge and their technologically realizable insights.
¶ 986.020 Elementary School Definitions
[986.021]{style="color: purple3"} []{#ver:986.021 label="ver:986.021"} My first mathematics and geometry teachers taught me games that I learned to play well enough to obtain swiftly the answers for which their (only-axiomatically-argued) assumptions called. Webster’s dictionary states tersely the definitions of the games they taught me. Webster’s definitions are carefully formulated by leading academic authorities and represent the up-to-the-minute concensus of what the educational system assumes geometry, mathematics, and science to consist.
[986.022]{style="color: purple3"} []{#ver:986.022 label="ver:986.022"} Webster defines geometry as “the mathematics of the properties, measurements, and relationships of points, lines, angles, surfaces, and solids” none of which we ourselves observe can exist experientially (ergo, science-verifiably), independently of the others; ergo, they cannot be isolatable “properties” or separate characteristics.
[986.023]{style="color: purple3"} []{#ver:986.023 label="ver:986.023"} Physics has found no surfaces and no solids; only localized regions of high-frequency, self-interfering, deflecting, and consequently self-knotting energy events. These self-interference patterns occur in pure principle of ultra-high-frequency intervals and on so minuscule a scale as to prohibit intrusion by anything so dimensionally gross and slow as our fingers. We cannot put our fingers between any two of all the numbers occurring serially between the integer 1 and the integer 2,000,000,000,000 two trillionas aggregated linearly in one inch. This is the approximate number of atomic domains (the x-illion-per-second, electron-orbited atoms’ individual spinout domains) tangentially arrayable in a row within an experience inch.
[986.024]{style="color: purple3"} []{#ver:986.024 label="ver:986.024"} Within each of the electron-orbited spheric domains the respective atomic nuclei are centered as remotely distant from their orbiting electrons as is our Sun from its orbiting planets. Within each of these nuclei complex, high-frequency events are occurring in pure principle of interrelationship.
[986.025]{style="color: purple3"} []{#ver:986.025 label="ver:986.025"} How do you see through a solid-glass window? Light passes through glass. Light is high-frequency radiation passing unobstructedly at 700 million miles per hour with lots of time and room “to spare” between the set of energy events that constitute the atomic-event constellation known as “glass.” (In lenses the light caroms off atoms to have its course deliberately and angularly altered.)
[986.026]{style="color: purple3"} []{#ver:986.026 label="ver:986.026"} Webster’s definition of mathematics is “the science of dealing with quanitites, forms, etc., and their relationships by the use of numbers and symbols.”
[986.027]{style="color: purple3"} []{#ver:986.027 label="ver:986.027"} Webster defines science as “systematized knowledge derived from observation and study. ”
[986.028]{style="color: purple3"} []{#ver:986.028 label="ver:986.028"} In respect to those definitions I was taught, between 1905 and 1913 at the private preparatory school then most highly regarded by Harvard, that “the properties of a point” are nonexistentthat a point is nondimensional or infradimensional, weightless, and timeless. The teacher had opened the day’s lesson by making a white chalk mark on the cleanly washed-off blackboard and saying, “This is a point.” I was next taught that a line is one-dimensional and consists of a “straight” row of non-dimensional pointsand I am informed that today, in 1978, all schoolchildren around the world are as yet being so taught. Since such a line lacks three-dimensionality, it too is nonexistent to the second power or to “the square root of nonexistence.” We were told by our mathematics teacher that the plane is a raft of tangentially parallel rows of nonexistent linesergo, either a third power or a “cube root of nonexistence”while the supposedly “real” cube of three dimensions is a rectilinear stack of those nonexistent planes and therefore must be either a fourth power or a fourth root of nonexistence. Since the cube lacked weight, temperature, or duration in time, and since its empty 12-edged frame of nonexistent lines would not hold its shape, it was preposterously nondemonstrable ergo, a treacherous device for students and useful only in playing the game of deliberate self-deception. Since it was arbitrarily compounded of avowedly nonexistent points, the socially accepted three-dimensional reality of the academic system was not “derived from observation and study”ergo, was to me utterly unscientific.
¶ 986.030 Abstraction
[986.031]{style="color: purple3"} []{#ver:986.031 label="ver:986.031"} The scientific generalized eternal principle of leverage can be experientially demonstrated, and its rate of lifting-advantage-gain per each additional modular increment of lifting-arm length can be mathematically expressed to cover any and all special case temporal realizations of the leverage principle. Biological species can be likewise generalizingly defined. So in many ways humanity has been able to sort out its experiences and identify various prominent sets and subsets of interrelationship principles. The special-case “oriole on the branch of that tree over there,” the set of all the orioles, the class of all birds, the class of all somethings, the class of all anythingsany one of which anythings is known as …that life’s experiences lead to the common discovery of readily recognized, differentiated, and remembered generalizable sets of constantly manifest residual interrelationship principlesswiftly persuaded mathematical thinkers to adopt the symbolism of algebra, whose known and unknown components and their relationships could be identified by conveniently chosen empty-set symbols. The intellectuals call this abstraction.
[986.032]{style="color: purple3"} []{#ver:986.032 label="ver:986.032"} Abstraction led to the discovery of a generalized family of plus- and-minus interrelationship phenomena, and these generalized interrelationships came to be expressed as ratios and equations whose intermultiplicative, divisible, additive, or subtractive results couldor mightbe experimentally (objectively) or experientially (subjectively) verified in substantive special case interquantation relationships.
¶ 986.040 Greek Geometry
[986.041]{style="color: purple3"} []{#ver:986.041 label="ver:986.041"} It was a very different matter, however, when in supposed scientific integrity mathematicians undertook to abstract the geometry of structural phenomena. They began their geometrical science by employing only three independent systems: one supposedly “straight”-edged ruler, one scribing tool, and one pair of adjustable-angle dividers.
[986.042]{style="color: purple3"} []{#ver:986.042 label="ver:986.042"} Realistically unaware that they were on a spherical planet, the Greek geometers were first preoccupied with only plane geometry. These Greek plane geometers failed to recognize and identify the equally important individual integrity of the system upon whose invisibly structured surface they were scribing. The Euclidean mathematicians had a geocentric fixation and were oblivious to any concept of our planet as an includable item in their tool inventory. They were also either ignorant ofor deliberately overlooked the systematically associative minimal complex of inter-self-stabilizing forces (vectors) operative in structuring any system (let alone our planet) and of the corresponding cosmic forces (vectors) acting locally upon a structural system. These forces must be locally coped with to insure the local system’s structural integrity, which experientially demonstrable force-interaction requirements are accomplishable only by scientific intertriangulations of the force vectors. Their assumption that a square or a cube could hold its own structural shape proves their oblivousness to the force (vector) interpatternings of all structurally stable systems in Universe. To them, structures were made only of stone wallsand stone held its own shape.
[986.043]{style="color: purple3"} []{#ver:986.043 label="ver:986.043"} The Ionian Greeks seem to have been self-deceived into accepting as an absolute continuum the surface of what also seemed to them to be absolutely solid items of their experiencewhether as randomly fractured, eroded, or ground-apart solids or as humanly carved or molded symmetrical shapes. The Ionian Greeks did not challenge the self-evident axiomatic solid integrity of their superficial-continuum, surface-face-area assumptions by such thoughts as those of the somewhat later, brilliantly intuitive, scientific speculation of Democritus, which held that matter might consist of a vast number of invisible minimum somethingsto which he gave the name “atoms.” All of the Euclidean geometry was based upon axioms rather than upon experimentally redemonstrable principles of physical behavior.
[986.044]{style="color: purple3"} []{#ver:986.044 label="ver:986.044"} Webster’s dictionary defines axiom (etymologically from the Greek “to think worthy”) as (1) a maxim widely accepted on its intrinsic merit, and (2) a proposition regarded as self-evident truth. The dictionary defines maxim as (1) a general truth, fundamental principle, or rule of conduct, and (2) a saying of a proverbial nature. Maxim and maximum possibly integratingly evolved as “the most important axiom.” . The assumption of commonly honored, customarily accredited axioms as the fundamental “building-blocks” of Greek geometry circumvented the ever-experimentally-redemonstrable qualifying requirement of all serious scientific considerations.
[986.045]{style="color: purple3"} []{#ver:986.045 label="ver:986.045"} The Ionian Greeks assumed as fundamental geometric components their line-surrounded areas. These areas’ surfaces could be rough, smooth, or polished just as the smooth surface of the water of the sea could be roughened without losing its identity to them as “the surface.” Looking upon plane geometry as the progenitor of subsequently-to-be-developed solid geometry, it seemed never to have occurred to the Euclideans that the surface on which they scribed had shape integrity only as a consequence of its being a component of a complex polyhedral system, the system itself consisting of myriads of subvisible structural systems, whose a priori structural integrity complex held constant the shape of the geometrical figures they scribed uponthe polyhedral system, for instance, the system planet Earth upon whose ground they scratched their figures, or the stone block, or the piece of bark on which they drew. Even Democritus’s brilliant speculative thought of a minimum thing smaller than our subdimensional but point-to-able speck was speculative exploration a priori to any experimentally induced thinking of complex dynamic interactions of a plurality of forces that constituted structuring in its most primitive sense. Democritus did not think of the atom as a kinetic complex of structural shaping interactions of energy events operating at ultra-high-frequency in pure principle.
[986.046]{style="color: purple3"} []{#ver:986.046 label="ver:986.046"} Cubical forms of wood and stone with approximately flat faces and corner angles seemed to the Euclidean-led Ionians to correspond satisfactorily with what was apparently a flat plane world to which trees and humanly erected solid wooden posts and stone columns were obviously perpendicularergo, logically parallel to one another. From these only-axiomatically-based conclusions the Ionians developed their arbitrarily shaped, nonstructural, geometrical abstractions and their therefrom-assumed generalizations.
[986.047]{style="color: purple3"} []{#ver:986.047 label="ver:986.047"} The Greeks’ generalized geometry commenced with the planar relationships and developed therefrom a “solid” geometry by in effect standing their planes on edge on each of the four sides of a square base and capping this vertical assembly with a square plane. This structure was then subdivided by three interperpendicularly coordinate lineseach with its corresponding sets of modularly interspaced and interparalleled planes. Each of these three sets of interparallel and interperpendicular planes was further subdivisible into modularly interspaced and interparallel lines. Their sets of interparallel and interperpendicular planar and linear modulations also inherently produced areal squares and volumetric cubes as the fundamental, seemingly simplest possible area-and-volume standards of uniform mensuration whose dimensioning increments were based exclusively on the uniform linear module of the coordinate systemwhose comprehensive interrelationship values remained constantergo, were seemingly generalizable mathematically quite independently of any special case experiential selection of special case lengths to be identified with the linear modules.
[986.048]{style="color: purple3"} []{#ver:986.048 label="ver:986.048"} The Euclidean Greeks assumed not only that the millions of points and instant planes existed independently of one another, but that the complex was always the product of endlessly multipliable simplexesto be furnished by an infinite resource of additional components. The persistence of the Greeks’ original misconceptioning of geometry has also so distorted the conditioning of the human brain-reflexing as to render it a complete 20th-century surprise that we have a finite Universe: a finite but nonunitarily-and-non-simultaneously accomplished, eternally regenerative Scenario Universe. In respect to such a scenario Universe multiplication is always accomplished only by progressively complex, but always rational, subdivisioning of the initially simplest structural system of Universe: the sizeless, timeless, generalized tetrahedron. Universe, being finite, with energy being neither created nor lost but only being nonsimultaneously intertransformed, cannot itself be multiplied. Multiplication is cosmically accommodated only by further subdivisioning.
[986.049]{style="color: purple3"} []{#ver:986.049 label="ver:986.049"} If the Greeks had tried to do so, they would soon have discovered that they could not join tetrahedra face-to-face to fill allspace; whereas they could join cubes face-to-face to fill allspace. Like all humans they were innately intent upon finding the “Building-Block” of Universe. The cube seemed to the Greeks, the Mesopotamians, and the Egyptians to be just what they needed to account their experiences volumetrically. But if they had tried to do so, they would have found that unit-dimensioned tetrahedra could be joined corner-to-corner only within the most compact omnidirectional confine permitted by the corner-to-corner rule, which would have disclosed the constant interspace form of the octahedron, which complements the tetrahedron to fill allspace; had they done so, the Ionians would have anticipated the physicists’ 1922 discovery of “fundamental complementarity” as well as the 1956 Nobel-winning physics discovery that the complementarity does not consist of the mirror image of that which it complements. But the Greeks did not do so, and they tied up humanity’s accounting with the cube which now, two thousand years later, has humanity in a lethal bind of 99 percent scientific illiteracy.
¶ 986.050 Unfamiliarity with Tetrahedra
[986.051]{style="color: purple3"} []{#ver:986.051 label="ver:986.051"} The distorted conditioning of human reflexing and reasoning persisted in overwhelming the academic point of viewand still does so up to this moment in history. This is nowhere more apparent than in the official reaction to the data and photographs taken on planet Mars by the planet Earth’s scientists from their multistage-rocket-dispatched Mariner 9 and Viking orbiters:
But even at the present limits of resolution, some surprising formations have been seen, the most inexplicable of which are the three-sided pyramids found on the plateau of Elysium. Scientists have tried to find a natural geological process that would account for the formation of these pyramids, some of which are two miles across at the base, but as yet their origin is far from being explained. Such tantalizing mysteries may not be fully solved until astronauts are able to make direct observations on the Martian surface.[^36]
[986.052]{style="color: purple3"} []{#ver:986.052 label="ver:986.052"} In 1977 the NASA scientists scrutinized the robot-photographed pictures of the close-in Martian scene and reported theto them surprise presence on Mars of two (two-mile-base-edged) three-sided pyramids the size of Mount Fuji. The NASA scientists were unfamiliar with the tetrahedron. They remarked that these forms, with whose simplest, primitive character they were unacquainted, must have been produced by wind-blown sand erosion, whereas we have discovered that tetrahedra are always and only a priori to nature’s processes of alteration of her simplest and most primitive polyhedral systems.
[986.053]{style="color: purple3"} []{#ver:986.053 label="ver:986.053"} Also suggestive of the same blindness to nature’s reality suffered by the academic world and the scientists who lead it, was van’t Hoff’s late-19th-century identification of the primitive significance of the tetrahedron in the structuring of organic chemistry. (See Sec. 931.60.) His hypothesis was at first scoffed at by scientists. Fortunately, through the use of optical instruments he was able to present visual proof of the tetrahedral configuration of carbon bondswhich experimentally reproduced evidence won him the first Nobel prize awarded a chemist. The Greeks of three millennia ago and today’s “educated” society are prone to assume that nature is primitively disorderly and that symmetrical shapes are accomplished only by human contriving.
¶ 986.060 Characteristics of Tetrahedra
[986.061]{style="color: purple3"} []{#ver:986.061 label="ver:986.061"} The tetrahedron is at once both the simplest system and the simplest structural system in Universe (see Secs. 402 and 620). All systems have a minimum set of topological characteristics of vertexes, faces, and edges (see Secs. 1007.22 and 1041.10). Alteration of the minimum structural system, the tetrahedron, or any of its structural-system companions in the primitive hierarchy (Sec. 982.61), may be accomplished by either external or internal contact with other systemswhich other systems may cleave, smash, break, or erode the simplest primitive systems. Other such polyhedral systems may be transformingly developed by wind-driven sandstorms or wave-driven pebble beach actions. Those other contacting systems can alter the simplest primitive systems in only two topological-system ways:
-
by truncating a vertex or a plurality of vertexes, and
-
by truncating an edge or a plurality of edges.
Faces cannot be truncated. (See Fig. 986.061.)
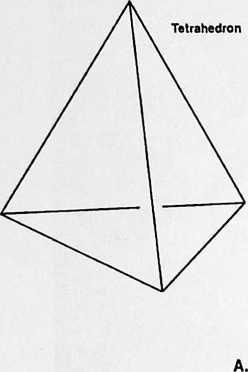
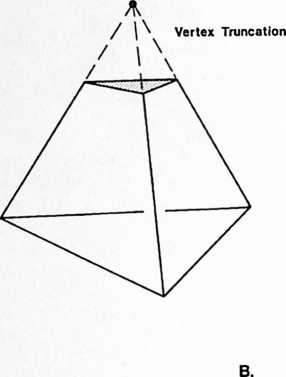
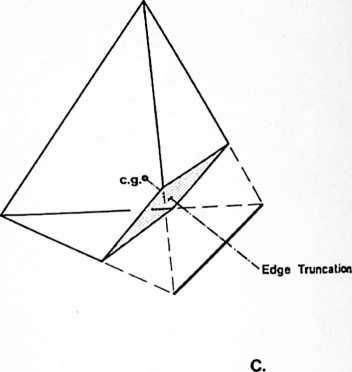
[986.062]{style="color: purple3"} []{#ver:986.062 label="ver:986.062"} As we have learned regarding the “Platonic solids” carvable from cheese (Sec. 623.10), slicing a polyhedron parallel to one of its faces only replaces the original face with a new face parallel to the replaced face. Whereas truncating a vertex or an edge eliminates those vertexes and edges and replaces them with faceswhich become additional faces effecting a different topological abundance inventory of the numbers of vertexes and edges as well. For every edge eliminated by truncation we gain two new edges and one new face. For every corner vertex eliminated by truncation our truncated polyhedron gains three new vertexes, three new edges, and one new face.
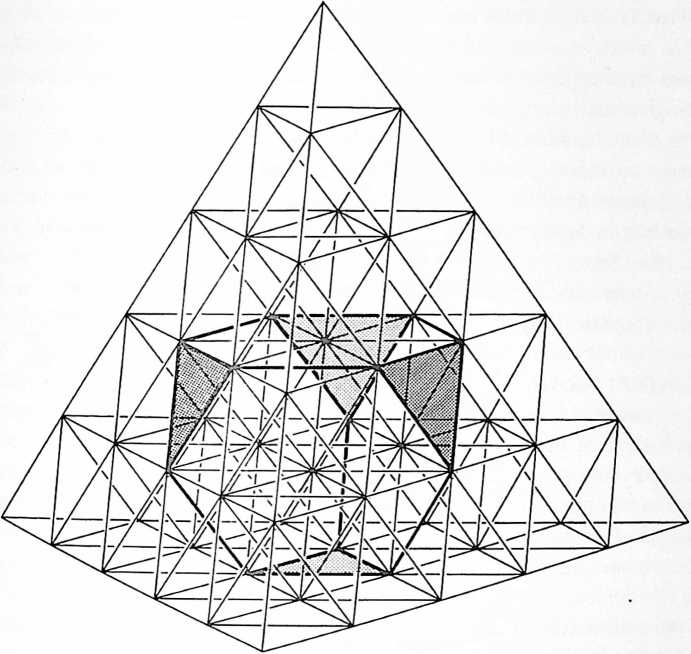
[986.063]{style="color: purple3"} []{#ver:986.063 label="ver:986.063"} The cheese tetrahedron (Sec. 623.13) is the only one of the primitive hierarchy of symmetrical polyhedral systems that, when sliced parallel to only one of its four faces, maintains its symmetrical integrity. It also maintains both its primitive topological and structural component inventories when asymmetrically sliced off parallel to only one of its four disparately oriented faces. When the tetrahedron has one of its vertexes truncated or one of its edges truncated, however, then it loses its overall system symmetry as well as both its topological and structural identification as the structurally and topologically simplest of cosmic systems.
[986.064]{style="color: purple3"} []{#ver:986.064 label="ver:986.064"} We may now make a generalized statement that the simplest system in Universe, the tetrahedron, can be design-altered and lose its symmetry only by truncation of one or more of its corners or edges. If all the tetrahedron’s four vertexes and six edges were to be similarly truncated (as in Fig. 1041.11) there would result a symmetrical polyhedron consisting of the original four faces with an addition of 10 more, producing a 14-faceted symmetrical polyhedron known as the tetrakaidecahedron, or Kelvin’s “solid,” which (as shown in Sec. 950.12 and Table 954.10) is an allspace filleras are also the cube, the rhombic dodecahedron, and the tetrahedral Mites, Sytes, and Couplers. All that further external alteration can do is produce more vertex and edge truncations which make the individual system consist of a greater number of smaller-dimension topological aspects of the system. With enough truncationsor knocking off of corners or edges the system tends to be come less angular and smoother (smoother in that its facets are multiplying in number and becoming progressively smaller and thus approaching subvisible identification). Further erosion can only “polish off more of the only microscopically-visible edges and vertexes. polished beach pebble, like a shiny glass marble or like a high-frequency geodesic polyhedral spheric structure, is just an enormously high-frequency topological inventory-event system.
[986.065]{style="color: purple3"} []{#ver:986.065 label="ver:986.065"} Joints, Windows, and Struts: As we have partially noted elsewhere (Secs. 536 and 604), Euler’s three primitive topological characteristicsvertexes, faces, and linesare structurally identifiable as joints, windows, and push-pull struts, respectively. When you cannot see through the windows (faces), it is because the window consists of vast numbers of subvisible windows, each subvisible-magnitude window being strut-mullion-framed by a complex of substructural systems, each with its own primitive topological and structural components.
[986.066]{style="color: purple3"} []{#ver:986.066 label="ver:986.066"} Further clarifying those structural and topological primitive com- ponentation characteristics, we identify the structural congruences of two or more joined-together-systems’ components as two congruent single vertexes (or joints) producing one single, univalent, universal-joint intersystem bonding. (See Secs. 704, 931.20, and Fig. 640.41B.) Between two congruent pairs of interconnected vertexes (or joints) there apparently runs only one apparent (because congruent) line, or interrelationship, or push-pull strut, or hinge.
[986.067]{style="color: purple3"} []{#ver:986.067 label="ver:986.067"} Returning to our early-Greek geometry initiative and to the as-yet-persistent academic misconditioning by the Greeks’ oversights and misinterpretations of their visual experiences, we recall how another non-Ionian Greek, Pythagoras, demonstrated and “proved” that the number of square areas of the unit-module-edged squares and the number of cubical module volumes of the unit-module-edged cubes correspond exactly with arithmetic’s second-powerings and third-powerings. The Greeks, and all mathematicians and all scientists, have ever since misassumed these square and cube results to be the only possible products of such successive intermultiplying of geometry’s unit-edge-length modular components. One of my early mathematical discoveries was the fact that all trianglesregular, isosceles, or scalene may be modularly subdivided to express second-powering. Any triangle whose three edges are each evenly divided into the same number of intervals, and whose edge-interval marks are cross-connected with lines that are inherently parallel to the triangle’s respective three outer edgesany triangle so treated will be subdivided by little triangles all exactly similar to the big triangle thus subdivided, and the number of small similar triangles subdividing the large master triangle will always be the second power of the number of edge modules of the big triangle. In other words, we can say “triangling” instead of “squaring,” and since all squares are subdivisible into two triangles, and since each of those triangles can demonstrate areal second-powering, and since nature is always most economical, and since nature requires structural integrity of her forms of reference, she must be using “triangling” instead of “squaring” when any integer is multiplied by itself. (See Sec. 990.)
[986.068]{style="color: purple3"} []{#ver:986.068 label="ver:986.068"} This seemed to be doubly confirmed when I discovered that any nonequiedged quadrangle, with each of its four edges uniformly subdivided into the same number of intervals and with those interval marks interconnected, produced a pattern of dissimilar quadrangles. (See Fig. 990.01.) In the same manner I soon discovered experimentally that all tetrahedra, octahedra, cubes, and rhombic dodecahedra regular or skewcould be unitarily subdivided into tetrahedra with the cube consisting of three tetra, the octahedron of four tetra, and the rhombic dodecahedron of six similar tetra; and that when any of these regular or skew polyhedras’ similar or dissimilar edges and faces were uniformly subdivided and interconnected, their volumes would always be uniformly subdivided into regular or skew tetrahedra, and that could and should be written and spoken of as and not as .
[986.069]{style="color: purple3"} []{#ver:986.069 label="ver:986.069"} Nature would use the tetrahedron as the module of subdivision because nature has proven to the physicists and the other physical scientists that she always chooses the most economic realization. Cubes require three times as much Universe as do tetrahedra to demonstrate volumetric content of systems because cubic identification with third-powering used up three times as much volume as is available in Universe. As a result of cubic mensuration science has had to invent such devices as “probability” and “imaginary numbers.” Thus “squaring” and “cubing,” instead of nature’s “triangling” and “tetrahedroning,” account for science’s using mathematical tools that have no physical-model demonstrabilityergo, are inherently “unscientific.”
¶ 986.070 Buildings on Earths Surface
[986.071]{style="color: purple3"} []{#ver:986.071 label="ver:986.071"} In the practical fortress and temple building of the earliest known Mesopotamians, Egyptians, and Greeks their cubes and omnirectilinear blocks seemed readily to fill allspace as they were assembled into fortress or temple walls with plumb bobs, water-and-bubble levels, straightedges, and right-triangle tools. No other form they knewother than the cubeseemed to fill allspace as demonstrated in practical masonry; wherefore they assumed this to be scientifically demonstrated proof of the generalizability of their mathematically abstracted plane- and solid-geometry system and its coordination.
[986.072]{style="color: purple3"} []{#ver:986.072 label="ver:986.072"} Because of the relatively diminutive size of humans in respect to the size of our planet, world-around society as yet spontaneously cerebrates only in terms of our immediate world’s seeming to demonstrate itself to be a flat plane base, all of the perpendiculars of whichsuch as trees and humans and human-built local structuresappear to be rising from the Earth parallel to one anotherergo, their ends point in only two possible directions, “up or “down.” …It’s “a wide, wide world,” and “the four corners of the Earth.”
[986.073]{style="color: purple3"} []{#ver:986.073 label="ver:986.073"} It was easy and probably unavoidable for humanity to make the self-deceptive blunders of assuming that a cube held its shape naturally, and not because the stone-cutters or wood-cutters had chosen quite arbitrarily to make it in this relatively simple form. Human’s thought readily acceptedand as yet doesthe contradictory abstract state “solid.” The human eye gave no hint of the energetic structuring of the atomic microcosm nor of the omnidynamic, celestial-interpositioning transformations of both macro- and micro-Universe.
[986.074]{style="color: purple3"} []{#ver:986.074 label="ver:986.074"} Prior to steel-framed or steel-reinforced-concrete construction methods, humans’ buildings that were constructed only of masonry could not be safely built to a height of over 20 storiesapproximately 200 feet high. Such a masonry building was Chicago’s turn-of-the-20th-century world-record Monadnock Building, whose base covered a small but whole city block. It is not until we reach a height of 100 storiesapproximately 1000 feet high that two exactly vertical square columns, each with base edges of 250 feet, built with exactly vertical walls, and touching one another only along one of each of their base edges, will show a one-inch space between them. The rate their vertical walls part from one another is only \sfrac{1}{100} of an inch for each foot of height.
[986.075]{style="color: purple3"} []{#ver:986.075 label="ver:986.075"} Masons’ and carpenters’ linear measuring devices are usually graduated only to \sfrac{1}{16}th of an inch, and never finer than \sfrac{1}{32}nd of an inch. Thus differentials of a thousandth of an inch are undetectable and are altogether inadvertently overlooked; ergo, they get inadvertently filled-in, or cross-joined, never to have been known to exist even on the part of the most skilled and conscientious of building craftsmen, whose human eyes cannot see intervals of less than \sfrac{1}{100}th of an inch.
[986.076]{style="color: purple3"} []{#ver:986.076 label="ver:986.076"} If two exactly-vertical-walled city skyscrapers are built side by side, not until they are two and one-half miles high (the height of Mount Fuji) will there be a space of one foot between the tops of their two adjacent walls. (See Fig. 986.076.) Of course, the farther apart the centers of their adjacent bases, the more rapidly will the tops of such high towers veer away from one another:
The twin towers of New York’s Verrazano Bridge are 693 feet high …soaring as high as a 70-story skyscraper …set almost a mile from each other, the two towers, though seemingly parallel, are an inch and five-eighths farther apart at their summits than at their bases because of the Earth’s curvature[^37]
[986.077]{style="color: purple3"} []{#ver:986.077 label="ver:986.077"} It is easy to understand how humans happened to think it “illogical” to have to consider that all the perpendiculars to a sphere are radii of that sphere ergo, never parallel to one another. Our humans-in-Universe scale is inherently self-deceptiveergo, difficult to cope with rigorously.
¶ 986.080 Naive Perception of Childhood
[986.081]{style="color: purple3"} []{#ver:986.081 label="ver:986.081"} The inventory of experimentally demonstrated discoveries of science which had accrued by the time of my childhood gave me reason to question many of the “abstractions” of geometry as I was being instructed in that subject. Axioms were based on what only seemed “self-evident, such as the stone block or the “cubical” wooden play blocks of my nursery. To society they “obviously held their shape.” I do not think that I was precocious or in any way a unique genius. I had one brother; he was three years younger than I. His eyesight was excellent; mine was atrocious. I did not get my first eyeglasses until my younger brother was running around and talking volubly. He could see things clearly; I could not. Our older sister could also see things clearly. I literally had to feel my way along tactilelyin order to recognize the “things” of my encountered environment ergo, my deductions were slow in materializing. My father called my younger brother “slickly-prickly” and he called me “slow-and-solid”terms he adopted from “The Jaguar and the Armadillo” in Kipling’s Just So Stories (Kipling 1902).
[986.082]{style="color: purple3"} []{#ver:986.082 label="ver:986.082"} I was born cross-eyed on 12 July 1895. Not until I was four-and-a-half years old was it discovered that I was also abnormally far-sighed. My vision was thereafter fully corrected with lenses. Until four-and-a-half I could see only large patternshouses, trees, outlines of peoplewith blurred coloring. While I saw two dark areas on human faces, I did not see a human eye or a teardrop or a human hair until I was four. Despite my newly gained abilityin 1899to apprehend details with glasses, my childhood’s spontaneous dependence upon only big-pattern clues has persisted. All that I have to do today to re-experience what I saw when I was a child is to take off my glasses, which, with some added magnification for age, have exactly the same lens corrections as those of my first five-year-old pair of spectacles. This helps me to recall vividly my earliest sensations, impressions, and tactical assumptions.
[986.083]{style="color: purple3"} []{#ver:986.083 label="ver:986.083"} I was sent to kindergarten before I received my first eyeglasses. The teacher, Miss Parker, had a large supply of wooden toothpicks and semidried peas into which you could easily stick the sharp ends of the toothpicks. The peas served as joints between the toothpicks. She told our kindergarten class to make structures. Because all of the other children had good eyesight, their vision and imagination had been interconditioned to make the children think immediately of copying the rectilinearly framed structures of the houses they saw built or building along the road. To the other children, horizontally or perpendicularly parallel rectilinear forms were structure. So they used their toothpicks and peas to make cubic and other rectilinear models. The semidried peas were strong enough to hold the angles between the stuck-in toothpicks and therefore to make the rectilinear forms hold their shapesdespite the fact that a rectangle has no inherent self-structuring capability.
[986.084]{style="color: purple3"} []{#ver:986.084 label="ver:986.084"} In my poor-sighted, feeling-my-way-along manner I found that the triangleI did not know its namewas the only polygon I did not know that word eitherthat would hold its shape strongly and rigidly. So I naturally made structural systems having interiors and exteriors that consisted entirely of triangles. Feeling my way along I made a continuous assembly of octahedra and tetrahedra, a structured complex to which I was much later to give the contracted name “octet truss.” (See Sec. 410.06). The teacher was startled and called the other teachers to look at my strange contriving. I did not see Miss Parker again after leaving kindergarten, but three-quarters of a century later, just before she died, she sent word to me by one of her granddaughters that she as yet remembered this event quite vividly.
[986.085]{style="color: purple3"} []{#ver:986.085 label="ver:986.085"} Three-quarters of a century later, in 1977, the National Aeronautics and Space Administration (NASA), which eight years earlier had put the first humans on the Moon and returned them safely to our planet Earth, put out bids for a major space-island platform, a controlled-environment structure. NASA’s structural specifications called for an “octet truss”my invented and patented structural name had become common language, although sometimes engineers refer to it as “space framing. ” NASA’s scientific search for the structure that had to provide the most structural advantages with the least pounds of material ergo, least energy and seconds of invested timein order to be compatible and light enough to be economically rocket-lifted and self-erected in spacehad resolved itself into selection of my 1899 octet truss. (See Sec. 422.00.)
[986.086]{style="color: purple3"} []{#ver:986.086 label="ver:986.086"} It was probable also that my only-insectlike, always-slow, cross-referencing strategy of touching, tasting, smelling, listening, and structurally testing by twisting and pounding and so forthto which I spontaneously resorted made me think a great deal about the fact that when I broke a piece of glass or a stone or a wooden cube apart, it did not separate naturally into little cubes but usually into sharp pointed shapes. In the earliest of my memories I was always suspicious of the integrity of cubes, which only humans seemed to be introducing into the world. There were no cubical roses, eggs, trees, clouds, fruits, nuts, stones, or anything else. Cubes to me were unnatural: I observed humans deliberately sawing ice into large rectilinear cakes, but window glass always broke itself into predominantly triangular pieces; and snowflakes formed themselves naturally into a myriad of differently detailed, six-triangled, hexagonal patterns.
[986.087]{style="color: purple3"} []{#ver:986.087 label="ver:986.087"} I was reacting normally in combining those spontaneous feelings of my childhood with the newly discovered knowledge of the time: that light has speed (it is not instantaneous, and comes in smallest packages called photons); that there is something invisible called electricity (consisting of “invisible behaviors” called electrons, which do real work); and that communication can be wireless, which Marconi had discovered the year I was bornand it is evident that I was reacting normally and was logically unable to accept the customarily honored axioms that were no longer “self-evident.”
[986.088]{style="color: purple3"} []{#ver:986.088 label="ver:986.088"} My contemporaries and I were taught that in order to design a complete and exact sphere and have no materials left over, we must employ the constant known as , which I was also taught was a “transcendentally irrational number,” meaning it could never be resolved. I was also informed that a singly existent bubble was a sphere; and I asked, ‘To how many places does nature carry out when she makes each successive bubble in the white-cresting surf of each successive wave before nature finds out that can never be resolved?’ …And at what moment in the making of each separate bubble in Universe does nature decide to terminate her eternally frustrated calculating and instead turn out a fake sphere? I answered myself that I don’t think nature is using or any of the other irrational fraction constants of physics. Chemistry demonstrates that nature always associates or disassociates in whole rational increments… Those broken window shards not only tended to be triangular in shape, but also tended to sprinkle some very fine polyhedral pieces. There were wide ranges of sizes of pieces, but there were no pieces that could not “make up their minds” or resolve which share of the original whole was theirs. Quite the contrary, they exploded simultaneously and unequivocally apart.
[986.089]{style="color: purple3"} []{#ver:986.089 label="ver:986.089"} At first vaguely, then ever more excitedly, precisely, and inclusively, I began to think and dream about the optimum grand strategy to be employed in discovering nature’s own obviously elegant and exquisitely exact mathematical coordinate system for conducting the energetic transactions of eternally regenerative Universe. How does nature formulate and mass-produce all the botanical and zoological phenomena and all the crystals with such elegant ease and expedition?
¶ 986.090 The Search for Natures Coordinate System
[986.091]{style="color: purple3"} []{#ver:986.091 label="ver:986.091"} Several things were certain: nature is capable of both omnidirectional disorderly, dispersive, and destructive expansion and omnidirectional collective, selective sorting and constructive contraction; and rays of candlelight are not parallel to one another. I decided to initiate my search for nature’s coordinate system by assuming that the coordinate system must be convergently and divergently interaccommodative. That the seasons of my New England childhood brought forth spectacular transformations in nature’s total interpatterning; that the transformations were not simultaneous nor everywhere the same; that there were shaded and Sun-shined-upon area variables; and that they were all embraced by a comprehensive coordination altogether made me dream of comprehending the comprehensively accommodating coordinate system that had no separate departments of chemistry, physics, biology, mathematics, art, history, or languages. I said nature has only one department and only one language.
[986.092]{style="color: purple3"} []{#ver:986.092 label="ver:986.092"} These thoughts kept stimulating my explorations for the totally accommodative coordinate system. Einstein’s conclusionthat the definitive, maximum possible speed of light rendered astronomical phenomena an aggregate of nonsimultaneous and only partially overlapping, differently enduring energy events greatly affected the increasing inventory of my tentative formulations of the interaccommodative requirements of the cosmic coordination system which I sought. I was driven by both consciously and subconsciously sustained intuition and excitement. This was very private, however. I talked to no one about it. It was all very remote from that which seemed to characterize popular interest.
[986.093]{style="color: purple3"} []{#ver:986.093 label="ver:986.093"} The youthful accruals of these long-sustained private observations, cogitations, and speculations were enormously helpful when I decided at the age of 32, in my crisis year of 1927, to abandon the game of competitive survival (a game I had been taught to believe in as thought-out, managed, and evolved entirely by others) and instead to rely completely upon my own thinking and experience-suggested inclinations …to find out how Universe is organized and what it is doing unbeknownst to humans. Why are humans here in Universe? What should we be doing to fulfill our designed functioning in Universe? Surely all those stars and galaxies were not designed only to be romantic scenery for human moods. What am I designed to be able to comprehend about Universe? What are we humans designed to be able to do for one another and for our Universe?
[986.094]{style="color: purple3"} []{#ver:986.094 label="ver:986.094"} Expanding Universe: My determination to commit myself completely to the search for nature’s raison d’etre and for its comprehensive coordinate system’s mathematics was greatly reinforced by the major discovery of the astronomer E. P. Hubble in 1924. He discovered an expanding macrocosmic system with all the myriads of galaxies and their respective stellar components at all times maintaining the same interangular orientations and relative interdistancings from one another while sum-totally and omnisymmetrically expanding and moving individually away from one another, and doing so at astronomical speeds. This discovery of Hubble’s became known as Expanding Universe.
[986.095]{style="color: purple3"} []{#ver:986.095 label="ver:986.095"} The only way humans can expand their houses is by constructing lopsided additions to their rectilinearly calculated contriving. People found that they could “blow up” rubber-balloon spheres to increase their radii, but they couldn’t blow up their buildings except by dynamite. They called their wooden “2 x 4,” and “2 x 6,” and “2 x 8-inch” cross-section, wooden-timber nail-ups “balloon framing,” but why they selected that name was difficult to explain.
[986.096]{style="color: purple3"} []{#ver:986.096 label="ver:986.096"} My insights regarding nature’s coordinate system were greatly enhanced by two of Milton Academy’s greatest teachers: Homer LeSourd in physics and William Lusk Webster Field (“Biology Bill”) in biology. During the summer vacation of 1906, at 11 years of age I designed and built my first small but exciting experimental dwelling on our family’s small midPenobscot Bay island. Living all my youthful summers on that island, with its essential boat-building, boat-modifying, boat-upkeep, and boat-sailing, followed by five years as a line officer in the regular U.S. Navy with some of my own smaller-craft commands, some deck-officering on large craft of the new era’s advanced technology ships, together with service involving airplanes, submarines, celestial navigation, ballistics, radio, and radiotelephone; then resignation from the Navy followed by five more private-enterprise years developing a new building system, inventing and installing its production tools, managing the production of the materials, and erecting therewith 240 residences and small commercial buildingsaltogether finally transformed my sustained activity into full preoccupation with my early-boyhood determination some day to comprehend and codify nature’s omniintertransformative, omnidirectional, cosmic coordination system and its holistic, only-experientially-proven mathematics. In 1928, inspired and fortified by Hubble’s Expanding Universe discovery, I gave the name and its symbol 4-D to my mathematical preoccupations and their progressively discovered system codifying. In 1936 I renamed my discipline “Energetic Vectorial Geometry.” In 1938 I again renamed it “Energetic-synergetic Geometry,” and in 1970 for verbal economy contracted that title to “Synergetics.” (See Fig. 986.096.)
¶ 986.100 Sequence of Considerations
[986.101]{style="color: purple3"} []{#ver:986.101 label="ver:986.101"} At the outset of my lifelong search for nature’s omnirational coordination system of mathematical interaccounting and intertransformability I proceeded through a sequence of considerations which may be enumerated as follows:
¶ 986.110 Consideration 1: Energetic Vectors
[986.111]{style="color: purple3"} []{#ver:986.111 label="ver:986.111"} I first determined to employ only vectors for lines. I realized that operationally all lines are always trajectories of energy events, either as the energy invested by humans in the work of carving or depositing linearly which we call “drawing” a lineor as the inanimately articulated energy of force lines.
[986.112]{style="color: purple3"} []{#ver:986.112 label="ver:986.112"} Vectors always represent energy forces of given magnitude operating at given angles upon given entities at given loci, and vectors may always be demonstrated by lines representing given mass moving at given velocity in unique angular direction in respect to a given axis of observation. Vectors do not occur singly: They occur only as the total family of forces interacting in any given physical circumstance.
[986.113]{style="color: purple3"} []{#ver:986.113 label="ver:986.113"} Vectors always have unique length, that length being the product of the mass and the velocity as expressed in a given modular system of measurement. Vectors do not have inherent extendibility to infinityas did the lines of my boyhood’s schoolteachers. Vectors are inherently terminal. Vectors bring into geometry all the qualities of energetic reality lacking in Euclidean geometry: time and energyenergy differentially divergent as radiation (velocity) and energy integratively convergent as matter (mass). Velocity and mass could be resolved into numerically described time and temperature components.
¶ 986.120 Consideration 2: Avogadro’s Constant Energy Accounting
[986.121]{style="color: purple3"} []{#ver:986.121 label="ver:986.121"} Avogadro discovered that under identical conditions of pressure and heat all elements in their gaseous state always consist of the same number of molecules per given volume. Since the chemical elements are fundamentally different in electron-proton componentation, this concept seemed to me to be the “Grand Central Station” of nature’s numerical coordinate system’s geometric volume that numerically exact volumes contain constant, exact numbers of fundamental energy entities. This was the numerical and geometrical constancy for which I was looking. I determined to generalize Avogadro’s experimentally proven hypothesis that “under identical conditions of heat and pressure all gases disclose the same number of molecules per given volume.” (See Secs. 410.03–04.)
[986.122]{style="color: purple3"} []{#ver:986.122 label="ver:986.122"} Here were Physical Universe’s natural number quantations being constantly related to given volumes. Volumes are geometrical entities. Geometrically defined and calculated volumes are polyhedral systems. Polyhedra are defined by edge lines, each of which must be a vector.
[986.123]{style="color: purple3"} []{#ver:986.123 label="ver:986.123"} Within any given volumetrically contained gaseous state the energy kinetics of molecules are everywhere the same. The outward pressure of air against the enclosing tube wall and casing of any one automobile tire is everywhere the same. Pressure and heat differentials involve isolated conditionsisolated by containers; ergo, special cases. To me this meant that we could further generalize Avogadro by saying that “under identical, uncontained, freely self-interarranging conditions of energy all chemical elements will disclose the same number of fundamental somethings per given volume.” This constant-volume-population-and-omniequilibrious-energy relationship would require physically demonstrable, substantive, geometrical combining of a given number of unique energetic-event entities per unit volume with constant-angularly-defined positional orientation integrities. This meant that the vectorially structured shapes of the volumes accommodating given numbers of most primitive energy events must be experientially demonstrable.
¶ 986.130 Consideration 3: Angular Constancy
[986.131]{style="color: purple3"} []{#ver:986.131 label="ver:986.131"} I said that since vectors are physically modelable structural components, they produce conceptual structural models of energy events, and since my hypothetical generalization of Avogadro’s law requires that “all the conditions of energy be everywhere the same,” what does this condition look like as structured in vectorial geometry? Obviously all the vectors must be the same length and all of them must interact at the same angles. I said: It will make no difference what length is employed so long as they are all the same length. Linear size is special case. Special case occurs only in time. Angles are cosmically constant independently of time-size considerations.
¶ 986.140 Consideration 4: Isotropic Vector Model
[986.141]{style="color: purple3"} []{#ver:986.141 label="ver:986.141"} I said, Can you make a vector model of this generalization of Avogadro? And I found that I had already done so in that kindergarten event in 1899 when I was almost inoperative visually and was exploring tactilely for a structural form that would hold its shape. This I could clearly feel was the triangle with which I could make systems having insides and outsides. This was when I first made the octet truss out of toothpicks and semidried peas, which interstructuring pattern scientists decades later called the “isotropic vector matrix,” meaning that the vectorial lengths and interanglings are everywhere the same. (See Sec. 410.06.)
[986.142]{style="color: purple3"} []{#ver:986.142 label="ver:986.142"} This matrix was vectorially modelable since its lines, being vectors, did not lead to infinity. This isotropic vector matrix consists of six-edged tetrahedra plus 12-edged octahedramultiples of six. Here is an uncontained omniequilibrious condition that not only could be, but spontaneously would be, reverted to anywhen and anywhere as a six-dimensional frame of transformative-evolution reference, and its vector lengths could be discretely tuned by uniform modular subdivisioning to accommodate any desired special case wavelength time-size, most economically interrelated, transmission or reception of physically describable information. (Compare Secs. 639.02 and 1075.10.)
[986.143]{style="color: purple3"} []{#ver:986.143 label="ver:986.143"} Since the vectors are all identical in length, their intersection vertexes become the nuclear centers of unit-radius spheres in closest-packed aggregationwhich closest packing is manifest by atoms in their crystal growth. All the foregoing brought the adoption of my vectorial geometry’s everywhere-the-same (isotropic) vector matrix as the unified field capable of accommodating all of Physical Universe’s intertransformative requirements.
¶ 986.150 Consideration 5: Closest Packing of Spheres
[986.151]{style="color: purple3"} []{#ver:986.151 label="ver:986.151"} I had thus identified the isotropic vector matrix with the uniform linear distances between the centers of unit radius spheres, which aggregates became known laterin 1922as “closest-packed” unit-radius spheres (Sec. 410.07), a condition within which we always have the same optimum number of the same “somethings”spheres or maybe atomsper given volume, and an optimally most stable and efficient aggregating arrangement known for past centuries by stackers of unit-radius coconuts or cannonballs and used by nature for all time in the closest packing of unit-radius atoms in crystals.
¶ 986.160 Consideration 6: Diametric Unity
[986.161]{style="color: purple3"} []{#ver:986.161 label="ver:986.161"} The installation of the closest-packed unit-radius spheres into their geometrical congruence with the isotropic vector matrix showed that each of the vectors always reaches between the spheric centers of any two tangentially adjacent spheres. This meant that the radius of each of the kissing spheres consists of one-half of the interconnecting vectors. Wherefore, the radius of our closest-packed spheres being half of the system vector, it became obvious that if we wished to consider the radius of the unit sphere as unity, we must assume that the value of the vector inherently interconnecting two unit spheres is two. Unity is plural and at minimum two. Diameter means dia-meter unit of system measurement is two.
Fig. 986.161 Diametric Unity: The vectors of the isotropic vector matrix interconnect the spheric centers of any two tangentially adjacent spheres. The radii of the two spheres meet at the kissing point and are each one-half of the system vector. Unity is plural and at minimum two.
[986.162]{style="color: purple3"} []{#ver:986.162 label="ver:986.162"} Fig. 986.161 shows one vector whose primitive value is two. Vectors are energy relationships. The phenomenon relationship exists at minimum between two entities, and the word unity means union, which is inherently at minimum two. “Unity is plural and at minimum two” also at the outset became a prime concept of synergetics vectorial geometry. (See Sec. 540.10)
[986.163]{style="color: purple3"} []
Diameter is the relative-conceptual-size determinant of a system. diameter is the prime characteristic of the symmetrical system. The separate single system = unity. Diameter describes unity. Unity = 2. (See Secs. 905.10 and 1013.10)
[986.164]{style="color: purple3"} []{#ver:986.164 label="ver:986.164"} One by itself is nonexistent. Existence begins with awareness. Awareness begins with observable otherness. (See Secs. 264 and 981.)
[986.165]{style="color: purple3"} []{#ver:986.165 label="ver:986.165"} Understanding means comprehending the interrelationship of the observer and the observed. Definitive understanding of interrelationships is expressed by ratios.
[986.166]{style="color: purple3"} []{#ver:986.166 label="ver:986.166"} At the outset of my explorations I made the working assumption that unity is two, as combined with the experimentally demonstrable fact that every system and every systemic special case sphere is at once both a concave and a convex sphere ergo, always inherently two spheres. Reflective concave surfaces convergently concentrate all impinging radiation, and reflective convex surfaces divergently diffuse all impinging radiation. Though concave and convex are inherently congruent as they are always-and-only coexisting, they are also diametrically opposed physical behavior phenomenaergo, absolutely different because the one diffuses the energies of Universe, producing macrocosmic dispersion, and the other concentrates the energies of Universe, producing microcosmic convergence. Concave and convex are explicitly two opposites cosituate (congruent) geometrically as one. This led me to the working assumption at the outset of mythus far-year exploration for nature’s own coordinate system, that unity is inherently plural and at minimum is to be dealt with as the value two, which twoness might well coexist with other numbers of inherent properties of primary-existence systems.
¶ 986.170 Consideration 7: Vector Equilibrium
[986.171]{style="color: purple3"} []{#ver:986.171 label="ver:986.171"} I then identified this closest-packed-spheres isotropic vector matrix as a generalized field condition of the everywhere-and-everywhen most economically interaccommodating of any plurality of nuclearly convergent-divergent, importively organizing, and exportingly info-dispensing energy events while also providing for any number of individually discrete, overlappingly co-occurrent, frequency differentiated info-interexchangingsergo, to be always accommodative of any number of co-occurrent, individual-pattern-integrity evolutionary scenarios.
[986.172]{style="color: purple3"} []{#ver:986.172 label="ver:986.172"} Thus the eternally regenerative Universe, embracing the minimum complex of intercomplementary transformations necessary to effect total regeneration, becomes comprehensively accommodated by the only generalizably definable Scenario Universe as the condition of the vector equilibrium, an everywhere-everywhen condition at which nature refuses to pause, but through which most economically accommodating field of operational reference she pulsates her complex myriads of overlapping, concurrent, local intertransformings and aberrative structurings. I then invented the symbol to identify vector equilibrium. Change: Add the logo image
¶ 986.180 Consideration 8: Concentric Polyhedral Hierarchy
[986.181]{style="color: purple3"} []{#ver:986.181 label="ver:986.181"} Thereafter I set about sorting out the relative numbers and volumes of the most primitive hierarchy of symmetrically structured polyhedral event “somethings” all of which are always concentrically congruent and each and all of which are to be discovered as vertexially defined and structurally coexistent within the pre-time-size, pre-frequency-modulated isotropic vector matrix. (See Sec. and Fig. 982.61.)
¶ 986.190 Consideration 9: Synergetics
[986.191]{style="color: purple3"} []{#ver:986.191 label="ver:986.191"} This book Synergetics (volumes 1 and 2) embraces the record of the lifetime search, research, sorting-outs, and structural-intertransforming experiments based upon the foregoing eight considerations, all of which I had adopted by 1927. This 1927 inventory has been progressively amplified by subsequent experience-induced considerations.
¶ 986.200 Narrative Exposition of Spherical Accommodation
¶ 986.201 Consideration 10: The Spheric Experience: Energetic-reality Accounting vs Abstract-cubic Accounting
[986.202]{style="color: purple3"} []{#ver:986.202 label="ver:986.202"} In Synergetics 1, Secs. 962 through 966, I developed the first-, second-, and third-power values of my numerical factors for converting the coordinate system’s edge lengths, square areas, and cubical volumes to my 1927-discovered synergetic system’s unit vectorial edge lengths, triangular areas, and tetrahedral volumes.[^38] (See Table 963.10.)
[986.203]{style="color: purple3"} []{#ver:986.203 label="ver:986.203"} The synergetics coordinate systemin contradistinction to the coordinate systemis linearly referenced to the unit-vector-length edges of the regular tetrahedron, each of whose six unit vector edges occur in the isotropic vector matrix as the diagonals of the cube’s six faces. We also recall that the eight corners of the cube are defined and structured omnitriangularly by the symmetrically interarrayed and concentric pairs of positive and negative tetrahedra (Figs. 110A and 110B).
[986.204]{style="color: purple3"} []{#ver:986.204 label="ver:986.204"} Since the cube-face diagonal is the edge of the six-vector-edged, four-planes-of-symmetry tetrahedron, and since synergetics finds the unit-vector-edged tetrahedron to be the simplest structural system in Universe, the tetrahedron’s vector edge logically becomes the most economically primitive simplex module of relative length in synergetics’ coordinate system of exploratory reference. Thus the tetrahedron’s unit vector edge of unity 2 is manifest as nature’s coordinate primitive-length module for assessing:
second-power triangular area,
as well as for assessing that vector’s
third-power tetrahedral volume, ,
These areas and volumes become the logical unit of areal and volumetric reference in accounting the relative geometrical area and volume values of the entire hierarchy of primitive, concentrically congruent, symmetrical polyhedra as these naturally occur around any vertex of the isotropic vector matrix, and that matrix’s experimentally demonstrable, maximum-limit set of seven axes of polyhedral symmetries, which seven symmetries (Sec. 1040) accommodate and characterize the energetic special case formulations of all great-circle gridding.
[986.205]{style="color: purple3"} []{#ver:986.205 label="ver:986.205"} The synergetics hierarchy of topological characteristics as presented in Table 223.64 of Synergetics 1 (which was contracted for with Macmillan in 1961 and published by them in 1975), discloses the rational values of the comprehensive coordinate system of nature, which my 60-year exploration discovered. In 1944 I published a paper disclosing this rational system. At that time I was counseled by some of my scientist friends, who were aware that I was continuing to make additional refinements and discoveries, that premature publication of a treatise of disclosure might result in the omission of one or more items of critical information which might be later discovered and which might make the difference between scientific acceptance or rejection of the disclosures. Reminded by those scientist-artist friends that we have only one opportunity in a lifetime out of many lifetimes to publish a primescience-reorienting discovery, I postponed publishing a comprehensive treatise until in 1970, at the age of 75, I felt it could no longer be delayed.
[986.206]{style="color: purple3"} []{#ver:986.206 label="ver:986.206"} The eleventh-hour publishing of Synergetics 1 coincided with my busiest years of serving other obligations over a period calling for a vast number of tactical decisions regarding the methodology of producing what proved to be a 780-page book. Typical of the problems to be swiftly resolved are those shortly to be herewith recounted. The accounting also discloses the always surprisingly productive events that ensue upon mistake-making that are not only discovered and acknowledged, but are re-explored in search of the significance of the mistakes’ having occurred.
[986.207]{style="color: purple3"} []{#ver:986.207 label="ver:986.207"} Because the -coordinate, three-dimensional system values are arrived at by successive multiplying of the dimensions, volume in that system is an inherently three-dimensional phenomenon. But in synergetics the primitive values start holistically with timeless-sizeless tetrahedral volume unity in respect to which the cube’s primitive value is 3, the octahedron’s relative timeless-sizeless value is 4, the rhombic triacontrahedron’s is 5, and the rhombic dodecahedron’s is 6. In synergetics, when time-size special-case realizations enter into the consideration, then the (only-interrelated-to-one-another) primitive volumes of the synergetic hierarchy are multiplied by frequency of the edge modulation to the third power. Since innate primitive volume is a base-times-altitude three-dimensional phenomenon, and since all the synergetics hierarchy’s time-size realization volumes are inherently sixdimensional, I was confronted with an exploratory tactical quandary.
[986.208]{style="color: purple3"} []{#ver:986.208 label="ver:986.208"} The problem was to arrive at the numerical volume value for the sphere in the synergetics hierarchy, and the dilemma was whether I should apply my synergetics’ volumetric constant to the first power or to the third power of the XYZ-coordinate system’s volumetric values as arrived at by the conventional XYZ-coordinate system’s method of calculating the volume of a sphere of radius vector = 1. This operation is recorded in Sec. 982.55 of Synergetics 1, where I mis-conceptualized the operation, and (without reviewing how I had calculated the constant for converting to synergetics) redundantly took the number , which I assumed (again in mistaken carelessness) to be the third-power value of the synergetics-conversion constant, and I applied it to the volumetric value of a sphere of unit vector diameter as already arrived at by conventional XYZ-referenced mathematics, the conventional -coordinate volumetric value for the volume of a sphere of radius 1 being , which multiplied by gave the product a value so close to 5 that I thought it might possibly have been occasioned by the unresolvability of tail-end trigonometric interpolations, wherefore I tentatively accepted 4.99 as probably being exactly 5, which, if correct, was an excitingly significant number as it would have neatly fitted the sphere into the hierarchy of primitive polyhedra (Sec. 982.61). My hindsight wisdom tells me that my subconscious demon latched tightly onto this 5 and fended off all subconsciously challenging intuitions.
[986.209]{style="color: purple3"} []{#ver:986.209 label="ver:986.209"} But what I had mistakenly assumed to be the third-power synergetics constant was in fact the ninth power of that constant, as will be seen in the following list of the synergetics constant raised to varying powers:
Table 986.209
Synergetics Power Constants
[986.210]{style="color: purple3"} []{#ver:986.210 label="ver:986.210"} In our always-experimental-evidenced science of geometry we need only show ratio of proportion of parts, for parts of primitive polyhedra have no independent existence. Ergo, no experimental proof is required for roots and roots. Though those numbers are irrational, their irrationality could not frustrate the falling apart of the polyhedral parts, because the parts are nonexistent except as parts of wholes, and exact proportionality is not required in the structuring.
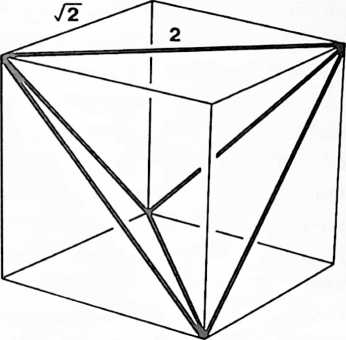
Fig. 986.210 Diagonal of Cube as Unity in Synergetic Geometry: In synergetic geometry mensural unity commences with the tetra edge as prime vector. Unity is taken not from the cube edge but from the edge of one of the two tetra that structure it. (Compare Fig. 463.01.) Proportionality exactly known to us is not required in nature’s structuring. Parts have no existence independent of the polyhedra they constitute.
[986.211]{style="color: purple3"} []{#ver:986.211 label="ver:986.211"} Whatever the workings of my subconscious may have been, the facts remain that I had erroneously concluded that the 5 was the tetravolume of the sphere whose diameter was our unit vector whose value was 2. In due course I received a letter from a mathematician, Ramsey Campbell, whose conventional calculations seemed to show that I was wrong. But I was not convinced that his conventional results were not also erroneous, inasmuch as they had been “cubically” arrived at rather than tetrahedrally referenced.
[986.212]{style="color: purple3"} []{#ver:986.212 label="ver:986.212"} At this point a young associate of mine, Robert Gripwho was convinced that I was misconvincedand who knew that I would alter my position only as confronted by physically demonstrable evidence, made a gallon-sized, water-holding tetrahedron and a sphere whose diameter was identical with the prime vector length of the tetrahedron’s edge. The water content the volumeof the sphere was indeed 4.43 units less than 5.7.
[986.213]{style="color: purple3"} []{#ver:986.213 label="ver:986.213"} The cubically-arrived-at spherical volume (A) of a sphere of diameter equal to the unit edge of the coordinate system’s cube is 4.188. To convert that spherical volume value (A) to that of sphere (B) whose diameter is equal to the diagonal of the face of the system’s cube, we multiply the volume of sphere (A) by the synergetics hierarchy s volumetric constant, which is obtained by taking synergetics’ unit vector linear constant 1.01 and raising it to its third-poweror volumetric dimension, which is , which equals . Multiplying the XYZ system’s cube-edge-diametered (A) sphere’s volume of 4.1888 by the synergetics volumetric constant of 1.0606 gives us 4.4429, which is the sought-for volume of the sphere (B). I thanked Mr. Campbell and acknowledged my error.
[986.214]{style="color: purple3"} []{#ver:986.214 label="ver:986.214"} I then said to my mathematical associates, Robert Grip and Chris Kitrick, that there is no single item that more effectively advances research than the unblocking of our thought processesthrough experiential evidence of a previously held erroneous assumption. Wherefore my intuition told me that my error may have been stubbornly clung to because there might be something very important to be discovered in this region of investigation. There is possibly some enlightening significance in the fact that I had intuitively applied (and again forsaking the first correction, had doubly reapplied) my third-power synergetics’ conversion factor to an already-three-dimensional cubic-volume quantation, which on the occasion of these retreatments had erroneously seemed to me to be as yet three powers short of the minimum primitive realizable somethingness.
[986.215]{style="color: purple3"} []{#ver:986.215 label="ver:986.215"} Why did I think as I did? Why was I puzzled? I was not confused about arithmetical operations per se. We conventionally arrive at the area of a square by multiplying the square’s edge length by itself, and we arrive at the volume of a cube by multiplying its edge length times itself twicethat is, we identify the square’s area by the second power of its edge length, and we identify a cube’s volume by the third power of its edge length. All that seems simple and clear … until we discover that the cube does not exist and cannot exist until it has at least three other observable attributes: weight, duration, and temperature. Given the quantitative inputs for those coordinate factors, the cube as yet fails to “exist,” because as calculated it is now “solid,” and physics has discovered and proven that no such solid phenomenon exists; wherefore the cubical domain has to be substantively populated by atoms which have a variety of interspacing and interpositioning behavioral patterns.
[986.216]{style="color: purple3"} []{#ver:986.216 label="ver:986.216"} Also, in order to exist the cube must have both tension and compression forces so arranged and quantated as to produce a self-stabilizing, independent behavior in the presence of the cosmic complex of coexisting force events. For it to exist there also must be introduced coordinate factors that account for the fact that this special case cube is keeping locatable company with the planet Earth with which it is traveling around the Sun at approximately 60,000 miles per hour.
[986.217]{style="color: purple3"} []{#ver:986.217 label="ver:986.217"} As the Earth and the Sun whirl circumferentially in company with the other hundred billion stars of the galactic system, and as all the while the galactic system keeps company with all the now-known billion such galaxies whose uniformly angled retreat from one another at an astronomical speed altogether constitutes what is called the Expanding Universe …if we wrote out the formula for integrating all those quantities and for realistically diagramming its geometry and its dimensions, we would have to admit that the dimensions of the cube did not as yet produce existence. There would as yet be required the set of coordinate factors stating when and where the cube was born, how old it was at the moment of its dimensioning, and what its exact remaining longevity would beand with all that, we have not disclosed its smell, its resonance factor, its electromagnetic-wave propagation length and frequencies. My quandary was one of adequately identifying and calculating the magnitude of relevant dimensions for the “considered set” (Section 509).
[986.218]{style="color: purple3"} []{#ver:986.218 label="ver:986.218"} My quandary also included, “Which exactly are the attributes that are being disclosed by the successive powerings?” With all the foregoing considerations I resolved upon the following set as that which I would employ in publishing Synergetics.
[986.219]{style="color: purple3"} []{#ver:986.219 label="ver:986.219"} Since our dimensional control is the prime vector, and since a vector’s relative size represents mass times velocity, and since mass has a priori both volume and weight, it inherently introduces one more dimension to velocity’s a priori two-dimensional product of time and distance. Ergo, vectors are in themselves primitive, pre-time-size, potentially energizable, three-dimensional phenomena. Any special case time-size phenomena must also be multiplied by frequency of subdivision of the primitive system taken volumetrically to the third power. We seem thus to have arrived at nine dimensionsi.e., ninth powering and we have altogether identified geometrical realization as being at least nine-dimensional.
[986.220]{style="color: purple3"} []{#ver:986.220 label="ver:986.220"} This is how I came to adopt my ninth-power factor for conversion from coordination to synergetics coordination. Employing the XYZ-coordinated volume of , I multiplied it by the appropriate factor (see table 986.209, where we find that ), which produced the inherently imperfect (only chord-describable rather than arc-describable) sphere of 4.998243305. This I knew was not a primitive three-dimensional or six-dimensional volume, and I assumed it to be the value of potential energy embraceable by a sphere of vector radius = 1. Ergo, both my conscious and subconscious searchings and accountings were operating faultlessly, but I was confusing the end product, identifying it as volume instead of as potential energy.
[986.221]{style="color: purple3"} []{#ver:986.221 label="ver:986.221"} I was astonished by my error but deeply excited by the prospect of reviewing the exponentially powered values. Looking over the remaining valid trail blazings, I ruminated that the proximity to 5 that provoked the figure might have other significancefor instance, as a real ninth-dimensional phenomenon. There was some question about that constant being a sixth-dimension figure: N3,N3 =N6, which operation I hadin my forgetfulness and carelessness inadvertently performed. Or the figure I had arrived at could be taken as nine-dimensional if you assume primitive demonstrability of minimum something always to have a combined a priori volumetric-and-energetic existence value, which is indeed what synergetics vectorial structuring does recognize to be naturally and demonstrably true. (See Sec. 100.20.)
[986.222]{style="color: purple3"} []{#ver:986.222 label="ver:986.222"} Synergetics demonstrates that the hierarchy of vectorially defined, primitive, triangularly self-stabilized, structural-system polyhedra is initially sixth-dimensional, being both a vectorially six-way coordinate system (mass X velocity) as well as being tetrahedrallyergo, four-dimensionally-coordinate[^39]ergo, TV6 N4 =Ni0 somethings; and that they grow expansively in time-sizeergo, in volume at the rate of F3 ergo, in time-size Dw • D3 =D13, a 13-dimensional special-case-somethingness of reality.
[986.223]{style="color: purple3"} []{#ver:986.223 label="ver:986.223"} We have learned in synergetics by physical experiment that in agglomerating unit-radius, closest-packed spheres around a nuclear sphere of the same unit radius, successively concentric symmetrical layers of the nuclear surroundment occur in a pattern in which the number of spheres in the outer shell is always the second power of the frequency of modular-system subdivision of the vector-defined edges of the system, and that when the primitive interhierarchy’s relative volumetric values are multiplied by frequency to the third powerand an additional factor of sixit always gives the symmetrical system’s total cumulative volume growth, not only of all its progressively concentric, closest-packed, unit-radius spheres’ combined shells, but also including the volume of the unit-radius, closest-packed sphere shells’ interstitial spaces, as altogether embraced by the exterior planes of the primitive polyhedra of reference. (See Sec. 971 and, in the drawings section, Fig. 970.20, “Dymax Nuclear Growth” (10 June 1948), and “Light Quanta Particle Growth” (7 May 1948); also drawings published in 1944 appearing as end papers to Synergetics 2.)
¶ 986.231 System Spinnability
[986.231]{style="color: purple3"} []{#ver:986.231 label="ver:986.231"} Synergetics assumes an a priori to time-size, conceptually primitive, relative volumetric value of all the hierarchy of primitive polyhedra; and it also assumes that when we introduce frequency, we are also introducing time and size (see Secs. 782.50 and 1054.70), and we are therefore also introducing all the degrees of freedom inherent in time-size realizations of energetic-system behavioras for instance the phenomenon of inherent system spinnability.
[986.232]{style="color: purple3"} []{#ver:986.232 label="ver:986.232"} With the introduction of the phenomenon of system spinnability around any one or several or all of the hierarchy of concentric symmetric systems’ seven axes of symmetry (Sec. 1040), we observe experientially that such inherent system spinnability produces a superficially spherical appearance, whose time-size realizations might be thought of as being only the dynamic development in time-size aspects of the primitive static polyhedral states. We recall the scientific nondemonstrability of the Greek sphere as defined by them (Secs. 981.19 and 1022.11). We also recall having discovered that the higher the frequency of the unit-radius-vertexed, symmetrical polyhedra of our primitive cosmic hierarchy, the more spherical do such geodesic-structured polyhedra appear (compare Sec. 986.064). I realized that under these recalled circumstances it could be safely assumed that a sphere does not exist in the primitive hierarchy of pre-time-size polyhedral conceptioning, whose timeless-sizelessergo, eternal perfection alone permitted consideration of the vector equilibrium’s isotropic vector matrix as the fourdimensional frame of reference of any time-size intertransforming aberrations of realizable physical experience. Such perfection can be only eternal and timeless.
[986.233]{style="color: purple3"} []{#ver:986.233 label="ver:986.233"} Timeless but conceptually primitive polyhedra of differently-lengthed-and-radiused external vertexes can be dynamically spinnable only in time, thereby to produce circular profiles some of whose longer radii dominantly describe the superficial, illusory continuity whose spherical appearance seems to be radially greater than half the length of the prime vector. (See Fig. 986.314.)
[986.234]{style="color: purple3"} []{#ver:986.234 label="ver:986.234"} Thus the only-superficially-defined spherical appearance is either the consequence of the multiplicity of revolving vertexes of the polyhedron occurring at a distance outwardly of the unit vector radius of the prime polyhedral hierarchy, or it could be inherent in the centrifugal deformation of the polyhedral structure. Wherefore I realized that my having unwittingly and redundantly applied the synergetics constant of the sixth powerrather than only of the third powerand my having applied that sixth-power factor to the theretofore nonexistent static sphere of the Greeks’ energy-and-time deprived three-dimensionality, was instinctively sound. Thus the erroneous result I had obtained must not discourage my intuitive urge to pursue the question further. I had inadvertently produced the slightly-greater-than-vector-radiused, high-frequency “spheric” polyhedron.
[986.235]{style="color: purple3"} []{#ver:986.235 label="ver:986.235"} It seemed ever more evident that it could be that there is no true sphere in Universe. This seemed to be confirmed by the discovery that the sum of the angles around all the vertexes of any system will always be 720 degrees one tetraless than the number of the system’s external vertexes times 360 degrees (Sec. 224). It could be that the concept conjured up by the mouthed-word sphere itself is scientifically invalid; ergo, it could be that the word sphere is not only obsolete but to be shunned because it is meaningless and possibly disastrously misleading to human thought.
¶ 986.240 The Sphere Experimentally Defined
[986.241]{style="color: purple3"} []{#ver:986.241 label="ver:986.241"} The best physically demonstrable definition of the “spheric” experience is: an aggregate of energy events approximately equidistant, multidirectionally outwardly from approximately the same central event of an only approximately simultaneous set of external eventsthe more the quantity of external points measuringly identified and the more nearly simultaneous the radius-measuring events, the more satisfactorily “spherical.” With each of all the outward unit-radius events most economically and most fully triangularly interchorded with their most immediate neighborschords being shorter than their corresponding arcswe find that the “spheric” experience inherently describes only high-frequency, omnitriangularly faceted polyhedra. By geometrical definition these are geodesic structures whose volumes will always be something less than a theoretically perfect omni-arc-embraced sphere of the same radius as an omni-chord-embraced geodesic sphere’s uniformly radiused outer vertexes.
[986.242]{style="color: purple3"} []{#ver:986.242 label="ver:986.242"} As is demonstrated in Sec. 224, the sum of the angles around all the vertexes of any system will always be 720 degrees less than the number of vertexes multiplied by 360 degrees. By the mathematicians’ definition a perfect arc-embraced sphere would have to have 360 degrees around every point on its surface, for the mathematicians assume that for an infinitesimal moment a sphere’s surface is congruent with the tangent plane. Trigonometry errs in that it assumes 360 degrees around every spherical surface point.
¶ 986.300 Minimum-Maximum System Limits
[986.301]{style="color: purple3"} []{#ver:986.301 label="ver:986.301"} Consideration 11: Maximum-limit Case
[986.302]{style="color: purple3"} []{#ver:986.302 label="ver:986.302"} The explorer gains assurance by discovering the relevant minimum-maximum limit casesthe min-max limits of the variablesof the system under consideration.
[986.303]{style="color: purple3"} []{#ver:986.303 label="ver:986.303"} For instance, we have learned through experimental evidence, the cosmic hierarchy of primitive polyhedra has a limit set of seven axes of great-circle symmetries and spinnabilities. They are the 3, 4, 6 ( ), 12, 10, 15, 6 (icosa) great-circle-spinnable systems. (See Table 986.304 and Sec. 1040.) Within that inherently limited hierarchy of seven symmetries, the triacontahedron, with its 15 different great circles’ self-hemispherings and 120 triangular interconfigurings, produces the maximum-limit number of identical polyhedral surface self-facetings of all great-circle systems in Universe (Sec. 400).
Table 986.304: Limit Set of Seven Axes of Spinnability
+:-------------------+:-----------------+
| Generalized Set | |
+--------------------+------------------+
| of All Symmetrical | Spinnable System |
+--------------------+------------------+
| Systems: | Great Circles: |
+--------------------+------------------+
| #1 | ::: minipage |
| | > 3 |
| | ::: |
+--------------------+------------------+
| #2 | ::: minipage |
| | > 4 |
| | ::: |
+--------------------+------------------+
| #3 | ::: minipage |
| | > 6 ( ) |
| | ::: |
+--------------------+------------------+
| #4 | ::: minipage |
| | > 12 |
| | ::: |
+--------------------+------------------+
| #5 | ::: minipage |
| | > 10 |
| | ::: |
+--------------------+------------------+
| #6 | ::: minipage |
| | > 15 |
| | ::: |
+--------------------+------------------+
| #7 | ::: minipage |
| | > 6 (icosa) |
| | ::: |
+--------------------+------------------+
(Compare Secs. 1041.01 and 1042.05.)
¶ 986.310 Strategic Use of Min-max Cosmic System Limits
[986.311]{style="color: purple3"} []{#ver:986.311 label="ver:986.311"} The maximum limit set of identical facets into which any system can be divided consists of 120 similar spherical right triangles whose three corners are 60 degrees at A, 90 degrees at C, and 36 degrees at B. Sixty of these right spherical triangles are positive (active), and 60 are negative (passive). (See Sec. 901.)
[Section thru \cosbhebron ,]{.smallcaps} BOQECRHEDRON, RHOMBIC TRI SCON T HEBRON , 120 TRIANGLES ENENICONTAHEDRC.N, USING, ONE qRERT CIRCLE OF THE 15 QRERT CIRCLES OF THE [IcosrheoROn]
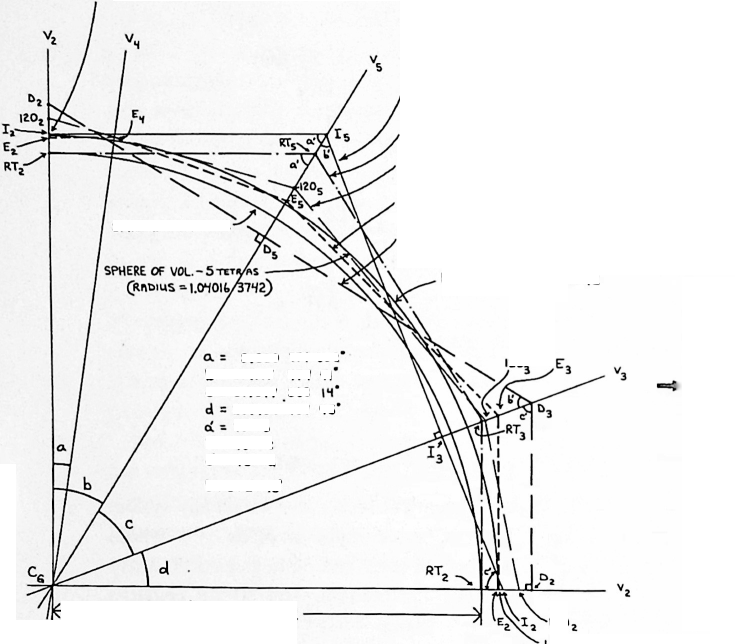
[986.312]{style="color: purple3"} []{#ver:986.312 label="ver:986.312"} These 120 right spherical surface triangles are described by three different central angles of degrees for arc AB, degrees for arc BC, and degrees for arc AC which three central-angle arcs total exactly 90 degrees. These 120 spherical right triangles are self-patterned into producing 30 identical spherical diamond groups bounded by the same central angles and having corresponding flat-faceted diamond groups consisting of four of the 120 angularly identical (60 positive, 60 nega tive) triangles. Their three surface corners are 90 degrees at C, degrees at B, and degrees at (See Fig. 986.502.)
[986.313]{style="color: purple3"} []{#ver:986.313 label="ver:986.313"} These diamonds, like all diamonds, are rhombic forms. The 30-symmetrical-diamond system is called the rhombic triacontahedron, its 30 mid-diamond faces (right-angle cross points) are approximately tangent to the unit-vector-radius sphere when the volume of the rhombic triacontahedron is exactly tetravolume-5. (See Fig. 986.314.)
[986.314]{style="color: purple3"} []{#ver:986.314 label="ver:986.314"} I therefore asked Robert Grip and Chris Kitrick to prepare a graphic comparison of the various radii and their respective polyhedral profiles of all the symmetric polyhedra of tetravolume 5 (or close to 5) existing within the primitive cosmic hierarchy (Sec. 982.62)i.e. other than those of tetravolumes 1, 2, 3, 4, and 6which carefully drafted drawing of the tetravolume-5 polyhedra (and those polyhedra “approximately” tetravolume 5) my colleagues did prepare (see Fig. 986.314). These exactly tetravolume-5 polyhedra are, for example
-
the icosahedron with outer edges of unit vector length;
-
the icosahedron of outer vertex radius of unit vector length;
-
the regular dodecahedron of unit vector edge; and
-
the regular dodecahedron of unit vector radius
all of which show that they have only a slightly greater radius length than that of the prime vector.
Fig. 986.314 Polyhedral Profiles of Selected Polyhedra of Tetravolume-5 and Approximately Tetravolume-5: graphic display of the radial proximity to one another of exact and neighboring tetravolume-5 polyhedra, showing central angles and ratios to prime vector.
+---------------------+--------------+--------------+--------------+
| ::: minipage | ::: minipage | ::: minipage | ::: minipage |
| D5 | 0 997 | 020 | ::: |
| ::: | ::: | ::: | |
+:====================+:=============+:=============+:=============+
| D2 | . 113 | | 23l» |
+---------------------+--------------+--------------+--------------+
| D3 | . 191 | | |
+---------------------+--------------+--------------+--------------+
| 12O„5 | | Ott | |
+---------------------+--------------+--------------+--------------+
| • RT-, | 999 | | |
+---------------------+--------------+--------------+--------------+
| RTS | . 179 | 9t3 | |
+---------------------+--------------+--------------+--------------+
| [rt3]{.smallcaps} | . Ot9 | | 19H |
+---------------------+--------------+--------------+--------------+
| | . 095 | | |
+---------------------+--------------+--------------+--------------+
| X3 | | | |
+---------------------+--------------+--------------+--------------+
| | | | |
+---------------------+--------------+--------------+--------------+
| E2 | | E39 | |
+---------------------+--------------+--------------+--------------+
| E5 | | | |
+---------------------+--------------+--------------+--------------+
| E3 | . 112 | | |
+---------------------+--------------+--------------+--------------+
| [e9]{.smallcaps} | | b9S | |
+---------------------+--------------+--------------+--------------+
[986.315]{style="color: purple3"} []{#ver:986.315 label="ver:986.315"} The chart of the polyhedral profiles (Fig. 986.314) shows the triacontahedron of tetravolume 5 having its mid-diamond-face point at a distance outward radially from the volumetric center that approximately equals the relative length of the prime vector. I say “approximately” because the trigonometrically calculated value is instead of 1, a radial difference, whichthough possibly caused in some very meager degree by the lack of absolute resolvability of trigonometric calculations themselves is on careful mathematical review so close to correct as to be unalterable by any known conventional trigonometric error allowance. It is also so correct as to hold historical significance, as we shall soon discover. Such a discrepancy is so meager in relation, for instance, to planet Earth’s spheric diameter of approximately 8,000 miles that the spherical surface aberration would be approximately the same as that existing between sea level and the height of Mount Fuji, which is only half the altitude of Mount Everest. And even Mount Everest is invisible on the Earth’s profile when the Earth is photographed from outer space. The mathematical detection of such meager relative proportioning differences has time and again proven to be of inestimable value to science in first detecting and then discovering cosmically profound phenomena. In such a context my “spherical energy content” of , instead of exactly , became a thought-provoking difference to be importantly remembered.
[986.316]{style="color: purple3"} []{#ver:986.316 label="ver:986.316"} By careful study of the Grip-Kitrick drawings of tetravolume-5 polyhedra it is discovered that the graphically displayed zones of radial proximity to one another of all the tetravolume-5 symmetric polyhedra (Fig. 986.314) describe such meager radial differences at their respective systems outermost points as to suggest that their circumferential zone enclosed between the most extremely varied and the most inwardly radiused of all their axially spun vertexes of the exact tetravolume-5 polyhedra may altogether be assumed to constitute the zone of limit cases of radiantly swept-out and pulsating tetravolume-5 kinetic systems.
[986.317]{style="color: purple3"} []{#ver:986.317 label="ver:986.317"} Recognizing that polyhedra are closed systems and that there are only seven cases of symmetrical subdivisioning of systems by the most economical great-circle spinnings (and most economically by the chords of the great-circle arcs), we discover and prove structurally that the maximum-limit abundance of a unit-symmetrical-polyhedral-system’s identical facetings is the rhombic triacontahedron, each of whose 30 symmetrical diamond planar faces may be symmetrically subdivided into four identical right triangles , and we find that the triacontahedron’s 120-spherical-right-triangled frame of system reference is the maximum-limit case of identical faceting of any and all symmetrical polyhedral systems in Universe. This maximum-limit-system structuring proof is accomplished by the physically permitted, great-circle-spun, hemispherical self-halvings, as permitted by any and all of the seven cosmic limit cases of symmetric systems’ being spun-defined around all the respective system’s geometrically definitive (ergo, inherent) axes of symmetrical spinnability. It is thus that we learn experimentally how all the symmetric systems of Universe self-fractionate their initial system unities into the maximum number of omniangularly identical surface triangles outwardly defining their respective internal-structure tetrahedra whose anglescentral or surfaceare always independent of a system’s time-size considerations. And because they are independent of time-size considerations, such minimum-maximum limit-case ranges embrace all the symmetrical polyhedral systems’ generalized-primitive-conceptuality phenomena.
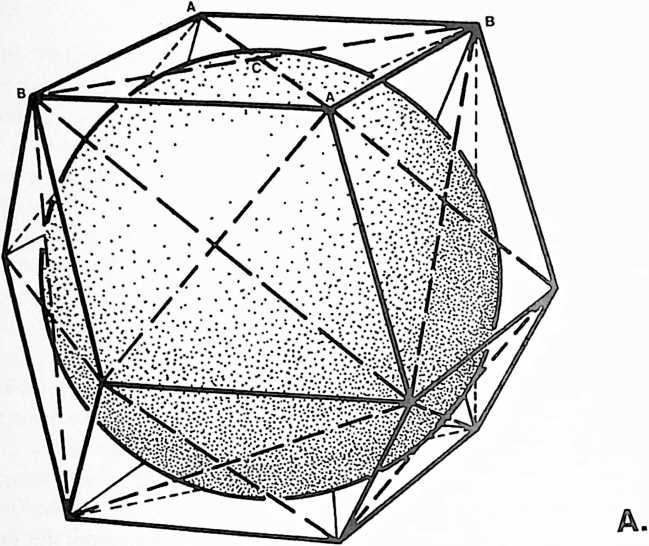
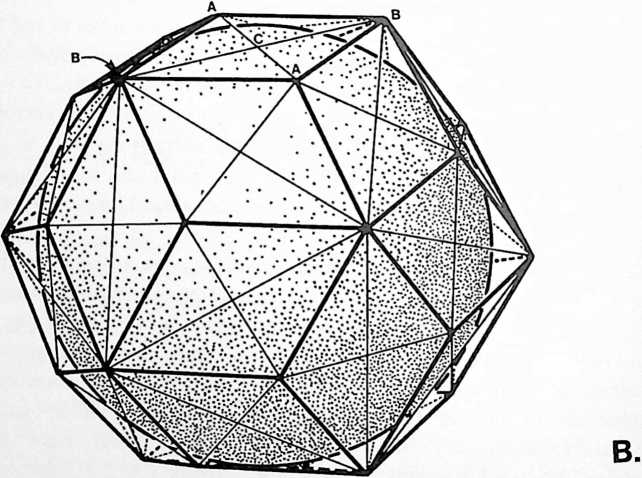
Fig. 986.405 Respective Subdivision of Rhombic Dodecahedron (A) and Rhombic Triacontahedron (B) into Diamond-faced Pentahedra: O is at the respective volumetric centers of the two polyhedra, with the short axes A-A and the long axes B-B (diagrams on the right). The central and surface angles of the two pentahedra differ as shown.
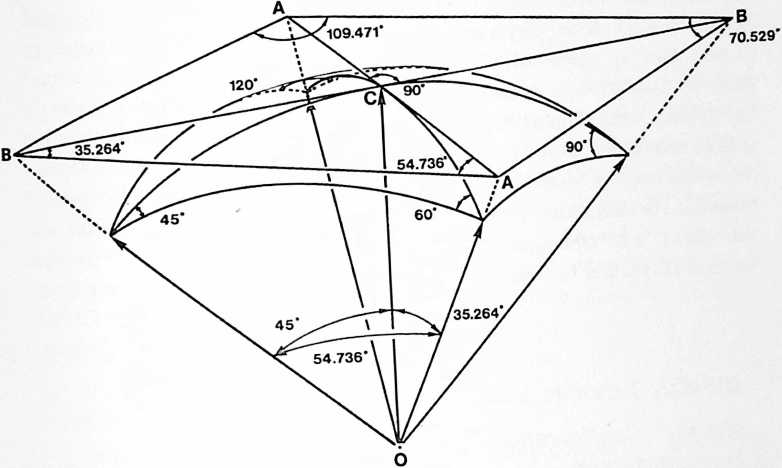
¶ 986.400 Quanta Module
[986.401]{style="color: purple3"} []{#ver:986.401 label="ver:986.401"} Consideration 12: Dynamic Spinning of Rhombic Triacontahedron
[986.402]{style="color: purple3"} []{#ver:986.402 label="ver:986.402"} I then speculated that the only-by-spinning-produced, only superficially apparent “sphericity” could be roundly aspected by spinning the rhombic triacontahedron of tetravolume 5. This rational volumetric value of exactly 5 tetravolumes placed the rhombic triacontahedron neatly into membership in the primitive hierarchy fainily of symmetric polyhedra, filling the only remaining vacancy in the holistic rational-number hierarchy of primitive polyhedral volumes from 1 through 6, as presented in Table 1053.51A.
[986.403]{style="color: purple3"} []{#ver:986.403 label="ver:986.403"} In the isotropic vector matrix system, where R = radius and , PV = 1 =Rergo, = prime vector radius, which is always the unity of . In the 30-diamond-faceted triacontahedron of tetravolume 5 and the 12-diamond-faceted dodecahedron of tetravolume 6, the radius distances from their respective symmetric polyhedra’s volumetric centers 0 to their respective mid-diamond faces (i.e., their short-and-long-diamond-axes’ crossing points) are in the rhombic triacontahedral case almost exactly PVR i.e., PVRand in the rhombic dodecahedral case exactly PVR, .
[986.404]{style="color: purple3"} []{#ver:986.404 label="ver:986.404"} In the case of the rhombic dodecahedron the mid-diamond-face point is exactly distance from the polyhedral system’s volumetric (nucleic) center, while in the case of the rhombic triacontahedron the point is at approximately distance from the system’s volumetric (nucleic) center. The distance outward to from the nucleic center of the rhombic dodecahedron is that same length as the prime unit vector of the isotropic vector matrix. This aspect of the rhombic triacontahedron is shown at Fig. 986.314.
[986.405]{style="color: purple3"} []{#ver:986.405 label="ver:986.405"} The symmetric polyhedral centers of both the rhombic dodecahedron and the rhombic triacontahedron may be identified as 0, and both of their respective external diamond faces’ short axes may be identified as and their respective long axes as B-B. Both the rhombic dodecahedron’s and the triacontahedron’s external diamond faces and their respective volumetric centers 0 describe semiasymmetric pentahedra conventionally labeled as OABAB. The diamond surface faces of both OABAB pentahedra are external to their respective rhombic-hedra symmetrical systems, while their triangular sides (four each) are internal to their respective rhombic-hedra systems. The angles describing the short /-/ axis and the long B-B axis, as well as the surface and central angles of the rhombic dodecahedron’s OABAB pentahedron, all differ from those of the triacontahedron’s OABAB pentahedron.
¶ 986.410 Quanta Module
[986.411]{style="color: purple3"} []{#ver:986.411 label="ver:986.411"} The respective 12 and 30 pentahedra OABAB of the rhombic dodecahedron and the triacontahedron may be symmetrically subdivided into four right-angled tetrahedra ABCO, the point being surrounded by three right angles ABC, BCO, and ACO. Right-angle is on the surface of the rhombic-hedra system and forms the face of the tetrahedron ABCO, while right angles and are internal to the rhombic-hedra system and from two of the three internal sides of the tetrahedron ABCO. The rhombic dodecahedron consists of 48 identical tetrahedral modules designated ABCOd. The triacontahedron consists of 120 (60 positive and 60 negative) identical tetrahedral modules designated ABCOt, for which tetrahedron ABCOt we also introduce the name T Quanta Module.
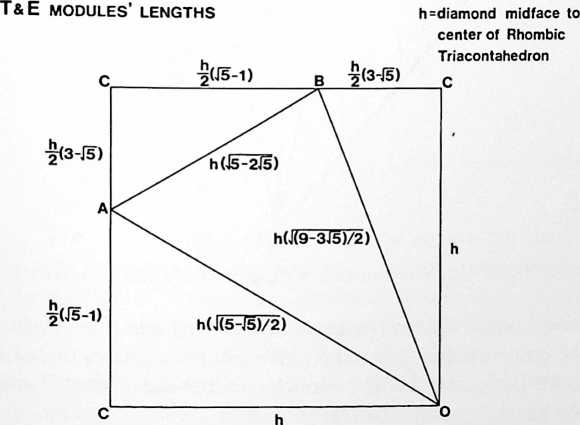
Fig. 986.411A and Quanta Modules: Edge Lengths: This plane net for the Quanta Module and the Quanta Module shows their edge lengths as ratioed to the octa edge. Octa edge = tetra edge = unity.
T & E [modules’ angles]
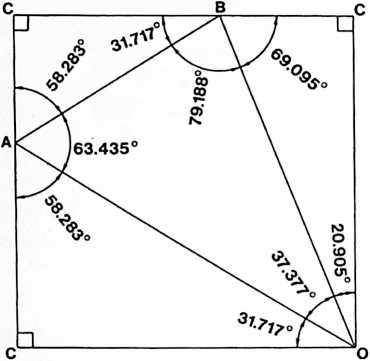
Fig. 986.41 IB and Quanta Module Angles: This plane net shows the angles and the foldability of the Quanta Module and the Quanta Module.
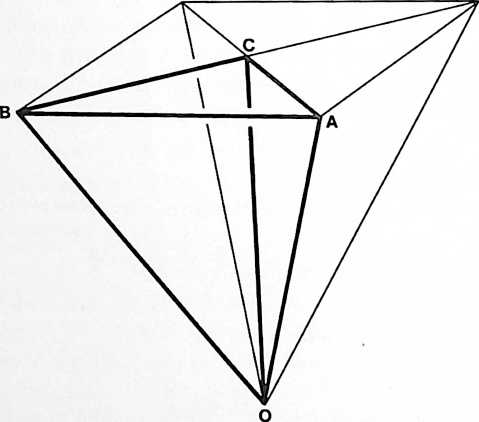
Fig. 986.411C and Quanta Modules in Context of Rhombic Triacontahedron
[986.412]{style="color: purple3"} []{#ver:986.412 label="ver:986.412"} The primitive tetrahedron of volume 1 is subdivisible into 24 Quanta Modules. The triacontahedron of exactly tetravolume 5, has the maximum-limit case of identical tetrahedral subdivisibilityi.e., 120 subtetra. Thus we may divide the 120 subtetra population of the symmetric triacontahedron by the number 24, which is the identical subtetra population of the primitive omnisymmetrical tetrahedron: . Ergo, volume of the Quanta Module = volume of the Quanta Module.
[986.413]{style="color: purple3"} []{#ver:986.413 label="ver:986.413"} The rhombic dodecahedron has a tetravolume of 6, wherefore each of its 48 identical, internal, asymmetric, component tetrahedra has a regular tetravolume of = . The regular tetrahedron consists of 24 quanta modules (be they ,[^40] or Quanta Modules; therefore , having \sfrac{1}{8}-tetravolume, also equals three quanta modules. (See Fig. 986.413.)
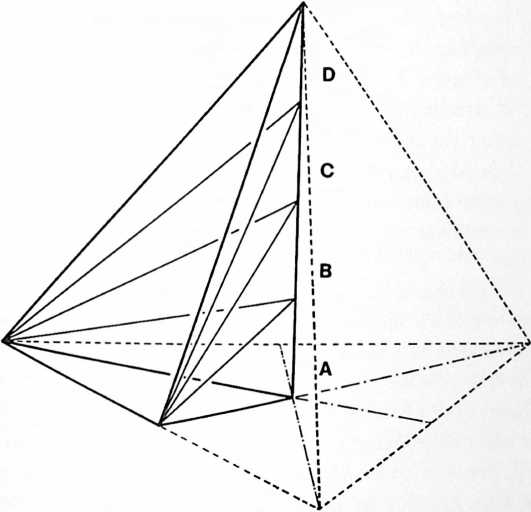
Fig. 986.413 Regular Tetrahedron Composed of 24 Quanta Modules: Compare Fig. 923.10B.
[986.414]{style="color: purple3"} []{#ver:986.414 label="ver:986.414"} The vertical central-altitude line of the regular, primitive, symmetrical tetrahedron may be uniformly subdivided into four vertical sections, eac of which we may speak of as quarter-prime-tetra altitude units each of w ic altitude division points represent the convergence of the upper apexes of the equivolume modules (as illustrated in Fig. 923.10B whereprior to the discovery of the “Einstein” Module additional modules were designated through , and will hence forth be designated as successive groups). The vertical continuance of these unit-altitude differentials produces an infinite series of equivolume modules, which we identify in vertical series continuance by groups of four repetitive groups, as noted parenthetically above. Their combined group-of-four, externally protracted, altitude increase is always equal to the total internal altitude of the prime tetrahedron.
[986.415]{style="color: purple3"} []{#ver:986.415 label="ver:986.415"} The rhombic triacontahedron has a tetravolume of 5, wherefore each of its 120 identical, internal, asymmetric, component tetrahedra , the Quanta Module, has a tetravolume of \sfrac{5}{120}= \sfrac{1}{24} tetravolume ergo, the volume of the Quanta Module is identical to that of the and Quanta Modules. The rhombic dodecahedron’s 48 asymmetric tetrahedra equal three of the rhombic triacontahedron’s 120 Quanta Module asymmetric tetrahedra. The rhombic triacontahedrons ABCO Quanta Module tetrahedra are each \sfrac{1}{24} of the volume of the primitive “regular” tetrahedronergo, of identical volume to the Quanta Module. The Mod, like the Mod, is structurally modeled with one of its four corners omnisurrounded by three right angles.
[986.416]{style="color: purple3"} []{#ver:986.416 label="ver:986.416"} 1 Module = 1 Module = 1 Module = 1 Module = 1 Module = any one of the unit quanta modules of which all the hierarchy of concentric, symmetrical polyhedra of the family are rationally comprised. (See Sec. 910).
[986.417]{style="color: purple3"} []{#ver:986.417 label="ver:986.417"} I find that it is important in exploratory effectiveness to remember as we find an increasingly larger family of equivolume but angularly differently conformed quanta modulesthat our initial exploration strategy was predicated upon our generalization of Avogadro’s special-case (gaseous) discovery of identical numbers of molecules per unit volume for all the different chemical-element gases when individually considered or physically isolated, but only under identical conditions of pressure and heat. The fact that we have found a set of unit-volume, all-tetrahedral modulesthe minimum-limit structural systemsfrom which may be aggregated the whole hierarchy of omnisymmetric, primitive, concentric polyhedra totally occupying the spherically spun and interspheric accommodation limits of closest-packable nuclear domains, means that we have not only incorporated all the min-max limit-case conditions, but we have found within them one unique volumetric unit common to all their primitive conformational uniqueness, and that the volumetric module was developed by vectoriali.e., energeticpolyhedral-system definitions.
[986.418]{style="color: purple3"} []{#ver:986.418 label="ver:986.418"} None of the tetrahedral quanta modules are by themselves allspace-filling, but they are all groupable in units of three (two A’s and one Bwhich is called the Mite) to fill allspace progressively and to combine these units of three in nine different waysall of which account for the structurings of all but one of the hierarchy of primitive, omniconcentric, omnisymmetrical polyhedra. There is one exception, the rhombic triacontahedron of tetravolume 5 i.e., of 120 quanta modules of the class, which Quanta Modules as we have learned are of equivolume to the and Modules.
[986.419]{style="color: purple3"} []{#ver:986.419 label="ver:986.419"} The 120 Quanta Modules of the rhombic triacontahedron can be grouped in two different ways to produce two different sets of 60 tetrahedra each: the 60 tetrahedra and the 60 tetrahedra. But rhombic triacontahedra are not allspace-filling polyhedra. (See Fig. 986.419.)
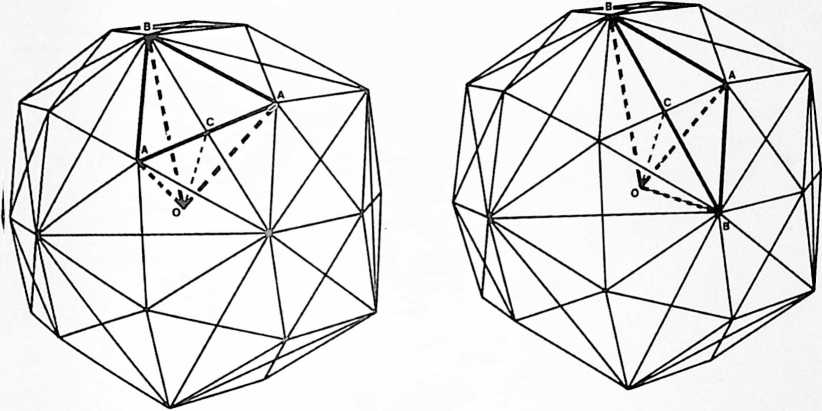
¶ 986.420 Min-max Limit Hierarchy of Pre-time-size Allspace-fillers
[986.421]{style="color: purple3"} []{#ver:986.421 label="ver:986.421"} Of all the allspace-filling module components, the simplest are the three-quanta-module Mites, consisting of two Quanta Modules (one positive and one negative) and of one Quanta Module (which may be either positive or negative). Thus a Mite can be positive or negative, depending on the sign of its Quanta Module. The Mites are not only themselves tetrahedra (the minimum-sided polyhedra), but they are also the simplest minimum-limit case of allspace-filling polyhedra of Universe, since they consist of two energy-conserving Quanta Modules and one equivolume energy dispersing Quanta Module. The energy conservation of the Quanta Module is provided geometrically by its tetrahedral form, four different right-triangled facets being all foldable from one unique flat-out whole triangle (Fig. 913.01), which triangle’s boundary edges have reflective properties that bounce around internally to those triangles to produce similar smaller triangles: Ergo, the Quanta Module acts as a local energy holder. The Quanta Module is not foldable out of one whole triangle, and energies bouncing around within it tend to escape. The Quanta Module acts as a local energy dispenser. (See Fig. 986.421.)
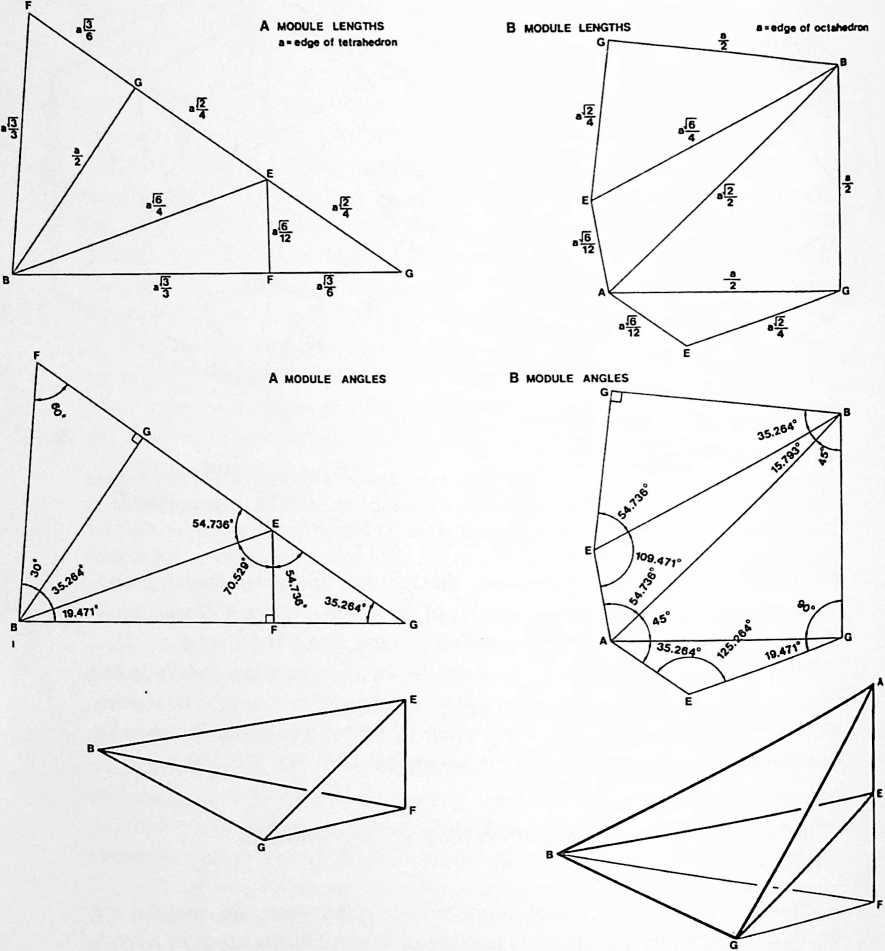
[986.422]{style="color: purple3"} []{#ver:986.422 label="ver:986.422"} Mite: The simplest allspace-filler is the Mite (see Secs. 953 and 986.418). The positive Mite consists of 1 + mod, 1 - mod, and 1 + mod; the negative Mite consists of 1 +mod, 1 A mod, and 1 B-mod. Sum-total number of modules
MITE( (See color plate 17.)
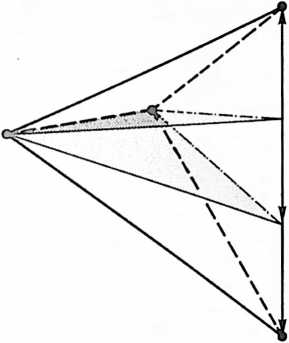
[986.423]{style="color: purple3"} []{#ver:986.423 label="ver:986.423"} Around the four corners of the tetrahedral Mites are three right triangles. Two of them are similar right triangles with differently angled acute corners, and the third right triangle around that omni-right-angled corner is an isosceles.
[986.424]{style="color: purple3"} []{#ver:986.424 label="ver:986.424"} The tetrahedral Mites may be inter-edge-bonded to fill allspace, but only because the spaces between them are inadvertent capturings of Mite shaped vacancies. Positive Mite inter-edge assemblies produce negative Mite vacancies, and vice versa. The minimum-limit case always provides inadvertent entry into the Negative Universe. Sum-total number of modules is1\sfrac{1}
[986.425]{style="color: purple3"} []{#ver:986.425 label="ver:986.425"} Mites can also fill allspace by inter-face-bonding one positive and one negative Mite to produce the Syte. This trivalent interface bonding requires twice as many Mites as are needed for bivalent inter-edge-bonding. Total number of modules is
[986.426]{style="color: purple3"} []{#ver:986.426 label="ver:986.426"} Syte: The next simplest allspace-filler is the Syte. (See Sec. 953.40.) Each Syte consists of one of only three alternate ways of face-bonding two Mites to form an allspace-filling polyhedron, consisting of 2 A + mods, 2 A-mods, 1 B+mod, and 1 B-mod. Sum-total number of modules
[986.427]{style="color: purple3"} []{#ver:986.427 label="ver:986.427"} Two of the three alternate ways of combining two Mites produce tetrahedral Sytes of one kind:
while the third alternate method of combining will produce a hexahedral Syte.
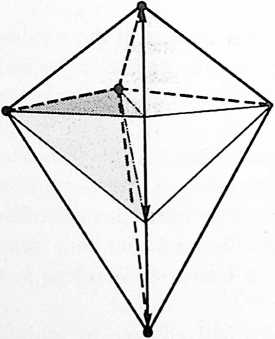
[986.428]{style="color: purple3"} []{#ver:986.428 label="ver:986.428"} Kite: The next simplest allspace-filler is the Kite. Kites are pentahedra or half-octahedra or half-Couplers, each consisting of one of the only two alternate ways of combining two Sytes to produce two differently shaped pentahedra, the Kate and the Kat, each of 4 + mods, 4 mods, 2 + mods, and 2 - mods. Sum-total number of modules
[986.429]{style="color: purple3"} []{#ver:986.429 label="ver:986.429"} Two Sytes combine to produce two Kites as
KATE (See color plate 20) KAT (See color plate 21)
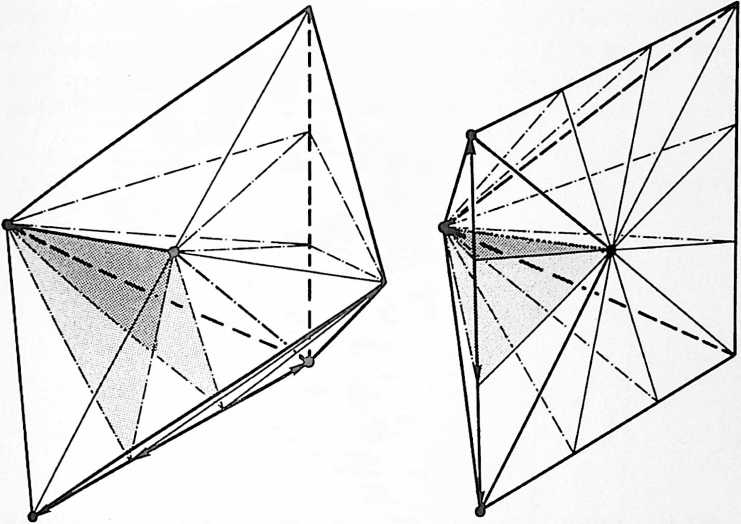
[986.430]{style="color: purple3"} []{#ver:986.430 label="ver:986.430"} Octet: The next simplest allspace-filler is the Octet, a hexahedron consisting of three Sytesergo, 6 + mods, 6 - mods, 3 + mods, and 3 - mods. Sum-total number of modules
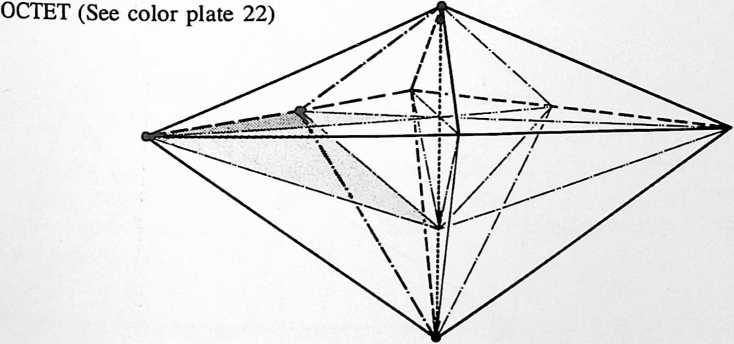
[986.431]{style="color: purple3"} []{#ver:986.431 label="ver:986.431"} Coupler: The next simplest allspace-filler is the Coupler, the asymmetric octahedron. (See Secs. 954.20–.70.) The Coupler consists of two Kites ergo, 8 + mods, 8 - mods, 4 + mods, and 4 B - mods. Sum-total number of modules
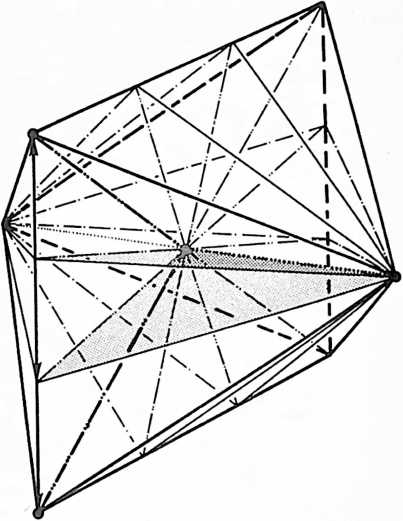
[986.432]{style="color: purple3"} []{#ver:986.432 label="ver:986.432"} Cube: The next simplest allspace-filler is the Cube, consisting of four Octetsergo, 24 + mods, 24 - mods, 12 + mods, and 12 - mods. Sum-total number of modules
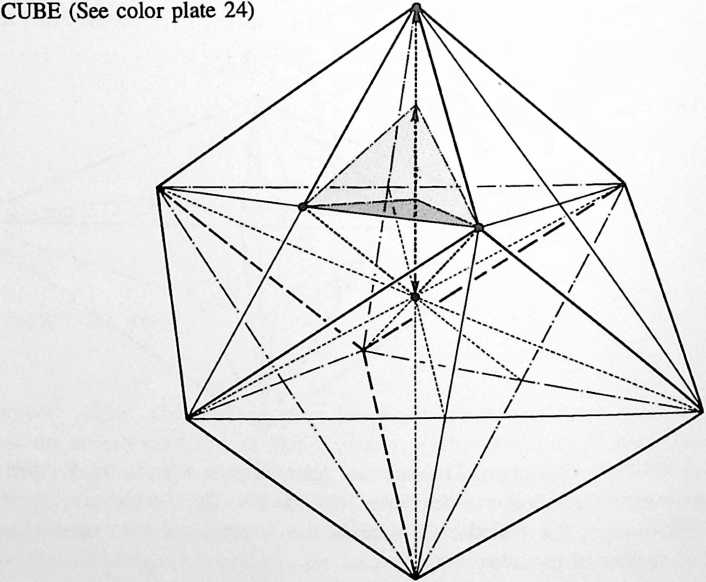
[986.433]{style="color: purple3"} []{#ver:986.433 label="ver:986.433"} Rhombic Dodecahedron: The next and last of the hierarchy of primitive allspace-fillers is the rhombic dodecahedron. The rhombic dodecahedron is the domain of a sphere (see Sec. 981.13). The rhombic dodecahedron consists of 12 Kitesergo, 48/ + mods, 48/ - mods, 24 + mods, and 24 B mods. Sum-total number of modules
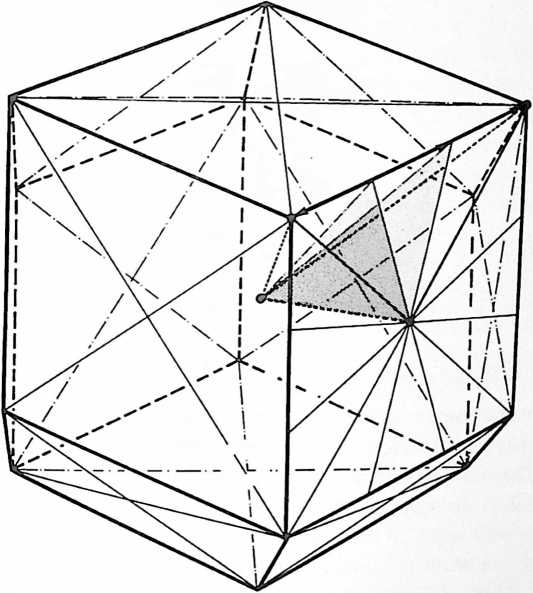
[986.434]{style="color: purple3"} []{#ver:986.434 label="ver:986.434"} This is the limit set of simplest allspace-fillers associable within one nuclear domain of closest-packed spheres and their respective interstitial spaces. There are other allspace-fillers that occur in time-size multiplications of nuclear domains, as for instance the tetrakaidecahedron. (Compare Sec. 950.12.)
¶ 986.440 Table: Set of Simple Allspace-fillers
This completes one spheric domain (i.e., sphere plus interstitial space) of one unit-radius sphere in closest packing, each sphere being centered at every other vertex of the isotropic vector matrix.
+:-------------+:------------+:-------------+:-------------------+:-------------------+:----------+
| Name: | Face | Type Hedra | A Quanta Modules | B Quanta Modules | Sum- |
| | | | | | |
| | Triangles | | | | Total |
| | | | | | |
| | | | | | Modules |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| MITE | | tetrahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| SYTE | | | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| BITE | | tetrahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| RITE | | tetrahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| LITE | | hexahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| KITE | | | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| KATE | | pentahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| KAT | | pentahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| OCTET | | hexahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| COUPLER | | octahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| CUBE | | hexahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| RHOMBIC | | | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
| DODECAHEDRON | | dodecahedron | | | |
+--------------+-------------+--------------+--------------------+--------------------+-----------+
(For the minimum time-size special case realizations of the two-frequency systems, multiply each of the above Quanta Module numbers by eight.)
¶ 986.450 Energy Aspects of Spherical Modular Arrays
[986.451]{style="color: purple3"} []{#ver:986.451 label="ver:986.451"} The rhombic dodecahedron has an allspace-filling function as the domain of any one sphere in an aggregate of unit-radius, closest-packed spheres; its 12 mid-diamond-face points are the points of intertangency of all unit-radius, closest-packed sphere aggregates; wherefore that point is the midpoint of every vector of the isotropic vector matrix, whose every vertex is the center of one of the unit-radius, closest-packed spheres.
[986.452]{style="color: purple3"} []{#ver:986.452 label="ver:986.452"} These 12 inter-closest-packed-sphere-tangency pointsthe pointsare the 12 exclusive contacts of the “Grand Central Station” through which must pass all the great-circle railway tracks of most economically interdistanced travel of energy around any one nuclear center, and therefrom through the pointsto other spheres in Universe. These points of the rhombic dodecahedron’s mid-diamond faces are also the energetic centers-of-volume of the Couplers, within which there are 56 possible unique interarrangements of the A and Quanta Modules.
[986.453]{style="color: purple3"} []{#ver:986.453 label="ver:986.453"} next discover that two ABABO pentahedra of any two tangentially adjacent, closest-packed rhombic dodecahedra will produce an asymmetric octahedron OABABO with and O being the volumetric centers (nuclear centers) of any two tangentially adjacent, closest-packed, unit-radius spheres. We call this nucleus-to-nucleus, asymmetric octahedron the Coupler, and we found that the volume of the Coupler is exactly equal to the volume of one regular tetrahedroni.e., 24 Quanta Modules. We also note that the Coupler always consists of eight asymmetric and identical tetrahedral Mites, the minimum simplex allspace-filling of Universe, which Mites are also identifiable with the quarks (Sec. 1052.360).
[986.454]{style="color: purple3"} []{#ver:986.454 label="ver:986.454"} We then discover that the Mite, with its two energy-conserving Quanta Modules and its one energy-dispersing Quanta Module (for a total combined volume of three quanta modules), serves as the cosmic minimum allspace-filler, corresponding elegantly (in all ways) with the minimumlimit case behaviors of the nuclear physics’ quarks. The quarks are the smallest discovered “particles”; they always occur in groups of three, two of which hold their energy and one of which disperses energy. This quite clearly identifies the quarks with the quanta module of which all the synergetics hierarchy of nuclear concentric symmetric polyhedra are co-occurrent.
[986.455]{style="color: purple3"} []{#ver:986.455 label="ver:986.455"} In both the rhombic triacontahedron of tetravolume 5 and the rhombic dodecahedron of tetravolume 6 the distance from system center 0 at is always greater than CO, and is always greater than/40.
[986.456]{style="color: purple3"} []{#ver:986.456 label="ver:986.456"} With this information we could reasonably hypothesize that the triacontahedron of tetravolume 5 is that static polyhedral progenitor of the only-dynamically-realizable sphere of tetravolume 5, the radius of which (see Fig. 986.314) is only .04 of unity greater in length than is the prune vector radius OC, which governs the dimensioning of the triacontahedron’s 30 midface cases of 12 right-angled corner junctions around mid-diamond-vertex C, which provides the 12 right angles around Cthe four right-angled corners of the Quanta Module’s faces of their 120 radially arrayed tetrahedra, each of which Quanta Module has a volume identical to that of the A and Quanta Modules.
[986.457]{style="color: purple3"} []{#ver:986.457 label="ver:986.457"} We also note that the radius is the same unitary prime vector with which the isotropic vector matrix is constructed, and it is also the unit-vector-radius distance outwardly from , which is always the common system center of all the members of the entire cosmic hierarchy of omniconcentric, symmetric, primitive polyhedra. In the case of the rhombic triacontahedron the 20 lines’ distances outwardly from are greater than , and the 12 lines’ distances are even greater in length outwardly from than. Wherefore I realized that, when dynamically spun, the great-circle chord lines and are centrifugally transformed into arcs and thus sprung apart at B, which is the outermost vertex ergo, most swiftly and forcefully outwardly impelled. This centrifugal spinning introduces the spherical excess of 6 degrees at the spherical system vertex B. (See Fig. 986.405.) Such yielding increases the spheric appearance of the spun triacontahedron, as seen in contradistinction to the diamond-faceted, static, planar-bound, polyhedral state aspect.
[986.458]{style="color: purple3"} []{#ver:986.458 label="ver:986.458"} The corners of the spherical triacontahedron’s 120 spherical arccornered triangles are 36 degrees, 60 degrees and 90 degrees, having been sprung apart from their planar-phase, chorded corners of degrees, degrees, and 90 degrees, respectively. Both the triacontahedron’s chorded and arced triangles are in notable proximity to the well-known 30-, 60-, and 90-degree-cornered draftsman’s flat, planar triangle. I realized that it could be that the three sets of three differently-distanced-outwardly vertexes might average their outward-distance appearances at a radius of only four percent greater distance from thus producing a moving-picture-illusioned “dynamic” sphere of tetravolume 5, having very mildly greater radius than its static, timeless, equilibrious, rhombic triacontahedron state of tetravolume 5 with unit-vector-radius integrity terminaled at vertex .
[986.459]{style="color: purple3"} []{#ver:986.459 label="ver:986.459"} In the case of the spherical triacontahedron the total spherical excess of exactly 6 degrees, which is one-sixtieth of unity = 360 degrees, is all lodged in one corner. In the planar case degrees have been added to 30 degrees at corner and subtracted from 60 degrees at corner . In both the spherical and planar trianglesas well as in the draftsman’s triangle the 90-degree corners remain unchanged.
[986.460]{style="color: purple3"} []{#ver:986.460 label="ver:986.460"} The 120 Quanta Modules radiantly arrayed around the center of volume of the rhombic triacontahedron manifest the most spherical appearance of all the hierarchy of symmetric polyhedra as defined by any one of the seven axially rotated, great circle system polyhedra of the seven primitive types of great-circle symmetries.
[986.461]{style="color: purple3"} []{#ver:986.461 label="ver:986.461"} What is the significance of the spherical excess of exactly 6 degrees? In the transformation from the spherical rhombic triacontahedron to the planar triacontahedron each of the 120 triangles releases 6 degrees. . 720 degrees = the sum of the structural angles of one tetrahedron = 1 quantum of energy. The difference between a high-frequency polyhedron and its spherical counterpart is always 720 degrees, which is one unit of quantum ergo, it is evidenced that spinning a polyhedron into its spherical state captures one quantum of energyand releases it when subsiding into its pre-time-size primitive polyhedral state.
¶ 986.470 Geodesic Modular Subdivisioning
[986.471]{style="color: purple3"} []{#ver:986.471 label="ver:986.471"} series of considerations leads to the definition of the most spherical-appearing limit of triangular subdivisioning:
-
recalling that the experimentally demonstrable “most spherically-appearing” structure is always in primitive reality a polyhedron;
-
recalling that the higher the modular frequency of a system the more spheric it appears, though it is always polyhedral and approaching not a “true sphere” limit but an unlimited multiplication of its polyhedral facetings;
-
recalling that the 120 outer surface triangles of the icosahedron’s 15 great circles constitute the cosmic maximum limit of system-surface omni-triangular-self-subdivisioning into centrally collected tetrahedron components; and
-
recalling that the icosahedron’s 10- and 6-great-circle equators of spin further subdivide the 15 great circles’ outer 120 triangles into four different right triangles, ADC, CDE, CFE, and (see Fig. 901.03),
then it becomes evident that the icosahedron’s three sets of symmetrical great-circle spinnabilitiesi.e., (which totals 31 great circle self-halvings)generate a total of 242 unit-radius, external vertexes, 480 external triangles, and 720 internal triangles (which may be considered as two congruent internal triangles, each being one of the internal triangular faces of the 480 tetrahedra whose 480 external triangular faces are showing in which case there are 1440 internal triangles). The 480 tetrahedra consist of 120 OCAD, Y2.0OCDE, 120 OCEF, and 120 tetrahedra. (See Fig. 986.471.) The 480 internal face-congruent tetrahedra therefore constitute the “most spheric-appearing” of all the hemispheric equators’ self-spun, surface-subdividing entirely into triangles of all the great circles of all the primitive hierarchy of symmetric polyhedra.
[986.472]{style="color: purple3"} []{#ver:986.472 label="ver:986.472"} In case one thinks that the four symmetrical sets of the great circles of the spherical (which total 25 great circles in all) might omnisubdivide the system surface exclusively into a greater number of triangles, we note that some of the subdivision areas of the 25 great circles are not triangles (see quadrant in Fig. 453.01third printing of Synergetics 1of which quadrangles there are a total of 48 in the system); and note that the total number of triangles in the 25-great-circle system is 288 ergo, far less than the 31 great circles’ 480 spherical right triangles; ergo, we become satisfied that the icosahedron’s set of 480 is indeed the cosmic maximum-limit case of system-self-spun subdivisioning of its self into tetrahedra, which 480 consist of four sets of 120 similar tetrahedra each.
[986.473]{style="color: purple3"} []{#ver:986.473 label="ver:986.473"} It then became evident (as structurally demonstrated in reality by my mathematically close-toleranced geodesic domes) that the spherical trigonometry calculations’ multifrequenced modular subdividing of only one of the icosahedron’s 120 spherical right triangles would suffice to provide all the basic trigonometric data for any one and all of the unit-radius vertex locations and their uniform interspacings and interangulations for any and all frequencies of modular subdividings of the most symmetrical and most economically chorded systems’ structuring of Universe, the only variable of which is the special case, time-sized radius of the special-case system being considered.
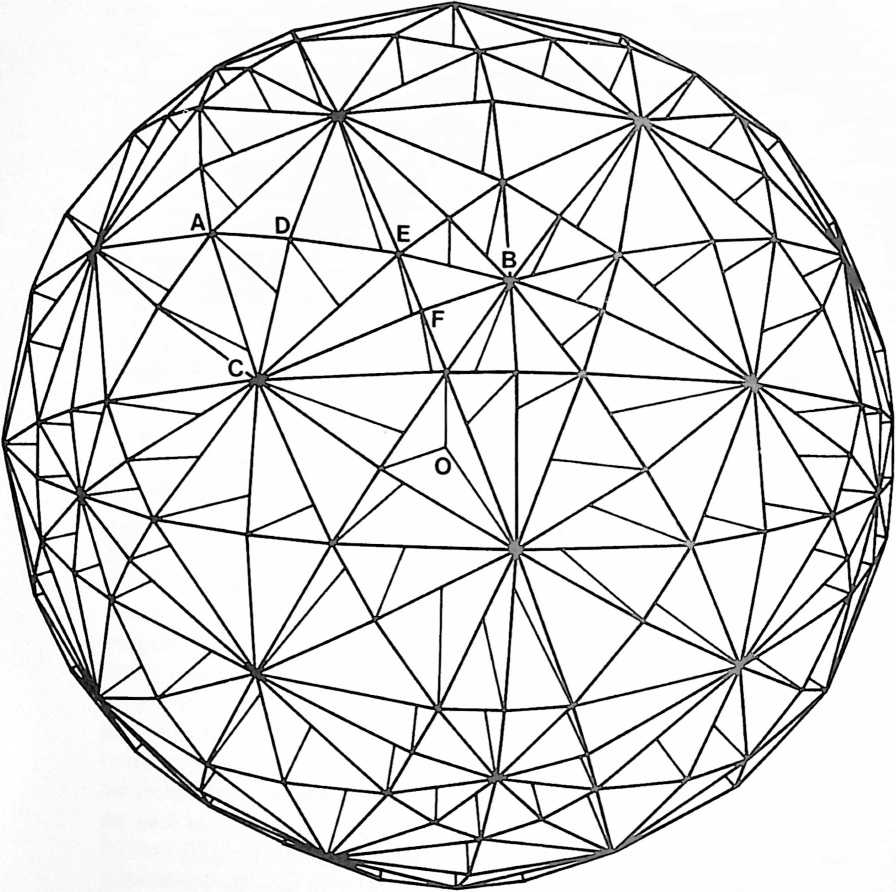
Fig. 986.471 Modular Subdivisioning of Icosahedron as Maximum Limit Case: The 120 outer surface right spherical triangles of the icosahedron’s 6, 10, and 15 great circles generate a total of 242 external vertexes, 480 external triangles, and 480 internal face-congruent tetrahedra, constituting the maximum limit of regular spherical system surface omnitriangular self-subdivisioning into centrally collected tetrahedral components.
[986.474]{style="color: purple3"} []{#ver:986.474 label="ver:986.474"} This surmise regarding nature’s most-economical, least-effort design strategy has been further verified by nature’s own use of the same geodesics mathematics as that which I discovered and employed in my domes. Nature has been using these mathematical principles for eternity. Humans were unaware of that fact. I discovered these design strategies only as heretofore related, as an inadvertent by-product of my deliberately undertaking to find nature’s coordination system. That nature was manifesting icosahedral and coordinate patterning was only discovered by other scientists after I had found and demonstrated geodesic structuring, which employed the synergetics’ coordinate-system strategies. This discovery by others that my discovery of geodesic mathematics was also the coordinate system being manifest by nature occurred after I had built hundreds of geodesic structures around the world and their pictures were widely published. Scientists studying X-ray diffraction patterns of protein shells of viruses in 1959 found that those shells disclosed the same patterns as those of my widely publicized geodesic domes. When Dr. Aaron Klug of the University of Londonwho was the one who made this discoverycommunicated with me, I was able to send him the mathematical formulae for describing them. Klug explained to me that my geodesic structures are being used by nature in providing the “spherical” enclosures of her own most critical design-controlling programming devices for realizing all the unique biochemical structurings of all biologywhich device is the DNA helix.
[986.475]{style="color: purple3"} []{#ver:986.475 label="ver:986.475"} The structuring of biochemistry is epitomized in the structuring of the protein shells of all the viruses. They are indeed all icosahedral geodesic structures. They embracingly guard all the DNA-RNA codified programming of all the angle-and-frequency designing of all the biological, life-accommodating, life-articulating structures. We find nature employing synergetics geometry, and in particular the high-frequency geodesic “spheres,” in many marine organisms such as the radiolaria and diatoms, and in structuring such vital organs as the male testes, the human brain, and the eyeball. All of these are among many manifests of nature’s employment on her most critically strategic occasions of the most cosmically economical, structurally effective and efficient enclosures, which we find are always mathematically based on multifrequency and three-way-triangular gridding of the “spherical” because high-frequencedicosahedron, octahedron, or tetrahedron.
[986.476]{style="color: purple3"} []{#ver:986.476 label="ver:986.476"} Comparing the icosahedron, octahedron, and tetrahedronthe isosahedron gives the most volume per unit weight of material investment in its structuring; the high-frequency tetrahedron gives the greatest strength per unit weight of material invested; and the octahedron affords a happybut not as stablemix of the two extremes, for the octahedron consists of the prime number 2, ; whereas the tetrahedron is the odd prime number 1 and the icosahedron is the odd prime number 5. Gear trains of even number reciprocate, whereas gear trains of an odd number of gears always lock; ergo, the tetrahedral and icosahedral geodesic systems lock-fasten all their structural systems, and the octahedron’s compromise, middle-position structuring tends to yield transformingly toward either the tetra or the icosa locked-limit capabilitieseither of which tendencies is pulsatively propagative.
¶ 986.480 Consideration 13: Correspondence of Surface Angles and Central Angles
[986.481]{style="color: purple3"} []{#ver:986.481 label="ver:986.481"} It was next to be noted that spherical trigonometry shows that nature’s smallest common denominator of system-surface subdivisioning by any one type of the seven great-circle-symmetry systems is optimally accomplished by the previously described 120 spherical-surface triangles formed by the 15 great circles, whose central angles are approximately
whereas their surface angles are 36 degrees at A, 60 degrees at B, and 90 degrees at C.
[986.482]{style="color: purple3"} []{#ver:986.482 label="ver:986.482"} We recall that the further self-subdividing of the 120 triangles, as already defined by the 15 great circles and as subdividingly accomplished by the icosahedron’s additional 6- and 10-great-circle spinnabilities, partitions the 120 triangles into 480 right triangles of four types: ADC, CDE, CFE, and EFBwith 60 positive and 60 negative pairs of each. (See Figs. 901.03 and
[986.314.)]{style="color: purple3"} []{#ver:986.314.) label="ver:986.314.)"} We also recall that the 6- and 10-great-circle-spun hemispherical gridding further subdivided the 120 right trianglesACB formed by the 15 great circles, which produced a total of 12 types of surface angles, four of them of 90 degrees, and three whose most acute angles subdivided the 90-degree angle at into three surface angles: ACD31.7 degrees; DCE37.4 degrees; and ECB20.9 degrees, which three surface angles, we remember, correspond exactly to the three central angles COB, BOA, and COA, respectively, of the triacontahedron’s tetrahedral Quanta Module ABCO??.
¶ 986.500 Quanta Module
[986.501]{style="color: purple3"} []{#ver:986.501 label="ver:986.501"} Consideration 14: Great-circle Foldable Discs
[986.502]{style="color: purple3"} []{#ver:986.502 label="ver:986.502"} With all the foregoing events, data, and speculative hypotheses in mind, I said I think it would be worthwhile to take 30 cardboard great circles, to divide them into four 90-degree quadrants, then to divide each of the quadrants into three anglesCOA, 20.9 degrees; AOB, 37.4 degrees; and BOC, 31.7 degreesand then to score the cardboard discs with fold lines in such a manner that the four lines will be negatively out- folded, while the lines and will be positively infolded, so that when they are altogether folded they will form four similar-arc-edged tetrahedra with all of their four radii edges centrally congruent. And when 30 of these folded great-circle sets of four Quanta Module tetrahedra are each triple-bonded together, they will altogether constitute a sphere. This spherical assemblage involves pairings of the three intercongruent interface triangles AOC, COB, and BOA; that is, each folded great-circle set of four tetra has each of its four internal triangular faces congruent with their adjacent neighbor’s corresponding AOC, COB, and interior triangular faces. (See Fig. 986.502.)
Fig. 986.502 Thirty Great-circle Discs Foldable into Rhombic Triacontahedron System: Each of the four 90-degree quadrants, when folded as indicated at and B, form separate Quanta Module tetrahedra. Orientations are indicated by letter on the great-circle assembly at D.
[image]{.image .placeholder original-image-src="
images/v2/900.00/image45
" original-image-title=""} [image]{.image .placeholder original-image-src="
images/v2/900.00/image46
" original-image-title=""} [image]{.image .placeholder original-image-src="
images/v2/900.00/image47
" original-image-title=""}
[986.503]{style="color: purple3"} []{#ver:986.503 label="ver:986.503"} I proceeded to make 30 of these 360-degree-folding assemblies and used bobby pins to lock the four edges together at the centers of the diamond-shaped outer faces. Then I used bobby pins again to lock the 30 assemblies together at the 20 convergent vertexes and the 12 convergent sphere-surface vertexes. Altogether they made a bigger sphere than the calculated radius, because of the accumulated thickness of the foldings of the construction paper’s double-walled (trivalent) interfacing of the 30 internal tetrahedral components. (See Fig. 986.502D.)
[986.504]{style="color: purple3"} []{#ver:986.504 label="ver:986.504"} Instead of the just previously described 30 assemblies of four identical spherically central tetrahedra, each with all of their 62 vertexes in the unit-radius spheres, I next decided to make separately the 120 correspondingly convergent (non-arc-edged but chorded) tetrahedra of the tetravolume-5 rhombic triacontahedron, with its 30 flat diamond faces, the center of which outer diamond faces is criss-crossed at right angles at by the short axis A-A of the diamond and by its long axis B-B, all of which diamond bounding and criss-crossing is accomplished by the same 15 great-circle planes that also described the 30 diamonds’ outer boundaries. As noted, the criss-crossed centers of the diamond faces occur at C, and all the points are at the prime-vector-radius distance outwardly from the volumetric center of the rhombic triacontahedron, while is 1.07 of vector unity and is 1.17 of vector unity outward, respectively, from the rhombic triacontahedron’s symmetrical system’s center of volume O. (See Figs. 986.504A and 986.504B.)
[986.505]{style="color: purple3"} []{#ver:986.505 label="ver:986.505"} To make my 120 tetrahedra I happened to be using the same construction paperboard I had used before in making the 30 arc-edged great-circle components. The construction paperboard happened to come in sheets 24 by 36 inches, i.e., two feet by three feet. In making the previously described spherical triacontahedron out of these 24-by-36-inch sheets, I had decided to get the most out of my material by using a 12-inch-diameter circle, so that I could lay out six of them tangentially within the six 12-inch-square modules of the paperboard to produce the 30 foldable great circles. This allowed me to cut out six intertangent great circles from each 24-by-36-inch construction paper sheet. Thirty great circles required only five sheets, each sheet producing six circles. To make the 12 separate Quanta Module tetrahedra, I again spontaneously divided each of the same-size sheets into six squares with each of the six circles tangent to four edges of each square (Fig. 986.505).
[image]{.image .placeholder original-image-src="
images/v2/900.00/image48
" original-image-title=""}
[image]{.image .placeholder original-image-src="
images/v2/900.00/image49
" original-image-title=""}
Fig. 986.504 Profile of Quadrants of Sphere and Rhombic Triacontahedron: Central angles and ratios of radii are indicated at . Orientation of modules in spherical assembly is indicated by letters at B.
\. / n
Fig. 986.505 Six Intertangent Great-circle Discs in 12-inch Module Grid: The four 90-degree quadrants are folded at the central angles indicated for the Quanta Module.
[986.506]{style="color: purple3"} []{#ver:986.506 label="ver:986.506"} In starting to make the 120 separate tetrahedra (60 positive, 60 negativeknown as Quanta Modules) with which to assemble the triacontahedronwhich is a chord-edged polyhedron vs the previous “spherical” form produced by the folded 15-great-circle patterningI drew the same 12-inch-edge squares and, tangentially within the latter, drew the same six 12-inch-diameter circles on the five 24-by-36-inch sheets, dividing each circle into four quadrants and each quadrant into three subsections of 20.9 degrees, 37.4 degrees, and 31.7 degrees, as in the Quanta Modules.
[986.507]{style="color: purple3"} []{#ver:986.507 label="ver:986.507"} I planned that each of the quadrants would subsequently be cut from the others to be folded into one each of the 120 Quanta Module tetrahedra of the triacontahedron. This time, however, I reminded myself not only to produce the rhombic triacontahedron with the same central angles as in the previous spheric experiment’s model, but also to provide this time for surfacing their clusters of four tetrahedra around their surface point at the mid-crossing point of their 30 flat diamond faces. Flat diamond faces meant that where the sets of four tetra came together at C, there would not only have to be four 90-degree angles on the flat surface, but there would be eight internal right angles at each of the internal flange angles. This meant that around each vertex corner of each of the four Quanta Modules coming together at the diamond face center there would have to be three 90-degree angles.
[986.508]{style="color: purple3"} []{#ver:986.508 label="ver:986.508"} Looking at my “one-circle-per-each-of-six-squares” drawing, I saw that each sheet was divided into 24 quadrant blanks, as in Fig. 986.508A. Next I marked the centers of each of the six circles as point 0, 0 being the volumetric center of the triacontahedral system. Then I realized that, as trigonometrically calculated, the flat, diamond-centered, right-angled, centrally criss-crossed point of the triacontahedron’s outer faces had to be at our primitive unit-vector-length distance outwardly from the system center O, whereas in the previous arc-edged 30-great-circle-folded model the outer vertex had been at full-spherical-system-radius distance outwardly from O. In the spherical 15-great-circle-model, therefore, the triacontahedron’s mid-flat-diamond-face would be at .07 lesser radial distance outwardly from 0 than would the diamond corner vertexes and vertex itself at a lesser radial distance outwardly from than diamond corner vertex B. (See Fig. 986.504A.)
[986.509]{style="color: purple3"} []{#ver:986.509 label="ver:986.509"} Thinking about the corner of the described tetrahedron consisting entirely of 90-degree angles as noted above, I realized that the line to must produce a 90-degree-angle as projected upon the line OC", which latter ran vertically outward from to , with being the volumetric center of the symmetrical system (in this case the rhombic triacontahedron) and with C" positioned on the perimeter exactly where vertex had occurred on each of the previous arc-described models of the great circles as I had laid them out for my previous 15 great-circle spherical models. I saw that angle must be 90 degrees. I also knew by spherical trigonometry that the angle would have to be 20.9 degrees, so I projected line outwardly from at 20.9 degrees from the vertical square edge OC.
[986.510]{style="color: purple3"} []{#ver:986.510 label="ver:986.510"} At the time of calculating the initial layout I made two mistaken assumptions: first, that the 0.9995 figure was critically approximate to 1 and could be read as 1; and second (despite Chris Kitrick’s skepticism bom of his confidence in the reliability of his calculations), that the .0005 difference must be due to the residual incommensurability error of the inherent irrationality of the mathematicians’ method of calculating trigonometric functions. (See the Scheherazade Numbers discussed at Sec. 1230.) At any rate I could not lay out with drafting tools a difference of 0.0005 of six inches, which is 0.0030 of an inch. No draftsman can prick off a distance even ten times that size. (I continue to belabor these mistaken assumptions and the subsequent acknowledgments of the errors because it is always upon the occasion of my enlightened admission of error that I make my greatest discoveries, and I am thus eager to convey this truth to those seeking the truth by following closely each step of this development, which leads to one of the most exciting of known discoveries.)
[image]{.image .placeholder original-image-src="
images/v2/900.00/image50
" original-image-title=""}
[image]{.image .placeholder original-image-src="
images/v2/900.00/image51
" original-image-title=""}
Fig. 986.508 Six Intertangent Great-circle Discs: Twelve-inch module grids divided into 24 quadrant blanks at A. Profile of rhombic triacontahedron superimposed on quadrant at B.
[986.511]{style="color: purple3"} []{#ver:986.511 label="ver:986.511"} In order to produce the biggest model possible out of the same 24-by-36-inch construction paper blanks, I saw that vertex / of this new Quanta Module model would have to lie on the same 12-inch circle, projecting horizontally from perpendicularly (i.e., at right angles), upon at C. I found that the point of 90-degree impingement of on occurred slightly inward (.041, as we learned later by trigonometry), vertically inward, from X. The symbol now occurs on my layout at the point where the previous spherical model’s central diamond vertex had been positionedon the great-circle perimeter. Trigonometric calculation showed this distance between and to be 0.041 of the length of our unit vector radius. Because (1) the distance is established by the right-angled projection of upon OX; and because (2) the length is also the prime vector of synergetics’ isotropic vector matrix itself, we found by trigonometric calculation that when the distance from to is 0.9995 of the prime vector’s length, that the tetravolume of the rhombic triacontahedron is exactly 5.
[986.512]{style="color: purple3"} []{#ver:986.512 label="ver:986.512"} When the distance from to is 0.9995, then the tetravolume of the rhombic triacontahedron is exactly 5. in our model layout is now exactly the same as the vector radius of the isotropic vector matrix of our “generalized energy field.” rises vertically (as the right-hand edge of our cut-out model of our eventually-to-be-folded Quanta Module’s model designing layout) from the eventual triacontahedron’s center to what will be the mid-diamond face point C. Because by spherical trigonometry we know that the central angles of our model must read successively from the right-hand edge of the layout at 20.9 degrees, 37.4 degrees, and 31.7 degrees and that they add up to 90 degrees, therefore line runs horizontally leftward, outward from to make angle 90 degrees. This is because all the angles around the mid-diamond criss-cross point are (both externally and internally) 90 degrees. We also know that horizontal is the same prime vector length as vertical OC. We also know that in subsequent folding into the Quanta Module tetrahedron, it is a mathematical requirement that vertical be congruent with horizontal in order to be able to have these edges fold together to be closed in the interior tetrahedral form of the T Quanta Module. We also know that in order to produce the required three 90-degree angles (one surface and two interior) around congruent and C of the finished Quanta Module, the line CB of our layout must rise at 90 degrees vertically from at the leftward end of the horizontal unit vector radius OC. (See Fig. 986.508C.)
[986.513]{style="color: purple3"} []{#ver:986.513 label="ver:986.513"} This layout now demonstrates three 90-degree corners with lines vertical and horizontal and of the same exact length, which means that the rectangle COCC" must be a square with unit-vector-radius edge length OC. The vertical line CC" rises from of horizontal until it encounters line OB, whichto conform with the triacontahedron’s interior angles as already trigonometrically established must by angular construction layout run outwardly from at an angle of 31.7 degrees above the horizontal from until it engages vertical CC" at B. Because by deliberate construction requirement the angle between vertical and has been laid out as 20.9 degrees, the angle A OB must be 37.4 degreesbeing the remainder after deducting both 20.9 degrees and 31.7 degrees from the 90-degree angle lying between vertical and horizontal . All of this construction layout with horizontally equaling vertically, and with the thus-far-constructed layout’s corner angles each being 90 degrees, makes it evident that the extensions of lines and C B will intersect at 90 degrees at point C", thus completing the square OC CC of edge length OC, which length is exactly of the prime vector of the isotropic vector matrix’s primitive cosmic-hierarchy system.
[986.514]{style="color: purple3"} []{#ver:986.514 label="ver:986.514"} Since ACO, COC, and are all 90-degree angles, and since vertical = horizontal CO in length, the area COC C" must be a square. This means that two edges of each of three of the four triangular faces of the Quanta Module tetrahedron, and six of its nine prefolded edges (it has only six edges after folding), are congruent with an exactly square paperboard blank. The three triangles OCA, OAB, and will be folded inwardly along and to bring the two and CO edges together to produce the three systemically interior faces of the Quanta Module.
[986.515]{style="color: purple3"} []{#ver:986.515 label="ver:986.515"} This construction method leaves a fourth right-triangular corner piece AC"B, which the dividers indicatedand subsequent trigonometry confirmedto be the triangle exactly fitting the outer ABC-triangular-shaped open end of the folded-together Quanta Module OABC. O" marks the fourth corner of the square blank, and trigonometry showed that C"A =C B and C"B =AC, while of triangle by construction is congruent with of triangle of the original layout. So it is proven that the vector-edged square COCC" exactly equals the surface of the Quanta Module tetrahedron CABO. (See Fig. 986.515.)
[986.516]{style="color: purple3"} []{#ver:986.516 label="ver:986.516"} The triangle is hinged to the Quanta Module along the mutual edge AB, which is the hypotenuse of the small right triangle. But as constructed the small right triangle cannot be hinged (folded) to close the Quanta Module tetrahedron’s open-end triangular area ABC~ despite the fact that the hinged-on triangle and the open triangle are dimensionally identical. is exactly the right shape and size an ar and can be used to exactly close the outer face of the Quanta tetrahedron, but only ifit is cut off along line and is then tume so that its faces are reversed and its corner is now where its corner been. This is to say that if the square COCC" is made of a cardboard sheet with a red top side and a gray underside, when we complete the tetrahedron folding as previously described, cut off the small corner triangle AC B ong lineB?l, reverse its face and its acute ends, and then address it to the small tn angular open end of the tetrahedron CABO, it will fit exactly into place, but with the completed tetrahedron having three gray faces around vertex and one red outer face CAB. (See Fig. 986.508C.)
Fig. 986.515 Quanta Module Foldable from Square: One of the triangular corners may be hinged and reoriented to close the open end of the folded tetrahedron.
[986.517]{style="color: purple3"} []{#ver:986.517 label="ver:986.517"} Following this closure procedure, when the triangles of each of the squares are cut off from COCC along line AB. and right triangle is reversed in face and its right-angle corner C" is made congruent with the right-angle corner of the Quanta Module’s open-end triangle, then the corner of the small triangle goes into congruence with the corner of the open-end triangle, and the corner of the small triangle goes into congruence with the corner of the open-end trianglewith the 90-degree corner becoming congruent with the small triangle’s right-angle corner C". When all 120 of these Quanta Module tetrahedra are closed and assembled to produce the triacontahedron, we will have all of the 360 gray faces inside and all of the 120 red faces outside, altogether producing an externally red and an internally gray rhombic triacontahedron.
[986.518]{style="color: purple3"} []{#ver:986.518 label="ver:986.518"} In developing the paper-folding pattern with which to construct any one of these 120 identical Quanta Module tetrahedra, we inadvertently discovered it to be foldable out of an exact square of construction paper, the edge of which square is almost (0.9995 of the prime vector 1) identical in length to that of the prime vector radius of synergetics’ closest-packed unitradius spheres, and of the isotropic vector matrix, and therefore of the radii and chords of the vector equilibriumwhich synergetics’ vector (as with all vectors) is the product of mass and velocity. While the unit-vector length of our everywhere-the-same energy condition conceptually idealizes cosmic equilibrium, as prime vector (Sec. 540.10) it also inherently represents everywhere-the-same maximum cosmic velocity unfettered in vacuoergo, its linear velocity (symbolized in physics as lower-case c) is that of all radiationwhether beamed or piped or linearly focusedthe velocity of whose unbeamed, omnidirectionally outward, surface growth rate always amounts to the second-powering of the linear speed. Ergo, omniradiance’s wave surface growth rate is .
[986.519]{style="color: purple3"} []{#ver:986.519 label="ver:986.519"} Since the edge length of the exactly 5.0000 volumed Quanta Module surface square is .9995 of the prime vector 1.0000 a, the surfacefield energy of the Quanta Module of minimum energy containment is V2, where 1.0000 a V is the prime vector of our isotropic vector matrix. The differenceis minimal but not insignificant; for instance, the mass of the electron happens also to be .0005 of the mass of the proton.
¶ 986.520 Einsteins Equation
[986.521]{style="color: purple3"} []{#ver:986.521 label="ver:986.521"} Remembering that in any given dimensional system of reference the vector’s length represents a given mass multiplied by a given velocity, we have in the present instance the physical evidence that the surface area of the Quanta Module tetrahedron exactly equals the area of the edge length “squared.” In this case of the Quanta Module the edge length of .9995 of the foldable square (the visibly undetectable) is .0005 less than the length of the prime vector of 1.000.
[986.522]{style="color: purple3"} []{#ver:986.522 label="ver:986.522"} The generalized isotropic vector matrix’s prime vector to the second power“squared”becomes physically visible in the folded-square tetra modules. (Try making one of them yourself.) This visible “squaring” of the surface area of the exactly one-energy-quantum module tetrahedron corresponds geometrically to what is symbolically called for in Einstein’s equation, which language physics uses as a nonengineering-language symbolism (as with conventional mathematics), and which does not preintermultiply mass and velocity to produce a vector of given length and angular directionergo, does not employ the integrated vectorial component ergo, must express in separate components as (mass) times the velocity of energy unfettered in vacuo to the second power, . However, we can say , the engineering expression V2 being more economical. When 7” = the T Quanta Module, and when the Quanta Module = one energy quantum module, we can say:
one module= 0.9995^
[986.523]{style="color: purple3"} []{#ver:986.523 label="ver:986.523"} In the Einstein equation the velocitylower-case c of all radiation taken to the second power is omnidirectionalergo, its quasispheric surface-growth rate is at the second power of its radial-linear-arithmetic growth rateergo, . (Compare Secs. 1052.21 and 1052.30.) Thus Einstein’s equation reads , where is the basic one quantum or one photon energy component of Universe.
[986.524]{style="color: purple3"} []{#ver:986.524 label="ver:986.524"} With all the foregoing holding true and being physically demonstrable, we find the vector minus .0005 of its full length producing an exactly square area that folds into a tetrahedron of exactly one quantum module, but, we must remember, with a unit-integral-square-surface area whose edge length is .0005 less than the true V2 vector, i.e., less than Mc~. But don t get discouraged; as with the French Vive la Difference, we find that difference of .0005 to be of the greatest possible significance …as we shall immediately learn.
¶ 986.540 Volume-surface Ratios of Quanta Module and Other Modules
[986.541]{style="color: purple3"} []{#ver:986.541 label="ver:986.541"} Now, reviewing and consolidating our physically exploratory gains, we note that in addition to the .9995 F2-edged “square -surfaced Quanta Module tetrahedron of exactly the same volume as the Quanta Modules, we also have the Quanta Moduleor the “Einstein Module”whose square edge is exactly vector V = 1.0000 a, but whose volume is when the Quanta Module’s volume is exactly 1.0000 a, which volume we have also learned is uncontainable by chemical structuring, bonding, and the mass-attraction law.
[986.542]{style="color: purple3"} []{#ver:986.542 label="ver:986.542"} When the prime-unit vector constitutes the radial distance outward from the triacontahedron’s volumetric center to the mid-points of each of its mid-diamond faces, the volume of the rhombic triancontahedron is then slightly greater than tetravolume 5, being actually tetravolume 5.007758031. Each of the rhombic triacontahedron’s 120 internally structured tetrahedra is called an Quanta Module, the “E” for Einstein, being the transformation threshold between energy convergently self-interfering as matter = M, and energy divergently dispersed as radiation = c2. Let us consider two rhombic triacontahedra: (1) one of radius .9995 of exact tetravolume 5; and (2) one of radius 1.0000 of tetravolume . The exact prime-vector radius 1.0000 rhombic triacontahedron volume is .007758031 (l/129th) greater than the tetravolume 5i.e., tetravolume . This means that each Quanta Module is when the Quanta Module is 1.0000.
[986.543]{style="color: purple3"} []{#ver:986.543 label="ver:986.543"} The 0.000517 radius difference between the .999483-radiused rhombic triacontahedron of exactly tetravolume 5 and its exquisitely minute greater radius-1.0000 prime vector, is the exquisite difference between a local-in-Universe energy-containing module and that same energy being released to become energy radiant. Each of the 120 right-angle-cornered Quanta Modules embraced by the tetravolume-5 rhombic triacontahedron is volumetrically identical to the and Quanta Modules, of which the Modules hold their energy and the Modules release their energy (Sec. 920). Each quanta module volume is .04166 i.e., V24 Change: fix of one regular primitive tetrahedron, the latter we recall being the minimum symmetric structural system of Universe. To avoid decimal fractions that are not conceptually simple, we multiply all the primitive hierarchy of symmetric, concentric, polyhedral volumes by 24 after which we can discuss and consider energetic-synergetic geometry in always-whole-rational-integer terms.
[986.544]{style="color: purple3"} []{#ver:986.544 label="ver:986.544"} We have not forgotten that radius 1 is only half of the prime-unit vector of the isotropic vector matrix, which equals unity 2 (Sec. 986.160~). Nor have we forgotten that every square is two triangles (Sec. 420.08); nor that the second-powering of integers is most economically readable as “triangling”; nor that nature always employs the most economical alternativesbut we know that it is momentarily too distracting to bring in these adjustments of the Einstein formula at this point.
[986.545]{style="color: purple3"} []{#ver:986.545 label="ver:986.545"} To discover the significance of the “difference” all we have to do is make another square with edge length of exactly 1.000 (a difference completely invisible at our one-foot-to-the-edge modeling scale), and now our tetrahedron folded out of the model is an exact geometrical model of Einstein’s , which, expressed in vectorial engineering terms, reads ; Change: fix however, its volume is now greater than that of one exact energy quanta module. We call this tetrahedron model folded from one square whose four edge lengths are each exactly one vector long the Module, naming it for Einstein. It is an exact vector model of his equation.
[986.546]{style="color: purple3"} []{#ver:986.546 label="ver:986.546"} The volumetric difference between the Module and the Module is the difference between energy-as-matter and energy-as-radiation. The linear growth of 0.0005 transforms the basic energy-conserving quanta module (the physicists’ particle) from matter into one minimum-limit photon” of radiant energy as light or any other radiation (the physicists wave).
[986.547]{style="color: purple3"} []{#ver:986.547 label="ver:986.547"} Einsteins equation was conceived and calculated by him to identify the energy characteristics derived from physical experiment, which defined the minimum radiation unitthe photon = Mc2. The relative linear difference of 0.000518 multiplied by the atoms’ electrons’ nucleus-orbiting diameter of one angstrom (a unit on only Ao-millionth Change: fix of an inch) is the difference between it is matter or it is radiation… Vastly enlarged, it is the same kind of difference existing between a soap bubble existing and no longer existing“bursting,” we call it because it reached the critical limit of spontaneously coexistent, cohesive energy as-atoms-arrayed-in-liquid mole cules and of atoms rearranged in dispersive behavior as gases. This is the gen eralized critical threshold between it is and it isn’t. …It is the same volume-to-tensional-surface-enclosing-capability condition displayed by the soap bubble, with its volume increasing at a velocity of the third power while its surface increases only as velocity to the second power. Its tension embracement of molecules and their atoms gets thinned out to a one-molecule layer, after which the atoms, behaving according to Newton s mass-interattraction law, become circumferentially parted, with their interattractiveness decreasing acceleratingly at a second-power rate of the progressive arithme tical distance apart attained an increase that suddenly attains critical demass point, and there is no longer a bubble. The same principle obtains in respect to the Quanta Module-> E Quanta Modulei.e., matter transforming into radiation.
[986.548]{style="color: purple3"} []{#ver:986.548 label="ver:986.548"} The difference between the edge length of the square from which we fold the Quanta Module and the edge length of the square from which we fold the Quanta Module is exquisitely minute: it is the difference between the inside surface and the outside surface of the material employed to fabricate the model. In a 20-inch-square model employing aluminum foil \sfrac{1}{200}th of an inch thick, the Module would be congruent with the outside surface and the Module would be congruent with the inside surface, and the ratio of the edge lengths of the two squares is as 1 is to 0.0005, or 0.0005 of prime vector radius of our spherical transformation. This minuscule modelable difference is the difference between it is and it isntwhich is to say that the dimensional difference between matter and radiation is probably the most minute of all nature’s dimensioning: it is the difference between inside-out and outside-out of positive and negative Universe.
[image]{.image .placeholder original-image-src="
images/v2/900.00/image54
" original-image-title=""}
[986.549]{style="color: purple3"} []{#ver:986.549 label="ver:986.549"} Because we have obtained an intimate glimpse of matter becoming radiation, or vice versa, as caused by a minimum-structural-system tetrahedron’s edge-length growth of only 129\sfrac{1}{2} quadrillionths of an inch, and because we have been paying faithful attention to the most minute fractions of difference, we have been introduced to a whole new frontier of synergetics exploration. We have discovered the conceptual means by which the 99 percent of humanity who do not understand science may become much more intimate with nature’s energetic behaviors, transformations, capabilities, and structural and de-structural strategies.
[986.550]{style="color: purple3"} []{#ver:986.550 label="ver:986.550"} Table: Relative Surface Areas Embracing the Hierarchy of Energetic Quanta Modules: Volumes are unit. All Module Volumes are 1, except the radiant Module, whose Surface Area is experimentally evidenced Unity:
ENERGY PACKAGE SURFACE AREA
-
Vector (linear)
-
= Mass x velocity = Energy Package
V2 = Energy package’s surface
1 Unit vector of isotropic vector matrix
Vector x Vector = Surface (Energy as local energy system-containment capability) = Outer array of energy packages[^41].
Mass =F = Relative frequency of primitive-system-subdivision energy-event occupation.
“SURFACE” AREA
VOLUME
A Quanta Module
T Quanta Module “Einstein” Module
B Quanta Module
C Quanta Module
D Quanta Module
A Module
B Module
C Module D Module
AModule
BModule
CModule
DModule
.9957819158 .9989669317 1.0000000000 1.207106781 1.530556591
1.896581995
2.280238966 2.672519302 3.069597104 3.469603759
3.871525253 4.27476567 4.678952488 5.083841106
11 HOLD
1 J ENERGY 1.00155 1
1
1
1
1 I RELEASE
1 ENERGY
1
1
1 1
1
(For a discussion of and Modules see Sec. 986.413.)
¶ 986.560 Surprise Nestability of Minimod into Maximod T
[986.561]{style="color: purple3"} []{#ver:986.561 label="ver:986.561"} The great circles of icosahedral symmetries (Fig. 901.03) produce the spherical-surface right triangle AC"B; CAB is sub-divisible into four spherical right triangles CDA, CDE, DFE, and EFB. Since there are 120 triangles, there are 480 subdivision-right-surface triangles. Among these subdivision-right triangles there are two back-to-back 90-degree surface angles at DCDA and CDEand two back-to-back 90-degree surface angles at FCFE and EFB. The surface chord of the central angle is identical in magnitude to the surface chord of the central angle EOB, both being 13.28 degrees of circular azimuth. Surface chord of central angle and surface chord of central angle are identical in magnitude, both being 10.8 degrees azimuth. In the same manner we find that surface chord of central angle constitutes the mutual edge of the two surface right triangles and BFE, the central-angle magnitude of being 7.77 degrees azimuth. Likewise, the central angles and COF of the surface chords and are of the same magnitude, 20.9 degrees. All the above data suggest a surprising possibility: that the small corner triangle ACB itself can be folded on its three internal chord lines CD, CE, and EF, while joining its two edges and CF, which are of equal magnitude, having central angles of 20.9 degrees. This folding and joining of to and ofB to cancels out the congruent-letter identities and to produce the tetrahedron ABEC. (See Fig. 986.561.)
[986.562]{style="color: purple3"} []{#ver:986.562 label="ver:986.562"} We find to our surprise that this little flange-foldable tetrahedron is an identically angled miniature of the Quanta Module OABC‘ and that it can fit elegantly into the identically angled space terminating at within the inner reaches of vacant OABC, with the miniature tetrahedron’s corner becoming congruent with the system’s center O. The volume of the Minimod is approximately Vis that of the Maximod Quanta Module or of the or B Modules.
¶ 986.570 Range of Modular Orientations
[986.571]{style="color: purple3"} []{#ver:986.571 label="ver:986.571"} Now we return to Consideration 13 of this discussion and its discovery of the surface-to-central-angle interexchanging wave succession manifest in the cosmic hierarchy of ever-more-complex, primary structured polyhedraan interchanging of inside-out characteristics that inherently produces positive-negative world conditions; ergo, it propagatesinside-to-outside-to-inpulsed frequencies. With this kind of self-propagative regenerative function in view, we now consider exploring some of the implications of the fact that the triangle is foldable into the Quanta Module and is also nestable into the Quanta Module, which produces many possibilities:
-
The triangle ACB will disconnect and reverse its faces and complete the enclosure of the Quanta Module tetrahedron.
-
The 120 Quanta Modules, by additional tension-induced twist, take the triangles ends end-for-end to produce the additional radius outwardly fromO to convert the Quanta Modules into “Einstein” Quanta Modules, thus radiantly exporting all 120 modules as photons of light or other radiation.
-
The triangle might disconnect altogether, fold itself into the miniature Quanta Module, and plunge inwardly to fill its angularly matching central tetrahedral vacancy.
-
The outer triangle may just stay mishinged and flapping, to leave the tetrahedron’s outer end open.
-
The outer triangle might come loose, fold itself into a miniature T Quanta Module, and leave the system.
-
The 120 miniature Quanta Modules might fly away independently as, for instance, cosmic rays, i.e., as minimum modular fractions of primitive systems.
-
All 120 of these escaping miniature Quanta Modules could reassemble themselves into a miniature */i2o Change: fix triacontahedron, each of whose miniature Module’s outer faces could fold into mini-mini Modules and plunge inwardly in ever-more-concentrating demonstration of implosion, ad infinitum.
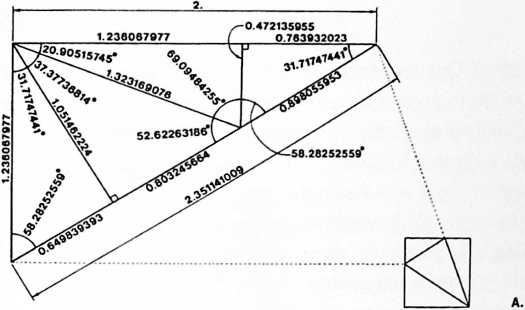
Fig. 986.56] and Modules: Minimod Nestabilities: Ratios of Angles and Edges: The top face remains open: the triangular lid will not close, but may be broken off and folded into smaller successive minimod tetra without limit.
There are 229,920 other possibilities that any one of any other number of the 120 individual Module tetrahedra could behave in any of the foregoing seven alternate ways in that vast variety of combinations and frequencies. At this borderline of ultrahigh frequency of intertransformability between matter and electromagnetic radiation we gain comprehension of how stars and fleas may be designed and be born.
¶ 986.580 Consideration 15: Surface Constancy and Mass Discrepancy
[986.581]{style="color: purple3"} []{#ver:986.581 label="ver:986.581"} Those triangles appear in the upper left-hand corner of either the Module’s or the Module’s square areas COC C", one of which has the edge length 0.994 and the other the edge length of 1.0000 a V. Regardless of what those triangles may or may not do, their areas, together with the areas of the triangles ACO, ABO, and BCO, exactly constitute the total surface area of either the Module or the Module.
Surface of Module = .994K2
Surface of Module = 1.00000 a V2
[986.582]{style="color: purple3"} []{#ver:986.582 label="ver:986.582"} The outer triangle of the Quanta Module is an inherent energy conserver because of its foldability into one (minimum-something) tetrahedron. When it folds itself into a miniature Module with the other 119 T Modules as a surface-closed rhombic triacontahedron, the latter will be a powerful energy conserverperhaps reminiscent of the giant-to-dwarf-Star behavior. The miniature Module behavior is also similar to behaviors of the electron’s self-conservation. This self-conserving and self-contracting property of the Quanta Modules, whose volume energy (ergo, energy quantum) is identical to that of the and Modules, provides speculative consideration as to why and how electron mass happens to be only /1836 the mass of the proton.
[986.583]{style="color: purple3"} []{#ver:986.583 label="ver:986.583"} Certain it is that the Quanta Module-»E Quanta Module threshold transformation makes it clear how energy goes from matter to radiation, and it may be that our little corner triangle is telling us how radiation retransforms into matter.
[986.584]{style="color: purple3"} []{#ver:986.584 label="ver:986.584"} The volume of the Quanta Module is identical with the volumes of the and Quanta Modules, which latter we have been able to identify with the quarks because of their clustering in the cosmically minimum, allspace-filling three-module Mites as + , , and , with both s holding their energy charges and discharging its energy in exact correspondence with the quark grouping and energy-holding-and-releasing properties, with the Modules’ energy-holding capabilities being based on their foldability from only one triangle, within which triangle the reflection pattern ing guarantees the energy conserving. (See Secs. 921 and 986.414)
[986.585]{style="color: purple3"} []{#ver:986.585 label="ver:986.585"} As we study the hierarchy of the surface areas of constant volume 1 and their respective shapes, we start with the least-surface Quanta Module which is folded out of one whole triangle, and we find that no other triangle is enclosed by one triangle except at the top of the hierarchy, where in the upper left-hand corner we find our Minimod or Minimod tetrahedron foldable out of our little triangle AC"B, whose fold-line patterning is similar to that of the triangle from which the Quanta Module is folded. In between the whole foldable triangular blank of the Quanta Module and the whole fold able triangular blank of the Minimod or Minimod E, we have a series of only asymmetrical folding blanksuntil we come to the beautiful squares o the and E Quanta Modules, which occur just before we come to the mangles of the minimod tetrahedra, which suggests that we go from radiation to matter with the foldable triangle and from matter to radiation when we get to the squares (which are, of course, two triangles).
¶ 986.600 Surface-Volume Ratios in the Atomic Theater
¶ 986.610 Considerations, Recalls, and Discoveries
[986.611]{style="color: purple3"} []{#ver:986.611 label="ver:986.611"} Our inventory of considerations, recalls, and discoveries is now burgeoning but remains omniinterrelevant. Wherefore we continue recalling and reconsidering with a high probability factor that we will make further discovery based on our past experience.
[986.620]{style="color: purple3"} []{#ver:986.620 label="ver:986.620"} Demass Breakpoint Model of Macrotude-microtude Difference Between Matter and Radiation
[986.621]{style="color: purple3"} []{#ver:986.621 label="ver:986.621"} Let me here introduce a physical experiment that will give us a personal feeling of appreciation of the importance to all humanity of all humanity’s being able to see with its own eyes what Einstein’s equation represents the breakpoint between matter and radiation (critical mass and atomic-energy release) and above all to give all humanity experienceable, knowable access to all that science has ever discovered regarding Universe, plus much more than science has ever discovered. With all this experienceability of most advanced scientific discovery all humanity will come to appreciate the otherwise utterly incredible exquisiteness of mathematical exactitude with which Universe (which is nature) functions.
[986.622]{style="color: purple3"} []{#ver:986.622 label="ver:986.622"} What we employ for such self-instruction at a human-sense-detectable level to appreciate the meager difference between the “T” square’s 0.9995 edge length and the “E” square’s 1.00000 edge length is to perform the physical task of producing two squares, which the human eyes can see and fingers can feel are of different sizes. Unaided by a lens, only the most skilled human eyes can see something that is one one-hundredth of an inch (expressed as 0.01 inch). carpenter works at no finer than nd of an inch. To make a difference of 0.0005 undeniably visible to any average human we would have to use the popularly adopted Vieth of an inch, which is that of the common school ruler. This \sfrac{1}
{16}th of an inch is expressed decimally as 0.0625. To make 0.005 of an inch visible we multiply it by 100, which makes it 0.05. One hundred inches is eight and a half feetthe average room-ceiling height. If we make two squares with 100-inch edges (8\sfrac{1}{2} feet “square”) out of wooden planks and timber, we cannot hold their dimensions to such a close tolerance of error because the humidity and temperature variations will be greater than 0.05 inch. Even if we make the 8\sfrac{1}{2}-foot squares of steel and aluminum plate, the expansion and contraction under common weather temperature changes will be greater than 0.05 inch.
[986.623]{style="color: purple3"} []{#ver:986.623 label="ver:986.623"} Using machine tools machinists can “dress” their products to tolerances as fine as 0.0001 inch.
[986.624]{style="color: purple3"} []{#ver:986.624 label="ver:986.624"} Fiberglass-and-epoxy resin is the substance that has the minimum presently known temperature-and-humidity-caused expansion and contraction rates of all practically producible materials. Wherefore: two square plates two inches thick with edge lengths of 8\sfrac{1}{2}feet could be machine-tool “dressed” and placed vertically fac e to face in a temperature-controlled slot with one of each of both of their bott om innermost 90-degree corners jammed tightly into a “machined” corner slot, wh ich would then make it possible to “see” with human eyes the difference in squa re size between the “T” and the “E” squares.
[986.625]{style="color: purple3"} []{#ver:986.625 label="ver:986.625"} Even if we “machi n ed” two steel cubes with an edge-length difference of .0005 inch, they would s t ack one on top of the other with their two vertical surfaces appearing as a pol i shed continuumthe space between them being also subvisible.
[986.626]{style="color: purple3"} []{#ver:986.626 label="ver:986.626"} But nature’s energy-as-matter transformed into energy-as-radiation are operations conducted at a size scale far different from our experientially imagined experime nts. Nature operates her matter-to-radiation energy exchanging at the atomic leve l. The nucleus of the atom is where energy-as-matter is self-interferingly knotte d together in most primitive polyhedral-patterning event systems. The atomic nucl eus diameter is\sfrac{1}{100,000}the diameter of its electron-orbited domainwhich domain is spoken of by scientists as “the atom. ” One atomic diameter is called the angstrom and is the prime measurement unit of the physicists macrophysicists or microphysicists, astro or nuclear, as they might well be desig nated.
[986.627]{style="color: purple3"} []{#ver:986.627 label="ver:986.627"} Referring to those two8\sfrac{1}{2}-foot (the size of Barnu m’s circus human giant) in height and 2-inches-thick square plates of machine-dre ssed fiberglass-epoxy resin and their minimum-human-sense-detectability differenc e of dimension, we find that the angstrom-atomic theater of energyexchanging perf ormance is only\sfrac{1}{126,500,000,000}the size of the minimum average human sense detectability. This figure, put into human-experience-sensing terms, is the distance that a photon of light expanding radially at 186,000 miles per second wi ll travel-reach between the time humans are born and the time they reach their ni neteenth birthday.
[986.628]{style="color: purple3"} []{#ver:986.628 label="ver:986.628"} What is important for us to realize here is that s ynergetics mathematics, beginning with the most primitive hierarchy of min-max ge ometrical relationships, expresses relationships that exist independently of t im e-size. So we humans can think intimately about structural principles of any s iz e. These primitive structural principles disclose inherent geometrical nuclei in respect to which all of Universe’s convergent-divergent, gravitational and ra dia tional, contracting into matter and expanding into electromagnetics, and vice ver sa, together with their terminal angular and frequency knotting and unknottin g e vents comprehensively and comprehendingly occur. And since the sum-total of b oth macro- and micro-physical science evidences 100-percent conservation of the energ y of eternally regenerative Scenario Universe, each smallest differential f racti on is of infinite importance to the integrity of Universe.
[986.629]{style="color: purple3"} []{#ver:986.629 label="ver:986.629"} And since Physical Universe demonstrates the principle of least effort, i.e., maximum efficiency to be infallibly operative, Universe does the most important tasks in the m ost exquisite manner; ergo, it is in the most exquisitely minute fractions that she hides her most important secrets. For all the foregoing synergetics’ disc los ure of a means of comprehending and operating independently of size provides h um an mind with not only a cosmic advantage but with all the responsibility such a c osmic decision to invest such an advantage in us implies. With these thoughts we address ourselves now to considering not only the critical cosmic surface-volume relationships but also their unique behavior differentials.
¶ 986.630 Interkinetic Limits
[986.631]{style="color: purple3"} []{#ver:986.631 label="ver:986.631"} In a structural system’s in terbalancing of compression and tension forces the tensed components will always embrace the compression componentsas does gravity always comprehensiv ely embrace all radiationergo, tension is always outermost of all sys tems, macrocosmic or microcosmic.
[986.632]{style="color: purple3"} []{#ver:986.632 label="ver:986.632"} Take any bendable substance and b e nd it. As you do so, the outer part of the bend stretches and the inner part co m presses. Tension always has the greater radiusergo, leverage advant a geergo, gravity is always comprehensive of radiation (Compare Sec. 10 51.50)
[986.633]{style="color: purple3"} []{#ver:986.633 label="ver:986.633"} In experiential structural reality the so-called sphere is alw ays and only an ultra-high-frequency geodesic polyhedron; ergo, it is always c ho rd-circumferenced and chord-convergent-vertexed rather than arc-circumferenced an d arc-vertexed; ergo, it is always and only quasispherical, which quasispherica l structural form is experimentally demonstrable as enclosing the most volume wit h the least surface of any and all symmetrical, equiangular, structural systems. Be cause of the foregoing we find it desirable to rename the spheric experience, u s ing from now on the word sphericin lieu of the nonexistent, experimentall y nondemonstrable “sphere.”
[986.634]{style="color: purple3"} []{#ver:986.634 label="ver:986.634"} As an asymmetrical or polarized struc t ural system, the hemispheric-ended cylinder has the same surface-to-volume rati o as that of a sphere with an identical diameterthe latter cylinders as well as their hemispherical terminals consist structurally only of high-frequ enc y, triangularly chorded stuructures. The spheric and the hemispheric-terminal led cylinders alike contain the most volume with the least surface of all symmet rica l polyhedra. At the other extreme of the surface-to-volume ratio, the equian gula r tetrahedron encloses the least volume with the most surface of any and all omni symmetrical structural systems. The more asymmetrical the tetrahedron, the m ore surface is required to envelop a given volume. It may be assumed, therefore, that with a given quantity of the same energy invested as molecularly structured , sys tem-containing capability, it is less tensionally stressful to enclose are gular equiangular tetrahedron than it is to enclose any asymmetrical tetrahedron .
[986.635]{style="color: purple3"} []{#ver:986.635 label="ver:986.635"} In respect to total surface areas of asymmetrical tetrahedra of un it (i.e., iden tical volume) enclosure, it is experimentally demonstrable that the greater the d ifference between the most acute angle and the most obtuse of its 12 surface angl es, the greater the surface-to-volume ratio will be, and therefore th e greater t he tensional stressing of its outermost cohering components ergo, the greater the challenge to the containment of its structural-system integ rity. (Se e Sec. 923 and Fig. 923.10.) According to Newton’s law the mass interatt raction of two separate bodies deteriorates exponentially as the distance apart d ecrease s arithmetically; ergo, the relative interproximity of the atoms within an y mole cule, and the relative interproximity of the molecules as structurally inte rarra yed within any and all volume-containment systemsand the resulta nt s tructural-integrity coherences of those systemstrend accelerating ly toward their theoretical atom-and-molecule-interattractive-proximity limits. T he se chemical-structure-integrity limits are visibly demonstrated to the human ey e s by the bursting of bubbles or of children’s overfilled balloons or of any othe r internally overpressured fluid-pneumatic, molecular-membraned containers when t he membrane impinging and ricocheting interkinetic acceleration of an increasingl y introduced population of contained gas molecules separates the molecules of the container membrane beyond their critical-proximity limits. These critical-atomic-and-molecular-proximity limits are mathematically and gravitationally similar to the proximity limits governing the velocity and distance outward from planet Eart h’s surface at which a rocket-launched vehicle can maintain its orbit and not fal l back into the Earth.
¶ 986.700 Spheric Nature of Electromagnetic Waves
[986.701]{style="color: purple3"} []{#ver:986.701 label="ver:986.701"} Conside ration 16: and Realization of Synergetic Significance
[986.702]{style="color: purple3"} []{#ver:986.702 label="ver:986.702"} Since we have l earned that nature’s second-powering is triangling and not squaring (Sec. 990), a nd since each square is always two similar triangles, we must express Einstein’ s equation, whereis the product ofand c2, as: $$E = 2V^{2}$$
¶ 986.710 Recapitulation of Geometry-and-energy Recalls
[986.711]{style="color: purple3"} []{#ver:986.711 label="ver:986.711"} I must add to the inventory of only-synergetically-interrevealing significant disco veries of this chronicle a recapitulation of additional “recalls”:
-
The absolute constancy of cheese polyhedra;
-
that the tetrahedron is the quantum of energy;
-
that the nonpolar vertexes of the polar-edge-“tuned” tetrehedron can connect any other two points in Universe;
-
that the unit-volume progression of quanta modules accounts for electromagnetic intertuning;
-
that the tetrahedron in turning itself inside-out accounts for electromagnetic-wave propagation;
-
that polyhedra should be reidentified as polyvertexia, the simplest of which is the tetravertex;
-
that the tetravertex is the simplest spheric system;
-
that the vector equilibrium provides a field for universal energy accommodation; and
-
that the vector equilibrium shell growth rate predicts the proton and neutron population of the elements.
¶ 986.720 Absolute Constancy: Cheese Polyhedra
[986.721]{style="color: purple3"} []{#ver:986.721 label="ver:986.721"} My first o bservation of the polyhedral hierarchy was introduced in Sec. 223.64, Table 224.2 0, and Fig. 400.30. That hierarchy may be considered as cheese polyhedra in which there is an experimental redemonstrability of absolute constancy of areal, volume tric, topological, and symmetry characteristics, which constancy is exclusively u nique to triangles and tetrahedra and is maintained despite any and all asymmetri cal aberrations of those triangles and tetrahedra, as caused by per s pective distortion; by interproportional variations of relative len g ths and angles as manifest in isosceles, scalene, acute, or obtuse system aspect s (see quadrangular versus triangular accounting in Figs. 990.01 and *100.301 .),*by truncatings parallel to triangle edges or para llel to tetrahedron faces; or by frequency modulations, in contradi s tinction to complete loss of symmetry and topological constancy of all polygons o ther than the triangle and of all polyhedra other than the tetrahedron as cause d by any special-case, time-size alterations or changes of the perspective point fr om which the observations of those systems are taken.
[986.722]{style="color: purple3"} []{#ver:986.722 label="ver:986.722"} In connectio n with this same cheese tetrahedron recall we remember (1) that we could push in on the faceof the tetrahedron at a given rate of radial contraction of the sys te m, while pulling out face# at a matching rate of radial expansion of the syste m , which “couple” of local alterations of the system left the tetrahedron unalt ered in shape or size throughout the transformation (Sec. 623) and just as it was both before and after the “coupled” transformings took place, the only altered consequence of which was that the tetrahedron’s center of volume had migrated; an d we remember (2) that we could also push in on the same tetrahedron’s faceand pull out on face/) at a coupled rate other than the coupled rate of radial expans ion and contraction of the A-B face-coupling s intercomplementary transformings; by all of which we learn that the tetrahedron can accommodate two disparate rates of change without in any way altering its own size and only alter ing its center-of-volume positioning in respect to any other system components of the local Universe consideration. (See color plate 26.)
[986.723]{style="color: purple3"} []{#ver:986.723 label="ver:986.723"} It must be no ted, however, that because of the generalized nonsimultaneity of cosmic events , there exists an inherent lag between the pushing in of faceand the pulling o u t of face, which induces an inherent interim wave-depression or a wave-breaki ng pulsating of the coupling functionings of the tetrahedron’s accommodation of t ransmission of two disparately frequenced energetic communications.
[986.724]{style="color: purple3"} []{#ver:986.724 label="ver:986.724"} S econd, I recallas in Secs. 920.01 and 921.10 and Fig. 923. 10that the tetrahedron is the quantum of energy.
[986.725]{style="color: purple3"} []{#ver:986.725 label="ver:986.725"} Third, I recall that t he single-tuned-length axis of the edge-axis- rotatable tetrahedro n’s two nonaxi s polar vertexes may be deployed to connect up with any two other p oints in Univ erse without altering the tetrahedron s unit volume or its tuned-axi s length. (S ee Sec. 961.30.)
[986.726]{style="color: purple3"} []{#ver:986.726 label="ver:986.726"} Fourth, I recall that the tetrahedron’ s 24Module s and the latter’s B, C, D; A, B, C, D; A", B", C", D" …a(see Fig. *986.726,*which is a detail and relabeli ng of Fig. 923.10B) together with theandModules provid e transformative sig nificance of being the constant-unit-volume progression of ev er-more-asymmetrica lly-transforming stages of the constant-unit-volume tetrahedra , with the uniform -stage transforming being provided by five of the six edges of each of the consta nt-volume tetrahedra being covaryingly and ever-progressively-d isparately altere dwith the sixth edge alone of each and all stages of the transformati on remaining unaltered in frequency and wavelength magnitude. The concurrent constant-volume-and-wavelength transformings, and system rotating aro und and angular tilting of the constant, unaltered-in-length, sixth edge’s axial altitude in respect to the all-other-in-Universe experiences’ omniinterangular or ientations, altogether both permit and accommodate any two oth er points X andi n Universe being interconnected not only with one another, but also with the two pointsandthat define the unaltered sixth edgeof the c onstant-volume an d constant-/lB-edge-length, omni-Universe-interconnecting tetrah edron *ABXY ;*all of which permits the constant sixth edgelength to serve as the anywhere and anywhen in Universe to be established transceiver’s wave-leng th-defining and frequency-selecting and tuning interconnecting any given two poin ts in Universe with any two other points in Universe; ergo, with all other points in Universe, g ranted only sufficient elapsed time for rotational realization of t he frequency of repetition of the wavelength vector’s velocity factor to reach an y given loci in Universe with a given volumetric-unit quantum of energy. (This is the signific ance of Fig. 923.10.) 
Fig. 986.726 Constant-iinit-volume Progressions of Asymmetric Tetrahedra: Change: fix I n this progression of ever-more-asymmetric tetrahedra, only the sixth edge remain s constant. Tetrahedral wavelength and tuning permits any two points in Universe to connect with any other two points in Universe.
[986.727]{style="color: purple3"} []{#ver:986.727 label="ver:986.727"} Fifth, I recall a s recounted in Sec. 961.40 that the more elongated the unit-volume tetrahedron of only one-edge-length-constancy (the sixth edge), the less becomes the unit-volume tetrahedron’s least-altitude aspect as related to its other interdimensional aspects, wherefore there is attained a condition wherein the controlling sixth edge’s wavelength is greater than half the tetrahedron’s least-altitude aspect at which condition the tetrahedron spontaneously turns itself inside-out, ergo, turns itself outnot out of Universe, but out of tune-in-able range. Prior to this spontaneous tuning-out range we have a vast range of now-partially-tuned-in-and-now-tuned-out, which altogether propagates finitely packaged, tuned-in energy information occurring in packages yet recurring in constant, contained wavelength intervals that introduce what has hitherto been considered to be the paradoxical aspect of electromagnetic phenomena, of which it has been misassumed that as of any one moment we can consider our electromagnetic phenomena as be ing continuous-wave phenomena or as discontinuous-particle phenomen aboth simultaneous. We thus learn that no such paradox exists. (Comp are Secs. 541 .30, 961.46-48, 973.30, and 1072.32.) [986.728]{style="color: purple3"} []{#ver:986.728 label="ver:986.728"} Sixth, we r ecall that th ere are no solids or absolute continuums; ergo, there are no physic ally demonstr able faces or sides of *hedra;*ergo, we reidentify the system-conceptioning experiences heretofore spoken of as polyhedra, by the name *polyvertexia,*t he simplest of which is the *tetravertex,*or “four-fix” sy stem.
[986.729]{style="color: purple3"} []{#ver:986.729 label="ver:986.729"} Seventh, we recall that the tetravertex is not only the simple st limit casei.e., the topologically most economically definable poly vertex system casebut also the simplest spheric-system experience cas e. (See Secs. 1024.10-25, 105 3.40-62, 1054. 1054.30, and Fig. 1054.40.)
[986.730]{style="color: purple3"} []{#ver:986.730 label="ver:986.730"} The Spheric Experience: We now scientifically redefine the spheric experience as an aggregate of vertex-direction-pointed-to (fixed) subtune-in-able microevent centers surrounding a system center at equal-radius distances from the system center. Four such surrounding, vertex-convergence-indicated, microevent fixes are redemonstrably proven to be the minimum number of such a microcenter-surrounding aggregate geometrically adequate to constitute systemic subdivision of Universe into macrocosm and microcosm by convergent envelopment , which inherently excludes the thus-constituted system’s macrocosm and inherently includes the thus-constituted system’s microcosm, in which spheric experiencing the greater the population of equi-radiused-from-system-center microevent fixes, the more spheric the experience, and the earliest and simplest beyond the tetrahedron being the hierarchy of concentric, symmetric, primitive polyhedra.
¶ 986.740 Microenergy Transformations of Octet Truss
[986.741]{style="color: purple3"} []{#ver:986.741 label="ver:986.741"} The se last nine major recalls (Sec. *986.711)*are directly related to the matt er-to-radiation transitional events that occur as we transit between the T and t heQuanta Modules. First, we note that bubbles are spherics, that bubble envelo pes are liquid membranes, and that liquids are bivalent. Bivalent tetrahedral agg regates produce at minimum the octet truss. (See Sec. 986.835et seq.) The octet truss’s double-bonded vertexes also require two layers of closest-packed, u nit-radius spheres, whose two layers of closest-packed spheres produce an octet t russ whose interior intermembranes are planar while both the exterior and interio r membranes are domical.
[986.742]{style="color: purple3"} []{#ver:986.742 label="ver:986.742"} Sufficient interior pressure will stretch ou t the bivalent two-sphere layer into univalent one-sphere layering, which mean s transforming from the liquid into the gaseous state, which also means transfor mi ng from interattractive proximity to inadequate interattractive proximity ergo, to self-diffusing, atoms-dispersing gaseous molecules. This is to say that the surface-to-volume relationship as we transform fromQuanta Modu le toQua nta Module is a transformative, double-to-single-bond, liquid-to-gas t ransition. Nothing “bursts.” …Bursting is a neat structural-to-destructur al atomic rearrangement, not an undefinable random mess.
[986.743]{style="color: purple3"} []{#ver:986.743 label="ver:986.743"} Small-mole culed, gase ous-state, atomic-element, monovalent integrities, wherein the atoms are within m ass-interattractive critical-proximity range of one another, interco nstitute a c loud that may entrap individual molecules too large for escape throu gh the small -molecule interstices of the cloud.cloud is a monovalent atomic cr owd. Water is a bivalent crowd of atoms. Clouds of gasses, having no external mem brane, ten d to dissipate their molecule and atom populations expansively, except, for insta nce, within critical proximity of planet Earth, whose Van Allen belts an d ionosp here are overwhelmingly capable of retaining the atmospheric aggregates whose minienergy events such as electrons otherwise become so cosmically disperse d as to be encountered only as seemingly “random” rays and particles.
[986.744]{style="color: purple3"} []{#ver:986.744 label="ver:986.744"} This cosmic dispersion of individual microenergy event components alp ha particles, beta particles, and so onleads us to wh at is seemingly the most entropic disorderly state, which is, however, only the interpenetration of the outer ramparts of a plurality of differently tuned or ve ctored isotropic-vector-matrix systems.
¶ 986.750 Universal Accommodation of Vector Equilibrium Field: Expanding Universe
[986.751]{style="color: purple3"} []{#ver:986.751 label="ver:986.751"} Recalling (a) that we gave the vector equilibrium its name because na ture avoids the indeterminate (the condition of equilibrium) by always transformi ng or pulsating four-dimensionally in 12 different ways through the omnicentrals tate, as in one plane of which a pendulum swings throughthe vertical; and recalling (b) that each of the vertexes of the isotropic vector matrix could serve as the nuclear center of a ; and recalling (c ) also that th e limits of swing, pulse, or transform through aberrations of all the nucleus-concentric hierarchy of polyhedra have shown themselves to be of m odest aberrati onal magnitude (see the unzipping angle, etc.); and r ecalling (d) al so that post-Hubble astronomical discoveries have found more than a million galax ies, all of which are omniuniformly interpositioned angularly and are omniuniform ly interdistanced from one another, while all those distances are seemingly incre asing uniformly; all of which recalls together relate to, explain, an d engender the name Expanding Universe.
[986.752]{style="color: purple3"} []{#ver:986.752 label="ver:986.752"} We realize t hat these last f our recalls clearly identify the isotropic vector matrix as bein g the operative geometrical field, not only when atoms are closest packed with o ne another but a lso when they are scattered entropically into the cosmically gre atest time-size galaxies consisting of all the thus-far-discovered-to-exist star s, which consist of the thus-far-discovered evidence of existent atoms within ea ch star’s cosmic regionwith those atoms interarrayed in a multitude of all-altemately, equi-degrees-of-freedom-and-frequency-permitted, evolutionary patterning displays ranging from interstellar gasses and dusts to planets and st ars, from asteroids to planetary turtles …to coral …to fungi … et al…Wherefore the Expanding Universe of uniformly interpositioned galaxi es informs us that we are witnessing the isotropic vector matrix and its local v ector equilibria demon strating integrity of accommodation at the uttermost time-size macrolimits thus far generalizable within this local 20-billion-year-episod e sequence of eternall y regenerative Universe, with each galaxy’s unique multibi llions of stars, and e ach of these stars’ multibillions of atoms all intertransf orming locally to demonstrate the adequacy of the isotropic vector matrix and it s local vector equilib ria to accommodate the totality of all local time aberrati ons possible within th e galaxies’ total system limits, which is to say within ea ch of their vector equ ilibrium’s intertransformability limits.
[986.753]{style="color: purple3"} []{#ver:986.753 label="ver:986.753"} Each of the galaxies is centered within a major domain within the greater isotropic vector matrix geometrical fieldwhich major ’s respective fields are subdividingly multiplied by isotropic matrix field centerings to the extent of the cumulative num ber of tendencies of the highest frequency components of the systems permitted by the total time-size enduring magnitude of the local systems’ individual endurance time limits.
[986.754]{style="color: purple3"} []{#ver:986.754 label="ver:986.754"} In the seemingly Expanding Universe the equidistant galaxies are apparently receding from each other at a uniform rate, as accounted for by the pre-time-size matrix which holds for the largest scale of the total tim e. This is what we mean by multiplication only by division within each domain and its total degrees of freedom in which the number of frequencies available can accommodate the full history of the cosmogony.
[986.755]{style="color: purple3"} []{#ver:986.755 label="ver:986.755"} The higher the frequency, the lower the aberration. With multiplication only by division we can accommodate the randomness and the entropy within an entirely regenerative Universe. The high frequency is simply diminishing our point of view.
[986.756]{style="color: purple3"} []{#ver:986.756 label="ver:986.756"} The Expanding Universe is a misnomer. What we have is a progressively diminishing point o f view as ever more time permits ever greater frequency of subdivisioning of the totally tunable Universe.
[986.757]{style="color: purple3"} []{#ver:986.757 label="ver:986.757"} What we observe sum-totally is not a uniformly Expanding Universe, but a uniformly-contracting-magnitude viewpoint of multiplication only by division of the finite but non-unitarily-conceptual, eternally regenerative Scenario Universe. (See Secs. 987.066and 1052.62.)
[986.758]{style="color: purple3"} []{#ver:986.758 label="ver:986.758"} Because the higher-frequency events have the shortest wavelengths in aberration limits, their field of articulation is more local than the low-frequency, longer-wavelengths aberration limit even tsergo, the galaxies usually have the most intense activities closer into and around the central region s: all their entropy tendency is accommodate d by the total syntropy of the astro physical greatest-as-yet-identified duration limit.
[986.759]{style="color: purple3"} []{#ver:986.759 label="ver:986.759"} We may now direct our attention to the microscosmic, no-time size, closest-packed unity (versus the Galactic Universe macro-interdistanced unity). This brings us to the prefrequency, timeless-sizeless ’s hierarchy and t o the latter’s contractability into the geometrical tetrahedron and to that quadrivalent tetrahedron’s ability to turn itself inside-out in pure principle to become the novent tetrahedron the “Black Hole”the presently-non-tuned-in phenomena. And now we w itness the full regenerative range of generalized accommodatability of the ’s isotropic matrix and its gamut of special case realizations occurring as local Universe episodes ranging from photons to mol ecules, from red giants to white dwarfs, to the black-hole, self-insideouting, and self-reversing phase of intertransformability of eternally regenerative Universe.
[986.760]{style="color: purple3"} []{#ver:986.760 label="ver:986.760"} Next we reexplore and recall our discovery of the initial timesize frequencymultiplication by division onlywhich produce s the frequency layers of 12, 42 , 92 closest-packed spheres around a nuclear sphere…And here we have evidencible proof of the persistent adequacy of the ’s local field to accommodate the elegantly simple structural regenerating of the prime chemical elements, with the successive shell populations demonstrating physically the exact proton-neutron population accounting of the first minimum-limit case of most symmetrical shell enclosings, which corresponds exactly with the ever-experimentally-redemonstrable structural model assemblies shown in Sec. 986.770.
¶ 986.770 Shell Growth Rate Predicts Proton and Neutron Population of the Elements
[986.771]{style="color: purple3"} []{#ver:986.771 label="ver:986.771"} Thus far we have discovered the physical modelability of Einstein’s equation and the scientific discovery of the modelability of the transformation from matter to radiation, as well as the modelability of the difference between w aves and particles. In our excitement over these discoveries we forget that other s may think synergetics to be manifesting only pure coincidence of events in a p ure-scientists’ assumed-to-be model-less world of abstract mathematical expressions, a world of meaningless but alluring, simple geometrical relationships. Hoping to cope with such skepticism we introduce here three very realistic models whose complex but orderly accounting refutes any suggestion of their being three successive coincidences, all occurring in the most elegantly elementary field of human exploration that of the periodic table of unique number behaviors of the proton and neutron populations in successive stages of the complexity of the chemical elements themselves.
[986.772]{style="color: purple3"} []{#ver:986.772 label="ver:986.772"} If we look at Fig. 222.01 (Synergetics 1) , which shows the three successive layers of closest-packed spheres around the prime nuclear sphere, we find the successive layer counts to be that is, they are “frequency to the second power times 10 plus 2.” While we have been aware for 40 years that the outermost layer of these concentric layers is 92 , and that its first three layers add to $$12 + 42 + 92 = 146$$ which 146 is the number of neutrons in uranium, and uranium is the 92nd element as with all elements, it combines its total of inner-layer neutrons with its oute r-layer protons. In this instance of uranium we have combined the 149 with 92, wh ich gives us Uranium-238 , from which count we can knock out fo ur neutrons from eight of the triangular faces without disturbing symmetry to giv e us Uranium-234 .
[986.773]{style="color: purple3"} []{#ver:986.773 label="ver:986.773"} Recently, however, a scientist w ho had been studying synergetics and attending my lectures called my attention to the fact that the first closest-packed layer 12 around the nuclear sphere and the second embracing closest-packed layer of 42 follow the same neutron count, combining with the outer layer number of protonsas in the 92 uranium-layer caseto provide a physically conceptual model of magnesium and molybdenum. (See Table 419.21.)
[986.774]{style="color: purple3"} []{#ver:986.774 label="ver:986.774"} We can report that a number of scientists or scientific-minded laymen are communicating to us their discovery of oth er physics-evolved phenomena as being elegantly illustrated by synergetics in a conceptually lucid manner.
[986.775]{style="color: purple3"} []{#ver:986.775 label="ver:986.775"} Sum-totally we can say that the curve of such events suggests that in the coming decades science in general will have discovered that synergetics is indeed the omnirational, omniconceptual, multialtermatived, omnioptimally-efficient, and always experimentally reevidenceable, comprehensive coordinate system employed by nature.
[986.776]{style="color: purple3"} []{#ver:986.776 label="ver:986.776"} With popular concept ion of synergetics being the omniconceptual coordinate system of nature will come popular comprehension of total cosmic technology, and therefore popular comprehension that a competent design revolution structurally and mechanicallyemploying the generalized principles governing cosmic technology can indeed render all humanity comprehensivelyi.e., physically and metaphysicallysuccessful, i.e., becoming like “hydrogen” or “leverage”regular member functions of an omnisuccessful Universe.
¶ 986.800 Behavioral Proclivities of Spheric Experience
¶ 986.810 Discard of Abstract Dimensions
[986.811]{style="color: purple3"} []{#ver:986.811 label="ver:986.811"} Inspired by the modelability, I did more retrospective reconsideration of what I have been concerned with mathematically throughout my life. This reviewing led me to (1) more discoveries, clarifications, and definitions regarding spheres; (2) the discard of the concept of axioms; and (3) the dismissal of th ree-dimensional reality as being inherently illusoryand the discard of many of mathematics’ abstract devices as being inherently “roundabout,” “obscurational,” and “inefficient.”
[986.812]{style="color: purple3"} []{#ver:986.812 label="ver:986.812"} Reversion to axioms and three-dimensional “reality” usually occurs on the basis of “Let’s be practical …let’s yield to our ill-informed reflex-conditioning …the schoolbooks can’t be wrong …no use in getting out of step with the system …we’ll lose our jobs …we’ll be called nuts.”
[986.813]{style="color: purple3"} []{#ver:986.813 label="ver:986.813"} Because they cannot qualify as laws if any exceptions to them are found, the generalizable laws of Universe are inherently eternal-timeless-sizeless. Sizing requires time. Time is a cosmically designed consequence of humanity’s having been endowed with innate slowness of apprehension and comprehension, which lags induce time-lapse-altered concepts . (Compare Sec. 529.09.)
[986.814]{style="color: purple3"} []{#ver:986.814 label="ver:986.814"} Time-lapsed apprehension of any and all energy-generated, human-sense-reported, human-brain-image-coordinated, angular-directional realization of any physical experiences, produces (swing-through-zero) momentums of misapprehending, which pulsatingly unbalances the otherwise equilibri ous, dimensionless, timeless, zero-error, cosmic intellect perfection thereby only inferentially identified to human apprehending differentiates the conceptioning of all the special case manifests of the generalized laws experienced by each and every human individual.
[986.815]{style="color: purple3"} []{#ver:986.815 label="ver:986.815"} Academic thought, overwhelmed by the admitted observational inexactitude of special case human-brain-sense experiences, in developing the particular logic of academic geometry (Euclidean or non-Euclidean), finds the term “identical” to be logically prohibited and adopts the word “similar” to identify like geometrical entities. In synergetics, because of its clearly defined differences between generalized primitive conceptuality and special-case timesize realizations, the word “identical” becomes logically permitted. This is brought about by the difference between the operational procedures of synergetics and the abstract procedures of all b ranches of conventional geometry, where the word “abstract” deliberately means “nonoperational,” because only axiomatic and non-physically-demonstrable.
[986.816]{style="color: purple3"} []{#ver:986.816 label="ver:986.816"} In conventional geometry the linear characteristics and the relative sizes of lin es dominate the conceptioning and its nomenclatureas, for instance, using the term “equiangular” triangle because only lengths or sizes of lines vary in time. Lines are unlimited in size and can be infinitely extended, whereas angles are discrete fractions of a discrete whole circle. Angles are angles independently of the lengths of their edges. (See Sec. 986.816) Lengths are always special time-size cases: angles are eternally generalized…We can say with scientific accuracy: “identical equiangular triangles.” (See Fig. 986.816.)
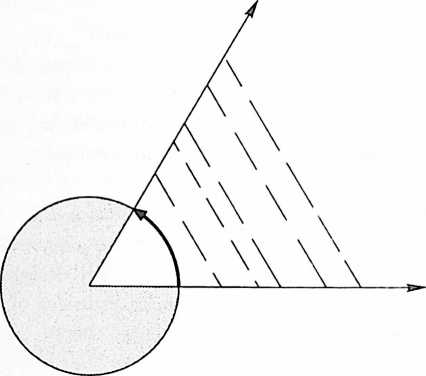
[986.817]{style="color: purple3"} []{#ver:986.817 label="ver:986.817"} In summary, lines are “size” phenomena and are unlimited in length. Size measuring requires “time.” Primitive synergetics deals only in angles, w hich are inherently whole fractions of whole circular azimuths.
[986.818]{style="color: purple3"} []{#ver:986.818 label="ver:986.818"} Angles are angles independent of the length of their edges. Triangles are triangles independent of their size. Time is cyclic. Lacking one cycle there is no time sense. Angle is only a fraction of one cycle.
[986.819]{style="color: purple3"} []{#ver:986.819 label="ver:986.819"} Synergetics procedure is always from a given whole to the particular fractional angles of the whole system considered. Synergetics employs multiplication only by division…only by division of finite but non-unitarily-conceptual Scenario Universe, subdivided into initially whole primitive systems that divide whole Universe into all the Universe outside the system, all the Universe inside the system, and the little bit of Universe that provides the relevant set of special case stars of experience that illuminatingly define the vertexes of the considered primitive generalized system of consideration. (See Sec. 509.) Conventional geometry “abstracts” by employment of nonexistentergo, nondemonstrable parts, and it compound s a plurality of those nonexistents to arrive at supposedly real objects.
[986.820]{style="color: purple3"} []{#ver:986.820 label="ver:986.820"} Because the proofs in conventional geometry depend on a plurality of divider-stepped-off lengths between scribed, punched, or pricked indefinably sized point-speck holes, and because the lengths of the straightedge-drawn lines are extendible without limit, conventional geometry has to assume that any two entities will never be exactly the same. Primitive synergetics has only one length: that of the prime unit vector of the and of the isotropic vector matrix.
[986.821]{style="color: purple3"} []{#ver:986.821 label="ver:986.821"} Synergetics identifies all of its primitive hierarchy and their holistic subdivisions only by their timeless-sizeless relative angular fractional subdivisions of six equiangular triangles surrounding a point, which hexagonal array equals 360 degrees, if we assume that the three angles of the equiangular triangle always add up to 180 degrees. Synergetics conducts all of its calculations by spherical trigonometry and deals always with the central and surface angles of t he primitive hierarchy of pre-time-size relationships of the symmetrically concentric systems around any nucleus of Universeand their seven great-circle symmetries of the 25 and 31 great-circle systems (Sec. 1040). The foldability of the four great-circle planes demonstrates the four sets of hexagons omnisurrounding the cosmic nucleus in omni-60-degree angular symmetry. This we call th e . (See Sec. 840.) Angular identities may be operationally assumed to be identical: There is only one equiangular triangle, all of its angles being 60 degrees. The 60-ness comes from the 60 positive and 60 negative, maximum number of surface triangles or Quanta Modules per cosmic system into which convergent-divergent nuclear unity may be subdivided. The triangle, as physically demonstrated by the tube necklace polygons (Sec. 608), is the only self-stabilizing structure, and the equiangular triangle is the most stable of all triangular structures. Equiangular triangles may be calculatingly employed on an “identical” basis.
¶ 986.830 Unrealizability of Primitive Sphere
[986.831]{style="color: purple3"} []{#ver:986.831 label="ver:986.831"} As is shown elsewhere (Sec. 1022.11), synergetics finds that the abstract Greek “sphere” do es not exist; nor does the quasisphere the sense-reported “spheric” experiencings of humansexist at the primitive stage in company with t he initial cosmic hierarchy of timeless-sizeless symmetric polyhedra as defined b y the six positive and six negative cosmic degrees of freedom and their potential force vectors for adequately coping with all the conditions essential to maintain the individual integrity of min-max primitive, structural, presubdivision systems of Universe.
[986.832]{style="color: purple3"} []{#ver:986.832 label="ver:986.832"} The sphere is only dynamically developed either by profiles of spin or by multiplication of uniformly radiused exterior vertexes of ever-higher frequency of modular subdivisioning of the primitive system’s initial symmetry of exterior topology. Such exclusively time-size events of sufficiently high frequency of modular subdivisioning, or high frequency of revolution, can transform any one of the primitive (eternal, sizeless, timeless) hierarchy of successive = 272, 1, 272, 3, 4, 5, 6-tetravolumed concentrically symmetric polyhedra into quasispherical appearances. In respect to each such ever-higher frequency of subdividing or revolving in time, each one of the primitive hierarchy polyhedra’ s behavioral appearance becomes more spherical.
[986.833]{style="color: purple3"} []{#ver:986.833 label="ver:986.833"} The volume of a static quasisphere of unit vector length (radius =1) is . Each quasisphere is subexistent because it is not as yet spun and there is as yet no time in which to spin it. Seeking to determine anticipatorily the volumetric value of the as-yet-only-potential sphere’s as-yet-to-be-spun domain (as recounted in Secs. 986.206-214 ), I converted my synergetics constant to its ninth power, as already recounted and as intuitively motivated to accommodate the energetic factors involved, which gave me the number (see Sec. 982.55), and with this ninth-powered constant multiplied the incipient sphere’s already-third-powered volume of , which produced the twelfth-powered value , which seems to tell us that synergetics’ experimentally evidenceable only-by-high-frequencyspinning polyhedral sphere has an unattainable but ever-more-closely-approached limit tetra volume-5.000 with however a physically imperceptible volumetric shortfall of tetra volume-5, the limit being the maximum attain able twelfth-powered dynamismbeing a sphericity far more perfect than that of any of the planets or fruits or any other of nature’s myriads of quasispheres, which shortfallers are the rule and not the exceptions. The primitively nonconceptual, only-incipient sphere’s only-potentially-to-be-demonstrated domain, like the square root of minus one, is therefore a useful, approximate-magnitude, estimating tool, but it is not structurally demonstrable. The difference in magnitude is close to that of the and Quanta Modules.
[986.834]{style="color: purple3"} []{#ver:986.834 label="ver:986.834"} Since structure means an interself-stabilized complex-of-events patterning (Sec. 600.01), the “spheric” phenomenon is conceptuallyseasonally experience a ble only as a time-size high-frequency recurrence of events, an only-by-dynamic s weepout domain, whose complex of involved factors is describable only at the twelfth-power stage. Being nonstructural and involving a greater volumetric sweepo u t domain than that of their unrevolved structural polyhedral domains, all quasi spheres are compressible.
[986.835]{style="color: purple3"} []{#ver:986.835 label="ver:986.835"} Independently occurring single bubbles are dynamic and only superficially spherical. In closest packing all interior bubbles of the bubble aggregate become individual, 14-faceted, tension-membrane polyhedra, which are structured only by the interaction with their liquid monomer, closed-system membranes of all the trying-to-escape, kinetically accelerated, interior gas moleculeswhich interaction can also be described as an omniembracing restraint of the trying-to-escape gaseous molecules by the sum-total of interatomic, critical-proximity-interattracted structural cohesion of the tensile strength of the bubble’s double-molecule-layered (double-bonded) membranes, which comprehensive closed-system embracement is similar to the cosmically total, eternally integral, nonperiodic, omnicomprehensive embracement by gravitation of the always-and-only periodically occurring, differentiated, separate, and uniquely frequenced nonsimultaneous attempts to disintegratingly escape Universe enacted by the individually differentiated sum-total entities (photons) of radiation. Gravity is always generalized, comprehensive, and untunable. Radiation is always special case and tunable.
[986.836]{style="color: purple3"} []{#ver:986.836 label="ver:986.836"} Bubbles in either their independent spherical shape or t heir aggregated polyhedral shapes are structural consequences of the omnidirectionally outward pressing (compression) of the kinetic complex of molecules in th e ir gaseous, single-bonded, uncohered state as comprehensively embraced by molecules in their liquid, double-bonded, coherent state. In the gaseous state the molecules operate independently and disassociatively, like radiation quanta ergo, less effective locally than in their double-bonded, integrated , gravity-like, liquid-state embracement.
¶ 986.840 Primitive Hierarchy as Physical and Metaphysical
[986.841]{style="color: purple3"} []{#ver:986.841 label="ver:986.841"} special case is time-size. Generalization is eternal and is independent of time-size “Spheres,” whether as independent bubbles, as high-frequency geodesic polyhedral structures, or as dynamically spun primitive polyhedra, are always and only special case time-size (frequency) physical phenomena. The omnirational primitive-numbered-tetravolume-interrelationships hierarchy of concentric symmetric polyhedra is the only generalized conceptuality that is both physical and metaphysical. This is to say that the prime number and relative abundance characteristics of the topology, angulation, and the relative tetravolume involvements o f the primitive hierarchy are generalized, conceptual metaphysics. Physically evidenced phenomena are always special case, but in special cases are manifests of generalized principles, which generalized principles themselves are also always metaphysical.
¶ 986.850 Powerings as Systemic-integrity Factors
[986.851]{style="color: purple3"} []{#ver:986.851 label="ver:986.851"} Synergetics is everywhere informed by and dependent on experimental evidence which is in herently witnessablewhich means conceptual and synergetics’ primitive structural polyhedra constitute an entire, infra-limit-to-ultra-limit, systemic, conceptual, metaphysical hierarchy whose entire interrelationship val ues are the generalizations of the integral and the “internal affairs” of all systems in Universeboth nucleated and non-nucleated. Bubbles and subatomic , , , and Quanta Modules are non-nucleated containment systems. Atoms are nucleated systems.
[986.852]{style="color: purple3"} []{#ver:986.852 label="ver:986.852"} The systemically internal interrelationship values of the primitive cosmic hierarchy are all independent of time-size factorings, all of which generalized primitive polyhedra’s structurings are accommodated by and are governed by six positive and six negative degrees of freedom. There are 12 integrity factors that definitively cope with those 12 degrees of freedom to produce integral structural systemsboth physical and meta physicalwhich integrity factors we will henceforth identify as powerings.
[986.853]{style="color: purple3"} []{#ver:986.853 label="ver:986.853"} That is, we are abandoning altogether the further employment of th e word dimension, which suggests (a) special case time-size lengths, and (b) that some of the describable characteristics of systems can exist a lone and not as part of a minimum system, which is always a part of a priori eternally regenerative Universe. In lieu of the no longer scientifically tenable concept of “dimension” we are adopting words to describe time-size realizations of generali zed, timeless, primitive systems as event complexes, as structural selfstabilizations, and structural intertransformings as first, second, third, etc ., local powering states and minimum local systemic involvement with conditions of the cosmic totality environment with its planetary, solar, galactic, complex-galactic, and supergalactic systems and their respective macro-micro isotropicities.
[986.854]{style="color: purple3"} []{#ver:986.854 label="ver:986.854"} In addition to the 12-powered primitive structurings of the positive and negativ e primitive tetrahedron, the latter has its primitive hierarchy of six intertransformable, tetravolumed, symmetrical integrities which require six additional powerings to produce the six rational-valued, relative-volumetric do mains. In addit ion to this 18-powered state of the primitive hierarchy we discover the integral ly potential six-way intertransformabilities of the primitive hiera rchy, any one of which requires an additional powering factor, which brings us th us far to 24 powering states. Realization of the intertransformings requires time-size, special case, physical transformation of the metaphysical, generalized, timeless-size less, primitive hierarchy potentials.
[986.855]{style="color: purple3"} []{#ver:986.855 label="ver:986.855"} It is demonstrably evidenceable that the physically realized superimposed intertransformability potentials of th e primitive hierarchy of systems are realizable only as observed fr om other systems. The transformability cannot be internally observed. All primit ive systems h ave potential external observability by other systems. “Otherness” systems hav e their own inherent 24-powered constitutionings which are not additional poweringsjust more of the same.
[986.856]{style="color: purple3"} []{#ver:986.856 label="ver:986.856"} All systems have external relationships, any one of which constitutes an additional systemic complexity-compreh ending-and-defining-and-replicating power factor. The number of additional power ing factors involved in systemic self-systems and otherness systems i s determine d in the same manner as that of the fundamental interrelationships of self- and otherness systems, where the number of system interrelationships is\sfrac{n^2 - n}{2} [986.857]{style="color: purple3"} []{#ver:986.857 label="ver:986.857"} Not including the\sfrac
{n^2 - n}{2}additional intersystems-relationshi p powerings, beyond the 24 systemically integral powers, there are six additional , only-otherness-viewable (and in some cases only multi-otherness viewable and re alizable), unique behavior potentials of all primitive hierarchy systems, each of which behaviors can be comprehensively accounted for only by additional powerings . They are:
25th-power = axial rotation of the system
26th-power = orbital travel of the system
27th-power = expansion-contraction of the system
28th-power = torque (axial twist) of the system
29th-power = inside-outing (involuting-evoluting) of the system
30th-power = intersystem precession (axial tilting) of the system
31st-power = external interprecessionings amongst a plurality of systems
32nd-power = self-steering of a system within the galaxy of systems (precessionally accomplished)
33rd-power = universal synergistic totality comprehensive of all intersystem effects and ultimate micro- and macroisotropicity of -ness
¶ 986.860 Rhombic Dodecahedron 6 Minus Polyhedron 5 Equals Unity
[986.861]{style="color: purple3"} []
High-frequency, triangulated unit-radius-vertexed, geodesically interchorded, sph erical polyhedral apparencies are also structural developments in time-size. Ther e are therefore two kinds of spherics: the high-frequency-event-stabilized, geode sic, structural polyhedron and the dynamically spun, only superficially “apparen t” spheres. The static, structural, multifaceted, polyhedral, geodesic sphere’s vertexes are uniformly radiused only by the generalized vector, whereas the only superficially spun and only apparently profiled spheres have a plurality of verte xial distances outward from their systemic center, some of which distances are gr eater than unit vector radius while some of the vertexes are at less than unit ve ctor radius distance. (See Fig. 986.314.) [986.862]{style="color: purple3"} []{#ver:986.862 label="ver:986.862"} Among the symmetrical polyhedra having a tetravolume of 5 and also having radii a little more or a litt le less than that of unit vector radius, are the icosahedron and the enenicontahe dron whose mean radii of spherical profiling are less than four percent vector-ab errant. There is, however, one symmetrical primitive polyhedron with two sets of its vertexes at greater than unit radius distance outwardly from their system’s n ucleic center; that is the rhombic dodecahedron, having, however, a tetravolume o f 6. The rhombic dodecahedron’s tetravolume of 6 may account for the minimum inte rsystemness in pure principle, being the space between omni-closest-packed unitra dius spheres and the spheres themselves. And then there is one symmetric primitiv e polyhedron having a volume of exactly tetravolume 5 and an interpattern radius ofof one unit vector; this is the T Quanta Module phase rhombic triacontah edron. There is also an additional rhombic triacontahedron of exact vector radius and a tetravolume of, which is just too much encroachment upon the r hombic dodecahedron 6 minus the triacontahedron, or one volu metric unit of unassigned cosmic “fail-safe space”: BANG radiation-e ntropy and eventual turnaround precessional fall-in to syntropic photosynthetic t ransformation into one of matter’s four states: plasmic, gaseous, liquid, crystal line.
[986.863]{style="color: purple3"} []{#ver:986.863 label="ver:986.863"} All the hierarchy of primitive polyhedra were developed by pr o gressive great-circle-spun hemispherical halvings of halvings and trisectings o f halvings and quintasectings (see Sec. 100.1041) of halvings of the init ia l primitive tetrahedron itself. That the rhombic triacontahedron of contact-fa ce t radius of unit vector length had a trigonometrically calculated volume ofp roved in due course not to be a residual error but the “critical difference” be tween matter and radiation. This gives us delight in the truth whatever it may be , recalling that all the discoveries of this chronicle chapter were consequent on ly to just such faith in the truth, no matter how initially disturbing to misinfo rmed and misconditioned reflexes it may be.
¶ 986.870 Nuclear and Nonnuclear Module Orientations
[986.871]{style="color: purple3"} []{#ver:986.871 label="ver:986.871"} The rhombic triacontahedron may be fashioned of 120 trivalently bonded T Quanta Modul e tetrahedra, or of either 60 bivalently interbonded positive T Modules or of 60 bivalently interbonded negativeModules. In the rhombic triacontahedron we have only radiantly arrayed basic energy modules, arrayed around a single spheric nucl ear-inadequate volumetric domain with their acute “corners” pointed inwardly to ward the system’s volumetric center, and their centers of mass arrayed outwardly of the systemergo, prone to escape from the system.
[986.872]{style="color: purple3"} []{#ver:986.872 label="ver:986.872"} In th e tetrahedron constructed exclusively ofModules, and in the octahedron co n structed ofandModules, the asymmetric tetrahedral modules are in rad ical groups, with their acute points arrayed outwardly of the system and their ce nters of mass arrayed inwardly of the systemergo, prone to maintain t heir critical mass interattractive integrity. The outer sharp points of theandM odules are located at the centers of the four or six corner spheres defining the tetrahedron and octahedron, respectively. The fact that the tetrahedron’s and oct ahedron’sandModules have their massive centers of volume pointing inwardly of the system all jointly interarrayed in the concentric layers of the, where as in the rhombic triacontahedron (and even more so in the half-Couplers of the r hombic dodecahedron) we have the opposite condition which facts powerf ully suggest that the triacontahedron, like its congruent icosahedron’s nonnuclea r closest-possible-packed omniarray, presents the exclusively radiational aspect of a “one” or of a “no” nuclear-sphere-centered and isolated most “spheric” polyhedral system to be uniquely identified with the nonnuclear bubble, the one-m olecule-deep, kinetically-escape-prone, gas-molecules-containing bubble.
[986.8721]{style="color: purple3"} []{#ver:986.8721 label="ver:986.8721"} In the case of the rhombic dodecahedra we find that the centers of vol ume of the ir half-Couplers’andModules occur almost congruently with their r espective closest-packed, unit-radius sphere’s outward ends and thereby concentra te their energies at several spherical-radius levels in respect to a common nucle ar-volum e-adequate centerall of which suggests some significant relat ionship of this condition with the various spherical-radius levels of the electro n “she lls.”
[986.873]{style="color: purple3"} []{#ver:986.873 label="ver:986.873"} The tetrahedron and octahedron present the “gravitat ional” model of self-and-otherness interattractive systems which inherently pro vide wit nessable evidence of the systems’ combined massive considerations or con stellati ons of their interbindings.
[986.874]{style="color: purple3"} []{#ver:986.874 label="ver:986.874"} The highly varied alternatean dModu le groupings permitted within the same primitive rhombic dodecahedron, ve ctor eq uilibrium, and in the Couplers, permit us to consider a wide spectrum of c omplex edly reorientable potentials and realizations of intermodular behavioral pr ocliv ities lying in proximity to one another between the extreme radiational or g ravi tational proclivities, and all the reorientabilities operative within the sam e s uperficially observed space (Sec. 954). All these large numbers of potential a lt ernatives of behavioral proclivities may be circumferentially, embracingly arra y ed entirely within the same superficially observed isotropic field.
¶ 987.00 Multiplication Only by Division
•[987.00-987.416 Multiplicati on by Division Scenario] [987.010]{style="color: purple3"} []{#ver:987.010 label="ver:987.010"} Operational Scenario in Proof of Multiplica tion Only by Progressive Divisioning of Simplest Vectorially Structured Polyhedra
[987.011]{style="color: purple3"} []{#ver:987.011 label="ver:987.011"} Six equi-zero-magnitude, mass-times-velocity-produced vectors repres enting the six equi-energetic, differently angled (i.e., differently directioned ) cosmic forces that always cointeract to freshly reinitiate minimum local struc turing in Universe, constitute the minimum-maximum cosmic set of coordinates nec essary to formulate a definitive system.system is the first finite unitarily c onceptual subdivision of finite but nonunitarily conceptual Scenario Universe. (S ee Sec. 400.011 and especially Fig. 401.)
[987.012]{style="color: purple3"} []{#ver:987.012 label="ver:987.012"} system is a polyhedral p atternregular or irregular that definitively closes back u pon itself topologically to subdivide Universe locally into four parts: (1) all t he Universe outside the system, the macrocosm; (2) all the Universe within the s ystem, the microcosm; (3) the convex-outside little bit of the Universe of which the system itself is constituted; and (4) the concave-inside little bit of the Un iverse of which the system is constituted.
[987.013]{style="color: purple3"} []{#ver:987.013 label="ver:987.013"} The tetrahedron, with it s six equi-lengthed vector edges and four vertexes and with its four triangular win dows, is experimentally demonstrable to be the topologically simplest structu ral system of Universe.
¶ 987.020 Topological Uniqueness
[987.021]{style="color: purple3"} []{#ver:987.021 label="ver:987.021"} Recognizing that angles are conceptual independent of the lengths of the lines converging to form them, i t follows that a triangle or a tetrahedron or any polygons or polyhedra are con c eptualand conceptually differentquite independen t of the time-size lengths of the lines defining the polyhedra. All primitive non-space-time differences are exclusively angular and topological.
[987.022]{style="color: purple3"} []{#ver:987.022 label="ver:987.022"} Th e topological variables of systems are identified exclusively as the unique number of vertexes (points), faces (areas), and edges (lines) of the system considered.
¶ 987.030 Finite Synergetics
[987.031]{style="color: purple3"} []{#ver:987.031 label="ver:987.031"} Starting with mass = zero an d velocity = zero (i.e.,MV= 0), as the energy-quantum product of the six v ectors of the minimum structural system in Universe (that is, each of the tetrahe dron’s six equi-lengthed edges individually = 0), the mathematical art and scienc e known as Synergeticsprovides a cosmically comprehensive mathematical str ategy of employing always and only physically demonstrable, omnidimensional, quan tum-compatible multiplication only by divisionof a no-gain-no-loss, no-beg inning-no-ending, omnicomplexedly and nonsimultaneously overlapping, ceaselessly and differently intertransforming, eternally self-regenerative, 100-percent-effic ient, energetic Universe.
[987.032]{style="color: purple3"} []{#ver:987.032 label="ver:987.032"} The omnidirectionally multiplying amplifi c ation of information in Universe is arrived at only by discretely progressive s u bdivision of the structural system that has been already experimentally and ope r ationally demonstrated to be the simplestthe regular tetrahedron. [987.033]{style="color: purple3"} []{#ver:987.033 label="ver:987.033"} Synergetics progressively divides and progressively discovers the omnira tional tetrahedral-related volumes (see Table 1033.192for table of tetravo lume values) and the other topological and angular characteristics of the great-c ircle-spun, hemisystem cleavages and their respective fractionation resultants. T his progressive synergetic division and discovery describes the entire primitive hierarchy of timeless-sizeless, omnisymmetrical, omniconcentric, omniintertransfo rmative, intercommensurable,[^42]systemic p olyhedral structures. (See cosmic hierarchy at Table 982.62.)
¶ 987.040 Macro-medio-micro Mensuration Limits
[987.041]{style="color: purple3"} []{#ver:987.041 label="ver:987.041"} Primitive unity is at minimum a union of two uniquely individual quantum vectorizations of each member of the primitive minimum polyhedral system hierarchy, each of whose p olyhedra described by the quantum vectorizations are complementarily intravolumed and intra-energetic. The quantum-vectored polyhedra of the primitive hierarchy ar e always relativevolumetrically, topologically, and vectorially
microto the tetrahedron as the minimum structural system of U niverse, and macroto the icosahedron as the maximum volume fo r the least energy investment structural system of Universe.
[987.042]{style="color: purple3"} []{#ver:987.042 label="ver:987.042"} Micro tetraand macro icosaalways and only coact as cosmic unity equaling at least two. This incommensurable pair serves as the two only separately ration albut proportionately constant and interequatable mensura tion reference limits in all geometrical, topological, chemical, and quantum-coo rdinate scientific interconsiderability.
[987.043]{style="color: purple3"} []{#ver:987.043 label="ver:987.043"} The medio octahedron serves as the average, between-limits, most structurally expedient, and most fre q uently employed of the three prime structural systems of Universe. It is signi fic ant that the limit case pair micro tetraand macro icosaare bot h pri me numbers and 5 whereas the medio octais a second power of 2, the only prime even number in Universe: 22= 4.
[987.044]{style="color: purple3"} []{#ver:987.044 label="ver:987.044"} The self-regeneration of the nonsimultaneously and only-partially -ov erlappingly-episoded, beginningless and endless Scenario Universe inherently req uires in pure principle an eternal incommensurability ofat minim um t wooverall symmetrical and concentric system intertransformative beha viors and characteristic phases.
¶ 987.050 Intercommensurable Functions of Jitterbug
[987.051]{style="color: purple3"} []{#ver:987.051 label="ver:987.051"} The vector equilibrium of tetravolume-20 = prime 5 x prime , is rationally coordinate with the tetrahedron representing the prime number 1 and w ith the octahedron representing the prime number 2. But the 20-tetra-volume () is inherently incommensurable with the icosahedron, which represents the prime number 5 compounded with V2 even though the and icosa are concentrically and omnisymmetrically intertransformable (see Secs. 461.02-06).
[987.052]{style="color: purple3"} []{#ver:987.052 label="ver:987.052"} The mathematical span between the second power of 2, and the second root of 2, (V2)which is the s ame proportional relationship as that existing between V2 and 1is th e constant proportional accommodating median between tetra 1 and octa 2 and between the first two prime numbers: between the most primitive odd and even, betwee n the most primitive yes and no of the primitive binary systemergo, of all computer mathematics.
[987.053]{style="color: purple3"} []{#ver:987.053 label="ver:987.053"} The 2 as constant proportional equity median is clearly evidenced as each of the ’s six square unit-length-vector-edged faces jitter-buggingly transform into the two unit-vector-edged equilateral triangles. We recall that the diagonal of each square was the hypotenuse of a right-angle-apexed, unit-vector-edged isosceles triangle whose hypotenuse jitterbuggin gly contracted in length to the length of each of the unit-vector edges. We have the well-known formula for the second power of the hypotenuse equaling the sum of the second powers of the right triangle’s right-angle sides, and since the right-angle-apexed isosceles triangle’s sides were of unit-vector length = 1, the secon d powers of both equal 1. The sum of their second powers was 2, and the length of the square’s hypotenuse diagonal = VT. Ergo, the total linear alteration of the >icosa was the contraction of V2. This introduces one of nature’s most profound incommensurability equations, wherein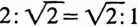 
[987.054]{style="color: purple3"} []{#ver:987.054 label="ver:987.054"} Proportionately expressed this equation reads: : icosa = 2: V?= V2 : 1 Fractionally expressed the equation reads: [ ]{.underline}_ 2_ V2 icosa V2 1 Thus we have a sublime equation of constant proportionality of otherwise inherently incommensurate value sets.
[987.055]{style="color: purple3"} []{#ver:987.055 label="ver:987.055"} In the jitterbug, as the 20-tetravolume contracts symmetrically through the icosahedral phase with a tetravolume o f 18.51 229587, and then ever symmetrically contracts to the bivalent octahedral phase of tetra-volume-4, the six-membered axis of the concentric system does not rotate while the other 18 nonaxis “equatorial” members rotate around the axis. (Fig. 460.08.)
[987.056]{style="color: purple3"} []{#ver:987.056 label="ver:987.056"} As the system contraction continues beyond the octahedron stage of tetravolume-4, the axis also torques and contracts as the octahedron either (1) contracts symmetrically and rotationally into the regular tetrahedron of tetravolume-1 (or counterrotates into the alternate regular tetrahedron of tetra volume-1), or (2) flattens by contraction of its axis to form zerovolume, edge-congruent pair of triangular patterns; thereafter the triangle’s three corners are foldable alternately into the quadrivalent positive or the quadrivalent negative regular tetrahedron of tetravolume-1.
[987.057]{style="color: purple3"} []{#ver:987.057 label="ver:987.057"} Since all 24 internal radiation vectors had been removed before the jitterbugging, leaving only the 24 external gravitation vectors, the transformation is systematically comprehensive and embraces all the complex unities of the and icosa and their only-proportionally-equatable, separately rational, geometrical membership sets. Though the tetra and icosa are incommensurable with each other, the octahedron is transformatively com mensurable with either.
[987.058]{style="color: purple3"} []{#ver:987.058 label="ver:987.058"} The inherent volumetric incommensurability of and icosa (and their respective four- and three-unique-symmetrical-g reat-ci rcle-system sets), compounded with the ability of the octahedron to intertransformably interconnect these two otherwise incommensurables, produces the energetic oscillations, resonances, and intertransformings of the eternally regenerative Universe. This eternal disquietude regeneration of Universe is also accommodated by the fact that the tetra and are a priori incommensurable with the icosa. Despite this the rhombic triacontahedron of tetravolume-5 (as a product of the icosa’s 15-great-circle cleavaging), while under the oscillatory pressuring, is volumetrically and rationally coordinate with the tetrahedron and the state we speak of as matter and when it is under the negative tensive pressure of the oscillatory Universe, it transforms from matter to radiation. (See scenario of and Modules at Sec. 986.)
¶ 987.060 Isotropic Limits
[987.061]{style="color: purple3"} []{#ver:987.061 label="ver:987.061"} Cosmic regeneration, metaphysical and physical, involves phases of maximum asymmetry or of random pattern uniqueness. The self-regeneration propagated by the eternal war of incommensurability occurs at the medio phase of Universe; the propagation commences at the middle and proceeds syntropically outward or recedes syntropically inward from the maxi-entropic center in both macro and micro directions with the ultrasyntropic isotropic macrophase being manifest in the interspacing of the galaxies and with the infra syntropic, isotropic microphase being manifest kinetically in time-size as “cosmic background radiation” and statically (timelessly, sizelessly) in the closest packing of unit radius spheres, like the aggregates of atoms of any one element.
[987.062]{style="color: purple3"} []{#ver:987.062 label="ver:987.062"} The median turbulence and kaleidoscopically nonrepetitive, random, individually unique, local patterning events occur between the four successive, symmetrically orderly, “click-stop” phases of the hierarchy of primitive polyhedra: , icosa, octa, and tetra. Between the four maximum symmetrical phases the (overall symmetrical, internally asymmetrical) evolutionary events of Universe are empirically and operationally manifest by the jitterbugging: they are infinitely different as multiplication only by division is infinitely employed. Time-size infinity is embraced by primitive finity.
[987.063]{style="color: purple3"} []{#ver:987.063 label="ver:987.063"} In the jitterbug the local patterning events of Universe rotate outwardly to the macro isotropicity of , which can rotate beyond macro to converge symmetrically again through the central phase of the icosaocta transformation. The maximum inc ommensurability occurs between the latter two, whereafter octa transforms to tetra. The tetra occurs at the microphase of radiation isotropicity and itself transforms and rotates via the negative tetra, expanding again through the negative phases of the octa’s duo-twoness octa icosa alternate .
[987.064]{style="color: purple3"} []{#ver:987.064 label="ver:987.064"} is potentially pattern-divisible both positively and negatively and both internally and surfacewise. Icosahedron is potentially pattern-divisible both positively and negatively and both internally and surfacewise. The octahedron has internal comprehensive (duo-tet) twoness of 22, 2, V2. Tetrahedron is likewise both positively and negatively integrally intertransformable.
[987.065]{style="color: purple3"} []{#ver:987.065 label="ver:987.065"} The incommensurability of the icosa derives from its lack of a nucleus. The is inherently nucleated. The primitive tetra is nonnuclear but acquires a nucleus with frequency. The icosa cannot acquire a nucleus whatever the frequency. (See Sec. 466 and Fig. 466.01for jitterbug transformation pumping out of nuclear sphere.)
[987.066]{style="color: purple3"} []{#ver:987.066 label="ver:987.066"} Since multiplication is accomplished only by division, we observe that the macroisotropicity of seemingly Expanding Universe is equally explicable as the shrinking relative magnitude of the system viewpoint of the observer. (See Secs. 986.756-57 and 1052.62.)
[987.067]{style="color: purple3"} []{#ver:987.067 label="ver:987.067"} Octaphase: The eternally inherent incommensurability of the regenerative turmoil of eternally self-regenerative Universe occurs always at its mediophase of intertransforming between and icosa and between icosa and tetra: at these mediophases the never-repeating maxi-asymmetry patterns are generated.
¶ 987.070 Topological Minima
[987.071]{style="color: purple3"} []{#ver:987.071 label="ver:987.071"} In synergetics all topological characteristics are interconformationally conceptual independent of size; for instance, a vertex is one of the convergence loci of a system’s inherent plurality of conceptual interrelationships.
[987.072]{style="color: purple3"} []{#ver:987.072 label="ver:987.072"} Since vertexes are omnidimensional, system topology deals with the loci of interrelationship convergences at anyone of the system set of defining loci with a closest-packing-of-spheres-imposed maximum of 12 unit-radius convergences around any one unit-radius locus sphere. In the latter case vertexes may be predominantly identified as spheres of unit radius an may identify a prime nucleated system.
[987.073]{style="color: purple3"} []{#ver:987.073 label="ver:987.073"} The minimum conceptual system in Universe is the regular tetrahedron, which consists of a minimum of four vertexes that can be represented as four approximately intertangent, equiradius spheres. Vertex-representing spheres do not occur in Universe or become conceptually considerable in sets of less than four. (This process is described at Secs. 100.331 and 411. minimum of four successive events and three intervals is required to define a frequency cycle; see Sec. 526.23.) In the same way linesor edges, as they are spoken of in topologyoccur only in sets of six, as the most economic interrelationships of vertexes of polyhedral systems.
[987.074]{style="color: purple3"} []{#ver:987.074 label="ver:987.074"} The minimum system in Universe is the tetrahedron; its unitradius spheres at each of the four vertexes have a minimum of six intersystem vertexial relationships. We have learned that topological system vertex interrelationships always occur in sets of six. The formula for the number of system interrelationships is\sfrac
{n^2 - n}{2}whereinis the number of system vertexes (or unit radius spheres). tetrahedron has four vertexes: 42=16, minus n4 = 12, divided by 2 = 6i.e., the number of unique vertex interrelationship lines of the minimum structural systemthe tetra hedronis six.
[987.075]{style="color: purple3"} []{#ver:987.075 label="ver:987.075"} Although Alfred North Whitehead and Bertrand Russell did not recognize the full conceptual implications, their “new mathematics” of set theory and empty sets were tour de force attempts by the leading abstract non-conceptual mathematicians of their day to anticipate the inevitable historical convergence of their mathematics with the inherently conceptual topology of Euler, as well as with the phase rule of Gibbs in chemistry, the simplified quantum mechanics of Dirac in physics, and the homogenizing biochemistry a nd physics of virology’s DNA-RNA design programmingall remotely but inexorably rendezvousing with Boltzmann’s, Einstein’s, and Hubble’s astrophysics and cosmology to constitute unitary science’s unitary self-regenerative, untenably equilibrious, cosmic-coordinate system to be embraced and accommodated by the epistemography of synergetics.
[987.076]{style="color: purple3"} []{#ver:987.076 label="ver:987.076"} What are known in the terminology of topology as faces the polyhedron’s hedrasides or facetsare known in synergetics as windows, being the consequences of system-vertex interrelationship lines framing or viewing “windows of nothingness” windows opening to a nonconvergence, to nonrelatedness, to the untuned-in. Nothingness is the at-present-untuned-ininformation of each special case individual’s special local-in-Universe, momentary, tuned-in, preoccupying consideration. Vertexes are tuned-in; hedraare untuned-in, ergo out. Hedrafaces are system outs.
[987.077]{style="color: purple3"} []{#ver:987.077 label="ver:987.077"} Unit radius spheres are unit-wavelength, tuned-in, event loci; topological faces (Greek *hedra)*are all the windows looking out upon all the rest of the Universe’s presently-untuned-in information in respect to the considered or tuned-in system.
[987.078]{style="color: purple3"} []{#ver:987.078 label="ver:987.078"} Since two system-interrelationship lines (vectorially energetic in pure principle) cannot pass through the s ame point at the same time, the windows’ “corners” are always superimposed time-crossing aspects one crossing behind or in front of, but not touching, the other. The topological windows of synergetics are polygonal aspects of the system’s interrelationships and not of physical lines.
[987.079]{style="color: purple3"} []{#ver:987.079 label="ver:987.079"} Synergetics’ experimentally produced, minimum-structural-system subdivisions of Universe have four tuned-in vertexial loci, four windows looking toward all the untuned-in complementary balance of Universe, and six vertexial interrelationship vector lines, with all the latter occurring as outermost system features. The minimum nonnucleated structural system does not require internal vertexes.
At c: Gasesare monovalent, single-bonded, omniflexible, inadequate-interattraction, separatist, compressible. At [b:]{.smallcaps}Liquidsare bivalent, double-bonded, hinged, flexible, viscous integrity. At [a:]{.smallcaps}Rigidsare trivalent, triple-bonded, rigid, highest tension coherence.
¶ 987.080 Vertexial Spheres Form Rigids
[987.081]{style="color: purple3"} []{#ver:987.081 label="ver:987.081"} In addition to the four vertexial spheres of the precleavage primitive tetrahedron, we find after the cleavage all six vertexial unit-radius-vertex spheres of the octahedron also occurring in the outermost structure of the nonnucleated system. Neither the primitive tetrahedron nor the primitive octahedron have internal or nuclear unit-radi us-vertex spheres. For an illustration of these structural “rigids” see Fig. 987.081.
¶ 987.100 Great-circle-spun Symmetries and Cleavagings
¶ 987.110 Intercommensurability Functions
[987.111]{style="color: purple3"} []{#ver:987.111 label="ver:987.111"} In the great-circle-spun cleavaging of synergetics’ multiplication only by division there are seven primitive symmetries of spinnability. (See Sec. 1040.) Four symmetries belong directly to the separate tetrahedral commensurability, and three symmetries belong to the separate icosahedral commensurability, with the integrity of eternal interrelationship being provided by the symmetrically contractive, concentric intertransformability of the two sets of symmetry at the jitterbug >icosa stage. This symmetrically embraced intertransformable stage corresponds to the constant interproportionality stage of the and icosa manifest as
¶ 987.120 Sequence of Symmetries and Cleavagings
[987.121]{style="color: purple3"} []{#ver:987.121 label="ver:987.121"} Table
Symmetry Sequence
Cleavage SequenceCleavage #1 Cleavage #4 Cleavages #2 & 3
Symmetry #1:
three great circles
Symmetry #2:
four great circles
TETRA
Symmetry #3:
six great circles ( )
Symmetry #4:
great circles
Thereafter we have the jitterbug transformation of the icosa and the further progressive halvings of: ICOSA Symmetry #5 six great circles (icosa) Symmetry #6 great circles Symmetry # 7 great circles (producing the Modules and & Modules) Cleavage #6 Cleavage #5 Cleavage #7 (See also Secs. 1025.14, 1040, 1041.10.)
[987.122]{style="color: purple3"} []{#ver:987.122 label="ver:987.122"} Starting with the regular tetrahedron the progressive primitive subdividing of synergetics is initially accomplished only by the successive equatorial halvings of the progressively halved-out parts of the first four of the only seven cosmic symmetries of axial spin of the primitive structural systems.
¶ 987.130 Primary and Secondary Great-circle Symmetries
[987.131]{style="color: purple3"} []{#ver:987.131 label="ver:987.131"} There are seven other secondarysymmetries based on the pairing into spin poles of vertexes produced by the complex secondary crossings of one another of the seven original great circle symmetries.
[987.132]{style="color: purple3"} []{#ver:987.132 label="ver:987.132"} The primary and secondary icosa symmetries altogether comprise great circles. (See Fig. 987.132E.)
[987.133]{style="color: purple3"} []{#ver:987.133 label="ver:987.133"} The crossing of the primary 12 great circle s of the at (see Fig. 453.01, as revised in third printing) results in 12 ne w axes to generate 12 new great circles. (See color plate 12.)
[987.134]{style="color: purple3"} []{#ver:987.134 label="ver:987.134"} The crossing of the primary 12 great circles of the and the four great circles of the at (Fig. 453.01) results in 24 new axes to generate 24 new great circles . (See color plate 13.)
[987.135]{style="color: purple3"} []{#ver:987.135 label="ver:987.135"} The crossing of the primary 12 great circle s of the and the six great circles of the at(Fig. 453.01) results in 12 new axes to generate 12 new great circles. (See color plate 14.)
[987.136]{style="color: purple3"} []{#ver:987.136 label="ver:987.136"} The remaining crossing of the primary 12 great circles of the at F (Fig. 453.01) results in 24 more axes to generate 24 new great circles. (See color plate 15.)
[987.137]{style="color: purple3"} []{#ver:987.137 label="ver:987.137"} The total of the above-mentioned secondarygreat circles of th e is 96 new great circles (See Fig. 987.137B.)
¶ 987.200 Cleavagings Generate Polyhedral Resultants
¶ 987.210 Symmetry #1 and Cleavage #1
[987.211]{style="color: purple3"} []{#ver:987.211 label="ver:987.211"} In Symmetry #1 and Cleavage #1 three great circlesthe lines in Figs. 987.210through F are successively and cleavingly spun by using the midpoints of each of the tetrahedron’s six edges as the six poles of three intersymmetrical axes of spinning to fractionate the primitive tetrahedron, first into the 12 equi-vector-edged octa, eight Eighth-octa (each of 16-tetra-volume), and four regular tetra (each of 1-tetravolume).
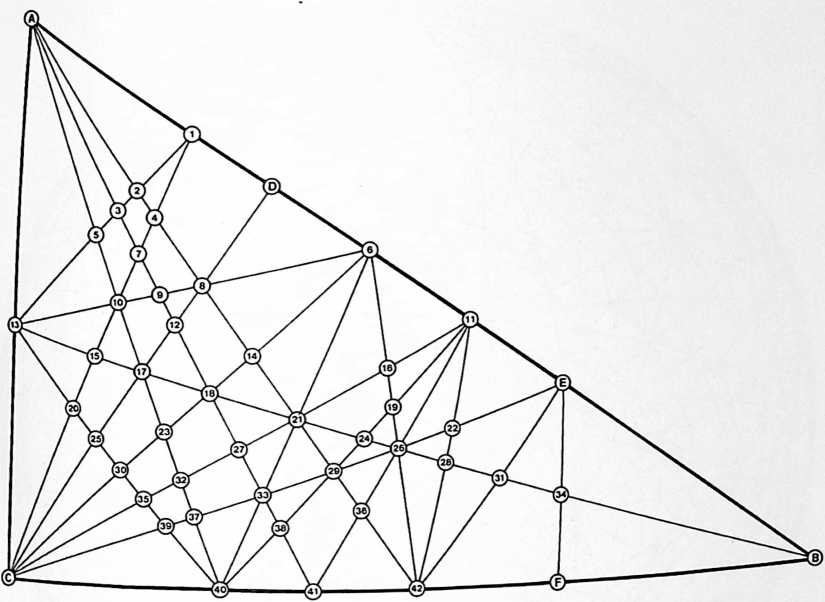
987.132E and at Fig. 901.03. It is the key to the trigonometric tables for the spherical central angles, the spherical face angles, the planar edge lengths, and the planar face angles presented at Table 987.132G.
[987.212]{style="color: purple3"} []{#ver:987.212 label="ver:987.212"} simple example of Symmetry #1 appears at Fig. 835.11. Cleavage #1 is illustrated at Fig. 987.210E.
[987.213]{style="color: purple3"} []{#ver:987.213 label="ver:987.213"} Figs. 987.210A-E demonstrate Cleavage #1 in the following sequences: (1) The red great circling cleaves the tetrahedron in to two asymmetric but identically formed and identically volumed “chef’s hat” halves of the initial primitive tetrahedron (Fig. 987.210A).(2) The blue gr eat circling cleavage of each of the two “chef’s hat” halves divides them into four identically formed and identically volumed “iceberg” asymmetrical quarterings of the initial primitive tetrahedron (Fig. 987.210B).(3) The yellow gr eat circling cleavage of the four “icebergs” into two conformal types of equi-volumed one-Eighthings of the initial primitive tetrahedronfour of these one-Eighthings being regular tetra of half the vector-edge-length of the origi nal tetra and four of these one-Eighthings being asymmetrical tetrahedra quarter octa with five of their six edges having a length of the unit vector = 1 and the sixth edge having a length of V2=. (Fig. 987.210C.)
[image]{.image .placeholder original-image-src="
images/v2/900.00/image66
" original-image-title=""} Fig. *987.137B Composite of Primary and Secondary Vector Equilibrium Great Circle Sets:*This is a black-and-white version of color plate 16. The Basic Equilibrium 48triangle as presented at Fig. 453.01 appears here shaded in the spherical grid. In this composite vector equilibrium spherical matrix all the 25 primary gr eat circles appear together with the four sets of secondary great circles. (The f our sets of secondary vector equilibrium great circles are shown successively at color plates 12–15.) Fig. 987.137C Net Diagram of Angles and Edges for Basic E q uilibrium 48Triangle in Vector Equilibrium Grid: This is a coded detail of t he basic spherical triangle shown shaded in Fig. 987.137B and at Fig. 453.01. It is the key to the trigonometry tables for the spherical central angles, the spher ical face angles, the planar edge lengths, and the planar face angles presented a t Table 987.137D. (The drawing shows the spherical phase: angle and edge ratios are given for both spherical and planar phases.) 
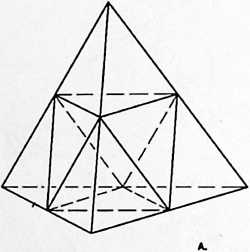
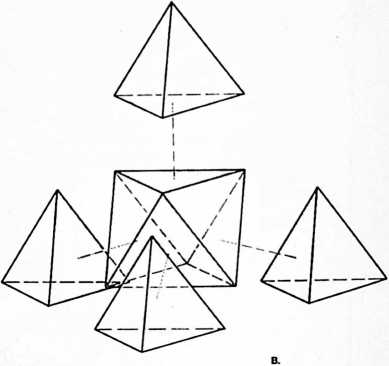
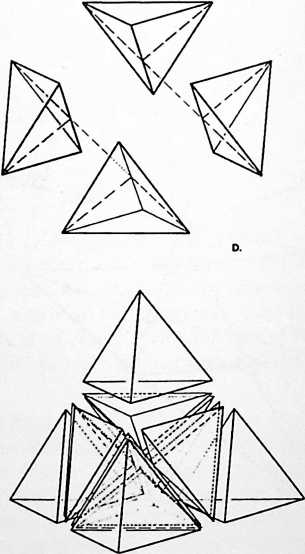F.
¶ 987.220 Symmetry #2 and Cleavage #4:
[987.221]{style="color: purple3"} []{#ver:987.221 label="ver:987.221"} In Symmetry #2 and Cleavage #4 the four-great-circle cleavage of the octahedron is accomplished thr ough spinning the four axes between the octahedron’s eight mid-face polar points, which were produced by Cleavage #2. This symmetrical four-great-circle spinning introduces the nucleated 12 unit-radius spheres closest packed around one unit-ra dius sphere with the 24 equi-vector outer-edge-chorded and the 24 equi-vector-len gthed, congruently paired radiia system called the vector equilibrium . The has 12 external vertexes around one center-of-volume vertex, and altoget her they locate the centers of volume of the 12 unit-radius spheres closest packe d around one central or one nuclear event’s locus-identifying, omnidirectionally tangent, unit-radius nuclear sphere.
[987.222]{style="color: purple3"} []{#ver:987.222 label="ver:987.222"} The vectorial and gravitational proclivities of nuclear convergence of all synergetics’ system interrelationships intercoordinatingly and intertransformingly permit and realistically account all radiant entropic growth of systems as well as all gravitational coherence, symmetrical contraction, and shrinkage of systems. Entropic radiation and dissipation growth and syntropic gravitational-integrity convergency uniquely differentiate synergetics’ natural coordinates from the XYZcentimeter-gram-second abstract coordinates of conventional formalized science with its omni interperpendicular and omniinterparallel nucleus-void frame of coordinate ev ent referencing.
[987.223]{style="color: purple3"} []{#ver:987.223 label="ver:987.223"} Symmetry #2 is illustrated at Fig. 841.15A.
¶ 987.230 Symmetries #1 & 3; Cleavages #1 <& 2
[987.231]{style="color: purple3"} []{#ver:987.231 label="ver:987.231"} Of the seven equatorial symmetries first employed in the progression of self-fractionations or cleavages, we use the tetrahedron s six mid-edge poles to serve as the three axes of spinnability. These three great-circle spinnings delineate the succession of cleavages of the 12 edges of the tetracontained octahedron whose six vertexes are congruent with the regular tetrahedron’s six mid-edge polar spin points. The octahedron resulting from the first cleavage has 12 edges; they produce the additional external surface lines necessary to describe the two-frequency, non-time-size subdividing of the primitive one-frequency tetrahedron. (See Sec. 526.23 , which describes how four happenings’ loci are required to produce and confirm a system discovery.) Fig. 987.210 Subdivision of Tetrahedral Unity: Symmetry #1:
-
Initial tetrahedron at two-frequency stage.
-
Tetrahedron is truncated: four regular corner tetra surround a central octa. The truncations are not produced by great-circle cleavages. show great-circle cleavages of the central octahedron. (For clarity, the four corner tetra are not shown.) Three successive great-circle cleavages of the tetrahedron are spun by the three axes connecting the midpoints of opposite pairs of the tetras six edges.
-
First great-circle cleavage produces two Half-Octa.
-
Second great-circle cleavage produces a further subdivision into four irregular tetra called “Icebergs.”
-
Third great-circle cleavage produces the eight Eighth-Octahedra of the original octa.
-
Eight Eighth-Octa and four corner tetras reassembled as initial tetrahedron.
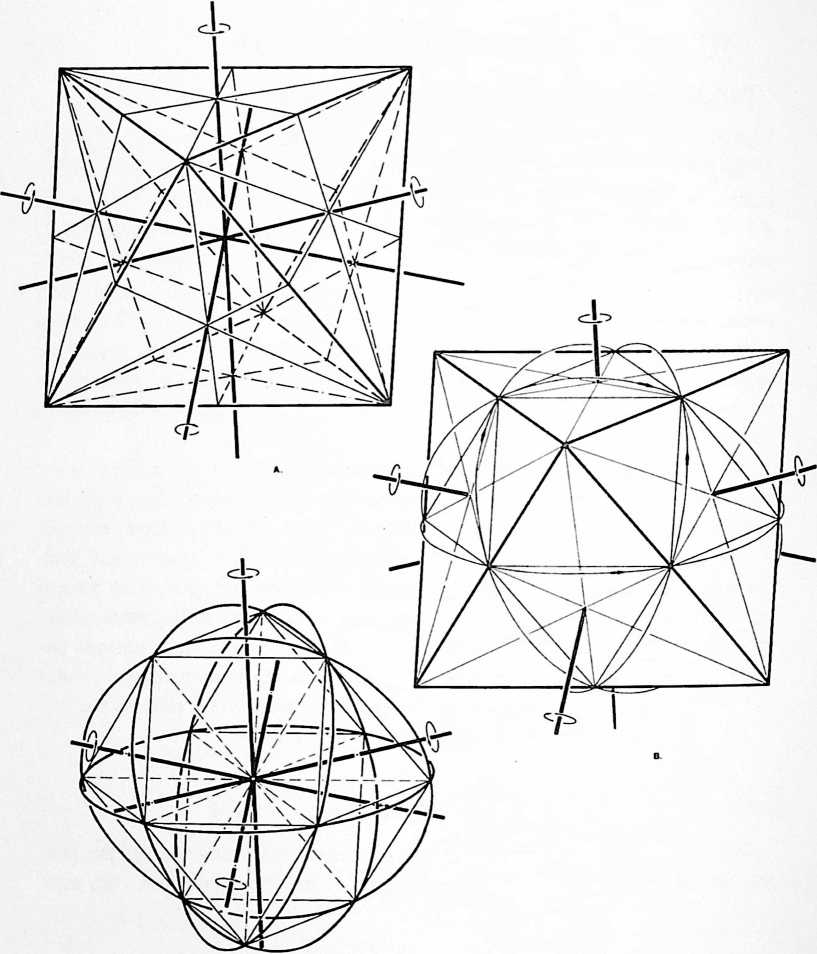Fig. 987.221 Four-great-circle Systems of Octahedron and Vector Equilibrium : Symmetry #2:
-
Six-great-circle fractionation of octahedron (as shown in Figs. 987.240B and C) defines centers of octa faces; interconnecting the pairs of opposite octa faces provides the octahedron’s four axes of symmetryhere shown extended.
-
Four mid-face-connected spin axes of octahedron generate four great circle trajectories.
-
Octahedron removed to reveal inadvertent definition of vector equilibrium by octahedron’s four great circles. The four great circles of the octahedron and the four great circles of the vector equilibrium are in coincidental congruence. (The vector equilibrium is a truncated octahedron; their triangular faces are in parallel planes.)
[987.232]{style="color: purple3"} []{#ver:987.232 label="ver:987.232"} The midpoints of the 12 edges of the octahedron formed by the first c leavage provide the 12 poles for the further great-circle spinning and Cleavage # 2 of both the tetra and its contained octa by the six great circles of Symmetry #3. Cleavage #2 also locates the center-of-volume nucleus of the tetra and separates out the center-of-volume-surrounding 24Quanta Modules of the tetra and the 48 Quanta Modules of the two-frequency, tetracontained octa. (See Sec. 942 for orientations of theandQuanta Modules.)
¶ 987.240 Symmetry #3 and Cleavage #3
[987.241]{style="color: purple3"} []{#ver:987.241 label="ver:987.241"} Symmetry #3 and Cleavage #3 mutually employ the six-polar-paired, 12 mid-edge points of the tetra-contained octa to produce the six sets of great-circle spinnabilities that in turn combine to define the two (one positive, one negative) tetrahedra that are inters ymmetrically arrayed with the common-nuclear-vertexed location of their eight equ i-interdistanced, outwardly and symmetrically interarrayed vertexes of the “cube ”the otherwise nonexistent, symmetric, square-windowed hexahedron whose overall most economical intervertexial relationship lines are by themselves unstructurally (non-triangularly) stabilized. The positive and negative tetrahedra are internally trussed to form a stable eight-cornered structure superficially de lineating a “cube” by the most economical and intersymmetrical interrelationshi ps of the eight vertexes involved. (See Figs. 987.240 and 241.)
[image]{.image .placeholder original-image-src="
images/v2/900.00/image78
" original-image-title="" width="2.99306in" height="1.4in"} [image]{.image .placeholder original-image-src="
images/v2/900.00/image79
" original-image-title=""} Fig. 987.241 Subdivision of Tetrahedral Unity: Octet: Duo-Tet Cube: Rhombic Dodecahedron: [987.242]{style="color: purple3"} []{#ver:987.242 label="ver:987.242"} In this positive-negative superficial cube of tetravolu me-3 there is combined an eight-faceted, asymmetric hourglasspolyhedron of tetravolume-1 \sfrac{1}{2}, which occurs interiorly of the interacting tetrahed ra s edge lines, and a complex asymmetric doughnutcored hexahedron of tetr avolume-1 \sfrac{1}{2}, which surrounds the interior tetra’s edge lines but occ urs entirely inside and completely fills the space between the superficially desc ribed “cube defined by the most economical interconnecting of the eight vertexes and the interior 1\sfrac{1}{2}-tetravolume hourglasscore. (See Fig. 987.242E.) [987.243]{style="color: purple3"} []{#ver:987.243 label="ver:987.243"} An illustration of Symmetry #3 appears at Fig. 455.11A.
[image]{.image .placeholder original-image-src="
images/v2/900.00/image74
" original-image-title=""} [image]{.image .placeholder original-image-src="
images/v2/900.00/image75
" original-image-title=""} **E.**Fig. 987.230 Subdivision of Tetrahedral Unity: Symmetry #3:
-
The large triangle is the tetrahedron face. The smaller inscribed triangle is formed by connecting the mid-points of the tetra edges and represents the octa face congruent with the plane of the tetra face.
-
Connecting the midpoints of the opposite pairs of the internal octahedron’s 12 edges provides the six axes of spin for the six great circle system of Symmetry #3. The perpendicular bisectors at and are projections resulting from the great circle spinning. also shows an oblique view of the half-Tetra or “Chef’s Caps” separated by the implied square. (For other views of Chef’s Caps compare Figs. B. 100.103B and 527.08A&B.)
-
The six great circle fractionations subdivide the tetrahedron into 24 Quanta Modules.
-
Exploded view of the tetrahedron’s 24 Quanta Modules.
-
Further explosion of tetrahedron’s Quanta Modules.
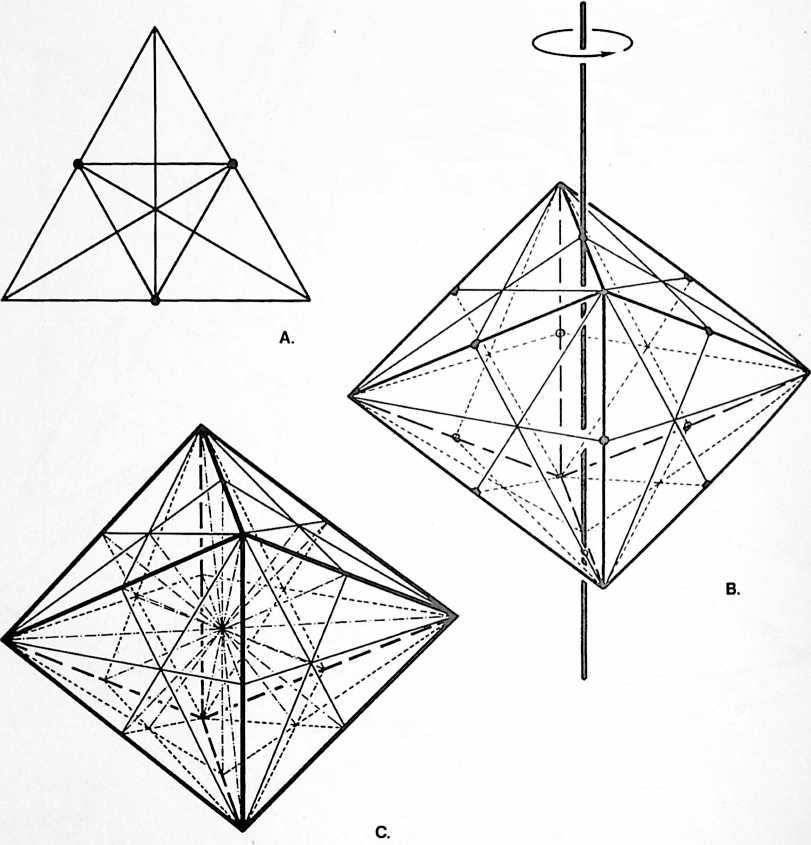Fig. 987.240 Subdivision of Tetrahedral Unity: Symmetry #3: Subdivision of Internal Octahedron:
-
Bisection of tetrahedron face edges describes a congruent octahedron face.
-
The spinning of the internal octahedron on axes through the opposite mid-edges generates the six great circle system of Symmetry #3.
-
The six great circle fractionations subdivide the octahedron into 48 Asymmetric Tetrahedra; each such Asymmetric Tetrahedron is comprised of one Quanta Module and one quanta Module.
-
Exploded view of octahedron’s 48 Asymmetric Tetrahedra.
[image]{.image .placeholder original-image-src="
images/v2/900.00/image77
" original-image-title=""}
¶ 987.250 Other Symmetries
[987.251]{style="color: purple3"} []{#ver:987.251 label="ver:987.251"} An example of Symmetry #4 app ears at Fig. 450.10. An ample of Symmetry #5 appears at Fig. 458.12B. An example of Symmetry #6 appears at Fig. 458.12A. An example of Symmetry #7 appears at Fig. 455.20.
¶ 987.300 Interactions of Symmetries: Spheric Domains
¶ 987.310 Irrationality of Nucleated and Nonnucleated Systems
[987.311]{style="color: purple3"} []{#ver:987.311 label="ver:987.311"} The six great circles of Symmetry #3 interact with the three great circles of Symmetry # 1 to produce the 48 similar-surface triangles
-
Eighth-Octa composed of six asymmetric tetrahedra. Each asymmetric tetrahedron is composed of one Quanta Module and one Quanta Module. The drawing is labeled to show the relationship of the Modules and the Modules. Vertex is at the center of volume of the octahedron and is at the midface of any of the octahedron’s eight triangular faces.
-
Proximate assembly of Eighth-Octa and Quarter-Tetra to be face bonded together as Octet.
-
Octet: (Oc-Tet = octahedron + tetrahedron.) An Eighth-Octa is face bonded with a Quarter-Tetra to produce the Octet. (See Sec. 986.430.) The Octet is composed of 12 Quanta Modules and 6 Quanta Modules. (Compare color plate 22.)
-
E. Duo-Tet Cube: Alternate assemblies of eight Octets form Duo-Tet Cube. Each Duo-Tet Cube = 3-tetravolumes.
-
Rhombic Dodecahedron: Two Duo-Tet Cubes disassociate their Octet components to be reassembled into the Rhombic Dodecahedron. Rhombic Dodecahedron = 6-tetravolumes.
[image]{.image .placeholder original-image-src="
images/v2/900.00/image80
" original-image-title=""}
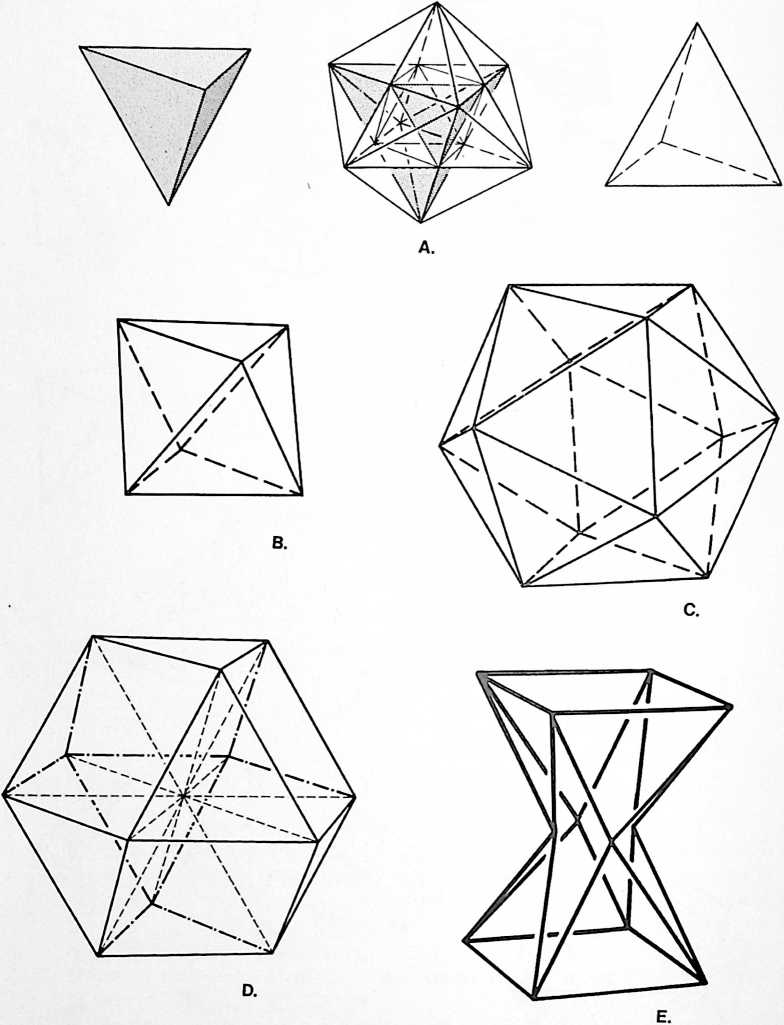
[987.312]{style="color: purple3"} []{#ver:987.312 label="ver:987.312"} These 48 asymmetric tetrahedra combine themselves into 12 sets of four asymmetric tetra each. These 12 sets of four similar (two positive, two negative) asymmetric tetrahedra combine to define the 12 diamond facets of the rhombic dodecahedron of tetravolume-6. This rhombic dodecahedron s hierarchical significance is elsewhere identified as the allspace-filling domain of each closest-packed, unit-radius sphere in all isotropic, closest-packed, unitradius sphere aggregates, as the rhombic dodecahedrons domain embraces both the unit-radius sphere and that sphere’s rationally and exactly equal share of the intervening intersphere space.
[987.313]{style="color: purple3"} []{#ver:987.313 label="ver:987.313"} The four great circles of Symmetry #2 produce a minimum nucleated system of 12 unit-radius spheres closest packed tangentially around each nuclear unit-radius sphere; they also produce a polyhedral system of six square windows and eight triangular windows; they also produce four hexagonal planes of symmetry that all pass through the same nuclear vertex spheres exact center.
[987.314]{style="color: purple3"} []{#ver:987.314 label="ver:987.314"} These four interhexagonalling planes may also be seen as the tetrahedron of zero-time-size-volume because all of the latters equi-edge lengths, its face areas, and system volumes are concurrently at zero.
[987.315]{style="color: purple3"} []{#ver:987.315 label="ver:987.315"} This four-great-circle interaction in turn defines the 24 equi-lengthed vectorial radii and 24 equi-lengthed vector chords of the . The 24 radii are grouped, by construction, in two congruent sets, thereby to appear as only 12 radii. Because the 24 radial vectors exactly equal energetically the circumferentially closed system of 24 vectorial chords, we give this system the name vector equilibrium. Its most unstable, only transitional, equilibrious state serves nature’s cosmic, ceaseless, 100-percent-energy-efficient, self regenerative integrity by providing the most expansive state of intertransformation accommodation of the original hierarchy of primitive, pre-time-size, “click-stop” rational states of energy-involvement accountabilities. Here we have in the the eight possible phases of the initial positive-negative tetrah edron occurring as an inter-double-bonded (edge-bonded), vertex-paired, self-inter-coupling nuclear system.
1\sfrac{1}{2}-tetravolumes of “substance” within the eight vertexes and 1-tetravolumes of complementation domain within the eight vertexes. The overall cubic domain consists of three tetravolumes: one outside-out (116) and one inside-out (16). The same star polyhedron appears within a vector equilibrium net at Fig. 1006.32.
-
Octahedron: tetravolume-4
-
Icosahedron; tetravolume-18.51229586
-
Vector equilibrium: tetravolume-20
-
Eight-faceted asymmetric Hourglass Polyhedron: tetravolume-116. These complex asymmetric doughnut-cored hexahedra appear within the star polyhedron at .
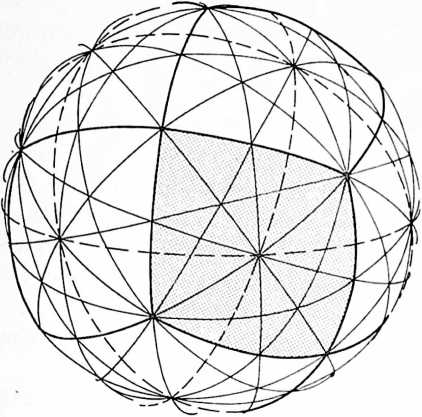
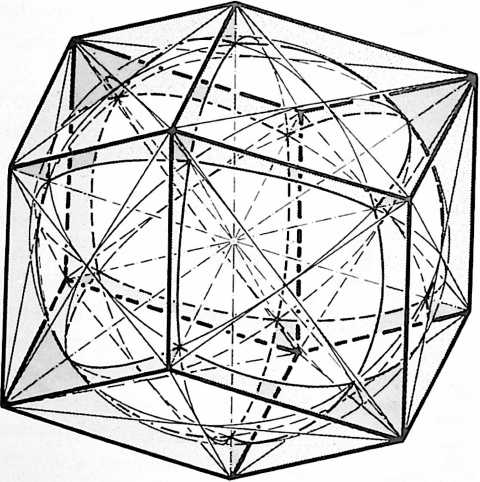
[987.316]{style="color: purple3"} []{#ver:987.316 label="ver:987.316"} With the nucleated set of 12 equi-radius vertexial spheres all closest packed around one nuclear unit-radius sphere, we found we had eight tetrahedra and six Half-octahedra defined by this assembly, the total volume of which is 20. But all of the six Half-octahedra are completely unstable as the 12 spheres cornering their six square windows try to contract to produce six diamonds or 12 equiangular triangles to ensure their interpatterning stability. (See Fig. 987.240.)
[987.317]{style="color: purple3"} []{#ver:987.317 label="ver:987.317"} If we eliminate the nuclear sphere, the mass interattraction of the 12 surrounding spheres immediately transforms their superficial interpatterning into 20 equiangular triangles, and this altogether produces the self-structuring pattern stability of the 12 symmetrically inter arrayed, but non-spherically-nucleated icosahedron.
[987.318]{style="color: purple3"} []{#ver:987.318 label="ver:987.318"} When this denucleation happens, the long diagonals of the six squares contract to unit-vector-radius length. The squares that were enclosed on all four sides by unit vectors w e re squares whose edgesbeing exactly unityhad a diagonal hypotenuse whose length was the second root of twoergo, when is transformed to the icosahedron by the removal of the nuclear sphere, six of its-lengthed, interattractive-relationship lines transform into a length of 1, while the other 24 lines of circumferential interattraction remain constant at unit-vector-radius length. The difference between the second root of two (which is , i.e., the difference is ) occurs six times, which amounts to a total system contraction of . This in turn means that the original $$24 + 8.485284 = 32.485284$$ overall unit-vector-lengths of containing bonds of the are each reduced by a length of to an overall of exactly 30 unit-vector-radius lengths.
[987.319]{style="color: purple3"} []{#ver:987.319 label="ver:987.319"} This excess of gravitational tensional-embracement capability constitutes the excess of intertransformative stretchability between the ’s two alter natively unstable, omnisystem’s stable states and its first two similarly stable, omni triangulated states.
[987.320]{style="color: purple3"} []{#ver:987.320 label="ver:987.320"} Because the increment of instability tolerance of most comprehensive intertransformative events of the primitive hierarchy is an irrational increment, the nucleus-void icosahedron as a structural system is inherently incommensurable with the nucleated and its family of interrational values of the octahedral, tetrahedral, and rhombic dodecahedral states.
[987.321]{style="color: purple3"} []{#ver:987.321 label="ver:987.321"} The irrational differences existing between nucleated and nonnucleated systems are probably the difference between proton-nucleated and proton-neutron systems a nd nonnucleated-nonneutroned electron systems, both having identical numbers of external closest-packed spheres, but having also different over all, system-domain, volumetric, and system-population involvements.
[987.322]{style="color: purple3"} []{#ver:987.322 label="ver:987.322"} There is another important systemic difference between ’s proton-neutron system and the nonnucleated icosahedron’s electron system: the icosahedron is arrived at by removing the nucleus, wherefore its contraction will not permit the multilayering of spheres as is permitted in the multilayerability of the ergo, it cannot have neutron populating as in the ; ergo, it permits only single-layer, circumferential closest packings; ergo, it permits only single spherical orbiting domains of equal number to the outer layers of -nucleated, closest-packed systems; ergo, it permits only the behavioral patterns of the electrons.
[987.323]{style="color: purple3"} []{#ver:987.323 label="ver:987.323"} When all the foregoing is comprehended, it is realized that the whole concept of multiplication of information by division also embraces the concept of removing or separating out the nucleus sphere (vertex) from the ’s structurally unstable state and, as the jitterbug model shows, arriving omnisymmetrically throughout th e transition at the structural stability of the icosahedron. The icosa hedron experimentally evidences its further self-fractionation by its three different polar great-circle hemispherical cleavages that consistently follow the process of progressive self-fractionations as spin-halved successively around respective #5 , #6, and #7 axes of symmetry. These successive halvings develop various fractions corresponding in arithmetical differentiation degrees, as is shown in this exploratory accounting of the hierarchy of unit-vector delineating multiplication of information only by progressive subdividing of parts.
[987.324]{style="color: purple3"} []{#ver:987.324 label="ver:987.324"} When the tetrahedron is unity of tetravolume-1 (see Table 223.64), then (in contradistinction to the vector-radiused of tetravolume-20)
-
the vector-diametered VE = +2\sfrac{1}{2} or = -2\sfrac{1}
-
a rational, relative primitive prime number 5 tetravolume is also only realizable with half of its behavioral potentials in the presently-tune-in-able macrocosm and the other half of its total 5 behavioral potential existent in the presently-tune-out-able microcosm; thus,
-
an overall tetravolume potential -2\sfrac{1}{2}ergo, + 5 - 2\sfrac{1}{2}= +2\sfrac{1}{2} or
-
an overall -5 tetravolume potential +2\sfrac{1}{2}ergo, -5 + 2\sfrac{1}{2}= -2\sfrac{1}
[987.325]{style="color: purple3"} []{#ver:987.325 label="ver:987.325"} The positive and negative tetrahedra, when composited as symmetrically concentric and structurally stable, have eight symmetrically interarranged ver texes defining the corners of what in the past has been mistakenly identified as a primitive polyhedron, popularly and academically called the “cube” or hexahedron. Cubes do not exist primitively because they are structurally unstable, having no triangularly-self-stabilizing system pattern. They occur frequently in nature’s crystals but only as the superficial aspect of a conglomerate complex of omni triangulated polyhedra.
[987.326]{style="color: purple3"} []{#ver:987.326 label="ver:987.326"} This positive-negative tetrahedron complex defines a hexahedron of overall volume-31\sfrac{1}{2}inside and1\sfrac{1}{2} outside its intertrussed system’s inside-and-outside-vertex-defined domain.
-
The three-great-circle symmetrical cleavaging (#1) of the primitive tetrahedron produces the vector-edged octahedron of tetravolume-4.
-
The vector-radiused rhombic triacontahedron, with its unit-vector-radius perpendicular to its midface center produces a symmetrical polyhedron of tetra volume-5.
-
With its 12 diamond-face-centers occurring at unit-vector-radius, the rhombic dodecahedron has a tetravolume-6.
The rhombic dodecahedron exactly occupies the geometric domain of each unit-vector-radius sphere and that sphere’s external share of the symmetrically identical spaces intervening between closest-packed unit-radius spheres of any and all aggregates of unit-radius, closest-interpacked spheres. In this closest-packed condition each sphere within the aggregate always has 12 spheres symmetrically closest packed tangentially around it. The midpoints of the 12 diamond faces of the rhombic dodecahedron’s 12 faces are congruent with the points of tangency of the 12 surrounding spheres. All the foregoing explains why unit-radius rhombic dodecahedra fill allspace when joined together.
[987.327]{style="color: purple3"} []{#ver:987.327 label="ver:987.327"} Repeating the foregoing more economically we may say that in this hierarchy of omnisymmetric primitive polyhedra ranging from through 2, 2\sfrac{1}{2},
3, 4, 5, and 6 tetravolumes, the rhombic dodecahedron’s 12 diamondface-midpoints occur at the points of intertangency of the 12 surrounding spheres. It is thus disclosed that the rhombic dodecahedron is not only the symmetric domain of both the sphere itself and the sphere’s symmetric share of the space intervening between all closest-packed spheres and therefore also of the nuclear domains of all isotropic vector matrixes (Sec. 420 ), but the rhombic dodecahedron is also the maximum-limit-volumed primitive polyhedron of frequency-1.
¶ 987.400 Interactions of Symmetries: Secondary Great-circle Sets
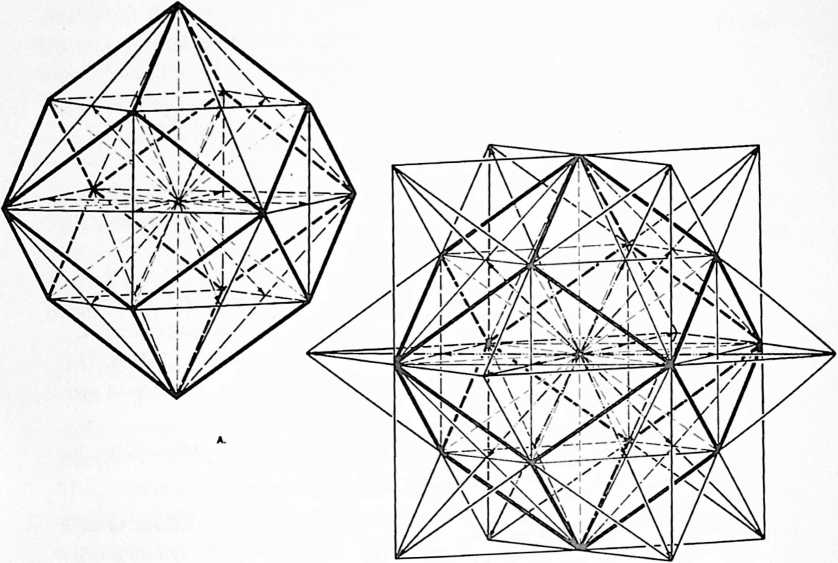
¶ 987.410 Icosa Phase of Rationality
[987.411]{style="color: purple3"} []{#ver:987.411 label="ver:987.411"} The 96 secondary gre at circles of the divide the chorded edge of the (which is the unit vector radius of synergetics) into rational linear fractions of the edge lengthi.e., \sfrac{1}{2}, \sfrac{3}{10}, \sfrac{1}{4}, \sfrac{1}{6}, \sfrac{1}{10} and these fractions embrace all the intercombinings of the first four prime numbers .
[987.412]{style="color: purple3"} []{#ver:987.412 label="ver:987.412"} For an illustration of how the four great circles of 60-degree central angles subdivide the central-angle chord increments, see Fig. 987.412.
[987.413]{style="color: purple3"} []{#ver:987.413 label="ver:987.413"} Next recalling the jitterbug transformation of the into the icosa with its inherent incommensurability brought about by the transformation ratio, and recognizing that the transformation was experimentally demonstrable by the constantly symmetrical contracting jitterbugging, we proceed to fractionate the icosahedron by the successive 15 great circles, six great circles (icosa type), and 10 great circles whose self-fractionation produces the Modules* as well as the and Modules.
[987.414]{style="color: purple3"} []{#ver:987.414 label="ver:987.414"} But it must be recalled that the experimentally demonstrable jitterbug model of transformation from to icosa can be accomplished through either a clockwise or counter clockwise twisting, which brings about 30 similar but positive and 30 negative omniintertriangulated vector edge results.
[987.415]{style="color: purple3"} []{#ver:987.415 label="ver:987.415"} The midpoints of each of these two sets of 30 vertexes in turn provide the two alternate sets of 30 poles for the spin-halving of the 15 great circles of Symmetry #6, whose spinning in turn generates the 120 right spherical triangles (60 positive, 60 negative) of t he icosahedral system.
[987.416]{style="color: purple3"} []{#ver:987.416 label="ver:987.416"} The 120 right triangles, evenly grouped into 30s pherical diamonds, are transformed into 30 planar diamonds of central angles iden tical to those of the 30 spherical diamonds of the 15 great circles of the icosa . When the radius to the center of the face of the rhombic triacontahedron equals … of the unit vector radius of Synergetics (1.000), the rhombic triacontahedron has a tetravolume of 5 and each of its 120 Quanta Modules h as a volume of one Module. When the radius equals 1, the volume of the rhombic triacontahedron is slightly larger (5.007758029), and the corresponding Module has a volume of of the Module. (See Sec. 986.540.) radius to radius = 2, or twice prime vector radius. This produces the stellated rhombic dodecahedron of tetravolume-12.
- The stellated rhombic dodecahedron vertexes are congruent with the mid-edge points of the cube of tetravolume-24. composite of three two-frequency Couplers (each individually of tetravolume-8) altogether comprises a star complex of tetravolume-12, sharing a common central rhombic dodeca domain of tetravolume-6. The stellated rhombic dodeca of tetravolume-12 is half the volume of the 24-tetravolume cube that inscribes it. (Compare the Duo-Tet Cube at Fig. 987.242A.)
See Sec. 988.
¶ 988.00 Icosahedron and Octahedron: Quanta Module
¶ 988.100 Octa-icosa Matrix
[988.110]{style="color: purple3"} []{#ver:988.110 label="ver:988.110"} The icosahedron positioned in the octahedron describes the Quanta Modules. (See Fig. 988.100.) Other references to the Quanta Modules may be found at Secs. 100.105, 100.322, Table 987.121, and 987.413.
[988.111]{style="color: purple3"} []{#ver:988.111 label="ver:988.111"} As skewed off the octa-icosa ma trix, they are the volumetric counterpart of the and Quanta Modules as manifest in the nonnucleated icosahedron. They also correspond to the \sfrac{1}{120}th tetrahedron of which the triacontahedron is composed. For their foldable angles and edge-length ratios see Figs. 988.111A-B.
[988.12]{style="color: purple3"} []{#ver:988.12 label="ver:988.12"} The icosahedron inscribed within the octahedron is shown at Fig. 988.12.
[988.13]{style="color: purple3"} []{#ver:988.13 label="ver:988.13"} The edge lengths of the Quanta Module are shown at Fig. 988.13A.
[988.14]{style="color: purple3"} []{#ver:988.14 label="ver:988.14"} The angles and foldability of the Quanta Module are shown at Fig. 988.13B. upon the planar they reveal the following rational fraction edge increments:
+:-----------------------+:-----------------------+:-------------+:----------+
| | | | |
+------------------------+------------------------+--------------+-----------+
| B-31 _ 1 | [B-C]{.underline} _ 1 | ::: minipage | B-33_ 3 |
| | | > B-32 _ 1 | |
| D-D 10 | D-D 6 | > | D-D 10 |
| | | > D-D 4 | |
| | | ::: | |
+------------------------+------------------------+--------------+-----------+
| [B-D]{.underline} _ 1 | [B-E]{.underline} _ 1 | ::: minipage | B-67 _ 3 |
| | | > B-62 _ 1 | |
| D-D 2 | D-D 6 | > | D-D 10 |
| | | > D-D 4 | |
| | | ::: | |
+------------------------+------------------------+--------------+-----------+
| B-73 _ 3 | [B-H]{.underline} _ 1 | | |
| | | | |
| D-D 8 | D-D 2 | | |
+------------------------+------------------------+--------------+-----------+
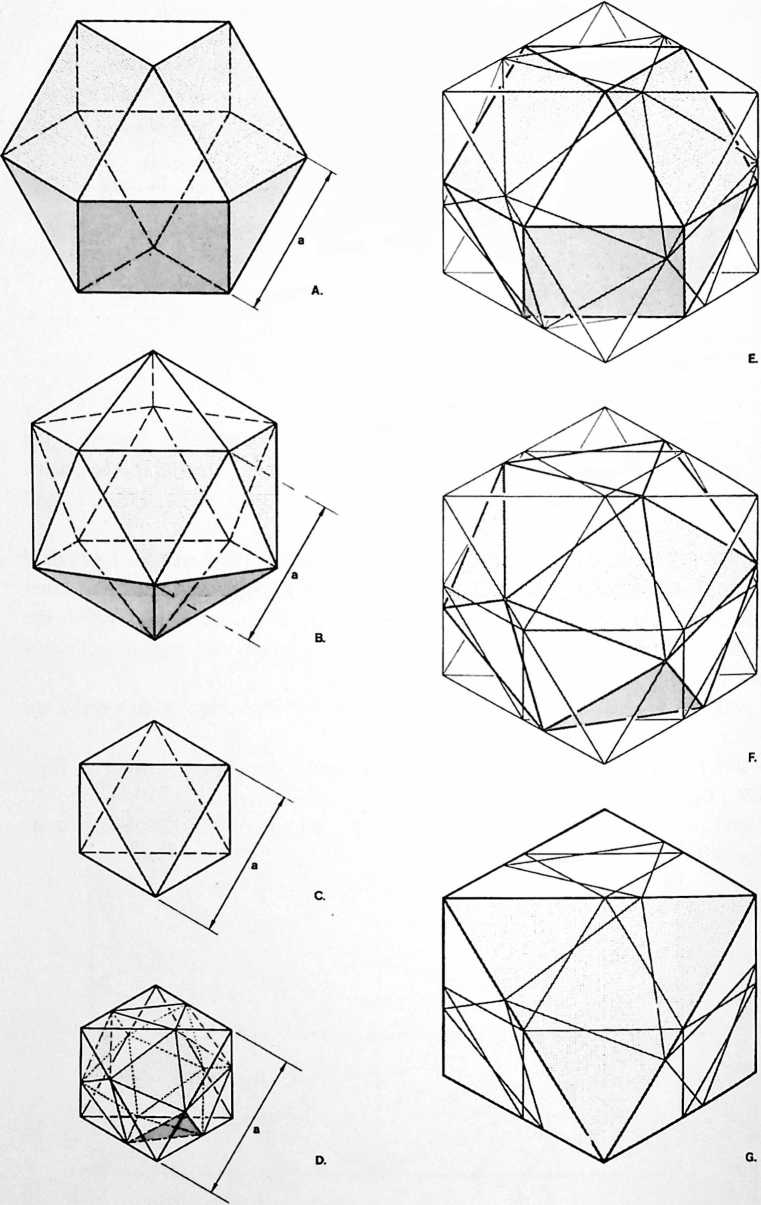
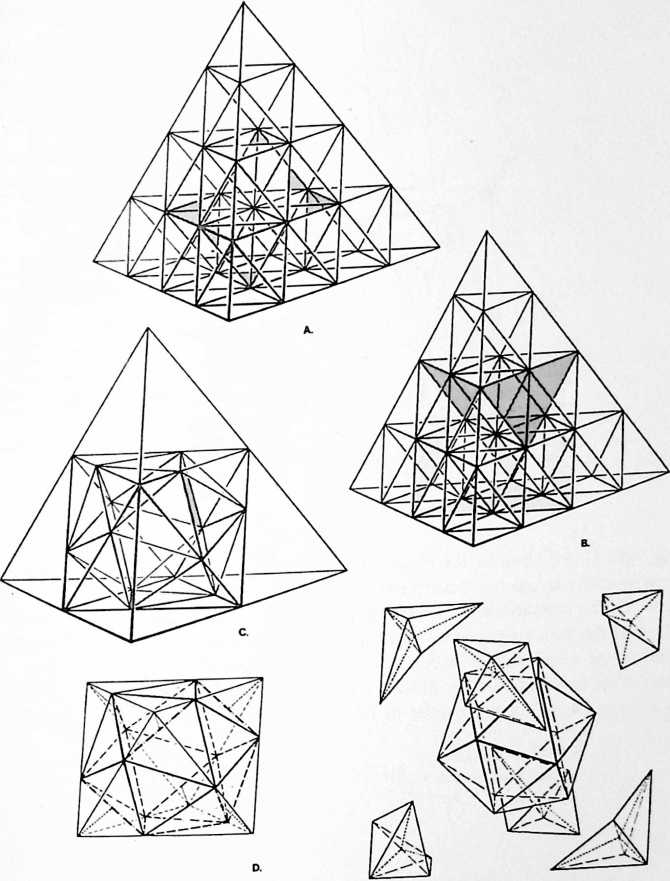
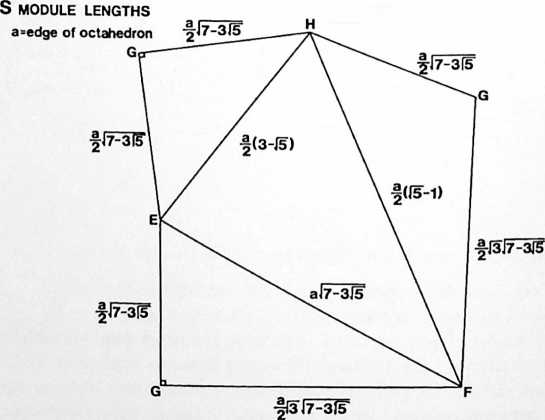
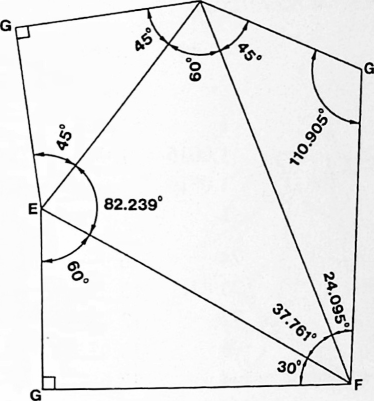
[988.20]{style="color: purple3"} []{#ver:988.20 label="ver:988.20"} Table: Volume-area Ratios of Modules and Polyhedra of the Primitive Hierarchy:
*Volume* *Area* *Volume /Area* *ArealVolume*
Module * *
P
Tetrahedron
Icosahedron**
Cube
Octahedron
Rhombic dodecahedron
Icosahedron
* Volume and area of Module considered as unity.
** Icosahedron inside octahedron.
¶ 990.00 Triangular and Tetrahedral Accounting
[990.01]{style="color: purple3"} []{#ver:990.01 label="ver:990.01"} All scientists as yet say “squared,” when they encounter the expression “,” and “ cubed,” when they encounter “.” But the number of squares enclosed by equi-module-edged subdivisions of large gridded squares is the same as the number of triangles enclosed by equi-module-edged subdivisions of large gridded triangles. This remains true regardless of the grid frequency, except that the triangular grids take up less space. Thus we may say ,“triangling” instead of,“squaring” and arrive at identical arithmetic results, but with more economical geometrical and spatial results. (See Illus. 990.01 and also 415.23.)
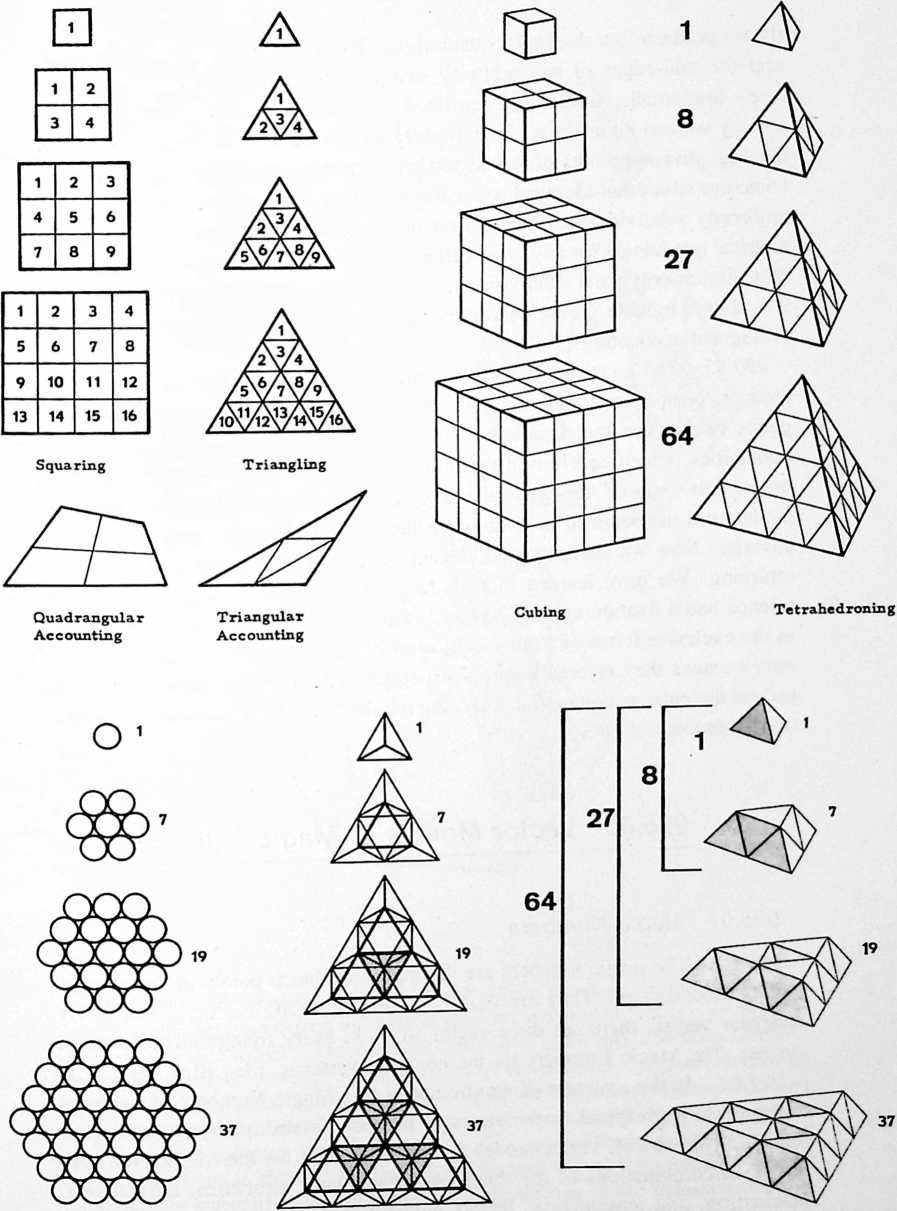
[990.02]{style="color: purple3"} []{#ver:990.02 label="ver:990.02"} Corresponding large, symmetrical agglomerations of cubes or tetrahedra of equi-modular subdivisions of their edges or faces demonstrate the same rate of third-power progression in their symmetrical growth ( etc.). This is also true when divided into small tetrahedral components for each large tetrahedron or in terms of small cubical components of each large cube. So we may also say “tetrahedroning” instead of “cubing” with the same arithmetical but more economical geometrical and spatial results.
[990.03]{style="color: purple3"} []{#ver:990.03 label="ver:990.03"} We may now say “one to the second power equals one,” and identify that arithmetic with the triangle as the geometrical unit. Two to the second power equals four: four triangles. And nine triangles and 16 triangles, and so forth. Nature needs only triangles to identify arithmetical “powering” for the self-multiplication of numbers. Every square consists of two triangles. Therefore, “triangling” is twice as efficient as “squaring.” This is what nature does because the triangle is the only structure. If we wish to learn how nature always operates in the most economical ways , we must give up “squaring” and learn to say “triangling,” or use the more generalized “powering.”
[990.04]{style="color: purple3"} []{#ver:990.04 label="ver:990.04"} There is another very trustworthy characteristic of synergetic accounting. If we prospectively look at any quadrilateral fig ure that does not have equal edges, and if we bisect and interconnect those mid-edges, we always produce four dissimilar quadrangles. But when we bisect and inter connect the mid-edges of any arbitrary triangleequilateral, isosceles , or scalene four smaller similar and equisized triangles will always result. There is no way we can either bisect or uniformly subdivide and then interconnect all the edge division points of any symmetrical or asymmetrical triangle and not come out with omni-identical triangular subdivisions. There is no way we can uniformly subdivide and interconnect the edge division points of any asymmetrical quadrangle (or any other different-edge-length polygons) and produce omnisimilar polygonal subdivisions. Triangling is not only more economical; it is always reliable. These characteristics are not available in quadrangular or orthogonal accounting.
[990.05]{style="color: purple3"} []{#ver:990.05 label="ver:990.05"} The increasingly vast, comprehensive, and rational order of arithmetical, geometrical, and vectorial coordination that we recognize as synergetics can reduce the dichotomy, the chasm between the sciences and the humanities, which occurred in the mid-nineteenth century when science gave up models because the generalized case of exclusively three-dimensional models did not seem to accommodate the scientists’ energy-experiment discoveries. Now we suddenly find elegant field modelability and conceptuality returning. We have learned that all local systems are conceptual. Because science had a fixation on the “square,” the “cube,” and the 90-degree angle as the exclusive forms of “unity,” most of its constants are irrational. This is only because they entered nature’s structural system by the wrong portal. If we use the cube as volumetric unity, t he tetrahedron and octahedron have irrational number volumes.
¶ 995.00 Vector Models of Magic Numbers
¶ 995.01 Magic Numbers
[995.02]{style="color: purple3"} []{#ver:995.02 label="ver:995.02"} The magic numbers are the high abundance points in the atomic-isotope occurrences. They are! For every nonpolar vertex, there are three vector edges in every triangulated structural system. The Magic Numbers are the nonpolar vertexes. (See Illus. 995.31.)
[995.03]{style="color: purple3"} []{#ver:995.03 label="ver:995.03"} In the structure of atomic nuclei, the Magic Numbers of neutrons and protons correspond to the states of increased stability. Synergetics provides a symmetrical, vector-model system to account for the Magic Numbers based on combinations of the three omnitriangulated structures: tetrahedron, octahedron, and icosahedron. In this model system, all the vectors have the value of one-third. The Magic Numbers of the atomic nuclei are accounted for by summing up the total number of external and internal vectors in each set of successive frequency models, then dividing the total by three, there being three vectors in Universe for every nonpolar vertex.
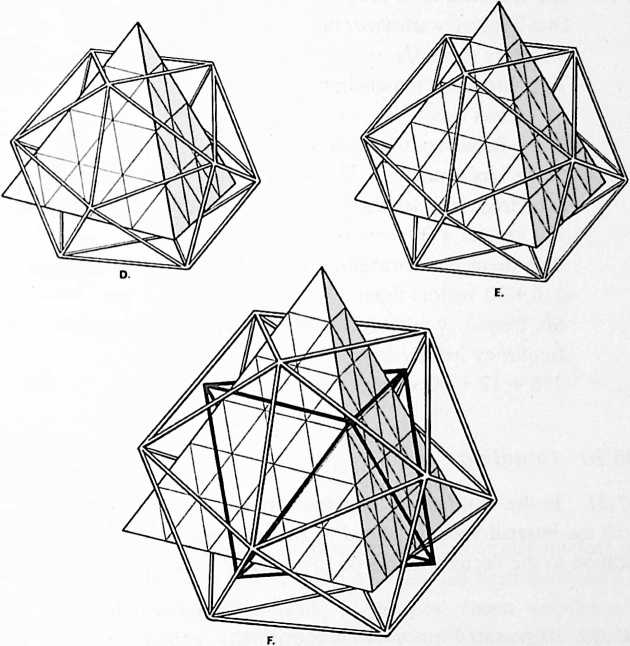
¶ 995.10 Sequence
[995.11]{style="color: purple3"} []{#ver:995.11 label="ver:995.11"} The sequence is as follows: Change: fix layout One-frequency tetrahedron: (MagicNumber:)
6 vectors times 1/3 = 2 Two-frequency tetrahedron: 24
vectors times 1/3 = 8
Three-frequency tetrahedron: 60 vectors times 1/3 = 20 Four-frequency tetrahedron + One-frequency icosahedron: 120 vectors + 30 vectors times 1/3 = 50 Five-frequency tetrahedron + One-frequency icosahedron: 216 + 30 vectors times 1/3 = 82 Six-frequency tetrahedron + One-frequency octahedron + One-frequency icosahedron: 336 + 12+ 30 vectors times 1/3 = 126
[995.11A]{style="color: purple3"} []{#ver:995.11A label="ver:995.11A"} The sequence is as follows: *(Magic Numbers)*One-frequency tetrahedron: 6 vectors times=2 Two-frequency tetrahedron: 24 vectors times =& Three-frequency tetrahedron: 60 vectors times 1/3 =20 Thr ee frequency tetrahedron + t wo-frequency tetrahedron: 60 vectors + 24 vectors ti mes V3 =28 Four-frequency tetrahedron + one-frequency icosahe d ron: 120 vectors + 30 vectors times V3 =50 Five-frequency tet r ahedron + one-frequency tetra hedron + one-frequency icosahedron: 210 + 6 + 30 ve ctors times V3 =82 Six-frequency tetrahedron + one-frequency oc tahedron + o ne-frequency icosahedron: 336+ 12 + 30 vectors times\sfrac{1}{3} = 126
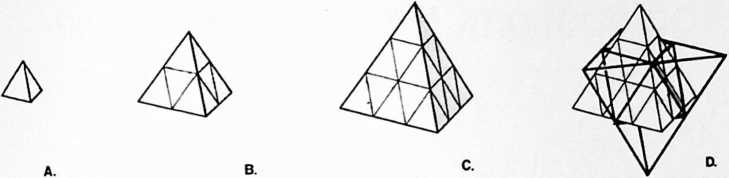
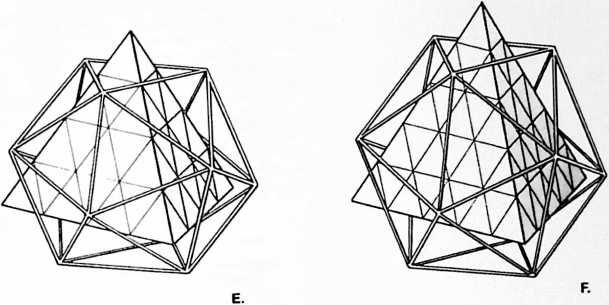
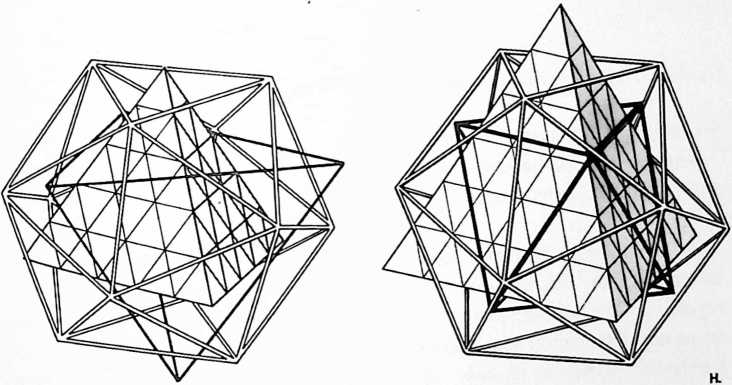
[995.12]{style="color: purple3"} []{#ver:995.12 label="ver:995.12"} Magic Number 28: The Magic Number 28, which introduces the cube and the octahedron to the series, was inadvertently omitted from Synergetics 1. The three-frequency tetrahedron is surrounded by an enlarged two-frequency tetrahedron that shows as an outside frame. This is a negative tetrahedron shown in its halo aspect because it is the last case to have no nucleus. The positive and negative tetrahedra combine to provide the eight corner points for the triangulated cube. The outside frame also provides for an octahedron in the middle. (See revised Figs. 995.03A and 995.31A.)
[995.20]{style="color: purple3"} []{#ver:995.20 label="ver:995.20"} Counting
[995.21]{style="color: purple3"} []{#ver:995.21 label="ver:995.21"} In the illustration, the tetrahedra are shown as opaque. Nevertheless, all the internal vectors defined by the isotropic vector matrix are counted in addition to the vectors visible on the external faces of the tetrahedra.
¶ 995.30 Reverse Peaks in Descending Isotope Curve
[995.31]{style="color: purple3"} []{#ver:995.31 label="ver:995.31"} There emerges an impressive pattern of regularly positioned behaviors of the relative abundances of isotopes of all the known atoms of the known Universe. Looking like a picture of a mountainside ski run in which there are a series of ski-jump upturns of the run, there is a series of sharp upward-pointing peaks in the overall descent of this relative abundance of isotopes curve, which originates at its highest abundance in the lowest-atomic-numbered elemental isotopes.
[995.32]{style="color: purple3"} []{#ver:995.32 label="ver:995.32"} The Magic Number peaks are approximately congruent with the atoms of highest structural stability. Since the lowest order of number of isotopes are the most abundant, the inventory reveals a reverse peak in the otherwise descending curve of relative abundance.
[995.33]{style="color: purple3"} []{#ver:995.33 label="ver:995.33"} The vectorial modeling of synergetics demonstrates nuclear physics with lucid comprehension and insight into what had been heretofore only instrumentally apprehended phenomena. In the post-fission decades of the atomic-nucleus explorations, with the giant atom smashers and the ever more powerful instrumental differentiation and quantation of stellar physics by astrophysicists, the confirming evidence accumulates.
[995.34]{style="color: purple3"} []{#ver:995.34 label="ver:995.34"} Dr. Linus Pauling has found and published his spheroid clusters designed to accommodate the Magic Number series in a logical system. We find him although without powerful synergetic toolsin the vicinity of the answer. But we can now identify these numbers in an absolute synergetic hierarchy, which must transcend any derogatory suggestion of pure coincidence alone, for the coincidence occurs with mathematical regularity, symmetry, and a structural logic that identifies it elegantly as the model for the Magic Numbers.