¶ 800.00 Operational Mathematics
¶ 801.00 Sensorial: Sweepout
¶ 801.01 Alternate Faculties of Sensation
[801.02]{style="color: purple3"} []{#ver:801.02 label="ver:801.02"} Information is experience. Experience is information. We have all experienced the information given to us directly through our own sensing faculties or relayed to us by others through our sensing faculties, but as originally sensed directly by others and not by ourselves. The only way that we know that we “are,” that we are alive in Universe, is through information apprehended by our own sensorial faculties. We can hear, see, taste, smell, and touch-feel. We have all experienced the information-relaying relationships between the old life and the new life. The old life is excited to see how early the new life develops, coordinates, and responds both consciously to external information and subconsciously to internally programmed instructions of the brain or of the genes. The old life tries to speed the development of the new life’s communicated comprehending by pointing to first the child’s and then the “old life” speaker’s eye and saying, “eye, eye, eye,” “mouth, mouth, mouth,” and “ear, ear, ear,” while pointing to those instruments until the child responds by making a similar sound. However, it is seldom that we observe parents thus engaged with their children refer to their internal organs, such as the endocrine glands. In fact, parents may not even know of these glands, let alone where they are situated. Such word-coaching by oldsters of youngsters relies almost exclusively upon identification of superficial characteristics and comprehends only in superficial degree those organs to which they refer.
[801.03]{style="color: purple3"} []{#ver:801.03 label="ver:801.03"} Let us imagine a scientifically conducted experiment designed to disclose the unique behavioral characteristics of each of those four prime sensing faculties without which we could not apprehend Universe and could not have sense of being.
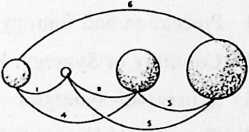
[801.04]{style="color: purple3"} []{#ver:801.04 label="ver:801.04"} Let us suppose that you are blindfolded and that your mouth, nostrils, and ears are also simultaneously bound closed. Only your tactile sensing is operative. To find out about yourself and local Universe, you would begin by reaching out around you with your arms-extended hands. You could learn environmental conditions through your hands. You could lean forward, and the sense of balance would tell you how far you can reach without shifting your base position. You discover that you are prospecting with your sensitive skin terminals, as does an insect with all its radially and circumferentially orientable feelers. Your most extreme and mobile skin feelers are your toes and your fingers. You are trying to get terminal reach information before you move on from your safe base. You will not risk shifting your weight until you are certain that you will be supported. You will not move into a place so small you cannot tum around and escape. Without changing your base, and standing with all your weight on your left foot, you learn that you can stretch out and sweep out with your arms while at the same time sweeping space and testing the ground’s firmness with your right leg. Thus you learn that there is a maximum range of information gathering, which is the distance between the right foot’s big toe and your left hand’s middle fingertip. Most of us have a toe-to-fingertip reach of about six or eight feet. In these sense-limited conditions, our only way of finding out about Universe is tactile, through touch alone. Very quickly, we become super-sensitive with our feet and hands, particularly with our feet and legs in gravitational balancing. Every child learns this in summer while at camp. At home, his parents won’t let him stay up after dark, but maybe at night he is very fond of a path that goes down to the water. He starts going on that path and finds himself running along in the dark. Even though you can’t see, you remember well the pattern of turns, depressions, hills, and dales. Your feet feel familiar with the path; the rhythm of steps and heartbeats subconsciously monitors your memory-bank control of your running along that familiar path barefootedly in the dark. We find experimentally that we can remember patterns tactilely and feel very safe following them. We are even able to run back and forth over a local complex of familiar ground and we can run at about 10 miles per hour. Wherefore our static tactile information-gathering, which commands a maximum spherical range of 10 feet in diameter, is augmented by the 10-miles-per-hour dynamic range-minding capability.
[801.05]{style="color: purple3"} []{#ver:801.05 label="ver:801.05"} Ecology is the science of cataloguing, ordering, and inspecting patterns of life. Different kinds of life demonstrate different kinds of patterns. There is a difference of radius of sweepout of wolves, seagulls, and man. If we humans had only the tactile sense to go by in our ecological patterning, we could only sweep out a fairly small territory, but we could get so used to it that we would probably run around in the known territory.
[801.06]{style="color: purple3"} []{#ver:801.06 label="ver:801.06"} But now suppose that you cover up all your skin and uncover your nostrils and your mouth. Your eyes and ears are still covered and your feet and hands are now tied down so you cannot move. You have only olfactory information. Under these conditions, men’s measurements are governed by three factors: (1) the radius of the permeation of gases within gases; (2) the concentration and viscosity of such gases, such as orange groves, pine woods, and so forth; and (3) the wind. Men coming in from months at sea have smelled orange groves and pine trees at somewhere around a mile offshore in still air. Such gases remain sufficiently concentrated to be detectable at a mile. (Of course, dogs can smell at greater distances than our human standing-still olfactory range of about a mile.) If the wind is blowing, the velocity is enhanced so we get smoke from forest fires at great distances. In great, 400-miles-per-hour, high altitude, jet stream winds, the smellable concentration can persist to a range of even 100 miles. Whereas our tactile sense’s static range is 10 feet, which equals about 1/Vth of a mile; and its dynamic velocity range augmentation is 10 miles per hour, we find our olfactoral static range of information-gathering is 100 miles and its dynamic range is 400 miles per hour.
[801.07]{style="color: purple3"} []{#ver:801.07 label="ver:801.07"} If we now shut off the mouth and nostrilswith eyes and skin also blanked outand we then open up only the ears, we cannot see, smell, or feel; we have only sounds to reckon by. Men have heard sounds at very great distances. Sounds will bounce on the water, into the atmosphere, and back on the water again. Sound is a wave phenomenon that men have heard at ranges up to 100 miles, as in the case of the atomic bomb. The speed of sound in the air is about 700 miles per hour; the static hearing range is about 100 miles, while the dynamic hearing range is 1,100 miles per hour (700 m.p.h. + 400 m.p.h. jet-stream wind = 1,100 m.p.h.).
[801.08]{style="color: purple3"} []{#ver:801.08 label="ver:801.08"} We next shut off the tactile, olfactory, and oral sensing, then uncover and open our eyes. Men see stars that are billions of miles away. We know the velocity of light is 186,000 miles per second, or about 700 million miles per hour. We find that the visual sensing is in an entirely different order of magnitude. The tactile, olfactory, and oral faculties as a group are so minuscule as compared to the range of the visual that they cannot even be considered together.
¶ 801.09 Human Sense Ranging and Information Gathering
Radius of Static Ranging:
Dynamic Velocity:
Tactile 1/1,000th of a mile 10 miles per hour
Olfactory 1 mile 400 miles per hour
Aural 100 miles 1,100 miles per hour
Visual 6,000,000,000,000,000,000 miles [^26] 700,000,000 miles per hour If we try to plot two curves of these static and dynamic human sensing capabilities on a chart, we will have no trouble in positioning the first three senses; but to reach the point on the chart at which the sight capabilities occur, we will have to take an airplane and fly for many days to reach those positions. It is clear that as we recede from the first three sets of points, they will tend gradually to appear as one. This disparity has not been taught to us. We were told that our senses were approximately equal and alternate capabilities. Court imposed “damage costs” for their respective losses are approximately equal. We found out the disparity ourselves by examining the limit-case conditions, which can only be discovered by physical experience. This method of discovery is called “operational procedure.”
¶ 801.10 Sense Coordination of the Infant
[801.11]{style="color: purple3"} []{#ver:801.11 label="ver:801.11"} One of the most surprising things about a newborn child is that it is already tactilely coordinated. Even in the first day, the baby is so well coordinated tactilely that if you put your finger against its palm, the baby will close its hand firmly and deftly around your finger, although it is not using its ears or eyes at all. If you will now exert a tiny bit of tension effort to remove your finger, the child will respond at once by opening its hand. The infant will repeat the closing and opening response to your initiatives as many times as you may wish to initiate. This should not surprise us if we realize that the baby has been in tactile communication with its mother for months before evacuating her womb, within which, however, its visual, olfactory, and aural faculties were muted and inoperative. Not much time after birth the child employs for the first time its olfactory glands and starts searching the mother’s breast and the source of milk. Quite a few days later it begins to hear; and very much later, it sees. The sequence in which the child’s faculties become employed corresponds to the order of increased range of its respective faculties of information apprehending.
[801.12]{style="color: purple3"} []{#ver:801.12 label="ver:801.12"} Thus we find the child successively coordinating the first three faculties: the tactile, the olfactory, and the aural. He begins to learn how they work together and quite rapidly gets to be very skillful in coordinating and handling the information coming to him through these senses. It is only days later that he begins to use his sight. He tries tactilely, olfactorily, and aurally to confirm what he sees to be reality. He cannot do so over any great distance because neither his arms and hands nor his tasting mouth will reach very far. Months later, the child crawls to check tactilely, olfactorily, and aurally on phenomena still further away; and thereby to coordinatingly sort out his information inputs; and thereby develop a scheme ofand a total sense of reality and repetitive event expectancy. He crawls over to the chair to find that his eyes have reported to him correctly that the chair is indeed there. He begins to check up and coordinate on more distant objects, and he finds his visual ability to be reliable. The child seeing the Fourth of July fireworks for the first time sees a flash and then hears a boom. Maybe that doesn’t mean so much to him, because boom (aural) and flash (optical) may be different phenomena; but when he sees a man hammering a fence post, he has by this time been hammering a whole lot and he knows the sound that makes. He may not be very sure of the fireworks in the sky, the flash and the boom, but he is really very confident about the sound of the hammering of the fence post. When he sees the man hammer and then hears the sound a fraction later, he begins to realize that there is some lag in the rates in which he gets information from different faculties. His eye gets it faster than his ear.
[801.13]{style="color: purple3"} []{#ver:801.13 label="ver:801.13"} The three postnatal senses the child coordinates are secondary. The first prenatal one, the tactile, is primary. The real emphasis of the judgment of life is on the tactile, the primary, the thing you can touch[^27]. The ranges of the first three senses are so close together, and sight is so different, that we may best rank them as #1, touch, being a primary set; with both #2, olfactoral coupled with #3, aural, as a secondary set; and #4 sight, as a tertiary set: wherefore in effect, touch is the yesterday set; while the olfactoral and aural (what you are smelling, eating, saying, and hearing) are the now set; while sight (what only may be next) is the future set. (We can seem to see, but we have not yet come to it.) Whereas reality is eternally now, human apprehending demonstrates a large assortment of lags in rates of cognitions whose myriadly multivaried frequencies of myriadly multivaried, positivenegative, omnidirectional aberrations, in multivaried degrees, produce such elusively off-center effects as possibly to result in an illusionary awareness of an approximately unlimited number of individually different awareness patterns, all of whose relative imperfections induce the illusion of a reality in which “life” is terminal, because physically imperfect; as contrasted to mind’s discovery of an omni-interaccommodative complex of a variety of different a priori, cosmic, and eternal principles, which can only be intellectually discovered, have no weight, and apparently manifest a perfect, abstract, eternal design, the metaphysical utterly transcendent of the physical.
[801.14]{style="color: purple3"} []{#ver:801.14 label="ver:801.14"} The 186,000-miles-per-second speed of light is so fast that it was only just recently measured, and it doesn’t really have much meaning to us. You don’t have a sense of 700 million miles per hour. If you did get to “see” that way, you would be spontaneously conscious of seeing the Sun eight minutes after the horizon had obscured it; ergo, consciously seeing an arc around the Earth’s curvature. We are not seeing that way as yet. To explain our sight, we call it “instantaneous.” We say we can see instantaneously. This fact has misled us very greatly. You insist that you are seeing the black-and-white page of this book, do you not? You’re not. You have a brain-centered television set, and the light is bouncing off the page. The resultant comes back through your optical system and is scanned and actually goes back into the brain, and you are seeing the page in your brain. You are not seeing the page out in front of you. We have gotten used to the idea that we see outside of ourselves, but we just don’t do so. It only takes about a billionth of a second for the light to bounce off the page and get in the brain to be scanned, so the child is fooled into thinking that he is seeing outside of himself. And we are misinforming ourselves in discounting the lag and assuming that we see it “over there.” No one has ever seen outside themselves.
¶ 801.20 The Omnidirectional TV Set
[801.21]{style="color: purple3"} []{#ver:801.21 label="ver:801.21"} Children looking at TV today look at it quite differently from the way it was to the first generation of TV adults. It begins to be very much a part of the child’s life, and he tends to accredit it the way adults accredit what they get from their eyes. When children are looking at a baseball game, they are right there in the field. All of our vision operates as an omnidirectional TV set, and there is no way to escape it. That is all we have ever lived in. We have all been in omnidirectional TV sets all our lives, and we have gotten so accustomed to the reliability of the information that we have, in effect, projected ourselves into the field. We may insist that we see each other out in the field. But all vision actually operates inside the brain in organic, neuron-transistored TV sets.
[801.22]{style="color: purple3"} []{#ver:801.22 label="ver:801.22"} We have all heard people describe other people, in a derogatory way, as being “full of imagination.” The fact is that if you are not full of imagination, you are not very sane. All we do is deal in brain images. We traffic in the memory sets, the TV sets, the recall sets, and certain incoming sets. When you say that you see me or you say “I see you,” or “I touch you,” I am confining information about you to the “tactile you.” If I had never had a tactile experience (which could easily be if I were paralyzed at conception), “you” might be only where I smell you. “You” would have only the smellable identity that we have for our dogs. You would be as big as you smell. Then, if I had never smelled, tasted, nor experienced tactile sensing, you would be strictly the hearable you.
[801.23]{style="color: purple3"} []{#ver:801.23 label="ver:801.23"} What is really important, however, about you or me is the thinkable you or the thinkable me, the abstract metaphysical you or me, what we have done with these images, the relatedness we have found, what communications we have made with one another. We begin to realize that the dimensions of the thinkable you are phenomenal, when you hear Mozart on the radio, that is, the metaphysicalonly intellectually identifiableeternal Mozart who will always be there to any who hears his music. When we say “atom” or think “atom” we are intellect-to-intellect with livingly thinkable Democritus, who first conceived and named the invisible phenomenon “atom.” Were exclusively tactile Democritus to be sitting next to you, surely you would not recognize him nor accredit him as you do the only-thinkable Democritus and what he thought about the atom. You say to me: “I see you sitting there.” And all you see is a little of my pink face and hands and my shoes and clothing, and you can’t see me, which is entirely the thinking, abstract, metaphysical me. It becomes shocking to think that we recognize one another only as the touchable, nonthinking biological organism and its clothed ensemble.
[801.24]{style="color: purple3"} []{#ver:801.24 label="ver:801.24"} Reconsidered in these significant identification terms, there is quite a different significance in what we term “dead” as a strictly tactile “thing,” in contrast to the exclusively “thinking” you or me. We can put the touchable things in the ground, but we can’t put the thinking and thinkable you in the ground. The fact that I see you only as the touchable you keeps shocking me. The baby’s spontaneous touching becomes the dominant sense measure, wherefore we insist on measuring the inches or the feet. We talk this way even though these are not the right increments. My exclusively tactile seeing inadequacy becomes a kind of warning, despite my only theoretical knowledge of the error of seeing you only as the touchable you. I keep spontaneously seeing the tactile living you. The tactile is very unreliable; it has little meaning. Though you know they are gentle, sweet children, when they put on Hallowe’en monster masks they “look” like monsters. It was precisely in this manner that human beings came to err in identifying life only with the touchable physical, which is exactly what life isn’t.
¶ 810.00 One Spherical Triangle Considered as Four
¶ 811.00 Bias on One Side of the Line
[811.01]{style="color: purple3"} []{#ver:811.01 label="ver:811.01"} We have all been brought up with a plane geometry in which a triangle was conceived and defined as an area bound by a closed line of three edges and three angles. A circle was an area bound by a closed line of unit radius. The area outside the closed boundary line was not only undefinable but was inconceivable and unconsidered.
[811.02]{style="color: purple3"} []{#ver:811.02 label="ver:811.02"} In the abstract, ghostly geometry of the Greeks, the triangle and circle were inscribed in a plane that extended laterally to infinity. So tiny is man and so limited was man’s experience that at the time of the Greeks, he had no notion that he was living on a planet. Man seemed obviously to be living on an intuitively expansive planar world around and above which passed the Sun and stars, after which they plunged into the sea and arose again in the morning. This cosmological concept of an eternally extended, planar-based Earth sandwiched between heaven above and hell below made infinity obvious, ergo axiomatic, to the Greeks.
[811.03]{style="color: purple3"} []{#ver:811.03 label="ver:811.03"} The Greek geometers could not therefore define the planar extensibility that lay outside and beyond the line of known content. Since the surface outside of the line went to infinity, you could not include it in your computation. The Greeks’ concept of the geometrical, bound-area of their triangle or their circle lay demonstrably on only one bound-area side of the line. As a consequence of such fundamental schooling, world society became historically biased about everything. Continually facing survival strategy choices, society assumed that it must always choose between two or more political or religious “sides.” Thus developed the seeming nobility of loyalties. Society has been educated to look for logic and reliability only on one side of a line, hoping that the side chosen, on one hand or the other of indeterminately large lines, may be on the inside of the line. This logic is at the head of our reflexively conditioned biases. We are continually being pressed to validate one side of the line or the other.
[811.04]{style="color: purple3"} []{#ver:811.04 label="ver:811.04"} You can “draw a line” only on the surface of some system. All systems divide Universe into insideness and outsideness. Systems are finite. Validity favors neither one side of the line nor the other. Every time we draw a line operationally upon a system, it returns upon itself. The line always divides a whole system’s unit area surface into two areas, each equally valid as unit areas. Operational geometry invalidates all bias.
¶ 812.00 Spherical Triangle
[812.01]{style="color: purple3"} []{#ver:812.01 label="ver:812.01"} The shortest distance between any two points on the surface of a sphere is always described by an arc of a great circle. A triangle drawn most economically on the Earth’s surface or on the surface of any other sphere is actually always a spherical triangle described by great-circle arcs. The sum of the three angles of a spherical triangle is never 180 degrees. Spherical trigonometry is different from plane trigonometry; in the latter, the sum of any triangle’s angles is always 180 degrees. There is no plane flat surface on Earth, wherefore no plane triangles can be demonstrated on its surface. Operationally speaking, we always deal in systems, and all systems are characterized projectionally by spherical triangles, which control all our experimental transformations.
[812.02]{style="color: purple3"} []{#ver:812.02 label="ver:812.02"} Drawing or scribing is an operational term. It is impossible to draw without an object upon which to draw. The drawing may be by depositing on or by carving awaythat is, by creating a trajectory or tracery of the operational event. All the objects upon which drawing may be operationally accomplished are structural systems having insideness and outsideness. The drawn-upon object may be either symmetrical or asymmetrical. A piece of paper or a blackboard is a system having insideness and outsideness.
[812.03]{style="color: purple3"} []{#ver:812.03 label="ver:812.03"} When we draw a triangle on the surface of Earth (which previously unscribed area was unit before the scribing or drawing), we divide Earth’s surface into two areas on either side of the line. One may be a little local triangle whose three angles seem to add up to 180 degrees, while the other big spherical triangle complementing the small one to account together for all the Earth’s surface has angles adding up to 900 degrees or less. This means that each corner of the big triangle complementing the small local one, with corners seeming to be only 60 degrees each, must be 300 degrees each, for there are approximately 360 degrees around each point on the surface of a sphere. Therefore the sum of all the three angles of the big Earth triangles, which inherently complement the little local 60-degree-per-corner equilateral triangles, must be 900 degrees. The big 900-degree triangle is also an area bounded by three lines and three angles. Our schooled-in bias renders it typical of us to miss the big triangle while being preoccupied only locally with the negligibly sized triangular area.
[812.04]{style="color: purple3"} []{#ver:812.04 label="ver:812.04"} If you inscribe one triangle on a spherical system, you inevitably describe four triangles. There is a concave small triangle and a concave big triangle, as viewed from inside, and a convex small triangle and a convex big triangle, as viewed from outside. Concave and convex are not the same, so at minimum there always are inherently four triangles.
[812.05]{style="color: purple3"} []{#ver:812.05 label="ver:812.05"} Background Nothingness: One spherical triangle ABC drawn on the Earth’s surface inadvertently produces four triangles as the corners of the surface triangle are inherently related to the center of the Earth D, and their lines of interrelatedness together with the three edge lines of the surface triangle describe a tetrahedron. (See Fig. 812.03.) Drawing a triangle on the surface of the Earth (as described at Sec. 810) also divides the surface of the Earth into two areasone large, one smallboth of which are bound by a closed line with three edges and three angles. The large triangle and the small triangle have both concave and convex aspectsergo, four triangles in all. Euler did not recognize the background nothingness of the outside triangles. (See Sec. 505.81.)
[812.06]{style="color: purple3"} []{#ver:812.06 label="ver:812.06"} Under the most primitive pre-time-size conditions the surface of a sphere may be exactly subdivided into the four spherical triangles of the spherical tetrahedron, each of whose surface corners are 120-degree angles, and whose “edges” have central angles of 109. The area of a surface of a sphere is also exactly equal to the area of four great circles of the sphere. Ergo, the area of a sphere’s great circle equals the area of a spherical triangle of that sphere’s spherical tetrahedron: wherefore we have a circular area exactly equaling a triangular area, and we have avoided use of pi (if).
¶ 813.00 Square or Triangle Becomes Great Circle at Equator
[813.01]{style="color: purple3"} []{#ver:813.01 label="ver:813.01"} If we draw a closed line such as a circle around Earth, it must divide its total unit surface into two areas, as does the equator divide Earth into southern and northern hemispheres. If we draw a lesser-sized circle on Earth, such as the circle of North latitude 70, it divides Earth’s total surface into a very large southern area and a relatively small northern area. If we go outdoors and draw a circle on the ground, it will divide the whole area of our planet Earth into two areasone will be very small, the other very large.
[813.02]{style="color: purple3"} []{#ver:813.02 label="ver:813.02"} If our little circle has an area of one square foot, the big circle has an area of approximately five quadrillion square feet, because our 8,000-mile-diameter Earth has an approximately 200-million-square-mile surface. Each square mile has approximately 25 million square feet, which, multiplied, gives a five followed by fifteen zeros: 5,000,000,000,000,000 square feet. This is written by the scientists as 5 x 1015 square feet; while compact, this tends to disconnect from our senses. Scientists have been forced to disconnect from our senses due to the errors of our senses, which we are now able to rectify. As we reconnect our senses with the reality of Universe, we begin to regain competent thinking by humans, and thereby possibly their continuance in Universe as competently functioning team membersmembers of the varsity or University team of Universe.
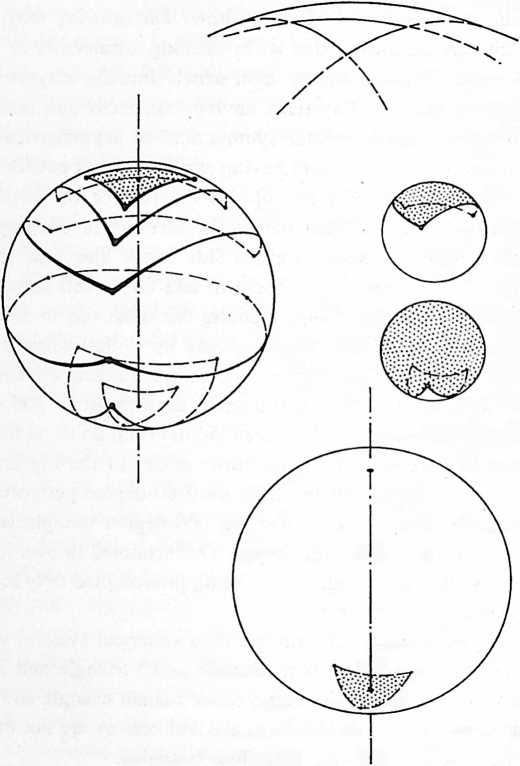
Fig. 812.03: The Greeks defined a triangle as an area bound by a closed line of three edges and three angles. A triangle drawn on the Earth’s surface is actually a spherical triangle described by three great-circle arcs. It is evident that the arcs divide the surface of the sphere into two areas, each of which is bound by a closed line consisting of three edges and three angles, ergo dividing the total area of the sphere into two complementary triangles. The area apparently “outside” one triangle is seen to be “inside” the other. Because every spherical surface has two aspectsconvex if viewed from outside, concave if viewed from withineach of these triangles is, in itself, two triangles. Thus one triangle becomes four when the total complex is understood. “Drawing” or “scribing” is an operational term. It is impossible to draw without an object upon which to draw. The drawing may be by depositing on or by carving away, that is, by creating a trajectory or tracery of the operational event. All the objects upon which drawing may be operationally accomplished are structural systems having insideness and outsideness. The drawn-upon object may be symmetrical or asymmetrical, a piece of paper or a blackboard system having insideness and outsideness.
[813.03]{style="color: purple3"} []{#ver:813.03 label="ver:813.03"} If, instead of drawing a one-square-foot circle on the ground–which means on the surface of the spherical Earthwe were to draw a square that is one foot on each side, we would have the same size local area as before: one square foot. A square as defined by Euclid is an area bound by a closed line of four equal-length edges and four equal and identical angles. By this definition, our little square, one foot to a side, that we have drawn on the ground is a closed line of four equal edges and equal angles. But this divides all Earth’s surface into two areas, both of which are equally bound by four equal-length edges and four equal angles. Therefore, we have two squares: one little local one and one enormous one. And the little one’s corners are approximately 90 degrees each, which makes the big square’s corners approximately 270 degrees each. While you may not be familiar with such thinking, you are confronted with the results of a physical experiment, which inform you that you have been laboring under many debilitating illusions.
[813.04]{style="color: purple3"} []{#ver:813.04 label="ver:813.04"} If you make your small square a little bigger and your bigger one a little smaller by increasing the little one’s edges to one mile each, you will have a local one square milea customary unit of western United States ranches and the big square will be approximately 199,999,999 square miles. As you further increase the size of the square, using great-circle lines, which are the shortest distances on a sphere between any two points, to draw the square’s edges, you will find the small square’s corner angles increasing while the big one’s corner angles are decreasing. If you now make your square so that its area is one half that of the Earth, 100 million square miles, in order to have all your edges the same and all your angles the same, you will find that each of the corners of both squares is 180 degrees. That is to say, the edges of both squares lie along Earth’s equator so that the areas of both are approximately 10 million square miles.
¶ 814.00 Complementarity of System Surfaces
[814.01]{style="color: purple3"} []{#ver:814.01 label="ver:814.01"} The progressive enlargement of a triangle, a pentagon, an octagon, or any other equi-edged, closed-line figure drawn on any system’s surface produces similar results to that of the enlarging square with 180 degrees to each corner at the equator. The closed-line surface figure will always and only divide the whole area into two complementary areas. Each human making this discovery experimentally says spontaneously, “But I didn’t mean to make the big triangle,” or “the big square,” or indeed, the big mess of pollution. This lack of intention in no way alters these truths of Universe. We are all equally responsible. We are responsible not only for the big complementary surface areas we develop on systems by our every act, but also for the finite, complementary outward tetrahedron automatically complementing and enclosing each system we devise. We are inherently responsible for the complementary transformation of Universe, inwardly, outwardly, and all around every system we alter.
¶ 820.00 Tools of Geometry
[821.01]{style="color: purple3"} []{#ver:821.01 label="ver:821.01"} The Early Greek geometers and their Egyptian and Babylonian predecessors pursued the science of geometry with three basic tools; the dividers, the straightedge, and the scriber. They established the first rule of the game of geometry, that they could not introduce information into their exploration unless it was acquired empirically as constructed by the use of those tools. With the progressive interactive use of these three tools, they produced modular areas, angles, and linear spaces.
[821.02]{style="color: purple3"} []{#ver:821.02 label="ver:821.02"} The basic flaw in their game was that they failed to identify and define as a tool the surface on which they inscribed. In absolute reality, this surface constituted a fourth tool absolutely essential to their demonstration. The absolute error of this oversight was missed at the time due to the minuscule size of man in relation to his planet Earth. While there were a few who conceived of Earth as a sphere, they assumed that a local planar condition existed which the vast majority of humans assumed to be extended to infinity, with a four-cornered Earth plane surrounded by the plane of water that went to infinity.
[821.03]{style="color: purple3"} []{#ver:821.03 label="ver:821.03"} They assumed the complementary tool to be a plane. Because the plane went to infinity in all planar directions, it could not be defined and therefore was spontaneously overlooked as a tool essential to their empirical demonstrating. What they could not define, yet obviously needed, they identified by the ineffable title “axiomatic,” meaning “Everybody knows that.” Had they recognized the essentiality of defining the fourth tool upon which they inscribed, and had they recognized that our Earth was sphericalergo, finite; ergo, definitethey could and probably would have employed strategies completely different from that of their initiation of geometry with the exclusive use of the plane. But to the eastern Mediterranean world there lay the flat, infinite plane of the Earth at their feet on which to scratch with a scriber.
[821.10]{style="color: purple3"} []{#ver:821.10 label="ver:821.10"} Dividers: The ends of two sticks can be bound together to serve as dividers. A straightedge stick could be whittled by a knife and sighted for straightness and improved by more whittling.
[821.11]{style="color: purple3"} []{#ver:821.11 label="ver:821.11"} The opening of the dividers could be fixed by binding on a third stick between the other two ends, thus rigidifying by triangulation. Almost anyone at sea or in the desert could start playing this game.
¶ 825.00 Greek Scribing of Right-Angle Modularity in a Plane
[825.01]{style="color: purple3"} []{#ver:825.01 label="ver:825.01"} It was easy for the Greeks to use their fixed dividers to identify two points on the plane marked by the divider’s two ends: and B, respectively. Employing their straightedge, they could inscribe the line between these two points, the line/IB. Using one end of the dividers as the pivot point at one end of the line, A, a circle can be described around the original line terminal: circle A. Using point as a center, a circle can be described around it, which we will call circle B. These two circles intersect one another at two points on either side of the line AB. We will call the intersection points and C.
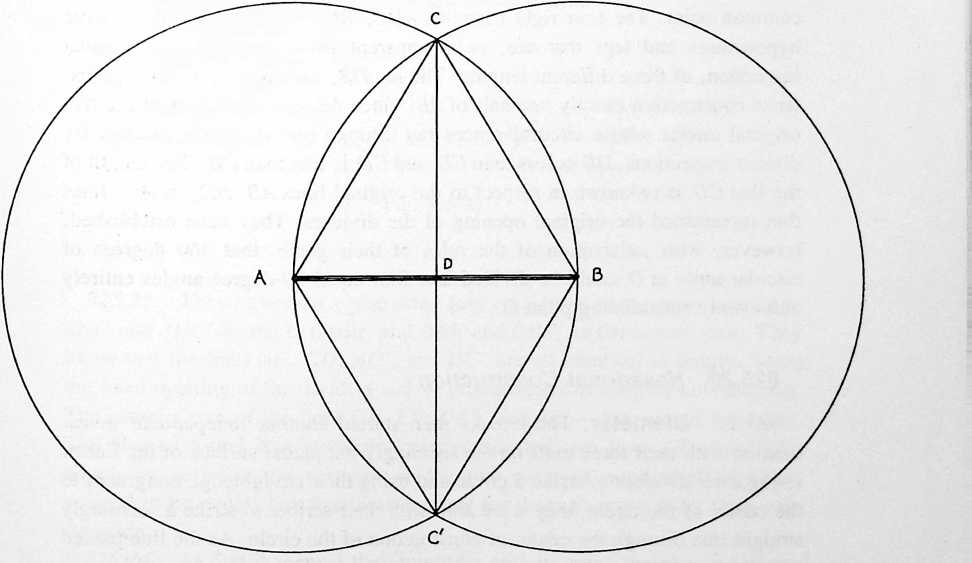
Fig. 825.01.
[825.02]{style="color: purple3"} []{#ver:825.02 label="ver:825.02"} By construction, they demonstrated that points and C were both equidistant from points and B. In this process, they have also defined two equilateral triangles ABC and ABC, with a congruent edge along the line AB and with points and equidistant on either side from points and B, respectively.
¶ 825.10 Right Triangle
[825.11]{style="color: purple3"} []{#ver:825.11 label="ver:825.11"} They then used a straightedge to connect points and with a line that they said bisected line AB perpendicularly, being generated by equidistance from either point on either side. Thus the Greeks arrived at their right triangle; in fact, their four right triangles. We will designate as point!) the intersection of the lines CC and AB. This gave the Greeks four angles around a common point. The four right triangles ADC, BDC, ADC, and BDC have hypotenuses and legs that are, as is apparent from even the most casual inspection, of three different lengths. The leg Z)B, for instance, is by equidistance construction exactly one-half of AB, since/IB was the radius of the two original circles whose circumferences ran through one another’s centers. By divider inspections, DB is less than CD and CD is less than CB. The length of the line CD is unknown in respect to the original lines AB, BD, or AC, lines that represented the original opening of the dividers. They have established, however, with satisfaction of the rules of their game, that 360 degrees of circular unity at could be divided into four equal 90-degree angles entirely and evenly surrounding point/).
¶ Hexagonal Construction
[825.21]{style="color: purple3"} []{#ver:825.21 label="ver:825.21"} Diameter: The Greeks then started another independent investigation with their three tools on the seemingly flat planar surface of the Earth. Using their dividers to strike a circle and using their straightedge congruent to the center of the circle, they were able with their scriber to strike a seemingly straight line through the center of construction of the circle. As the line passed out of the circle in either direction from the center, it seemingly could go on to infinity, and therefore was of no further interest to them. But inside the circle, as the line crossed the circumference at two points on either side of its center, they had the construction information that the line equated the opening of the dividers in two opposite directions. They called this line the diameter: DIA + METER.
[825.22]{style="color: purple3"} []{#ver:825.22 label="ver:825.22"} Now we will call the center of the constructed circle and the two intersections of the line and the circumference andB. That AD =DB is proven by construction. They know that any point on the circumference is equidistant from D. Using their dividers again and using point >1 as a pivot, they drew a circle around A; they drew a second circle using as a pivot. Both of these circles pass through D. The circle around A intersects the circle around at two points, and C. The circle around intersects the circle around at two points, and E. The circle around and the circle around are tangent to one another at the point D.
[825.23]{style="color: purple3"} []{#ver:825.23 label="ver:825.23"} They have now constructed four equilateral triangles in two pairs: ADC and ADC as the first pair, and DBS and DBE as the second pair. They know that the lines AC, CD, AC, and DC are all identical in length, being the fixed opening of the dividers and so produced and proven by construction. The same is true of the lines DE, EB, DE, and BE they are all the same. The Greeks found it a tantalizing matter that the two lines CE and CE, which lie between the vertexes of the two pairs of equilateral triangles, seemed to be equal, but there was no way for them to prove it by their construction.
[825.24]{style="color: purple3"} []{#ver:825.24 label="ver:825.24"} At first it seemed they might be able to prove that the increments CE and CE are not only equal to one another, but are equal to the basic radius of the circle AD; therefore, the hexagon ACEBEC would be an equilateral hexagon; and hexagons would be inherently subdivisible into six 60degree equilateral triangles around the central point, and all the angles would be of 60 degrees.
[825.25]{style="color: purple3"} []{#ver:825.25 label="ver:825.25"} There seemed to be one more chance for them to prove this to be true, which would have provided an equiangular, equiedged, triangularly stable structuring of areal mensuration. This last chance to prove it was by first showing by construction that the line ADB, which runs through the point of tangency of the circles A andB, is a straight line. This was constructed by the straightedge as the diameter of circle D. This diameter is divided by four equal half-radii, which are proven to be half-radii by their perpendicular intersection with lines both of whose two ends are equidistant from two points on either side of the intersecting lines. If it could be assumed that: (1) the lines CE and CE were parallel to the straight line ADB running through the point of tangency as well as perpendicular to both the lines CO and EE; and (2) if it could be proven that when one end between two parallels is perpendicular to one of the parallels, the other end is perpendicular to the other parallel; and (3) if it could be proven also that the perpendicular distances between any two parallels were always the same, they could then have proven CE = CD = DEDE, and their hexagon would be equilateral and equiradial with radii and chords equal.
¶ 825.26 Pythagorean Proof
[825.261]{style="color: purple3"} []{#ver:825.261 label="ver:825.261"} All of these steps were eventually taken and proven in a complex of other proofs. In the meantime, they were diverted by the Pythagoreans’ construction proof of “the square of the hypotenuse of a right triangle’s equatability with the sum of the squares of the other two sides,” and the construction proof that any non-right triangle’s dimensional values could be obtained by dropping a perpendicular upon one of its sides from one of its vertexes and thus converting it into two right triangles each of which could be solved arithmetically by the Pythagoreans’ “squares” without having to labor further with empirical constructs. This arithmetical facility induced a detouring of strictly constructional explorations, hypotheses, and proofs thereof.
[825.27]{style="color: purple3"} []{#ver:825.27 label="ver:825.27"} Due to their misassumed necessity to commence their local scientific exploration of geometry only in a supposed plane that extended forever without definable perimeter, that is, to infinity, the Ionians began using their right-triangle exploration before they were able to prove that six equilateral triangles lie in a circle around point D. They could divide the arithmetical 360 degrees of circular unity agreed upon into six 60-degree increments. And, as we have already noted, if this had been proven by their early constructions with their three tools, they might then have gone on to divide all planar space with equilateral triangles, which models would have been very convenient in connection with the economically satisfactory point-locating capability of triangulation and trigonometry.
[825.28]{style="color: purple3"} []{#ver:825.28 label="ver:825.28"} Euclid was not trying to express forces. We, however inspired by Avogadro’s identical-energy conditions under which different elements disclosed the same number of molecules per given volumeare exploring the possible establishment of an operationally strict vectorial geometry field, which is an isotropic (everywhere the same) vector matrix. We abandon the Greek perpendicularity of construction and find ourselves operationally in an omnidirectional, spherically observed, multidimensional, omni-intertransforming Universe. Our first move in spherical reality scribing is to strike a quasi-sphere as the vectorial radius of construction. Our dividers are welded at a fixed angle. The second move is to establish the center. Third move: a surface circle. The radius is uniform and the lesser circle is uniform. From the triangle to the tetrahedron, the dividers go to direct opposites to make two tetrahedra with a common vertex at the center. Two tetrahedra have six internal faces = hexagon = genesis of bow tie –genesis of modelability = vector equilibrium. Only the dividers and straightedge are used. You start with two eventsany distance apart: only one module with no subdivision; ergo, timeless; ergo, eternal; ergo, no frequency. Playing the game in a timeless manner. (You have to have division of the line to have frequency, ergo, to have time.)
[825.29]{style="color: purple3"} []{#ver:825.29 label="ver:825.29"} Commencing proof upon a sphere as representative of energy convergent or divergent, we may construct an equilateral triangle from any point on the surface. If we describe equilateral (equiangular) triangles whose chords are identical to the radii, the same sphere may be intersected alternately by four great-circle planes whose circles intercept each other, respectively, at 12 equidistant points in such a manner that only two circles intersect at any one point. As this system is described, each great circle becomes symmetrically subdivided into six equal-arc segments whose chords are identical to the radii. From this four-dimensional tribisection, any geometrical form may be described in whole fractions.
¶ 825.30 Two-Way Rectilinear Grid
[825.31]{style="color: purple3"} []{#ver:825.31 label="ver:825.31"} To the Greeks, a two-way, rectilinearly intersecting grid of parallel lines seemed simpler than would a three-way grid of parallel lines. (See Chapter 11, “Projective Transformation.”) And the two-way grid was highly compatible with their practical coordinate needs for dealing with an assumedly flat-plane Universe. Thus the Greeks came to employ 90-degreeness and unique perpendicularity to the system as a basic additional dimensional requirement for the exclusive, and consequently unchallenged, three-dimensional geometrical data coordination.
[825.32]{style="color: purple3"} []{#ver:825.32 label="ver:825.32"} Their arithmetical operations were coordinated with geometry on the assumption that first-power numbers represented linear module tallies, that second-power N2 = square increments, and that third-power N3 = cubical increments of space. First dimension was length expressed with one line. Two dimensions introduced width expressed with a cross of two lines in a plane. Three dimensions introduced height expressed by a third line crossing perpendicularly to the first two at their previous crossing, making a three-way, three-dimensional cross, which they referred to as the coordinate system. The most economical distance measuring between the peripheral points of such systems involved hypotenuses and legs of different lengths. This three-dimensionality dominated the 2,000-year scientific development of the c.gt.s. “Comprehensive Coordinate System of Scientific Mensurations.” As a consequence, identifications of physical reality have been and as yet are only awkwardly characterized because of the inherent irrationality of the peripheral hypotenuse aspects of systems in respect to their radial XYZ interrelationships.
[825.33]{style="color: purple3"} []{#ver:825.33 label="ver:825.33"} Commanded by their wealth-controlling patrons, pure scientists have had to translate their theoretical calculations of physical-system behaviors into coordinate relationship with physical reality in order to permit applied science to reduce theoretical inventions to physical practice and use. All of the analytic geometers and calculus mathematicians identify their calculus-derived coordinate behaviors of theoretical systems only in terms of linear measurements taken outwardly from central points of reference; they locate the remote event points relative to those centers only by an awkward set of perpendicularities emanating from, and parallel to, the central grid of perpendicular coordinates. The irrationality of this peripheral measuring in respect to complexedly orbited atomic nuclei has occasioned the exclusively mathematical processing of energy data without the use of conceptual models.
¶ 826.00 Unity of Peripheral and Radial Modularity
[826.01]{style="color: purple3"} []{#ver:826.01 label="ver:826.01"} Had the Greeks originally employed a universal model of x-dimensional reality as their first tool upon and within which they could further inscribe and measure with their divider, scriber, and straightedge, they would have been able to arrive at unity of circumferential as well as radial modularity. This would have been very convenient to modern physics because all the accelerations of all the constantly transforming physical events of Universe are distinguished by two fundamentally different forms of acceleration, angular and linear.
[826.02]{style="color: purple3"} []{#ver:826.02 label="ver:826.02"} Hammer Throw: When a man accelerates a weight on the end of a cord by swinging it around his head, the weight is restrained by the cord and it accumulates the energy of his exertions in the velocity it maintains in a circular pattern. This is angular acceleration, and its velocity rates and angular momentum are calculated in central-angle increments of the circular movement accomplished within given units of time. When the weight’s cord is released by its human accelerator, it then goes into linear acceleration and its accomplished distance is measured in time increments following its release and its known release velocity, which calculations are modified by any secondary restraints.
Fig. 826.02.
[826.02A]{style="color: purple3"} []{#ver:826.02A label="ver:826.02A"} Hammer Throw: The picture of the hammer throw and gyroscope appearing in Synergetics 1 was incomplete. The complete sequence of six line drawings appears here in revised Fig. 826.02A.
Fig. 826.02A Hammer Throw: The weight on the cord accumulates energy as the man swings it around his head in a circular pattern that illustrates angular acceleration. When the weight is released it goes into linear acceleration as modified by any secondary restraints.
[826.03]{style="color: purple3"} []{#ver:826.03 label="ver:826.03"} The angular accelerations relate then to the myriad of circular or elliptical orbitings of components of systems around their respective centers or focii, and are intimate to original acceleration-generating factors such as the “hammer thrower” himself and his muscle as the metabolic powering by the beef he ate the day before, which gained its energy from vegetation it had eaten, which gained its energy from the Sun’s radiation by photosynthesis–all of whose attendant relative efficiencies of energy relaying were consequent upon the relative design efficacies and energy divergence to complementary environment conditions of the total synergetically effective system with the eventually total regenerative Universe itself.[^28]
[826.04]{style="color: purple3"} []{#ver:826.04 label="ver:826.04"} Science as a Tool: The linear measurements represent the radial going-away accelerations or resultants of earlier or more remote events as well as of secondary restraints. The rigid rectilinear angularity of the 90degree-central-angle mensuration instituted by the Greeks made impossible any unit language of direct circumferential or peripheral coordination between angular and linear phenomena. As a consequence, only the radial and linear measurements have been available to physics. For this reason, physics has been unable to make simultaneous identification of both wave and particle aspects of energy events.
[826.05]{style="color: purple3"} []{#ver:826.05 label="ver:826.05"} The Greeks’ planar inception of geometry and its diversion first into theoretical mathematical calculations and ultimate abandonment of models has occasioned the void of ignorance now existing between the sciences and the humanities imposed by the lack of logical and unitarily moduled conceptual systems. This, in turn, has occasioned complete social blindness to either the facts or the potential benefits of science to humanity. Thus science has now come to represent an invisible monster to vast numbers of society, wherefore society threatens to jettison science and its “obnoxious” technology, not realizing that this would lead swiftly to genocide. Central to this crisis of terrestrially situate humans is the necessity for discovering and employing a comprehensively comprehendible universal coordinate system that will make it swiftly lucid to world society that science and technology are only manipulative tools like inanimate and cut-offable hands which may be turned to structuring or destructuring. How they are to be employed is not a function of the tools but of human choice. The crisis is one of the loving and longing impulse to understand and be understood, which results as informed comprehension. It is the will to structure versus ignorant yielding to fear-impulsed reflexive conditioning that results from being born utterly helpless. Intellectual information-accumulating processing and anticipatory faculties are necessary, and are only slowly discovered as exclusively able to overcome the ignorantly feared frustrating experiences of the past. Science must be seen as a tool of fundamental advantage for all, which Universe requires that man understand and use exclusively for the positive advantage of all of humanity, or humanity itself will be discarded by Universe as a viable evolutionary agent.
[826.06]{style="color: purple3"} []{#ver:826.06 label="ver:826.06"} It is to this dilemma that we address ourselves; not being interested in palliatives, we backtrack two and a half millennia to the turning of the road where we entered in the hope of regaining the highway of lucid rationality. Using the same Greek tools, but not starting off with a plane or the subsequently substituted blackboard of the pedagogues working indoors and deprived of direct access to the scratchable Earth surface used by the Near Eastern ancients[^29], we will now institute scientific exploration in the measurement of physical reality.
¶ 826.10 Otherness Restraints and Elliptical Orbits
[826.11]{style="color: purple3"} []{#ver:826.11 label="ver:826.11"} Angular acceleration is radically restrained accumulation of circular momentum, angular deceleration is the local depletion of angular momentum.
[826.12]{style="color: purple3"} []{#ver:826.12 label="ver:826.12"} Release from angular acceleration appears to be linear acceleration, but the linearity is only theoretical. Linear acceleration is the release from the restraint of the nearest accelerator to the angularly accelerative or decelerative restraint of the integrated vectorial resultant of all the neighboringly dominant, forever-otherness restraints in Universe. Linear acceleration never occurs, because there is no cosmic exemption of otherness.
[826.13]{style="color: purple3"} []{#ver:826.13 label="ver:826.13"} The hammer thrower releases his “hammer’s” ball-and-rod assembly from his extended arm’s-end grasp, seemingly allowing the hammer to take a tangentially linear trajectory, but Earth’s gravitational pull immediately takes over and converts the quasistraight trajectory into an elliptical arc of greater orbiting radius than before. But the arc is one of ever-decreasing radius as the Earth’s gravity takes over and the hammer thrower’s steel ball seemingly comes to rest on the Earth’s surface, which is, however, in reality traveling around the Earth’s axis in synchronized consonance with the other huddled together atoms of the Earth’s surface. Near the Earth’s equator this would be at a circular velocity of approximately 1000 miles an hour, but near the Earth’s poles the velocity would be only inches per hour around the Earth’s axis. Both Earth, hammer thrower, and thrown hammer are traveling at 60,000 miles an hour around the Sun at a radial restraint distance of approximately 92 million miles, with the galaxies of Universe’s other nonsimultaneously generated restraints of all the othernesses’ overlappingly effective dominance variations, as produced by degrees of neighboring energy concentrations and dispersions. It is the pulsation of such concentrations and dispersions that brings about the elliptical orbiting.
[826.14]{style="color: purple3"} []{#ver:826.14 label="ver:826.14"} This is fundamental complementarity as intuited in Einstein’s curved space prior to the scientific establishment of generalized complementarity, which we may now also speak of as the “generalized otherness” of Universe. This is why there can be only curved space. (See Sec. 1009.52.)
[826.15]{style="color: purple3"} []{#ver:826.15 label="ver:826.15"} Isaac Newton’s first law of motion, “A body persists in a state of rest or in a straight line except as affected by other forces,” should now be restated to say, “Any one considered body persists in any one elliptical orbit until that orbit is altered to another elliptical orbit by the ceaselessly varying interpositionings and integrated restraint effects imposed upon the considered body by the ever-transforming generalized cosmic otherness.” A body is always responding orbitally to a varying plurality of otherness forces.
¶ 830.00 Foldability of Great Circles
¶ 831.00 Sheet of Paper as a System
[831.01]{style="color: purple3"} []{#ver:831.01 label="ver:831.01"} Our steel dividers have sharp, straight-edged legs, each tapering into sharp points. We can call these dividers “scissors.” Scissors are dividers of either linear or angular, i.e. circular, differentiation. We can even make our explorations with some superficial accommodation of the Greeks’ propensity for using a plane. For instance, we can take a finite piece of paper, remembering (operationally), however, that it has “thickness” and “edges,” which are in fact small area faces. If it is a rectilinear sheet of typewriter paper, we recognize that it has four minor faces and two major faces. The major faces we call “this side” and “the other side,” but we must go operationally further in our consideration of what the “piece of paper” is. Looking at its edges with a magnifying glass, we find that those surfaces round over rather brokenly, like the shoulders of a hillside leading to a plateau. We find the piece of paper to be fundamentally the same kind of entity as that which we have watched the baker make as he concocts, stirs, and thickens his piecrust dough, which, after powdering with flour, can be formed into a spherical mass and set upon a flour-powdered surface to be progressively rolled into a thick sheet that may be cut into separate increments of the same approximate dimensions as the “sheet” of typewriter paper.
¶ 831.10 Moebius Strip
[831.11]{style="color: purple3"} []{#ver:831.11 label="ver:831.11"} In the same operational piecrust-making strictness of observation, we realize that the phase of topology that Moebius employed in developing his famous strip mistakenly assumed that the strip of paper had two completely nonconnected faces of such thinness as to have no edge dimension whatsoever. When we study the Moebius strip of paper and the method of twisting one of its ends before fastening them together and scribing and cutting the central line of the strip only to find that it is still a single circle of twice the circumference and half the width of the strip, we realize that the strip was just a partially flattened section of our piecrust, which the baker would have produced by making a long hard roll, thinner than a breadstick and flattened out with his wooden roller. What Moebius really did was to take a flattened tube, twist one of its ends 180 degrees, and rejoin the tube ends to one another. The scribed line of cutting would simply be a spiral around the tube, which made it clear that the two alternate ends of the spirals were joined to one another before the knifing commenced.
¶ Cutting Out Circular Cookies
[831.21]{style="color: purple3"} []{#ver:831.21 label="ver:831.21"} We can use the leverage of the sheet length of flatness of the paper against the fulcrum of the sheet of paper’s thinness to fold it as a relatively flat system, even as the baker could fold over the unbaked piecrust. Or we can scribe upon the paper with our geometrical tools in an approximately accurate measuring manner. What we have done is to flatten our system in a measurefully knowing manner. For operational accommodation, but always by construction, we can for the moment consider the papers surface as did the Greeks their infinitely extending plane, but we are aware and will always be responsible for “the rest of the system” with which we are working, though we are momentarily preoccupied with only a very local area of the whole.
[831.22]{style="color: purple3"} []{#ver:831.22 label="ver:831.22"} We can scribe a circle around the pivotal / -end of the dividers, and we can do so in an approximate “plane.” We can strike or scribe the approximately straight diameter through the circle’s center. We can now use our divider-scissors to divide the finite circle of paper from the finite balance of the paper system lying outside the circlethat is, we can scissor or “cut” out the area contained by the circle from the balance of the paper, as the baker cuts out circular, wafer-thin cookies. We are at all times dividing reality multidimensionally, no matter how relatively diminutive some of its dimensions may be.
[831.23]{style="color: purple3"} []{#ver:831.23 label="ver:831.23"} Because we are dealing with multidimensional reality, we must note operationally that in cutting out our circular piece of paper, we are also cutting our original piece of typewriter paper into two pieces, the other piece of which has a circular hole in its overall rectilinear area. We must keep ourselves conscious of this complementary consequence even though we are for the moment interested only in the cut-out circular piece pricked with the original center of the divider-generated circumference. (The Maori, whose prime love was the Pacific Ocean, looked upon islands as holes in their ocean and upon what man calls harbors or bays as protrusions of the ocean inserted into the land.) Now, from our cut-out circle and our inventory of construction-produced information, we learn experimentally that we can lift any point of the perimeter of the circle and fold it over so that the point of the perimeter is congruent with any other point on the perimeter; in doing so, we find that we are always folding the circular system of paper into two semicircles whose hinge lines always run through the points of origin.
[831.24]{style="color: purple3"} []{#ver:831.24 label="ver:831.24"} By construction, we can demonstrate that the circle of paper may be folded along its constructionally scribed diameter, and because all of its perimeter points are equidistant from the center of the circle, the semicircular edges are everywhere congruent. We find that we can fold the circle along any of its infinite number of diameters and the two half-circle circumferences (or perimeters = run arounds = racetracks) will always be congruent as folded together. The same infinity of diameters could be used to fold the paper-circle diameters in the opposite direction on the underside of the original plane.
[831.25]{style="color: purple3"} []{#ver:831.25 label="ver:831.25"} Having deliberately colored our original paper’s two opposite major sides with two different colors, red and white, we will see that our set of paper-circle folding along its infinity of diameters resulted in red half-circles, while the folding in the opposite direction produced all white half-circles. We also discover that as we fold from flat whole circle to congruence with the other half-circle, among any of the infinity of diameters along which to fold, the circumference of any one side of the circle moves toward the circumference on the other half, and as it travels 180 degrees around its diameter hinges, its perimeter thus describes a hemisphere of points all equidistant from the same center of all the hinges.
[831.26]{style="color: purple3"} []{#ver:831.26 label="ver:831.26"} Having worked from a unitary plane and employing the infinity of diameters to fold in opposite directions, we discover that all the combined red and white opposite semicircular foldings altogether have produced a sphere consisting of two complementary hemispheres, one red and one white, which altogether represent all the rotatings of the equidistant circumferences, always from the same common center of all the diameters, which fact we know by construction of the diameters by our straightedge along which we scribed through the original center mark of our generation of the circle.
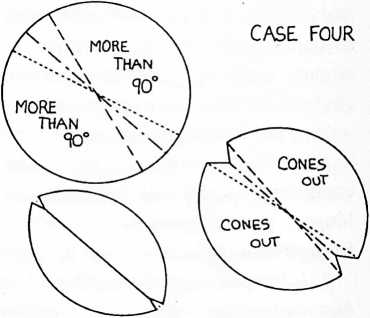
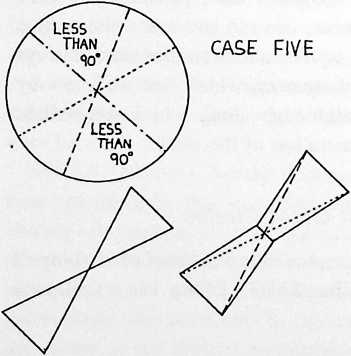
¶ 831.30 Six Cases of Foldability of Great Circles
[831.31]{style="color: purple3"} []{#ver:831.31 label="ver:831.31"} There are six cases of folding employed in the proof of sixthing of the circleor hexagoning the circle. (See Illus 831.31.) Case 1 is a limit case with congruence of all diameters.
Fig. 831.31 Foldability of Great Circles.
¶ 835.00 Bow-Tie Construction of Spherical Octahedron
[835.01]{style="color: purple3"} []{#ver:835.01 label="ver:835.01"} With one of the sharp points (A) of dividers (AB) fixed at a point (X) on a flat sheet of paper, sharp point is rotated cuttingly around until an equiradius circle of paper is cut out. It is discovered experimentally that if any point on the circular perimeter is folded over to any other point on the circle’s perimeter, that the circle of paper always folds in such a manner that one-half of its perimeterand one-half of its areais always congruent with the other half; and that the folded edge always runs through the exact center point X of the circle and constitutes a diameter line of the circle. This demonstrates that a diameter line always divides both the whole circular area and the circle’s perimeter-circumference into two equal halves. If one diameter’s end corner W of the circle, folded into halves, is folded over once more to congruence with the corner W at the other end of the diameter, once again it will be constructively proved that all of the circle’s perimeter is congruent with itself in four folded-together layers, which operational constructing also divides the whole circle into four equal parts, with the second folded diameter /-/ perpendicular to the first diameter, ergo producing four right-angled corners at the center of the circle as marked by the two diameter fold lines, W-W and Y-Y. If we now open the paper circle and turn it over to its reverse side, we fold in a third diameter line T-T by making circumference point W congruent with circumference point Y (which inadvertently makes point W congruent with /), we will find that we have exactly halved the right angles WXY and W XY, so that the perimeter distances WT or TY are each exactly half the perimeter distance WY, and either W T or TY are each one-half the perimeter distances of either WY, YW, W Y, or YW.
[835.02]{style="color: purple3"} []{#ver:835.02 label="ver:835.02"} If we now turn the paper circle over once more we find that the spring in the fold lines of the paper will make point and I" approach each other so that the whole circle once again may be folded flat to produce four congruent surfaces of the paper folded into an overall composite quarter circle with the two quarter-circle outer layers, and four one-eighth circle’s two inner layers coming to congruent fold-around terminal tangency at the midpoint and center of the folded, right-angle, quarter-circle packet, with W congruent with Y and W congruent with Y and congruent with T. Thus it is proven that with three diameter foldlines the whole circle can be subdividingly folded into six arc-and-central-angle increments, ergo also unfoldable again into wholecircle flatness. (See Illus. 835.02.)
[835.03]{style="color: purple3"} []{#ver:835.03 label="ver:835.03"} We know that every point on the perimeter of the folded semicircle is equidistant from the point of origin. We may now go to one end of the folded-edge diameter and fold the paper in such a manner that two ends of the diameter are congruent. This will fold the paper circle into four quadrants which, by construction congruence, are exactly equal. The legs of the 90degree angle formed around the origin of the circle by this second folding are the same in length, being the same radius as that of the circle, ergo, of the halved diameter produced by the second folding. The angle edges and the radii are identical. When we open the quarter-circle of four faces folded together into the semicircle, we find that the second fold edge, which produced the 90-degree angle, is the radius of the diameter perpendicular to the first diameter folded upon. The points where this perpendicular diameter’s ends intersect the circumference of the circle are equidistant, by construction, from the diameter ends of the first folded-edge diameter of the semicircle. This folded semicircle, with its secondary fold-mark of verticality to its origin, can be partially folded again on that perpendicular radius so that the partially folded semicircle and its partially folded, vertically impinging fold-line constitute an angularly winged unit, with appearance similar to the outer hard covers of a partially opened book standing bottomless with the book’s hard covers vertically perpendicular to a table. This flying-winged, vertically hinged pair of double-thickness quarter-circles will be found to be vertically stable when stood upon a table, that is, allowed to be pulled vertically against the table by gravity. In structural effect, this winged quarter-pair of open, standing “book covers” is a tripod because the two diameter ends, and B, and the circle’s origin point, C, at the middle represent three points, A, B, C, in triangular array touching the table, which act as a triangle base for the tripod whose apex is at the perimeter, T, of the semicircle at the top terminal of the vertical fold. The tripod’s legs are uneven, one being the vertical radius of the original circle, TC, and the other two being the equidistance chords, and b, running from the top of the vertical “book” column’s back and leading directly to the two wing terminals, and B, of the first folded diameter of the original circle. The weight of the paper on either side of the vertical fold extended on only one side of any line produces weight or gravitational effect to keep the vertical edge vertical, not allowing it to lean farther in the direction of the legs due to the relative structural rigidity of the paper itself.
[835.04]{style="color: purple3"} []{#ver:835.04 label="ver:835.04"} We will now take five additional pieces of paper, making six in all, producing the circles on each of the same radius with our dividers welded and using the scissor function of the dividers’ cuttingly ground straightedges. We cut the circles out and fold them in the manner already described to produce the vertically standing, angular interaction of the four quadrants of paper, standing as a vertically edged tripod with double thicknesses of the paper in arced flanges acting as legs to stabilize their verticality. We now have six such assemblies. We can take any two of them that are standing vertically and bring the vertical edges of their tripods together. (We know that they are the same size and that the vertical hinges are dimensionally congruent because they are all of the same radius length produced by the dividers.) We move two of their vertically folded edges into tangential congruence, i.e., back-to-back. The vertical perimeter terminals of their vertically folded hinges and their circle-center origins at the bottom of the hinges are congruent.
[835.05]{style="color: purple3"} []{#ver:835.05 label="ver:835.05"} To hold their vertical hinges together and to free our hands for other work, we slip a bobby pin over their four thicknesses of paper, holding their two angles together in the pattern of a cross as viewed vertically from above or below. This construction produces a quadripod. Now I can grasp this cross between two of my fingers inserted into the angles of the cross and lift it from the table, turning it upside down in my hands and finding the other side of the cross, all four lines of which are in the same (approximately flat) plane, in contradistinction to the way the cross looked when those four folded edges sat on the table and had four arcing lines running in four different directions from their vertical congruence. I will insert a bobby pin to hold together the cross at its folded-line intersection. With its flat cross down, it will now stand as the partial profiling of a hemisphere. When I put the arced cross down on the table, it will roll around as would half a wooden ball. Placing it on the table in this roll-around hemisphere attitude, I can stabilize it with underprops so that the plane of four folded edges coming together on top will be approximately horizontal and parallel to the table top.
[835.06]{style="color: purple3"} []{#ver:835.06 label="ver:835.06"} I may now take one of the four additional quadri-folded, partially opened, hinged, quarter-circle, double-thickness assemblies first described as able to stand vertically by themselves. Each of the four can be made to stand independently with one of its 90-degree, quarter-circle wings lying horizontally on the table and its other quarter-fold wing standing approximately vertically. The four quarter-circles on the table can be slid together to form a whole circle base; bobby pins can be inserted at their four circumference terminals to lock them together in a circle; and their four approximately vertical flanges can be hinged into true verticality so that they form two half-circle arcs, passing through one another perpendicularly to one another. They will have a common vertical radius (by construction) at the common top terminal, and all of their four vertical hinges’ two crossing bobby pins can be inserted to lock this vertex together. This assembly of four of the six units with circular base can now be superimposed upon the first pair of hinges sitting on the table with hemisphere down and its planar cross up. The four cross ends of that first assembly can be hinged around into congruence with the 90degree circumference points of the top assembled four units, with everything firmly congruent by construction.
[835.07]{style="color: purple3"} []{#ver:835.07 label="ver:835.07"} We will now take bobby pins and fasten the folded flanking edge ends of the top-four assembly congruent with each of the four edges of the hemispherical cross group on the table.
[835.08]{style="color: purple3"} []{#ver:835.08 label="ver:835.08"} Fastened by bobby pins at the congruent perimeter terminals of the folded cross lines, this top assembly stabilizes the previously unstable angular space between any two of the cross-forming hemispherical groups propstabilized, bowl down, with the plane of its four-way hinge cross horizontal and parallel to the table. The angle between any two of the horizontally crossed assembly members is now stabilized at exactly one-quarter of a circle by the integrity of construction procedures of our experiment. This produces one complete horizontal circle with 90-degree triangular webbing of doublefolded paper perpendicular to two other perpendicularly intersecting vertical circles, each of which also consist of four 90-degree triangular webs of double-thickness paper, each of all 12 of which 90-degree triangular webs structurally stabilizes the six radial hinges of the three axes of this spherically profiled system assembly, prop-stabilized not to roll on the table.
[835.09]{style="color: purple3"} []{#ver:835.09 label="ver:835.09"} In effect, we have the original six circular pieces reassembled with one another as two sets of three circles symmetrically intercepting one another. We know that each of the six-quadrantly folded units fit into the remaining angular spaces because, by construction, each of the angles was folded into exactly one-quarter of a circle and folded together exactly to complete their circle. And we know that all the radial hinges fit together because they are constructionally of equal length. We have now a triangularly stabilized structure constituting what is called the spherical octahedron. Its vertical axis has polar terminals we call north and south. South is congruent with the table, and north is at the apex of the assembly. It has four equatorial points lying in a plane horizontal to the table. It is called the spherical octahedron because it has an external pattern subdivided exactly, evenly, and symmetrically by eight spherical triangles, four in the northern hemisphere and four in the southern hemisphere.
[835.10]{style="color: purple3"} []{#ver:835.10 label="ver:835.10"} We find that the construction has three distinct planes that are all symmetrical and perpendicular to one another; the horizontal equatorial plane and two vertical planes intersect each other on the north-south polar axis perpendicularly to one another, which perpendicularity is constructurally inherent. Each of the perpendicularly intersecting great circles is seen to be of a double thickness due to the folding of the six original paper great circles, which now appear, deceptively, as three, but are not continuous planes, being folded to make their hinges congruent. (See illus. 835.10.)
[835.11]{style="color: purple3"} []{#ver:835.11 label="ver:835.11"} The spherical octahedron provides the basis for the frame of reference of the constructionally proven verticality of its axis in respect to its equatorial plane and the equidistance of the poles from all the perimeter points. (See Illus. 835.11.)
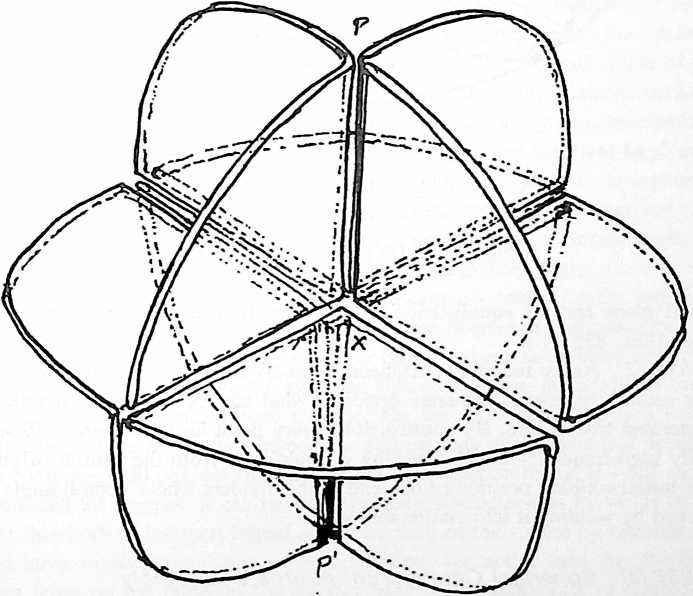
Fig. 835.10 Six Great Circles Folded to Form Octahedron.
Fig. 835.11 The Spherical Octahedron.
[835.12]{style="color: purple3"} []{#ver:835.12 label="ver:835.12"} As we rotate this octahedron rapidly on any one of its three axes, the rotated perimeters generate optically what can be called a dynamically generated true sphere. By construction, every point on the sphere’s dynamically high-frequency event-occurring is equidistant from the central origin–our initial scribing position of one end of the dividers whose central angle we locked by welding it into unalterability.
¶ 836.00 Spherical Octahedron: Alternate Assembly
[836.01]{style="color: purple3"} []{#ver:836.01 label="ver:836.01"} In addition to the foregoing operational development of the octahedron, we discover that the assembling of the spherical octahedron called for a fundamental asymmetry of procedure. That is, we assemble two of its quadrantly folded great circles to form one hemisphere and four of the quadrantly folded great circles to form the other hemisphere. In this method, the equator has to be included in either the northern or the southern hemisphere.
[836.02]{style="color: purple3"} []{#ver:836.02 label="ver:836.02"} Therefore, in attempting to find some other method of assembly, we find that the spherical octahedron can be alternatively assembled in three sets of two quadrantly folded great circles. This is done by following all of the general procedures for developing the six quadrantly folded circles and their stand-up-ability as open book backs, producing a tripoding stability with the angle hinged by the variability of the vertical book-back spine.
[836.03]{style="color: purple3"} []{#ver:836.03 label="ver:836.03"} We will now make three pairs of these valiantly angled, quadrantly folded circles. We find that instead of standing one of them as a book with its hinge-spine vertical, the book can be laid with one of its faces parallel to the table and the other pointing approximately vertically, outward from the table. Due to the relative inflexibility of the double-folded angle of the great-circle construction paper, the book can be laid on its front face or its back face. We will take two of them sitting on the front face of the book with their backs reaching outwardly, vertically away from the table. We move two in front of us, one right and one left. We will rotate the right-hand one counterclockwise, 90 degrees around its vertical axis. Then we move the quadrant angle of the right-hand one into congruence with the quadrant angle of the left-hand one. We stabilize the variable angle of the right-hand one between its vertical and horizontal parts by fastening with two bobby pins the constructionally produced stable quadrant of the folded parts of the right-hand unit. This gives us a constructionally proven one-eighth of a sphere in an asymmetrical assembly, having the 180-degree axis of the sphere lying congruent with the table. On one end of the axis, we have the stabilized quadrant angle; on the other end of the axis, we have the open, unstabilized angle.
[836.04]{style="color: purple3"} []{#ver:836.04 label="ver:836.04"} With the other four of our six quadrantly folded circles, we make two more paired assemblies in exactly the same manner as that prescribed for the first paired assembly. We now have three of these assemblies with their axes lying on the table; on the left-hand side of all three, there will be found the stabilized, spherical-octant triangle. On the left side, there is a folded quadrant, where the angle between the vertical axis of the spherical octant is approximately 90 degrees from the folded axis lying on the tablebut an unstabilized 90 degrees; it can be stabilized into 90-degreeness by virtue of the fact that both of its open folded edges are radii of the sphere by construction and have an accommodating, open hinge-line. We notice then that the three axes lying on the table, as the interior edge of the semicircle of double-ply folded paper, represent the three axes of the octahedron as well as the 90-degree coordinates of the international scientific standards of comprehensive mensurationas, for instance, theX axis represents the height, Y the width, and Z the breadth. Geographically, this would represent the north and south poles and the four perpendicular quadrants of the equator.
[836.05]{style="color: purple3"} []{#ver:836.05 label="ver:836.05"} Our operational-construction method employs the constant radius and identifies every point on the circumference and every point on the internal radii. This is in contradistinction to analytic geometry, in which the identification is only in terms of the coordinates and the perpendiculars to them. Analytic geometry disregards circumferential construction, ergo, is unable to provide for direct identification of angular accelerations.
[836.06]{style="color: purple3"} []{#ver:836.06 label="ver:836.06"} These three subassemblies of the six folded quadrants are inherently asymmetrical. It was the fundamental asymmetry that made it possible to make the spherical octahedron with only three whole circles of paper, but we found it could only be accomplished symmetrically with six quadrantly folded great circles, with the symmetry being provided by the duality, by the twoness.
[836.07]{style="color: purple3"} []{#ver:836.07 label="ver:836.07"} All three assemblies are identically asymmetric. The loaded XYZ axes hold the Y axis vertically. Pick up the Y axis and turn it 90 degrees to the X axis. This brings one of the stabilized quadrants of the Y axis into congruence with one of the nonstabilized quadrants of the X axisto stabilize it. With the Y axis now at 90 degrees to the X axis, we can fasten the two assemblies into place with bobby pins.
[836.08]{style="color: purple3"} []{#ver:836.08 label="ver:836.08"} Take the Z axis assembly and hold it so that it is perpendicular to both the X and Y axes; this will bring the three constructionally proven folded quadrangles into congruence with the three folded, as yet unstabilized, 90degree sinuses of the X and Y axis assemblies.
¶ 840.00 Foldability of Four Great Circles of Vector Equilibrium
¶ 841.00 Foldability Sequence
[841.11]{style="color: purple3"} []{#ver:841.11 label="ver:841.11"} Using the method of establishing perpendiculars produced by the overlapping of unit-radius circles in the first instance of the Greeks’ exclusively one-planar initiation of their geometry (see Illus. 455.11), a diameter PP perpendicular to the first straightedge constructed diameter DD can be constructed. If we now fold the paper circles around DD and PP, it will be found that every time the circles are folded, the points where the perpendicular to that diameter intercept the perimeter are inherently congruent with the same perpendicular’s diametrically opposite end.
[841.12]{style="color: purple3"} []{#ver:841.12 label="ver:841.12"} The succession of positive and negative foldings in respect to the original plane folded around a plurality of diameters of that plane will define a sphere with inherent poles P and P, which occur at the point of crossing of the rotated perpendiculars to the folded-upon diameters, thePP points being commonly equidistant from the first prime, as yet unfolded circle cut out from the first piece of paper. This constructional development gives us a sphere with a polar axis PP perpendicular to the original plane’s circle at the center of that circle. We can also fold six great circles of unit radius, first into halfcircle, 180-degree-arc units, and then halve-fold those six into 90-degree “bookends,” and assemble them into a spherical octahedron with three axes, and we can rotate the octahedron around axisPP and thus generate a spherical surface of uniform radii.
[841.13]{style="color: purple3"} []{#ver:841.13 label="ver:841.13"} We could also have constructed the same sphere by keeping point of the dividers at one locus in Universe and swinging point in a multiplicity of directions around (see Illus. 841.15). We now know that every point on the surface of an approximate sphere is equidistant from the same center. We can now move point of the dividers from the center of the constructed sphere to any point on the surface of the sphere, but preferably to point P perpendicular to an equatorially described plane as in 841.11 and 841.12. And we can swing the free point to strike a circle on the surface of the sphere around point P. Every point in the spherical surface circle scribed by is equidistant chordally from A which is pivotally located atP, that is, as an apparently straight line from passing into and through the inside of the spherical surface to emerge again exactly in the surface circle struck by B, which unitary chordal distance is, by construction, the same length as the radius of the sphere, for the opening of our divider’s ends with which we constructed the sphere was the same when striking the surface circle around surface point A.
[841.14]{style="color: purple3"} []{#ver:841.14 label="ver:841.14"} We now select any point on the spherical surface circle scribed by point of the dividers welded at its original radius-generating distance with which we are conducting all our exploration of the spheres and circles of this operational geometry. With point of the dividers at the north-polar apex, of the spherical octahedron’s surface, which was generated by rotating the symmetrical assembly of six 90-degree, quadrangularly folded paper circles. Axis PP is one of its three rectilinearly interacting axes as already constructively described.
[841.15]{style="color: purple3"} []{#ver:841.15 label="ver:841.15"} We now take any point, J, on the spherical surface circle scribed by the divider’s point around its rotated point at P. We now know that A’ is equidistant chordally from P and from the center of the sphere. With point of our dividers on J, we strike point on the same surface circle as J, which makes J equidistant from K, P, and X, the center of the sphere. Now we know by construction integrity that the spherical radii XJ, XK, and XP are the same length as one another and as the spherical chords PA, JK, and JP. These six equilength lines interlink the four points X, P, J, and to form the regular equiedged tetrahedron. We now take our straightedge and run it chordally from point J to another point on the same surface circle on which JK and are situated, but diametrically opposite K. This diametric positioning is attained by having the chord-describing straightedge run inwardly of the sphere and pass through the axis PP, emerging from the sphere at the surface-great-circle point R. With point of the dividers on point R of the surface circle–on which also lies diametrically point Kwe swing point of the dividers to strike point also on the same spherical surface circle around P, on which now lie also the points , and/?, with points diametrically opposite J, as is known by construction derived information. Points R, S, P, and X now describe another regular tetrahedron equiedged with tetrahedron JKPX; there is one common edge, PX, of both tetrahedra. PX is the radius of the spherical, octahedrally constructed sphere on whose surface the circle was struck around one of its three perpendicularly intersectioned axes, and the three planes through them intersect congruently with the three axes by construction. PX is perpendicular to the equatorial plane passing through W, Y, W, Y of the spherical octahedron’s three axes PP, WW, and YY.
Fig. 841.15A Realization of Four Great Circles of Vector Equilibrium.
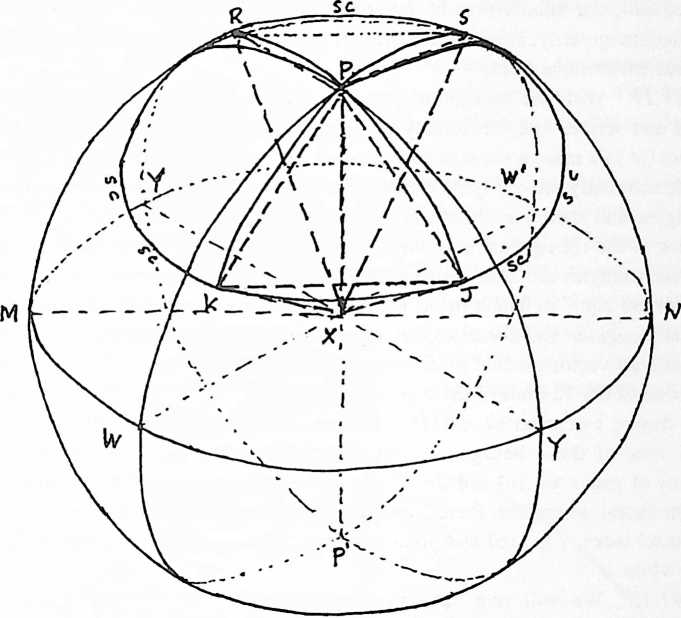
Fig. 841.15B Fixed Radius Striking a Small Circle on the Surface of a Sphere.
[841.16]{style="color: purple3"} []{#ver:841.16 label="ver:841.16"} We may now take the congruent radius edgePX of the two tetrahedra and separate it into the two radii (PX)1 and (PX)2 and rotate their two P ends (PM) and (PN), away from one another around the sphere’s center, X, until (PM) and (PX) are diametrically opposite one another. Therefore, points (PM) and (PN) are now lying in the octahedron’s equatorial plane WXWY. We may now rotate points J, K, R, and 5 around the (PM), X (PN) axis until points J, K, R, and S all lie in the octahedral plane WY W X, which converts the opened unitary construction first into a semifolded circle and then into a circle congruent with the octahedron’s equatorial plane, all of which six- hinged transformation was permitted as all the seven points (PM), J, K, (PN) , S, R, Xwere at all times equidistant from one another, with no restraints placed on the motion. We now have the hexagonally divided circle as a constructionally proven geometrical relationship; and therefore we have what the Greeks could not acquire: i.e., a trisected 180-degree angle; ergo a six-equiangular subdivision of spherical unity’s 360 degrees into 60-degree omniequiangularity; ergo a geometrically proven isotropic vector matrix operational evolvement field.
[841.17]{style="color: purple3"} []{#ver:841.17 label="ver:841.17"} With our operationally considerate four tools of divider, straightedge and scriber and measurably manipulable scribable system as a material object (in this case, a sheet of paper; later, four sheets of paper), and with our constructionally proven symmetrical subdivision of a circle into six equilateral triangles and their six chord-enclosed segments, we now know that all the angles of the six equilateral triangles around center X are of 60 degrees; ergo, the six triangles are also equiangular. We know that the six circumferential chords are equal in length to the six radii. This makes it possible to equate rationally angular and linear accelerations, using the unit-radius chord length as the energy-vector module of all physical-energy accelerations. We know that any one of the 12 lines of the equilaterally triangled circle are always either in 180-degree extension of, or are parallel to, three other lines. We may now take four of these hexagonally divided circles of paper. All four circular pieces of paper are colored differently and have different colors on their opposite faces; wherefore, there are eight circular faces in eight colors paired in opposite faces, e.g., red and orange, yellow and green, blue and violet, black and white.
[841.18]{style="color: purple3"} []{#ver:841.18 label="ver:841.18"} We will now take the red-orange opposite-faced construction paper circle. We fold it first on its (PM)-(PN) axis so that the red is hidden inside and we see only an orange half-circle’s two-ply surface. We next unfold it again, leaving the first fold as a crease. Next we fold the circle on its RX axis so that the orange face is inside and the red is outside the two-ply, halfcircled foldup. We unfold again, leaving two crossing, axially folded creases in the paper. We next fold the same paper circle once more, this time along its JS axis in such a manner that the orange is inside and once again only the red surface is visible, which is the two-ply, half-circle folded condition.
[841.19]{style="color: purple3"} []{#ver:841.19 label="ver:841.19"} We now unfold the red-orange opposite-faced colored-paper circle, leaving two positive and one negative creases in it. We will find that the circle of paper is now inclined by its creases to take the shape of a double tetrahedron bow tie, as seen from its openings end with the orange on the inside and the red on the outside. We may now insert a bobby pin between points (PM) and (PN), converting this hexagonally subdivided and positivelynegatively folded circle back into the mutually congruent PX edge, two (hinge-bonded, bivalent) tetrahedra: JKPX and RSPX.
[841.20]{style="color: purple3"} []{#ver:841.20 label="ver:841.20"} We may now fold the other three circles into similar, edgebonded, tetrahedral bow-tie constructions in such a manner that number two is yellow outside and green inside; number three of the 60-degree-folded bowties is blue outside and violet inside; and the fourth bow tie, identical to the other three bow ties’ geometrical aspects of 60-degree equiangularity and equiradius chord edges, is black outside and white inside.
[841.21]{style="color: purple3"} []{#ver:841.21 label="ver:841.21"} We may take any two of these bow tiessay, the orange inside and the green insideand fasten each of their outside corners with bobby pins, all of their radii being equal and their hinges accommodating the interlinkage.
[841.22]{style="color: purple3"} []{#ver:841.22 label="ver:841.22"} Each of these paired bow-tie assemblies, the orange-green insiders and the violet-white insiders, may now be fastened bottom-to-bottom to each other at the four external fold ends of the fold cross on their bottoms, with those radial crosses inherently congruent. This will reestablish and manifest each of the four original circles of paper, for when assembled symmetrically around their common center, they will be seen to be constituted of four great circles intersecting each other through a common center in such a manner that only two circular planes come together at any other than their common centerpoint and in such a manner that each great circle is divided entirely into six equilateral triangular areas, with all of the 12 radii of the system equilengthed to the 24 circumferential chords of the assembly. Inasmuch as each of the 12 radii is shared by two great circle planes, but their 24 external chords are independent of the others, the seeming loss of 12 radii of the original 24 is accounted for by the 12 sets of congruent pairs of radii of the respective four hexagonally subdivided great circles. This omniequal line and angle assembly, which is called the vector equilibrium, and its radii-chord vectors accommodate rationally and simultaneously all the angular and linear acceleration forces of physical Universe experiences.
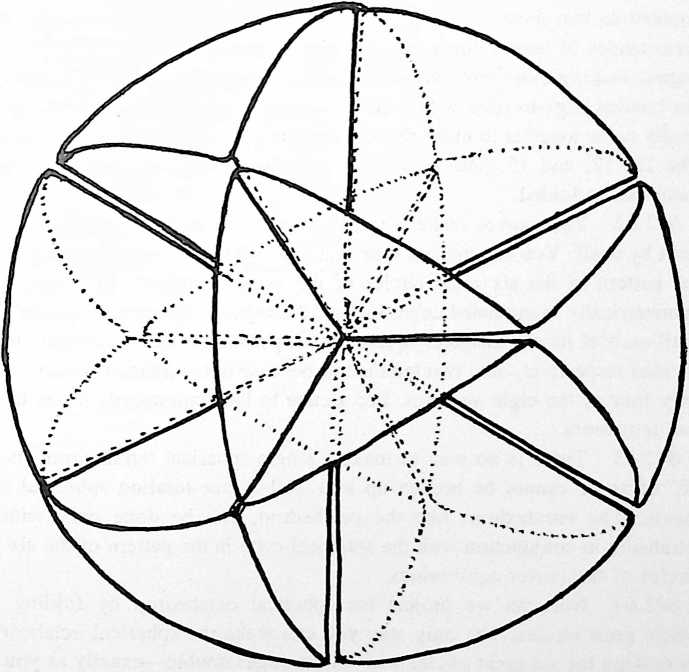Fig. 841.22 Foldability of Four Great Circles of Vector Equilibrium.
¶ 841.30 Trisection by Inherent Axial Spin of Systems
[841.31]{style="color: purple3"} []{#ver:841.31 label="ver:841.31"} The 12 great circles of the vector equilibrium’s hemispherical self-halvings inherentlyand inadvertentlycentrally trisect each of the vector equilibrium’s eight equiangle spherical triangles, centrally subdividing those triangles into twelve 30-degree angles.
Fig. 841.30 Trisection by Inherent Axial Spin: The 12 great circles of the vector equilibrium inherently trisect each of its eight equiangular faces, centrally subdividing each of them into twelve 30-degree angles.
¶ 842.00 Generation of Bow Ties
[842.01]{style="color: purple3"} []{#ver:842.01 label="ver:842.01"} When we consider the “jitterbug” vector equilibrium contracting into the icosahedron, bearing in mind that it is all double-bonded, we discover that, when the jitterbug gets to the octahedron phase, there really are two octahedra there. …Just as when you get three great circles, each one is doubled so that there are really six. …In making my tests, taking whole great circles of paper, doing my spherical trigonometry, learning the central angles, making those bow ties as a complex, which really amounts to tetrahedra bonded edge-to-edge with a common center, they link up as a chain and finally come together to make the icosahedron in a very asymmetrical manner. The 10, 12, and 15 great circles re-establish themselves, and every one of them can be folded.
[842.02]{style="color: purple3"} []{#ver:842.02 label="ver:842.02"} You cannot make a spherical octahedron or a spherical tetrahedron by itself. You can make a spherical cube with two spherical tetrahedra in the pattern of the six great circles of the vector equilibrium. It becomes a symmetrically triangulated cube. In fact, the cube is not structurally stabilized until each of its six unstable, square-based, pyramidal half-octahedra are subdivided respectively into two tetrahedra, because one tetrahedron takes care of only four of the eight vertexes. For a cube to be triangulated, it has to have two tetrahedra.
[842.03]{style="color: purple3"} []{#ver:842.03 label="ver:842.03"} There is no way to make a single spherical tetrahedron: its 109 of angle cannot be broken up into 360-degree-totaling spherical increments. The tetrahedron, like the octahedron, can be done only with two tetrahedra in conjunction with the spherical cube in the pattern of the six great circles of the vector equilibrium.
[842.04]{style="color: purple3"} []{#ver:842.04 label="ver:842.04"} Nor can we project the spherical octahedron by folding three whole great circles. The only way you can make the spherical octahedron is by making the six great circles with all the edges doubleexactly as you have them in the vector equilibriumas a strutted edge and then it contracts and becomes the octahedron.
[842.05]{style="color: purple3"} []{#ver:842.05 label="ver:842.05"} There is a basic cosmic sixness of the two sets of tetrahedra in the vector equilibrium. There is a basic cosmic sixness also in an octahedron minimally-great-circle-produced of six great circles; you can see only three because they are doubled up. And there are also the six great circles occurring in the icosahedron. All these are foldable of six great circles which can be made out of foldable disks.
[842.06]{style="color: purple3"} []{#ver:842.06 label="ver:842.06"} This sixness corresponds to our six quanta: our six vectors that make one quantum.
[842.07]{style="color: purple3"} []{#ver:842.07 label="ver:842.07"} There are any number of ways in which the energy can go into the figure-eight bow ties or around the great circle. The foldability reveals holdings patterns of energy where the energy can go into local circuits or go through the points of contact.