¶ 400.00 System
¶ 400.01 Definition: System
[400.011]{style="color: purple3"} []{#ver:400.011 label="ver:400.011"} A system is the first subdivision of Universe. It divides all the Universe into six parts: first, all the universal events occurring geometrically outside the system; second, all the universal events occurring geometrically inside the system; third, all the universal events occurring nonsimultaneously, remotely, and unrelatedly prior to the system events; fourth, the Universe events occurring nonsimultaneously, remotely, and unrelatedly subsequent to the system events; fifth, all the geometrically arrayed set of events constituting the system itself; and sixth, all the Universe events occurring synchronously and or coincidentally to and with the systematic set of events uniquely considered.
[400.02]{style="color: purple3"} []{#ver:400.02 label="ver:400.02"} A system is the first subdivision of Universe into a conceivable entity separating all that is nonsimultaneously and geometrically outside the system, ergo irrelevant, from all that is nonsimultaneously and geometrically inside and irrelevant to the system; it is the remainder of Universe that conceptually constitutes the system’s set of conceptually tunable and geometrical interrelatability of events.
[400.03]{style="color: purple3"} []{#ver:400.03 label="ver:400.03"} Conceptual tuning means occurring within the optical “rainbow” range of human’s sensing within the electromagnetic spectrum and wherein the geometrical relationships are imaginatively conceivable by humans independently of size and are identifiable systematically by their agreement with the angular configurations and topological characteristics of polyhedra or polyhedral complexes.
[400.04]{style="color: purple3"} []{#ver:400.04 label="ver:400.04"} All systems are polyhedra. Systems having insideness and outsideness must return upon themselves in a plurality of directions and are therefore interiorally concave and exteriorally convex. Because concaveness reflectively concentrates radiation impinging upon it and convexity diffuses radiation impinging upon it, concavity and convexity are fundamentally different, and therefore every system has an always and only coexisting inward and outward functionally differentiated complementarity. Any one system has only one insideness and only one outsideness.
[400.05]{style="color: purple3"} []{#ver:400.05 label="ver:400.05"} In addition to possessing inherent insideness and outsideness, a system is inherently concave and convex, complex and finite. A system may be either symmetrical or asymmetrical. A system may consist of a plurality of subsystems. Oneness, twoness, and threeness cannot constitute a system, as they inherently lack insideness and outsideness. Twoness constitutes wavilinear relatedness. Threeness constitutes planar relatedness, which is inherently triangular. Three triangular planes alone cannot differentiate, distinguish, or constitute a system. At minimum, it takes four triangular planes having inherent fourness of vertexes to constitute differential withinness and withoutness. Fourness of geometrically contiguous and synchronous event foci and their coincidentally defined four triangular planes, along with their six common edges provided by the six wavilinear vectors connecting the four event foci, altogether inherently differentiate, distinguish, initially institute, and constitute prime or minimum withinness and withoutness.
[400.06]{style="color: purple3"} []{#ver:400.06 label="ver:400.06"} Thought is systemic. Cerebration and intellection are initiated by differential discernment of relevance from nonrelevance in respect to an intuitively focused-upon complex of events which also intuitively suggests inherent and potentially significant system interrelatedness.
[400.07]{style="color: purple3"} []{#ver:400.07 label="ver:400.07"} Human thoughts are always conceptually and definitively confined to system considerability and comprehension. The whole Universe may not be conceptually considered by thought because thinkability is limited to contiguous and contemporary integrity of conformation of consideration, and Universe consists of a vast inventory of nonsynchronous, noncontiguous, noncontemporary, noncoexisting, irreversibly transforming, dissimilar events.
[400.08 Unit]{style="color: purple3"} []{#ver:400.08 Unit label="ver:400.08 Unit"} means system integrity. Organic means regenerative system integrity. As minimum or prime systems consist of four event foci and their always and only coexisting fourness of triangularly defined planar facets, along with their sixness of a wavilinearly defined minimum set of unique componentation relatedness, unity is inherently plural. Unity is plural. A system is a local phenomenon in the Universe. Each of the conceivable or imaginable awareness or thinkability entities or phenomena inducing or producing onenesses or twonesses are subvisible and potentially further subdivisible, or as yet unresolved, ergo unrecognized systems. Functions always and only co-occur as subsystem relativistics, characteristics, inherencies, and proclivities. Functions occur only as parts of systems. Universe is constituted of a complex plurality of nonsimultaneous and only partially overlappingly occurring systems, not one system.
[400.09]{style="color: purple3"} []{#ver:400.09 label="ver:400.09"} All the interrelationships of system foci are conceptually represent able by vectors (see Sec. 521). A system is a closed configuration of vectors. It is a pattern of forces constituting a geometrical integrity that returns upon itself in a plurality of directions. Polyhedral systems display a plurality of polygonal perimeters, all of which eventually return upon themselves. Systems have an electable plurality of view-induced polarities. The polygons of polyhedra peregrinate systematically and sometimes wavilinearly around three or more noncongruent axes.
[400.10]{style="color: purple3"} []{#ver:400.10 label="ver:400.10"} Absolutely straight lines or absolutely flat planes would, theoretically, continue onwardly or spread areally outward to infinity. The difference between infinity and finity is governed by the taking out of angular sinuses, like pieces of pie cut out of surface areas around a point in an otherwise absolute and infinitely extendable plane, and joining together the open gap’s radial edges. This is the way lampshades and skirts are made. Joining the sinused fan-edges together makes a cone. If two cones are made and their respective open circle edges are brought together, a finite or closed system results. It has two poles and two polar domains. The two poles and their polar cone surface domains, as well as the defined insideness and outsideness, are inherent and primary characteristics of all systems.
[400.11]{style="color: purple3"} []{#ver:400.11 label="ver:400.11"} All systems are continually importing as well as exporting energy. Physics has found only myriad pattern integrities of comprehensively nonsimultaneous and only partially overlapping evolution; of disintegrative “heres” and reintegrative “theres,” which are omnilocal vari-intertransformabilities of limited duration identities of an apparently eternal, physical Universe regenerating mathematically treatable energy quanta.
[400.20]{style="color: purple3"} []{#ver:400.20 label="ver:400.20"} Comprehensibility of Systems: All systems are subject to comprehension, and their mathematical integrity of topological characteristics and trigonometric interfunctioning can be coped with by systematic logic.
[400.21]{style="color: purple3"} []{#ver:400.21 label="ver:400.21"} A system is the antithesis of a nonsystem. A nonsystem lacks omnidirectional definition. Nonsystems such as theoretical planes or straight lines cannot be found experimentally. We are scientifically bound to experientially discovered and experimentally demonstrable systems thinking.
[400.22]{style="color: purple3"} []{#ver:400.22 label="ver:400.22"} General systems theory treats with phenomena that are holistically comprehensible. The objects of our experience are finite systems. Their superficial outlines close back upon themselves multidirectionally as a systematic continuity of relevantly contiguous events.
[400.23]{style="color: purple3"} []{#ver:400.23 label="ver:400.23"} Maximum system complexity consists of a dissimilarly quantified inventory of unique and nonintersubstitutable components. That is, Euler’s irreducible-system aspects of vertexes, areas, and edges exhibit the respective dissimilar quantities [4, 4,]{style="color: purple3"} []{#ver:4, 4, label="ver:4, 4,"} and 6 in the minimum prime system, the tetrahedron. This demonstrates the inherent synergy of all systems, since their minimum overall inventory of inherent characteristics is unpredicted and unpredictable by any of the parts taken separately. Systems are unpredicted by oneness, twoness, or threeness. This explains how it happens that general systems theory is a new branch of science.
[400.24]{style="color: purple3"} []{#ver:400.24 label="ver:400.24"} General systems theory is another example of evolution by inadvertence. It developed fortuitously to accommodate the unprecedented and vastly complex undertakings of the late twentieth century, such as the 10 million separate and only partially overlapping “critical path,” tasks that had to be accomplished and tested to foolproof reliability en route to countdown to eventual blastoff, Moon landing, and safe return to Earth, which found all conventional mathematical theory wanting. It required the development of the computer and star-focused instruments and computer programming arts together with operational research, which guess-improvises the inventory of parameter of variables that must be progressively programmed into the system in order further to reduce the magnitude of tolerated errors consequent to trial “bird” (rocket vehicle) “flight” (trajectory) control as the vehicles are progressively zeroed-in to progressive target rendezvous with celestial entities. Neither differential and integral calculus, nor “probability” statistics, nor any branch of specialized hard science has accredited synergy as an a priori assumption. General systems theory, which recognizes synergy as inherent, was discovered and named by the biologically inspired Ludwig von Bertalanffy.
[400.25]{style="color: purple3"} []{#ver:400.25 label="ver:400.25"} Every system, as a subdivision of the total experience of Universe, must accommodate traffic of inbound and outbound events and inward-outward relationships with other systems’ aspects of Universe. Effective thinking is systematic because intellectual comprehension occurs only when the interpatternings of experience events’ star foci interrelationships return upon themselves. Then the case history becomes “closed.” A system is a patterning of enclosure consisting of a conceptual aggregate of recalled experience items, or events, having inherent insideness, outsideness, and omniaroundness.
[400.26]{style="color: purple3"} []{#ver:400.26 label="ver:400.26"} Systems are aggregates of four or more critically contiguous relevant events having neither solidity nor surface or linear continuity. Events are systemic.
[400.30]{style="color: purple3"} []{#ver:400.30 label="ver:400.30"} Tigers Skin: Typical of all finitely conceptual objects, or systems, the tiger’s skin can be locally pierced and thence slotted open. Thereafter, by elongating the slot and initiating new subslots therefrom in various directions, the skin gradually can be peeled open and removed all in one piece. Adequate opening of the slots into angular sinuses will permit the skin to lie out progressively flat. Thus, the original lunar gash from the first puncture develops into many subgashes leading from the original gash into any remaining domical areas of the skin. The slitting of a paper cone from its circular edge to its apex allows the paper to be laid out as a flat “fan” intruded by an angular sinus. A sinus is the part of an angle that is not the angle’s diverging sides. Sinus means in Latin a “withoutness”an opening out a definitively introduced “nothingness.”
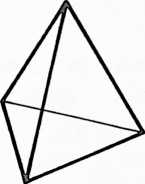
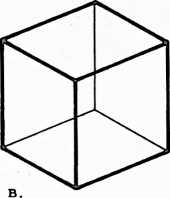
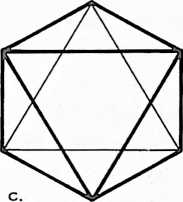
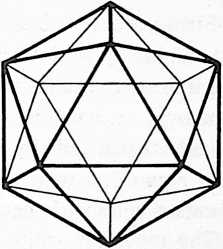
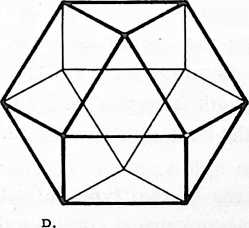
Fig. 400.30 Topological relationships of faces, vertexes, and edges of various polyhedra:
-
Tetrahedron: 4 faces, 4 vertexes, 6 edges.
-
Cube: 6 faces, 8 vertexes, 12 edges.
-
Vector Equilibrium (cuboctahedron): 14 faces, 12 vertexes, 24 edges.
-
Rhombic dodecahedron: 12 faces, 14 vertexes, 24 edges.
-
Icosahedron: 20 faces, 12 vertexes, 30 edges.
-
Pentagonal dodecahedron: 12 faces, 20 vertexes, 30 edges.
Note that in each case by Euler’s topological formula: or . In any system, two vertexes may be considered polarized. These vertexes are then subtracted to balance the equation. This is another suggestion of the inherent two-ness of the Universe.
[400.31]{style="color: purple3"} []{#ver:400.31 label="ver:400.31"} The surface contour of any object or systembe it the skin of a complex creature such as a crocodile, or the skin of a simple prune, or a sugar-cube wrapping, or a dodecahedron, or any formal angular polyhedra–can thus be “skinned” and laid out flat.
[400.40]{style="color: purple3"} []{#ver:400.40 label="ver:400.40"} Finiteness of Systems: Definition: Single systems occurring initially and minimally as four synchronously related event fociergo, inherently as tetrahedra, regular or irregularare omnitriangulated and may be either symmetrical or asymmetrical. In single symmetrical systems, all the vertexes are equidistant radially from their common volumetric centers, and the centers of area of all their triangular facets are also equidistant from the system’s common volumetric center.
[400.41]{style="color: purple3"} []{#ver:400.41 label="ver:400.41"} The minimum single symmetrical system is the regular tetrahedron, which contains the least volume with the most surface as compared to all other symmetrical single systems. There are only three single symmetrical systems: the regular tetrahedron, with a “unit” volume-to-skin ratio of 1 to 1; the regular octahedron, with a volume-to-surface ratio of 2 to 1; and the regular icosahedron, with a volume-to-surface ratio of 3.7 to 1. Single asymmetrical systems contain less volume per surface area of containment than do symmetrical or regular tetrahedra. The more asymmetrical, the less the volume-to-surface ratio. Since the structural strength is expressed by the vector edges, the more asymmetrical, the greater is the containment strength per unit of volumetric content.
[400.42]{style="color: purple3"} []{#ver:400.42 label="ver:400.42"} Since the minimum system consists of two types of tetrahedra, one symmetrical (or regular) and the other asymmetrical (or irregular); and since also the asymmetrical have greater enveloping strength per units of contained event phenomena, we will differentiate the two minimum-system types by speaking of the simplest, or minimum, single symmetrical system as the mini-symmetric system; and we will refer to the minimum asymmetric system as the mini-asymmetric system. And since the mini-symmetric system is the regular tetrahedron, which cannot be compounded face-to-face with other unit-edged symmetric tetrahedra to fill allspace, but, in order to fill allspace, must be compounded with the tetrahedron’s complementary symmetrical system, the octahedron, which is not a minimum system and has twice the volume-to-surface ratio of the tetrahedron of equal edge vector dimension; and since, on the other hand, two special-case minimum asymmetric tetrahedra, the Quanta Modules and the Quanta Modules (see Sec. 920), have equal volume and may be face-compounded with one another to fill allspace, and are uniquely the highest common volumetric multiple of allspace-filling; and since the single asymmetrical tetrahedron formed by compounding two symmetrical tetrahedral Modules and one asymmetrical tetrahedral Module will compound with multiples of itself to fill all positive space, and may be turned inside out to form its noncongruent negative complement (which may also be compounded with multiples of itself to fill all negative space), this three-module, minimum asymmetric (irregular) tetrahedral system, which accommodates both positive or negative space and whose volume is exactly Vs that of the regular tetrahedron; and exactly 732 the volume of the regular octahedron; and exactly Vieo the volume of the regular vector equilibrium of zero frequency; and exactly V1280 the volume of the vector equilibrium of the initial of all frequencies, the integer 2, which is to say that, expressed in the omnirational terms of the highest common multiple allspace-filling geometry’s or Modules, the minimum realizable nuclear equilibrium of closest-packing symmetry of unit radius spheres packed around one spherewhich is the vector equilibrium (see Sec. 413 )consists of or Modules, and .
[400.43]{style="color: purple3"} []{#ver:400.43 label="ver:400.43"} Since the two-A-Module, one-B-Module minimum asymmetric system tetrahedron constitutes the generalized nuclear geometrical limit of rational differentiation, it is most suitably to be identified as the prime minimum rational structural system: also known as the [mite]{.smallcaps} (see “Modelability,” Sec. 950 ). The [mite]{.smallcaps} is the mathematically demonstrable microlimit of rational fractionation of both physically energetic structuring and metaphysical structuring as a single, universal, geometrically discrete system-constant of quantation. The [mite]{.smallcaps} consists of two Modules and one Module, which are mathematically demonstrable as the minimum cosmic volume constant, but not the geometrical shape constant. The shape differentiability renders the volume-to-surface ratio of the Modules more envelopingly powerful than the volume-to-surface ratio of the Modules; ergo, the most powerful local-energy-impounding, omnirationally quantatable, microcosmic structural system.
[400.44]{style="color: purple3"} []{#ver:400.44 label="ver:400.44"} The [mite]{.smallcaps} may be turned inside out by having each of its two Modules and one Module turn themselves inside out and recombine to fill all negative space. It is also to be observed that one all-negative-space-filling and one all-positive-space-filling [mite]{.smallcaps} may be face-associated structurally to produce yet another single minimum system asymmetric tetrahedral, all-positive-and-negative space filler whose modular volumetric unity value of six corresponds with the six-ness of vectorial edges of the minimum system’s tetrahedral four foci event relationships.
[400.45]{style="color: purple3"} []{#ver:400.45 label="ver:400.45"} It is characteristic of a single prime system that the aggregate of angles convergent around its vertexes must be concave or convex with respect to the position from which they are viewedconcave if viewed from the inside, convex when viewed from outside.
[400.46]{style="color: purple3"} []{#ver:400.46 label="ver:400.46"} There are in all systems the additive twoness of the poles and the multiplicative twoness of the coexistent concavity and convexity of the system’s insideness and outsideness.
[400.47]{style="color: purple3"} []{#ver:400.47 label="ver:400.47"} Planet Earth is a system. You are a system. The “surface,” or minimally enclosing envelopmental relationship, of any system such as the Earth is finite.
[400.50]{style="color: purple3"} []{#ver:400.50 label="ver:400.50"} Other Characteristics of Systems: Prime Rational Integer Characteristics: Electromagnetic frequencies of systems are sometimes complex but always exist in complementation of gravitational forces to constitute the prime rational integer characteristics of physical systems.
[400.51]{style="color: purple3"} []{#ver:400.51 label="ver:400.51"} Systems may be symmetrical or asymmetrical.
[400.52]{style="color: purple3"} []{#ver:400.52 label="ver:400.52"} Systems are domains of volumes. Systems can have nuclei, and prime volumes cannot.
[400.53]{style="color: purple3"} []{#ver:400.53 label="ver:400.53"} Interconnection of Systems: If two adjacent systems become joined by one vertex, they still constitute two systems, but universally interjointed. If two adjacent systems are interconnected by two vertexes, they remain two systems, interlocked by a hinge. If two adjacent systems become adjoined by three vertexes, they become one complex system because they have acquired unit insideness and outsideness.
[400.54]{style="color: purple3"} []{#ver:400.54 label="ver:400.54"} If two adjacent systems are interpositioned with their respective centers of volume congruent and all their respective vertexes equidistant from their common center of volumes, they become one system. If their respective vertexes are at different distances radially from their common center of volumes, they become one complex system. If the complex system’s respective interpositioned systems are all symmetric, then they become one complex symmetric system.
[400.55]{style="color: purple3"} []{#ver:400.55 label="ver:400.55"} Polyhedra: Polyhedra consist only of polyhedra. Polyhedra are always pro tem constellations of polyhedra. Polyhedra are defined only by polyhedra and only by a minimum of four polyhedra.
[400.56]{style="color: purple3"} []{#ver:400.56 label="ver:400.56"} All systems are polyhedra: All polyhedra are systems.
[400.57]{style="color: purple3"} []{#ver:400.57 label="ver:400.57"} The observed or tuned-in polyhedra whose plurality of corners, faces, and edges and frequency of subdividing are tunably discernible to the tuning-in station (the observer) consist of corners that are infra-threshold-tunable polyhedra and whose faces or openings are ultra-threshold tunables.
[400.60]{style="color: purple3"} []{#ver:400.60 label="ver:400.60"} Motion of Systems: Systems can spin. There is at least one axis of rotation of any system.
[400.61]{style="color: purple3"} []{#ver:400.61 label="ver:400.61"} Systems can orbit. Systems can contract and expand. They can torque; they can turn inside out; and they can interprecess their parts.
[400.62]{style="color: purple3"} []{#ver:400.62 label="ver:400.62"} Systems are, in effect, spherical gears. Their internal-external pulsating and rotating “teeth” consist in reality of both circumferential and radial waves of various frequencies of subdivision of spherical unity. They often fail to mesh with other local systems. Some of them mesh only in special aspects. The universally frequent nonmeshing of geometrical sizes and rates of wavelengths and frequencies produces an omnicondition in which the new system’s center, as each is created, must continually occupy an omnidirectionally greater domain.
¶ 400.65 Summary: Six Positive and Negative Motions
[400.651]{style="color: purple3"} []{#ver:400.651 label="ver:400.651"} Energetic Functions: Twoness is synergetic. The twoness of inherent otherness of awareness is synergetic. Twoness inherently induces the dynamic quality of oscillatory propagation unpredicted by one-integer-plus-one-integer as empty set. Synergetic twoness and the primitive topological complexity of minimum systems themselves and the presently-non-tuned-in but always inherently coexisting macro-micro otherness inherently produces the ever-interaccommodative, intertransforming, ceaseless restlessness, an intercomplementary characteristic inherent in energetic functions.
[460.652]{style="color: purple3"} []{#ver:460.652 label="ver:460.652"} Resultants of pluralities of copotentials of initial freedoms of unique, reciprocally displacing event patterning, of necessity, occasion fundamental conversion of Euler’s empty integer plus twoness into the synergetic or unpredictedinherent nuclear cohesion.
[400.653]{style="color: purple3"} []{#ver:400.653 label="ver:400.653"} Structural Functions: Structural functions are summarized at Sec. 610.10. (Compare also Sec. 502.05.)
[400.654]{style="color: purple3"} []{#ver:400.654 label="ver:400.654"} Summary: There are six basic motions in Universe. All of them are positive and negative: active and passive. The first five are individually experienceable and popularly familiar; the lastprecession is less popularly familiar:
Spin: Spinning is horizontal or vertical axial rotation. Spinnability has to be totally independent of the system’s local surface transformations.
Orbit: No path of travel may be 180-degree linear in a multibodied, gravity-cohered, omnimotional Universe. The initial reality of all travel is orbital as a composite resultant of all tensive restraints. As the Sun’s pull on the Earth produces orbiting, orbiting electrons produce directional field pulls. As 99.99 percent of the bodies in motion in physical Universe are operating orbitally, orbiting must be thought of as normal. (Spinning and orbiting together is dancing.) Orbits are regenerative feedback circuits.
inside-out: Anything with a hole in it turns inside-out. The tetrahedron turns inside-out through any of its four space-window faces. Kissing humans turn partially inside-out as they “pucker” their lips.
Expansion-contraction: Expansion is radiant divergence, and contraction is gravitational convergence.
Torque: Torque and countertorque are local twists in which one pole spins right and the other pole spins left.
Precession: Precession is the effect of bodies in motion on other bodies in motion in interrelationship patterns of other than 180 degrees. Reactions and resultants are precessional, bringing about orbits and not straight lines. For instance, the effect of the Sun traveling around our galaxy center at 700,000 miles per hour upon the Earth cotraveling with the Sun; the precessional effect of gravity between the two is an effect at 90 degrees to the Sun pull, which makes the Earth both spin and orbit around the Sun.
¶ 400.66 Basic Motions and Degrees of Freedom
[460.661]{style="color: purple3"} []{#ver:460.661 label="ver:460.661"} There are six positive and six negative exercises of the motion freedoms (see Sec. [400.654),]{style="color: purple3"} []{#ver:400.654), label="ver:400.654),"} but the freedoms themselves come from the fact that the minimum structural system in Universe consists of six vectors: the tetrahedron. The tetrahedron has a minimum of six edges.
[460.662]{style="color: purple3"} []{#ver:460.662 label="ver:460.662"} The tetrahedron is a fourfold symmetry: As the minimum something it has four faces of symmetry and four vertexes of symmetry and six edge vectors providing the minimum degrees of freedom. Any one face has three edges, and the total of six edge vectors in the structure defines the set of events. With every turn to play in Universe we always get six moves: So the minimum something is the minimum play. (Compare Sec. 537.10, Fig. 608.01, and Sec. 825.27.)
[460.663]{style="color: purple3"} []{#ver:460.663 label="ver:460.663"} The minimum six vectors can be interarrayed at all kinds of angles provided they all add to 720 degreesthe variable interangling provides the degrees of freedom. We find in topology that all minimum systems have vertexes, faces, and edges and that the number of edges in Universe is always evenly divisible by six. These are the six active and passive degrees of freedom, and they are always there. They do not operate in a plane; they are omnidirectionally interarranged.
[460.664]{style="color: purple3"} []{#ver:460.664 label="ver:460.664"} The six basic motions are complex consequences of the six degrees of freedom. If you want to have an instrument held in position in respect to any cosmic body such as Earth, it will take exactly six restraints: no more, no less. If we have only five restraints, then the tetrahedron will change its shape. Shape requires six restraints. Exactly six systemic interrestraints produce structure. Six restraints are essential to structure and to pattern stability.
[460.665]{style="color: purple3"} []{#ver:460.665 label="ver:460.665"} Anything that holds its shape has a minimum of six positive and negative integral restraints so that the system itself can spin or the system itself can orbit. The system itself can inside-out. These are system behaviors, and the six degrees of restraint are integral.
[460.666]{style="color: purple3"} []{#ver:460.666 label="ver:460.666"} The six basic integral system cosmic motions have six internal structure-producing restraints and six external unique motion-producing restraints. (If a system is frozen as part of a larger system, it will have to lose one of its restraints.) Internally and externally there are 12 alternate optimally equieconomical degrees of cosmic freedom, all of which must be coped with to produce cosmic order.
¶ 400.70 Visibility and Invisibility of Systems
[400.71]{style="color: purple3"} []{#ver:400.71 label="ver:400.71"} There are six uniquely differentiable components of all systems and of all thoughts: (1) insideness; (2) outsideness; and (3) (4) (5) (6) the four star events (see Sec. 510) that do the systemic defining of the insideness and the outsideness, which inadvertently display:
six interrelationships, which in turn inadvertently define:
four triangle windows, which, again inadvertently, reveal the untunedin programs potentially occurring between the six most economical omniinterrelationships whose triangular edge-defining lines inadvertently exclude the macro-outsideness and definingly include the micro-insideness.
[400.72]{style="color: purple3"} []{#ver:400.72 label="ver:400.72"} Therefore there are six parts of Universe: four of them are always humanly conceptualizable and always define the successively considerable domains of human thought, while the other two of the six cosmic parts are always untuned-in, ergo invisible; i.e., the ultramacrotunable otherness and the inframicrotunable otherness.
[400.73]{style="color: purple3"} []{#ver:400.73 label="ver:400.73"} The visibility of conceptuality is always so preoccupying of human senses and minds as to render spontaneously forgettable our only-progressively-acquired knowledge of the vast ranges of the known-to-exist but nonsimultaneously tunable ergo, invisibleotherness of Scenario Universe.
¶ 401.00 Twelve Vectors of Restraint, Six Positive and Six Negative, Define Minimum System
(See drawings section.)[]
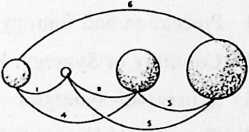
[401.01]{style="color: purple3"} []{#ver:401.01 label="ver:401.01"} At the top of Illus. 401.01 (see also Illus. 401.00 in drawings section ), we see something like a ping-pong ball attached to a string. The ping-pong ball represents me, and the string is gravity (or mass attraction), with its other end tethered to a point that represents all the rest of Universe that isn’t me. Because of mass attraction, the one thing that I cannot do is escape absolutely from Universe. I may try to exert terrific acceleration and shoot out through a hole in the Galaxies, beyond the Pleiades, where the stars seemingly are so scarce that as I look back from fantastically far out, all the stars of Universe seem to be collected in approximately one bright spot. The single string of the model, long though it may be, represents the combined mass attraction exerted upon me by all the stars of Universe.
[401.02]{style="color: purple3"} []{#ver:401.02 label="ver:401.02"} Tetherball: There is an old game called tetherball, played by tennis players lacking a tennis court. There is a tennis ball fastened powerfully to a strong, slender cord 19 feet long suspended from the top of a pole 22 feet in height above the ground level. There is a circular marker on the pole at the 11’ 4” height. The server bats the ball in a clockwise circumferential direction around the pole, attempting to wind its cord completely around the pole above the 11’’ 4” mark. The opponent can intercept and attempt to wind the ball counterclockwise. Obviously, a tethered ball on a long string is free to describe any omnigeometric forms of circles, spheres, or giraffes, but it cannot get away from the Universe. This is called one restraint: the fundamental “otherness” essential to initial “awareness” of the observer. (Nothing to observe: no awareness: only nothingness.) Otherness always imposes a minimum of one restraint, weak though it may be, on all awareness, which is the beginning of “Life.”
[401.03]{style="color: purple3"} []{#ver:401.03 label="ver:401.03"} But the imagined experience of cosmically long journeys teaches me that the possibility of finding such a hole in the celestial myriadicity to attain such a unified paralactic bunching of all island nebulae is a futile search. Therefore, I resign myself to acknowledgment of at least two a priori restraints that inescapably affect my relative cosmic freedom. Hoping to save myself vast cosmic time, and accepting my present position in Universe, I try to process the known data on the mass dimensions of all the known stars and try to divide them all into two opposite hemispherical teamsthose to my right and those to my left. Then assuming all the right-hand hemisphere group’s mass attraction to be accumulatively resolved into one mass-attractive restraint tied to my right arm’s wrist, and all the other cosmic hemisphere’s equal tensions tied to my left arm’s wrist, I find myself used like a middleman in a ropeless tug of war, liable to have my arms pulled out of my armpits. So I tie both the tension lines around my waist. Now I am in the same dynamic situation as a ping-pong ball suspended in the middle of a one-string fiddle. Because all strings, no matter how tautly strung, can still vibrate, I can still move. But I find that with two restraints I can move about in circles, cloverleafs, or figures-of-eight, but always and only in a plane that is perpendicular to the string of which I am in the middle.
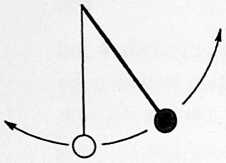
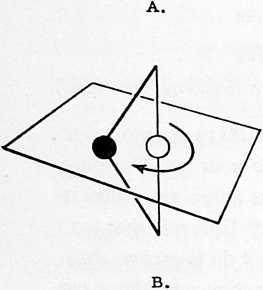
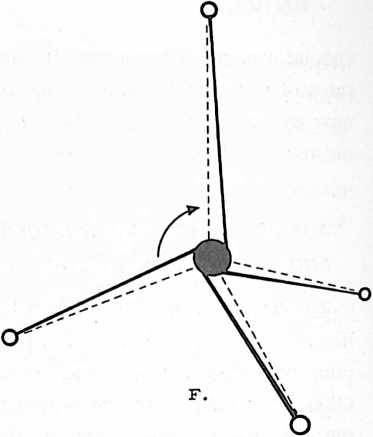
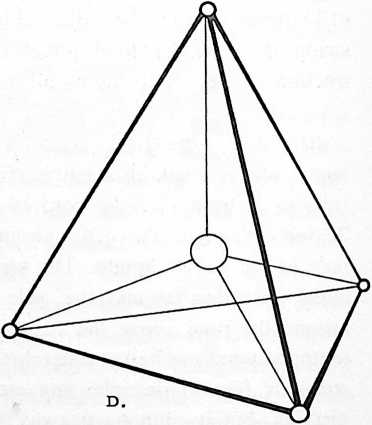
Fig. 401.01 Four Vectors of Restraint Define Minimum System:
Investigation of the requirements for a minimum system.
-
One vector of restraint allows ball to define complete sphere a three-dimensional system.
-
Two vectors: a planea two-dimensional system.
-
Three vectors: a linea one-dimensional system.
-
Four vectors: a pointno displacement.
-
Note the possibility of turbining with the position otherwise fixed by the four vectors of restraint.
-
The four vectors define the tetrahedron: the first identifiable “system” a primary or minimum subdivision of Universe. The ball lies at the center of gravity within the tetrahedron.
[401.04]{style="color: purple3"} []{#ver:401.04 label="ver:401.04"} Now I conclude that the various motions of the stars make it illogical to assume any persistence of the two hemispherical star sphere groupings. The star accelerations produce the inertial advantage of awayness to which my mass-attraction tethers were attached. I therefore conclude that it is more probable that such dynamic inertia will persist in three groups. Now I have three restraints, and the ping-pong ball “me” acts as if it were in the middle of a drumhead, or as tensilely suspended at the center of area of a triangle by three strings fastened at the triangle’s corners. The ping-pong ball “me” can still move, but only in a line perpendicular to the plane of the drumhead or web triangle. I am constrained by three converging lines as I oscillate to and fro between the opposite apexes of two dynamically described, base-to-base, positive or negative tetrahedra formed by the resonating drumhead’s terminal oscillations.
[401.05]{style="color: purple3"} []{#ver:401.05 label="ver:401.05"} With only one restraint, the ball was moving omnidirectionally or multidimensionally. With two restraints, it was moving in a plane; with three restraints, it moves only in a line. I now conclude that it is more probable that I can concentrate all the restraints operating upon me from all the stars because of the multidirectional pull of all the stars actually pulling me. I conclude that there is much redundancy but that four restraints is closer to a matter of reality than three restraints. When we attach a fourth restraint perpendicular to the center of the drumhead and pull it only in the “fro” direction, the ping-pong ball “me” seems at last to be immobilized. With four restraints the ping-pong ball “me” can no longer move either toward or away from any other parts of the Universe. But the ball can twist locally, that is, it can rotate in place around an axis, and that axis itself can incline at many angles, as does the gyroscope top, without alteration of its volumetric center position in respect to the four vertexial star groups. Because the vectors are coming together in nonequilateral quadrangles, i.e., in trapezoids, the restraints are not intertriangulated, and we have learned experimentally that only triangles are stable. (See Sec. 610, Triangulation.) Therefore, it is possible for the ball to “turbine,” rotate, and precess locally in place without altering the geometrical position at volume center of the celestial tetrahedron from whose four corners the four vectors of restraint were imposed. The six edges of the celestial spherical tetrahedron represent the three mass-attraction restraints imposed on each of the tetrahedron’s four corner mass centers as each being in normal acceleration is precessionally restrained from exiting from Universe. Each of the four corners’ group massiveness is restrained by all three of the other tetrahedral corner mass centers. Any one of the mass-moment acceleration tendencies to part company with the others is overpowered three-to-one by the three others. Thus the cohering integrity of Universe is manifest to us by consideration of the celestial advantage points from which our four central restraints were mounted. Though the ping-pong “me” ball can be twisted and torqued in place, it cannot be moved from its tetrahedral center position. To prevent local in-position twist and torque, each of the four corner tensional restraints will have to be multiplyingly replaced by three restraints, all springing from three external points at each of the four tetrahedral corners; and each of the three tensions from any one of the four corners must cross the others triangularly and be attached tangentially to the ball at the center. These 12 now completely restrain any motion of the central ball in relation to the other four.
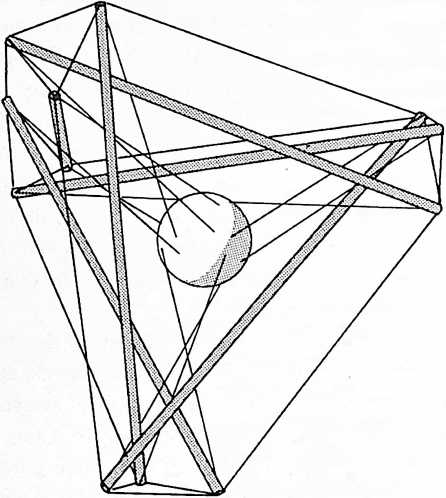
Fig. 401.05 The six compression members are the acceleration vectors trying to escape from Universe at either end by action and reaction, while the ends of each would-be escapee are restrained by three tensors; while the ball at the center is restrained from local torque and twist by three triangulated tensors from each of the four corners tangentially affixed.
[401.06]{style="color: purple3"} []{#ver:401.06 label="ver:401.06"} The purpose of our investigation was to find the requirements of a minimum system. Our experimental model demonstrates that it takes four vectors to define a point with the ping-pong ball at the center of gravity and center of volume of the regular tetrahedron. It takes 12 such vectors to both position and locally immobilize. It takes six external push vectors and six external pull vectors to define the minimum nuclear structural system: a primary subdivision of Universe. To summarize, the celestial tetrahedron has six positive and six negative internal vectors and six positive and six negative external vectors.
[401.07]{style="color: purple3"} []{#ver:401.07 label="ver:401.07"} Four external “star” foci effecting complete immobilization of the “me” ball are the same four event foci that we learned earlier (Sec. 400.05) always constitute the minimum number of events necessary to define the insideness and outsideness of a system.
[401.08]{style="color: purple3"} []{#ver:401.08 label="ver:401.08"} Tetherball: In the “me” ball in Universe 12 structural restraints are necessary to eliminate all the degrees of freedom because all the initial four restraints are connected to the surface of the “me” sphere and not to its center. The four points of tangency describe a square, and they permit local twist and torque because a square is unstable. So each tension has to be replaced by three tension restraints to produce a tensegrity structure within which the “me” ball may be omninonredundantly immobilized.
¶ 402.00 Tetrahedron as System
[402.01]{style="color: purple3"} []{#ver:402.01 label="ver:402.01"} The tetrahedron as a real system consists of one concave tetrahedron and a second convex tetrahedron, plus a third tetrahedron for all the Universe outside the system-as-tetrahedron, and a fourth tetrahedron complementarily accounting for all Universe inside the system-as-tetrahedron. All the angles are the same on the inside as on the outside.
[402.02]{style="color: purple3"} []{#ver:402.02 label="ver:402.02"} A tetrahedron is a triangularly faceted polyhedron of four faces. It is unique as a system, for it is the minimum possible system.
¶ 403.00 Stable and Unstable Systems
[403.01]{style="color: purple3"} []{#ver:403.01 label="ver:403.01"} There are stable systems and unstable systems. (For a discussion of stable and unstable structures, see Sec. 608, Stability: Necklace.)
[403.02]{style="color: purple3"} []{#ver:403.02 label="ver:403.02"} Conceptuality: Unstable systems are conceptual as momentary positional relationships of unstructured-component event aggregates; for example, amongst the stars comprising the Big Dipperin Ursa Majorthe second and third stars in the dipper’s handle are, respectively, 100- and 200-light-years away from Earth and, though seemingly to us in the same plane, are not all so; and they are both moving in opposite directions and so in due course they will no longer seem to be in the same constellation. In the same way, four airplanes flying in different directions may be within visible range of one another, but are far too remote for mass inter-attraction to become critical and pull them into one another. Stable systems are conceptual as structured, which means componently omni-intertriangulated critical-proximity, interrelevant, coordinate, constellar event aggregates.
[403.03]{style="color: purple3"} []{#ver:403.03 label="ver:403.03"} Generalized Principles: If the only momentary and optically illusory system consideration proves to be unstable, it does not manifest generalized principle. If systems are stable, they are inherent in and accommodate all generalized principles.
¶ 410.00 Closest Packing of Spheres
[410.01]{style="color: purple3"} []{#ver:410.01 label="ver:410.01"} Natures Coordination
[410.011]{style="color: purple3"} []{#ver:410.011 label="ver:410.011"} About 1917, I decided that nature did not have separate, independently operating departments of physics, chemistry, biology, mathematics, ethics, etc. Nature did not call a department heads’ meeting when I threw a green apple into the pond, with the department heads having to make a decision about how to handle this biological encounter with chemistry’s water and the unauthorized use of the physics department’s waves. I decided that it didn’t require a Ph.D. to discern that nature probably had only one department and only one coordinate, omnirational, mensuration system.
[410.02]{style="color: purple3"} []{#ver:410.02 label="ver:410.02"} I determined then and there to seek out the comprehensive coordinate system employed by nature. The omnirational associating and disassociating of chemistryalways joining in whole low-order numbers, as for instance and never persuaded me that if I could discover nature’s comprehensive coordination, it would prove to be omnirational despite academic geometry’s fortuitous development and employment of transcendental irrational numbers and other “pure,” nonexperimentally demonstrable, incommensurable integer relationships.
[410.03]{style="color: purple3"} []{#ver:410.03 label="ver:410.03"} I was dissatisfied with abstract, weightless, unstable, ageless, temperatureless, straight-line-defined squares and cubes as models for calculating our omnicurvilinear experience. I was an early rebel against blockheads and squares. Reviewing the history of chemical science, I became intuitively aware that the clue to vectorial, volumetric, geometrical coordination with physical reality and all the fundamental energetic experiences of reality, such as temperature, time, and force, might be found in Avogadro’s experimental proof of his earlier hypothesis, which stated that all gases under identical conditions of heat and pressure will always disclose the same number of molecules per given volume. Here was disclosed a “Grand Central Station” accommodating all corners; despite “fundamental” or elementarily unique differences of identity, all accommodated on a common volume (space)-to-number basis. One molecule of any element: One space. A cosmic democracy.
[410.04]{style="color: purple3"} []{#ver:410.04 label="ver:410.04"} I felt intuitively that inasmuch as the variety of gases experimented with often consisted of only one unique chemical element, such as hydrogen or oxygen, and that inasmuch as these gases also could be liquefied, and also inasmuch as most of the elements are susceptible to some heat- or pressure-produced transformation between their liquid, crystalline, and vapor, or incandescent, states, it might also be hypothetically reasonable to further generalize Avogadro’s hypothesis by assuming that, under identical energy conditions, all elements may disclose the same number of “somethings” per given volume. Such a generalized concept is not limited to pressure and heat: we wanted to be much more inclusive, so we said we assume that the conditions of energy are identical; this includes not only the pressure and heat conditions of thermodynamics, which developed before electromagnetics became an applied realization, but also the conditions of electromagnetics as constant.
[410.05]{style="color: purple3"} []{#ver:410.05 label="ver:410.05"} I went on from there to reason that vectors, being the product of physical energy constituents, are “real,” having velocity multiplied by mass operating in a specific direction; velocity being a product of time and size; and mass being a volume-weight relationship. On impact, mass at velocity transforms into heat and work. These energy factors can be translated not only into work, but into heat or into time as well. Furthermore, electromagnetic scientists had found that all their EMF (electromotive force) problems could be graphed vectorially; the fact that “graphable” or “modelable” vectors can interact modelably in real Universe space seemed to promise that the equations of nature’s omnicoordinate transactions, expressed in omni-space-intruding vectorial models, might produce real models of reality of nature’s Grand Central Station of omnicoordination.
[410.06]{style="color: purple3"} []{#ver:410.06 label="ver:410.06"} So I then went on to say that, if all the energy conditions were everywhere the same, then all the vectors would be the same length and all of them would interact at the same angle. I then explored experimentally to discover whether this “isotropic vector matrix,” as so employed in matrix calculus, played with empty sets of symbols on flat sheets of paper, could be realized in actual modeling. Employing equilength toothpicks and semi-dried peas, as I had been encouraged to do in kindergarten at the age of four (before receiving powerful eyeglasses and when I was unfamiliar with the right-angled structuring of buildings as were the children with normal vision), I fumbled tactilely with the toothpicks and peas until I could feel a stable structure, and thus assembled an omnitriangulated complex and so surprised the teachers that their exclamations made me remember the event in detail. I thus rediscovered the octet truss whose vertexes, or convergent foci, were all sixty-degree-angle interconnections, ergo omniequilateral, omniequiangled, and omni-intertriangulated; ergo, omni structured. Being omnidirectionally equally interspaced from one another, this omni-intertriangulation produced the isotropic matrix of foci for omni-closest-packed sphere centers. This opened the way to a combinatorial geometry of closest-packed spheres and equilength vectors.
[410.07]{style="color: purple3"} []{#ver:410.07 label="ver:410.07"} Over and over again, we are confronted by nature obviously formulating her structures with beautiful spherical agglomerations. The piling of oranges, coconuts, and cannonballs in tetrahedral or half-octahedral pyramids has been used for centuries and possibly for ages. Almost a half-century ago, F. W. Aston, the British scientist first identified for physics the most economical uniradius spherical interagglomerations as the “closest packing of spheres,” which had fresh interest for the physicist and crystallographer because of the then recently discovered microscopic realization that nature frequently employed omni-intertriangulated systems, which hold mathematical clues to the principles of symmetrical coordination governing natural structure, the dynamic vectorial geometry of the atomic nucleus, as well as of the atoms themselves.
¶ 410.10 Omnitriangulation of Sixty Degrees
[410.11]{style="color: purple3"} []{#ver:410.11 label="ver:410.11"} The closest packing of unit radius spheres always associates in omnitriangulations of 60 degrees, whether in planar or omnidirectional arrays. Six unit radius spheres pack most tightly around one sphere on a billiard table. Twelve unit radius spheres compact around one sphere in omnidirectional closest packing.
[410.12]{style="color: purple3"} []{#ver:410.12 label="ver:410.12"} If we take three billiard balls on a flat table, we find that they compact beautifully into a triangle. If we arrange four of them on a billiard table in a square, they tend to be restless and roll around each other. If compacted into a condition of stability, the four form a 60-degree-angled diamond shape made of two stable triangles.
¶ 411.00 Four Spheres as Minimum System
[411.01]{style="color: purple3"} []{#ver:411.01 label="ver:411.01"} The South Seas islander piling his coconuts, the fruit dealer selling oranges, and the cannoneer stacking equiradius cannonballs, or the much earlier round-rock-slinging soldiers were probably the first to learn about the closest packing of spheres. The stacking of balls in symmetrical rows and layers leads inevitably to a stable pyramidal aggregate.
[411.02]{style="color: purple3"} []{#ver:411.02 label="ver:411.02"} Closest packing of spheres does not begin with a nucleus. Closest packing begins with two balls coming together.
[411.03]{style="color: purple3"} []{#ver:411.03 label="ver:411.03"} One ball cannot zoom around alone in Universe. Without otherness, there is no consciousness and no direction. If there were only one entity say it is a sphere called *“me”*there would be no Universe: no otherness: no awareness: no consciousness: no direction. Once another entity let’s say a sphereis sighted, there is awareness and direction. There is no way to tell how far away the other sphere may be or what its size may be. Size sense comes only with a plurality of comparative experiences.
[411.04]{style="color: purple3"} []{#ver:411.04 label="ver:411.04"} As a single sphere, now aware of an otherness sphere somewhere out there, "me” has to rotate about without restraint and can observe its rotation in relation to the otherness, but could misassume the otherness sphere to be zooming around it, as there are no third, or more, othernesses by which to judge.
[411.05]{style="color: purple3"} []{#ver:411.05 label="ver:411.05"} When moved unknowingly toward another by mass attraction, the “other” ball and the "me” ball, either or both of which could have been rotating as they approach one another, each misassumes the other to be growing bigger, until finally they touch each other. Now they can roll around upon one another, and they might be cotraveling together, but there is not as yet anywhere to go because there is no otherness than their joint selves relative to which to travel. They can’t go through each other and they can’t get away from each other. They are only free to rotate upon each other, and because of friction they must do so cooperatively.
[411.06]{style="color: purple3"} []{#ver:411.06 label="ver:411.06"} When a third ball looms into sight, providing a sense of direction for the tangently rolling-upon-each-other first couple, the third one and the first two are mass-attracted toward each other and finally make contact. The newcorner third sphere may roll around on one of the first couple until it rolls into the valley between the first two. The third ball then gets locked into the valley between the first two by double mass attraction, and now becomes tangent to both of the first two.
[411.07]{style="color: purple3"} []{#ver:411.07 label="ver:411.07"} The three balls, each one tangent to both of the others, now form an equiangular triangular group with a small opening at their center. The friction of each of their double contacts with the other two gives them a geartooth interaction effect. With two gears, one can turn clockwise and the other can tum counterclockwise. Even numbers of gears reciprocate; odd numbers of gears block one another. Thus our three balls can no longer roll circumferentially around each other; they can only rotate cooperatively on the three axes formed between each of their two tangent contact points. The friction between their surface contacts forces all three to rotate unidirectionally about their respective contact axes, which are parallel to the edges of the equilateral triangle defined by the three sphere centers; i.e., the three spheres can now only co-rotate over and into the hole at the center of the triangle, and out and away upwardly again from the bottom of the center hole. Thus the three balls can involute or evolute axially, like a rubber doughnut in respect to the hole at their triangular center, but they cannot rotate circumferentially.
Fig. 411.05 Four Spheres Lock as Tetrahedron:
-
A single sphere is free to rotate in any direction.
-
Two tangent spheres although free to rotate in any direction must do so cooperatively.
-
Three spheres can rotate cooperatively only about respective axes which are parallel to the edges of the equilateral triangle defined by joining the sphere centers, i.e. each sphere rotates toward the center of the triangle.
-
Four spheres lock together. No rotation is possible, making the minimum stable closest-packed-sphere system: the tetrahedron.
[411.08]{style="color: purple3"} []{#ver:411.08 label="ver:411.08"} Finally, a fourth ball appears in Universe and is mass-attracted to tangency with one of the three previously triangulated spheres, then rolls on one of the joined balls until it falls into the valley formed by the hole at the top center of the triangulated three; but being of equal diameter with the other three balls, it cannot fall through that hole whose radius is less than those of the associated spheres. Thus nested in the central valley, the fourth sphere now touches each of the other three and vice versa. The four closest-packed spheres make a closest-packing array. They are mass-attractively locked together as a tetrahedron.[^8] No further interrotation is possible. As a tetrahedron, they form the minimum stable structural system and provide the nuclear matrix for further mass attraction and closest-packed growth of additional spheres falling into their four-surface triangular nests. This produces increasing numbers of closest-packed nests. Thus do atoms agglomerate in closest packing in tetrahedrally conformed arrays, often truncated asymmetrically at corners and along edges to obscure the tetrahedral origin of the collection.
[411.10]{style="color: purple3"} []{#ver:411.10 label="ver:411.10"} Unpredicted Degrees of Freedom: Reviewing the history of self-discoveries of restraints progressively and mutually interimposed upon one another by the arrival of and association with successive othernesses, self may discover through progressive retrospections and appreciate the significance of theretofore unrecognized and unrealized degrees of cosmic freedom successively and inadvertently deducted from the original total inventory of unexpended self-potentials with which the individual is initially, always and only, endowed. Only with the progressive retrospection inventoryings induced only by otherness-developed experience of awareness does the loss of another degree of freedom become consciously subtracted from the previous experience inventory of now consciously multiplying rememberable events.
[411.11]{style="color: purple3"} []{#ver:411.11 label="ver:411.11"} With the discovery of principles through progressive deprivations dawns new awareness of the elective employability of the principles initially separated out from their special-case experiencing to self-control more and more of the pattern of events.
[411.12]{style="color: purple3"} []{#ver:411.12 label="ver:411.12"} Only through relationships with otherness can self learn of principles; only by discovery of the relationships existing between self and othernesses does inspiration to employ principles objectively occur. There is nothing in self per se, or in otherness per se, that predicts the interrelatedness behaviors and their successively unique characteristics. Only from realization of the significance of otherness it can be learned further that only by earnest commitment to others does self become inadvertently behaviorally advantaged to effect even greater commitment to others, while on the other hand all self-seeking induces only ever greater self-loss.
[411.20]{style="color: purple3"} []{#ver:411.20 label="ver:411.20"} Discovery as a Function of Loss: It is a basic principle that you only discover what you had had by virtue of losing it. Due to our subconscious organic coordination, you don’t know what you are losing until you lose it. Naught can be so advantageous as thoughtfully considered loss and resolve to employ the principles thereby discovered for others. You don’t know how much you have to give until you start trying to give. The more you try to give effectively to advantage others, the more you will possess to give, and vice versa.
[411.21]{style="color: purple3"} []{#ver:411.21 label="ver:411.21"} Retrospective awareness of losses can bring preoccupation with self, blinding self to recognition of the synergetic gains that, by virtue of the second-power law, have brought group advantage gains in which the individual has attained fourth-power continuance potential often way offsetting individual freedom losses, particularly in view of the group’s discovery that as a group it can enjoy all the original freedoms individually lost but never realized by the individual to existergo, unemployable consciously by the individual, who was more of a victim of the unknown freedoms than an enjoyer.
[411.22]{style="color: purple3"} []{#ver:411.22 label="ver:411.22"} Only as group structuring occurs do the discovered cosmic freedoms become consciously employableemployable effectively only for all and not for self. It is when this retrospective discovering is made by the grouped-in individual and he tries to employ the freedoms exclusively for self or exclusive subdivisions of the group, that his attempts become inherently unfulfillable and scheduled for ultimate failure.
[411.23]{style="color: purple3"} []{#ver:411.23 label="ver:411.23"} Self-seeking brings a potential loss that engenders first caution, then fear: fear of change; change being inexorable, fear increases and freezes. Self-seeking always eventuates in self-destruction through inability to adapt.
[411.30]{style="color: purple3"} []{#ver:411.30 label="ver:411.30"} Intergeared Mobility Freedoms: Only with the arrival of the second otherness do individuals become aware of the loss of mutual any where-around-one-another rollability, and then discover that they have also lost the ability to go in all directions, for they cannot go through each other. It is inferred that they haven’t lost mutually accomplishable omnidirectional mobility. (Here is an example of one of those comprehendings from an apprehending.) With the acquisition of the second otherness, self discovers what it has lost which self didn’t know it had, until the loss brought retrospective awareness of the lost freedom: an inter-anywhere-roll-aroundness with the first other.
[411.31]{style="color: purple3"} []{#ver:411.31 label="ver:411.31"} With the mutually interattracted threeness, each having two contacts with their two otherness partners, they learn, as a fourth otherness nests into their triangular opening, that they have now lost a frictionally intergeared mutually evoluting-involuting rotational freedom (torus). Now blocked by the frictionally intergeared fourth otherness, the mutual omnidirectionality of the structural system so produced by that structural system can be discovered only by the self-observation of the realization of another structural system’s cumulative repetition repeating the evolutionary accumulation of its own fourfolding; observing that the other structural system can move omnidirectionally, their observed rotations and magnitude changes can be explained only by the omnidirectional freedom only mutually experienceable by the whole individual structural system as it had been originally and only subconsciously experienced by the individual self. Naught has been lost. Much has been mutually gained. Each can take off from and return to the others.
[411.32]{style="color: purple3"} []{#ver:411.32 label="ver:411.32"} The variations of the features of second-structural-system otherness can be explained only by the self-structural system assumption of increasing distance of travel of the otherness to and away, or by the other system’s experiencing a freedom theretofore unself-realized: that of individual expansion and contraction. For any one of the four members of a structural-system team can expand and contract coordinatedly at individual rates, mutual rates, or interpaired rates, provided one does not become so small as to “fall through,” the triangular opening at its nest bottom. (If it fell through, one otherness would start rotating hingewise around the axis of tangent contact with the next-largest, without touching the fourth and next-smallest-to-self.)
[411.33]{style="color: purple3"} []{#ver:411.33 label="ver:411.33"} Thus the self-structural system discloses by observation of otherness’s system changing features that its own system had been enjoying, as with freedoms of which it was previously unconscious.
[411.34]{style="color: purple3"} []{#ver:411.34 label="ver:411.34"} Our inventory of intergeared mobility freedoms is fourfold. It is four-dimensional:
-
omnidirectionality of united movement;
-
roll-aroundness (orbiting);
-
polarized evoluting-and-involuting, and polarized spin; and
-
inward-outward expandability singly, doubly, three- or four-partite.
[411.35]{style="color: purple3"} []{#ver:411.35 label="ver:411.35"} The inward-outward expandability is the basis of convergencedivergence and radiation-gravitation pulsationwhich seems furthest from man’s awareness. This is what science has discovered: a world of waves in which waves are interpenetrated by waves in frequency modulation. There is a systemic interrelationship of basic fourness always accompanied by a sixness of alternatives of freedoms.
[411.36]{style="color: purple3"} []{#ver:411.36 label="ver:411.36"} When a sphere gets so small that it can roll through a hole between other close packed spheres, the omnidirectionality of any one individual would not be impeded under the following circumstances:
-
The individual mass-attracted by any threeness being drawn through the hole of any other threeness.
-
Where a fourth otherness could be attracted by a momentary critical- proximity threeness.
-
We learn there is individuality and magnitude change; then we learn that, due to the energy losses and gains of systems occasioned by the continual variations of omnidirectional proximities and omnivariability of expansion-contraction system accumulating rates, there is a degree of freedom phenomena rate as well as a terminal condition.
[411.37]{style="color: purple3"} []{#ver:411.37 label="ver:411.37"} Rate occurs only when there is terminal. Rate is a modulation between terminals. With termination, a system’s integrity is brought about by the individually covarying magnitudes and the omnidirectional experience pulls on the system.
[411.38]{style="color: purple3"} []{#ver:411.38 label="ver:411.38"} The degree of freedom that is lost is discoverable only retrospectively by the very fact of the loss. It is an inverse synergetic behavior wherein no feature of the self part predicted the successive behaviors of the whole and where the individual part freedoms were only mutually disclosed by their subsequently realized loss.
¶ 412.00 Closest Packing of Rods
[412.01]{style="color: purple3"} []{#ver:412.01 label="ver:412.01"} Just as six balls may be closest packed around a nuclear ball in a plane, six rods or wires may be closest packed around a nuclear rod or wire in a cluster. When the seven wires are thus compacted in a parallel bunch, they may be twisted to form a cable of hexagonal cross section, with the nuclear wire surrounded by the other six. The hexagonal pattern of cross section persists as complete additional layers are symmetrically added to the cluster. These progressive symmetrical surroundments constitute circumferentially finite integrities in universal geometry.
[412.02]{style="color: purple3"} []{#ver:412.02 label="ver:412.02"} Surface Tension Capability: We know by conclusive experiments and measuring that the progressive subdivision of a given metal fiber into a plurality of approximately parallel fibers provides tensile behavior capabilities of the smaller fibers at increased magnitudes up to hundreds- and thousands-fold that of the unit solid metal section. This is because of the increased surface-to-mass ratios and because all high tensile capability is provided by the work hardening of the surfaces. This is because the surface atoms are pressed into closer proximity to one another by the drawing tool through which the rod and wire are processed.
¶ 413.00 Omnidirectional Closest Packing
[413.01]{style="color: purple3"} []{#ver:413.01 label="ver:413.01"} In omnidirectional closest packing of equiradius spheres around a nuclear sphere, 12 spheres will always symmetrically and intertangentially surround one sphere with each sphere tangent to its immediate neighbors. We may then close-pack another symmetrical layer of identical spheres surrounding the original 13. The spheres of this outer layer are also tangent to all of their immediate neighbors. This second layer totals 42 spheres. If we apply a third layer of equiradius spheres, we find that they, too, compact symmetrically and tangentially. The number of spheres in the third layer is 92.
NO. RODS PER CLUSTER 1 7 19 37 61 91 127
NO. RODS OUTER LAYER 6 12 18 24 30 36
TOTAL ROD AREAS 314.159 314.159 314.159 314.159 314.159 314.159 314.159
DIAM. OF SINGLE ROD 20.000 7.556 4.588 3.288 2.561 2.099 1.775
AREA OF SINGLE ROD 314.159 44.880 16.535 8.491 5.150 3.452 2.474
PERIM. OF SINGLE ROD 62.832 23.748 14.415 10.330 8.045 6.594 5.575
TOTAL PERIMETER OF RODS IN BUNDLE 62.832 166.24 273.88 382.19 489.88 600.07 708.08
TOTAL PERIMETER OF RODS IN OUTER LAYER 62.832 142.49 172.98 185.93 193.08* 197.83* 205.39*
MIN. DIAMETER OF HEXAGONAL BUNDLE 20.649 20.483 20.373 20.302 20.277 20.218
MAX. DIAMETER OF HEXAGONAL BUNDLE 22.668 22.940 23.016 23.046 23.089 23.095
TOTAL AREA OF RODS OUTER LAYER ONLY 269.279 198.416 152.834 123.604 103.569 89.053
NOTE THAT PERIMETERS OF OUTER LAYER RODS ALONE EXCEEDS THREE TIMES PERIMETER OF LARGE ROD.
Fig. 412.01 Closest Packing of Rods.
[413.02]{style="color: purple3"} []{#ver:413.02 label="ver:413.02"} Equi-radius spheres closest packed around a nuclear sphere do not form a supersphere, as might be expected. They form a symmetrical polyhedron of 14 faces: the vector equilibrium.
3 Frequency Triangle A.
Fig. 413.01 Vector Equilibrium: Omnidirectional Closest Packing Around a Nucleus: Triangles can be subdivided into greater and greater numbers of similar units. The number of modular subdivisions along any edge can be referred to as the frequency of a given triangle. In triangular grids each vertex may be expanded to become a circle or sphere showing the inherent relationship between closest packed spheres and triangulation. The frequency of triangular arrays of spheres in the plane is determined by counting the number of intervals (A) rather than the number of spheres on a given edge. In the case of concentric packings or spheres around a nucleus the frequency of a given system can either be the edge subdivision or the number of concentric shells or layers. Concentric packings in the plane give rise to hexagonal arrays (B) and omnidirectional closest packing of equal spheres around a nucleus (C) gives rise to the vector equilibrium (D).
[413.03]{style="color: purple3"} []{#ver:413.03 label="ver:413.03"} If we add on more layers of equiradius spheres to the symmetrical polyhedron of 14 faces close-packed around one sphere, we find that they always compact symmetrically and tangentially, and that this process of enclosure may seemingly be repeated indefinitely. Each layer, however, is in itself a finite or complete and symmetrical embracement of spheres. Each of these embracing layers of spheres constitutes a finite system. Each layer always takes the 14-face conformation and consists of eight triangular and six square faces. Together with the layers they enclose and the original sphere center, or nucleus, these symmetrically encompassing layers constitute a concentric finite system.
[413.04]{style="color: purple3"} []{#ver:413.04 label="ver:413.04"} As additional layers are added, it is found that a symmetrical pattern of concentric systems repeats itself. That is, the system of three layers around one sphere, with 92 spheres in the outer layer, begins all over again and repeats itself indefinitely with successively enclosing layers in such a way that the successive layers outside of the 92-sphere layer begin to penetrate the adjacent new nuclear systems. We find then that only the concentric system of spheres within and including the layer of 92 are unique and individual systems. We will pursue this concept of a finite system in universal geometry still further (see Sec. 418, et seq.) in order to relate it to the significance of the 92 self-regenerative chemical elements.
¶ 414.00 Nucleus
[414.01]{style="color: purple3"} []{#ver:414.01 label="ver:414.01"} In closest packing of equiradius spheres, a nucleus by definition must be tangentially and symmetrically surrounded. This means that there must be a ball in every possible tangential and optically direct angular relationship to the nucleus. This does not happen with the first layer of 12 balls or with the second layer of 42 balls. Not until the third layer of 92 balls is added are all the tangential spaces filled and all the optically direct angles of nuclear visibility intercepted. We then realize a nucleus.[^9]
[414.02]{style="color: purple3"} []{#ver:414.02 label="ver:414.02"} It will also be discovered that the third layer of 92 spheres contains eight new potential nuclei; however, these do not become realized nuclei until each has two more layers enveloping itone layer with the nucleus in it and two layers enclosing it. Three layers are unique to each nucleus. This tells us that the nuclear group with 92 spheres in its outer, or third, layer is the limit of unique, closest-packed symmetrical assemblages of unit wavelength and frequency. These are nuclear symmetry systems.
[414.03]{style="color: purple3"} []{#ver:414.03 label="ver:414.03"} It is characteristic of a nucleus that it has at least two surrounding layers in which there is no nucleus showing, i.e., no potential. In the third layer, however, eight potential nuclei show up, but they do not have their own three unique layers to realize them. So the new nuclei are not yet realized, they are only potential.
[414.04]{style="color: purple3"} []{#ver:414.04 label="ver:414.04"} The nucleus ball is always two balls, one concave and one convex. The two balls have a common center. Hydrogen’s one convex proton contains its own concave nucleus.
¶ 415.00 Concentric Shell Growth Rates
[415.01]{style="color: purple3"} []{#ver:415.01 label="ver:415.01"} Minimal Most Primitive Concentric Shell Growth Rates of Equiradius, Closest-Packed, Symmetrical Nucleated Structures: Out of all possible symmetrical polyhedra produceable by closest-packed spheres agglomerating, only the vector equilibrium accommodates a one-to-one arithmetical progression growth of frequency number and shell number developed by closest-packed, equiradius spheres around one nuclear sphere. Only the vector equilibrium“equanimity” accommodates the symmetrical growth or contraction of a nucleus-containing aggregate of closest-packed, equiradius spheres characterized by either even or odd numbers of concentric shells.
[415.02]{style="color: purple3"} []{#ver:415.02 label="ver:415.02"} Odd or Even Shell Growth: The hierarchy of progressive shell embracements of symmetrically closest-packed spheres of the vector equilibrium is generated by a smooth arithmetic progression of both even and odd frequencies. That is, each successively embracing layer of closest-packed spheres is in exact frequency and shell number atunement. Furthermore, additional embracing layers are accomplished with the least number of spheres per exact arithmetic progression of higher frequencies.
[415.03]{style="color: purple3"} []{#ver:415.03 label="ver:415.03"} Even-Number Shell Growth: The tetrahedron, octahedron, cube, and rhombic dodecahedron are nuclear agglomerations generated only by even-numbered frequencies:
+:------------------------------+:-------------------------+
| Nuclear tetrahedron: | = 4 (34 around one) |
| | |
| | = 8 (130 around one) |
+-------------------------------+--------------------------+
| Nuclear octahedron: | F = 2 (18 around one) |
| | |
| | = 4 (66 around one) |
+-------------------------------+--------------------------+
| Nuclear cube: | = 4 (210 around one) |
| | |
| | F = 6 (514 around one) |
+-------------------------------+--------------------------+
| Nuclear rhombic dodecahedron: | = 4 (74 around one) |
| | |
| | = 8 (386 around one) |
+-------------------------------+--------------------------+
Chart 415.03 Rate of Occurrence of Symmetrically Nucleated Polyhedra of Closest Packing
[415.10]{style="color: purple3"} []{#ver:415.10 label="ver:415.10"} Yin-Yang As Two (Note to Chart 415.03): Even at zero frequency of the vector equilibrium, there is a fundamental twoness that is not just that of opposite polarity, but the twoness of the concave and the convex, i.e., of the inwardness and outwardness, i.e., of the microcosm and of the macrocosm. We find that the nucleus is really two layers because its inwardness turns around at its own center and becomes outwardness. So we have the congruence of the inbound layer and the outbound layer of the center ball.
F = 0
10x0 = 0
0 + 2 = 2 (at zero frequency)
Because people thought of the nucleus only as oneness, they for long missed the significant twoness of spherical unity as manifest in the atomic weights in the Periodic Table of the Elements.
[415.11]{style="color: purple3"} []{#ver:415.11 label="ver:415.11"} When they finally learned that the inventory of data required the isolation of the neutron, they were isolating the concave. When they isolated the proton, they isolated the convex.
[415.12]{style="color: purple3"} []{#ver:415.12 label="ver:415.12"} As is shown in the comparative table of closest-packed, equiradius nucleated polyhedra, the vector equilibrium not only provides an orderly shell for each frequency, which is not provided by any other polyhedra, but also gives the nuclear sphere the first, or earliest possible, polyhedral symmetrical enclosure, and it does so with the least number spheres; whereas the octahedron closest packed requires 18 spheres; the tetrahedron, 34; the rhombic dodecahedron, 92; the cube, 364; and the other two symmetric Platonic solids, the icosahedron and the dodecahedron, are inherently, ergo forever, devoid of equiradius nuclear spheres, having insufficient radius space within the triangulated inner void to accommodate an additional equiradius sphere. This inherent disassociation from nucleated systems suggests both electron and neutron behavior identification relationships for the icosahedron’s and the dodecahedron’s requisite noncontiguous symmetrical positioning outwardly from the symmetrically nucleated aggregates. The nucleation of the octahedron, tetrahedron, rhombic dodecahedron, and cube very probably plays an important part in the atomic structuring as well as in the chemical compounding and in crystallography. They interplay to produce the isotopal Magic Number high point abundance occurrences. (See Sec. 984.10 hangeadd ref)
[415.13]{style="color: purple3"} []{#ver:415.13 label="ver:415.13"} The formula for the nucleated rhombic dodecahedron is the formula for the octahedron with frequency plus four (because it expands outwardly in four-wavelength leaps) plus eight times the closest-packed central angles of a tetrahedron. The progression of layers at frequency plus four is made only when we have one ball in the middle of a five-ball edge triangle, which always occurs again four frequencies later.
[415.14]{style="color: purple3"} []{#ver:415.14 label="ver:415.14"} The number of balls in a single-layer, closest-packed, equiradius triangular assemblage is always 2.
[N2-N]{.underline}
[415.15]{style="color: purple3"} []{#ver:415.15 label="ver:415.15"} To arrive at the cumulative number of spheres in the rhombic dodecahedron, you have to solve the formula for the octahedron at progressive frequencies plus four, plus the solutions for the balls in the eight triangles.
[415.16]{style="color: purple3"} []{#ver:415.16 label="ver:415.16"} The first cube with 14 balls has no nucleus. The first cube with a nucleus occurs by the addition of 87-ball corners to the eight triangular facets of a four-frequency vector equilibrium.
[415.17]{style="color: purple3"} []{#ver:415.17 label="ver:415.17"} Nucleated Cube: The “External” Octahedron: The minimum allspace-filling nuclear cube is formed by adding eight Eighth-Octahedra to the eight triangular facets of the nucleated vector equilibrium of tetravolume-20, with a total tetravolume involvement of quanta modules. This produces a cubical nuclear involvement domain (see Sec. 1006.30) of tetravolume-24: quanta modules. (See Sec. 463.05 and Figs. [415.17A-F.)]{style="color: purple3"} []
[415.171]{style="color: purple3"} []{#ver:415.171 label="ver:415.171"} The nuclear cube and its six neighboring counterparts are the volumetrically maximum members of the primitive hierarchy of concentric, symmetric, pre-time-size, subfrequency-generalized, polyhedral nuclear domains of synergetic-energetic geometry.
[415.172]{style="color: purple3"} []{#ver:415.172 label="ver:415.172"} The construction of the first nuclear cube in effect restores the vector-equilibrium truncations. The minimum to be composited from closest- packed unit radius squares has 55 balls in the vector equilibrium. The first nucleated cube has 63 balls in the total aggregation.
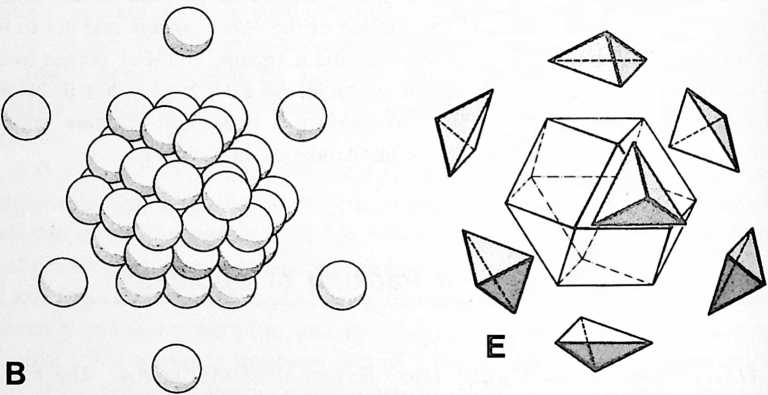
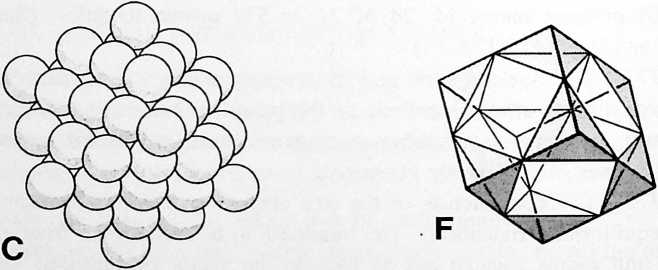
Fig. [415.17 Nucleated Cube: The “External" Octahedron: ABC]{style="color: purple3"} []{#ver:415.17 Nucleated Cube: The External\" Octahedron: ABC label="ver:415.17 Nucleated Cube: The External" Octahedron: ABC"} show that eight additional closest-packed spheres are required to form the minimum allspace-filling nuclear cube to augment the nuclear vector equilibrium. DEF show the eight Eighth-Octa required to complete the polyhedral transformation. (Compare Fig. 1006.32.)
[415.20]{style="color: purple3"} []{#ver:415.20 label="ver:415.20"} Organics: It could be that organic chemistries do not require nuclei.
[415.21]{style="color: purple3"} []{#ver:415.21 label="ver:415.21"} The first closest-packed, omnitriangulated, ergo structurally stabilized, but non-nuclear, equiradius-sphered, cubical agglomeration has 14 spheres. This may be Carbon 14, which is the initially closest-packed, omnisymmetrical, polyhedral fourteenness, providing further closest-packability surface nests suitable for structurally mounting hydrogen atoms to produce all organic matter.
[415.22]{style="color: purple3"} []{#ver:415.22 label="ver:415.22"} The cube is the prime minimum omnisymmetrical allspace filler. But the cube is nonstructural until its six square faces are triangularly diagonaled. When thus triangularly diagonaled, it consists of one tetrahedron with four one-eighth octahedra, of three isosceles and one equilateral-faced tetrahedron, outwardly applied to the nuclear equilateral tetrahedron’s four triangular faces. Thus structurally constituted, the superficially faced cube is prone to closest-packing self-associability. In order to serve as the carbon ring (with its six-sidedness), the cube of 14 spheres (with its six faces) could be joined with six other cubes by single atoms nestable in its six square face centers, which singleness of sphericity linkage potential is providable by Hydrogen 1.
[415.23]{style="color: purple3"} []{#ver:415.23 label="ver:415.23"} In the atoms, we are always dealing in equiradius spheres. Chemical compounds may, and often do, consist of atomic spheres with a variety of radial dimensions. Since each chemical element’s atoms are characterized by unique frequencies, and unique frequencies impose unique radial symmetries, this variety of radial dimensionality constitutes one prime difference between nuclear physics and chemistry.
[415.30]{style="color: purple3"} []{#ver:415.30 label="ver:415.30"} Eight New Nuclei at Fifth Frequency of Vector Equilibrium: Frequency five embraces nine nuclei: the original central nucleus plus eight new nuclei occurring at the centers of volume of the eight tetrahedra symmetrically surrounding the nucleus, with each of the nine enclosed with a minimum of two layers of spheres.
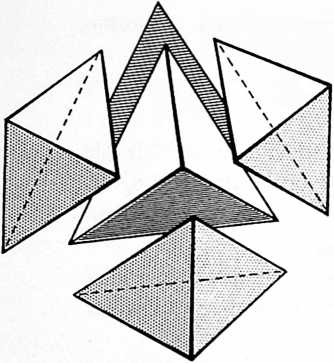
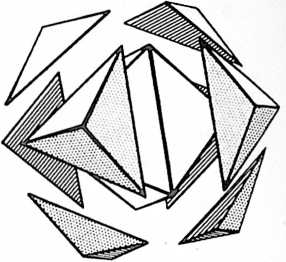
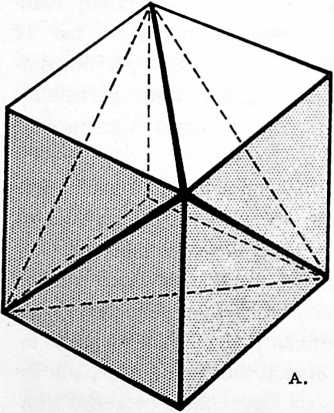
Fig. 415.22 Rational Volumes of Tetrahedroning:
-
The cube may be formed by placing four 1/s-octahedra with their equilateral faces on the faces of a tetrahedron. Since tetrahedron volume equals one, and Vs- octahedron equals V2, the volume of the cube will be: 1 + 4(1/2) = 3.
-
The rhombic dodecahedron may be formed by placing eight V-i-tetrahedra with their equilateral faces on the faces of an octahedron. Since the octahedron volume equals four and V4-tetrahedron equals V4, the volume of the rhombic dodecahedron will be: 4+8(V4)=6.
[415.31]{style="color: purple3"} []{#ver:415.31 label="ver:415.31"} The vector equilibrium at /= 12; at/2 = 42; /3 = 93; f4= 162 spheres in the outer shell; and atf5 = 252 we get eight new nuclei. Therefore, their eightness of “begetness” relates to the eight triangles of the vector equilibrium.
[415.32]{style="color: purple3"} []{#ver:415.32 label="ver:415.32"} Six nucleated octahedra with two layer omni-enclosure of their nuclei does not occur until /6 = 362 in the outer shell of the vector equilibrium. At this stage we have six new nuclei, with 14 nuclei surrounding the 15th, or original, nucleus.
[415.40]{style="color: purple3"} []{#ver:415.40 label="ver:415.40"} Begetted Eightness: The “begetted” eightness as the systemlimit number of nuclear uniqueness of self-regenerative symmetrical growth may well account for the fundamental octave of unique interpermutative integer effects identified as plus one, plus two, plus three, plus four, as the inter- permutated effects of the integers one, two, three, and four, respectively; and as minus four, minus three, minus two, minus one, characterizing the integers five, six, seven, and eight, respectively. The integer nine always has a neutral, or zero, intermutative effect on the other integers. This permutative, synergetic or interamplifying or dimensioning effect of integers upon integers, together with the octave interinsulative accommodation produced by the zero effect of the nineness, is discussed experientially in our section on Indigs in Chapter 12, Numerology.
[415.41]{style="color: purple3"} []{#ver:415.41 label="ver:415.41"} The regenerative initial eightness of first-occurring potential nuclei at the frequency-four layer and its frequency-five confirmation of those eight as constituting true nuclei, suggest identity with the third and fourth periods of the Periodic Table of Chemical Elements, which occur as
1st period = 2 elements
2nd period = 8 elements
3rd period = 8 elements
[415.42]{style="color: purple3"} []{#ver:415.42 label="ver:415.42"} Starting with the center of the nucleus: plus one, plus two, plus three, plus four, outwardly into the last layer of nuclear uniqueness, whereafter the next pulsation becomes the minus fourness of the outer layer (fifth action); the sixth event is the minus threeness of canceling out the third layer; the seventh event is the minus twoness canceling out the second layer; the eighth event is the minus oneness returning to the center of the nucleusall of which may be identified with the frequency pulsations of nuclear systems.
[415.43]{style="color: purple3"} []{#ver:415.43 label="ver:415.43"} The None or Nineness/Noneness permits wave frequency propagation cessation. The Nineness/Zeroness becomes a shutoff valve. The Zero/Nineness provides the number logic to account for the differential between potential and kinetic energy. The Nineness/Zeroness becomes the number identity of vector equilibrium, that is, energy differentiation at zero. (See Secs. 1230 et seq. and the Scheherazade Number.)
[415.44]{style="color: purple3"} []{#ver:415.44 label="ver:415.44"} The eightness being nucleic may also relate to the relative abundance of isotopal magic numbers, which read 2, 8, 20, 50, 82, 126…
[415.45]{style="color: purple3"} []{#ver:415.45 label="ver:415.45"} The inherent zero-disconnectedness accounts for the finite energy packaging and discontinuity of Universe. The vector equilibria are the empty set tetrahedra of Universe, i.e., the tetrahedron, being the minimum structural system of Universe independent of size, its four facet planes are at maximum remoteness from their opposite vertexes and may have volume content of the third power of the linear frequency. Whereas in the vector equilibrium all four planes of the tetrahedra pass through the same opposite vertexwhich is the nuclear vertex and have no volume, frequency being zero: .
[415.50]{style="color: purple3"} []{#ver:415.50 label="ver:415.50"} Vector-Equilibrium Closest-Packing Configurations: The vector equilibrium has four unique sets of axes of symmetry:
-
The three intersymmetrical axes perpendicular to, i.e., normal to, i.e., joining, the hemispherically opposite six square faces;
-
The four axes normal to its eight triangular faces;
-
The six axes normal to its 12 vertexes; and
-
the 12 axes normal to its 24 edges.
The tetrahedron, vector equilibrium, and octahedron, with all their planes parallel to those of the tetrahedron, and therefore derived from the tetrahedron, as the first and simplest closest-packed, ergo omnitriangulated, symmetrical structural system, accept further omnidirectional closest packing of spheres. Because only eight of its 20 planar facets are ever parallel to the four planes of the icosahedron, the icosahedron refuses angularly to accommodate anywhere about its surface further omnidirectional closest packing of spheres, as does the tetrahedron.
[415.51]{style="color: purple3"} []{#ver:415.51 label="ver:415.51"} Consequently, the (no-nucleus-accommodating) icosahedron formed of equiradius, triangularly closest-packed spheres occurs only as a one-sphere-thick shell of any frequency only. While the icosahedron cannot accommodate omnidirectionally closest-packed multishell growth, it can be extended from any one of its triangular faces by closest-packed sphere agglomerations. Two icosahedra can be face-bonded.
[415.52]{style="color: purple3"} []{#ver:415.52 label="ver:415.52"} The icosahedron has three unique sets of axes of symmetry:
-
The 15 intersymmetric axes perpendicular to and joining the hemispherically opposite mid-edges of the icosahedron’s 30 identical, symmetrically interpatterned edges;
-
The 10 intersymmetric axes perpendicular to the triangular face centers of the hemispherically opposite 20 triangular faces of the icosahedron; and
-
The six intersymmetric axes perpendicularly interconnecting the hemispheric opposites of the icosahedron’s 12 vertexes, or vertexial corner spheres of triangular closest packing.
[415.53]{style="color: purple3"} []{#ver:415.53 label="ver:415.53"} While the 15-axes set and the 6-axes set of the icosahedron are always angularly askew from the vector equilibrium’s, four out of its 10 axes of symmetry are parallel to the set of four axes of symmetry of the vector equilibrium. Therefore, the icosahedron may be face-extended to produce chain patterns conforming to the tetrahedron, octahedron, vector equilibrium, and rhombic dodecahedron in omnidirectional, closest-packing coordinationbut only as chains; for instance, as open linear models of the octahedron’s edges, etc.
[415.55]{style="color: purple3"} []{#ver:415.55 label="ver:415.55"} Nucleus and Nestable Configurations in Tetrahedra: In any number of successive planar layers of tetrahedrally organized sphere packings, every third triangular layer has a sphere at its centroid (nucleus). The dark ball rests in the valley between three balls, where it naturally falls most compactly and comfortably. The next layer is three balls to the edge, which means two-frequency. There are six balls in the third layer, and there very clearly is a nest right in the middle. There are ten balls in the fourth layer: but we cannot nest a ball in the middle because it is already occupied by a dark centroid ball. Suddenly the pattern changes, and it is no longer nestable.
[415.56]{style="color: purple3"} []{#ver:415.56 label="ver:415.56"} At first, we have a dark ball at the top; then a second layer of three balls with a nest but no nucleus. The third layer with six balls has a nest but no nucleus. The fourth layer with ten balls has a dark centroid ball at the nucleus but no nestable position in the middle. The fifth layer (five balls to the edge; four frequency) has 15 balls with a nest again, but no nucleus. This 35-sphere tetrahedron with five spheres on each edge is the lowest frequency tetrahedron system that has a central sphere or nucleus. (See Fig. A, illustration 415.55. )
[415.57]{style="color: purple3"} []{#ver:415.57 label="ver:415.57"} The three-frequency tetrahedron is the highest frequency single-layer, closest-packed sphere shell without a nuclear sphere. This three-frequency, 20-sphere, empty, or nonsphere nucleated, tetrahedron may be enclosed by an additional shell of 100 balls; and a next layer of 244 balls totaling 364, and so on. (See Fig. B, illustration 415.55.)
[415.58]{style="color: purple3"} []{#ver:415.58 label="ver:415.58"} Basic Nestable Configurations: There are three basic nestable possibilities shown in Fig. C. They are (1) the regular tetrahedron of four spheres; (2) the one-eighth octahedron of seven spheres; and (3) the quarter tetrahedron, with a 16th sphere nesting on a planar layer of 15 spheres. Note that this “nesting” is only possible on triangular arrays that have no sphere at their respective centroids. This series is a prime hierarchy. One sphere on three is the first possibility with a central nest available. One sphere on six is the next possibility with an empty central nest available. One sphere on 10 is impossible as a ball is already occupying the geometrical center. The next possibility is one on 15 with a central empty nest available.
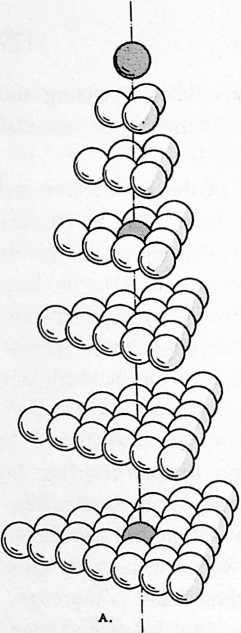
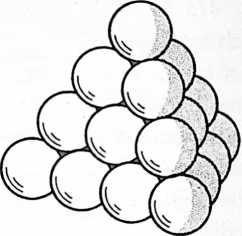
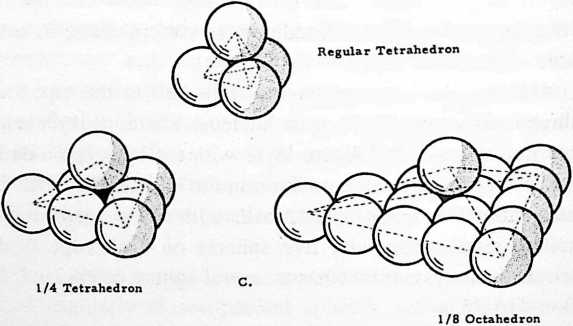
Fig. 415.55 Tetrahedral Closest Packing of Spheres: Nucleus and Nestable Configurations:
-
In any number of successive planar layers of tetrahedrally organized sphere packings, every third triangular layer has a sphere at its centroid (a nucleus). The 36- sphere tetrahedron with five spheres on an edge (four-frequency tetrahedron) is the lowest frequency tetrahedron system which has a central sphere or nucleus.
-
The three-frequency tetrahedron is the highest frequency without a nucleus sphere.
-
Basic “nestable” possibilities show how the regular tetrahedron, the V-i- tetrahedron and the 1/s-octahedron may be defined with sets of closest packed spheres. Note that this “nesting” is only possible on triangular arrays which have no sphere at their respective centroids.
[415.59]{style="color: purple3"} []{#ver:415.59 label="ver:415.59"} Note that the 20-ball empty set (see Fig. B, illustration 415.55 ) consists of five sets of four-ball simplest tetrahedra and can be assembled from five separate tetrahedra. The illustration shows four four-ball tetrahedra at the vertexes colored “white.” The fifth four-ball tetrahedron is dark colored and occupies the central octahedral space in an inverted position. In this arrangement, the four dark balls of the inverted central tetrahedron appear as center balls in each of the four 10-ball tetrahedral faces.
¶ 416.00 Tetrahedral Precession of Closest-Packed Spheres
[416.01]{style="color: purple3"} []{#ver:416.01 label="ver:416.01"} You will find, if you take two separate parallel sets of two tangent equiradius spheres and rotate the tangential axis of one pair one-quarter of a full circle, and then address this pair to the other pair in such a manner as to bring their respective intertangency valleys together, that the four now form a tetrahedron. (See Fig. B, illustration 416.01.)
[416.02]{style="color: purple3"} []{#ver:416.02 label="ver:416.02"} If you next take two triangles, each made of three balls in closest packing, and twist one of the triangles 60 degrees around its center hole axis, the two triangular groups now may be nested into one another with the three spheres of one nesting in the three intersphere tangency valleys of the other. We now have six spheres in symmetrical closest packing, and they form the six vertexes of the octahedron. This twisting of one set to register it close- packedly with the other, is the first instance of two pairs intemested to form the tetrahedron, and in the next case of the two triangles twisted to intemest- ability as an octahedron, is called interprecessing of one set by its complementary set.
[416.03]{style="color: purple3"} []{#ver:416.03 label="ver:416.03"} Two pairs of two-layer, seven-ball triangular sets of closest- packed spheres precess in a 60-degree twist to associate as the cube. (See Fig. A, illustration 416.01.) This 14-sphere cube is the minimum cube that may be stably produced by closest-packed spheres. While eight spheres temporarily may be tangentially glued into a cubical array with six square hole facades, they are not triangulated; ergo, are unstructured; ergo, as a cube are utterly unstable and will collapse; ergo, no eight-ball cube can be included in a structural hierarchy.
[416.04]{style="color: purple3"} []{#ver:416.04 label="ver:416.04"} The two-frequency (three spheres to an edge), two-layer tetrahedron may also be formed into a cube through 90-degree interprecessional effect. (See Fig. A.)
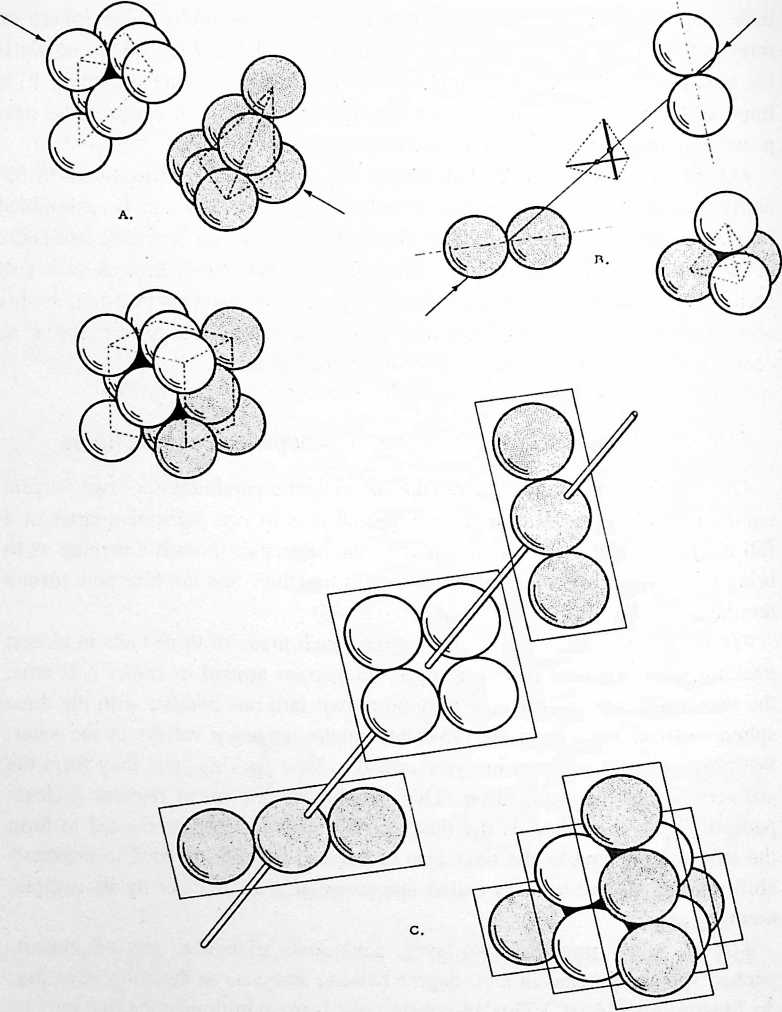
Fig. 416.01 Tetrahedral Precession of Closest Packed Spheres:
-
Two pairs of seven-ball, triangular sets of closest packed spheres precess in 60 degree twist to associate as the cube. This 14-sphere cube is the minimum structural cube which may be produced by closest-packed spheres. Eight spheres will not close-pack as a cube and are utterly unstable.
-
When two sets of two tangent balls are self-interprecessed into closest packing, a half-circle inter-rotation effect occurs. The resulting figure is the tetrahedron.
-
The two-frequency (three-sphere-to-an-edge) equare-centered tetrahedron may also be formed through one-quarter-circle precessional action.
¶ 417.00 Precession of Two Sets of 60 Closest-Packed Spheres
[417.01]{style="color: purple3"} []{#ver:417.01 label="ver:417.01"} Two identical sets of 60 spheres in closest packing precess in 90- degree action to form a seven-frequency, eight-ball-to-the-edge tetrahedron with a total of 120 spheres; exactly 100 spheres are on the outer shell, exactly 20 spheres are in the inner shell, and there is no sphere at the nucleus. This is the largest possible double-shelled tetrahedral aggregation of closest-packed spheres having no nuclear sphere. As long as it has the 20-sphere tetrahedron of the inner shell, it will never acquire a nucleus at any frequency.
[417.02]{style="color: purple3"} []{#ver:417.02 label="ver:417.02"} The 120 spheres of this non-nuclear tetrahedron correspond to the 120 basic triangles that describe unity on a sphere. They correspond to the 120 identical right-spherical triangles that result from symmetrical subdividing of the 20 identical, equilateral, equiangular triangles of ei±er the spherical or planar-faceted icosahedron accomplished by the most economical connectors from the icosahedron’s 12 vertexes to the mid-edges of the opposite edges of their respective triangles, which connectors are inherently perpendicular to the edges and pass through one another at the equitriangles’ center and divide each of the equilaterals into six similar right triangles. These 120 triangles constitute the highest common multiple of system surface division by a single module unit area, as these 30 , 60, 90triangles are not further divisible into identical parts.
[417.03]{style="color: purple3"} []{#ver:417.03 label="ver:417.03"} When we first look at the two unprecessed 60-ball halves of the 120-sphere tetrahedron, our eyes tend to be deceived. We tend to look at them “three-dimensionally,” i.e., in the terms of exclusively rectilinear and perpendicular symmetry of potential associability and closure upon one another. Thus we do not immediately see how we could bring two oblong quadrangular facets together with their long axes crossing one another at right angles.
[417.04]{style="color: purple3"} []{#ver:417.04 label="ver:417.04"} Our sense of exclusively perpendicular approach to one another precludes our recognition that in 60-degree (versus 90-degree) coordination, these two sets precess in 60-degree angular convergence and not in parallel- edged congruence. This 60-degree convergence and divergence of mass- attracted associabilities is characteristic of the four-dimensional system.
¶ 418.00 Analogy of Closest Packing, Periodic Table, and Atomic Structure
[418.01]{style="color: purple3"} []{#ver:418.01 label="ver:418.01"} The number of closest-packed spheres in any complete layer around any nuclear group of layers always terminates with the digit 2. First layer, 12; second, 42; third, 92 …162, 252, 362, and so on. The digit 2 is always preceded by a number that corresponds to the second power of the number of layers surrounding the nucleus. The third layer’s number of 92 is comprised of the 3 multiplied by itself (i.e., 3 to the second power), which is 9, with the digit 2 as a suffix.
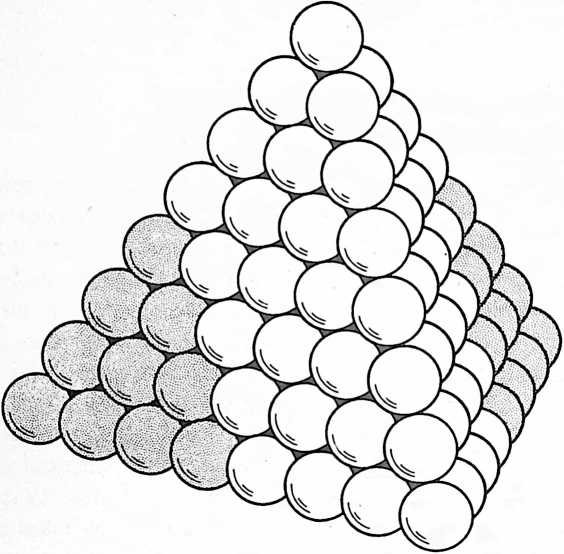
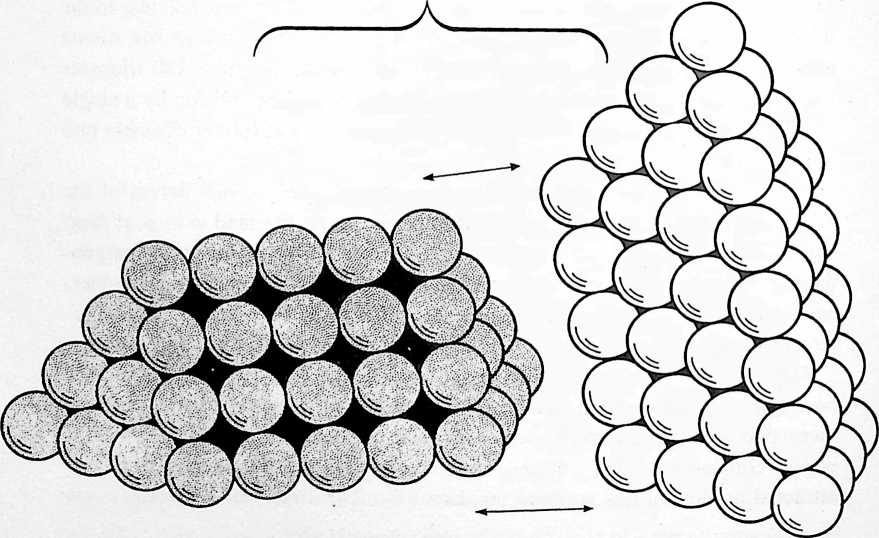
Fig- 417.01 Precession of Two Sets of 60 Closest-Packed Spheres as Seven-Frequency Tetrahedron: Two identical sets of 60 spheres in closest packing precess in 90-degree action to form a seven-frequency, eight-ball-edged tetrahedron with a total of 120 spheres, of which exactly 100 spheres are on the surface of the tetrahedron and 20 are inside but have no geometrical space accommodation for an equiradius nuclear sphere. The 120-sphere, nonnucleated tetrahedron is the largest possible double-shelled tetrahedral aggregation of closest-packed spheres having no nuclear sphere.
[418.02]{style="color: purple3"} []{#ver:418.02 label="ver:418.02"} This third layer is the outermost of the symmetrically unique, nuclear-system patterns and may be identified with the 92 unique, self-regenerative, chemical-element systems, and with the 92nd such elementuranium.
[418.03]{style="color: purple3"} []{#ver:418.03 label="ver:418.03"} The closest-sphere-packing system’s first three layers of 12, 42, and 92 add to 146, which is the number of neutrons in uraniumwhich has the highest nucleon population of all the self-regenerative chemical elements; these 146 neutrons, plus the 92 unengaged mass-attracting protons of the outer layer, give the predominant uranium of 238 nucleons, from whose outer layer the excess two of each layer (which functions as a neutral axis of spin) can be disengaged without distorting the structural integrity of the symmetrical aggregate, which leaves the chain-reacting Uranium 236.
[418.04]{style="color: purple3"} []{#ver:418.04 label="ver:418.04"} All the first 92 chemical elements are the finitely comprehensive set of purely abstract physical principles governing all the fundamental cases of dynamically symmetrical, vectorial geometries and their systematically self-knotting, i.e., precessionally self-interfered, regenerative, inwardly shunting events.
[418.05]{style="color: purple3"} []{#ver:418.05 label="ver:418.05"} The chemical elements are each unique pattern integrities formed by their self-knotting, inwardly precessing, periodically synchronized selfinterferences. Unique pattern evolvement constitutes elementality. What is unique about each of the 92 self-regenerative chemical elements is their nonrepetitive pattern evolvement, which terminates with the third layer of 92.
[418.06]{style="color: purple3"} []{#ver:418.06 label="ver:418.06"} Independent of their isotopal variations of neutron content, the 92 self-regenerative chemical elements belong to the basic inventory of cosmic absolutes. The family of prime elements consists of 92 unique sets of from one to 92 electron-proton counts inclusive, and no others.
¶ 419.00 Superatomics
[419.01]{style="color: purple3"} []{#ver:419.01 label="ver:419.01"} Those subsequently isolated chemical elements beyond the 92 prime self-regenerative chemical elements constitute super-atomics. They are the non-self-regenerative chemical elements of negative Universe.
[419.02]{style="color: purple3"} []{#ver:419.02 label="ver:419.02"} Negative Universe is the complementary but invisible Universe. To demonstrate negative Universe, we take one rubber glove with an external green surface and an internal red surface. On the green surface a series of 92 numbers is patterned; and on the red surface a continuance of 93, 94, through to 184, with number 184 at the inside end of the pinkyeach of the inner surface numbers being the inner pole of the outer pole point number positionings. The positions of the numbers on the inside correspond to the positions of the numbers on the outside. The numbering starts with the position of the five fingernails, then their successive first joints, and then their successive second joints from the tips: 5, 10, 15, and 20 numbers accommodated by the digits. The other 62 members are arranged in four rows of 12 each around the back and front of the palm of the hand. There is a final row of 14 at the terminal edge of the glove openingthis makes a total of 92. Now we can see why the 92 numbers on the outside were discoverable in a random manner requiring very little physical effort. It was just a matter of which part of your gloved hand you happened to be looking at. But if we become curious about what may be on the inside of the glove we discover that the glove is powerfully resilient. It takes a great deal of power to turn it up, to roll back the open edge and it takes increasing amounts of power to cope with the increasing thickness of the rubber that rolls up as the glove opens. The elements from 93 on are revealed progressively by the numbers.
[419.03]{style="color: purple3"} []{#ver:419.03 label="ver:419.03"} The discovery of the first 92 self-regenerative chemical elements was not by the numbers starting with one, but in a completely random sequence. In the super-atomics, beyond Uranium, number 92, the split- second-lived chemical elements have been discovered in a succession that corresponds to their atomic numberfor example, the 94th discovery had the atomic weight of 94; the 100th discovery was atomic weight 100, etc.
[419.04]{style="color: purple3"} []{#ver:419.04 label="ver:419.04"} This orderly revelation is in fundamental contrast to the discoveries of the 92 self-regenerative elements and their naturally self-regeneratively occurring isotopes. The discovery of the post-uranium elements has involved the employment of successively greater magnitudes of energy concentration and focusing. As each of the super-atomic trans-uranium elements was isolatingly discovered, it disintegrated within split seconds. The orderliness of the succession of the discovery of super-atomics corresponds to the rate of increase of the magnitudes of energy necessary to bring them into split-second identifiability before they revert to their insideergo, invisible to outsideposition.
[419.05]{style="color: purple3"} []{#ver:419.05 label="ver:419.05"} []{#ver:419.05 label="ver:419.05"} Every layer of a finite system has both an interior, concave, associability potential and an exterior, convex, associability potential. Hence the outer layer of a vector-equilibrium-patterned atom system always has an additional full number “unemployed associability” count. In the example cited above (Sec. 418.03), an additional 92 was added to the 146 as the sum of the number of spheres in the first three shells. The total is 238, the number of nucleons in uranium, whose atomic weight is 238. Four of the nucleons on the surface of one of the square faces of the vector equilibrium’s closest-packed aggregation of nucleons may be separated out without impairing the structural-stability integrity of the balance of the aggregate. This leaves a residue of 236 nucleons, which is the fissionable state of uraniumwhich must go on chain-reacting due to its asymmetry.
¶ 419.10 Nuclear Domain and Elementality
[419.11]{style="color: purple3"} []{#ver:419.11 label="ver:419.11"} Where the primitive polyhedron considered is the vector equilibrium, the closest-packed-sphere-shell growth rate is governed by the formula (Sec. 222). Where the most primitive polyhedron is the tetrahedron, the growth rate is governed by the formula ; in the cases of the octahedron and the cube see Sec. 223.21. The formula is reliably predictable in the identification of the chemical elements and their respective neutron inventories for each shell. The identifications are related exclusively to the unique nuclear domain pattern involvements.
[419.12]{style="color: purple3"} []{#ver:419.12 label="ver:419.12"} When a new nucleus becomes completely surrounded by two layers, then the exclusively unique pattern surroundment of the first nucleus is terminated. Thereafter, at three enclosure levels or more, the initial nucleus is no longer the unique nucleus. The word elemental relates to the original unique patterning around any one nucleus of closest-packed spheres. When we get beyond the original unique patterning, we find the patternings repeating themselves, and we enter into the more complex structurings of the molecular world.
[419.13]{style="color: purple3"} []{#ver:419.13 label="ver:419.13"} Uranium-92 is the limit case of what we call inherently self- regenerative chemical elements. Beyond these we get into demonstrations of non-self-regenerative elements with the split-second life of Negative Universe. These demonstrations are similar to having a rubber ball with a hole in its skin and stretching that hole’s rubber outwardly around the hole until we can see the markings on the inner skin that correspond to markings on the outer skinbut when we release the ball, the momentarily outwardly displayed markings on the inside will quickly resume their internal positions.
[419.14]{style="color: purple3"} []{#ver:419.14 label="ver:419.14"} As we see in Sec. 624, the inside-outing of Universe occurs only at the tetrahedral level. In the nucleated, tetrahedral, closest-packed-sphereshell growth rates the outward layer sphere count increases as frequency to the second power times two plus twowith the outer layer also always doubled in value.
¶ 419.20 Elemental Identification of First and Second Shell
[419.21]{style="color: purple3"} []{#ver:419.21 label="ver:419.21"} The outer layer of the vector equilibrium aggregates always equals the shell wave frequencies to the second power times 10 plus two. The sum of all the layers equals the number of neutrons of the elements, and the outer layer is always complemented by an equal number of active nucleons, which, if added to the sum of the previously encompassed neutron layer, equals the isotope number.
[419.22]{style="color: purple3"} []{#ver:419.22 label="ver:419.22"} The omnidirectional closest packing of spheres in all six symmetrical conformations of the primitive hierarchy of polyhedra probably provides models for all the chemical elements in a hierarchy independent of size in which the sum of the spheres in all the layers and the nuclear sphere equals the most prominent number of neutrons, and the number in the outer layer alone equals the number of protons of each atom. In the VE symmetry of layer growth the sum of the spheres is one and the outer layer is one: the initial sphere represents the element hydrogen, with the atomic number 1, having one neutron and one proton. The second VE assembly layer, magnesium, with the atomic number 12, has 12 protons and 24 neutrons. The third layer, molybdenum, with the atomic number 42, has 42 protons and a majority of 54 neutrons. The fourth layer, uranium, with the atomic number 92, has 92 protons and an isotopal majority of 146 neutrons. (Compare Secs. 986.770 and 1052.32.)
[419.23]{style="color: purple3"} []{#ver:419.23 label="ver:419.23"} Table: Number of Protons and Neutrons in Magnesium, Molybdenum, and Uranium
+:------------------+:-------------+:------------+
| Element Protons | Neutrons | Abundance |
+-------------------+--------------+-------------+
| Hydrogen 1 | + 1 = 2 | |
+-------------------+--------------+-------------+
| Magnesium 12 | + 12 =24 | % |
+-------------------+--------------+-------------+
| ::: minipage | + 13 =25 | |
| > 12 | | |
| ::: | | |
+-------------------+--------------+-------------+
| ::: minipage | + 14 =26 | |
| > 12 | | |
| ::: | | |
+-------------------+--------------+-------------+
| Molybdenum. 42 | + 52 =94 | |
+-------------------+--------------+-------------+
| ::: minipage | + 53 =95 | |
| > 42 | | |
| ::: | | |
+-------------------+--------------+-------------+
| ::: minipage | + 54 =96 | |
| > 42 | | |
| ::: | | |
+-------------------+--------------+-------------+
| ::: minipage | + 55 =97 | |
| > 42 | | |
| ::: | | |
+-------------------+--------------+-------------+
| ::: minipage | + 56 =98 | |
| > 42 | | |
| ::: | | |
+-------------------+--------------+-------------+
| Uranium 92 | + 142 = 234 | |
+-------------------+--------------+-------------+
| ::: minipage | + 143 =235 | |
| > 92 | | |
| ::: | | |
+-------------------+--------------+-------------+
| ::: minipage | + 146 =238 | |
| > 92 | | |
| ::: | | |
+-------------------+--------------+-------------+
| | | |
+-------------------+--------------+-------------+
[419.30]{style="color: purple3"} []{#ver:419.30 label="ver:419.30"} Closest-sphere-packing Analogy to Atomic Structure: In 1978 Philip Blackmarr, a student of synergetics from Pasadena, proposed a novel analogy of closest-sphere-packing geometry to electron-proton-neutron interrelationships and atomic structure. He took note of the following four facts;
-
In the closest packing of unit radius spheres each spheric and interspheric space domain is equally and symmetrically embraced by allspace-filling rhombic dodecahedra. (Sec. 426.20.)
-
The concentrically embracing shells of the vector equilibrium have a successive population growth rate of , resulting in 12 spheres in the first layer, 42 in the second, 92 in the third, and 162 in the fourth. (See Chart 415.03.)
-
In the concentric successive shells of closest-packed spheres a new nucleus does not appear until the fifth frequencythe fifth shell layer. (Secs. 414 and 415.30.)
-
The ratio of the electron mass to the proton mass is 1 : 1836. (Sec. 433.02.)
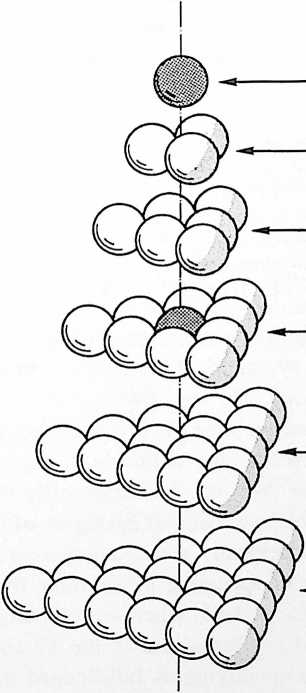NUCLEUS
1st SHELL OF 12 SPHERES
Fig. [419.30 Realized Nucleus Appears at Fifth Shell Layer:]{style="color: purple3"} []{#ver:419.30 Realized Nucleus Appears at Fifth Shell Layer: label="ver:419.30 Realized Nucleus Appears at Fifth Shell Layer:"} In concentric closest packing of successive shell layers potential nuclei appear at the third shell layer, but they are not realized until surrounded by two shells at the fifth layer.
2nd SHELL OF 42 SPHERES
3rd SHELL OF 92 SPHERES
4th SHELL OF 162 SPHERES
5th SHELL OF 252 SPHERES
Bearing those four facts in mind Blackmarr employed a symmetrical four- shell aggregate of 308 rhombic dodecahedra to represent the total allspace-filling domains of the 308 spheres of the maximum limit nuclear domain. He then intuitively divided the number 1836 by 6, the latter being the volume of the rhombic dodecahedron in respect to the volume of the tetrahedron as one. The number becomes significant as it represents the total number of neutron spheric domains in the vector equilibrium concentric shell packingless the number two of their integral number to serve as poles of the axis of spin of the symmetrical system. The spheres in the successive shell layers, 42, 92, 162add up to 308; . (Compare Sec. 418.)
[419.31]{style="color: purple3"} []{#ver:419.31 label="ver:419.31"} Blackmarr then hypothetically identified the electron as the volume of the unit-vector-edge tetrahedron as ratioed to the volume of the four-frequency vector equilibrium, representing a symmetrical and “solid” agglomeration of 308 rhombic dodecahedra (with two of the outer-layer rhombic dodecahedra assigned to serve as the symmetrically opposite poles of the system’s axis of spin), or of 308 unit-radius spheres and their interspaces. This evidences that the space filled by the 308 rhombic dodecahedra is the maximum, cosmic-limit, unit-vector, symmetrical polyhedral space occupiable by a single nucleus.
[419.32]{style="color: purple3"} []{#ver:419.32 label="ver:419.32"} /
The volume of the ELECTRON /The volume of the rhombic- 1 /
(which is that of one regular vector/ dodecahedron-composed four-fre- = / edged negative tetrahedron) / quency VECTOR EQUILIBRIUM / 1836
The volume of the POSITRON / The volume of the rhombic- 1 /
(which is that of one regular vector-/ dodecahedron-composed four-fre- = /
edged positive tetrahedron) / quency VECTOR EQUILIBRIUM /1836
[419.33]{style="color: purple3"} []{#ver:419.33 label="ver:419.33"} Here is an elegant realization that two spheres of the outer-layer spheres (or rhombic dodecahedra) of the symmetrical system have to serve as the polar axis of the system spin. (See Secs. 223 and 1044.)
[419.34]{style="color: purple3"} []{#ver:419.34 label="ver:419.34"} Thus by experimental evidence we may identify the electron with the volume of the regular, unit-vector-radius-edge tetrahedron, the simplest symmetrical structural system in Universe. We may further identify the electron tetrahedra with the maximum possible symmetrical aggregate of concentrically-packed, unit-radius spheres symmetrically surrounding a single nucleusthere being 12 new potential nuclei appearing in the three-frequency shell of 92 spheres, which three-frequency shell, when surroundingly embraced by the four-frequency shell of 162 spheres, buries the 12 candidate new nuclei only one shell deep, whereas qualifying as full-fledged nuclei in their own right requires two shells all around each, which 12, newborn nuclei event calls for the fifth-frequency shell of 252 spheres.
[419.35]{style="color: purple3"} []{#ver:419.35 label="ver:419.35"} Together with the closest-packed spheres of the outer layer of the icosahedron of frequencies 1 and 4 (and of the outer layers of the closest-packed spheres of the oneand only onenucleus-embracing, symmetrically and closest-packed, unit-radius sphere aggregates in the form of the octahedron, rhombic dodecahedron, rhombic triacontahedron, and enenicontahedron) as well as the already identified four-frequency vector equilibrium, the rhombic dodecahedron is the maximum nuclear domain within which the pretime-size set of chemical-element-forming atoms’ proton-neutron-and-electron interrelationship events can and may occur.
[419.36]{style="color: purple3"} []{#ver:419.36 label="ver:419.36"} All of the foregoing is to say that the size of one spinnable proton consisting of 308 rhombic dodeca closest packed in the symmetrical form of the four-frequency vector equilibrium is 1836 times the size of one prime, pre-time-size, prefrequency, unit-vector-edge tetrahedron or of one electron. Multiplication only by division means that the time-size frequencies of the elements (other than hydrogen) occur as various concentric-shell symmetry phases of the single-nucleus-embracing, symmetrically closest-packed, single nucleus aggregates in the multiconcentric-layered forms of the vector equilibrium, tetrahedron, octahedron, rhombic dodecahedron, rhombic triacontahedron, and cube.
[419.37]{style="color: purple3"} []{#ver:419.37 label="ver:419.37"} Synergetics has long associated the electron with the icosahedron. Icosahedra cannot accommodate concentric shells; they occur as single-layer shells of closest-packed, unit-radius spheres. Since the proton has only the outer shell count, it may be identified with the icosa phase by having the total volume of the rhombic-dodecahedron-composed four-frequency vector equilibrium transformed from the 306 (non-axial) nucleon rhombic dodecahedron into each of the closest-packed, single-layer icosahedra shells as an emitted wave entity. The rhombic dodecahedron neutrons are packed into concentric layers of the vector equilibria to produce the various isotopes. For example:
+:-------------+:--------------------------+
| VE f1 - | = 12 neutrons |
| | |
| VE f2 | = 42 |
| | |
| VE f3 = | = [92]{.underline} |
| | |
| | 146 neutrons in Uranium |
+--------------+---------------------------+
| Icosa f3 - | = 92 protons |
| | |
| | (238 nucleons in Uranium) |
+--------------+---------------------------+
92 Tetra = 92 electrons in Uranium
¶ 420.00 Isotropic Vector Matrix
[420.01]{style="color: purple3"} []{#ver:420.01 label="ver:420.01"} When the centers of equiradius spheres in closest packing are joined by most economical lines, i.e., by geodesic vectorial lines, an isotropic vector matrix is disclosed“isotropic” meaning “everywhere the same,” “isotropic vector” meaning “everywhere the same energy conditions.” This matrix constitutes an array of equilateral triangles that corresponds with the comprehensive coordination of nature’s most economical, most comfortable, structural interrelationships employing 60-degree association and disassociation. Remove the spheres and leave the vectors, and you have the octahedron-tetrahedron complex, the octet truss, the isotropic vector matrix.
[420.02]{style="color: purple3"} []{#ver:420.02 label="ver:420.02"} The isotropic vector matrix is four-dimensional and 60-degree- coordinated. It provides an omnirational accounting system that, if arbitrarily accounted on a three-dimensional, 90-degree basis, becomes inherently irrational. The isotropic vector matrix demonstrates the ability of the symmetrically and asymmetrically terminaled, high-frequency energy vectors to accommodate the structuring of any shape. (See Sec. 932, “Constant Volume.”)
[420.03]{style="color: purple3"} []{#ver:420.03 label="ver:420.03"} Our extension of the Avogadro hypothesis (Sec. 410) generalizes that all energy conditions are the same. Inasmuch as vectors describe energy conditions, this would mean a volumetric aggregation of vectors in a structural complex in which all of the interacting vectors would have to be of the same length and all of their intersecting angles would have to be the same. This state of omnisameness of vectors stipulates the “isotropic,” meaning everywhere the same. This prescribes an everywhere state of equilibrium.
¶ 420.04 Equilibrium
[420.041]{style="color: purple3"} []{#ver:420.041 label="ver:420.041"} Nature is said to abhor an equilibrium as much as she abhors a perfect vacuum or a perfect anything. Heisenberg’s indeterminism and quasiprecision mechanics’ recognition of inherent inaccuracy of observation or articulation seems to suggest that the asymmetric deviations and aberrations relative to equilibrium are inherent in the imperfection of a limited life of humans with a tightly limited range of perceptible differentiation of details of its experience. Nature demonstrates her abhorrence of equilibrium when an airplane in flight slows to a speed that reduces the airfoil “lift” and brings the airplane’s horizontal flight forces into equilibrium with Earth gravity’s vertically Earthward pull. The plane is said then to stall, at which moment the plane’s indeterminate direction makes it unmanageable because the rudder and elevator surfaces lack enough passing air to provide steerability, and the plane goes swiftly through equilibrium and into an Earthward-spinning plunge. Despite the untenability of equilibrium, it seemed to me that we could approach or employ it referentially as we employed a crooked linethe deliberately nonstraight (see Sec. 522) line that approaches but never reaches the perfect or exact. A comprehensive energy system could employ the positive and negative pulsations and intertransformative tendencies of equilibrium. The vector equilibrium became the logical model of such omnidimensional, omniexperience-accommodation studies. Because we have learned that scientists have experimental evidence only of waves and wavilinearity and no evidence of straight lines, it became evident that the radial and circumferential vectors of the vector equilibrium must be wavilinear, which meant that as coil springs when compressioned will lessen in length and when tensed will be increased in lengthergo, the explosive disintegrative radial forces of Universe would compress and lessen in outward disintegrative length and would be well inside the closed-back-on-itself, hexagonally tensed, embracing vectors, indicating a higher effectiveness of tensile integrity of Universe over any locally disintegrative forces. The comprehensive vector-equilibrium system would also have to recognize all the topological interpatterning characteristics and components; also, as a quasi-equilibrious system, all of its structural component vectors would have to be approximately the same length; therefore, all the interangulation would have to be in aberration increments relative to 60 degrees as the equilibrious norm.
EARTH ORBIT IN MAN MADE ENVIRONMENT CONTROL: PRODUCT OF SUCCESSFUL APPLICATION OF HIGH PERFORMANCE PER UNIT OF INVESTED RESOURCES
PROFILE OF THE INDUSTRIAL REVOLUTION AS EXPOSED BY THE CHRONOLOGICAL RATE OF ACQUISITION OF THE BASIC INVENTORY OF COSMIC ABSOLUTES-THE 92 ELEMENTS
Fig. 419.03.
STEAMSHIP
AIRPLANE ROCKET
2010 A.O
J 103* LAWRENCIUM JI02* NOBELIUM JI01* MENDELEVIUM JlOO* FERMIUM f 99* EINSTEINIUM f 98* CALIFORNIUM 97* BERKELIUM 96* PROMETHIUM 95* AMERICIUM
NUMBER
TKHNKAL ACQUSmON BY SC1DKI 08 91 ATOMIC HI- MINTS B COMMITTO 1933 AMO WTH ATOMICS COMMJNd
40 MAGNESIUM 39 IRIDIUM 38 OSMIUM
37 PALLADIUM 36 RHODIUM 35 CERIUM
34 TANTALUM
33 COLUM8IUM
32 CHROMIUM 31 BERYLLIUM
30 YTTRIUM 29 TITANIUM 28 ZIRCONIUM 27 URANIUM 26 TUNGSTEN 25 TELLURIUM 24 MOLYBDENUM 23 MANGANESE 22 CHLORINE 21 OXYGEN 20 NITROGEN 19 FLUORINE 18 HYDROGEN 17 NICKEL 16 BISMUTH
15 ZINC 14 PLATINUM 13 COBALT
J IB RHENIUM
[1]{.underline} 87 HAFNIUM i [1]{.underline}86* PROTACTINIUM » 91
1 8S LUTETIUM Je-T RADON J W“ ACTINIUM 82* POLONIUM 81’ RADIUM 80 XEON 79 KRYPTON I 78 NEON [77 EUROPIUM J76 HEUUM T75 ARGON 174 GERMANIUM J 73 DYSPROSIUM p2 NEODYMIUM 171 PRASEODYMIUM [70 GADOLINIUM 69 SAMARIUM 68 HOLMIUM 67 SCANDIUM 66 THULIUM J65 YTTERBIUM [1]{.underline}64 GALLIUM 163 [Indium]{.smallcaps} 62 THALLIUM 161 RUBIDIUM [,]{.underline}60 CESIUM J59 RUTHENIUM [58 ERBIUM J 57 TERBIUM 156 LANTHANUM VANADIUM
I 94* CURIUM • 96 c- [usa]{.smallcaps}
93* PLUTONIUM • 94 [n’ usa]{.smallcaps}
I 92* NEPTUNIUM «9J «»*
J 91* ASTATINE »85 *’ [usa]{.smallcaps}
[ 90* FRANCIUM 87 *
89* TECHNETIUM • 43 »« USA
• 61
“18 A
J53 BROMINE
F51 [silicon]{.smallcaps}
f50 SELENIUM “3
CADMIUM “41
148 UTHIUM “3
J47 IODINE •5Z 1
46 BORON “5
45 BARIUM “56
44 STRONTIUM “38
43 CALCIUM "20 c«
42 POTASSIUM “19
41 SODIUM “11 Na
IlMMMTIVt TOTAL 08 MY INVENTIONS OF SCIENCE ANO TECHNOLOGY
•flfio 160 ifa l/lO I7bo 1750 I7>o
i/ro iiio
450
18*30 18*50
1.450 10.000
1870 1890 1910 19*30 1950 1970 AO
Copyright 1946 and 1964 by R. BUCKMINSTER FULLER
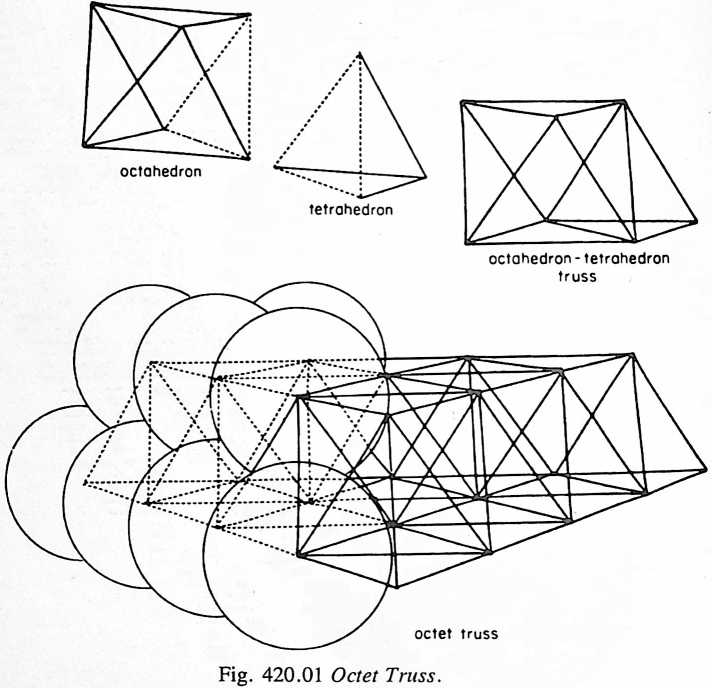
Fig. 420.02 When the centers of equiradius spheres in closest packing are joined with lines, an isotropic vector matrix is formed. This constitutes an array of equilateral triangles which is seen as the comprehensive coordination frame of reference of nature’s most economical, most comfortable structural interrelationships employing 60-degree association and disassociation. This provides an omnirational accounting system which, if arbitrarily accounted on a 90-degree basis, becomes inherently irrational. The isotropic vector matrix demonstrates the capability of accommodating all symmetrically and asymmetrically terminaled, high-frequency energy vectors of any structural shaping.
[420.05]{style="color: purple3"} []{#ver:420.05 label="ver:420.05"} The closest-packing-of-spheres model coincides with the observed real world’s atomic packing of like atoms with their own counterparts.
[420.06]{style="color: purple3"} []{#ver:420.06 label="ver:420.06"} We find that the space compartmentation formed by the vectors connecting the sphere centers always consists only of tetrahedra and octahedra. The spheres in closest packing coincide with the Eulerian vertexes; the vectors between the sphere centers are the Eulerian edges; and the triangles so formed are the “faces.”
[420.07]{style="color: purple3"} []{#ver:420.07 label="ver:420.07"} All of the polygons formed by the interacting vectors of the isotropic vector matrix consist entirely of equilateral triangles and squares. The squares occur as equatorial cross sections of the octahedra. The triangles occur as the external facets of both the tetrahedra and the octahedra.
[420.08]{style="color: purple3"} []{#ver:420.08 label="ver:420.08"} All the polygons are reducible to triangles and are not further reducible. All polyhedra are reducible to triangulation, i.e., to trusses and are not further reducible. Infinite polyhedra are infinitely faceted by basic trusses.
¶ 421.00 Function of Nucleus in Isotropic Vector Matrix
[421.01]{style="color: purple3"} []{#ver:421.01 label="ver:421.01"} Because the spacing of absolutely compacted spheres is tangential and hexagonal in great-circle cross section around any one sphere, the contact points are always spaced equidistant from the centers of the spheres and from their immediately neighboring points, respectively; wherefore the dimensions of a system of lines joining each and all adjacent spherical centers are identical to the universal radii of the identical spheres and, therefore, to each other. Such a universal system of identically dimensioned lines, growing outwardly from any one nuclear vertex, constitutes a universal vector system in dynamic equilibrium, for all the force lines are of equal magnitude.
[421.02]{style="color: purple3"} []{#ver:421.02 label="ver:421.02"} In the isotropic vector matrix, every vector leads from one nuclear center to another, and therefore represents the operational effect of a merging of any two or more force centers upon each other. Each vector is composed of two halves, each half belonging respectively to any two adjacent nuclear centers. Each half of the interconnecting vectors represents the radius of one of the two spheres tangent to one another at the vector midpoints.
[421.03]{style="color: purple3"} []{#ver:421.03 label="ver:421.03"} Unity as represented by the internuclear vector modulus is of necessity always of the value of two, for it represents union of a minimum of two energy centers. (See Sec. 240.40.)
[421.031]{style="color: purple3"} []{#ver:421.031 label="ver:421.031"} Function of Nucleus in Isotropic Vector Matrix: Every vector has two ends both of which join with other vectors to produce both structural systems and total cosmic integrity of regeneration. Every vector unites two ends.
[421.04]{style="color: purple3"} []{#ver:421.04 label="ver:421.04"} Each nuclear ball can have a neutral function among the aggregates. It is a nuclear ball whether it is in a planar array or in an omnidirectional array. It has a unique function in each of the adjacent systems that it bonds.
[421.05]{style="color: purple3"} []{#ver:421.05 label="ver:421.05"} The nucleus can accommodate wave passage without disrupting the fundamental resonance of the octaves. The tetrahedron is the minimum, ergo, prime, non-nucleated structural system of Universe. The vector equilibrium is the minimum, ergo prime, nucleated structural system of Universe.
[421.10]{style="color: purple3"} []{#ver:421.10 label="ver:421.10"} Corollary: Identically dimensioned nuclear systems and layer growths occur alike, relative to each and every absolutely compacted sphere of the isotropic vector matrix conglomerate, wherefore the integrity of the individual energy center is mathematically demonstrated to be universal both potentially and kinetically (Sec. 240.50 ).
¶ 421.20 Ideal Vectorial Geometry of Nucleated Systems
[421.21]{style="color: purple3"} []{#ver:421.21 label="ver:421.21"} It is experientially suggested that the structural interpatterning principles apparently governing all atomic associability behaviors are characterized by triangular and tetrahedral accommodation, wherein the tetrahedron’s six positive and six- negative vectorial edge forces match a total of 12 universal degrees of freedom. The tetrahedron’s exclusively edge-congruent-agglomeratability around any one nuclear point produces the vector equilibrium. These structural, pattern-governing, conceptualizable principles in turn govern all eternally regenerative design evolution, including the complex patterning of potential, symmetrically and asymmetrically limited, pulsative regenerations, only in respect to all of which are ideas conceivable. These patternings are experientially manifest in synergetics’ closed-system topological hierarchy through which we can explore the ramifications of the idealistic vectorial geometry characteristics of inherently nucleated systems and their experientially demonstrable properties. (For possible relevance to the periodic table of the elements see Sec. 955.30.)
¶ 422.00 Octet Truss
[422.01]{style="color: purple3"} []{#ver:422.01 label="ver:422.01"} In an isotropic vector matrix, there are only two clear-space polyhedra described internally by the configuration of interacting vectors: these are the regular tetrahedron and the regular octahedron operating as complementary space fillers. The single octahedron-tetrahedron deep truss system is known in synergetics as the octet truss.
[422.02]{style="color: purple3"} []{#ver:422.02 label="ver:422.02"} The octet truss, or the isotropic vector matrix, is generated by the asymmetrical closest-packed sphere conglomerations. The nuclei are incidental.
[422.03]{style="color: purple3"} []{#ver:422.03 label="ver:422.03"} When four tetrahedra of a given size are symmetrically intercombined by single bonding, each tetrahedron will have one of its four vertexes uncombined, and three combined with the six mutually combined vertexes symmetrically embracing to define an octahedron; while the four noncombined vertexes of the tetrahedra will define a tetrahedron twice the edge length of the four tetrahedra of given size; wherefore the resulting central space of the double-size tetrahedron is an octahedron. Together, these polyhedra comprise a common octahedron-tetrahedron system.
[422.04]{style="color: purple3"} []{#ver:422.04 label="ver:422.04"} The tetrahedronated octahedron and all other regular symmetrical polyhedra known are described repetitiously by compounding two types of rational fraction asymmetric elements of the tetrahedron and octahedron. These elements are known in synergetics as the and Quanta Modules. (See Sec. 920.)
[422.10]{style="color: purple3"} []{#ver:422.10 label="ver:422.10"} Force Distribution: In the three-way grid octet truss system, concentrated energy loads applied to any one point are distributed radially outward in nine directions and are immediately diffused into the finite hexagonally arranged six vectors entirely enclosing the six-way-distributed force. Each of the hexagon’s six vertexes distribute the loads 18 ways to the next outwardly encircling vectors, which progressively diffusing system ultimately distributes the original concentrated energy force equally to all parts of the system as with a pneumatic tire. Thus the system joins together synergetically to distribute and inhibit the forces.
[422.20]{style="color: purple3"} []{#ver:422.20 label="ver:422.20"} Geometry of Structure: Considered solely as geometry of structure, the final identification of the octet truss by the chemists and physicists as closest packing also identifies the octet truss and vector equilibria structuring as amongst the prime cosmic principles permeating and facilitating all physical experience.
¶ 423.00 60-Degree Coordination
[423.01]{style="color: purple3"} []{#ver:423.01 label="ver:423.01"} In the octet truss system, all the vectors are of identical length and all the angles around any convergence are the same. The patterns repeat themselves consistently. At every internal convergence, there are always 12 vectors coming together, and they are always convergent at 60 degrees with respect to the next adjacent ones.
[423.02]{style="color: purple3"} []{#ver:423.02 label="ver:423.02"} There are angles other than 60-degrees generated in the system, as for instance the square equatorial mid-section of the octahedron. These angles of other than 60-degrees occur between non-adjacently converging vectorial connectors of the system. The prime structural relationship is with the 60-degree angle.
[423.03]{style="color: purple3"} []{#ver:423.03 label="ver:423.03"} Fundamental 60-degree coordination operates either circumferentially or radially. This characteristic is lacking in 90-degree coordination, where the hypotenuse of the 90-degree angles will not be congruent and logically integratable with the radials.
[423.04]{style="color: purple3"} []{#ver:423.04 label="ver:423.04"} When we begin to integrate our arithmetical identities, as for instance n2 or n3, with a 60-degree coordination system, we find important coincidence with the topological inventories of systems, particularly with the isotropic vector matrix which makes possible fourth- and fifth-power modeling.
[423.10]{style="color: purple3"} []{#ver:423.10 label="ver:423.10"} Hexagon as Average of Angular Stabilizations: The irrational radian and pi [(tt)]{.smallcaps} are not used by nature because angular accelerations are in finite package impellments [^10] which are chordal (not arcs) and produce hexagons because the average of all angular stabilizations from all triangular interactions average at 60 degreesergo, radii and 60-degree chords are equal and identical; ergo, six 60-degree chords equal one frequency cycle; ergo, one quantum. Closest packed circles or spheres do not occupy all area or space, but six-triangled, nucleated hexagons do constitute the shortest route cyclic enclosure of closest-packed nucleation and do uniformly occupy all planar area or volumetric space.
¶ 424.00 Transformation by Complementary Symmetry
[424.01]{style="color: purple3"} []{#ver:424.01 label="ver:424.01"} The octet truss complex is a precessionally nonredundant, isotropic vector-tensor evolutionary relationship whose energy transformation accountings are comprehensively rationalradially and circumferentiallyto all chemical, biological, electromagnetic, thermodynamic, gravitational, and radiational behaviors of nature. It accommodates all transformations by systematic complementary symmetries of concentric, contractile, involutional, turbo-geared, rational, turbulence-accommodating, inside-outing, positive-to-negative-to-equilibrium, pulsative coordinate displacements.
[424.02]{style="color: purple3"} []{#ver:424.02 label="ver:424.02"} Thus we see both the rational energy quantum of physics and the topological tetrahedron of the isotropic vector matrix rationally accounting all physical and metaphysical systems and their transformative transactions.
[424.03]{style="color: purple3"} []{#ver:424.03 label="ver:424.03"} This indefinitely extending vector system in dynamic equilibrium provides a rational frame of reference in universal dimension for measurement of any energy conversion or any degree of developed energy factor disequilibrium or its predictable reaction developmentsof impoundment or releaseergo, for atomic characteristics.
¶ 425.00 Potentiality of Vector Equilibrium
[425.01]{style="color: purple3"} []{#ver:425.01 label="ver:425.01"} Where all the frequency modulations of the local vectors are approximately equal, we have a potentially local vector equilibrium, but the operative vector frequency complexity has the inherent qualities of accommodating both proximity and remoteness in respect to any locally initiated actions, ergo, a complex of relative frequencies and velocities of realization lags are accommodated (see Corollary at Sec. 240.37).
¶ 426.00 Spherics
[426.01]{style="color: purple3"} []{#ver:426.01 label="ver:426.01"} An isotropic vector matrix can be only omnisymmetrically, radiantly, and “broadcastingly” generated, that is, propagated and radiantly regenerated, from only one vector equilibrium origin, although it may be tuned in, or frequency received, at any point in Universe and thus regenerate local congruence with any of its radiantly broadcast vector structurings.
[426.02]{style="color: purple3"} []{#ver:426.02 label="ver:426.02"} An isotropic vector matrix can be only radiantly generated at a “selectable” (tunable) propagation frequency and vector-size (length) modular spacing and broadcast omnidirectionally or focally beamed outward from any vector-center-fixed origin such that one of its symmetrically regenerated vector-convergent fixes will be congruent with any other identical wavelength and frequency attuned and radiantly reachable vector-center fixes in Universe.
[426.03]{style="color: purple3"} []{#ver:426.03 label="ver:426.03"} In time-vectorable Universe, the maximal range of radiant- regenerative reachability in time is determined by the omnidirectional velocity of all radiation: , i.e., .[^11]
[426.04]{style="color: purple3"} []{#ver:426.04 label="ver:426.04"} Spherics: Employing the rhombic dodecahedron as the hub at the vector crossings of the octet truss (the isotropic vector matrix) provides unique economic, technical, and geometric advantages: its 12 facets represent the six pairs of planes perpendicular to the six degrees of freedom. (See Sec. 537.10.) Its 12 diamond faces also provide the even-numbered means of allowing the vectors to skew-weave around the nucleus at critical-proximity distances without touching the nucleus or one another. Because two or more lines cannot go through the same point at the same time, this function of the rhombic dodecahedron’s hub makes all the difference between regenerative success or failure of Universe. (See Figs. 955.52 and 426.04.)
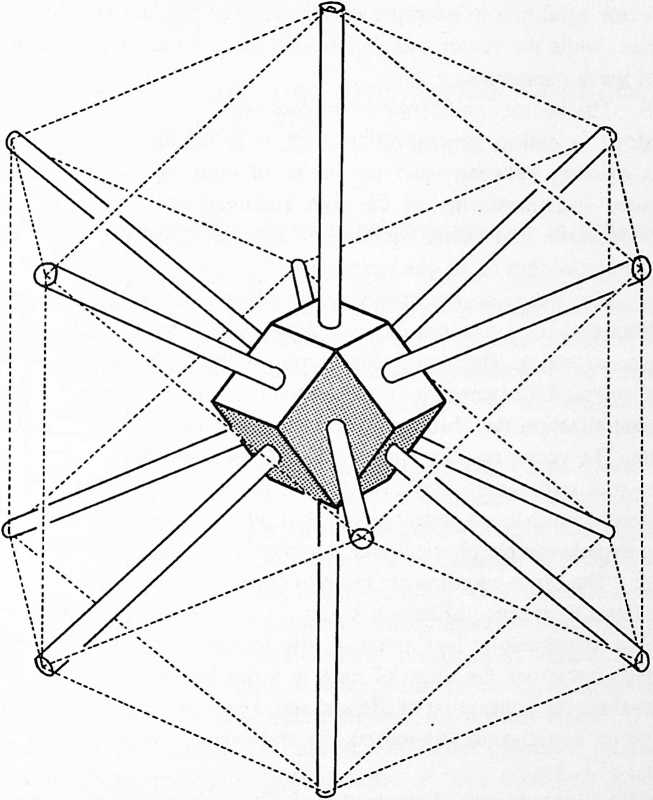
Fig. [426.04 Rhombic Dodecahedron as Hub at the Vector Crossings within the Isotropic Vector Matrix]{style="color: purple3"} []
[426.10]{style="color: purple3"} []{#ver:426.10 label="ver:426.10"} Definition of a Spheric: A “spheric” is any one of the rhombic dodecahedra symmetrically recurrent throughout an isotropic-vector-matrix geometry wherein the centers of area of each of the rhombic dodecahedra’s 12 diamond facets are exactly and symmetrically tangent at 12 omnisymmetrically interarrayed points lying on the surface of any one complete sphere, entirely contained within the spheric-identifying rhombic dodecahedra, with each of any such rhombic dodecahedra’s tangentially contained spheres symmetrically radiant around every other, i.e., every omnidirectionally alternate vertex of every isotropic vector matrix, with the 12 points of spherical tangency of each of the rhombic dodecahedra exactly congruent also with the 12 vertexes of the vector equilibrium most immediately surrounding the vertex center of the sphere, each of whose 12 vector equilibrium radii are the special set of isotropic vector matrix vectors leading outwardly from the sphere’s center vertex to the 12 most immediately surrounding vertexes.
[426.11]{style="color: purple3"} []{#ver:426.11 label="ver:426.11"} These 12 vertexes, which are omni-equidistant from every other vertex of the isotropic vector matrix, also occur at the diamond-face centers of the “spheric” rhombic dodecahedra and are also the points of tangency of 12 uniradius spheres immediately and omni-intertangentially surrounding (i.e., closest-packing) the sphere first defined by the first rhombic dodecahedron. Each rhombic dodecahedron symmetrically surrounds every radiantly alternate vertex of the isotropic vector matrix with the other radiantly symmetrical unsurrounded set of vertexes always and only occurring at the diamond-face centers of the rhombic dodecahedra.
[426.12]{style="color: purple3"} []{#ver:426.12 label="ver:426.12"} One radiantly alternate set of vertexes of the isotropic vector matrix always occurs at the spheric centers of omni-closest-packed, uniradius spheres; whereas the other radiantly alternate set of vertexes of the isotropic vector matrix always occurs at the spheric intertangency points of omni-closest-packed, uniradius spheres.
[426.20]{style="color: purple3"} []{#ver:426.20 label="ver:426.20"} Allspace Filling: The rhombic dodecahedra symmetrically fill allspace in symmetric consort with the isotropic vector matrix. Each rhombic dodecahedron defines exactly the unique and omnisimilar domain of every radiantly alternate vertex of the isotropic vector matrix as well as the unique and omnisimilar domains of each and every interior-exterior vertex of any aggregate of closest-packed, uniradius spheres whose respective centers will always be congruent with every radiantly alternate vertex of the isotropic vector matrix, with the corresponding set of alternate vertexes always occurring at all the intertangency points of the closest-packed spheres.
[426.21]{style="color: purple3"} []{#ver:426.21 label="ver:426.21"} The rhombic dodecahedron contains the most volume with the least surface of all the allspace-filling geometrical forms, ergo, rhombic dodecahedra are the most economical allspace subdividers of Universe. The rhombic dodecahedra fill and symmetrically subdivide allspace most economically, while simultaneously, symmetrically, and exactly defining the respective domains of each sphere as well as the spaces between the spheres, the respective shares of the inter-closest-packed-sphere interstitial space. The rhombic dodecahedra are called “spherics,” for their respective volumes are always the unique closest-packed, uniradius spheres’ volumetric domains of reference within the electively generatable and selectively “sizable” or tunable of all isotropic vector matrixes of all metaphysical “considering” as re-generatively reoriginated by any thinker anywhere at any time; as well as of all the electively generatable and selectively tunable (sizable) isotropic vector matrixes of physical electromagnetics, which are also reoriginatable physically by anyone anywhere in Universe.
[426.22]{style="color: purple3"} []{#ver:426.22 label="ver:426.22"} The rhombic dodecahedron’s 12 diamond faces are the 12 unique planes always occurring perpendicularly to the midpoints of all vector radii of all the closest-packed spheres whenever and wherever they may be metaphysically or physically regenerated, i.e., perpendicular to the midpoints of all vectors of all isotropic vector matrixing.
[426.30]{style="color: purple3"} []{#ver:426.30 label="ver:426.30"} Spherics and Modularity: None of the rhombic dodecahedra’s edges are congruent with the vectors of the isotropic vector matrix, and only six of the rhombic dodecahedra’s 14 vertexes are congruent with the symmetrically co-reoccurring vertexes of the isotropic vector matrix. The other eight vertexes of the rhombic dodecahedra are congruent with the centers of volume of the eight edge-interconnected tetrahedra omnisymmetrically and radiantly arrayed around every vertex of the isotropic vector matrix, with all the edges of all the tetrahedra always congruent with all the vectors of the isotropic vector matrix, and all the vertexes of all the tetrahedra always congruent with the vertexes of the isotropic vector matrix, all of which vertexes are always most economically interconnected by three edges of the tetrahedra.
[426.31]{style="color: purple3"} []{#ver:426.31 label="ver:426.31"} A spheric is any one of the rhombic dodecahedra, the center of each of whose 12 diamond facets is exactly tangent to the surface of each sphere formed equidistantly around each vertex of the isotropic vector matrix.
[426.32]{style="color: purple3"} []{#ver:426.32 label="ver:426.32"} A spheric has 144 and modules, and there are 24 Quanta Modules (see Sec. 920 and 940) in the tetrahedron, which equals th of a spheric. Each of the tetrahedron’s 24 modules contains Vi44th of a sphere, plus th of the nonsphere space unique to the individual domain of the specific sphere of which it is a th part, and whose spheric center is congruent with the most acute-angle vertex of each and all of the and Quanta Modules. The four corners of the tetrahedron are centers of four embryonic (potential) spheres.
[426.40]{style="color: purple3"} []{#ver:426.40 label="ver:426.40"} Radiant Valvability of Isotropic-Vector-Matrix-Defined Wavelength: We can resonate the vector equilibrium in many ways. An isotropic vector matrix may be both radiantly generated and regenerated from any vector-centered fixed origin in Universe such that one of its vertexes will be congruent with any other radiantly reachable center fix in Universe; i.e., it can communicate with any other noninterfered-with point in Universe. The combined reachability range is determined by the omnidirectional velocity of all radiation, within the availably investable time.
[426.41]{style="color: purple3"} []{#ver:426.41 label="ver:426.41"} The rhombic dodecahedron’s 144 modules may be reoriented within it to be either radiantly disposed from the contained sphere’s center of volume or circumferentially arrayed to serve as the interconnective pattern of six th-spheres, with six of the dodecahedron’s 14 vertexes congruent with the centers of the six individual th spheres that it interconnects. The six th spheres are completed when 12 additional rhombic dodecahedra are close-packed around it.
[426.42]{style="color: purple3"} []{#ver:426.42 label="ver:426.42"} The fact that the rhombic dodecahedron can have its 144 modules oriented as either introvert-extrovert or as three-way circumferential provides its valvability between broadcasting-transceiving and noninterference relaying. The first radio tuning crystal must have been a rhombic dodecahedron.
[426.43]{style="color: purple3"} []{#ver:426.43 label="ver:426.43"} Multiplying wavelength by frequency equals the speed of light. We have two experimentally demonstrable radiational variables. We have to do whatever we do against time. Whatever we may be, each we has only so much commonly experiencable time in scenario Universe within which to articulate thus and so. Therefore, the vector equilibrium’s radiant or gravitational “realizations” are always inherently geared to or tuned in with the fundamental time-sizing of mps, which unique time-size-length increments of available time can be divided into any desirable frequency. One second is a desirable, commonly experienceable increment to use, and within each unit of it we can reach miles in any non-frequency-interfered-with direction.
[426.44]{style="color: purple3"} []{#ver:426.44 label="ver:426.44"} Wavelength times frequency is the speed of all radiation. If the frequency of the vector equilibrium is four, its vector radius, or basic wavelength miles reachable within one second reach-miles. Electromagnetically speaking, the unarticulated vector equilibrium’s one- second vector length is always miles.
[426.45]{style="color: purple3"} []{#ver:426.45 label="ver:426.45"} We multiply our frequency by the number of times we divide the vector of the vector equilibrium, and that gives ; our reachable points in Universe will multiply at a rate of .
[426.46]{style="color: purple3"} []{#ver:426.46 label="ver:426.46"} All the relative volumetric intervaluations of all the symmetric polyhedra and of all uniradius, closest-packed spheres are inherently regenerated in omnirational respect to isotropic vector matrixes, whether the matrixes are inadvertently i.e., subjectivelyactivated by the size-selective, metaphysical-consideration initiatives, whether they are objectively and physically articulated in consciously tuned electromagnetic transmission, or whether they are selectively tuned to receive on that isotropic-vector-matrix-defined “wavelength.”
[426.47]{style="color: purple3"} []{#ver:426.47 label="ver:426.47"} Humans may be quite unconscious of their unavoidable employment of isotropic vector matrix fields of thought or of physical articulations; and they may oversimplify or be only subconsciously attuned to employ their many cosmically intertunable faculties and especially their conceptual and reasoning faculties. However, their physical brains, constituted of quadrillions times quadrillions of atoms, are always and only most economically interassociative, interactive, and intertransforming only in respect to the closest-packed isotropic vector matrix fields which altogether subconsciously accommodate the conceptual geometry picturing and memory storing of each individual’s evolutionary accumulation of special-case experience happenings, which human inventories are accumulatingly stored isotropic-vector-matrix-wise in the brain and are conceptually retrievable by brain and are both subconsciously and consciously reconsidered reflexively or by reflex-shunning mind.
¶ 427.00 Nuclear Computer Design
[427.01]{style="color: purple3"} []{#ver:427.01 label="ver:427.01"} Though I have found an omnidirectional vector equilibrium matrix and the complex of momentarily positively and negatively asymmetrical intertransformabilities pulsating through the equilibrious state, I knew that nature would never allow temporal humans to omniarrest cosmic kinetics at the timeless, i.e., eternal equilibrium zero. But experimenting in cryogenics, taking energy-as-heat out of the insulatingly isolated liquefied gaseous element system approaching absolute zero, we learn that as the temperature gets lower and lower, an increasingly orderly and an increasingly symmetrical, micro- geometrical patterning occursthe Platonic solids appear to become more symmetrically uniform. Contrariwise, when energy-as-heat is progressively reintroduced, the kinetics increase and the complex of conceptual behavior becomes progressively asymmetric. At lowest cryogenic temperatures the omnigrametric interpatterning approaches isotropic vector matrix equilibrium.
[427.02]{style="color: purple3"} []{#ver:427.02 label="ver:427.02"} The progressive energy-starving experimental strategy reveals that nature always transforms through, and relative centrally to, the omni-isotropic-vector-matrix equilibrium, while kinetically emphasizing the mildly off-center asymmetric aspects. Nature grows her crystals positively or negatively askewshe twists and spirals around the local, three-way great-circle grid systems in the alternate positive-negative geodesic complementations. Such kinetic considerations of closest packing are significant.
[427.03]{style="color: purple3"} []{#ver:427.03 label="ver:427.03"} The isotropic vector matrix equilibrium multiplies omnidirectionally with increasing frequency of concentric, vector-equilibrium-con- formed, closest-packed uniradius sphere shells, conceptually disclosing the cosmically prime unique sequence of developed interrelationships and behaviors immediately surrounding a prime nucleus. While the physicist processes his nuclear problems with nonconceptual mathematics, the conceptual isotropic vector matrix equilibria model provides a means of comprehending all the electromagnetic and nonelectromagnetic energy valving and angular shunting controls of the solid state transistors.
[427.04]{style="color: purple3"} []{#ver:427.04 label="ver:427.04"} With one layer of spheres around the nuclear sphere we will get one set of angular interrelationships of the surrounding spheres with the nucleus and with one another. With two layers of spheres around the nuclear sphere a different angular relationship between the nuclear sphere and its intersurrounding spheres occurs (see Sec. 415). At the third layer of enclosure some of the angular interrelationship patternings begin to repeat themselves. Thus we are able to inventory what we are going to call a nuclear set of unique interrelationship patterns.
[427.05]{style="color: purple3"} []{#ver:427.05 label="ver:427.05"} The isotropic vector matrix multiplies concentrically. But because vectors are discrete, the isotropic vector matrix’s lines do not go to infinity. Their length must always represent sum-totally the total energy of eternally regenerative physical Universe. No matter how high the internal frequency of finite Universe, the overall vector equilibrium is of unit magnitude. This magnitude corresponds to that of the speed of radiation uninterfered with in vacuo. We find that the different frequencies in their phases of symmetry identify precisely with what we now call the Magic Numbers identifying the successively reoccurring five peaks in relative abundance of atomic isotopes. (See Sec. 984.10.)
[427.06]{style="color: purple3"} []{#ver:427.06 label="ver:427.06"} I am confident that I have discovered and developed the conceptual insights governing the complete family of variables involved in realization by humanity of usable access to the ultimate computer …ultimate meaning here: the most comprehensive, incisive and swiftest possible information-storing, retrieving, and variably processing facility with the least possible physical involvement and the least possible investment of human initiative and cosmic energization.
[427.07]{style="color: purple3"} []{#ver:427.07 label="ver:427.07"} Science evolved the name “solid state” physics when, immediately after World War II, the partial conductors and partial resistorslater termed “transistors”were discovered. The phenomena were called “solid state” because, without human devising of the electronic circuitry, certain small metallic substances accidentally disclosed electromagnetic pattern-holding, shunting, route-switching, and frequency-valving regularities, assumedly produced by the invisible-to-humans atomic complexes constituting those substances. Further experiment disclosed unique electromagnetic circuitry characteristics of various substances without any conceptual model of the “subvisible apparatus.” Ergo, the whole development of the use of these invisible behaviors was conducted as an intelligently resourceful trial-and-error strategy in exploiting invisible and uncharted-by-humans natural behavior within the commonsensically “solid” substances. The addition of the word “state” to the word “solid” implied “regularities” in an otherwise assumedly random conglomerate. What I have discovered goes incisively and conceptually deeper than the blindfolded assumptions and strategies of solid state physicswhose transistors’ solid state regularities seemingly defied discrete conceptuality and scientific generalization and kinetic omnigramming.
¶ 427.10 Invisible Circuitry of Nature
[427.11]{style="color: purple3"} []{#ver:427.11 label="ver:427.11"} We have here the disclosure of a new phase of geometry employing the invisible circuitry of nature. The computer based on such a design could be no bigger than the subvisibly dimensioned domain of a pinhead’s glitter, with closures and pulsations which interconnect at the vector equilibrium stage and disconnect at the icosahedron stage in Milky-Way-like remoteness from one another of individual energy stars.
[427.12]{style="color: purple3"} []{#ver:427.12 label="ver:427.12"} As we get into cryogenicstaking energy-as-heat out of the systemthe geometries become more regular and less asymmetric, thus fortifying the assumptions of synergetics because the geometrically “twinkling” asymmetries of kinetics progressively subside and approach, but do not quite attain, absolute cessation at the isotropic vector equilibrium state.
[427.13]{style="color: purple3"} []{#ver:427.13 label="ver:427.13"} The atomically furnished isotropic vector matrix can be described as an omnidirectional matrix of “lights,” as the four-dimensional counterpart of the two-dimensional light-bulb-matrix of the Broadway-and-Forty-second- Street, New York City billboards with their fields of powerful little light bulbs at each vertex which are controlled remotely off-and-on in intensity as well as in color. Our four-dimensional, isotropic vector matrix will display all the atom “stars” concentrically matrixed around each isotropic vector equilibrium’s nuclear vertex. By “lighting” the atoms of which they consist, humans’ innermost guts could be illustrated and illuminated. Automatically turning on all the right lights at the right time, atomically constituted, center-of-being light, “you,” with all its organically arranged “body” of lights omnisurrounding “you,” could move through space in a multidimensional way just by synchronously activating the same number of lights in the same you-surrounding pattern, with all the four-dimensional optical effect (as with two-dimensional, planar movies), by successively activating each of the lights from one isotropic vector vertex to the next, with small, local “movement” variations of “you” accomplished by special local matrix sequence programmings.
[427.14]{style="color: purple3"} []{#ver:427.14 label="ver:427.14"} We could progressively and discretely activate each of the atoms of such a four-dimensional isotropic vector matrix to become “lights,” and could move a multidimensional control “form” through the isotropic multidimensional circuitry activating field. The control form could be a “sphere,” a “vector equilibrium,” or any other system including complex you-and-me, et al. This multidimensional scanning group of points can be programmed multidimensionally on a computer in such a manner that a concentric spherical cluster of four-dimensional “light” points can be progressively “turned on” to comprise a “substance” which seemingly moves from here to there.
[427.15]{style="color: purple3"} []{#ver:427.15 label="ver:427.15"} This indeed may be what Universe is doing! Employing a scanner of each of our atoms, this is one way humans could have been radio-transmitted and put aboard Earth from any place in Universe. The naked human eye cannot differentiate visually the separate dots of a matrix when their frequency of uniform-moduled spaced occurrence is greater than one hundred to the linear inch, or ten thousand to the square inch, or one million to the cubic inch. Let us radiantly activate isotropically and modularly grouped local atoms of a human’s physical organism in such a manner that only one million per cubic inch out of all the multibillions of actual atoms per cubic inch of which humans consist, are radiationally, ergo visibly, activated. The human, thus omni-internally illumined by the local one-in-one-million atomic “street lamps,” could be realistically scanned by discrete “depth-sounding” devices and programmed to move “visibly” through an omnidimensional, high- frequency, isotropic light matrix field “mass.”
[427.16]{style="color: purple3"} []{#ver:427.16 label="ver:427.16"} Employing as broadcastable channels the 25 great circles of the vector equilibrium all of which pass through all the “K” (kissing) points of intertangency of all uniform radius, closest-packed spheres of all isotropic vector matrixes; and employing as local holding patterns the 31 great circles of the icosahedron; and employing as a resonance field all the intertransforming spheres and between-sphere spaces; and employing the myriadly selectable, noninterfering frequencies of such propagatable intertransformation resonance; it is evidenced that the isotropic vector matrixes of various atomic elements may be programmed to receive, store, retrieve, and uniquely constellate to provide computer functioning of unprecedented capacity magnitude within approximately invisible atomic domains. The control mechanism for the operational programming of such microcosmic “computers” will be visible and dextrous and will be keyed by the Mite orientations of the prime-number-one-volumed “Couplers.” [^12]
[427.17]{style="color: purple3"} []{#ver:427.17 label="ver:427.17"} The ultra micro computer (UMC) employs step-up, step-down, transforming visible controls between the invisible circuitry of the atomic computer complex pinhead-size programmer and the popular outdoor, high-in-the-sky, “billboard” size, human readability.
¶ 430.00 Vector Equilibrium
¶ 430.01 Definition
[430.011]{style="color: purple3"} []{#ver:430.011 label="ver:430.011"} The geometric form most compactly developed from the closest packing of spheres around one nuclear sphere is not that of a composite sphere, but is always a polyhedron of 14 faces composed of six squares and eight triangles, with 12 vertexes extending in tangential radius from the original 12 spheres surrounding the nucleus sphere. (See illustration 413.01. )
[430.02]{style="color: purple3"} []{#ver:430.02 label="ver:430.02"} It is called the vector equilibrium because the radials and the circumferentials are all of the same dimension and the tendencies to both explode and implode are symmetrical. That the explosive and implosive forces are equal is shown by the four-dimensional hexagonal cross sections whose radial and circumferential vectors balance. The eight triangular faces reveal four opposite pairs of single-bonded tetrahedra in a positive and negative tetrahedral system array with a common central vertex and with coinciding radial edges. The four hexagonal planes that cross each other at the center of the vector-equilibrium system are parallel to the four faces of each of its eight tetrahedra. Six square faces occur where the six half-octahedra converge around the common vector-equilibrium nuclear vertex.
[430.03]{style="color: purple3"} []{#ver:430.03 label="ver:430.03"} In terms of vectorial dynamics, the outward radial thrust of the vector equilibrium is exactly balanced by the circumferentially restraining chordal forces: hence the figure is an equilibrium of vectors. All the edges of the figure are of equal length, and this length is always the same as the distance of any of its vertexes from the center of the figure. The lines of force radiating from its center are restrainingly contained by those binding inward arrayed in finite closure circumferentially around its peripherybarrel-hooping. The vector equilibrium is an omnidirectional equilibrium of forces in which the magnitude of its explosive potentials is exactly matched by the strength of its external cohering bonds. If its forces are reversed, the magnitude of its contractive shrinkage is exactly matched by its external compressive archwork’s refusal to shrink.
[430.04]{style="color: purple3"} []{#ver:430.04 label="ver:430.04"} The vector equilibrium is a truncated cube made by bisecting the edges and truncating the eight corners of the cube to make the four axes of the four planes of the vector equilibrium. The vector equilibrium has been called the “cuboctahedron” or “cubo-octahedron” by crystallographers and geometers of the non-experimentally-informed and non-energy-concerned past. As such, it was one of the original 23 Archimedean “solids.”
[430.05]{style="color: purple3"} []{#ver:430.05 label="ver:430.05"} The vector equilibrium is the common denominator of the tetrahedron, octahedron, and cube. It is the decimal unit within the octave system. Double its radius for octave expansion.
[430.06]{style="color: purple3"} []{#ver:430.06 label="ver:430.06"} The vector equilibrium is a system. It is not a structure. Nor is it a prime volume, because it has a nucleus. It is the prime nucleated system. The eight tetrahedra and the six half-octahedra into which the vector equilibrium may be vectorially subdivided are the volumes that are relevantly involved.
¶ 431.00 Volume
[431.01]{style="color: purple3"} []{#ver:431.01 label="ver:431.01"} The vector equilibrium consists of six one-half octahedra, each with a volume of two (), and eight tetrahedra each with a volume of one, so , which is its exact volume. (See illustration 222.30. )
[431.02]{style="color: purple3"} []{#ver:431.02 label="ver:431.02"} The volume of a series of vector equilibria of progressively higher frequencies is always frequency to the third power times 20, or 20F3, where F = frequency. When the vector equilibrium’s frequency is one (or radiationally inactive), its volume is .
[431.03]{style="color: purple3"} []{#ver:431.03 label="ver:431.03"} But frequency, as a word key to a functional concept, never relates to the word one because frequency obviously involves some plurality of events. As a one-frequency, ergo sub-frequency, system, the vector equilibrium is really subsize, or a size-independent, conceptual integrity. Therefore, frequency begins with twowhere all the radials would have two increments. When the edge module of a cube is one, its volume is one; when the edge module of a cube is two, its volume is eight. But when the edge module of a vector equilibrium is one, its volume is 20. A nuclear system is subsize, subfrequency. Equilibrious unity is 20; its minimum frequency state is . This is one of the properties of 60-degree coordination.
[431.04]{style="color: purple3"} []{#ver:431.04 label="ver:431.04"} Looking at a two-frequency vector equilibrium (with all the radials and edge units divided into two) and considering it as the domain of a point, we find that it has a volume of 480/1 and Modules. The formula of the third power of the frequency tells us the exact number of quanta in these symmetrical systems, in terms of quantum accounting and in terms of the and Modules (see Chapter 9, Modelability).
¶ 432.00 Powering
[432.01]{style="color: purple3"} []{#ver:432.01 label="ver:432.01"} The vector equilibrium makes it possible to make conceptual models of fourth-, fifth-, and sixth-dimensional omniexperience accounting by using tetrahedroning. If we have a volume of 20 around a point, then two to the fourth power (16) plus two to the second power (4) equals 20. We can then accommodate these powerings around a single point.
[432.02]{style="color: purple3"} []{#ver:432.02 label="ver:432.02"} Using frequency to the third power with a no-frequency nucleus, the vector equilibrium models all of the first four primes. For instance, the number 48 (in 480) is . Three is a prime number, and 16 is two to the fourth power: that is 48, and then times 10. Ten embraces the prime numbers five times the number two; so instead of having 16 times 2, we can call it 32, which is two to the fifth power. The whole 480-moduled vector equilibrium consists of the prime number one times two to the fifth power, times three, times five (). These are the first four prime numbers.
[432.03]{style="color: purple3"} []{#ver:432.03 label="ver:432.03"} Using frequency to the third power with a two-frequency nucleus, we have . If the frequency is two, we have two to the eighth power in the model times three times five ().
[432.04]{style="color: purple3"} []{#ver:432.04 label="ver:432.04"} In a three-frequency system, we would have three to the third power times three, which makes three to the fourth power, which we would rewrite as 25 x 34 x 5. We get two kinds of four-dimensionality in here. There is a prime dimensionality of three to the fourth power (34). And there is another kind of four-dimensionality if the frequency is four, which would be written 25 x 3 X 5. But since it is frequency to the third power, and since four is two times two (2 x 2) or two to the second power (22), we would add two to make two to the seventh power (27), resulting in 27 x 3 x 5. If the frequency is five, it would then be two to the fifth power (25) times three, because frequency is to the third power times five, which makes five to the fourth power. Quite obviously, multidimensionality beyond three dimensions is experienceably, i.e., conceptually, modelable in synergetics accounting.
¶ 433.00 Outside Layer of Vector Equilibrium
[433.01]{style="color: purple3"} []{#ver:433.01 label="ver:433.01"} The unique and constantly remote but-always-and-only co-occurring geometrical “starry” surroundment “outsideness” of the nucleated vector equilibrium is always an icosahedron, but always occurring only as a single layer of vertexes of the same frequency as that of the nuclear vector equilibrium’s outermost vertexial layer.
[433.02]{style="color: purple3"} []{#ver:433.02 label="ver:433.02"} There may be multilayer vector equilibriatwo-frequency, three-frequency, four-frequency, or whatever frequency. The circumferential vector frequency will always be identical to that of its radial vector frequency contraction of the vector equilibrium’s outer layer of unit radius spheres by local surface rotation of that outer layer’s six square arrays of non-closest-single-layer packing of tangent spheres inter-rearranging into closest triangular packing as in the vector equilibrium’s eight triangular facets, thus transforming the total outer layer into the icosahedron of equal outer edge length to that of the vector equilibrium, but of lesser interior radius than the vector equilibrium of the same outer edge length, and therefore of lesser interior volume than that of the vector equilibrium, ergo unable to accommodate the same number of interiorally-closest-packed, nuclear-sphere-centered unit radius spheres as that of the vector equilibrium. The icosahedron’s multifrequenced outer layer surface arrays of unit radius, closest-planar-packed spheres cannot accommodate either concentric layers of unit radius closest-packed spheres noreven at zero frequencycan the icosahedron’s 12-ball, omni-intertangentially triangulated outer shell accommodate one nuclear sphere of the same radius as that of its shell spheres. Icosahedral outer shell arrays of identical frequency to that of the vector equilibria of the same frequency, can therefore only occur as single-layer, symmetrical, enclosure arrays whose individual spheres cannot be tangent to one another but must be remotely equipositioned from one another, thus to form an omni-intertriangulated, icosahedrally conformed starry array, remotely and omnisurroundingly occupying the vector equilibrium’s sky at an omnistar orbit-permitting equidistance remoteness around the vector equilibrium whose outer shell number of spheres exactly corresponds to the number of the icosahedron’s “stars.” This geometrical dynamically interpositioning integrity of relationship strongly suggests the plurality of unique electron shell behaviors of all the chemical elements’ atoms, and the identical number relationships of the atoms’ outer layer protons and its electrons; and the correspondence of the vector equilibrium’s number of concentric closest-packed, nucleus-enclosing layers with the number of quantumjump-spaced electron orbit shells; and finally the relative volume relationship of equi-edged vector equilibria and icosahedra, which is, respectively, as is to , which suggests the relative masses of the proton and the electron, which is as 1 : \sfrac{1}{1851}.
¶ 440.00 Vector Equilibrium as Zero Model
[440.01]{style="color: purple3"} []{#ver:440.01 label="ver:440.01"} Equilibrium between positive and negative is zero. The vector equilibrium is the true zero reference of the energetic mathematics. Zero pulsation in the vector equilibrium is the nearest approach we will ever know to eternity and god: the zerophase of conceptual integrity inherent in the positive and negative asymmetries that propagate the differentials of consciousness.
[440.02]{style="color: purple3"} []{#ver:440.02 label="ver:440.02"} The vector equilibrium is of the greatest importance to all of us because all the nuclear tendencies to implosion and explosion are reversible and are always in exact balance. The radials and the circumferentials are in balance. But the important thing is that the radials, which would tend to explode since they are outwardly pushing, are always frustrated by the tensile finiteness of the circumferential vectors, which close together in an orderly manner to cohere the disorderly asundering. When the radial vectors are tensilely contractive and separately implosive, they are always prevented from doing so by the finitely closing pushers or compressors of the circumferential set of vectors. The integrity of Universe is implicit in the external finiteness of the circumferential set and its surface-layer, close-packing, radius-contracting proclivity which always encloses the otherwise divisive internal radial set of omnidirectional vectors.
[440.03]{style="color: purple3"} []{#ver:440.03 label="ver:440.03"} All the internal, or nuclear, affairs of the atom occur internally to the vector equilibrium. All the external, or chemical, compoundings or associations occur externally to the vector equilibrium. All the phenomena external to and more complex thanthe five-frequency vector equilibria relate to chemical compounds. Anything internal toor less complex than the five- frequency vector equilibrium relates principally to single atoms. Single atoms maintain omnisymmetries; whereas chemical compounds may associate as polarized and asymmetrical chain systems.
[440.04]{style="color: purple3"} []{#ver:440.04 label="ver:440.04"} The vector equilibrium is the anywhere, any when, eternally regenerative, event inceptioning and evolutionary accommodation and will never be seen by man in any physical experience. Yet it is the frame of evolvement. It is not in rotation. It is sizeless and timeless. We have its mathematics, which deals discretely with the chordal lengths. The radial vectors and circumferential vectors are the same size.
[440.05]{style="color: purple3"} []{#ver:440.05 label="ver:440.05"} The vector equilibrium is a condition in which nature never allows herself to tarry. The vector equilibrium itself is never found exactly symmetrical in nature’s crystallography. Ever pulsive and impulsive, nature never pauses her cycling at equilibrium: she refuses to get caught irrecoverably at the zero phase of energy. She always closes her transformative cycles at the maximum positive or negative asymmetry stages. See the delicate crystal asymmetry in nature. We have vector equilibriums mildly distorted to asymmetry limits as nature pulsates positively and negatively in respect to equilibrium. Everything that we know as reality has to be either a positive or a negative aspect of the omnipulsative physical Universe. Therefore, there will always be positive and negative sets that are ever interchangeably intertransformative with uniquely differentiable characteristics.
[440.06]{style="color: purple3"} []{#ver:440.06 label="ver:440.06"} The vector equilibrium is at once the concentric push-pull interchange, vectorial phase or zone, of neutral resonance which occurs between outwardly pushing wave propagation and inwardly pulling gravitational coherence.
[440.07]{style="color: purple3"} []{#ver:440.07 label="ver:440.07"} All the fundamental forms of the crystals are involved in the vector equilibrium. It is a starting-pointnot anything in its own right if it is a vector equilibrium.
[440.08]{style="color: purple3"} []{#ver:440.08 label="ver:440.08"} As the circumferentially united and finite great-circle chord vectors of the vector equilibrium cohere the radial vectors, so also does the metaphysical cohere the physical.
[440.09]{style="color: purple3"} []{#ver:440.09 label="ver:440.09"} Zerophase: Being the zerophase of energy the vector equilibrium is inherently invisible and non-empirically-discoverable, which accounts for its having been for so long unrecognized as the spontaneous equilibrious model. As specialists, scientists seek only the somethings. The vector equilibrium is the only model of nonbeing zero-inflection at the nonmoment of omniintertransformabilities, where anything can happen and must happen single-atomic ally within and multiatomically without. Specializing science, seeking only somethings, inherently overlooked the nonthing vector equilibrium. Vector equilibria in isotropic vector matrixes produce the discontinuity of particles, while the vector-weaving around the VE nuclei produce the continuity of wave phenomena.
[440.10]{style="color: purple3"} []{#ver:440.10 label="ver:440.10"} The vector equilibrium is the most abstract of all the always-and-only abstract scientific generalizations, for it is the heart of all interrelationships existing betweenand not in or ofany of all the empirically apprehended intertransforms of the ever-and-everywhere intertransforming Scenario Universe. The vector equilibrium is the zerophase ergo, inexpressibleinterrelationship of all Universe events.
[440.11]{style="color: purple3"} []{#ver:440.11 label="ver:440.11"} The word vacuum relates specifically to gaseous phenomena. Nature’s abhorrence of a vacuum induces physical relationships only in respect to the gaseous states. The vector equilibrium is the nothingness phase of all states of physical Universe: it is the generalization of nothingness, within which generalization the absolute vacuum is a special case event in the gaseous state. The vector equilibrium is such a physically abhorred nonstate as to be the eternal self-starterergo, the eternal re-self-starter, ever regenerating the off-zero perturbations, oscillations, and all the wave propagation of all humanly experienceable physical and metaphysical phenomena.
[440.12]{style="color: purple3"} []{#ver:440.12 label="ver:440.12"} The sense-coordinating brain of each and every human, like sound or light, has a limit speed of apprehending. There is no instant cerebral cognition. These apprehension lags automatically impose off-center human cognition, which occasions the sense of time in a timeless eternity. The sense of time occasions the conception of life and serial experience. The inherently invisible vector equilibrium self-starters life and ever regenerates life.
¶ 441.00 Vector Equilibrium as Zero Tetrahedron
[441.01]{style="color: purple3"} []{#ver:441.01 label="ver:441.01"} Emptiness at the Center: All four planes of all eight tetrahedra, i.e., 32 planes in all, are congruent in the four visible planes passing through their common vector equilibrium center. Yet you see only four planes. Both the positive and the negative phase of the tetrahedra are in congruence in the center. They are able to do this because they are synchronously discontinuous. Their common center provides the locale of an absolutely empty event.
[441.02]{style="color: purple3"} []{#ver:441.02 label="ver:441.02"} Vector equilibrium accommodates all the intertransformings of any one tetrahedron by polar pumping, or turning itself inside out. Each vector equilibrium has four directions in which it could turn inside out. It uses all four of them through the vector equilibrium’s common center and generates eight tetrahedra. The vector equilibrium is a tetrahedron exploding itself, turning itself inside out in four possible directions. So we get eight: inside and outside in four directions. The vector equilibrium is all eight of the potentials.
[441.021]{style="color: purple3"} []{#ver:441.021 label="ver:441.021"} Zerovolume Tetrahedron: The zerovolume phenomenon altogether avoids the operationally prohibited concept of a plurality of lines going through the same point at the same time. In the zerovolume tetrahedron each of the four great circles is folded into a “bow tie” pair of double-bonded tetra, each of which is double-bonded to the three others. The eight vertexes of the eight tetrahedra at each of their four open corners only seemingly pass through each other, whereas each converges to the other and turns around divergently outward at 60 degrees, thus producing a nucleus with an energy potential of eight but presenting the topologically visual aspect and enumeration of only one. (See Secs. 623.20, 1033.020 and 1053.810.)
[441.03]{style="color: purple3"} []{#ver:441.03 label="ver:441.03"} Terminal Condition: The formula for the number of balls in any one of the concentric layers of the vector equilibrium is always . The center ball of a vector equilibrium is the zero layer. The layer frequency is zero just as in the first layer the frequency is one. So zero times 10 is zero; to the second power is zero; plus two is two. So the center ball has a value of two. The significance is that it has its concavity and its convexity. It has both insideness and outsideness. Its center is as far as you can go inward. You turn yourself inside out and come out in the outside direction. Its inbound shell and its outbound shell are equally valid, and though you see them as congruent and as one, they are two. This central sphere center is a cosmic terminal condition.
[441.04]{style="color: purple3"} []{#ver:441.04 label="ver:441.04"} Let us consider a tetrahedron, which also always has an externality and an internality. At its internal center is its terminal turn-around- and-come-outward-again condition. This is exactly why in physics there is a cosmic limit point at which systems turn themselves inside out. They get to the outside and they turn themselves inside out and come the other way. This is why radiation does not go off into a higher velocity. Radiation gets to a maximum velocity unrestrained in vacuo and then turns itself inward againit becomes gravity. Then gravity comes to its maximum concentration and turns itself around and goes outwardbecomes radiation again.
[441.05]{style="color: purple3"} []{#ver:441.05 label="ver:441.05"} This Boltzmann’s import-export-import-export; entropy-syntropy- entropy-syntropy, cosmically complementary, human-heartlike, eternally pul- sative, evolutionary regeneration system, also locally manifests itself in the terrestrial biosphere as the ever alternatively, omni-interpulsing, barometric highs and lows of the weather.
[441.10]{style="color: purple3"} []{#ver:441.10 label="ver:441.10"} Coordinate Symmetry: In coordinate symmetry, as the faces of the tetrahedron move in toward the opposite vertex, the volume gets less at an exponential velocity of the third power, its surfaces diminish at a second- power rate of change, and its lines shorten at a covariation rate of the first power. When all four of the tetrahedral faces come to congruence with the same common nucleus of the vector equilibrium, all three of these different rates of size change come synchronously to common zero size. The constant tetrahedral fourness of vertexes and faces, sixness of edges, insideness and outsideness, convexity and concavitythese integrated constants of conceptuality never change.
[441.20]{style="color: purple3"} []{#ver:441.20 label="ver:441.20"} Turbining: In looking at a tetrahedron, we see that there are around any one vertex three faces and three edges in beautiful synchronization; we say that it all looks simple and logical. We find, however, that the inventory of three faces around each vertex comes out of a total inventory of four that are always available in the tetrahedron. On the other hand, the inventory of three edges around each vertex comes out of a total inventory of six that are available. So the sixness and the fourness are from very different total quantity inventories. Somehow, around any one vertex of the same system nature has arranged to synchronize them in a neat three-to-three balance while using them all in a total symmetry despite their being supplied from their differing inventories.
[441.21]{style="color: purple3"} []{#ver:441.21 label="ver:441.21"} Consider the case of the cheese tetrahedron (see Sec. 623.20), where we push one of the faces toward the opposite vertex. We can move that face in until it is congruent with the opposite vertex. There is now no volume, but we have agreed that the condition of symmetry is a constant of the abstractly conceptual system, the tetrahedron: the sixness and the fourness are still there, but they are empty. With one face congruent with the opposite vertex, we have all four planes of the tetrahedron going through the same exact point at the same time, or theoretically as close as we can ever get to exactly. We also have six edges of the tetrahedron going through the same point at the same time. We have agreed that this is a condition that can never happen in reality, but in the vector equilibrium, where there is no size, we have the only possible time when this would seem to occur.
[441.22]{style="color: purple3"} []{#ver:441.22 label="ver:441.22"} So we have the total inventory of four faces and six edges going through the same theoretical point at the same moment. We have said that this is a vector equilibrium and in a zero condition and it is nonreality. Nature would not permit it. But a moment later, those six edges turbine around that point one way or anotherand we have seen plenty of models of the lines turbining aroundbut we will have to say that there had to be a moment when this plane went from being a positive tetrahedron to being a negative tetrahedron, and it had theoretically to pass through that point.
[441.23]{style="color: purple3"} []{#ver:441.23 label="ver:441.23"} Very clearly, vector equilibrium is a zero-size tetrahedron. We have already had tetrahedron as an indestructible phenomenon independent of size. And then we have it getting into its own true zero vector equilibrium. It is a condition that nature apparently does not permit in our life, but what we call physical reality is always a positive and negative pulsating aberration of the whole a multifrequency-accommodating, vector equilibrium aberratability whole.
¶ 442.00 Polarization of Vector Equilibrium
[442.01]{style="color: purple3"} []{#ver:442.01 label="ver:442.01"} In closest packing of spheres, there are always between the spheres alternate spaces that are not being used, and so triangular space and space-available groups can be alternated from their original positions 60 degrees to alternate nestable positions. We find that you can take two halves of the vector equilibrium and rotate one of the halves 60 degrees. Instead of having the vector-equilibrium condition of alternate faces in symmetrical array around it, you will get a polarized system around the equatorial zone of which you will get a square and a square side by side and a triangle and a triangle side by side. By rotating the system 60 degrees, you will get a top polar triangle and a bottom polar triangle in the same orientation. If you rotate the vector equilibrium to the next 60-degree nestable position, suddenly it is omnisymmetrical again.
[442.02]{style="color: purple3"} []{#ver:442.02 label="ver:442.02"} It is in this polarized condition that a section through the vector equilibrium makes the famous chemical hex that the chemists have used for years. The chemists recognized it as a polarized system, but they did not recognize it as the vector equilibrium because chemists had not had any internal atomic experience like that. Apparently, then, all the chemical compounding in the organic chemistry relates to polarized systems.
¶ 443.00 Vector Equilibrium as Equanimity Model
[443.01]{style="color: purple3"} []{#ver:443.01 label="ver:443.01"} In order to reduce the concept of vector equilibrium to a single-name identity, we employ the word equanimity as identifying the eternal metaphysical conceptuality model that eternally tolerates and accommodates all the physically regenerative, intertransforming transactions of eternal, inexorable, and irreversible evolution’s complex complementations, which are unitarily unthinkable, though finite.
[443.02]{style="color: purple3"} []{#ver:443.02 label="ver:443.02"} The equanimity model permits metaphysically conceptual thinkability and permits man to employ the package-word Universe. Equanimity, the epistemological model, is the omni-intertransformative, angle- and frequency-modulatable, differential accommodator and identifies the direction toward the absolute, completely exquisite limit of zero-error, zero-time omnicomprehension toward which our oscillatory, pulsating reduction of tolerated cerebrally reflexed aberrations trends.
[443.03]{style="color: purple3"} []{#ver:443.03 label="ver:443.03"} Humanity’s physical brains’ inherent subjective-to-objective time lag reflexing induces the relatively aberrated observation and asymmetrical articulation tolerated by ever more inclusively and incisively demanding mind’s consciousness of the absolute exactitude of the eternally referential centrality at zero of the equanimity model. Thus mind induces human consciousness of evolutionary participation to seek cosmic zero. Cosmic zero is conceptually but sizelessly complex, though full-size-range accommodating.
[443.04]{style="color: purple3"} []{#ver:443.04 label="ver:443.04"} In the equanimity model, the physical and the metaphysical share the same design. The whole of physical Universe experience is a consequence of our not seeing instantly, which introduces time. As a result of the gamut of relative recall time-lags, the physical is always the imperfect experience, but tantalizingly always ratio-equated with the innate eternal sense of perfection.
¶ 445.00 Frequency of Vector Equilibrium
[445.01]{style="color: purple3"} []{#ver:445.01 label="ver:445.01"} As the most compact spherical agglomeration of unit radius spheres around a unit radius nuclear sphere, the vector equilibrium is indefinitely expandable, either by additional unit radius spheres, colonied, layer-embracement multiplication, or by uniform time-size increase. If expanded by unit radius, sphere-colonized, omni-embracing, concentric layer multiplication, additional new locally operative nuclei are progressively born with every four successive concentric generations of symmetrical, omni-embracing layer multiplication. We use here the concept of multiplication only by division of the conceptual sizeless whole in a greater number of coordinate parts.
[445.02]{style="color: purple3"} []{#ver:445.02 label="ver:445.02"} The eight-triangled, six-square, planar-faceted space volume of the vector equilibrium is always frequency to the third power times 20with frequency being of omni symmetric, radial-circumferential, modular sub- divisioning of the whole. The geometrical conceptioning of volume as used here is in contradistinction to the number of vari-frequenced, vectorequilibrium-forming, closest-packed spheres and their nonoccupied concave octahedra and concave vector equilibria-shaped intersphere interstices: these being the all and only shapes of inter-closest-packed unit radius sphere agglomeration interstices. (See illustration 1032.13.)
[445.03]{style="color: purple3"} []{#ver:445.03 label="ver:445.03"} When the frequency of the vector equilibrium is one (or radia- tionally inactive), its initial volume is always ; wherefore, with , , . When the frequency is, for instance, eight, the ; .
[445.04]{style="color: purple3"} []{#ver:445.04 label="ver:445.04"} The relative size of the vector equilibrium begins with the initial zerosize integrity of conceptuality and its omnidimensional modular subdivisibility for accounting any frequency of geometrical configuration transformative accounting. Vector equilibria, as with the tetrahedra and other polyhedra, are conceptually valid as vector equilibria or tetrahedra, independent of size. Size is where relativity becomes generated. The eternality of synergetics is the experienceable conceptuality whose imaginability is independent of individual human life’s successive special-case experiences of time and size relativity.
[445.05]{style="color: purple3"} []{#ver:445.05 label="ver:445.05"} Considering vector equilibrium as initial unity, 20 in respect to tetrahedral unity of one, it constitutes the total volumetric domain unique to any universal focus or point.
[445.06]{style="color: purple3"} []{#ver:445.06 label="ver:445.06"} We find that the vector equilibrium has a volume of 480 in terms of the and Quanta Modules.
[445.07]{style="color: purple3"} []{#ver:445.07 label="ver:445.07"} When the frequency of the vector equilibrium is 50 (that is, with 50 edge intervals and with radii at 50 intervals), the volume is frequency to the third power times unity of 480 and Quanta Modules: or and Quanta Modules. This will give us the exact number of quanta at any symmetrical stage growth. Here we witness experientially the quantum propagation of radiant wave after radiant wave identifiable with given wavelengths and frequencies of embracements.
[445.10]{style="color: purple3"} []{#ver:445.10 label="ver:445.10"} Frequency inherently involves a plurality of events, which means that frequency begins with two or more event experiences. Where frequency is one, it means frequency is none = N-one = frequency-is-not-one, because frequency is two-or-more. (None is Latin for number nine, which is also numerologically a zero.) A frequency of one in the vector equilibrium is like the vector equilibrium itself, a zero state, i.e., energetically inactive. Frequency of experience inherently involves intervals between experience. Intervals that are nonexperiences are not nothingness: they are number integrities like zero state. This zero-state integrity is brought home to human cognition by numerological arithmetic disclosure (see Chapter 12, Numerology) that every nine experiences in arithmetical system integrity (integer) accounting always has a zero operational effect in all intersystem multiplying or dividing calculations, and that nature’s number coordination coincides with its geometrical operational evolution, having only octave periodicity in which four positive entities accrue followed by the accrual of four negative entities and an interval zero state nine, which positive-negative accrual and intervailing accommodates rationally and elegantly both the wavilinear and discontinuity characteristics of all-experimentally acquired information to date regarding the electromagnetics and chemistry of both physical and metaphysical Universe.
[445.11]{style="color: purple3"} []{#ver:445.11 label="ver:445.11"} At eternal “outset,” the vector equilibrium’s frequency is none non, which is inactive, which is different in meaning from nonexistent. Zero is the inside-out phase of conceptual integrity; it is the eternal complementation of system. Quite the contrary to “nonexistent,” it means only “eternally existent” in contrast to “temporarily existent.” Experience is all temporary. Between experiences is the forever eternal metaphysical, which cannot be converted into existent. Zerophase, i.e., the absolute integrity, is a metaphysical potential in pure principle but is inherently inactive. The inactivity of zerophase can be converted into activity only by pure principle of energetic geometrical propagation of successive positive-negative-positive-negative aberrational pulsations which intertransform locally initiated Universe through vector-equilibrium complex frequency accommodations in pure principle. The propagative pulsations are unopposed by the inherent but eternal, limitless, unoccupied outwardness of absolute metaphysical integrity. The unlimited metaphysical conceptual equilibrium integrity permits the limited special-case realizations. The limited cannot accommodate the unlimited. The unlimited metaphysical can and does accommodate the limited and principles-dependent physical; but the physical, which is always experienceable and special-case, cannot accommodate the metaphysical independence and unlimited capability.
[445.12]{style="color: purple3"} []{#ver:445.12 label="ver:445.12"} The first layer of nuclear sphere embracement = . Twelve balls of the first layer. The center ball has a value of two for the outwardness-inwardness, concave-convex terminal condition. But the center ball’s frequency is zero.
[445.13]{style="color: purple3"} []{#ver:445.13 label="ver:445.13"} The number of vertexes in the vector equilibrium is always the same as the number of spheres in omnidirectional closest packing: but frequency is identifiable only as the interval between the sphere centers. Two spheres have only one interval, ergo, . Frequency to the second power times ten plus two .
[445.14]{style="color: purple3"} []{#ver:445.14 label="ver:445.14"} The vector equilibrium is the common denominator of the tetrahedron, octahedron, and cube. It is the modular domain of the nine-zero-punctuated octave system. Double the vector equilibrium’s modules radius for octaval volume accommodation.
[445.15]{style="color: purple3"} []{#ver:445.15 label="ver:445.15"} When we compare the two-frequency-edge moduled cube’s volume as quantized exclusively with cubes, to the vector equilibrium’s volume as quantized exclusively with tetrahedra, we find that the volume of the two- frequency cube equals eightwhich is two to the third power, expressed as . Whereas the volume of the two-frequency vector equilibrium equals 160, which is the integer two raised to the fifth power, , and then multiplied by five, , expressed as 5-25. (See illustration 966.05.)
[445.16]{style="color: purple3"} []{#ver:445.16 label="ver:445.16"} In 60-degree vector equilibrium accounting, when the edge module reads two, we have an energy potential (20) converted to an energy realized value of 20F3, F being 2, ergo, 23 = 8, ergo, 20 x 8 = 160, which is also expressible most economically in prime numbers as two to the fifth power times five.
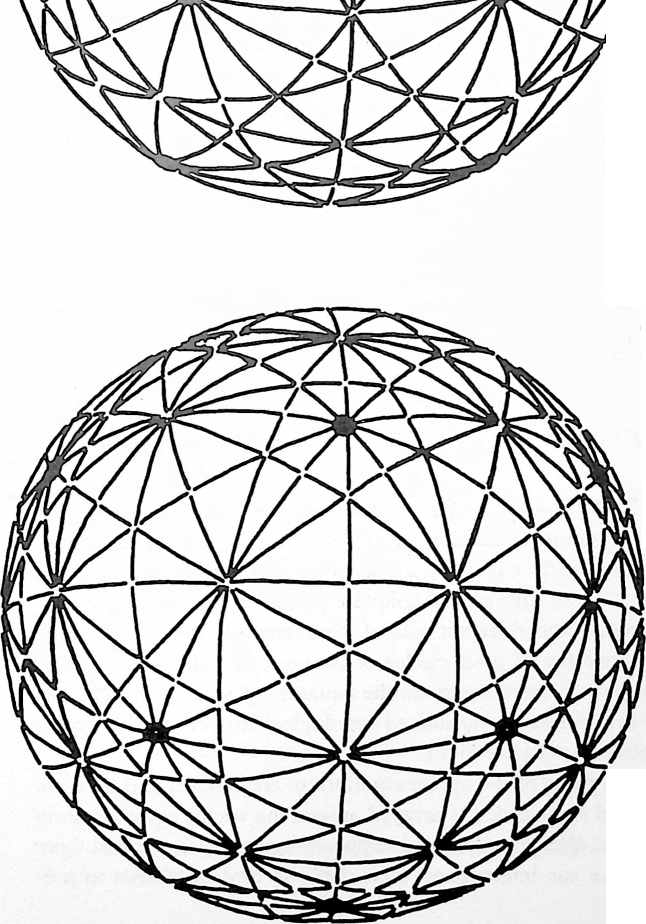
Fig. 445.13.
-
The 25 great-circle planes of the vector equilibrium shown as true circles on a sphere (Enlarged points of intersection represent the vertexes of the vector equilibrium.)
-
The 31 great-circle planes of the icosahedron shown as true circles on a sphere. (Enlarged points of intersection represent the vertexes of the icosahedron.)
[445.17]{style="color: purple3"} []{#ver:445.17 label="ver:445.17"} We thus understand the misassumption of mid-19th century science that the fourth and fifth dimensions were inherently nonmodelable. The misassumption was occasioned by science’s identification of dimensional uniqueness only with the rectilinearity of the cube, instead of with the vector equilibrium’s omni-sixty-degreeness and the isotropic vector matrix’s most economically mass-interattracted closest-self-packing unit radius sphere nucleation.
[445.18]{style="color: purple3"} []{#ver:445.18 label="ver:445.18"} Generalized omni-intertransformable modelability now faithfully permits popular human comprehension of all experimentally derived scientific knowledge regarding physical phenomena heretofore translated only into exclusively abstract mathematical schemes of notationally formalized and formulated treatment, study, discovery; objective physical application now becomes modelable with energy-vectored tetrahedroning. This means that omniconceptuality of the geometrical intertransformations of eternally self- regenerative Universe now returns to science. This also means that the om- nirational quantation we are discovering here means that children can conceptualize nuclear geometry even in their kindergarten years. This means in turn that nuclear physics will become lucidly explorable by humanity in its elementary spontaneously conceptioning and reasoning years.
¶ 450.00 Great Circles of the Vector Equilibrium and Icosahedron
[450.10]{style="color: purple3"} []{#ver:450.10 label="ver:450.10"} Great Circles of the Vector Equilibrium (see also drawings section )
[450.11]{style="color: purple3"} []{#ver:450.11 label="ver:450.11"} Four Sets of Axes of Spin: The omni-equi-edged and radiused vector equilibrium is omnisymmetrical, having 12 vertexes, six square faces, eight triangular faces, and 24 edges for a total of 50 symmetrically positioned topological features. These four sets of unique topological aspects of the vector equilibrium provide four different sets of symmetrically positioned polar axes of spin to generate the 25 great circles of the vector equilibrium. The 25 great circles of the vector equilibrium are the equators of spin of the 25 axes of the 50 unique symmetrically positioned topological aspects of the vector equilibrium (see also drawings section ).
[450.12]{style="color: purple3"} []{#ver:450.12 label="ver:450.12"} Six of the faces of the vector equilibrium are square, and they are only corner-joined and symmetrically arrayed around the vector equilibrium in respect to one another. We can pair the six opposite square faces so that there are three pairs, and we can interconnect their opposite centers of area to provide three axes, corresponding to the coordinates of Cartesian geometry. We can spin the vector equilibrium on each of these three intersymmetrically positioned axes of square symmetry to produce three equators of spin. These axes generate the set of three intersymmetrical great-circle equators of the vector equilibrium. Together the three great circles subdivide the vector equilibrium into eight octants (see also drawings section).
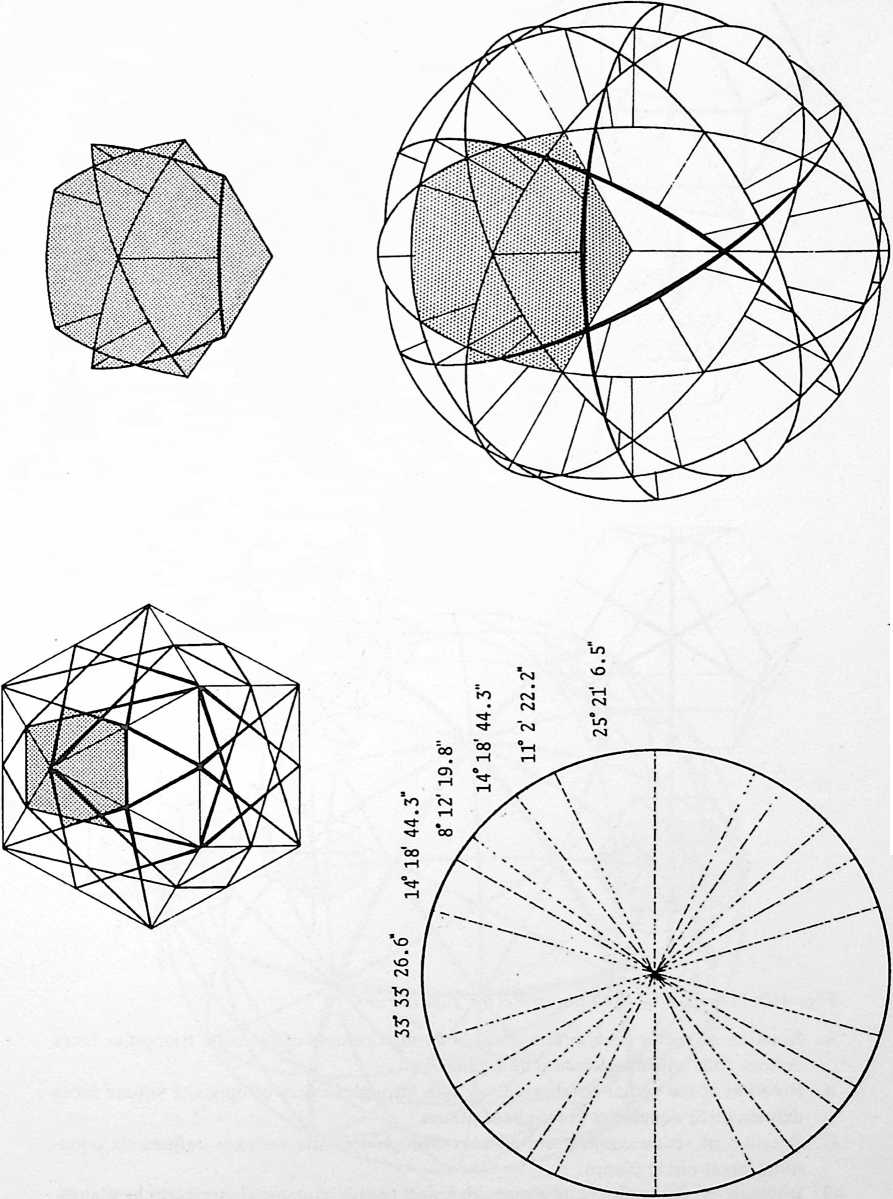
Fig. 450.10 The 12 Great Circles of the Vector Equilibrium Constructed from 12 Folded Units (Shown as Shaded).
The 12 Great Circles of the Vector Equilibrium
Fig. 450.11A Axes of Rotation of Vector Equilibrium:
-
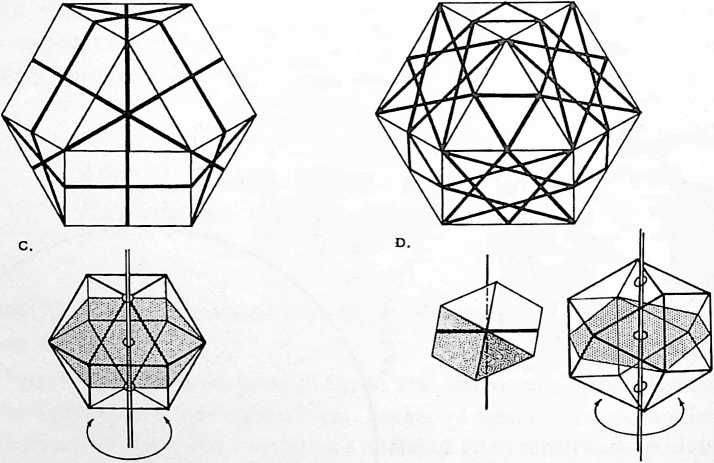
Rotation of vector equilibrium on axes through centers of opposite triangular faces defines four equatorial great-circle planes.
-
Rotation of the vector equilibrium on axes through centers of opposite square faces defines three equatorial great-circle planes.
-
Rotation of vector equilibrium on axes through opposite vertexes defines six equatorial great-circle planes.
-
Rotation of the vector equilibrium defining twelve equatorial great-circle planes, each of which passes through two opposite vertexes and two midpoints of the edges of two opposite triangular faces. The axes of rotation pass through opposite square faces.
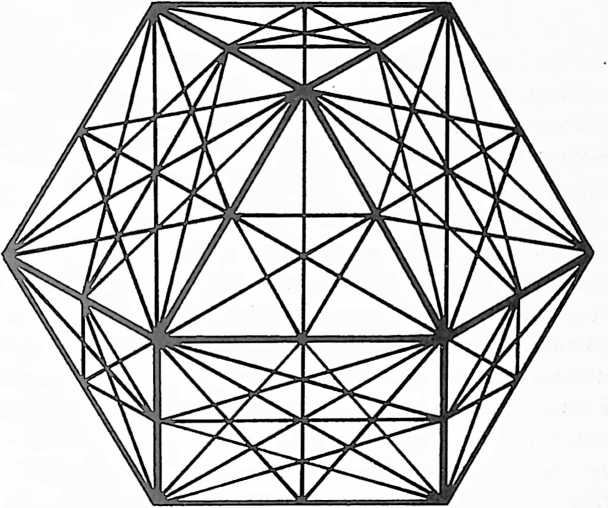
Fig. 450.1 1B Projection of 25 Great-Circle Planes in Vector Equilibrium System: The complete vector equilibrium system of 25 great-circle planes, shown as both a plane faced-figure and as the complete sphere (). The heavy lines show the edges of the original 14-faced vector equilibrium.
-
There are also eight symmetrically arrayed triangular faces of the vector equilibrium. We can pair the symmetrically opposite triangular faces so that there are four pairs, and we can interconnect their opposite centers of area to provide four intersymmetrically positioned axes. We can spin the vector equilibrium on each of these four axes of symmetry to produce four intersymmetrical equators of spin. These axes generate the set four intersymmetrical great-circle equators of the vector equilibrium.
-
When the 12 intersymmetrically positioned vertexes of the vector equilibrium are polarly interconnected, the lines of most economical interconnection provide six symmetrically interpositioned axes of spin. These six axes generate the set of six intersymmetrical great-circle equators of the vector equilibrium.
-
We may also most economically interconnect the 24 polarly opposed midpoints of the 24 intersymmetrically arrayed edges of the vector equilibrium to provide 12 sets of intersymmetrically positioned axes of spin. These axes generate the set of twelve intersymmetrical great-circle equators of the vector equilibrium.
-
As described, we now have sum-totally three square-face-centered axes, plus four triangular-face-centered axes, plus six vertex-centered axes, plus 12 edge-centered axes (3 + 4 + 6 + 12 = 25). There are a total of 25 com- plexedly intersymmetrical great circles of the vector equilibrium.
¶ 451.00 Vector Equilibrium: Axes of Symmetry and Points of Tangency in Closest Packing of Spheres
[451.01]{style="color: purple3"} []{#ver:451.01 label="ver:451.01"} It is a characteristic of all the 25 great circles that each one of them goes through two or more of the vector equilibrium’s 12 vertexes. Four of the great circles go through six vertexes; three of them go through four vertexes; and 18 of them go through two vertexes.
[451.02]{style="color: purple3"} []{#ver:451.02 label="ver:451.02"} We find that all the sets of the great circles that can be generated by all the axes of symmetry of the vector equilibrium go through the 12 vertexes, which coincidentally constitute the only points of tangency of closest- packed, uniform-radius spheres. In omnidirectional closest packing, we always have 12 balls around one. The volumetric centers of the 12 uniformradius balls closest packed around one nuclear ball are congruent with the 12 vertexes of the vector equilibrium of twice the radius of the closest-packed spheres.
[451.03]{style="color: purple3"} []{#ver:451.03 label="ver:451.03"} The network of vectorial lines most economically interconnecting the volumetric centers of 12 spheres closest packed around one nuclear sphere of the same radius describes not only the 24 external chords and 12 radii of. the vector equilibrium but further outward extensions of the system by closest packing of additional uniform-radius spheres omnisurrounding the 12 spheres already closest packed around one sphere and most economically interconnecting each sphere with its 12 closest-packed tangential neighbors, altogether providing an isotropic vector matrix, i.e., an omnidirectional complex of vectorial lines all of the same length and all interconnected at identically angled convergences. Such an isotropic vector matrix is comprised internally entirely of triangular-faced, congruent, equiedged, equiangled octahedra and tetrahedra. This isotropic matrix constitutes the omnidirectional grid.
[451.04]{style="color: purple3"} []{#ver:451.04 label="ver:451.04"} The basic gridding employed by nature is the most economical agglomeration of the atoms of any one element. We find nature time and again using this closest packing for most economical energy coordinations.
¶ 452.00 Vector Equilibrium: Great-Circle Railroad Tracks of Energy
[452.01]{style="color: purple3"} []{#ver:452.01 label="ver:452.01"} The 12 points of tangency of unit-radius spheres in closest packing, such as is employed by any given chemical element, are important because energies traveling over the surface of spheres must follow the most economical spherical surface routes, which are inherently great circle routes, and in order to travel over a series of spheres, they could pass from one sphere to another only at the 12 points of tangency of any one sphere with its closest-packed neighboring uniform-radius sphere.
[452.02]{style="color: purple3"} []{#ver:452.02 label="ver:452.02"} The vector equilibrium’s 25 great circles, all of which pass through the 12 vertexes, represent the only “most economical lines” of energy travel from one sphere to another. The 25 great circles constitute all the possible “most economical railroad tracks” of energy travel from one atom to another of the same chemical elements. Energy can and does travel from sphere to sphere of closest-packed sphere agglomerations only by following the 25 surface great circles of the vector equilibrium, always accomplishing the most economical travel distances through the only 12 points of closest-packed tangency.
[452.03]{style="color: purple3"} []{#ver:452.03 label="ver:452.03"} If we stretch an initially flat rubber sheet around a sphere, the outer spherical surface is stretched further than the inside spherical surface of the same rubber sheet simply because circumference increases with radial increase, and the more tensed side of the sheet has its atoms pulled into closer radial proximity to one another. Electromagnetic energy follows the most highly tensioned, ergo the most atomically dense, metallic element regions, wherefore it always follows great-circle patterns on the convex surface of metallic spheres. Large copper-shelled spheres called Van De Graaff electrostatic generators are employed as electrical charge accumulators. As much as two million volts may be accumulated on one sphere’s surface, ultimately to be discharged in a lightning-like leap-across to a near neighbor copper sphere. While a small fraction of this voltage might electrocute humans, people may walk around inside such high-voltage-charged spheres with impunity because the electric energy will never follow the concave surface paths but only the outer convex great-circle paths for, by kinetic inherency, they will always follow the great-circle paths of greatest radius.
[452.04]{style="color: purple3"} []{#ver:452.04 label="ver:452.04"} You could be the little man in Universe who always goes from sphere to sphere through the points of intersphere tangencies. If you lived inside the concave surface of one sphere, you could go through the point of tangency into the next sphere, and you could go right through Universe that way always inside spheres. Or you could be the little man who lives on the outside of the spheres, always living convexly, and when you came to the point of tangency with the next sphere, you could go on to that next sphere convexly, and you could go right through Universe that way. Concave is one way of looking at Universe, and convex is another. Both are equally valid and cosmically extensive. This is typical of how we should not be fooled when we look at spheresor by just looking at the little local triangle on the surface of our big sphere and missing the big triangle [^13] always polarly complementing it and defined by the same three edges but consisting of all the unit spherical surface area on the outer side of the small triangle’s three edges. These concave-convex, inside-out, and surface-area complementations are beginning to give us new clues to conceptual comprehending.
[452.05]{style="color: purple3"} []{#ver:452.05 label="ver:452.05"} As was theoretically indicated in the foregoing energy-path discoveries, we confirm experimentally that electric charges never travel on the concave side of a sphere: they always stay on the convex surface. In the phenomenon of electroplating, the convex surfaces are readily treated while it is almost impossible to plate the concave side except by use of a close matrix of local spots. The convex side goes into higher tension, which means that it is stretched thinner and tauter and is not only less travel-resistant, but is more readily conductive because its atoms are closer to one another. This means that electromagnetic energy automatically follows around the outside of convex surfaces. It is experimentally disclosed and confirmed that energy always seeks the most economical, ergo shortest, routes of travel. And we have seen that the shortest inter-sphere or inter-atom routes consist exclusively of the 25 great-circle geodesic-surface routes, which transit the 12 vertexes of the vector equilibrium, and which thus transit all the possible points of tangency of closest-packed spheres.
[452.06]{style="color: purple3"} []{#ver:452.06 label="ver:452.06"} There always exists some gap between the closest-packed spheres due to the nuclear kinetics and absolute discontinuity of all particulate matter. When the 12 tangency gaps are widened beyond voltage jumpability, the eternally regenerative conservation of cosmic energy by pure generalized principles will reroute the energies on spherically closed great-circle “holding patterns” of the 25 great circles, which are those produced by the central-angle foldings of the four unique great-circle sets altogether comprising the vector equilibrium’s 25 great circles.
[452.07]{style="color: purple3"} []{#ver:452.07 label="ver:452.07"} High energy charges in energy networks refuse to take the longest of the two great-circle arc routes existing between any two spherical points. Energy always tends to “short-circuit,” that is, to complete the circuit between any two spherical surface points by the shortest great-circle arc route. This means that energy automatically triangulates via the diagonal of a square or via the triangulating diagonals of any other polygons to which force is applied. Triangular systems represent the shortest, most economical energy networks. The triangle constitutes the self-stabilizing pattern of complex kinetic energy interference occasioned angular shuntings and three-fold or more circle interaction averaging of least-resistant directional resultants, which always trend toward equiangular configurations, whether occurring as free radiant energy events or as local self-structurings.
¶ 453.00 Vector Equilibrium: Basic Equilibrium LCD Triangle
[453.01]{style="color: purple3"} []{#ver:453.01 label="ver:453.01"} The system of 25 great circles of the vector equilibrium defines its own lowest common multiple spherical triangle, whose surface is exactly th of the entire sphere’s surface. Within each of these th-sphere triangles and their boundary arcs are contained and repeated each time all of the unique interpatterning relationships of the 25 great circles. Twenty-four of the 48 triangles’ patternings are “positive” and 24 are “negative,” i.e., mirror-images of one another, which condition is more accurately defined as “inside out” of one another. This inside-outing of the big triangles and each of their contained triangles is experimentally demonstrable by opening any triangle at any one of its vertexes and holding one of its edges while sweeping the other two in a 360-degree circling around the fixed edge to rejoin the triangle with its previous outsideness now inside of it. This is the basic equilibrium LCD triangle; for a discussion of the basic disequilibrium LCD triangle, see Sec. 905 .
’ AD ’ 28 16.3”
DE IS 47 3S.S
EG 28 16.3
GH 26 5.6
HC 33 54.4
BC 14 21.8
AB 1 30.0
BD 46 43.3
DC 00 00
DF 18 44.3
EF 12 19.8
EH 18 44.3
FH 2 22.2
K 21 6.5
+---+--------------+-----------------------+
| | ::: minipage | |
| | ::: | |
+:==+:=============+:======================+
| ’ | BAD | ’ 00 00.0’ |
+---+--------------+-----------------------+
| | ADB | 28 55.9 |
+---+--------------+-----------------------+
| | BDC | 31 4.1 |
+---+--------------+-----------------------+
| | CDF | 31 4.1 |
+---+--------------+-----------------------+
| | EDF | 28 55.9 |
+---+--------------+-----------------------+
| | DEF | 45 38.2 |
+---+--------------+-----------------------+
| | FEH | 28 43.7 |
+---+--------------+-----------------------+
| | HEG | 45 38.2 |
+---+--------------+-----------------------+
| | EGH | 00 00.0 |
+---+--------------+-----------------------+
| | EHG | 27 5.8 |
+---+--------------+-----------------------+
| | EHF | 5 48.5 |
+---+--------------+-----------------------+
| | FHC | 27 5.8 |
+---+--------------+-----------------------+
| | FCH | 14 21.8 |
+---+--------------+-----------------------+
| | DCF | 29 46.3 |
+---+--------------+-----------------------+
| | BCD | 15 51.8 |
+---+--------------+-----------------------+
| | DBC | 00 00.[0]{.underline} |
+---+--------------+-----------------------+
| | ABD | 00 00.0 |
+---+--------------+-----------------------+
| | DFE | 84 47 2.8 |
+---+--------------+-----------------------+
| | EFH | 12 5[7.2]{.underline} |
+---+--------------+-----------------------+
| | CFH | 84 47 3.8 |
+---+--------------+-----------------------+
| | DFC | 12 57.2 |
+---+--------------+-----------------------+
Fig-453.01 Great Circles of Vector Equilibrium Define Lowest Common Multiple the entire sphere and is the lowest common denominator (in 24 rights and 24 lefts) of the total spherical surface. The 48 LCD triangles defined by the 25 great circles of the vector equilibrium are grouped together in whole increments to define exactly the spherical surface areas, edges, and vertexes of the spherical tetrahedron, spherical cube, spherical octahedron, and spherical rhombic dodecahedron. The heavy lines are the edges of the four great circles of the vector equilibrium. Included here is the spherical trigonometry data for this lowest-common-denominator triangle of the 25-great-circle hierarchy of the vector equilibrium.
[453.02]{style="color: purple3"} []{#ver:453.02 label="ver:453.02"} Inside-Outing of Triangle: The inside-outing transformation of a triangle is usually misidentified as “left vs. right,” or “positive and negative,” or as “existence vs. annihilation” in physics (see drawings section ).
[453.03]{style="color: purple3"} []{#ver:453.03 label="ver:453.03"} The inside-outing is four-dimensional and often complex. It functions as complex intro-extroverting.
¶ 454.00 Vector Equilibrium: Spherical Polyhedra Described by Great Circles
[454.01]{style="color: purple3"} []{#ver:454.01 label="ver:454.01"} The 25 great circles of the spherical vector equilibrium provide all the spherical edges for five spherical polyhedra: the tetrahedron, octahedron, cube, rhombic dodecahedron, and vector equilibrium, whose corresponding planar-faceted polyhedra are all volumetrically rational, even multiples of the tetrahedron. For instance, if the tetrahedron’s volume is taken as unity, the octahedron’s volume is four, the cube’s volume is three, the rhombic dodecahedron’s is six, and the vector equilibrium’s is 20 (see drawings section).
[454.02]{style="color: purple3"} []{#ver:454.02 label="ver:454.02"} This is the hierarchy of rational energy quanta values in synergetics, which the author discovered in his youth when he first sought for an omnirational coordinate system of Universe in equilibrium against which to measure the relative degrees of orderly asymmetries consequent to the cosmic myriad of pulsatively propagated energetic transactions and transformations of eternally conserving evolutionary events. Though almost all the involved geometries were long well known, they had always been quantized in terms of the cube as volumetric unity and its edges as linear unity; when employed in evaluating the other polyhedra, this method produced such a disarray of irrational fraction values as to imply that the other polyhedra were only side-show geometric freaks or, at best, “interesting aesthetic objets d’art.” That second-powering exists today in academic brains only as “squaring” and third-powering only as cubing is manifest in any scientific blackboard discourse, as the scientists always speak of the they have just used as “x squared” and likewise always account as “x cubed” (see drawings section).
[454.03]{style="color: purple3"} []{#ver:454.03 label="ver:454.03"} The spherical tetrahedron is composed of four spherical triangles, each consisting of 12 basic, least-common-denominator spherical triangles of vector equilibrium (see drawings section).
[454.04]{style="color: purple3"} []{#ver:454.04 label="ver:454.04"} The spherical octahedron is composed of eight spherical triangles, each consisting of six basic-vector-equilibrium, least-common-denominator triangles of the 25 great-circle, spherical-grid triangles.
[454.05]{style="color: purple3"} []{#ver:454.05 label="ver:454.05"} The spherical cube is composed of six spherical squares with corners of 120each, each consisting of eight basic-vector-equilibrium, least-common-denominator triangles of the 25 great-circle spherical-grid triangles.
[454.06]{style="color: purple3"} []{#ver:454.06 label="ver:454.06"} The spherical rhombic dodecahedron is composed of 12 spherical diamond-rhombic faces, each composed of four basic-vector-equilibrium, least-common-denominator triangles of the 25 great-circle, spherical-grid triangles.
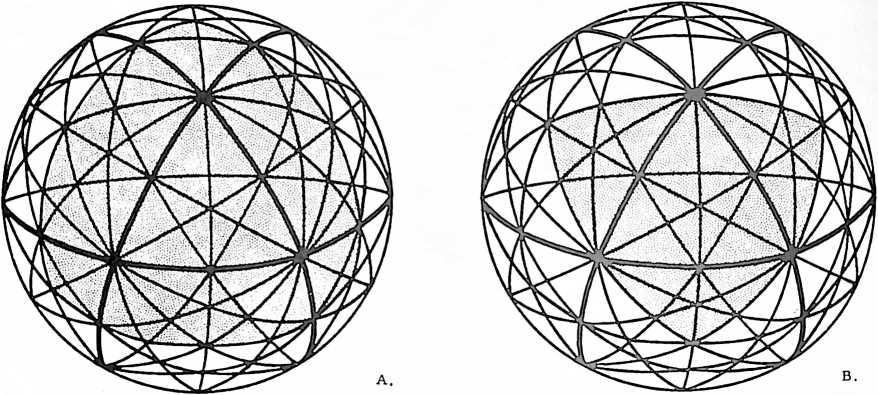
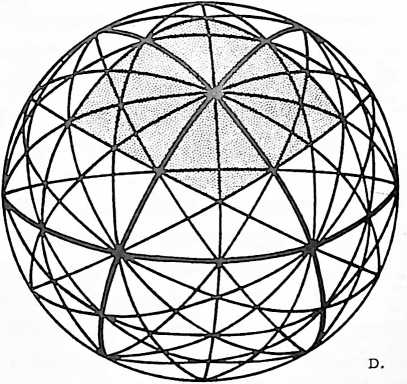
Fig. 454.06 Definition of Spherical Polyhedra in 25-Great-Circle Vector Equilibrium System: The 25 great circles of the spherical vector equilibrium provide all the spherical edges for four spherical polyhedra in addition to the vector equilibrium whose edges are shown here as heavy lines. The shading indicates a typical face of each as follows:
-
The edges of one of the spherical tetrahedron’s four spherical triangles consists of 12 VE basic LCD triangles.
-
The edges of one of the spherical octahedron’s eight spherical triangles consists of six VE basic LCD triangles.
-
The edges of one of the spherical cube’s six spherical squares consists of eight VE basic LCD triangles.
-
The edges of one of the spherical rhombic dodecahedron’s 12 spherical rhombic faces consists of four VE basic LCD triangles.
¶ 455.00 Great-Circle Foldabilities of Vector Equilibrium
[455.01]{style="color: purple3"} []{#ver:455.01 label="ver:455.01"} Foldability of Vector Equilibrium Four Great-Circle Bow Ties: All of the set of four great circles uniquely and discretely describing the vector equilibrium can be folded out of four whole (non-incised), uniformradius, circular discs of paper, each folded radially in 60-degree central angle increments, with two diametric folds, mid-circle, hinge-bent together and locked in radial congruence so that their six 60-degree arc edges form two equiangled spherical triangles, with one common radius-pairing fastened together at its external apex, that look like a bow tie. The pattern corresponds to the external arc trigonometry, with every third edgefold being brought into congruence to form great-circle-triangled openings at their top with their pointed lower ends all converging ice-cream-cone-like at the center of the whole uncut and only radially folded great circles. When the four bow ties produced by the folded circles are assembled together by radii congruence and locking of each of their four outer bow-tie corners to the outer bow-tie corners of one another, they will reestablish the original four great-circle edge lines of the vector equilibrium and will accurately define both its surface arcs and its central angles as well as locating the vector-equilibrium axes of symmetry of its three subsets of great-circle-arc-generating to produce, all told, 25 great circles of symmetry. When assembled with their counterpart foldings of a total number corresponding to the great-circle set involved, they will produce a whole sphere in which all of the original great circles are apparently restored to their completely continuing-around-the-sphere integrity.
[455.02]{style="color: purple3"} []{#ver:455.02 label="ver:455.02"} The sum of the areas of the four great-circle discs elegantly equals the surface area of the sphere they define. The area of one circle is . The area of the surface of a sphere is . The area of the combined four folded great-circle planes is also and all four great-circle planes go through the exact center of the sphere and, between them, contain no volume at all. The sphere contains the most volume with the least surface enclosure of any geometrical form. This is a cosmic limit at maximum. Here we witness the same surface with no volume at all, which qualifies the vector equilibrium as the most economic nuclear “nothingness” whose coordinate conceptuality rationally accommodates all radiational and gravitational interperturbational transformation accounting. In the four great-circle planes we witness the same surface area as that of the sphere, but containing no volume at all. This too, is cosmic limit at zero minimumness.
[455.03]{style="color: purple3"} []{#ver:455.03 label="ver:455.03"} It is to be noted that the four great-circle planes of the vector equilibrium passing exactly through its and one another’s exact centers are parallel to the four planes of the eight tetrahedra, which they accommodate in the eight triangular bow-tie concavities of the vector equilibrium. The four planes of the tetrahedra have closed on one another to produce a tetrahedron of no volume and no size at all congruent with the sizeless center of the sphere defined by the vector equilibrium and its four hexagonally intersected planes. As four points are the minimum necessary to define the insideness and out-sideness unique to all systems, four triangular facets are the minimum required to define and isolate a system from the rest of Universe.
[455.04]{style="color: purple3"} []{#ver:455.04 label="ver:455.04"} Four is also the minimum number of great circles that may be folded into local bow ties and fastened corner-to-corner to make the whole sphere again and reestablish all the great circles without having any surfaces double or be congruent with others or without cutting into any of the circles.
[455.05]{style="color: purple3"} []{#ver:455.05 label="ver:455.05"} These four great-circle sets of the vector equilibrium demonstrate all the shortest, most economical railroad “routes” between all the points in Universe, traveling either convexly or concavely. The physical-energy travel patterns can either follow the great-circle routes from sphere to sphere or go around in local holding patterns of figure eights on one sphere. Either is permitted and accommodated. The four great circles each go through six interspherical tangency points.
[455.10]{style="color: purple3"} []{#ver:455.10 label="ver:455.10"} Foldability of Vector Equilibrium Six Great-Circle Bow Ties: The foldable bow ties of the six great circles of the vector equilibrium define a combination of the positive and negative spherical tetrahedrons within the spherical cube as well as of the rhombic dodecahedron.
[455.11]{style="color: purple3"} []{#ver:455.11 label="ver:455.11"} In the vector equilibrium’s six great-circle bow ties, all the internal, i.e., central angles of 70 and 54, are those of the surface angles of the vector equilibrium’s four great-circle bow ties, and vice versa. This phenomenon of turning the inside central angles outwardly and the outside surface angles inwardly, with various fractionations and additions, characterizes the progressive transformations of the vector equilibrium from one great-circle foldable group into another, into its successive stages of the spherical cube and octahedron with all of their central and surface angles being both 90 degrees even.
[455.20]{style="color: purple3"} []{#ver:455.20 label="ver:455.20"} Foldability of 12 Great Circles into Vector Equilibrium: We can take a disc of paper, which is inherently of 360 degrees, and having calculated with spherical trigonometry all the surface and central angles of both the associated and separate groups of 3/4–12 great circles of the vector equilibrium’s 25 great circles, we can lay out the spherical arcs which always subtend the central angles. The 25 great circles interfere with and in effect “bounce off” or penetrate one another in an omnitriangulated, nonredundant spherical triangle grid. Knowing the central angles, we can lay them out and describe foldable triangles in such a way that they make a plurality of tetrahedra that permit and accommodate fastening together edge-to-edge with no edge duplication or overlap. When each set, 3-4-6-12, of the vector equilibrium is completed, its components may be associated with one another to produce complete spheres with their respective great-circle, 360-degree integrity reestablished by their arc increment association.
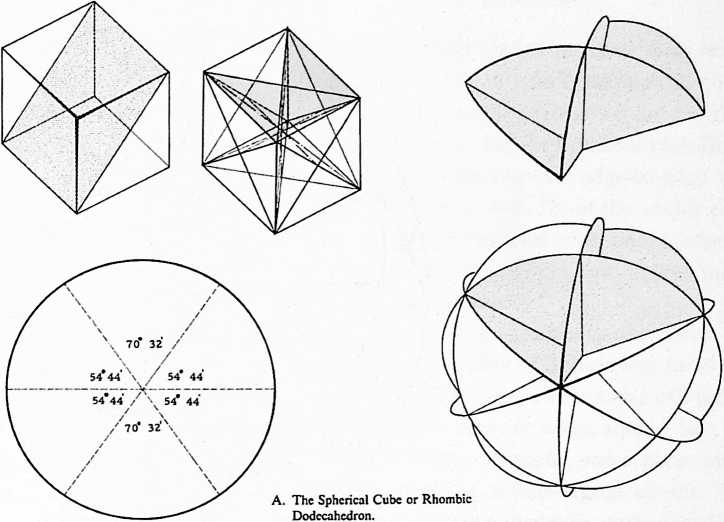
Fig. 455.11 Folding of Great Circles into Spherical Cube or Rhombic Dodecahedron and Vector Equilibrium: Bow-Tie Units:
-
This six-great-circle construction defines the positive-negative spherical tetrahedrons within the cube. This also reveals a spherical rhombic dodecahedron. The circles are folded into “bow-tie” units as shown. The shaded rectangle in the upper left indicates the typical plane represented by the six great circles.
-
The vector equilibrium is formed by four great circles folded into “bow-ties.” The sum of the areas of the four great circles equals the surface area of the sphere. (4r2).
Fig. 455.20 The 12 Great Circles of the Vector Equilibrium Constructed from 12 Folded Units.
[455.21]{style="color: purple3"} []{#ver:455.21 label="ver:455.21"} The 25 folded great-circle sections join together to reestablish the 25 great circles. In doing so, they provide a plurality of 360-degree local and long-distance travel routes. Because each folded great circle starts off with a 360-degree disc, it maintains that 360-degree integrity when folded into the bow-tie complexes. It is characteristic of electromagnetic wave phenomena that a wave must return upon itself, completing a 360-degree circuit. The great-circle discs folded or flat provide unitary-wave-cycle circumferential circuits. Therefore, folded or not, they act like waves coming back upon themselves in a perfect wave control. We find their precessional cyclic self-interferences producing angular resultants that shunt themselves into little local 360-degree, bow-tie “holding patterns.” The entire behavior is characteristic of generalized wave phenomena.
[455.22]{style="color: purple3"} []{#ver:455.22 label="ver:455.22"} In the case of the 12 great circles of the vector equilibrium, various complex transformative, anticipatory accommodations are manifest, such as that of the 12 sets of two half-size pentagons appearing in the last, most complex great-circle set of the vector equilibrium, which anticipates the formation of 12 whole pentagons in the six great-circle set of the 31 great circles of the icosahedron into which the vector equilibrium first transforms contractively.
¶ 456.00 Transformation of Vector Equilibrium into Icosahedron
[456.01]{style="color: purple3"} []{#ver:456.01 label="ver:456.01"} While its vertical radii are uniformly contracted from the vector equilibrium’s vertexial radii, the icosahedron’s surface is simultaneously and symmetrically askewed from the vector equilibrium’s surface symmetry. The vector equilibrium’s eight triangles do not transform, but its six square faces transform into 12 additional triangles identical to the vector equilibrium’s original eight, with five triangles cornered together at the same original 12 vertexes of the vector equilibrium.
[456.02]{style="color: purple3"} []{#ver:456.02 label="ver:456.02"} The icosahedron’s five-triangled vertexes have odd-number-imposed, inherent interangle bisectioning, that is, extensions of the 30 great-circle edges of any of the icosahedron’s 20 triangles automatically bisecting the apex angle of the adjacently intruded triangle into which it has passed. Thus extension of all the icosahedron’s 20 triangles’ 30 edges automatically bisects all of its original 60 vertexial-centered, equiangled 36-degree corners, with all the angle bisectors inherently impinging perpendicularly upon the opposite mid-edges of the icosahedron’s 20 equilateral, equiangled 72-degree-cornered triangles. The bisecting great-circle extensions from each of all three of the original 20 triangles’ apexes cross inherently (as proven elsewhere in Euclidian geometry) at the areal center of those 20 original icosahedral triangles. Those perpendicular bisectors subdivide each of the original 20 equiangled triangles into six right-angled triangles, which multiplies the total surface subdivisioning into 120 “similar” right-angled triangles, 60 of which prepositive and 60 of which are negative, whose corners in the spherical great-circle patterning are 90, 60, and 36, respectively, and their chordally composed corresponding planar polyhedral triangles are 90, 60, and 30 degrees, respectively. There is exactly 6 degrees of “spherical excess,” as it is formally known, between the 120 spherical vs. 120 planar triangles.
[456.03]{style="color: purple3"} []{#ver:456.03 label="ver:456.03"} This positive-negative subdivision of the whole system puts half the system into negative phase and the other half into positive phase, which discloses an exclusively external “surface” positive-negative relationship quite apart from that of the two surface polar hemispheres. This new aspect of complementarity is similar to the systematic omnicoexistence of the concave and convex non-mirror-imaged complementarity whose concavity and convexity make the 60 positive and 60 negative surface triangle subdivisions of spherical unity inherently noninterchangeable with one another when turned inside out, whereas they are interchangeable with one another by insideouting when in their planar-faceted polyhedral state.
[456.04]{style="color: purple3"} []{#ver:456.04 label="ver:456.04"} We thus find the split-phase positive-and-negativeness of odd- number-of-vertexial-angle systems to be inherently askewed and inside-outingly dichotomized omni symmetries. This surface phase of dichotomization results in superficial, disorderly interpatterning complementation. This superficially disarrayed complementation is disclosed when the 15 great circles produced by extension of all 30 edges of the icosahedron’s 20 triangles are folded radially in conformity to the central interangling of the 120 triangles’ spherical arc edges.
[456.05]{style="color: purple3"} []{#ver:456.05 label="ver:456.05"} The 15 great circles of the icosahedron interact to produce 15 “chains” of three varieties of four corner-to-corner, sausage-linked, right triangles, with four triangles in each chain. These 15 chains of 60 great-circle triangles are each interconnectible corner-to-corner to produce a total spherical surface subdivided into 120 similar spherical triangles. An experiment with 15 unique coloring differentiations of the 15 chains of three sequential varieties of four triangles each, will exactly complete the finite sphere and the 15 great-circle integrities of total spherical surface patterning, while utterly frustrating any systematically orderly surface patterning. The 15 chains’ 60 triangles’ inadvertent formation of an additional 60 similar spherical triangles occurring between them, which exactly subdivides the entire spherical surface into 120 symmetrically interpatterned trianglesdespite the local surface disorder of interlinkage of the three differently colored sets of four triangles composing the 15 chainsdramatically manifests the half-positive, half-negative, always and only coexisting, universal non-mirror-imaged complementarity inherently permeating all systems, dynamic or static, despite superficial disorder, whether or not visibly discernible initially.
[456.10]{style="color: purple3"} []{#ver:456.10 label="ver:456.10"} Icosahedron as Contraction of Vector Equilibrium: The icosahedron represents the 12-way, omniradially symmetrical, transformative, rotational contraction of the vector equilibrium. This can be seen very appropriately when we join the 12 spheres tangent to one another around a central nuclear sphere in closest packing: this gives the correspondence to the vector equilibrium with six square faces and eight triangular faces, all with 60-degree internal angles. If we had rubber bands between the points of tangency of those 12 spheres and then removed the center sphere, we would find the 12 tangent spheres contracting immediately and symmetrically into the icosahedral conformation.
[456.11]{style="color: purple3"} []{#ver:456.11 label="ver:456.11"} The icosahedron is the vector equilibrium contracted in radius so that the vector equilibrium’s six square faces become 12 ridge-pole diamonds. The ridge-pole lengths are the same as those of the 12 radii and the 24 outside edges. With each of the former six square faces of the vector equilibrium now turned into two equiangle triangles for a total of 12, and with such new additional equiangled and equiedged triangles added to the vector equilibrium’s original eight, we now have 20 triangles and no other surface facets than the 20 triangles. Whereas the vector equilibrium had 24 edges, we now have added six more to the total polyhedral system as it transforms from the vector equilibrium into the icosahedron; the six additional ridge poles of the diamonds make a total of 30 edges of the icosahedron. This addition of six vector edge lengths is equivalent to one great circle and also to one quantum. (See Sec. 423.10. )
[456.12]{style="color: purple3"} []{#ver:456.12 label="ver:456.12"} We picture the location of the vector equilibrium’s triangular faces in relation to the icosahedron’s triangular faces. The vector equilibrium could contract rotatively, in either positive or negative manner, with the equator going either clockwise or counterclockwise. Each contraction provides a different superposition of the vector equilibrium’s triangular faces on the icosahedron’s triangular faces. But the centers of area of the triangular faces remain coincidental and congruent. They retain their common centers of area as they rotate.
[456.13]{style="color: purple3"} []{#ver:456.13 label="ver:456.13"} We find that the 25 great circles of the icosahedron each pass through the 12 vertexes corresponding to the 25 great circles of the vector equilibrium, which also went through the 12 vertexes, as the number of vertexes after the rotational contraction remains the same.
[456.20]{style="color: purple3"} []{#ver:456.20 label="ver:456.20"} Single-Layer Contraction: The icosahedron, in order to contract, must be a single-layer affair. You could not have two adjacent layers of vector equilibria and then have them collapse to become the icosahedron. But take any single layer of a vector equilibrium with nothing inside it to push it outward, and it will collapse into becoming the icosahedron. If there are two layers, one inside the other, they will not roll on each other when the radius contracts. The gears block each other. So you can only have this contraction in a single layer of the vector equilibrium, and it has to be an outside layer remote from other layers.
[456.21]{style="color: purple3"} []{#ver:456.21 label="ver:456.21"} The icosahedron has only the outer shell layer, but it may have as high a frequency as nature may require. The nuclear center is vacant.
[456.22]{style="color: purple3"} []{#ver:456.22 label="ver:456.22"} The single-shell behavior of the icosahedron and its volume ratio of 18.63 arouses suspicions about its relation to the electron. We appear to have the electron kind of shells operating in the nucleus-free icosahedron and are therefore not frustrated from contracting in that condition.
¶ 457.00 Great Circles of Icosahedron
[457.01]{style="color: purple3"} []{#ver:457.01 label="ver:457.01"} Three Sets of Axes of Spin: The icosahedron has three unique symmetric sets of axes of spin. It provides 20 triangular faces, 12 vertexes, and 30 edges. These three symmetrically interpatterned topological aspectsfaces, vertexes, and mid-edgesprovide three sets of axes of symmetric spin to generate the spherical icosahedron projection’s grid of 31 great circles.
[457.02]{style="color: purple3"} []{#ver:457.02 label="ver:457.02"} The icosahedron has the highest number of identical and symmetric exterior triangular facets of all the symmetrical polyhedra defined by great circles.
[457.10]{style="color: purple3"} []{#ver:457.10 label="ver:457.10"} When we interconnect the centers of area of the 20 triangular faces of the icosahedron with the centers of area of their diametrically opposite faces, we are provided with 10 axes of spin. We can spin the icosahedron on any one of these 10 axes to produce 10 equators of spin. These axes generate the set of 10 great-circle equators of the icosahedron. We may also interconnect the midpoints of the 30 edges of the icosahedron in 15 sets of diametrically opposite pairs. These axes generate the 15 great-circle equators of the icosahedron. These two sets of 10 and 15 great circles correspond to the 25 great circles of the vector equilibrium.
[457.20]{style="color: purple3"} []{#ver:457.20 label="ver:457.20"} Six Great Circles of Icosahedron: When we interconnect the 12 vertexes of the icosahedron in pairs of diametric opposites, we are provided with six axes of spin. These axes generate the six great-circle equators of the icosahedron. The six great circles of the icosahedron go from mid-edge to mid-edge of the icosahedron’s triangular faces, and they do not go through any of its vertexes.
[457.21]{style="color: purple3"} []{#ver:457.21 label="ver:457.21"} The icosahedron’s set of six great circles is unique among all the seven axes of symmetry (see Sec. 1040), which include both the 25 great circles of the vector equilibrium and the 31 great circles of the icosahedron. It is the only set that goes through none of the 12 vertexes of either the vector equilibrium or the icosahedron. In assiduously and most geometrically avoiding even remote contact with any of the vertexes, they represent a new behavior of great circles.
[457.22]{style="color: purple3"} []{#ver:457.22 label="ver:457.22"} The 12 vertexes in their “in-phase” state in the vector equilibria or in their “out-of-phase” state in the icosahedra constitute all the 12 points of possible tangency of any one sphere of a closest-packed aggregate with another sphere, and therefore these 12 points are the only ones by which energy might pass to cross over into the next spheres of closest packing, thus to travel their distance from here to there. The six great circles of the icosahedron are the only ones not to go through the potential intertangency points of the closest-packed unit radius spheres, ergo energy shunted on to the six icosahedron great circles becomes locked into local holding patterns, which is not dissimilar to the electron charge behaviors.
[457.30]{style="color: purple3"} []{#ver:457.30 label="ver:457.30"} Axes of Symmetry of Icosahedron: We have now described altogether the 10 great circles generated by the 10 axes of symmetry occurring between the centers of area of the triangular faces; plus 15 axes from the midpoints of the edges; plus six axes from the vertexes. . There is a total of 31 great circles of the icosahedron.
[457.40]{style="color: purple3"} []{#ver:457.40 label="ver:457.40"} Spherical Polyhedra in Icosahedral System: The 31 great circles of the spherical icosahedron provide spherical edges for three other polyhedra in addition to the icosahedron: the rhombic triacontrahedron, the octahedron, and the pentagonal dodecahedron. The edges of the spherical icosahedron are shown in heavy lines in the illustration.
[457.41]{style="color: purple3"} []{#ver:457.41 label="ver:457.41"} The spherical rhombic triacontrahedron is composed of 30 spherical rhombic diamond faces.
[457.42]{style="color: purple3"} []{#ver:457.42 label="ver:457.42"} The spherical octahedron is composed of eight spherical triangles.
Fig. 457.30A Axes of Rotation of Icosahedron:
-
The rotation of the icosahedron on axes through midpoints of opposite edges define 15 great-circle planes.
-
The rotation of the icosahedron on axes through opposite vertexes define six equatorial great-circle planes, none of which pass through any vertexes.
-
The rotation of the icosahedron on axes through the centers of opposite faces define ten equatorial great-circle planes, which do not pass through any vertexes.
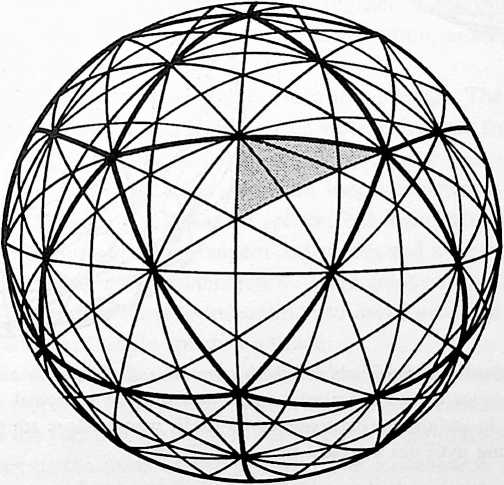
Fig. 457.30B Projection of 31 Great-Circle Planes in Icosahedron System: The complete icosahedron system of 31 great-circle planes shown with the planar icosahedron as well as true circles on a sphere (). The heavy lines show the edges of the original 20-faced icosahedron.
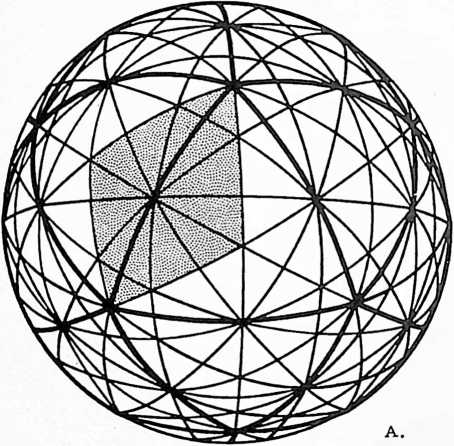
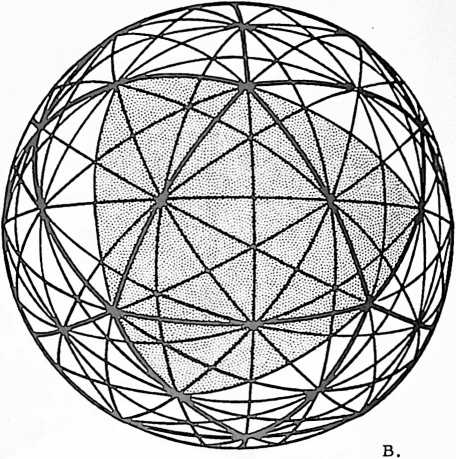
Fig. 457.40 Definition of Spherical Polyhedra in 31-Great-Circle Icosahedron System: The 31 great circles of the spherical icosahedron provide spherical edges for three other polyhedra in addition to the icosahedron itself, whose edges are shown as heavy lines. The shading indicates a typical face, as follows:
-
The rhombic triacontrahedron with 30 spherical rhombic faces, each consisting of four basic, least-common-denominator triangles.
-
The octahedron with 15 basic, least-common-denominator spherical triangles.
-
The pentagonal dodecahedron with ten basic, least-common-denominator spherical triangles.
- The spherical pentagonal dodecahedron is composed of 12 spherical pentagons.
¶ 458.00 Icosahedron: Great Circle Railroad Tracks of Energy
[458.01]{style="color: purple3"} []{#ver:458.01 label="ver:458.01"} Whereas each of the 25 great circles of the vector equilibrium and the icosahedron goes through the 12 vertexes at least twice; and whereas the 12 vertexes are the only points of intertangency of symmetric, unit-radius spheres, one with the other, in closest packing of spheres; and inasmuch as we find that energy charges always follow the convex surfaces of systems; and inasmuch as the great circles represent the most economical, the shortest distance between points on spheres; and inasmuch as we find that energy always takes the most economical route; therefore, it is perfectly clear that energy charges passing through an aggregate of closest-packed spheres, from one to another, could and would employ only the 25 great circles as the great-circle railroad tracks between the points of tangency of the spheres, ergo, between points in Universe. We can say, then, that the 25 great circles of the vector equilibrium represent all the possible railroad tracks of shortest energy travel through closest-packed spheres or atoms.
[458.02]{style="color: purple3"} []{#ver:458.02 label="ver:458.02"} When the nucleus of the vector equilibrium is collapsed, or contracted, permitting the 12 vertexes to take the icosahedral conformation, the 12 points of contact of the system go out of register so that the 12 vertexes that accommodate the 25 great circles of the icosahedron no longer constitute the shortest routes of travel of the energy.
[458.03]{style="color: purple3"} []{#ver:458.03 label="ver:458.03"} The icosahedron could not occur with a nucleus. The icosahedron, in fact, can only occur as a single shell of 12 vertexes remote from the vector equilibrium’s multi-unlimited-frequency, concentric-layer growth. Though it has the 25 great circles, the icosahedron no longer represents the travel of energy from any sphere to any tangent sphere, but it provides the most economical route between a chain of tangent icosahedra and a face-bonded icosahedral structuring of a “giant octahedron’s” three great circles, as well as for energies locked up on its surface to continue to make orbits of their own in local travel around that single sphere’s surface.
[458.04]{style="color: purple3"} []{#ver:458.04 label="ver:458.04"} This unique behavior may relate to the fact that the volume of the icosahedron in respect to the vector equilibrium with the rational value of 20 is 18.51 and to the fact that the mass of the electron is approximately one over 18.51 in respect to the mass of the neutron. The icosahedron’s shunting of energy into local spherical orbiting, disconnecting it from the closest-packed railroad tracks of energy travel from sphere to sphere, tends to identify the icosahedron very uniquely with the electron’s unique behavior in respect to nuclei as operating in remote orbit shells.
[458.05]{style="color: purple3"} []{#ver:458.05 label="ver:458.05"} The energy charge of the electron is easy to discharge from the surfaces of systems. Our 25 great circles could lock up a whole lot of energy to be discharged. The spark could jump over at this point. We recall the name electron coming from the Greeks rubbing of amber, which then discharged sparks. If we assume that the vertexes are points of discharge, then we see how the six great circles of the icosahedronwhich never get near its own vertexes may represent the way the residual charge will always remain bold on the surface of the icosahedron.
[458.06]{style="color: purple3"} []{#ver:458.06 label="ver:458.06"} Maybe the 31 great circles of the icosahedron lock up the energy charges of the electron, while the six great circles release the sparks. (See illustration 1032.13.)
[458.10]{style="color: purple3"} []{#ver:458.10 label="ver:458.10"} Icosahedron as Local Shunting Circuit: The icosahedron makes it possible to have individuality in Universe. The vector equilibrium never pauses at equilibrium, but our consciousness is caught in the icosahedron when mind closes the switch.
[458.11]{style="color: purple3"} []{#ver:458.11 label="ver:458.11"} The icosahedron’s function in Universe may be to throw the switch of cosmic energy into a local shunting circuit. In the icosahedron energy gets itself locked up even more by the six great circleswhich may explain why electrons are borrowable and independent of the proton-neutron group.
[458.12]{style="color: purple3"} []{#ver:458.12 label="ver:458.12"} The vector-equilibrium railroad tracks are trans-Universe, but the icosahedron is a locally operative system.
¶ 459.00 Great Circle Foldabilities of Icosahedron
[459.01]{style="color: purple3"} []{#ver:459.01 label="ver:459.01"} The great circles of the icosahedron can be folded out of circular discs of paper by three different methods: (a) 15 multi-bow ties of four tetrahedra each; (b) six pentagonal bow ties; and (c) 10 multi-bow ties. Each method defines certain of the surface arcs and central angles of the icosahedron’s great circle system, but all three methods taken together do not define all of the surface arcs and central angles of the icosahedron’s three sets of axis of spin (see drawings section).
[459.02]{style="color: purple3"} []{#ver:459.02 label="ver:459.02"} The 15 great circles of the icosahedron can be folded into multi-bowties of four tetrahedra each. Four times 15 equals 60, which is half the number of triangles on the sphere. Sixty additional triangles inadvertently appear, revealing the 120 identical spherical triangles which are the maximum number of like units which may be used to subdivide the sphere.
[459.03]{style="color: purple3"} []{#ver:459.03 label="ver:459.03"} The six great circles of the icosahedron can be folded from central angles of 36 degrees each to form six pentagonal bow ties. (See illustration 458.12.)
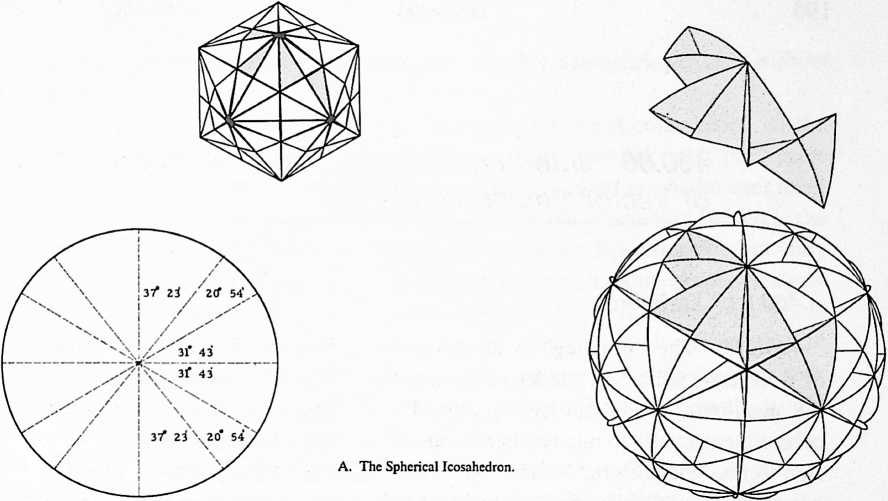
Fig. 458.12 Folding of Great Circles into the Icosahedron System:
-
The 15 great circles of the icosahedron folded into “multi-bow-ties” consisting of four tetrahedrons each. Four times 15 equals 60, which is 16 the number of triangles on the sphere. Sixty additional triangles inadvertently appear, revealing the 120 identical (although right- and left-handed) spherical triangles, which are the maximum number of like units that may be used to subdivide the sphere.
-
The six great-circle icosahedron system created from six pentagonal “bow-ties.”
¶ 460.00 Jitterbug: Symmetrical Contraction of Vector Equilibrium
[460.01]{style="color: purple3"} []{#ver:460.01 label="ver:460.01"} Definition
[460.011]{style="color: purple3"} []{#ver:460.011 label="ver:460.011"} The “jitterbug” is the finitely closed, external vector structuring of a vector-equilibrium model constructed with 24 struts, each representing the push-pull, action-and-reaction, local compression vectors, all of them cohered tensionally to one another’s ends by flexible joints that carry only tension across themselves, so that the whole system of only-locally-effective compression vectors is comprehensively cohered by omniembracing continuous four closed hexagonal cycles’ tension.
[460.02]{style="color: purple3"} []{#ver:460.02 label="ver:460.02"} When the vector-equilibrium “jitterbug” assembly of eight triangles and six squares is opened, it may be hand-held in the omnisymmetry conformation of the vector equilibrium “idealized nothingness of absolute middleness.” If one of the vector equilibrium’s triangles is held by both hands in the following manner with that triangle horizontal and parallel to and above a tabletop; with one of its apexes pointed away from the holder and the balance of the jitterbug system dangling symmetrically; with the opposite and lowest triangle, opposite to the one held, just parallel to and contacting the tabletop, with one of its apexes pointed toward the individual who is handholding the jitterbugand then the top triangle is deliberately lowered toward the triangle resting on the table without allowing either the triangle on the table or the triangle in the operator’s hands to rotate (keeping hands clear of the rest of the system), the whole vector equilibrium array will be seen to be both rotating equatorially, parallel to the table but not rotating its polar-axis triangles, the top one of which the operating individual is hand-lowering, while carefully avoiding any horizontal rotation of, the top triangle in respect to which its opposite triangle, resting frictionally on the table, is also neither rotating horizontally nor moving in any direction at all.
[460.03]{style="color: purple3"} []{#ver:460.03 label="ver:460.03"} While the equatorial rotating results from the top triangle’s rotationless lowering, it will also be seen that the whole vector-equilibrium array is contracting symmetrically, that is, all of its 12 symmetrically radiated vertexes move synchronously and symmetrically toward the common volumetric center of the spherically chorded vector equilibrium. As it contracts comprehensively and always symmetrically, it goes through a series of geometrical- transformation stages. It becomes first an icosahedron and then an octahedron, with all of its vertexes approaching one another symmetrically and without twisting its axis.
[460.04]{style="color: purple3"} []{#ver:460.04 label="ver:460.04"} At the octahedron stage of omnisymmetrical contraction, all the vectors (strut edges) are doubled together in tight parallel, with the vector equilibrium’s 24 struts now producing two 12-strut-edged octahedra congruent with one another. If the top triangle of the composite octahedron (which is the triangle hand-held from the start, which had never been rotated, but only lowered with each of its three vertexes approaching exactly perpendicularly toward the table) is now rotated 60 degrees and lowered further, the whole structural system will transform swiftly into a tetrahedron with its original 24 edges now quadrupled together in the six-edge pattern of the tetrahedron, with four tetrahedra now congruent with one another. Organic chemists would describe it as a quadrivalent tetrahedral structure.
[460.05]{style="color: purple3"} []{#ver:460.05 label="ver:460.05"} Finally, the model of the tetrahedron turns itself inside out and oscillates between inside and outside phases. It does this as three of its four triangular faces hinge open around its base triangle like a flower bud’s petals opening and hinging beyond the horizontal plane closing the tetrahedron bud below the base triangle.
[460.06]{style="color: purple3"} []{#ver:460.06 label="ver:460.06"} As the tetrahedron is opened again to the horizontal four-triangle condition, the central top triangle may again be lifted, and the whole contractive sequence of events from vector equilibrium to tetrahedron is reversed; the system expands after attaining the octahedral stage. When lifting of the topheld, nonhorizontally rotated triangle has resulted in the whole system expanding to the vector equilibrium, the equatorial rotational momentum will be seen to carry the rotation beyond dead-center, and the system starts to contract itself again. If the operating individual accommodates this momentum trend and again lowers the top triangle without rotating it horizontally, the rotation will reverse its original direction and the system will contract through its previous stages but with a new mix of doubled-up struts. As the lowering and raising of the top triangle is continuously in synchronization with the rotating-contracting-expanding, the rotation changes at the vector equilibrium’s “zero”this occasions the name jitterbug. The vector equilibrium has four axial pairs of its eight triangular faces, and at each pair, there are different mixes of the same struts.
[460.07]{style="color: purple3"} []{#ver:460.07 label="ver:460.07"} The jitterbug employs only the external vectors of the vector equilibrium and not its 12 internal radii. They were removed as a consequence of observing the structural stability of 12 spheres closest packed around a nuclear sphere. When the nuclear sphere is removed or mildly contracted, the 12 balls rearrange themselves (always retaining their symmetry) in the form of the icosahedron. Removal of the radial vectors permitted contraction of the modeland its own omnisymmetrical pulsation when the lowering and raising patterns are swiftly repeated. It will be seen that the squares accommodate the jitterbug contractions by transforming first into two equiangular triangles and then disappearing altogether. The triangles do not change through the transformation in size or angularity. The original eight triangles of the vector equilibrium are those of the octahedron stage, and they double together to form the four faces of the tetrahedron.
[460.08]{style="color: purple3"} []{#ver:460.08 label="ver:460.08"} In the jitterbug, we have a sizeless, nuclear, omnidirectionally pulsing model. The vector-equilibrium jitterbug is a conceptual system independent of size, ergo cosmically generalizable. (See Secs. 515.10 and 515.11.)
¶ 461.00 Recapitulation: Polyhedral Progression in Jitterbug
[461.01]{style="color: purple3"} []{#ver:461.01 label="ver:461.01"} If the vector equilibrium is constructed with circumferential vectors only and joined with flexible connectors, it will contract symmetrically, due to the instability of the square faces. This contraction is identical to the contraction of the concentric sphere packing when the nuclear sphere is removed. The squares behave as any four balls will do in a plane. They would like to rest and become a diamond, to get into two triangles. They took up more room as a square, and closer packing calls for a diamond. The 12 vertexes of the vector equilibrium simply rotate and compact a little. The center ball was keeping them from closer packing, so there is a little more compactibility when the center ball goes out.
[461.02]{style="color: purple3"} []{#ver:461.02 label="ver:461.02"} Icosahedron: The icosahedron occurs when the square faces are no longer squares but have become diamonds. The diagonal of the square is considerably longer than its edges. But as we rotate the ridge pole, the diamonds become the same length as the edge of the square (or, the same length as the edge of the tetrahedron or the edge of the octahedron). It becomes the octahedron when all 30 edges are the same length. There are no more squares. We have a condition of omnitriangulation.
[461.03]{style="color: purple3"} []{#ver:461.03 label="ver:461.03"} We discover that an icosahedron is the first degree of contraction of the vector equilibrium. We never catch the vector equilibrium in its true existence in reality: it is always going one way or the other. When we go to the icosahedron, we get to great realities. In the icosahedron, we get to a very prominent fiveness: around every vertex you can always count five.
[461.04]{style="color: purple3"} []{#ver:461.04 label="ver:461.04"} The icosahedron contracts to a radius less than the radii of the vector equilibrium from which it derived. There is a sphere that is tangent to the other 12 spheres at the center of an icosahedron, but that sphere is inherently smaller. Its radius is less than the spheres in tangency which generate the 12 vertexes of the vector equilibrium or icosahedron. Since it is no longer the same-size sphere, it is not in the same frequency or in the same energetic dimensioning. The two structures are so intimate, but they do not have the same amount of energy. For instance, in relation to the tetrahedron as unity, the volume of the icosahedron is in respect to the vector equilibrium’s volume of 20. The ratio is tantalizing because the mass of the electron in respect to the mass of the neutron is one over . That there should be such an important kind of seemingly irrational number provides a strong contrast to all the other rational data of the tetrahedron as unity, the octahedron as four, the vector equilibrium as 20, and the rhombic dodecahedron as six: beautiful whole rational numbers.
Fig. 460.08 Symmetrical Contraction of Vector Equilibrium: Jitterbug System: If the vector equilibrium is constructed with circumferential vectors only and joined with flexible connectors, it will contract symmetrically due to the instability of the square faces. This contraction is identical to the contraction of the concentric sphere packing when its nuclear sphere is removed. This system of transformation has been referred to as the “jitterbug.” Its various phases are shown in both left- and right-hand contraction:
-
Vector equilibrium phase: the beginning of the transformation.
-
Icosahedron phase: When the short diagonal dimension of the quadrilateral face is equal to the vector equilibrium edge length, 20 equilateral triangular faces are formed.
-
Further contraction toward the octahedron phase.
-
Octahedron phase: Note the doubling of the edges.
[461.05]{style="color: purple3"} []{#ver:461.05 label="ver:461.05"} The icosahedron goes out of rational tunability due to its radius being too little to permit it having the same-size nuclear sphere, therefore putting it in a different frequency system. So when we get into atoms, we are dealing in each atom having its unique frequencies.
[461.06]{style="color: purple3"} []{#ver:461.06 label="ver:461.06"} In the symmetrical jitterbug contraction, the top triangle does not rotate. Its vertex always points toward the mid-edge of the opposite triangle directly below it. As the sequence progresses, the top triangle approaches the lower as a result of the system’s contraction. The equator of the system twists and transforms, while the opposite triangles always approach each other rota- tionlessly. They are the polar group.
[461.07]{style="color: purple3"} []{#ver:461.07 label="ver:461.07"} Octahedron: When the jitterbug progresses to the point where the vector edges have doubled up, we arrive at the octahedron. At this stage, the top triangle can be pumped up and down with the equatorial vectors being rotated first one way and then the other. There is a momentum of spin that throws a twist into the systempositive and negative. The right-hand octahedron and the left-hand octahedron are not the same: if we were to color the vectors to identify them, you would see that there are really two different octahedra.
[461.08]{style="color: purple3"} []{#ver:461.08 label="ver:461.08"} Tetrahedron: As the top triangle still plunges toward the opposite triangle, the two corners, by inertia, simply fold up. It has become the tetrahedron. In the octahedron stage, the vectors were doubled up, but now they have all become fourfold, or quadrivalent. The eight tetrahedra of the original vector equilibrium are now all composited as one. They could not escape from each other. We started off with one energy action in the system, but we have gone from a volume of 20 to a volume of one.[^14] The finite closure of the four-great-circle, six-hexagon-vector “necklaces” were never “opened” or unfastened.
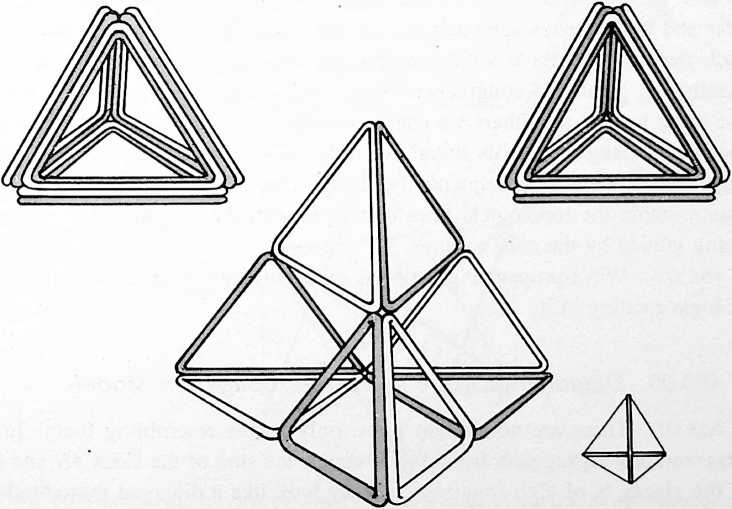
Fig. 461.08 Jitterbug System Collapses into Tetrahedron: Polarization: The “jitterbug” system, after reaching the octahedron phase, may be collapsed and folded into the regular tetrahedron. Note that because the vector equilibrium has 24 edges the tetrahedra have accumulated four edges at each of their six normal edges. The “jitterbug” can also be folded into a larger but incomplete tetrahedron. Note that in this case the two sets of double edges which suggest polarization.
[461.09]{style="color: purple3"} []{#ver:461.09 label="ver:461.09"} We have arrived at the tetrahedron as a straight precessional result. The quadrivalent tetrahedron is the limit case of contraction that unfolds and expands again symmetrically only to contract once more to become the other tetrahedron (like the pumping of the positive and negative octahedron). All of the jitterbug sequence was accomplished within the original domain of the vector equilibrium. The tensional integrity survives within the internal affairs domain of atoms.
[461.10]{style="color: purple3"} []{#ver:461.10 label="ver:461.10"} Deceptiveness of Topology: Quanta Loss By Congruence: (See poster, color plate 4.) The vector equilibrium jitterbug provides the articulative model for demonstrating the always omnisymmetrical, divergently expanding or convergently contracting intertransformability of the entire primitive polyhedral hierarchy, structuring-as-you-go, in an omnitriangularly oriented evolution.
[461.11]{style="color: purple3"} []{#ver:461.11 label="ver:461.11"} As we explore the interbonding (valencing) of the evolving structural components, we soon discover that the universal interjoining of systems and their foldabilitypermit their angularly hinged convergence into congruence of vertexes (single-bonding), or congruence of vectors (double-bonding), or congruence of faces (triple-bonding), or volumetric congruence (quadrivalent), but each of the multicongruences appears as only one vertex or one edge or one face aspect. The Eulerean topological accounting as presently practiced innocent of the inherent synergetical hierarchy of intertransformability accounts each of these multicongruent topological aspects as consisting of only one such aspect. This misaccounting has prevented the physicists and chemists from conceptual identification of their data with synergetics’ disclosure of nature’s comprehensively rational intercoordinate mathematical system.
[461.12]{style="color: purple3"} []{#ver:461.12 label="ver:461.12"} Only the topological analysis of synergetics can account for all the multicongruenttwo-, three-, fourfoldtopological aspects by accounting for the initial tetravolume inventories of the comprehensive rhombic dodecahedron and the vector equilibrium. The rhombic dodecahedron has an initial tetravolume of 48, and the vector equilibrium has an inherent tetravolume of 20. Their respective initial or primitive inventories of vertexes, vectors, and faces are always present (though often imperceptibly so) at all stages in nature’s comprehensive 48 convergence transformation.
[461.13]{style="color: purple3"} []{#ver:461.13 label="ver:461.13"} Although superficially the tetrahedron seems to have only six vectors, we witness in the jitterbug transformation that it has in fact 24. (See poster 4 and Fig. 461.08.) The sizeless, primitive tetrahedronconceptual independent of sizeis quadrivalent, inherently having eight potential alternate
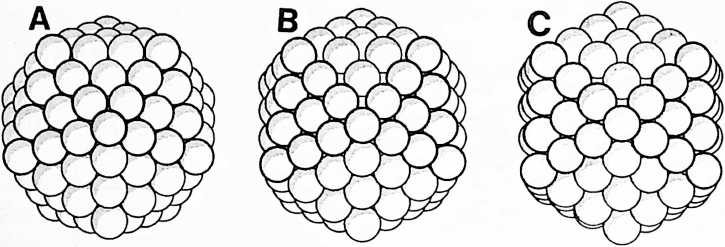
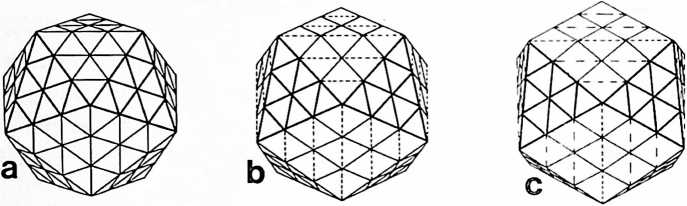
Fig. [466.00 Energy-valve Functions of Closest Sphere Packing:]{style="color: purple3"} []{#ver:466.00 Energy-valve Functions of Closest Sphere Packing: label="ver:466.00 Energy-valve Functions of Closest Sphere Packing:"} This series illustrates the skew-transformation of the 92-ball icosahedral aggregate to a vector equilibrium conformation and its return to the icosahedral state.
Figs. 466A-G illustrate closest-sphere-packing transformations.
Figs. 466a-g illustrate polyhedral resultants.
ways of turning itself inside out: four passive and four active, meaning that four positive and four negative tetrahedra are congruent.
[461.14]{style="color: purple3"} []{#ver:461.14 label="ver:461.14"} Only by recognizing the deceptiveness of Eulerean topology can synergetics account for the primitive total inventories of all aspects and thus conceptually demonstrate and prove the validity of Boltzmann’s concepts as well as those of all quantum phenomena. Synergetics mathematical accounting conceptually interlinks the operational data of physics and chemistry and their complex associabilities manifest in such disciplines as geology, biology, and others.
¶ 462.00 Rotation of Triangle in Cube
[462.01]{style="color: purple3"} []{#ver:462.01 label="ver:462.01"} To comprehend the complex of transformings demonstrated by the jitterbug we may identify each of the eight triangles of the vector equilibrium with the eight small cubes which comprise a two-frequency large cube’s eight corners. When the jitterbug transforms into an octahedron, the jitterbug vector equilibrium’s six square faces disappear leaving only the eight triangles of the vector equilibrium, each of which has moved inwardly at a symmetrical rate toward the common center of the vector equilibrium as the squares disappear and the triangles approach one another until their respective three edges each become congruent with one another, thus doubling their vector edges together in paralleled congruence. Since each of the eight triangles behaved the same way as the others we can now study how one behaved and we find that each triangle “did its thing” entirely within the domain of one of the eight cubes of the two-frequency big cube. Thus we learn that a triangle can rotate within the topological lines of a cube with the triangle’s three corners being guided by the cube’s edges.
[462.02]{style="color: purple3"} []{#ver:462.02 label="ver:462.02"} Wave-propagating action is cyclically generated by a cube with a triangle rotating in it.
¶ 463.00 Diagonal of Cube as Wave-Propagation Model
[463.01]{style="color: purple3"} []{#ver:463.01 label="ver:463.01"} There are no straight lines, only waves resembling them. In the diagram, any zigzag path from 4 to equals the sum of the sides and . If the zigzag is of high frequency, it may look like a diagonal that should be shorter than ABC. It is not.
[463.02]{style="color: purple3"} []{#ver:463.02 label="ver:463.02"} As the triangle rotates in the cube, it goes from being congruent with the positive tetrahedron to being congruent with the negative tetrahedron. It is an oscillating system in which, as the triangles rotate, their corners describe arcs (see Sec. 464.02) which convert the cube’s 12 edges from quasi-straight lines to 12 arcs which altogether produce a dynamically described sphere (a spherical cube) which makes each cube to appear to be swelling locally. But there is a pulsation arc-motion lag in it exactly like our dropping a stone in the water and getting a planar pattern for a wave (see Sec. 505.30), but in this model we get an omnidirectional wave pulsation. This is the first time man has been able to have a conceptual picture of a local electromagnetic wave disturbance.
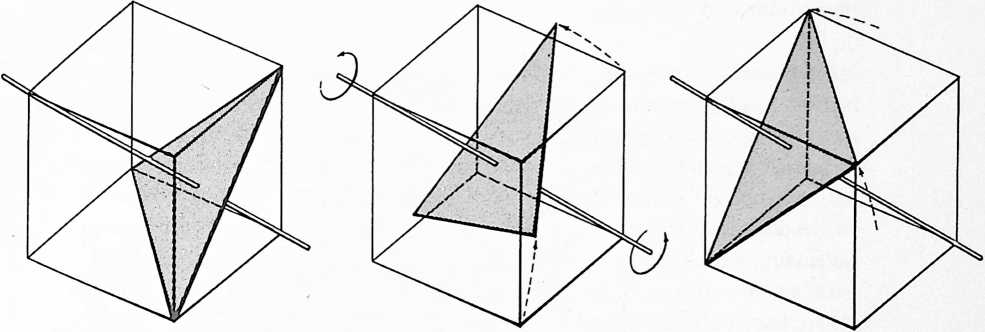
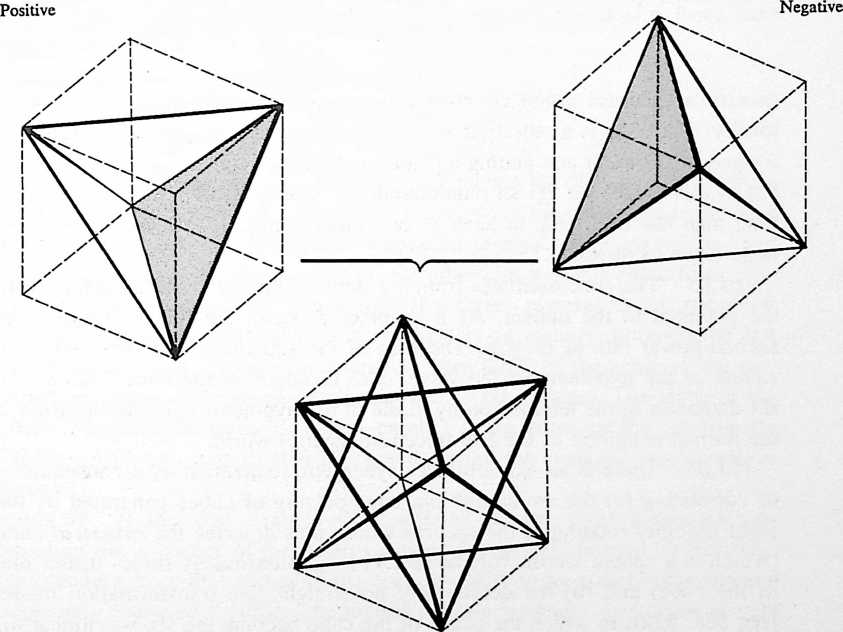
Fig. 462.00 The triangle formed by connecting diagonals of three adjacent faces of the cube is the face of the tetrahedron within the cube. If the triangle is rotated so that its vertexes move along the edges of the cube, its position changes from the positive to the negative tetrahedron. Two equal tetrahedra (positive and negative) joined at their common centers define the cube. The total available energy of a system is related to its surface area, involving the second power (square) of the radius. : The conjunction of any two similar systems results in a synergetic relationship: the second power of individual totals of cohesiveness of the systems.
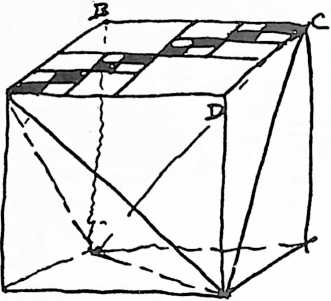
Fig. 463.01 There are no straight lines, only waves resembling them. In this diagram, any zigzag path from to equals the sum of the sides and . If zigzag is infinitely small, it looks like a diagonal that should be shorter than . It is not.
[463.03]{style="color: purple3"} []{#ver:463.03 label="ver:463.03"} The cube oscillates from the static condition to the dynamic, from the potential to the radiant. As it becomes a wave, the linear becomes the second-power rate of growth. The sum of the squares of the two legs = the square of the hypotenuse = the wave. The 12 edges of the cube become the six diagonals of the tetrahedron by virtue of the hypotenuse: the tetrahedron is the normal condition of the real (electromagnetic) world.
[463.04]{style="color: purple3"} []{#ver:463.04 label="ver:463.04"} There is an extraordinary synergetic realization as a consequence of correlating (a) the arc-describing, edge-pulsing of cubes generated by the eight triangles rotating in the spheres whose arcs describe the spherical cube (which is a sphere whose volume is approximately three times that of the cube) and (b) the deliberately non-straight line transformation model (see Sec. 522), in which the edges of the cube become the six wavilinear diagonals of the cube, which means the cube transforming into a tetrahedron. Synergetically, we have the tetrahedron of volume one and the cube of volume threeas considered separatelyin no way predicting that the cube would be transformed into an electromagnetic-wave-propagating tetrahedron. This is an energy compacting of 3; but sum-totally this means an energetic-volumetric contraction from the spherical cube’s volume of 8.142 to the tetrahedron’s one, which energetic compacting serves re-expansively to power the electromagnetic-wave-propagating behavior of the wavilinear-edged tetrahedron.
[463.05]{style="color: purple3"} []{#ver:463.05 label="ver:463.05"} We really find, learning synergetically, from the combined behaviors of the tetrahedron, the cube, and the deliberately-non-straight-line cubical transformation into a tetrahedron, how the eight cubical corners are self-truncated to produce the vector equilibrium within the allspace-filling cubical isotropic-vector-matrix reference frame; in so doing, the local vacatings of the myriad complex of closest-packing cube truncations produce a “fallout” of all the “exterior octahedra” as a consequence of the simultaneous truncation of the eight corners of the eight cubes surrounding any one point. As we learn elsewhere (see Sec. 1032.10), the exterior octahedron is the contracted vector equilibrium and is one of the spaces between spheres; the octahedron thus becomes available as the potential alternate new sphere when the old spheres become spaces. The octahedra thus serve in the allspace-filling exchange of spheres and spaces (see Sec. 970.20).
¶ 464.00 Triangle in Cube as Energetic Model
(see drawings section)
[464.01]{style="color: purple3"} []{#ver:464.01 label="ver:464.01"} The triangle formed by connecting the diagonals of the three adjacent square faces surrounding one corner, , of the cube defines the base triangular face of one of the two tetrahedra always coexisting within, and structurally permitting the stability of, the otherwise unstable cubic form. The triangle formed by connecting the three adjacent faces surrounding thefi corner of the same cube diametrically, i.e. polarly, opposite the first triangulated corner, defines the triangular face of the other of the two tetrahedra always coexisting within that and all other cubes. The plane of the green triangle remains always parallel to the plane of the red triangle even though it is rotated along and around the shaft (see drawings section).
[464.02]{style="color: purple3"} []{#ver:464.02 label="ver:464.02"} If the first triangle defined by the three diagonals surrounding the corner of the cube is rotated on the axis formed by the diagonal leading from that corner of the cube inwardly to its polarly opposite and oppositely triangled corner, the rotated triangle maintains its attitude at right angles to its axis, and its three vertexes move along the three edges of the cube until the green triangle reaches and become congruent with the red base triangle of the axially opposite corner. Thereafter, if the rotation continues in the same circular direction, the same traveling triangle will continue to travel pulsatingly, back and forth, becoming alternately the base triangle of the positive and then of the negative tetrahedron. As the triangle returns from its first trip away, its corners follow three additional edges of the cube. As the vertexes of the shuttling triangle follow the six cube edges, their apexes protrude and describe spherical arcs outwardly along the cubes’ edges running from cube corner to cube corner. Swift rotation of the triangle’s shaft not only causes the triangle to shuttle back and forth, but also to describe six of the 12 edges of the spherical cube producing an equatorially spheroid pulsation. The two equal tetrahedra are not only oppositely oriented, but their respective volumetric centers (positive and negative) are congruent, being joined at their common centers of volume, which coincide with that of the containing cube. Because each cube in the eight-cube, two-frequency big cube has both a positive and a negative tetrahedron in it, and because each tetrahedron has four triangular faces, each cube has eight equilateral triangular edges corresponding to the 12 diagonalling hypotenuses of each cube’s six faces (see drawings section).
[464.03]{style="color: purple3"} []{#ver:464.03 label="ver:464.03"} Each cube has four pairs of polarly opposite corners. There are four co-occurring, synchronously operative, triangularly shuttleable systems within each cube; with all of them synchronously operative, the cube’s 12 edges will be synchronously accommodating edge-arcings traveling 12 positively and 12 negatively, to produce the profile of two spherical cubes, one positive and one negative.
[464.04]{style="color: purple3"} []{#ver:464.04 label="ver:464.04"} Each vector equilibrium, when complemented by its coexistent share of one-eighth of its (concave) external octahedra, embraces eight cubes, each of which has four activable, axially shuttleable, electromagnetic-energy-generating potentials.
[464.05]{style="color: purple3"} []{#ver:464.05 label="ver:464.05"} Eight of these triangular shuttle cubes may be completed on each of the vector equilibrium’s eight triangular faces by adding one Vsth-Octa corner to each of them. Each th-Octa corner consists of six and six modules. As one such th-Octa, 6A-6B moduled, 90-apexed, equianglebased, isosceles tetrahedron is added to any of the vector equilibrium’s eight triangular faces, which contain the potential new nucleuswhich thus becomes a newborn active nucleuswhen so double-layer covered by the 12 *A’*s and 12 ’s energy modules, which altogether produce a total of 24 energy modules whenever the rotating triangle alternates its position, which combined 24 modules correspond to the 24 energy modules of one whole regular tetrahedral event, which is the quantum in nuclear physics.
[464.06]{style="color: purple3"} []{#ver:464.06 label="ver:464.06"} The vector equilibrium’s jitterbugging conceptually manifests that any action (and its inherent reaction force) applied to any system always articulates a complex of vector-equilibria, macro-micro jitterbugging, involving all the vector equilibria’s ever cosmically replete complementations by their always co-occurring internal and external octahedraall of which respond to the action by intertransforming in concert from “space nothingnesses” into closest-packed spherical “somethings,” and vice versa, in a complex three- way shuttle while propagating a total omniradiant wave pulsation operating in unique frequencies that in no-wise interfere with the always omni-co-occurring cosmic gamut of otherly frequenced cosmic vector-equilibria accommodations.
[464.07]{style="color: purple3"} []{#ver:464.07 label="ver:464.07"} In contradistinction to the sphere, the tetrahedron has the most surface with the least volume of any symmetrical form. The total available energy of a system is related to its surface area, involving the second power of the radius. . The mass congruence of any two similar systems results in a synergetic relationship with a second-powering of cohesiveness of the joined systems. This releases the fourfolded energy, which no longer has the two tetrahedra’s mass-interattraction work to do, and this in turn releases the energies outward to the tetrahedra’s highest-capacity surfaces. And since surface functions as the electromagnetic-energy carrier, and since the energy relayed to their surfaces alternates from the positive to the negative tetrahedron, and since the distance between their surface centers is only two A Module altitude wavelengths (each of which two A Module altitudes constitute and serve as one generalized electromagnetic wavelength with generatable frequency beginning at two), the rotation of the triangle within the cube passes through the common energy centers of the two tetrahedra and delivers its content to the other base surface, after which it pulses through center delivery of the opposite charge to the other surface, which altogether propagates potentially exportable, frequency-determinate, electromagnetic energy. The six cube-edge travelings of the triangles’ vertexes accomplished with each cycle of the triangle-in-cube shuttle coincides in number and is akin to the six vector edges comprising one tetrahedral quantum; the sixness of wavilinear and sometimes reangularly redirected traveling employs also the six basic degrees of freedom articulated by each and every one cosmic event.
[464.08]{style="color: purple3"} []{#ver:464.08 label="ver:464.08"} Thus we realize conceptually the ever-self-regenerative, omniidealized, eternal integrity of the utterly metaphysical, timeless, weightless, zerophase geometric frame of transformations referencing function, which is served by the vector equilibrium in respect to which all the aberrational dimensioning of all realization of the variety of relative durations, sensorial lags, recalls, and imaginings are formulatingly referenced to differentiate out into the special-case local experiences of the eternal scenario Universe, which each of us identifies to ourselves as the “Shape of Things” and which each individual sees differently yet ever intuits to be rigorously referenced to an invisibly perfect prototype in pure principle, in respect to which only approachable but never realizable “understanding” of one of us by others occurs: “And it Came to Pass (Fuller 1976).”
¶ 465.00 Rotation of Four Axes of Vector Equilibrium: Triangles, Wheels, and Cams
[465.01]{style="color: purple3"} []{#ver:465.01 label="ver:465.01"} We can have a vector equilibrium model made out of a tubular steel frame with each of the eight triangular faces connected by four axes with a journal to slide on the shafts and with each of the rods being perpendicular to two of the eight triangular faces. This is a four-dimensional, four-axis system. Just as a regular tetrahedron has four unique faces, so there are four unique perpendiculars to them, making a four-dimensional system.
[465.02]{style="color: purple3"} []{#ver:465.02 label="ver:465.02"} We can put a little rivet through the centers of area of the eight triangles, and we can let the brass rod run through the journals and slide on a wire. We can tie the corners of the triangles together with nylon threads. If we spin the model rapidly on one of the axes, all the triangles slide outwardly to form the vector equilibrium. If next we touch a finger or a pencil to any mid-face of one triangle in the spinning system, the whole system will contract symmetrically until it becomes an octahedron. But when we take the finger or pencil off again, centrifugal force will automatically open up the system to the vector-equilibrium condition again. The oscillating motion makes this an expanding and contracting system.
[465.03]{style="color: purple3"} []{#ver:465.03 label="ver:465.03"} We see that every one of the triangles in the vector equilibrium can shuttle back and forth, so that all the edges of the cube would be arced outwardly with pairs of arcing triangle corners shuttling in opposite directions by each other. With a swiftly oscillating system and a pulsating spherical expansion-contraction going on everywhere locally, the whole system becomes an optically pulsating sphere. We find that each one of the little triangles rotates as if it were swelling locally. Each one of their vertexes brings about a further spherical condition, so that in the whole system, all the wires locally bend outwardly temporarily to accommodate the whole motion. We may now put together a large omnidirectional complex of the sets of four-axis and eight vertex-interconnected transparent plastic triangles with alternate sets of red transparent and uncolored transparent plastic triangles. We can interconnect the triangles from set to set. We then find experimentally that if one force, such as a pencil, is applied to one triangle of one open vector equilibrium, that vector equilibrium closes to become an octahedron, and vice versa, throughout the whole system. Every vector equilibrium will become an octahedron and every octahedron will become a vector equilibrium. (Which is to say that every space becomes a sphere and every sphere becomes a space.)
[465.04]{style="color: purple3"} []{#ver:465.04 label="ver:465.04"} Since there is a force distribution lag in the system, it is exactly like dropping a stone into water and getting a planar pattern for a wave, but in this one, we get an omnidirectional wave. We can see the electromagnetic wave pattern as clearly demonstrated by one energy action in the system. This may be the first time man has been provided with omnidirectional conceptual comprehension of the separate and combining transformation events of local electromagnetic-wave-propagation events.
Fig. 465.00 Note that the eight triangular faces of the vector equilibrium are disposed about four-sided openings, i.e. square faces. It is possible to arrange 20 triangles in similar fashion around five-sided openings, i.e. pentagons. The shape is the icosidodecahedron. When a model is constructed with 20 spokes, i.e. ten axes, meeting at its center, which pass through the centers of each triangle, an unexpected behavior results. In the vector equilibrium model the triangles will rotate and contract towards its center, however, with the icosidodecahedron the entire structure remains fixed. It is not capable of contraction due to the fact that there is an odd number of triangles surrounding each opening. The diagrams show clearly why this is so. Any odd-numbered array of interlocked gears will not be free to rotate.
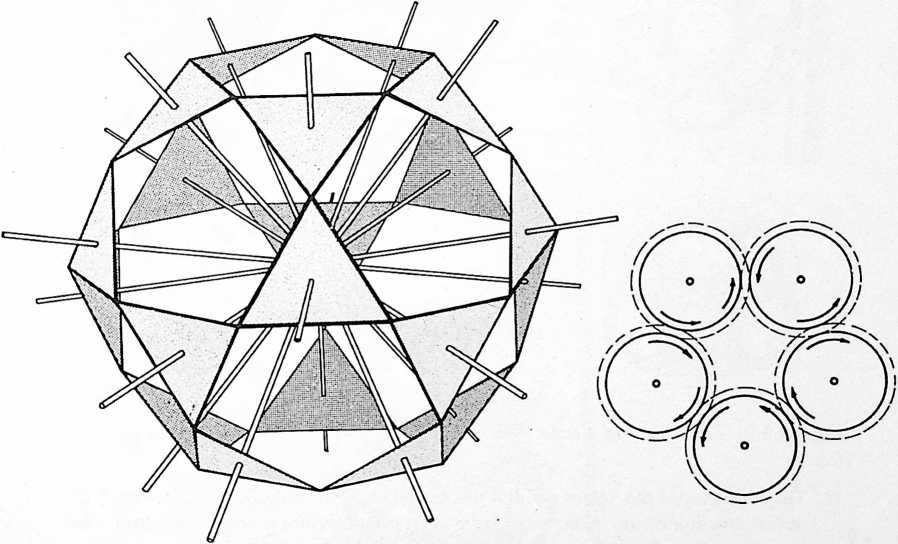
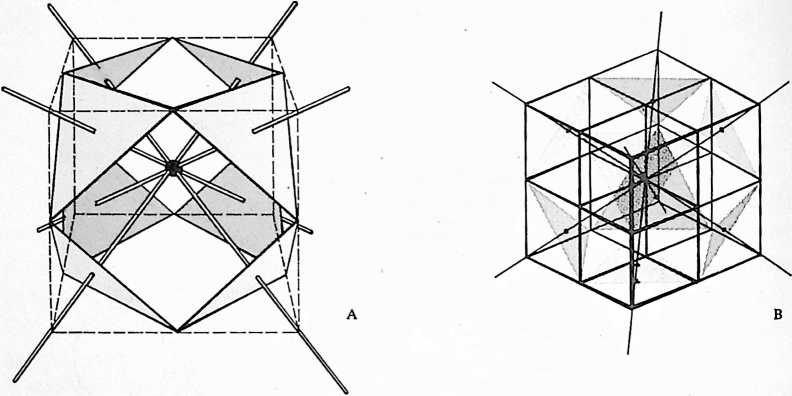
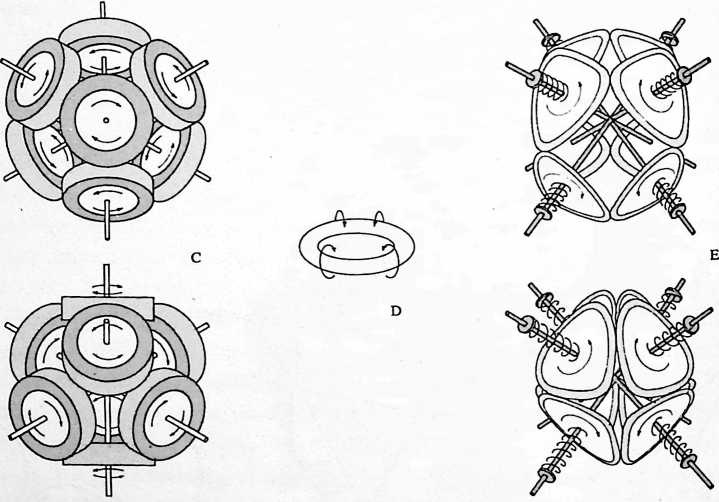
Fig. 465.01 Four Axes of Vector Equilibrium with Rotating Wheels or Triangular Cams:
-
The four axes of the vector equilibrium suggesting a four-dimensional system. In the contraction of the “jitterbug” from vector equilibrium to the octahedron, the triangles rotate about these axes.
-
Each triangle rotates in its own cube.
-
The four axes of the vector equilibrium shown with wheels replacing the triangular faces. The wheels are tangent to one another at the vertexes of the triangles, and when one wheel is turned, the others also rotate. If one wheel is immobilized and the system is rotated on the axes of this wheel, the opposite wheel remains stationary, demonstrating the polarity of the system.
-
Each wheel can be visualized as rotating inwardly on itself thereby causing all other wheels to rotate in a similar fashion.
-
If each wheel is conceived as a triangular cam shape, when they are rotated a continuous “pumping” or reciprocating action is introduced.
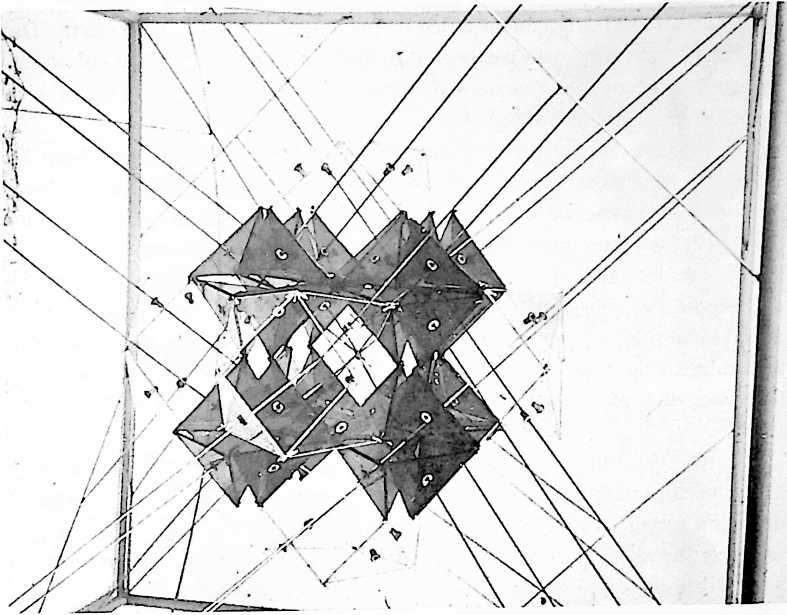
Fig. 465.03 Rotation of Four Axes of Vector Equilibrium: Articulation of Eight Triangular Faces.
[465.05]{style="color: purple3"} []{#ver:465.05 label="ver:465.05"} We must remember that in the local water where we drop the stone, the molecules run inwardly and outwardly toward the center of Earth gravitationally. The water does not move; it accommodates a wave moving through it. A wave inherently goes outward in a pattern without any of the locally accommodating molecules or atoms migrating elsewhere. It is not simultaneous; we are using our memory and afterimage. We make a single energy action at one point and a complete omnidirectional wave occurs. This is similar to the steel-frame cube with all the many triangles rotating in it. (See Sec. 462, et seq.)
[465.10]{style="color: purple3"} []{#ver:465.10 label="ver:465.10"} Wheels: Rubber Tires: If, instead of the eight triangular faces of the vector equilibrium, we substitute on the same shaft a little automobile tire on a wheel, we can bring tires in until each of the tires is frictionally touching the other tires at three points. If we have a train of gears, as one wheel goes one way, the next wheel can go the other way very comfortably. Around any hole there are four gears, and since there are fouran even numberwe find that the trains reciprocate. There is no blocking anywhere. When we rotate one wheel in the light-wheel system, the other wheels rotate responsively. They are in friction with one another. Or we can hold on to the bottom of one of the wheels and turn the rest of the system around it. If we do so, we find that the top wheel polarly opposite the one we are holding also remains motionless while all the other six rotate.
[465.20]{style="color: purple3"} []{#ver:465.20 label="ver:465.20"} Torus: If one of the mounted tires were just a rubber doughnut, it could be rotated inwardly like a torus; or it could be rotated outwardly like a big atomic-bomb mushroom cloud, opening in the center and coming in at the bottom. This is what we call an evoluting and involuting torus (see illustration 505.40, Pattern). These rubber tires of the eight-wheel assembly could not only rotate around on each other, but it is quite possible to make one wheel in such a way that it has little roller bearings along its rim that allow the rubber tires to rotate in the rim so that the tire could be involuting and evoluting. Therefore, if any one tire started to evolute, all the other tires would reciprocate.
[465.21]{style="color: purple3"} []{#ver:465.21 label="ver:465.21"} If we hold only an axis in our hand, we can rotate the system around it. But as we rotate it around, all the wheels are rolling. As we saw in the pumping vector equilibrium, the opposite triangles never torque in relation to each other. The opposite wheel of the one we are holding does the same.
Fig. 465.10 The vector equilibrium with wheels showing that when one wheel is immobilized (the lower wheel in photos) and the system is rotated about the axis shared by the fixed wheel and its opposite wheel, the opposite wheel remains stationary but the other six wheels rotate in concert. The polarity of the system is thus demonstrated.
With the bottom wheel stationary on the ground and another wheel immobilized by one holding it, we can rotate the system so that one wheel rolls around the other. But we find that no matter how much we move it equatorially, if we immobilize one wheel in our fingers, the one opposite it becomes immobilized, too. If we not only hold a wheel immobilized while another is turning, but also squeeze and evolute it, all of the wheels will also involute and evolute.
[465.22]{style="color: purple3"} []{#ver:465.22 label="ver:465.22"} It is quite possible to make an automobile tire and mount it in such a way that it looks triangular; that is, it will have a very small radius in its corners. I can take the same rubber and stretch it onto a triangular frame and also have the same little roller bearings so that it can involute and evolute. We will have a set of triangular tires that will pump from being the vector equilibrium into being the octahedron and back again. If we were then to immobilize one part of it, i.e., not let it involute and evolute, the rest of the system, due to rotation, would contract to become an octahedron so that it makes all the others reciprocate involuting and evoluting. We are able then to immobilize one axis, and the rest of the system except our opposite pole will both rotate and involute-evolute pulsatively.
[465.30]{style="color: purple3"} []{#ver:465.30 label="ver:465.30"} Four-Dimensional Mobility: We are now discovering that in omnimotional Universe, it is possible to make two moving systems that move four-dimensionally, comfortably, the way we see four sets of wheels (eight wheels altogether) moving quite comfortably. But if we fasten one vector equilibrium to another by a pair of wheelsimmobilizing one of them and having an axis immobilized the rest of the system can keep right on rolling around it. By fastening together two parts of the Universe, we do not stop the rest of the four-dimensional motion of Universe. In all other non-four-dimensional mechanical systems we run into a “three-dimensional” blockage: if anything is blocked, then everything is blocked. But in a four-dimensional system, this is not at all the case. We can have two atoms join one another perfectly well and the rest of Universe can go right on in its motion. Nothing is frustrated, although the atoms themselves may do certain polarized things in relation to one another, which begins to explain a lot of the basic experiences.
¶ 465.40 Triangular-cammed, In-out-and-around Jitterbug Model (Short Title)
[465.41]{style="color: purple3"} []{#ver:465.41 label="ver:465.41"} The four axes of the vector equilibrium provide the four-dimensionally articulatable model of motion freedoms unimpeded by other motions of either contiguous or remote systems of Universe while copermitting the concurrently articulating both omnidirectional wave propagation and gravitationally convergent embracement. We can also call it by the short title: triangular-cammed, in-out-and-around jitterbug model. (See Fig. 465.01.)
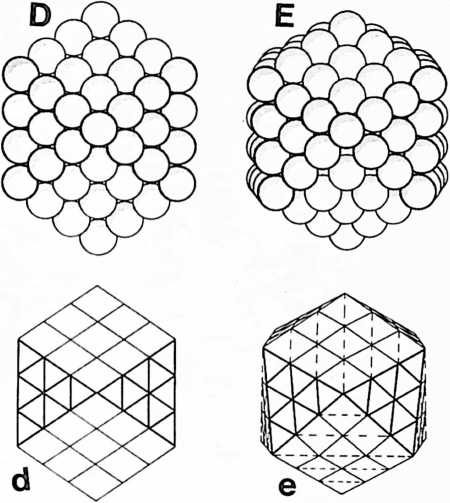
[465.42]{style="color: purple3"} []{#ver:465.42 label="ver:465.42"} The “opposite” of the engineers’ equal-and-opposite action and reaction is a strictly 180-degree linear conceptioning, conceived on a planar drawing. Macro is not opposite to micro: these are opposed, inward-and-outward, explosive-contractive, intertransformative accommodations such as those displayed by the eight-triangular-cammed, perimeter-tangent, contact-driven, involuting-evoluting, rubber doughnut jitterbug. In such a model macro and micro are not planarly opposed: they are the poles of inward-outward, omnidirectional, locally vertexing considerations of experience. (See Fig. 465.10.)
¶ 466.00 Energy-valve Functioning of Outer Shell of Nuclear Domains
[466.01.]{style="color: purple3"} []{#ver:466.01. label="ver:466.01."} An earlier version of Fig. 466.01 was first published by the author in 1944: it illustrates the energy-valving aspects of the closest-packed spheres interfunctionings as they occur within the three-frequency, 92-ball outer layer of the vector equilibrium as it “jitterbuggingly ” skew-transforms into the icosahedral state, then returns to the vector equilibrium state, passes through, and again transforms to the alternately skewed icosahedral staterepeat and repeat.
Fig. [466.01 Reciprocal Motion of Nine Internal Spheres Propagates Wave by Diagonal Elongation:]{style="color: purple3"} []
(The original version of this drawing was copyrighted by R. Buckminster Fuller in 1944.) This is a planar representation of the closest-packed spheres in the outer layer as they skew-transform between the icosahedral and vector equilibrium phases.
-
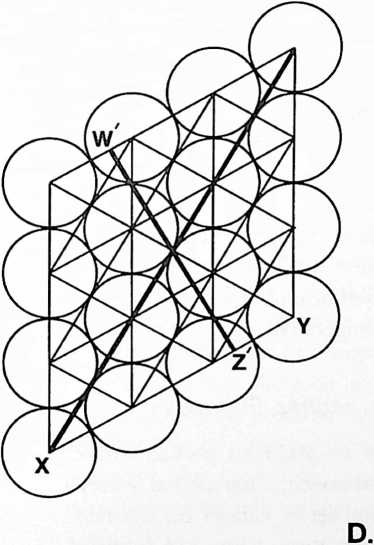
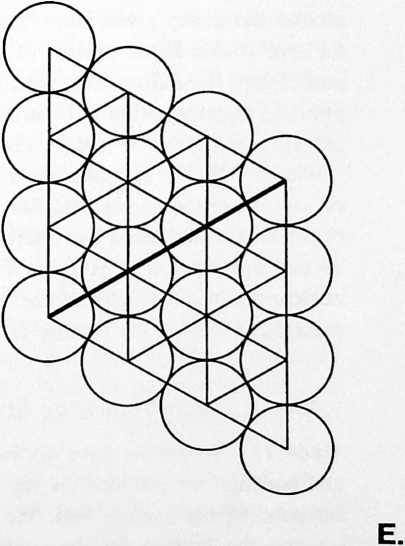
Apex sphere surrounded by two 16-ball grids and N, and by short-axis diamond and long-axis diamond D.
-
The 90-degree alignment of the 16 balls of any one of the six square faces of the vector equilibrium.
-
Plan view of the closest-sphere-packing aspects of any one of the vector equilibrium’s four pairs of nuclear tetrahedra as they begin to torque in the jitterbug process.
-
Short-axis diamond.
-
Long-axis diamond.
[466.02]{style="color: purple3"} []{#ver:466.02 label="ver:466.02"} The 90-degree interalignment of the 16 balls of any one of the six square faces of the vector equilibrium (Fig. B) is inherently unstable. The 16 balls resolve their instability by forming any one of two alternate types of most closely packed diamonds (Figs. D and E) with either a short cross axis or a long diagonal axis. Both types are equiedged, equiarea, and most densely packed, and they occupy less area than their equiedged square counterparts. This is quickly evidenced geometrically because both the square (Fig. B) and the diamond (Fig. D) have the same-length base edge , but the altitude of the square is greater than the altitude of the diamond.
[466.03]{style="color: purple3"} []{#ver:466.03 label="ver:466.03"} As displayed in a planar array, Fig. A, there is an apex sphere surroundingly shared by the innermost corners (vertexes) of two square-faced, 16-ball grids, and , as well as by the two diamondsthe short-axis diamond E and the long-axis diamond .
[466.04]{style="color: purple3"} []{#ver:466.04 label="ver:466.04"} The apex sphere s neighboring spheres are uncomfortable because is surrounded by seven spheres and not six. Only six can closest pack around one in any given plane. One of the two adjacent spheres or from the two square-faced grids will get pushed in, and the other one will be pushed out, depending upon which way the vector-equilibrium-to-icosahedron jitterbug transformation is rotating around apex sphere . The “in-and-out” pumping of spheres and acts as an energy-propagating valve.
[466.05]{style="color: purple3"} []{#ver:466.05 label="ver:466.05"} Fig. C is a plan view of the closest-sphere-packing manifestation of any one of the vector equilibrium’s four pairs of nuclear tetrahedra as they commence to torque in the jitterbug process. An isometric sketch of this net 39-baIl aggregation is given at Fig. 466.31. Note that this torqued pair of nuclear tetrahedra employs three of the vector equilibrium’s six axes. The two unengaged axes of the equator are starved and inoperative.
¶ 466.10 High-frequency Sphericity Approaches Flatness
[466.11]{style="color: purple3"} []{#ver:466.11 label="ver:466.11"} Where we have six balls in a planar array closest packed around one nucleus, we produce six top and six bottom concave tetrahedral valleys surrounding the nucleus ball. We will call the top set of valleys the northern set and the bottom set the southern set. Despite there being six northern valleys we find that we can nest only three close-packed (triangulated) balls in the valleys. This is because we find that the balls nesting on top of the valleys occupy twice as much planar area as that afforded by the six tetrahedral valleys. Three balls can rest together on the top in omni-close-packed tangency with one another and with the seven balls below them; and three balls can similarly rest omniintertangentially in the bottom valleys as their top and bottom points of tangency bridge exactly across the unoccupied valleys, allowing room for no other spheres. This produces the symmetrical nuclear vector equilibrium of 12 closest-packed spheres around one. (See Fig. 466.13A.)
[466.12]{style="color: purple3"} []{#ver:466.12 label="ver:466.12"} The three balls on the top can be lifted as a triangular group and rotated 60 degrees in a plane parallel to the seven balls of the hexagonal equatorial set below them; this triangular group can be then set into the three previously vacant and bridged-over valleys. As this occurs, we have the same 12 spheres closest packed around one with an overall arrangement with the two triangular sets of three on the top, three on the bottom, and six around the equator. The top and the bottom triangular sets act as poles of the system, whichas with all systemshas inherent free spinnability. In both of the two alternate valley occupations the northern polar triangle is surrounded alternately by three squares and three triangles, reading alternatelytriangle, square, triangle, square, triangle, square. (See Fig. 466.138.)
[466.13]{style="color: purple3"} []{#ver:466.13 label="ver:466.13"} In one polar triangular valley occupation the squares of the northern hemisphere will be adjacent to the triangles of the southern hemisphere. This is the vector-equilibrium condition. In the alternate valley nesting position at the equator the equatorial edges of the squares of the northern hemisphere will abut the squares of the southern hemisphere, and the triangles of the northern hemisphere will abut those of the southern, producing a polarized symmetry condition. In the vector-equilibrium condition we have always and everywhere the triangle-and-square abutments, which produces a four-dimensional symmetry system. (See Sec. 442 and Fig. 466.13C.)
[466.14]{style="color: purple3"} []{#ver:466.14 label="ver:466.14"} There is then a duality of conditions of the same 12 nucleus-surrounding first omni-inter-closest-packed layer: we have both a polarized symmetry phase and an equilibrious symmetry phase. Under these alternate conditions we have one of those opportunities of physical Universe to develop a pulsative alternation of interpatterning realizations, whereby the alternations in its equilibrium phase do not activate energy, while its polarized phase does activate energetic proclivities. The equilibrious phase has no associative proclivities, while the polarized phase has associative proclivities. In the polarized phase we have repulsion at one end and attraction at the other: potential switchings on and off of energetic physical Universe. (See Figure 466.13D.)
[466.15]{style="color: purple3"} []{#ver:466.15 label="ver:466.15"} When modular frequency enters into the alternately vector equilibrium polarized conformations, the vertexes of the multifrequenced nuclear system are occupied by uniradius spheres, whereat it is evidenced that the equatorial continuity set of spheres can be claimed either by the northern or southern set of triangles and squares, but they cannot serve both simultaneously. Here again we have alternating conditionsstarving or fulfilling of northern and southern hemispheres matching or nonmatching triangles and squares, with the central equilibrium condition having a large plurality of alternately realizable behaviors under variously modified conditions affected further as frequency increases the numbers of edge-vertex-occupying spheres.
Fig. 466.13
-
Twelve Closest-packed Spheres around One: Symmetrical nuclear vector equilibrium.
-
Twelve Closest-packed Spheres around One: Rotation of top triangular group.
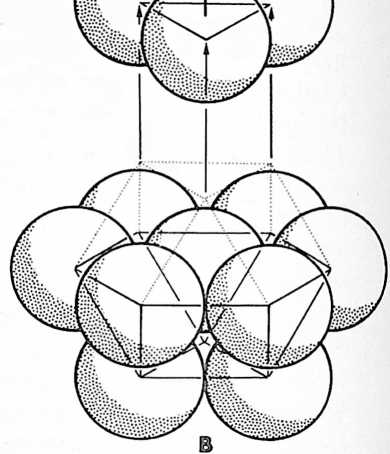
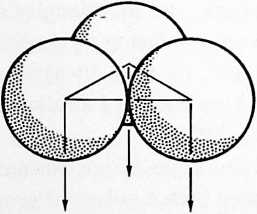
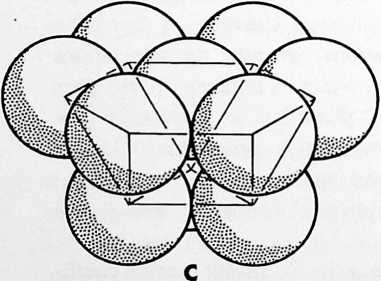
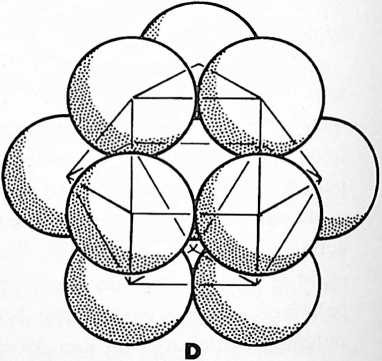
[466.16]{style="color: purple3"} []{#ver:466.16 label="ver:466.16"} As the frequencies of vector equilibria or icosahedra increase, the relative size of the occupied arcs of the great circles involved become of ever lesser magnitude. At a high frequency of larger spheresfor example, planet Earth the conditions of patterning around the 12 external vertexes of the vector equilibria or icosahedra appear to be approximately flat, in contrast to the sharp concavity/convexity of the nonfrequenced convergence of the four planes around the corners of the vector equilibrium and the convergence of the five planes around the corners of the icosahedron.
[466.17]{style="color: purple3"} []{#ver:466.17 label="ver:466.17"} In very-high-frequency nuclear systems the approach to flatness from the four planes to five planes tends to induce a 360-degreeness of the sums of the angles around the critical 12 vertexesin contrast to the 300-degree condition existing in both the unfrequenced vector equilibrium and icosahedron. That is what Fig. 466.01 is all about.
[466.18]{style="color: purple3"} []{#ver:466.18 label="ver:466.18"} In Figs. 466.01 and 466.41 there is introduced an additional 60-degree equilateral triangle, in surroundment of every directly-nuclear-emanating vertex . The 12 vector-equilibrium vertexes are always in direct linear relationship with the system nucleus (see Sec. 414). The additional degrees of angle produced by the high-frequency local flattening around vertexes introduces a disturbance-full exterior shell condition that occasions energetic consequences of a centrifugal character.
¶ 466.20 Centrifugal Forces
[466.21]{style="color: purple3"} []{#ver:466.21 label="ver:466.21"} As we get into ultra-ultra-high-frequency, and as we get to greater and greater sphericity, by virtue of the inherent spin, we can account for the vector equilibrium becoming the sphere of lesser radius, becoming the sphere of approximately tetravolume 5, while the relative flatness around the critical vertexes relates to the centrifugal forces involved.
[466.22]{style="color: purple3"} []{#ver:466.22 label="ver:466.22"} People think of centrifugal force as picturable by arrows expelled radially (perpendicularly) outward. But in fact centrifugal force operates as a hammer-thrower’s hammer does: it departs from the system tangentially, not radially. Since the outward tangent ends reach ever farther away, there is a net only-indirectly-radial force realized. This common misapprehension of the assumed 180-degreeness of centrifugal forces has greatly misled human thinking and has obscured comprehensions of precession.
- Twelve Closest-packed Spheres around One: Alternate nestability in polar triangular valley.
- Twelve Closest-packed Spheres around One: Alternate polarized symmetry of vector equilibrium.
[466.23]{style="color: purple3"} []{#ver:466.23 label="ver:466.23"} At certain high frequencies the energy displacements tend to occur that do not tend to occur at low- or no-frequency conditions, which brings us into the realm of possibly comprehending the photon-emitting radiation limits of operation within the 92 regenerative chemical elements and the split-second articulatability of trans-uranium nuclear systems when bombarded with ultra-ultra-high-frequency energy missiles. The lower the frequency, the higher the required bombardment energies.
¶ 466.30 Nuclear Tetrahedra Pairs: Closest-sphere-packing Functions
[466.31]{style="color: purple3"} []{#ver:466.31 label="ver:466.31"} In Fig. 466.01-C is a plan view of the closest-sphere-packing manifestation of any one of the vector equilibrium’s four pairs of nuclear tetrahedra as they commence to torque in the jitterbug process. An isometric sketch of this net 39-ball aggregation is given in Fig. 466.31. Note that this torqued, north-south-pole, axial pair of tetrahedra employs three of the vector equilibrium’s six axes. The other three unengaged axes lying in the equator are starved and inoperativeangularly acceleratable independently of the north-south axial motion.
[466.32]{style="color: purple3"} []{#ver:466.32 label="ver:466.32"} In Fig. 466.01-C we see the internal picture from the nucleus to the vertexes displaying the hexagonal pattern emerging at .
[466.33]{style="color: purple3"} []{#ver:466.33 label="ver:466.33"} There can be only one pair of tetrahedra operative at any one time. The other three pairs of tetrahedra function as standby auxiliaries, as in the triangular-cammed, in-out-and-around, rubber cam model described in Secs. 465.01 and 465.50.
[466.34]{style="color: purple3"} []{#ver:466.34 label="ver:466.34"} The active triangular face has to share its vertexes with those of the adjacent square-face grids. This transformation relates to the transformation of the octahedron and the rhombic dodecahedron.
[466.35]{style="color: purple3"} []{#ver:466.35 label="ver:466.35"} In the outer layer of 92 ballstwo of which are extracted for the axis of spinthere are eight triangular faces. There are four balls in the center of each of the six square faces.
We need 20 balls for a pair of complete polar triangles.
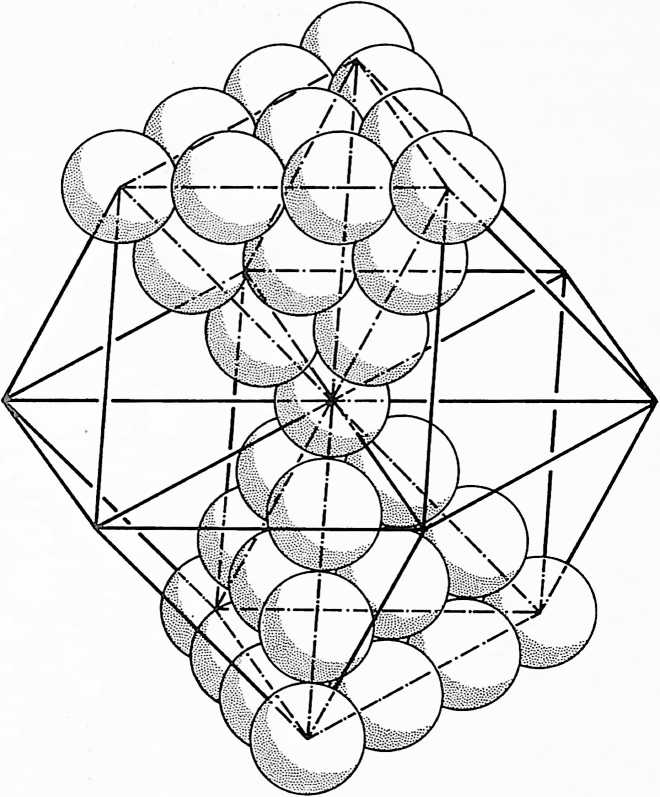
Fig. [466.31 Nuclear Tetrahedra Pairs:]{style="color: purple3"} []{#ver:466.31 Nuclear Tetrahedra Pairs: label="ver:466.31 Nuclear Tetrahedra Pairs:"} An isometric view of 39-ball aggregate of torqued, north-south pole, axial pair of tetrahedra at nucleus of vector equilibrium.
Thus there are only 12 available where 20 are required for a polar pair. In any one hemisphere the vertex balls used by a polar triangle make it impossible to form any additional polar units.
¶ 466.40 Universal Section of Compound Molecular Matrix
[466.41]{style="color: purple3"} []{#ver:466.41 label="ver:466.41"} The illustration at the back-end paper was first published by the author in 1944. It displays the surface shell matrix of an ultra-high-frequency sphere in which a local planar flatness is approached. The vertexes are energy centers, just as in the isotropic vector matrix where 12 exterior comer vertexes of the vector equilibria are always connected in 180-degree tangential direct radial alignment with the nuclear sphere.
[466.42]{style="color: purple3"} []{#ver:466.42 label="ver:466.42"} This compound molecular matrix grid provides a model for molecular compounding because it accommodates more than one tetrahedron.
[466.43]{style="color: purple3"} []{#ver:466.43 label="ver:466.43"} This matrix is not isotropic. It is anisotropic. It accommodates the domain of a nucleus.
¶ 470.00 Allspace-Filling Transformations of Vector Equilibrium
[470.01]{style="color: purple3"} []{#ver:470.01 label="ver:470.01"} In the closest packing of spheres, there are only two symmetric shapes occurring in the spaces between the spheres. They are what we call the concave octahedron and the concave vector equilibrium. One is an open condition of the vector equilibrium and the other is a contracted one of the octahedron. If we take vector equilibria and compact them, we find that the triangular faces are occupying a position in closest packing of a space and that the square faces are occupying the position in closest packing of a sphere. (For a further exposition of the interchange between spheres and spaces, see illustrations at Sec. 1032, “Convex and Concave Sphere Packing Voids.” )
[470.02]{style="color: purple3"} []{#ver:470.02 label="ver:470.02"} When we compact vector equilibria with one another, we find that two of their square faces match together. Within a square face, we have a half octahedron; so bringing two square faces together produces an internal octahedron between the two of them. At the same time, a set of external octahedra occurs between the triangular faces of the adjacent vector equilibria.
¶ 480.00 Tetrahedron Discovers Itself and Universe
[481.00]{style="color: purple3"} []{#ver:481.00 label="ver:481.00"} The initial self-and-other spherical associability (see Sec. 401 and illustration 401.01 ) produced first, associability; next, triangulation as structure; and then, tetrahedron as system. The inherent self-stretch-apartness reaction identified as mass attraction, and the inherent otherness of awareness, and the discovery of the self through the otherness, as a consequence of which awareness of relatedness, and curiosity about the interrelatedness of further unprecedented self-and-otherness discoveries, all initiate the tetrahedron’s self-discovering that it can turn itself inside out by employing the mass-coherent integrity of any three spheres’s intergeared frictionality to swallow involutingly the fourth sphere through the three’s central passage and to extrude it evolutingly outward again on the other side.
[482.00]{style="color: purple3"} []{#ver:482.00 label="ver:482.00"} Thus tetrahedron discovers that each of its four vertexes can be plunge-passaged through its innards to be extended on the opposite side of its four triangular faces. This automatically develops eight tetrahedral, self-transformation awarenesses and produces eight common nuclear-vertex tetrahedra of the vector equilibrium.
[483.00]{style="color: purple3"} []{#ver:483.00 label="ver:483.00"} Further self-examination of the tetrahedron discovers that the geometry of its insideness proves to be a concave octahedron, with four of the octahedron’s triangular faces represented by the four triangular windows at the face centers of the tetrahedron and the other triangular faces hidden from the view of outsiders, but clearly viewable from inside the tetrahedron’s system as the spherical triangular areas of the interior surfaces of the tetrahedron’s four corner balls; the edges of the triangles are defined as the great-circle arcs leading most economically between each ball’s three interior tangent contact points with each of the other three balls, respectively.
Fig. 470.02A 7?o/e ofTetrahedra and Octahedra in Vector Equilibrium:
-
Positive-negative tetrahedron system.
-
Vector equilibrium formed by four positive-negative tetrahedron systems with common central vertex and coinciding radial edges. Equilibrium of system results from positive-negative action of double radial vectors.
-
The relationship of space-filling tetrahedra and octahedra to the vector equilibrium defined by eight radially disposed tetrahedra.
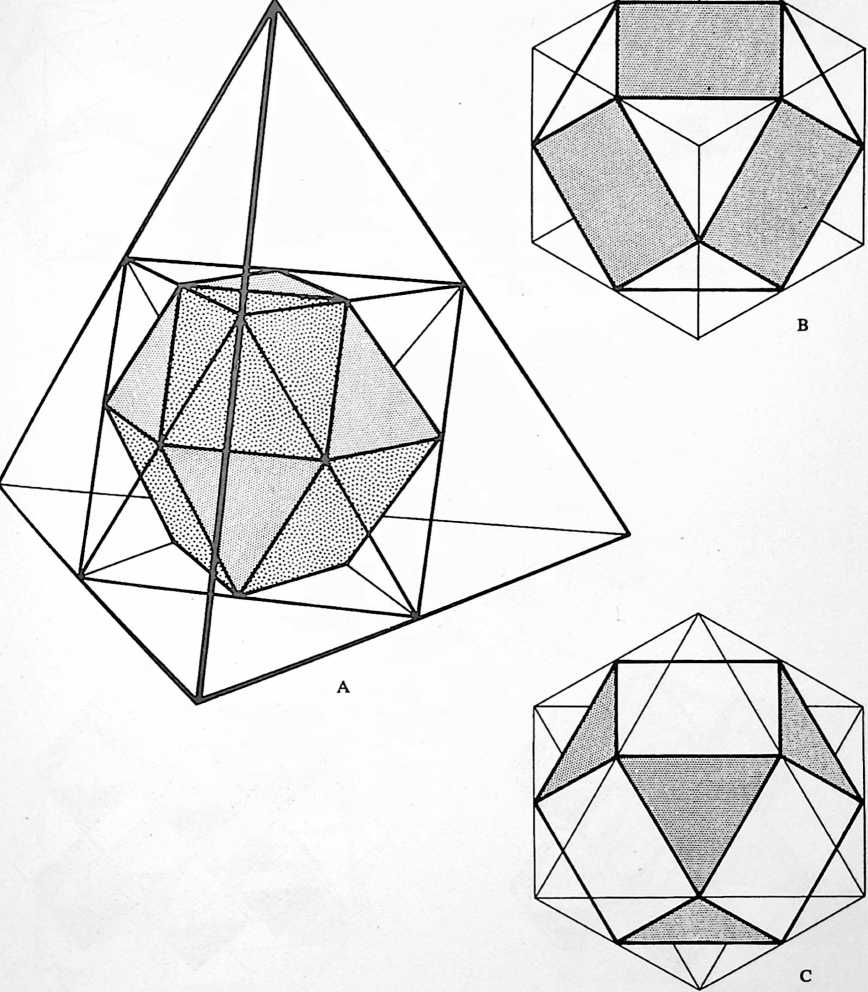
Fig. 470.02B Relationship of Vector Equilibrium to Cube and Octahedron:
-
Joining and interconnecting the midpoints of tetrahedron edges results in the octahedron. Joining and interconnecting the midpoints of the octahedron edges results in the vector equilibrium.
-
Relationship of vector equilibrium to cube.
-
Relationship of vector equilibrium to octahedron.
Fig. 470.02C Transformation of Vector Equilibrium and Octahedron as Space-Filling Jitterbug: Because the vector equilibrium and the octahedron will fill space, it is possible to envision a space-filling “jitterbug” transformation. If we combine vector equilibria on their square faces in a space-filling arrangement, the triangular faces form octahedral voids (1). As the vector equilibria contract, just as in the single “jitterbug,” they transform through the icosahedron phase (3) and end at the octahedron phase (5).
[484.00]{style="color: purple3"} []{#ver:484.00 label="ver:484.00"} And now we have the octahedron self-examinatingly discovered and more sharply defined by the 12 chords of the great-circle arcs being realized as shorter distances than arcs, as lines of sight, between their six common vertexes. Thereafter, awareness of the fourfold equatorial square symmetry of four of those octahedral, equidistanted six vertexes of the octahedron, and discovery of the three axes crossing one another at the octahedron’s center within the shortest distance centrally apart from the three sets of opposite vertexes or poles, thus establishing the one-quarter full circle as well as the one-sixth full circle angular self-fractionating as the octa-and-tetra interpump through the phases of the icosa into full extension of the vector equilibrium: “equanimity” of all potential systems and the extreme local domain of its local self-realization.
[485.00]{style="color: purple3"} []{#ver:485.00 label="ver:485.00"} Thereafter, self-recognition of its six half-octahedra aspects of its own six polar potentials, and thence the self-discovery of its integral four great-circle symmetry, and its vector equanimity of effectively opposed disintegrative propensities by its mass-attractive, full-circle closingness at high-leverage advantage of radius of lever arm self-wrapping around itself, as being more powerfully effective than its self-disintegratively employed equipotential disintegrativeness; whereby the ever self-multiplications at the second-power arithmetical rate of its associative propensities are realized by their initiation, in contradistinction to the immediate second-root rate of diminution of the energy potential whenever it even starts to disintegrate.
[486.00]{style="color: purple3"} []{#ver:486.00 label="ver:486.00"} Thus the self-discovery of the tetrahedral structural system and subsequent evolutionary realization of its inherent octahedral symmetry goes on further to discover its tetrahedron-octahedron complementarity of allspace-filling, and its development thereby of the universal isotropic vector matrix as a self-referring frame comprehensive of its relative aberrations of realizable exactitude which only approaches its ideal equanimity.
[487.00]{style="color: purple3"} []{#ver:487.00 label="ver:487.00"} Whereafter the self-discovery process goes on to identify all the hierarchy of geometrical intertransformings that are the subject of this book, and proceeds inherently, by synergetic strategy of commencing with totality of Universe self-realization, to its progressive omnirational differentiation of its ever symmetrically equated potentials. And all other geometrical proofs of the Greeks and their academic successors aboard our self-realizing planet are herewith usably embraced; and all the rules of geometrical self-development proofs in terms of a priori self-realization proofs are discovered to be germane but always holistically embraced in omnirational identity. Self is not a priori evident. Thus we have avoided mathematical axioms that hold certain recognized a priori self-recognized conditions to be self-evidently irreducible by further analysis.
[488.00]{style="color: purple3"} []{#ver:488.00 label="ver:488.00"} Instead of starting with partspoints, straight lines, and planesand then attempting to develop these inadequately definable parts into omnidirectional experience identities, we start with the whole system in which the initial “point” turned out to be self, which inherently embraced all of its parameters wrapped tightly in that initial underdeveloped, self-focused aspect of self and went on to self-develop through successively discovered relative awarenesses whereby the proof of totality and omni-integrity is not only always inherent, but all the rules of operational procedure are always totally observed.