¶ 1100.00 Triangular Geodesics Transformational Projection
¶ 1101.00 Triangular Geodesics Transformational Projection Model
¶ 1101.01 Description
[1101.02]{style="color: purple3"} []{#ver:1101.02 label="ver:1101.02"} The transformational projection is contained entirely within a plurality of great-circle-bounded spherical triangles (or quadrangles or multipolygons) of constant, uniform-edge-module (invariant, central-angle-incremented) subdivisioning whose constantly identical edge length permits their hinging into flat mosaic-tile continuities. The planar phase of the transformation permits a variety of hinged-open, completely flat, reorientable, unit-area, world mosaics. The transformational projection model demonstrates how the mosaic tiles migrate zonally. It demonstrates how each tile transforms cooperatively but individually, internally from compound curvature to flat surface without interborder-crossing deformation of the mapping data.
[1102.00 Construction of the Model]{style="color: purple3"} []
[1102.01]{style="color: purple3"} []{#ver:1102.01 label="ver:1102.01"} The empirical procedure modeling that demonstrates the transformational projection is constructed as follows:
[1102.02]{style="color: purple3"} []{#ver:1102.02 label="ver:1102.02"} There are three spring-steel straps of equal length, each of which is pierced with rows of holes located at equal intervals, one from the other, along the longitudinal center line of the straps’ flat surfaces; the first and last holes are located inward from the ends a distance equal to one-half the width of the steel straps’ flat surfaces.
[1102.03]{style="color: purple3"} []{#ver:1102.03 label="ver:1102.03"} Steel rods of equal length are inserted an equal distance through each of the holes in the straps in such a manner that each rod is perpendicular to the parallel surfaces of the strap and therefore parallel to the other rods. Each of the straps and their respective rods form, in effect, a long-toothed comb, with the comb’s straight back consisting of the steel strap.
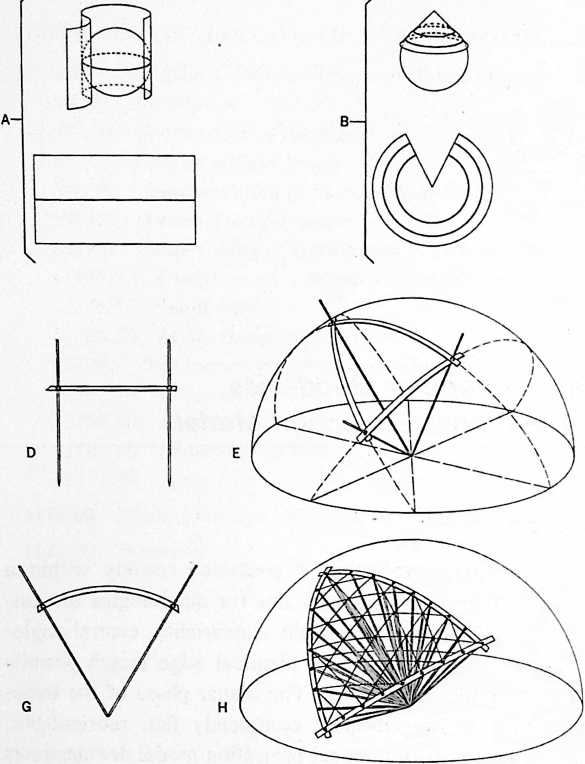
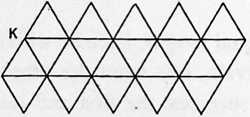
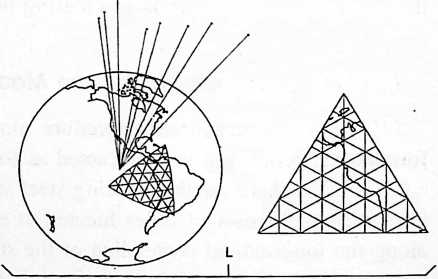
Fig. 1101.02 The projection system of the Dymaxion Airocean World Map divides the sphere into 20 equilateral spherical triangles, which are then flattened to form the icosahedron (J). These 20 triangles are each projected into a flat plane (D, E, F, G, H, I). This method results in a map having less visible distortion than any previously known map projection system to date. To flatten the globe it is simply necessary to “unfold” the icosahedron (K). The more conventional projection systems that are widely used include the Mercator projection (A), the conic projection (B), and the planar projection (C). All three of these systems give rise to considerable visual distortion, unlike the Dymaxion projection.

[1102.04]{style="color: purple3"} []{#ver:1102.04 label="ver:1102.04"} Assuming that the steel straps are flexible, and assuming that each of the rods is absolutely stiff (as when employed as a lever), if the rods have their long lower ends gathered toward one another, at one point the strap will yield by curving of its flat surface to the section of a cylinder whose axis is perpendicular to the plane of the rods and congruent with the rod ends. The strap is bent into an arc of a true circle whose radius is uniformly that of the uniform rod lengths. Each of the rods, as a radius of the circular arc, is perpendicular to the arc. That is, the rods are constantly perpendicular to the strap in either its flat condition or in any of its progressive arcings.
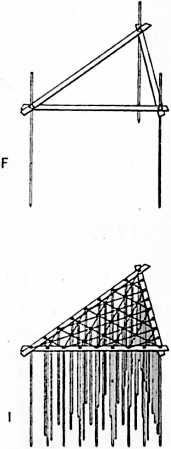
[1102.05]{style="color: purple3"} []{#ver:1102.05 label="ver:1102.05"} Next, one of ±e two ends of each of the three steel straps is joined to an end of one of the other two straps by means of their end rods being removed and one of the rods being reinserted through their mutual end holes as one strap is superimposed on the other with their respective end holes being brought into register, whereafter, hollow “stovepipe” rivets[^54] of complementary inside-outside diameters are fastened through the end holes to provide a journal through which one of the former end rods is now perpendicularly inserted, thus journaled pivotally together like a pair of scissors. The three straps joined through their registered terminal holes form an equilateral triangle of overlapping and rotatably journaled ends. (See Illus. 1101.02 F.)
[1102.06]{style="color: purple3"} []{#ver:1102.06 label="ver:1102.06"} It will next be seen that a set of steel rods of equal length may be inserted an equal distance through each of the holes of each of the straps, including the hollow journaled holes at the ends, in such a manner that each rod is perpendicular to the parallel surfaces of the straps; therefore, each rod is parallel to the others. All of the rods perpendicularly piercing any one of the straps are in a row, and all of their axes are perpendicular to one common plane. The three unique planes of the three rows of rods are perpendicular to each of the straps whose vertical faces form a triangular prism intersecting one another at the central axes of their three corner rods’ common hinge extensions. Each of the three planes is parallel to any one rod in each of the other two planes. (See Illus. 1101.02 I.)
¶ 1103.00 Flexing of Steel Straps
[1103.01]{style="color: purple3"} []{#ver:1103.01 label="ver:1103.01"} Assuming that each of the rods is absolutely stiff (as when employed as a lever) and that the rotatable journaling in their respective end holes is of such close tolerance that the combined effect of these two qualities of the model is such that any different directions of force applied to any two different rod ends would force the steel straps to yield into circular arc then it will be clear that the three journaled end rods permit the three corner angles of the triangle to change to satisfy the resulting force or motion differential.
[1103.02]{style="color: purple3"} []{#ver:1103.02 label="ver:1103.02"} If the rods in any one row in any one strap have their ends gathered toward one another, the strap will yield by curving its flat surfaces to the section of a cylinder whose axis is perpendicular to the plane of the rods. If all the rod ends of one strap are pulled together at one point (we refer to the one set of ends on either side of the strap), the strap, being equidistant along its center from that point, will form a segment of a circle, and each of the rods, being radii of that circle, will remain each perpendicular to the strap and all in a single plane perpendicular to the strap throughout the transformation.
[1103.03]{style="color: purple3"} []{#ver:1103.03 label="ver:1103.03"} Now if all the ends of all the rods on one face side or the other of the triangle (since released to its original flat condition of first assembly), and if all of the three rows in the planes perpendicular to each of the three straps forming the triangle are gathered in a common point, then each of the three spring-steel-strap and rod sets will yield in separate arcs, and the three planes of rods perpendicular to them will each rotate around its chordal axis formed between the two outer rivet points of its arc, so that the sections of the planes on the outer side of the chords of the three arcs, forming what is now a constant-length, equiedged (but simultaneously changing from flat to arced equiedged), equiangled (but simultaneously altering corner-angled), spherical triangle, will move toward one another, and the sections of the planes on the inner side of the chords of the three arcs forming the constant, equiedged (but simultaneously changing flat-to-arc equiedged), and equiangled (but simultaneously altering corner-angled), spherical triangle will rotate away from one another. The point to which all rod ends are gathered will thus become the center of a sphere on the surface of which the three arcs occur, as arcs of great circlesfor their planes pass through the center of the same sphere. The sums of the corner angles of the spherical triangles add to more than the 180 degrees of the flat triangle, as do all spherical triangles with the number of degrees and fractions thereof that the spherical triangle is greater than its chorded plane triangle being called the spherical excess, the provision of which excess is shared proportionately in each corner of the spherical triangle; the excess in each corner is provided in our model by the scissors-like angular increase permitted by the pivotal journals at each of the three corners of the steel-strap-edged triangle. (See Illus. 1101.02 H.)
[1103.04]{style="color: purple3"} []{#ver:1103.04 label="ver:1103.04"} The three arcs, therefore, constitute the edges of a spherical equilateral triangle, whose fixed-length steel boundaries are subdivided by the same uniform perimeter scale units of length as when the boundary lines were the “straight” edge components of the flat triangle. Thus we are assured by our model that the original triangle’s edge lengths and their submodular divisions have not been altered and that the finite closure of the triangle has not been violated despite its transformation from planar to spherical triangles.
¶ 1104.00 Constant Zenith of Flat and Spherical Triangles
[1104.01]{style="color: purple3"} []{#ver:1104.01 label="ver:1104.01"} The radii of the sphere also extend outwardly above the surface arcs in equidistance, being perpendicular thereto, and always terminate in zenith points in respect to their respective points of unique penetration through the surface of the sphere.
[1104.02]{style="color: purple3"} []{#ver:1104.02 label="ver:1104.02"} If we now release the rods from their common focus at the center of the sphere and the spring-steel straps return to their normal flatness, all the rods continue in the same perpendicularity to the steel bands throughout the transformation and again become parallel to one another and are grouped in three separate and axially parallel planes. What had been the external spherical zenith points remain in zenith in respect to each rod’s point of penetration through the now flat triangle’s surface edge. This is an important cartographic property[^55] of the transformational projection, which will become of increasing importance to the future high-speed, world-surface-unified triangulation through aerial and electromagnetic signal mapping, as well as to the spherical world-around data coordination now being harvested through the coordinately “positioned” communications satellites “flying” in fixed formation with Earth. They and Moon together with Earth co-orbit Sun at 60,000 mph.
¶ 1105.00 Minima Transformation
[1105.01]{style="color: purple3"} []{#ver:1105.01 label="ver:1105.01"} If the rods are pushed uniformly through the spring-steel straps so that increasing or decreasing common lengths of rod extend on the side of the triangle where the rods are gathered at a common point, then, as a result, varying ratios of radii length in respect to the fixed steel-strap arc length will occur. The longer the rods, the larger will be the sphere of which they describe a central tetrahedral segment, and the smaller the relative proportional size of the spherical surface triangle bounded by the steel springsas compared to the whole implicit spherical surface. Because the spherical triangle edge length is not variable, being inherent in the original length of the three identical steel springs, the same overall length can accommodate only an ever smaller spherical surface arc (central-angle subtension) whenever the radii are lengthened to produce a greater sphere.

Fig. 1105.01
[1105.02]{style="color: purple3"} []{#ver:1105.02 label="ver:1105.02"} If the ends of the rods gathered together are sufficiently shortened, they will finally attain a minimum length adequate to reach the common point. This minimum is attained when each is the length of the radius of a sphere relative to which the steel spring’s length coincides with the length of an arc of 120 degrees. This condition occurs uniquely in a spherical triangle where each of the three vertexes equals 180 degrees and each of the arcs equals 120 degrees, which is of course the description of a single great circle such as the equator.
[1105.03]{style="color: purple3"} []{#ver:1105.03 label="ver:1105.03"} Constituting the minima transformation obtainable by this process of gathering of rod ends, it will be seen that the minima is a flat circle with the rods as spokes of its wheel. Obviously, if the spokes are further shortened, they will not reach the hub. Therefore, the minima is not 0or no sphere at allbut simply the smallest sphere inherent in the original length of the steel springs. At the minima of transformation, the sphere is at its least radius, i.e., smallest volume.
[1105.04]{style="color: purple3"} []{#ver:1105.04 label="ver:1105.04"} As the rods are lengthened again, the implied sphere’s radius ergo, its volumegrows, and, because of the nonyielding length of the outer steel springs, the central angles of the arc decrease, as does also the relative size of the equilateral, equiangular spherical triangle as, with contraction, it approaches one of the poles of the sphere of transformation. The axis running between the two poles of most extreme transformation of the spherical triangle we are considering runs through all of its transforming triangular centers between itsnever attainedminimum-spherical-excess, smallest-conceivable, local, polar triangle on the ever-enlarging sphere, then reversing toward its largest equatorial, three-180-degree-corners, hemisphere area phase on its smallest sphere, with our triangle thereafter decreasing in relative spherical surface area as thenever attained smallest triangle and the sphere itself enlarge toward thealso never attainedcosmically largest sphere. It must be remembered that the triangle gets smaller as it approaches one pole, the complementary triangle around the other pole gets correspondingly larger. It must also be recalled that the surface areas of both the positive and negative complementary spherical triangles together always comprise the whole surface of the sphere on which they co-occur. Both the positive and negative polarcentered triangles are themselves the outer surface triangles of the two complementary tetrahedra whose commonly congruent internal axis is at the center of the same sphere whose total volume is proportionately subdivided between the two tetrahedra.
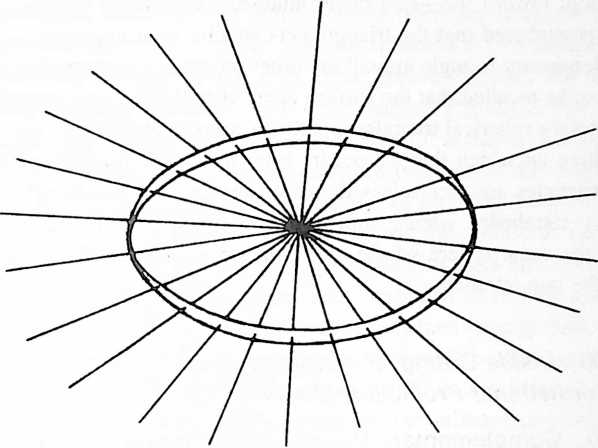
Fig. 1105.03.
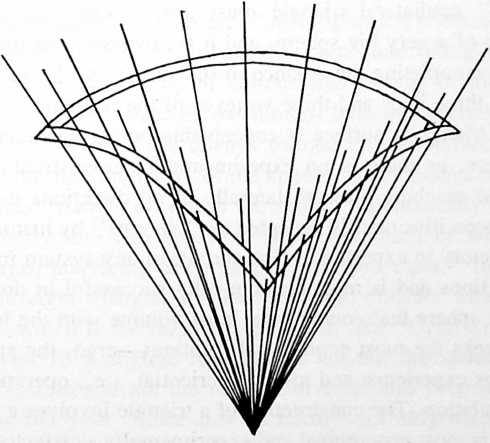
¶ 1106.00 Inside-Outing of Tetrahedron in Transformational Projection Model
[1106.10]{style="color: purple3"} []{#ver:1106.10 label="ver:1106.10"} Complementary Negative Tetrahedron: The rod ends can be increased beyond the phase that induced the 180-degree triangle, and the vertexes of the steel-spring surface triangle can go on to be increased beyond 180 degrees each, and thus form a negative triangle. This is to say that the original tetrahedron formed between the three vertexes of the spherical triangle on the sphere’s surfacewith the center of the sphere as the fourth point will have flattened to one plane when the vertexes are at 180 degrees; at that moment the tetrahedron is a hemisphere. By lengthening the radii again and increasing the triangle’s original “interior” angles, the tetrahedron will turn itself inside out. In effect, what seems to be a “small,” i.e., an only apparently “plane” equilateral triangle must always be a small equilateral spherical triangle of a very big sphere, and it is always complemented by the negative triangle completing the balance of the surface of the inherent sphere respective to the three lines and three vertexes of the triangle.
[1106.11]{style="color: purple3"} []{#ver:1106.11 label="ver:1106.11"} No triangular surface is conceivable occurring independently of its inherent sphere, as there is no experimentally demonstrable flat surface plane in Universe reaching outward laterally in all directions to infinity; although this has been illusionarily accepted as “obvious” by historical humanity, it is contradictory to experience. The surface of any system must return to itself in all directions and is most economically successful in doing so as an approximate true sphere that contains the most volume with the least surface. Nature always seeks the most economical solutionsergo, the sphere is normal to all systems experience and to all experiential, i.e., operational consideration and formulation. The construction of a triangle involves a surface, and a curved surface is most economical and experimentally satisfactory. A sphere is a closed surface, a unitary finite surface. Planes are never finite. Once a triangle is constructed on the surface of a spherebecause a triangle is a boundary line closed upon itself the finitely closed boundary lines of the triangle automatically divide the unit surface of the sphere into two separate surface areas. Both are bounded by the same three great-circle arcs and their three vertexial links: this is the description of a triangle. Therefore, both areas are true triangles, yet with common edge boundaries. It is impossible to construct one triangle alone. In fact, four triangles are inherent to the oversimplified concept of the construction of “one” triangle. In addition to the two complementary convex surface triangles already noted, there must of necessity be two complementary concave triangles appropriate to them and occupying the reverse, or inside, of the spherical surface. Inasmuch as convex and concave are opposites, one reflectively concentrating radiant energy and the other reflectively diffusing such incident radiation; therefore they cannot be the same. Therefore, a minimum of four triangles is always induced when any one triangle is constructed, and which one is the initiator or inducer of the others is irrelevant. The triangle initiator is an inadvertent but inherent tetrahedron producer; it might be on the inside constructing its triangle on some cosmic sphere, or vice versa.
[1106.12]{style="color: purple3"} []{#ver:1106.12 label="ver:1106.12"} It might be argued that inside and outside are the same, but this is not so. While there is an interminable progression of insides within insides in Experience Universe, there is only one outside comprehensive to all insides. So they are not the same, and the mathematical fact remains that four is the minimum of realizable triangles that may be constructed if any are constructed. But that is not all, for it is also experimentally disclosed that not only does the construction of one triangle on the surface of the sphere divide the total surface into two finite areas each of which is bound by three edges and three anglesergo, by two trianglesbut these triangles are on the surface of a system whose unity of volume was thereby divided into two centrally angled tetrahedra, because the shortest lines on sphere surfaces are great circles, and great circles are always formed on the surface of a sphere by planes going through the center of the sphere, which planes of the three-great-circle-arc-edged triangle drawn on the surface automatically divide the whole sphere internally into two spherical tetrahedra, each of which has its four trianglesergo, inscribing one triangle “gets you eight,” like it or not. And each of those eight triangles has its inside and outside, wherefore inscribing one triangle, which is the minimum polygon, like “Open Sesame,” inadvertently gets you 16 triangles. And that is not all: the sphere on which you scribed is a system and not the whole Universe, and your scribing a triangle on it to stake out your “little area on Earth” not only became 16 terrestrial triangles but also induced the remainder of Universe outside the system and inside the system to manifest their invisible or nonunitarily conceptual “minimum inventorying” of “the rest of Universe other than Earth,” each of which micro and macro otherness system integrity has induced an external tetrahedron and an internal tetrahedron, each with 16 triangles for a cosmic total of 64 (see Sec. 401.01).
[1106.20]{style="color: purple3"} []{#ver:1106.20 label="ver:1106.20"} Inside-Outing: Inside-outing means that any one of the four vertexes of the originally considered tetrahedron formed on the transformational projection model’s triangle, with its spherical center, has passed through its opposite face. The minima and the maxima of the spherical equiside and -angle triangle formed by the steel springs is seen to be in negative triangular complement to the smallest 60-degree+ triangle. The vertexes of even the maxima or minima are something greater than 60 degrees eachbecause no sphere is large enough to be flator something less than 300 degrees each.
[1106.21]{style="color: purple3"} []{#ver:1106.21 label="ver:1106.21"} The sphere is at its smallest when the two angles of complement are each 180 degrees on either side of the three-arc boundary, and the minima-maxima of the triangles are halfway out of phase with the occurrence of the minima and maxima of the sphere phases.
[1106.22]{style="color: purple3"} []{#ver:1106.22 label="ver:1106.22"} No sphere large enough for a flat surface to occur is imaginable. This is verified by modern physics’ experimentally induced abandonment of the Greeks’ definition of a sphere, which absolutely divided Universe into all Universe outside and all Universe inside the sphere, with an absolute surface closure permitting no traffic between the two and making inside self-perpetuating to infinity complexergo, the first locally perpetual-motion machine, completely contradicting entropy. Since physics has found no solids or impervious continuums or surfaces, and has found only finitely separate energy quanta, we are compelled operationally to redefine the spheric experience as an aggregate of events approximately equidistant in a high-frequency aggregate in almost all directions from one only approximate event (see Sec. 224.07). Since nature always interrelates in the most economical manner, and since great circles are the shortest distances between points on spheres, and since chords are shorter distances than arcs, then nature must interrelate the spheric aggregated events by the chords, and chords always emerge to converge; ergo, converge convexly around each spheric system vertex; ergo, the sums of the angles around the vertexes of spheric systems never add to 360 degrees. Spheres are high-frequency, geodesic polyhedra (see Sec. 1022.10).
[1106.23]{style="color: purple3"} []{#ver:1106.23 label="ver:1106.23"} Because (a) all radiation has a terminal speed, ergo an inherent limit reach; because (b) the minimum structural system is a tetrahedron; because (c) the unit of energy is the tetrahedron with its six-degrees-of-minimum-freedoms vector edges; because (d) the minimum radiant energy package is one photon; because (e) the minimum polar triangleand its tetrahedron’s contraction is limited by the maximum reach of its three interior radii edges of its spherical tetrahedron; and because (f) physics discovered experimentally that the photon is the minimum radiation package; therefore we identify the minimum tetrahedron photon as that with radius =c, which is the speed of light: the tetrahedron edge of the photon becomes unit radius = frequency limit.
[1106.24]{style="color: purple3"} []{#ver:1106.24 label="ver:1106.24"} The transformational projection model coupled with the spheric experience data prove that a finite minima and a finite maxima do exist, because a flat is exclusively unique to the area confined within a triangle’s three points. The almost flat occurs at the inflection points between spheric systems’ inside-outings and vice versa, as has already been seen at the sphere’s minima size; and that at its maxima, the moment of flatness goes beyond approximate flatness as the minima phase satisfies the four-triangle minima momentum of transformation, thus inherently eliminating the paradox of static equilibrium concept of all Universe subdivided into two parts: that inside of a sphere and that outside of it, the first being finite and the latter infinite. The continual transforming from inside out to outside in, finitely, is consistent with dynamic experience.
[1106.25]{style="color: purple3"} []{#ver:1106.25 label="ver:1106.25"} Every great circle plane is inherently two spherical segment tetrahedra of zero altitude, base-to-base.
[1106.30]{style="color: purple3"} []{#ver:1106.30 label="ver:1106.30"} Inside-Outing of Spheres: When our model is in its original condition of having its springs all flat (a dynamic approximation) and in one plane, in which condition all the rods are perpendicular to that plane, the rods may be gathered to a point on the opposite side of the spring-steel strap to that of the first gathering, and thus we see the original sphere turned inside out. This occurs as a sphere of second center, which, if time were involved, could be the progressive point of the observer and therefore no “different” point.
[1106.31]{style="color: purple3"} []{#ver:1106.31 label="ver:1106.31"} Considering Universe at minimum unity of two, two spheres could then seem to be inherent in our model. The half-out-of-phaseness of the sphere maxima and minima, with the maxima-minima of the surface triangles, find the second sphere’s phase of maxima in coincidence with the first’s minima. As the two overlap, the flat phase of the 180-degree triangles of the one sphere’s minima phase is the flat phase of the other sphere’s maxima. The maxima sphere and the minima sphere, both inside-outing, tend to shuttle on the same polar axis, one of whose smaller polar triangles may become involutional while the other becomes evolutional as the common radii of the two polar tetrahedra refuse convergence at the central sphere. We have learned elsewhere (see Sec. 517) that two or more lines cannot go through the same point at the same time; thus the common radii of the two polar tetrahedra must twistingly avert central convergence, thus accomplishing central core involutional-evolutional, outside-inside-outside, cyclically transformative travel such as is manifest in electromagnetic fields. All of this is implicit in the projection model’s transformational phases. There is also disclosed here the possible intertransformative mechanism of the interpulsating binary stars.
¶ 1107.00 Transformational Projection Model with Rubber-Band Grid
[1107.10]{style="color: purple3"} []{#ver:1107.10 label="ver:1107.10"} Construction: Again returning the model to the condition of approximate dynamic inflection at maxima-minima of the trianglei.e., to their approximately flat phase of “one” most-obvious triangle of flat springsteel stripsin which condition the rods are all perpendicular to the surface plane of the triangle and are parallel to one another in three vertical planes of rod rows in respect to the triangle’s plane. At this phase, we apply a rubberband grid of three-way crossings. We may consider the rubber bands of ideal uniformity of cross section and chemical composition, in such a manner as to stretch them mildly in leading them across the triangle surface between the points uniformly spaced in rows, along the spring-steel strap’s midsurface line through each of which the rods were perpendicularly inserted. The rubber bands are stretched in such a manner that each rubber band leads from a point distant from its respective primary vertex of the triangle to a point on the nearest adjacent edge, that is, the edge diverging from the same nearest vertex, this second point being double the distance along its edge from the vertex that the first taken point is along its first considered edge. Assuming no catenary sag or drift, the “ideal” rubber bands of no weight then become the shortest distances between the edge points so described. Every such possible connection is established, and all the tensed, straight rubber bands will lie in one plane because, at the time, the springs are flatand that one plane is the surface of the main spring-steel triangle of the model.
[1107.11]{style="color: purple3"} []{#ver:1107.11 label="ver:1107.11"} The rubber bands will be strung in such a way that every point along the steel triangle mid-edge line penetrated by the rods shall act as an origin, and every second point shall become also the recipient for such a linking as was described above, because each side feeds to the other sides. The “feeds” must be shared at a rate of one goes into two. Each recipient point receives two lines and also originates one; therefore, along each edge, every point is originating or feeding one vertical connector, while every other, or every second point receives two obliquely impinging connector lines in addition to originating one approximately vertically fed line of connection.
[1107.12]{style="color: purple3"} []{#ver:1107.12 label="ver:1107.12"} The edge pattern, then, is one of uniform module divisions separated by points established by alternating convergences with it: first, the convergence of one connector line; then, the convergence of three connector lines; and repeat.
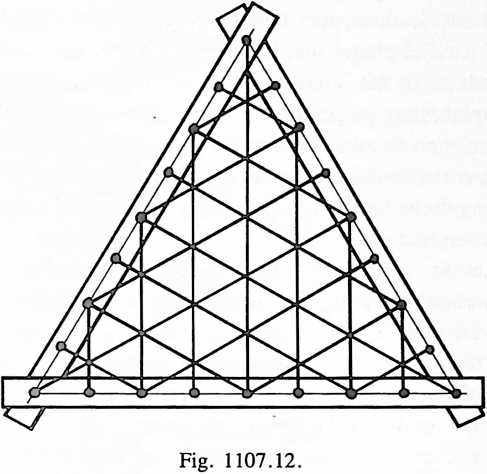
[1107.13]{style="color: purple3"} []{#ver:1107.13 label="ver:1107.13"} This linking of the three sides will provide a rubber-band grid of three-way crossings of equi-side and -angle triangular interstices, except along the edges of the main equiangle triangle formed by the spring-steel pieces, where half-equilateral triangles will occur, as the outer steel triangle edges run concurrently through vertexes to and through midpoints of opposite sides, and thence through the next opposite vertexes again of each of the triangular interstices of the rubber-band grid interacting with the steel edges of the main triangle.
[1107.14]{style="color: purple3"} []{#ver:1107.14 label="ver:1107.14"} The rubber-band, three-way, triangular subgridding of the equimodule spring-steel straps can also be accomplished by bands stretched approximately parallel to the steel-strap triangle’s edges, connecting the respective modular subdivisions of the main steel triangle. In this case, the rubber-band crossings internal to the steel-band triangle may be treated as is described in respect to the main triangle subtriangular gridding by rubber bands perpendicular to the sides.
[1107.20]{style="color: purple3"} []{#ver:1107.20 label="ver:1107.20"} Transformation: Aggregation of Additional Rods: More steel rods (in addition to those inserted perpendicularly through the steel-band edges of the basic triangle model) may now be insertedalso perpendicularly through a set of steel grommets attached at (and centrally piercing through) each of the points of the three-way crossings of the rubber bands (internal to the big triangle of steel) in such a manner that the additional rods thus inserted through the points of three-way crossings are each perpendicular to the now flat-plane phase of the big basic articulatable steel triangle, and therefore perpendicular to, and coincident with, each of the lines crossing within the big steel triangle face. The whole aggregate of rods, both at edges and at internal intersections, will now be parallel to one another in the three unique sets of parallel planes that intersect each other at 60 degrees of convergence. The lines of the intersecting planes coincide with the axes of the rods; i.e., the planes are perpendicular to the plane of the basic steel triangle and the lines of their mutual intersections are all perpendicular to the basic plane and each corresponds to the axis of one of the rods. The whole forms a pattern of triangularly bundled, equiangular, equilateral-sectioned, parallel-prism-shaped tube spaces.
[1107.21]{style="color: purple3"} []{#ver:1107.21 label="ver:1107.21"} Let us now gather together all the equally down-extending lengths of rod ends to one point. The Greeks defined a sphere as a surface equidistant in all directions from one point. All the points where the rods penetrate the steel triangle edges or the three-way-intersecting elastic rubberband grid will be equidistant from one common central point to which the rod ends are gathered and thus they all occur in a spherical, triangular portion of the surface of a common spherespecifically, within the lesser surfaced of the two spherical triangles upon that sphere described by the steel arcs.
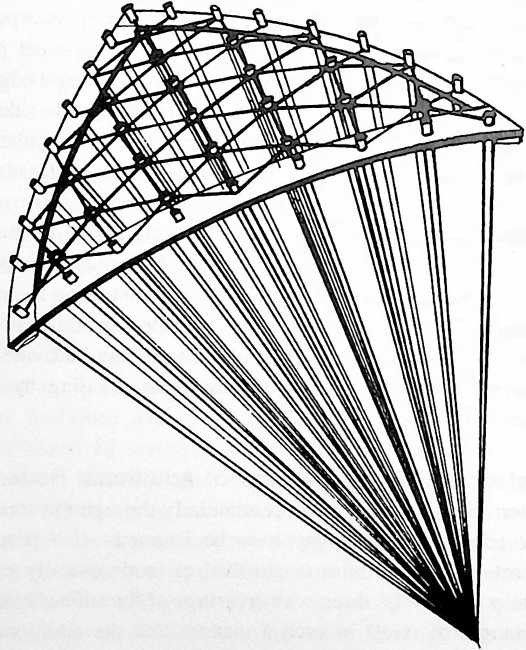
Fig. 1107.21.
Throughout the transformation, all the rods continue their respective perpendicularities to their respective interactions of the three-way crossings of the flexible grid lines of the basic steel triangle’s inherently completable surface.
[1107.22]{style="color: purple3"} []{#ver:1107.22 label="ver:1107.22"} If the frequency of uniform spacing of the perpendicularly and equidistantlypenetrating and extending rods is exquisitely multiplied, and the uniform intervals are thus exquisitely shortened, then when the rod ends are gathered to a common point opposite either end of the basic articulatable steel-band triangle, the gathered ends will be closer together than their previous supposedly infinitely close parallel positioning had permitted, and the opposite ends will be reciprocally thinned out beyond their previous supposedly infinite disposition. Both ends of the rods are in finite condition beyond infiniteand the parallel phase (often thought of as infinite) is seen to be an inflection phase between two phases of the gathering of the ends, alternately, to one or the other of the two spherical centers. The two spherical centers are opposite either the inflection or flat phase of the articulating triangle faces of the basic articulatable triangle of our geodesics transformational projection model.
[1107.30]{style="color: purple3"} []{#ver:1107.30 label="ver:1107.30"} Persistence of Perpendicularity: As the frequency of uniform spacing of the rods increases and as the ends are uniformly and infinitely extended, the distance each end must move to accomplish union is infinitely decreased. As this union takes place and the surface of the original triangle becomes a spherical-surface triangle of infinitely small dimension on an infinitely large sphere, the chords between the points of intersection of the rods’ triangle’s surface, and the arcs between the points of intersection, approach infinitely negligible difference. We discern that, while at the inflection point, the rods are at right angles to the chord-arc“negligible” mean; that they are not at right angles to the chord at the gathering-of-the-ends phase; and that they are always perpendicular to the mean-arc-chord “infinity”; and that the condition of perpendicularity is persistent throughout all the transformation phases. Perpendicularity does not “disappear” at the zero-inflection phase of inside-outing, or positive-to-negative transformation.
[1107.31]{style="color: purple3"} []{#ver:1107.31 label="ver:1107.31"} The above development of our transformational projection model is that of a flexible and two-way steel rod-bristle brush with ends extending evenly infinitelyin opposite (double infinity) directions and infinitely tightly packed, the bristles being mounted in the steel triangle and its rubberband-interlaced membrane, which is situated at a central position between two infinite ends and, perpendicular thereto, in both directions.
[1107.32]{style="color: purple3"} []{#ver:1107.32 label="ver:1107.32"} Because the rubber bands seek the shortest distances between their respective points of interaction, and because the steel arcs (to which they are attached at uniform intervals) each rotate uniformly (as planes of great circles of the same series of commonly expanding or contracting spheres) away from the other two sides (of the basic articulatable steel triangle) toward one of which two (rotated away from the sides) each rubber band leads (from its own receding position on its awaywardly rotating arc), each band therefore yields elastically, in axial elongation, to permit the continued three-way awayness rotation. Each will persist in finding the progressive set of shortest distances between the points of the spherical triangle’s respective perpendicular rod-penetrated surface.
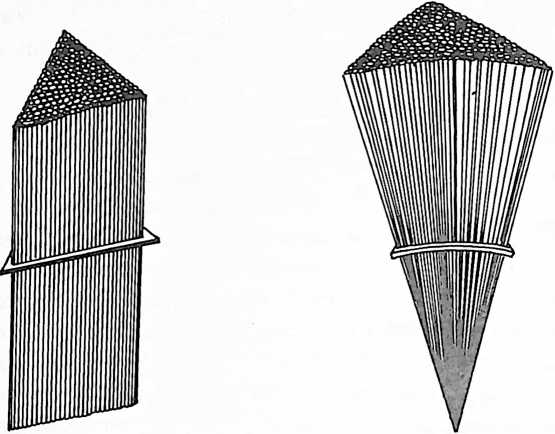
Fig. 1107.31.
[1107.40]{style="color: purple3"} []{#ver:1107.40 label="ver:1107.40"} Three-Way Crossings: Zigzags: Great circles represent the shortest distances between two points on spherical surfaces, and the chords of the arcs between points on spherical surfaces are the even shorter lines of Universe between those points. When the ends of the rods have been gathered together, the rubber bands will be found each to yield complexedly as an integrated resultant of least resistance to the other two bands crossing at each surface point of the grid. They yield respectively each to the other and to the outward thrusting of their rigidly constant steel rods, perpendicularly impinging from within upon the progressively expanding grid. The progressively integrated set of force resultants continuously sorts the rods into sets of rows in the great-circle planes connecting the uniform boundary scale subdivisions of the flexing and outwardly rotating steel-band arcs of the equi-side and -angle articulatable triangle.
[1107.41]{style="color: purple3"} []{#ver:1107.41 label="ver:1107.41"} How do we know empirically that this force-resultant integration is taking place? The stresses pair off into identical zigzags of two-way stress in every chord, in identical magnitude, through the six-functional phases of the six right spherical triangles primarily subdividing the basic equi-side and -angle articulatable steel triangle!
[1107.42]{style="color: purple3"} []{#ver:1107.42 label="ver:1107.42"} How do we know that this is true mathematically? Because the sum-total overall lengths of the vectors in direct opposition are identical, and the sums of their angles are identical!
¶ 1110.00 Zenith Constancy of Radial-Coordination
[1110.01]{style="color: purple3"} []{#ver:1110.01 label="ver:1110.01"} The zenith constancy of the transformational projection’s topological trigonometry discretely locates the common zenith points of any commonly centered, concentric-surfaced systems.
[1110.02]{style="color: purple3"} []{#ver:1110.02 label="ver:1110.02"} If camera-equipped telescopes were mounted aboard Earth-dispatched and -controlled satellites that were “locked” in fixed-formation flight positions around Earth, with one such fixed satellite hovering steadily over each vertex of a one-mile-edged world-triangulation grid, and if each telescope was trained so that the eyepiece of its eyepiece-to-optics’ axis would be pointed exactly toward the center of Earth and its outer optics’ end pointed exactly toward whatever star, if any, may be in exact zenith over the point on the surface of Earth above which the satellite was vertically positioned, a human on Earth at any of those points looking vertically outward into the heavens with a radarscope would discover that satellite as a blip in the middle of his scope-viewing tube’s grid.
[1110.03]{style="color: purple3"} []{#ver:1110.03 label="ver:1110.03"} Now let us have an around-the-world simultaneous clicking of the shutters of the cameras attached to each of the telescopes of each of those around-Earth, fixedly hovering photo-satellites with their telescopes pointed to whatever stars may be vertically outward from Earth at their respective omni-Earth-triangulated, one-mile-apart, grid vertexes. Let us assume the photographing telescopes to be very long-barreled to shield those not pointing at Sun from its intense luminosity. A composite mosaic of all those pictures could now be print-mounted spherically on the inside of a translucent 200-foot globe of Earth’s conventional geographic data of continents, islands, etc., together with the conventional latitude-longitude grid. Because they were photographed outside Earth’s cloud cover, they would present a composite and accurate spherical picture of what the navigators and astronauts call the celestial sphere, with the relative brilliance of the stars in evidence with astronomically calculatable corrections being made in the printing for the Sun’s luminosity effects.
FIGURES
AUG 15 1950
THIS PATTERN SHOWS
2-WAT COMPREHENSIVE
EQUILIBRIUM WITH 3 WAY YIELD AND
BASIC & FUNCTION
SATISFACTION WITHOUT INTERNAL
CONFLICT AND SINGLE
EXTERNAL COMPLEMENTARITY NEXT A
[1110.04]{style="color: purple3"} []{#ver:1110.04 label="ver:1110.04"} While this picture was orientationally unique to its one moment in eternity in respect to the Earth-to-celestial-sphere orientation, Earth data per se and the celestial sphere data per se remain constant at their magnitude of scrutability within the lifespan of any human.
[1110.05]{style="color: purple3"} []{#ver:1110.05 label="ver:1110.05"} Because of the accuracy with which this spherical picture was made, it would also be possible to take a transparent-plastic, 20-foot globe of Earth, with the latitude-longitude grid and the continents and islands outlined, together with the marker points identifying the respective positions of the satellite-mounted telescope cameras at the time of the photographing, and to position the 20-foot Earth globe within the 200-foot celestial sphere globe with the miniature Earth’s spherical center congruent with the spherical center of the 200-foot celestial sphere.
[1110.06]{style="color: purple3"} []{#ver:1110.06 label="ver:1110.06"} It is then possible to orient the miniature 20-foot-diameter Earth globe so that its polar axis is pointed toward the North Star, making a small correction to correspond with the astronomical correction for the small aberration well known to exist in this respect, which is negligible in this description of the properties of our triangular geodesics transformational projection. We may then rotate the miniature Earth 20-foot globe around its axis until a sighting from its exact center will register each of the satellite camera positions with each of the stars of the 200-foot celestial sphere that the satellites photographed in exact verticality outward from Earth.
[1110.07]{style="color: purple3"} []{#ver:1110.07 label="ver:1110.07"} Earth’s highest mountaintop is five miles above sea level, and the ocean’s deepest bottom is five miles below sea level. We could now modify the surface of our transparent-plastic, 20-foot model of Earth to show these aberrations, which indicate that some parts of Earth’s surface have a differential radial distance from Earth’s center; but it would be in evidence that the stars would be in zenith over the same latitude-longitude grid points as would all of the satellite photographic stations.
[1110.08]{style="color: purple3"} []{#ver:1110.08 label="ver:1110.08"} Finding that surface aberrations include only radial-distance variations and changes in the spherical-surface line-of-sight projections from the center, we will now introduce a clear-plastic shell model of a whale and of a crocodile, of such sizes that the crocodile is large enough to omnisurround or swallow the 20-foot miniature Earth globe, and that the whale is large enough to swallow the crocodile yet small enough to be inside the 200-foot-diameter, clear-plastic celestial sphere. With omnidirectional spoke-wires, we will now tensionally position the whale within the 200-foot celestial sphere, and we will tensionally wire-position the crocodile within the whale, and the 20-foot miniature Earth within the crocodile. The miniature Earth is oriented as before, its volumetric center exactly in congruence with the center of volume of the celestial sphere, with all of the stars at the time of the photographing in register with the same satellites that photographed them.
[1110.09]{style="color: purple3"} []{#ver:1110.09 label="ver:1110.09"} Now the whale’s and the crocodile’s surfaces will be at a great variety of different radii distances from the concentric volumetric centers of the 200-foot and 20-foot spheres. We are going now to coat the surfaces of the transparent whale and transparent crocodile with a photosensitive emulsion. Then we have a high-intensity light source flash at the common volumetric centers of the 20-foot and 200-foot spheres. This process will reproduce on the plastic skin of both the whale and the crocodileas well as on the celestial 200-foot sphere the triangular satellite-positioning grid together with the latitude-longitude grid and all Earth’s continental and insular outlines. Then, traveling with a pencil-beam strobic light on the outside of the 200-foot celestial sphere, we will point vertically inward against each of the stars, thus projecting their positions radially, i.e., vertically, inwardly to register on the skins of both the whale and the crocodile and on the 20-foot Earth globe. Now, with the human eye at the common concentric centers of volume of the 20-foot and 200-foot spheres, as well as both the whale and the crocodile, we may sight outwardlywhich is inherently radiallyin all directions, and observe that all the grids and all the geographical and celestial star data appear as one grid, being in exact radial register. We have all the same grids and data on all four of the concentric surfaces: 200-foot celestial sphere, whale, crocodile, and 20-foot Earth globe. That registering of all data is obviously independent of radial distance from the common center; ergo, the only variable in the system is the radius to any given point within the concentric systems.
[1110.10]{style="color: purple3"} []{#ver:1110.10 label="ver:1110.10"} As we have demonstrated with geodesic domes and spheres, what is meant by compound curvature is “omni-intertriangulated structuring (i.e., balanced connectors) of concave-convex surface points.” Given a unit radius sphere and the known central angle between any two radii of known length, then the length of the chord running between their outer ends may be calculated trigonometrically by running a line from the sphere center perpendicular to the mid-chord and solving for the right triangle thus formed, whose halved-chord outer edge is the side opposite its central angle, which is half the central angle originally given, and we know that the sine of an angle is the side opposite. When radius is assumed to be one, then the well-known sine of one-half the original angle given is the length of that half chord. With the chord length calculatable for a given central angle, it is easy to calculate the length of any line running between the outer end of one of the radii to a position on the other radius at a known distance outward from the spherical center. With this knowledge we can design struts, of suitable structural material say, aluminum tubesand we may triangularly interconnect all the vertex points of the triangular grid of the 200-foot sphere. Then we can triangularly interstrut all the grid points on the inside of the whale; then we can-interstrut all the grid vertexes of the crocodile; and finally we can inter-triangularly strut the 20-foot Earth globe.
[1110.11]{style="color: purple3"} []{#ver:1110.11 label="ver:1110.11"} Now again, viewing outwardly in all directions from the common volumetric centers of those concentric forms, we will see nothing changed because all the struts will be in register with all the lines of the four separate grids. If we now dissolve the plastic skins from all four shellsthe 200-foot celestial sphere, the whale, the crocodile, and the 20-foot globewe find that all four hold their shapes exactly as before and, being intertrussed (intertrussed and intertriangulated are the same words: truss: trace: and triangle) between vertexes of the grid, and the grid now being omnitriangularly interstructured, we may again sight outwardly from the volumetric center. A photograph of what we see will reveal only the same lines in exact register that we saw at the time of the original first spherical printing.
[1110.12]{style="color: purple3"} []{#ver:1110.12 label="ver:1110.12"} Since the speed of light permitted astronauts to understand and adopt the light-year in their observational data, we have learned of the great variation of radial distances outwardly to the different stars. In the Big Dipper, one star is 200 light-years farther from Earth than the next one on the handle, which is a distance of 200 quadrillion miles farther away from you and me than is the other. If we ran rods radially from the volumetric center of our model outward perpendicularly through each of the stars shown on the 200-foot celestial sphere to a distance perpendicular outwardly from the 200-footer equal to their distance away in light-years from Earth, with the 200-foot sphere’s 100-foot radius equaling that of the nearest star other than Sun, and assume that the camera had photographed only those stars visible to the naked eye, then a few of the rods would reach outwardly ten miles, but most of them would be much nearer in, with one of the Big Dipper’s one mile out and another a half-mile out. It would make a vastly varied porcupine if we intertriangularly interconnected the outer terminals of the lines of interconnection, which would as yet be in exact register with the original grid as seen from system center.
[1110.013]{style="color: purple3"} []{#ver:1110.013 label="ver:1110.013"} Now let us separate the four structures by opening up an approximate equator in the outer ones and rejoining the equatorial points. With this celestial porcupine rolled into our deepest ocean and then resting on the bottom, its top would reach outwardly above the ocean surface to the height of Mt. Everest; its densest, most high-frequency-trussed spherical core would be only 200 feet in diameter and would occur at ocean surface. The triangularly trussed 175-foot whale would hold its shape and size, as would the 60-foot crocodile and the little 20-foot miniature Earth. Obviously, they could not appear more differently.
[1110.14]{style="color: purple3"} []{#ver:1110.14 label="ver:1110.14"} Our triangular geodesics transformation projection would show all four of these dissimilar systems in the flat plane in exactly the same manner and in exact register with that of Earth alone as shown later in the icosahedral flat-out of the world map, but with a number (or numbers of different styles) shown at each grid vertex, which number indicates the radius distance of that vertex outwardly from the center point of the system “Earth.” Four different colors blue for the celestial, black for the whale, green for the crocodile, and brown for the 20-foot Earth globewould identify the relative radius distances outward from the congruent systems’ center, which occurs at each vertex of these four utterly different-shaped and -sized systemsall on the same map. This would provide all of the data necessary to reconstruct each of the four systems in exactly the same relative sizes. Every point in the four systems remains in exact perpendicular (zenith), whether in the spherical or planar flat-out phase or any interim transitional phase. This makes possible the design of an airplane or an ocean liner all on one synergetic-geodesic map. And the flat-out map may have its triangular mosaic pieces rearranged in many waysfor instance, to center the oceans or to center the lands. And the building of that airplane or ocean liner, as with the geodesic dome, will generate compound curvature, omnifinite, tensegrity trussing far stronger and lighter than the presently designed and built -parallel coordinate grids and their parallel-plane sectional designing.
[1110.15]{style="color: purple3"} []{#ver:1110.15 label="ver:1110.15"} With omnidirectional, complex, computerized, world-satellite sensing, comprehensive-resources inventorying and interrouting, the triangular geodesics transformational projection can alone bring visual comprehending and schematic-network elucidation.
[1110.16]{style="color: purple3"} []{#ver:1110.16 label="ver:1110.16"} Just as triangular geodesics transformational projection can alone reduce the astronomical to the cosmic middle ground of eye-comprehensible coordination with the mind explorations and formulations in metaphysics in general and mathematics in particular, especially in relation to computer programming, so too may the triangular geodesics transformational projection enlarge the complex invisible microcosmic patterns to eye and sense comprehensibility.
¶ 1120.00 Wrapability
[1120.01]{style="color: purple3"} []{#ver:1120.01 label="ver:1120.01"} One roll of paper being unrolled from any one fixed axis wraps up all the faces of a tetrahedron. Two rolls of paper being unrolled from two axes perpendicular to one another wrap up all the faces of the octahedron. Three rolls of paper being unrolled from three axes[^56] wrap up all the faces of the icosahedron.
[1120.02]{style="color: purple3"} []{#ver:1120.02 label="ver:1120.02"} If the paper were transparent and there were ruled lines on the transparent paper at uniform single intervals, the single lines of the transparent paper wrapping up the tetrahedron will enclose the tetrahedron without any of the lines crossing one another. In wrapping up the octahedron with two rolls of such transparent paper, the lines crossmaking a grid of diamonds. Wrapping the icosahedron with the three rolls of transparent, parallel-ruled paper, a three-way grid of omnitriangulation appears.
[1120.03]{style="color: purple3"} []{#ver:1120.03 label="ver:1120.03"} The wrapping of the six-edged tetrahedron with the single roll of paper leaves two opposite edges open, i.e., uncovered by the wrapping-paper roll. The other four opposite edges are closed, i.e., covered by the wrapping-paper roll.
[1120.04]{style="color: purple3"} []{#ver:1120.04 label="ver:1120.04"} The wrapping of the 12-edged octahedron with two rolls of paper leaves two sets of opposite edges open. The other eight opposite edges are closed.
[1120.05]{style="color: purple3"} []{#ver:1120.05 label="ver:1120.05"} The wrapping of the 30-edged icosahedron with three rolls of paper leaves three pairs of opposite edges open or uncovered. To cover those open edges, we need two more rolls. With five wrappings, all 30 edges become enclosed: with five wrappings, 10 faces are double-covered and 10 faces are triple-covered. Only the triple-covered have omnitriangular gridding by the parallel ruled lines. Thus we see that we need a sixth wrapping to make the omnitriangulated three-way grid. At the fif± wrapping, the three-way grid appears about the north and south poles with only a two-way grid on the equatorial triangles. The whole three-way grid six-times rewrapping in omnitriangular gridding at any desired frequency of subdivisioning can thus be accomplished with only one type of continuing, parallel-ruled strip.
[1120.06]{style="color: purple3"} []{#ver:1120.06 label="ver:1120.06"} Wrapping relates to the mid-edges of prime structural systems.
[1120.07]{style="color: purple3"} []{#ver:1120.07 label="ver:1120.07"} It takes three wrappings on three axes to produce the three-way grid on every face of a tetrahedron.
[1120.08]{style="color: purple3"} []{#ver:1120.08 label="ver:1120.08"} Wrapping of the octahedron with two rolls of paper left two opposite edges open. Two strips covered all the faces. Three strips covered all the edges. But a fourth strip is needed to complete the omnitriangulation of each face of the octahedron. (Compare the four axes of the octahedron with the eight faces perpendicular to the center of volume of the octahedron. We are dealing with the axes of the mid-faces.) There are four unique ways to wrap an octahedron from a roll. The three-way grid for each face requires four-way wrappings.
[1120.09]{style="color: purple3"} []{#ver:1120.09 label="ver:1120.09"} If we take a transparent sheet of paper whose width is the altitude of the equilateral triangles of the three universal prime structures, both of the edges can be stepped off with vectors of the same length. This produces a series of opposing, regular, uniform, equilateral triangles. The altitude of the equilateral triangle is the width of the transparent paper ruled with parallel lines parallel to the edges of the roll. Along the edge of one side of this roll, we step off increments the same length as the basic vectors of the triangles. We take the midpoint of the first triangle and drop a perpendicular across to the opposite edge of the roll. We step off increments of the same basic vector length. But the step-offs are staggered with the vertex of one triangle opposite the mid-edge of the other.
[1120.10]{style="color: purple3"} []{#ver:1120.10 label="ver:1120.10"} This is how the lines of the tetrahedron keep wrapping up like a spool. That is why in the tetrahedron the axes are all the mid-edges of the poles. One polar pair of opposite edges is left open because the system is polarized; therefore, you need the three wrappingsone to cover all the faces, the second to cover all the edges, and the third for omnitriangulation. Three axes = three-way grid = three vectors for every vertex.
[1120.11]{style="color: purple3"} []{#ver:1120.11 label="ver:1120.11"} A single wrapping defines the octahedron even though two faces are left uncovered. It is polarized by the empty opposite triangles. One-half vector lacks rigidity. The interference of two planes is required for the spin. But we have to deal with open edges as well as with open faces. The figure will stand stably because six of the 12 edges are double-spin, with two edges coming together in dihedral angles.
[1120.12]{style="color: purple3"} []{#ver:1120.12 label="ver:1120.12"} Because one pre-omnitriangulated strip whose width exactly equals the altitude of the tetrahedron can completely spool-wrap all four faces of the tetrahedron, and because a tetrahedron so wrapped has an axis running perpendicular to and outward throughthe two mid-unwrapped-edges of the tetrahedron spool, such a spool may be endlessly wrapped, being a tetrahedron and an omnidirectionally closed system; ergo all the data of evoluting inwardly and outwardly in observable Universe and its scenario of intertransformings could be continuously rephotographed with each cycle and could thus be fed linearly into and stored ina computer in the most economical manner to be recalled and rerun, thus coping with all manner of superimpositions and inclusions at recorded dial distances inward and outward as a minimal-simplicity device.
¶ 1130.00 Omnidirectional Typewriter
•[ 1130.00-1133.04 Typewriter Scenario]
¶ 1130.10 Model Studies
[1130.11]{style="color: purple3"} []{#ver:1130.11 label="ver:1130.11"} Hypothetical model studies are schematic probability studies. Some are planar area models, but many deal exclusively with linear probability. Comprehensive reality problems are not linear; they are omnidirectional. They deal with total system and total Universe. That is what world society is not attending to realistically and that’s why we are in trouble: Synergy shows that you cannot solve comprehensive problems with exclusively local planar or local linear models.
¶ 1130.20 Orbital Feedback Circuitry vs Critical Path
[1130.21]{style="color: purple3"} []{#ver:1130.21 label="ver:1130.21"} Conventional critical-path conceptioning is linear and self-under- informative. Only orbital system feedbacks are both comprehensively and incisively informative. Orbital critical feedback circuits are pulsative, tidal, importing and exporting. Critical-path elements are not overlapping linear modules in a plane: they are interspiralling complexes of regenerative feedbacks or circuits.
[1130.22]{style="color: purple3"} []{#ver:1130.22 label="ver:1130.22"} When we go out to the Earth-orbiting Moon and plan to get back into the biospheric-enshrouded Earth again, we are dealing in 60,000-miles-per-hour solar system spiraling as the solar system while part of our galaxy rotates around the galaxy center at 700,000 miles per hour. This, altogether with the intergalactic motion, means we can never come back to where we were even though we safely reach Earth.
[1130.23]{style="color: purple3"} []{#ver:1130.23 label="ver:1130.23"} People may think they are being realistically linear, but they are actually just increasing the radius of larger and larger spiral orbits. Each year is a Sun-spiraling circuit. Years are not linear. As humans complete their daily local circuits, the Earth spins about its axis and orbits the Sun; wherefore the critical path of progressive accomplishment that led to humans reaching the Moon and returning safely to Earth involves not a linear months-and-years progression but a complex of millions of spirals within spirals. With each year the multimillion-stranded rope of omniinterrelated local circuitry feedback closures integrates synergetically to produce a spirally orbiting, complex, system-defining set of Sun-Earth-Moon orbiting events, and this system finally reaches out to embrace the Moon as well as the Earth, all of which ever expands humanity’s local Universe involvement. (See Sec. 535.20.)
[1130.24]{style="color: purple3"} []{#ver:1130.24 label="ver:1130.24"} A structural system (even such a structural system as a building) can be thought of as a multi-great-circle-faced clock, a complex of feedback circuitry where the sum-total of interferences of the pushes and pulls are everywhere synergetically and locally regenerative. As the humans complete their daily local circuits, the Earth spins about its axis and concurrently orbits the Sun; wherefore the critical spiral path of progressive accomplishment that led to humans reaching the Moon and returning safely to Earth involves not a linear months-and-years progression but a complex of millions of spirals within spirals of an around-the-Sun-by-Earth orbiting and an around-the-Earth-by-Moon orbiting progression, wherein we progressively establish one feedback circuitry system overlapping another, and another, and so on as the year goes around.
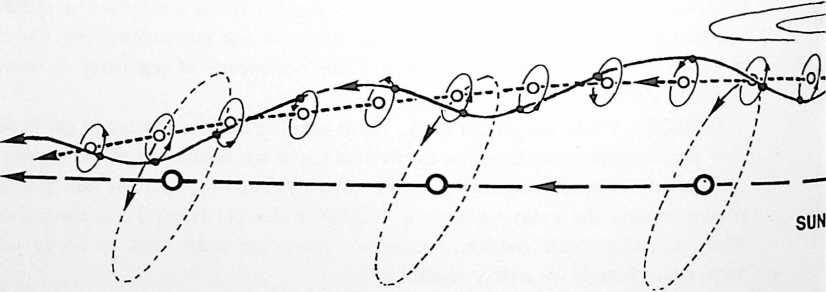
Fig. 1130.24 Reality is Spiro-orbital: All terrestrial critical path developments inherently orbit the Sun. No path can be linear. All paths are precessionally modulated by remotely operative forces producing spiralinear paths.
[1130.25]{style="color: purple3"} []{#ver:1130.25 label="ver:1130.25"} The reality is always systematically spiro-orbital. Orbit circuit. For instance, all terrestrial critical-path developments inherently orbit the Sun. No path can develop as curvature-free linearity. All paths are precessionally modulated by remotely operative forces that produce curvi-wavi-spiralinear paths. Increasingly complex curvi-wavi-spiralinear, system-embracing circuits are diffusiveergo, spinoff prone; ergo, system-mass reducing; ergo, ultimately bit-by-bit self-annihilative. Spun-off simplexes may come into critical interattractiveness with other diffusely detached simplexes to form other young complex systems, to syntropically initiate new, mass-increasing, cosmically-local-traveler, complex system-defining, new intercelestial orbiting circuits.
¶ 1131.00 Spool-wrapping of Tetrahedron
¶ 1131.10 Omnitriangulated Strip
[1131.11]{style="color: purple3"} []{#ver:1131.11 label="ver:1131.11"} Another model is the omnitriangulated strip tape whose width exactly equals the altitude of the regular tetrahedron’s triangular face. This strip’s surface has been entirely divided into a series of equilateral triangles, each of whose edges are of the same length as any edge of the regular tetrahedron. Employing this wavilinear-faced tape, we can completely and successively spool-wrap the entire surfaces of all four faces of the tetrahedron while also wrapping four of the tetrahedron’s six edges and exactly paralleling the wrapping tape along the other two edges of the tetrahedron. None of the four vertexes are embracingly wrapped, but all of them are tangentially wrapped.
[1131.12]{style="color: purple3"} []{#ver:1131.12 label="ver:1131.12"} The tetrahedron so wrapped has a wrapping axis running through, and perpendicular to, the midpoints of the two unwrapped edges of the tetrahedron spool. Being a regular tetrahedron, this spool may be used as a roller printing device, when its fixes are inked, to make a continuously printed strip of edge-to-edge equilateral triangles. Ergo, we have a device for projecting all of the omnidirectionally occurring and tetrahedrally observed data onto a minimum-surface system that is unwrappable onto a flat ribbon printout with four-dimensional coordination. In this method of projection the observer’s viewpoint always remains perpendicular to the outside surface of the system, as in the Dymaxion map projection, where any star remains in exact perpendicular zenith to the corresponding point on the map of the world, whether the map is stretched in one flat plane or whether it is the surface of complete unitary sphericity. The same triangles are going to come out flat and the same stars are in exact zenith over their respective points, as the radii remain perpendicular to the system independent of whether the triangular area edges are arcs or chords.
 Change: fix image
Change: fix image
[1131.13]{style="color: purple3"} []{#ver:1131.13 label="ver:1131.13"} The omnitriangulated strip is an extraordinary mathematical transformation in which you can graphically accommodate the omnidirectionality of all systems in an exactly coordinated mathematical accounting. It can project and print out on a strip all gravitational and radiational data, be they in the form of stars, Ashes, or anything. They are all coordinatably printoutable onto one continuous flat ribbon map. What we have is a true prototype of an omnidirectional typewriter. It can print out each omniembracing layer of each frequency layer of each convergent-divergent system. When you print out the omnidata on such a strip, it identifies specifically where and when each event in the transformation occurs.
¶ 1132.00 Great-circle Shunting and Switch Points
[1132.01]{style="color: purple3"} []{#ver:1132.01 label="ver:1132.01"} This omnidirectional, convergent-divergent, systems-reporting device can print out the most-economical-interrelationships trackings and information-coordinating routings of all systems, because it embraces the pattern of all 87 of the most economical and only available great-circle railroad tracks and no-loss-holding stations of energetic Universe; i.e., through all the closest-sphere-packed systems; i.e., through all the isotropic vector matrixes. In other words, if you want to go from here to there in Universe in the quickest and most economical way, while stopping over here and there for indefinite periods at no-extra-cost hotels, you have got to go through the 12 points of intertangency of the 25 great circles of fundamental symmetry that apply to all the atoms and their association in all seven of the fundamental symmetry subsets.
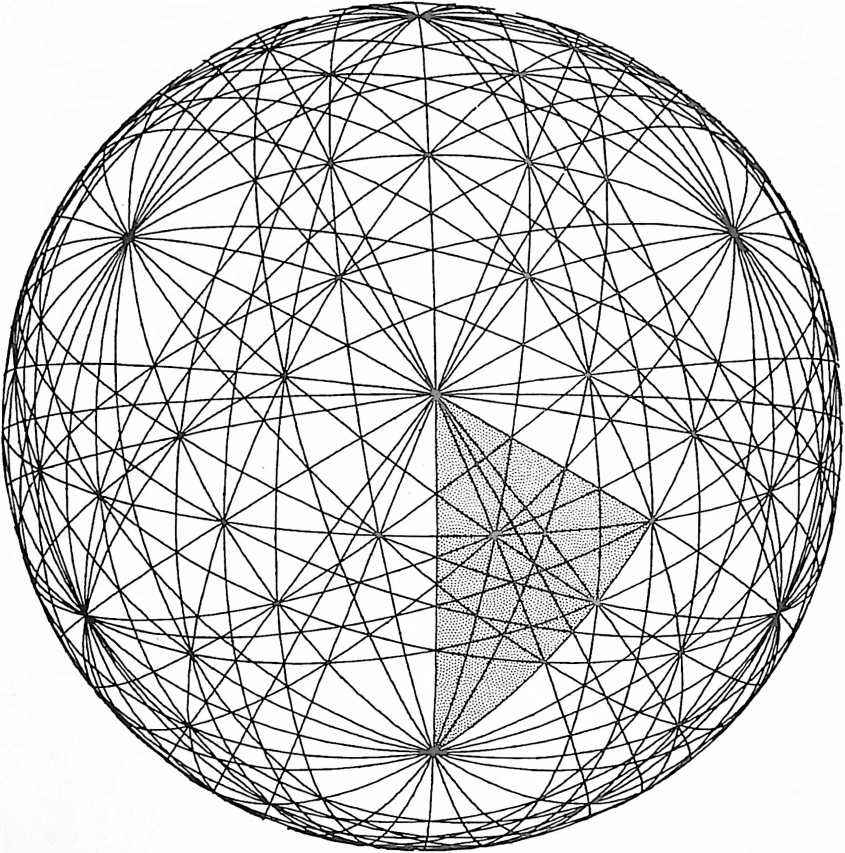
Fig. 1132.01B Composite of Vector Equilibrium and Icosahedron Great Circle Sets: This is a black-and-white version of color plate 32. The Basic Equilibrium 48 LCD triangle appears here shaded in the spherical grid. In this composite spherical matrix we see all the 25 primary vector equilibrium great circles and two sets skewed-positive and negative of the icosahedron 31 great circle sets. (31 x2=62. 62 + 25 = 87. But 14 of the 87 are redundant.) Four of the VE great circles are congruent with four of the icosa s 10-great circle set. Three of the VE great circles are congruent with three of the icosa’s 15-great-circle set. Thus seven positive are redundant and seven negative are redundant. (87 - 14 = 73.) There are 73 great circles in the composite set. (See color plate 32.)
This composite shows the vector equilibrium great circles and the icosahedron great circles in the two alternate ways of pumping the VE jitterbug pattern.

Fig. 1132.01 C Net Diagram of Angles and Edges for Basic Equilibrium 48 LCD Triangle in VE-Icosa Grcd: This is a coded detail of the basic spherical triangle shown shaded in Fig. 1132.0IB and at Fig. 453.01. It is the key to the trigonometry tables for the spherical central angles, the spherical face angles, the planar edge lengths, and the planar face angles presented at Table 1132.01D. (The drawing shows the spherical phase: angle and edge ratios are given for both spherical and planar VE.)
[1132.02]{style="color: purple3"} []{#ver:1132.02 label="ver:1132.02"} The 31 great circles of the icosahedron always shunt the energies into local-holding great-circle orbits, while the vector equilibrium opens the switching to omniuniverse energy travel. The icosahedron is red light, holding, no-go; whereas vector equilibrium is green light, go. The six great circles of the icosahedron act as holding patterns for energies. The 25 great circles of the vector equilibrium all go through the 12 tangential contact points bridging between the 12 atomic spheres always closest packed around any one spherical atom domain.
¶ 1132.10 Great-circle Railroad Tracks of Energy
[1132.11]{style="color: purple3"} []{#ver:1132.11 label="ver:1132.11"} Each of the 25 great circles of any one closest-packed sphere can be used by that special local sphere as an “until-ready,” local shunt-off, holding circuit track for any traveling energy entity. This is permitted by the fact that each and all of the 25 great circles are foldable into local, bow-tie, clover-leaf, figure-eight, “chain-of-sausages,” three-or-four-bladed-propeller- type patterns which, when totally interassembled, also provide full, uninterrupted, 360-degree, around-the-sphere circuitry. The energy entities can travel around locally on any one sphere’s holding tracks in these local 360-degree total shuntings for as long as is “convenient” to the system.
[1132.12]{style="color: purple3"} []{#ver:1132.12 label="ver:1132.12"} The 25 great circles of the vector equilibrium are the only omni-intersystem-connecting “railroad tracks” of energy in the Universe. When an energy entity holding locally on a local sphere gets a green light to get back on the grand-omni-interspheres’ system tracks, it can do so by crossing over one of the 12 inter-atomic-sphere bridges. As we have seen in Sec. 450, three of the vector equilibrium’s four unique sets of great circles, whose respective numbers total 25, disclose different rates of encounter with the 12 tangential “Grand Central Stations” through which the energy-entity travelers can transfer to other spheres of the omni-equiradiused, closest-packed-spherical-dynamics domains of any one elemental atomic class. Arranged in order of the number of encounters with (and entries into) the sphere-to-sphere, tangential grand-central transfer points per each great-circle cycle, they may be accounted as follows:
6 great circles go through 2 points per 360cycle
+:------------------------------------+:----------------------------------------------------------------+
| n ft u n | |
+-------------------------------------+-----------------------------------------------------------------+
| u n h ft | |
+-------------------------------------+-----------------------------------------------------------------+
| /j [h h]{.smallcaps} tt n | [6]{.underline} |
+-------------------------------------+-----------------------------------------------------------------+
| shunt holding | transfer opportunities |
+-------------------------------------+-----------------------------------------------------------------+
| circuits | ::: minipage |
| | > per each spheric moment, of which only 12 can be accommodated |
| | ::: |
+-------------------------------------+-----------------------------------------------------------------+
[1132.13]{style="color: purple3"} []{#ver:1132.13 label="ver:1132.13"} Because only 12 of 16 station transfers can be accommodated, each sphere has inherently eternal retention of four energy entities. Four energy entities comprise the minimum system-defining constellationi.e. the tetrahedronwhich is exactly one energy quantum. Thus we see that the 16 potential encounters of the 25 great-circle sphere may be identified as 16/4 =4 energy quanta, of which only three may be accommodated at the exits: wherefore a fourth quantum is always retained. No sphere or atom can be exhausted.
[1133.00 Information Control System of Universe]{style="color: purple3"} []
[1133.01]{style="color: purple3"} []{#ver:1133.01 label="ver:1133.01"} In the vector equilibrium’s total of 25 great-circle circuitings, we find at any one moment four different sets of great-circle holding patterns and four energy quanta per sphere, but with exit accommodation for only three quanta. With all these beautiful local holding-circuit switches and stop-and-go controls we begin to comprehend conceptually the method by which nature can shunt, valve, hold, and transmit all information in Universe. This is the information-control system of the Universe. This is the way spheres transmit through closest-packing patterns.
[1133.02]{style="color: purple3"} []{#ver:1133.02 label="ver:1133.02"} This is why transistors work; it explains why somebody was suddenly able to discover that a tiny piece of metal embraced an energy-quanta valving system having reliable regularities. Science unthinkingly spoke of this phenomenon as “solid state physics,” partially because individual humans could not see those beautiful little atoms and electrons doing their acts on their railroad tracks and their respective local great-circle energy holding patterns, and partially because science has been flying blind on instruments. For over a century science has been maintaining stubbornly that there was nothing to see by looking out of the windows. They said nature does not use models in the invisible microcosm; she uses only abstract equations. This “nonconceptuality viewpoint” was fortified to the public by use of the term “solid state physics.”
[1133.03]{style="color: purple3"} []{#ver:1133.03 label="ver:1133.03"} In the behaviors of the vector equilibrium’s 25 great circles we have the basis for the design of a nuclear omnidirectional typewriter, a programmable computer smaller than a pinhead, which is capable of storing, retrieving, and printing out all humanly acquirable information. Synergetics mathematics has the ability to convert the spherically arranged information and project it onto flat conceptual-information-printout arrays of negligible distortion. The least-possible-distorted transformational projection is icosahedral treatment employed in the Dymaxion airocean world map system. The simplest frame of reference, however, is that of the spherical tetrahedron, which transforms into the flat, omnitriangulated-grid, strip-wrapped, four-dimensionally-symmetrical tetrahedron. The tetrahedron produces a conveniently linear, four-dimensional roller printout.
[1133.04]{style="color: purple3"} []{#ver:1133.04 label="ver:1133.04"} These transformational projections afford the most economical, least distorted means of translating the symmetrically omnidirectional into a flat symmetrical projection. The prime structural system of Universe, the tetrahedron, unwraps linearly to print out all possible variations of angle and frequency modulation. Here we have a conceptualizing model that can be reliably programmed to conceptualize atomic structurings at humanly discernible magnitudes. This kind of atomic-level behavior is exactly what all the computer model specialists have been missing ergo, the magnitude of the chasm between their projective equation strategies and synergetics’ four-dimensional conceptual integrity independent of size and its inherent ability to deal discretely with closest-packed atomic system proclivities and behaviors.